Deret fourier dan pemakaiannya - USD Repository

DERET FOURIER DAN PEMAKAIANNYA

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh:

Veronika Fitri Rianasari NIM. 041414012

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

2008

HALAMAN PERSEMBAHAN

Whatever you do, do it heartily, as to the Lord and not to men.

(Colossians 3:23)

And we know that in all things God works for the good of those who

love Him, who have been called according to His purpose. (Rome 8:28)

Dengan penuh syukur kupersembahkan karyaku ini kepada Tuhan Yesus dan Bunda Maria Bapak, Ibu, dan saudara-saudaraku tercinta Masku Nobertus Ribut Santoso Kalian adalah anugerah terindah dalam hidupku

ABSTRAK

Veronika Fitri Rianasari, 2008. Deret Fourier dan Pemakaiannya. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Fungsi yang didefinisikan pada interval

(

, periodik dengan periode

) (x

f −L,L

)

L

2 , dan kontinu sepotong-sepotong dalam interval tersebut, dapat dinyatakan dalam bentuk deret Fourier sebagai berikut

∑

∞ =

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₊

+ 1

0 cos sin

n

n

n x

L n b x L n a

a π π , dimana

( )

xdx f L a

L

L

∫

−

= 2

1

0 ,

( )

dx

L x n x f L a

L

L n

π

cos 1

∫

−

= , dan

( )

dx

L x n x f L b

L

L n

π

sin 1

∫

−

=

untuk n adalah bilangan bulat positif.

Sebuah teorema yang penting yang dibahas dalam skripsi ini yaitu teorema mengenai kekonvergenan deret Fourier. Teorema tersebut menyatakan bahwa deret Fourier dari fungsi f

( )

x yang mempunyai periode 2 , kontinu π sepotong-sepotong dalam interval −π ≤x≤π, dan mempunyai turunan kiri dan turunan kanan di setiap titik pada interval tersebut akan konvergen ke

jika x titik kontinuitas, dan konvergen ke

( )

x

f

( ) ( )

2

− + + f x

x f

jika x titik diskontinuitas.

Dalam studi ini dibahas pemakaian deret Fourier dalam bidang fisika, khususnya pada osilasi paksa, konduksi panas, dan getaran dawai. Persamaan diferensial biasa dari osilasi paksa berbentuk

, dimana berupa fungsi kontinu sepotong-sepotong dalam suatu interval . Persamaan tersebut merupakan persamaan diferensial linear non homogen orde dua dengan koefisien konstan. Pada osilasi paksa, deret Fourier digunakan untuk merepresentasikan gaya luar yang bekerja pada sistem, sehingga akhirnya dapat diperoleh penyelesaian dari persamaan diferensial biasa dari osilasi paksa. Persamaan diferensial parsial dari konduksi panas berbentuk

) ( '

" cy ky F t y

m + + = F(t)

(

F(t)

)

2 2 2

x u c t u

∂ ∂ = ∂ ∂

. Sedangkan persamaan diferensial parsial dari getaran dawai berbentuk

2 2 2 2 2

x u c t

u

∂ ∂ = ∂ ∂

. Pada konduksi panas dan getaran dawai, deret Fourier digunakan untuk menentukan solusi bagi kedua persamaan diferensial biasa yang persamaannya diperoleh dari metode hasilkali dua fungsi untuk mencari penyelesaian masalah nilai batas pada persamaan diferensial parsial dari masing-masing kasus.

ABSTRACT

Veronika Fitri Rianasari, 2008. Fourier Series and Its Use. Thesis. Mathematics Education Study Program, Mathematics and Science Education Department, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

Function f(x) defined in interval

(

−L,L

)

, periodic function with period 2L, and piecewise continuous in its interval, can be expressed in the Fourier Series form as follows

∑

∞ =

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₊

+ 1

0 cos sin

n

n

n x

L n b x L n a

a π π ,

( )

xdx f L a

L

L

∫

−

= 2

1

0 ,

( )

dx

L x n x f L a

L

L n

π

cos 1

∫

−

= , and

( )

dx

L x n x f L b

L

L n

π

sin 1

∫

−

=

for n is a positive integer.

An important theorem discussed in this thesis is a theorem about convergence of Fourier series. The theorem defined that the Fourier series of

that have period

( )

x

f 2 , piecewise continuous in interval π −π ≤ x≤π, and left derivative and right derivative of f

( )

x at each point in the interval exist converges to f

( )

x if x is continuity point, and converges to

( ) ( )

2

− + + f x

x f

if x is discontinuity point.

This study discussed the use of the Fourier series in physics, particularly forced oscillations, heat conduction, and string vibration. Ordinary differential equation from forced oscillations is of the form , is a piecewise continuous function in an interval. It is second order nonhomogeneous linear differential equation with constant coefficients. In the forced oscillations, the Fourier series is used to represent the external force

) ( '

" cy ky F t y

m + + = F(t)

(

F(t)

)

acting on a spring-mass system so it is obtained the solution of ordinary differential equation from forced oscillations. Partial differential equation from heat conduction is of the form

2 2 2

x u c t u

∂ ∂ = ∂ ∂

. Moreover, partial differential equation from string vibration is

of the form ₂

2 2 2 2

x u c t

u

∂ ∂ = ∂ ∂

. In the heat conduction and string vibration, the Fourier series is used to decide the solution for two ordinary differential equations in which the equations are obtained from product of two functions method, so it is obtained the solution of the boundary value problem in the partial differential equation from the heat conduction and string vibration.

KATA PENGANTAR

Puji dan syukur ke hadirat Allah Bapa di Surga karena penulis dapat menyelesaikan skripsi dengan judul “Deret Fourier dan Pemakaiannya”. Skripsi ini disusun untuk memenuhi salah satu syarat memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan di Universitas Sanata Dharma Yogyakarta.

Selama penyusunan skripsi ini banyak kesulitan dan hambatan yang penulis alami. Namun dengan bantuan berbagai pihak semua kesulitan dan hambatan tersebut dapat teratasi. Untuk itu, dalam kesempatan ini penulis dengan tulus hati ingin mengucapkan terima kasih yang tak terhingga kepada :

1. Tuhan Yesus dan Bunda Maria yang selalu menjaga, melindungi, dan menuntun langkahku. Puji syukur atas segala berkat dan anugerah yang telah dianugerahkan selama ini.

2. Bapak Drs. A. Tutoyo, M.Sc. selaku dosen pembimbing yang dengan tulus telah membimbing, mengarahkan, dan memberikan masukan serta kritikan yang berharga kepada penulis selama proses penyusunan skripsi ini.

3. Bapak Dr. St. Suwarsono selaku Ketua Program Studi Pendidikan Matematika dan selaku dosen penguji yang telah banyak memberikan bantuan selama penulis menempuh kuliah serta atas masukan dan kritikan yang bermanfaat untuk penyempurnaan skripsi ini.

4. Bapak Dr. Susento, M.S. selaku dosen penguji yang telah membimbing selama penulis menempuh kuliah serta atas masukan dan kritikan yang bermanfaat untuk penyempurnaan skripsi ini.

5. Segenap dosen JPMIPA, khususnya dosen-dosen Program Studi Pendidikan Matematika, Universitas Sanata Dharma yang telah mendidik, membagi pengetahuan dan pengalaman yang sangat bermanfaat kepada penulis.

6. Bapak Sunardjo dan Bapak Sugeng di sekretariat JPMIPA atas segala bantuan, keramahan, dan kerja samanya selama penulis menempuh kuliah hingga penyelesaian skripsi ini.

7. Bapak Markus Ramen Sudiran, Ibu Khatarina Mariani, saudara-saudaraku Irwan Wijayanto, Agustinus Heru Apriyanto, Theresia Renny Andarwati, dan Sr. Yoanne Dian Retnosari, CB atas doa, cinta, kasih sayang, perhatian, nasehat, dan semangat yang diberikan selama ini. Semoga skripsi ini dapat menjadi hadiah kecil yang membanggakan.

8. Nobertus Ribut Santoso yang tak pernah kunjung henti memberi cinta, kasih sayang, doa, dan dukungan kepada penulis selama ini.

9. Teman-teman PMAT angkatan 2004 di JPMIPA. Terima kasih atas bantuan, semangat, keceriaan dan kebersamaan selama kuliah.

10.Teman-teman Kost Flamboyan, Resti, Ayu, Monik, Putu, Windru, Lusi, Weni, Asih, Darti, Heni, Meli, dan Ria. Terima kasih atas bantuan, semangat, dan perhatian yang diberikan selama ini.

11.Teman-teman KMPKS (Keluarga Mahasiswa/i Pelajar Katolik Sumatera bagian Selatan) khususnya paduan suara KMPKS Voice yang selalu memberi dukungan, semangat , dan keceriaan kepada penulis.

12.Seluruh staf perpustakaan USD Paingan, atas segala bantuan, kerja sama, dan keramahan yang telah diberikan selama ini.

13.Semua pihak yang tidak dapat disebutkan satu persatu yang telah rela membantu dan mendukung penulis hingga selesainya proses penyusunan skripsi ini.

Penulis menyadari masih banyak kekurangan dan kesalahan dalam skripsi ini. Karena itu penulis sangat mengharapkan masukan dan saran dari pembaca demi perbaikan skripsi ini. Akhir kata, penulis berharap semoga skripsi yang tidak sempurna ini bermanfaat bagi setiap pembaca.

Penulis

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

ABSTRAK ... vi

ABSTRACT ... vii

PERNYATAAN PERSETUJUAN PUBLIKASI ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xii

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Perumusan Masalah ... 7

C. Tujuan Penulisan ... 7

D. Manfaat Penulisan ... 7

E. Pembatasan Masalah ... 8

F. Metode Penulisan ... 8

G. Sistematika Penulisan ... 8

BAB II DERET FOURIER ... 10

A. Pengertian Deret Fourier ... 10

B. Menghitung Koefisien Fourier dengan Rumus Euler ... 17

C. Ekspansi Fungsi Menjadi Deret Fourier ... 23

D. Fungsi Genap dan Fungsi Ganjil ... 28

E. Penguraian Setengah Kisaran ... 35

F. Konvergensi Uniform ... 43

G. Sifat Koefisien Deret Fourier ... 52

H. Kekonvergenan Deret Fourier ... 56

BAB III PEMAKAIAN DERET FOURIER ... 66

A. Pemakaian pada Osilasi Paksa ... 66

B. Pemakaian pada Konduksi Panas ... 78

C. Pemakaian pada Getaran Dawai ... 86

BAB IV PENUTUP ... 98

DAFTAR PUSTAKA ... 102

BAB I PENDAHULUAN

A. Latar Belakang

Fenomena periodik sangat sering dijumpai di dalam fisika dan penerapan rekayasanya, dan suatu masalah praktis yang penting adalah merepresentasikan fungsi periodik yang muncul dengan fungsi-fungsi periodik yang sederhana seperti sinus dan kosinus. Hal ini membawa deret Fourier, yang suku-sukunya adalah fungsi sinus dan kosinus. Temuan Jean-Baptiste Joseph Fourier (yang mengembangkan temuan Euler dan Daniel Bernoulli) merupakan salah satu kejadian paling penting di dalam perkembangan matematika terapan.

Fungsi f

( )

x dikatakan periodik jika ada bilangan positif ρ sedemikian rupa sehingga f

(

x+ρ

)

= f

( )

x untuk semua x. Bilangan ρ ini dinamakan periode fungsi f(x). Grafik fungsi periodik diperoleh melalui pengulangan periodik grafiknya untuk sembarang selang yang panjangnya ρ.

x f(x)

ρ

Fungsi periodik yang telah kita kenal adalah fungsi sinus dan kosinus, dan kita lihat bahwa fungsi f

( )

x =c (c = konstanta) juga merupakan fungsi periodik , sebab fungsi ini memenuhi f

(

x+ρ

)

= f

( )

x untuk setiap ρ positif.

Contoh-contoh lain dari fungsi periodik bisa dilihat pada gambar berikut :

f(x)

x

p e r i o d e

x

p e r i o d e

f(x)

Jika suatu fungsi memiliki periode ρ, maka

(

x

)

f

[

(

x

)

]

f

(

x

)

f

( )

x f +2ρ = +ρ +ρ = +ρ = , dan juga

(

x

)

f

[

(

x

)

]

f

(

x

)

f

( )

x f +3ρ = +2ρ +ρ = +ρ = ,

dan seterusnya , sehingga untuk setiap bilangan bulat n berlaku f

(

x+nρ

)

= f

( )

x untuk semua x. Jika f(x) dan g(x) masing-masing adalah fungsi periodik dengan periode ρ, maka berdasarkan sifat linearitas berlaku h

( )

x =a⋅ f

( )

x +b⋅g

(

x

)

juga merupakan fungsi periodik dengan periode ρ.

Fungsi periodik yang dijumpai di dalam masalah rekayasa sering kali agak rumit, oleh karena itu kita berusaha untuk merepresentaskan fungsi itu ke dalam bentuk yang lebih sederhana. Berikut adalah fungsi-fungsi sederhana yang berperiode 2 : π

Deret yang diperoleh akan berbentuk

K

+ +

+ +

+a x b x a x b x

a_{0 1}cos ₁sin ₂cos2 ₂sin2

dengan adalah bilangan real. Deret ini dinamakan deret trigonometrik, sedangkan dan disebut koefisien deret trigonometrik. Dengan menggunakan notasi sigma, kita dapat menuliskan deret itu sebagai

. Himpunan fungsi-fungsi yang menyusun deret

trigonometrik sering dinamakan sistem trigonometrik. Hampir semua fungsi periodik yang berperiode

K K, , , ,

,

, _{1 2 1 2}

0 a a b b a

n

a b_n

(

∑

∞

=

+ +

1

0 cos sin

n

n

n nx b nx

a

a

)

( )

x

f 2 yang banyak dijumpai dalam penerapan π (misalnya dalam kaitan dengan getaran dan konduksi panas) dapat direpresentasikan oleh deret trigonometrik.

Dalam penerapan, khususnya dalam getaran dan konduksi panas, penuh dengan masalah-masalah yang harus dimodelkan dengan persamaan diferensial. Persamaan diferensial adalah persamaan yang memuat derivatif atau diferensial dari satu atau lebih fungsi yang belum diketahui. Jika fungsi yang belum diketahui dalam persamaan diferensial bergantung hanya pada satu variabel bebas maka persamaan itu disebut persamaan diferensial biasa. Bentuk umum persamaan diferensial biasa yaitu:

0 ) ,..., ,

, , , (

3 3 2 2

=

n n dx y d dx

y d dx

y d dx dy y x

f ,

variabel bebas, maka persamaan itu disebut persamaan diferensial parsial. Bentuk umum persamaan diferensial parsial yaitu :

0 ) ,..., ,

, , , , , ,

( ₂

2 2 2 2

= ∂ ∂ ∂

∂ ∂ ∂

∂ ∂ ∂ ∂ ∂ ∂ ∂

n n y z y

z y x

z x

z y z x z z y x

f ,

dengan x dan y menyatakan variabel bebas, sedangkan z menyatakan variabel tak bebas.

Persamaan diferensial biasa mempunyai penerapan pada getaran pegas. Untuk lebih memahami penerapan persamaan diferensial biasa pada getaran pegas, perhatikan contoh berikut.

Contoh 1.1 : Sebuah benda bermassa m tergantung dari keadaan seimbang pada sebuah pegas dengan konstanta pegas k. Sebuah gaya luar bekerja pada pegas tersebut sebesar

( )

⎪ ⎩ ⎪ ⎨ ⎧

< < −

< < − =

π π

π π

t t t

F

0 jika 2

0 jika

2 _{, F(t+2π)=F}

( )

_t

dan terdapat gaya redaman sebesar c satuan seperti terlihat pada gambar di bawah ini :

+ ) (t F

c m k

Untuk menentukan keadaan stabil dari masalah di atas berarti menentukan penyelesaian dari persamaan diferensial biasa berikut:

) ( '

" cy ky F t y

m + + = .

Karena gaya luar bukan berupa suatu fungsi sinus atau kosinus murni maka langkah pertama yang harus dilakukan yaitu merepresentasi gaya luar dengan suatu deret Fourier. Setelah ditentukan deret Fourier dari gaya luar tersebut, maka langkah selanjutnya yaitu menentukan penyelesaian dari persamaan diferensial yang telah terbentuk.

) (t F

) (t F

Persamaan diferensial parsial banyak dijumpai dalam kaitan dengan berbagai masalah fisik seperti konduksi panas, teori mengenai getaran dan berbagai bidang fisik lainnya yang penuh dengan masalah-masalah yang harus dimodelkan dengan persamaan diferensial parsial. Untuk lebih memahami penerapan persamaan diferensial parsial pada konduksi panas, perhatikan contoh berikut.

Contoh 1.2 : Tentukan suhu u

( )

x,t dalam suatu kawat yang telah diisolasi, yang panjangnya L cm, dan kedua ujungnya dipertahankan pada suhu

, jika diasumsikan suhu awalnya

C

o 0

( )

⎪ ⎩ ⎪ ⎨ ⎧

< < −

< < =

L x L x

L

L x x

x f

2 jika

2 0

jika

dalam satuan oC.

Untuk menentukan suhu u

( )

x,t dalam kawat tersebut berarti menentukan penyelesaian dari persamaan diferensial parsial berikut

t u c t u

2 2 2

∂ ∂ = ∂ ∂

...(1)

yang harus memenuhi syarat awal dan syarat batas di atas.

Suatu metode umum untuk menyelesaikan masalah tersebut yaitu dengan menggunakan metode hasil kali dua fungsi. Pada metode ini diasumsikan solusinya berbentuk hasil kali dua fungsi, yang masing-masing hanya tergantung pada salah satu peubah saja. Jadi, persamaan (1) diuraikan menjadi

( )

x t F

( ) ( )

x G x

u , = ⋅ ...(2)

Substitusi persamaan (2) ke dalam persamaan (1) menghasilkan persamaan diferensial biasa untuk F dan G, dan akhirnya diperoleh takhingga banyaknya solusi F = F_n dan G=G_n, sedemikian rupa sehingga fungsi

merupakan solusi untuk persamaan diferensial parsial (1) yang memenuhi syarat batas. Agar solusi terebut juga memenuhi syarat awal, harus dibentuk deret takhingga bagi yang koefisien-koefisiennya merupakan koefisien Fourier untuk fungsi

( )

x t F

( )

x G

( )

x u_n , = _n ⋅ _n

n u

( )

x

f yang merepresentasikan syarat awal. Dari contoh di atas, dapat dilihat bahwa dalam mencari penyelesaian persamaan diferensial diperlukan pengetahuan bagaimana mengekspansi suatu fungsi menjadi deret trigonometri.

yang melibatkan persamaan diferensial biasa maupun parsial. Karena alasan itulah penulis tertarik untuk mengkaji lebih jauh deret Fourier secara teoritik dan pemakaian deret Fourier dalam menentukan penyelesaian persamaan diferensial khususnya pada osilasi paksa , konduksi panas, dan getaran dawai.

B. Perumusan Masalah

Dengan latar belakang yang telah diungkapkan diatas, dapat dirumuskan beberapa masalah :

1. Apakah yang dimaksud dengan deret Fourier?

2. Bagaimana pemakaian deret Fourier dalam bidang fisika?

C. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah :

1. Penulis dapat memahami deret Fourier secara teoritik.

2. Penulis dapat menggunakan deret Fourier dalam menyelesaikan persoalan-persoalan dalam bidang fisika.

D. Manfaat Penelitian

E. Pembatasan Masalah

Materi yang akan dibahas pada skripsi ini mencakup konsep deret Fourier, dan teorema kekonvergenan deret Fourier. Dalam pembahasan akan dibahas juga tentang pemakaian deret Fourier dalam osilasi paksa , konduksi panas, dan getaran dawai.

F. Metode Penulisan

Metode yang akan digunakan dalam membahas topik tersebut adalah metode studi pustaka.

G. Sistematika Penulisan

Penulisan ini terbagi dalam beberapa bab, yakni : Bab I Pendahuluan

Pada bab ini dikemukakan hal-hal yang melatarbelakangi penulisan skripsi, beserta perumusan masalah, tujuan penulisan, manfaat penulisan, pembatasan masalah, metode penulisan, dan sistematika penulisan.

Bab II Deret Fourier

Bab III Pemakaian Deret Fourier

Pada bab ini diuraikan mengenai pemakaian deret Fourier dalam bidang fisika, khususnya pemakaian deret Fourier pada osilasi paksa, konduksi panas, dan getaran dawai.

Bab IV Kesimpulan

BAB II DERET FOURIER

A. Pengertian Deret Fourier 1. Fungsi Periodik

Fungsi f(x) disebut mempunyai periode ρ atau periodik dengan periode

ρ jika untuk semua nilai x, f

(

x+ρ

)

= f

( )

x dengan ρ adalah bilangan positif. Nilai terkecil dari ρ disebut sebagai periode terkecil atau periode dari . Jika fungsi periodik mempunyai periode terkecil

) (x f

) (x

f ρ, ini sering dinamakan

periode primitif dari fungsi . Jika f(x) dan g(x) masing-masing adalah fungsi periodik dengan periode

) (x f

ρ, maka berdasarkan sifat linearitas berlaku

juga merupakan fungsi periodik dengan periode

( )

x a f

( )

x b g

( )

x

h = ⋅ + ⋅ ρ.

Contoh 2.1:

Fungsi cos mempunyai periode x 2 , π 4 , π 6 , ..., π 2nπ, ... (n = 1, 2, 3, ...), karena cos

(

x+2π

)

=cos

(

x+4π

)

=cos

(

x+6π

)

=cos

(

x+2nπ

)

=cosx. Walaupun demikian, 2 adalah periode terkecil atau periode dari π cos . x

Contoh 2.2:

Periode dari fungsi sinnx atau fungsi cosnx, dengan n = 1, 2, 3, ... adalah

n

π

2 ,

karena

( )

(

)

⎟

⎠ ⎞ ⎜

⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜

⎝ ⎛ + =

+ =

=

n x f n x n nx

nx x

f cos cos 2π cos 2π 2π dan

( )

sin sin

(

2

)

sin 2 2 ⎟.

⎠ ⎞ ⎜

⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜

⎝ ⎛ + =

+ =

=

n x f n x n nx

nx x

f π π π

Contoh 2.3:

Periode dari tanx yang didefinisikan pada interval ⎟ ⎠ ⎞ ⎜

⎝ ⎛−

2 , 2

π π

adalah π , karena

( )

x = x=

(

x+π

)

= f

(

x+π

)

f tan tan .

Contoh 2.4:

Fungsi f

( )

x =c (c = konstanta) mempunyai sebarang bilangan positif sebagai periodenya, sehingga dapat dikatakan bahwa f

( )

x =c merupakan fungsi periodik tanpa periode primitif.

Contoh 2.5:

Tentukan periode dari fungsi berikut: a. f

( )

t =sin2t

b.

( )

k nt t

f =cos2π

Jawab:

a. Fungsi sinus dan kosinus merupakan fungsi periodik dengan periode 2 , π maka f

( )

t =sin2t=sin

(

2t+2π

)

=sin2

(

t+π

)

= f

(

t+π

)

. Oleh karena itu, periodik dengan periode

t 2 sin

π.

b. Karena

( )

⎟

⎠ ⎞ ⎜ ⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + =

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₊

= =

n k t f n k t k

n k

nt k

nt t

f cos2π cos 2π 2π cos2π , maka

k nt

π

2

cos periodik dengan periode

n k

.

c. Fungsi tangen dan cotangen merupakan fungsi periodik dengan periode π.

Misal:

( )

(

)

⎟

⎠ ⎞ ⎜ ⎝ ⎛ + =

+ =

=

2 2 tan 2

tan 2

tan t t π t π

x

h , maka

2 1

π

ρ = , dan

( )

x = x=

(

+ x

)

=

(

+

(

x+ π

)

)

=

(

+

(

x+π

)

)

g 1 cos2

2 1 2

2 cos 1 2 1 2 cos 1 2 1 cos2

=cos2

(

x+π

) (

=g x+π

)

, maka ρ₂ =π.

Oleh karena itu, periode dari f

( )

t =tan2t+cos2t adalah KPK π π⎟=π ⎠ ⎞ ⎜ ⎝ ⎛

2

, .

Contoh 2.6:

Gambarkan grafik dari fungsi berikut yang dipandang periodik dengan periode diketahui.

a.

( )

, periode = 6

0 3

3 0

, 3 , 3

< ≤ −

< ≤ ⎩

⎨ ⎧ − =

x x x

f

-3

-3 3

3 f(x)

x

b. f

( )

t = t , periode 2 untuk π −π <t<π Jawab:

-π π

f(t)

t

Dari contoh-contoh di atas dapat dilihat bahwa tidak semua fungsi periodik kontinu untuk setiap bilangan real yang diberikan. Sebelum membahas mengenai definisi deret Fourier terlebih dahulu akan dibicarakan mengenai pengertian fungsi kontinu sepotong-sepotong.

Definisi 2.1 (fungsi kontinu sepotong-sepotong) : Fungsi disebut fungsi kontinu sepotong-sepotong atau kontinu bagian demi bagian pada interval

[ ]

bila dipenuhi syarat-syarat berikut :

) (x f

b a,

1. Interval

[ ]

a,b dapat dibagi menjadi sebanyak hingga sub interval sehingga kontinu pada setiap sub interval tersebut.

) (x f

2. Limit dari jika x mendekati ujung-ujung dari sub interval ada dan terhingga.

Atau dapat dikatakan bahwa mempunyai sebanyak hingga titik diskontinu.

) (x f

Contoh 2.7 : Sebuah fungsi f(x) didefinisikan dengan

⎩ ⎨ ⎧− =

, 1

, 1 ) (x

f . Fungsi kontinu pada selang

[

karena pada

selang tersebut fungsi bernilai -1. Demikian pula pada selang

[

fungsi kontinu karena fungsi bernilai 1.

4 2

2 0

≤ ≤

< ≤

x x

) (x

f 0,2

)

) (x

f 2,4

]

) (x

f f(x)

Dan pada x=2 terdapat dua limit yaitu

• f(x)=−1,0≤ x<2

1 1 lim ) ( lim

2

2− = → −− =−

→ x

x

x

f , f(x)=−1

(

0≤t<2

)

mempunyai limit kiri untuk

, 2

=

x

• f(x)=1,2≤ x≤4

1 1 lim ) ( lim

2 2+ = → + =

→ x

x f x

, f(x)=1

(

2≤t≤4

)

mempunyai limit kanan untuk

. 2

=

x

Jadi, fungsi f(x) tersebut kontinu sepotong-sepotong pada 0≤ x≤4.

Contoh 2.8 : Perlihatkan bahwa

⎪ ⎩ ⎪ ⎨ ⎧

− − =

, 3

, 2

, ) (

2

t t t t f

3 2

2 1

1 0

≤ ≤

< ≤

< ≤

t t

t

kontinu

sepotong-sepotong dalam selang tertutup

[ ]

0,3 .

Fungsi f(t) kontinu dalam selang

[

0,1

)

karena pada selang itu , juga kontinu dalam selang . Demikian juga pada selang

2 ) (t t

f = f(t)

[

1,2

)

[ ]

2,3 .

• f(t)=t2,0≤t <1

, 1 lim ) (

lim 2

1 1

=

= ₋

− _→

→ f t t t

t

(

)

1 0 )

(t =t2 ≤t <

• f(t)=2−t,1≤t<2

, 1 2 lim ) ( lim

1

1+ = →+ − =

→ f t t t

t ( ) 2

(

1 2

)

< ≤ −

= t t

t

f mempunyai limit kanan untuk

. 1

=

t

Pada t =2,

• f(t)=2−t,1≤t<2

0 2 lim ) ( lim

2 2

= − = ₋

− _→

→ f t t t

t

, f(t)=2−t

(

1≤t <2

)

mempunyai limit kiri untuk ,

2

=

t

• f(t)=3−t,2≤t≤3

1 3 lim ) ( lim

2

2+ = → + − =

→ f t t t

t

, f(t)=3−t

(

2≤t≤3

)

mempunyai limit kanan untuk

. 2

=

t

Jadi, fungsi f(t) kontinu sepotong-sepotong dalam selang 0≤t≤3.

1. Definisi Deret Fourier

Fungsi periodik yang dijumpai di dalam masalah rekayasa sering kali agak rumit, oleh karena itu kita berusaha untuk merepresentaskan fungsi itu ke dalam bentuk yang lebih sederhana. Berikut adalah fungsi-fungsi sederhana yang berperiode 2 : π

1, cos , x sinx, cos2x, sin2x, K, cosnx, sinnx, K. Deret trigonometri yang didefinisikan oleh

K

+ +

+ +

+a x b x a x b x

a_{0 1}cos ₁sin ₂cos2 ₂sin2

mempunyai periode 2 dengan π adalah bilangan real. Dengan menggunakan notasi sigma, kita dapat menuliskan deret itu sebagai

K K, , , ,

,

, _{1 2 1 2}

(

)

∑

∞

=

+ +

1

0 cos sin

n

n

n nx b nx

a

a , dan disebut koefisien-koefisien deret

trigonometri.

n

a b_n

Definisi 2.2 (deret Fourier) : Misalkan f(x) didefinisikan pada interval

(

−π,π

)

, periodik dengan periode 2π , dan kontinu sepotong-sepotong pada

interval tersebut, maka deret Fourier dari didefinisikan sebagai berikut: )

(x f

) (x f

(

)

∑

∞ =

+ +

1

0 cos sin

n

n

n nx b nx

a a

dengan harga-harga koefisien Fourier , dan ditentukan oleh rumus-rumus Euler sebagai berikut:

0

a a_n b_n

( )

xdx f

a

∫

−

= π

π

π

2 1 0

( )

x nxdx f

an cos

1

∫

−

= π

π

π n=1, 2, 3, ...

( )

x nxdx f

b_n 1

∫

sin

−

= π

π

π

A. Menghitung Koefisien- Koefisien Fourier dengan Rumus Euler

Misalkan f(x) adalah fungsi periodik dengan periode 2 . Akan π ditentukan deret trigonometri dari fungsi itu,

( )

∑

∞

(

)

=

+ +

=

1

0 cos sin

n

n

n nx b nx

a a

x

f dengan n=1, 2, 3, ... ....(1)

Langkah I

Langkah pertama yaitu menentukan dengan mengintegralkan kedua ruas pada persamaan (1) dari

0 a

π

− sampai π.

( )

x dx a

(

a nx b nx

)

dx

f n n n

∫

∑

∫

− ∞ = − ⎥⎦ ⎤ ⎢ ⎣ ⎡ _{+ +} = π π π π 1

0 cos sin

Kemudian dilakukan pengintegralan suku demi suku ( untuk lebih jelas akan dibahas pada konvergensi uniform), didapat:

( )

∫

∑

∫

∫

∫

∞₌ − − − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = 1

0 cos sin

n

n

n nxdx b nxdx

a dx a dx x f π π π π π π π π

[ ]

∑

∞ = − − − _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡ + = 1 0 cos sin n n n n nx b n nx a x a π π π π π π

( )

(

)

∑

∞

(

)

(

)

= ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎥⎦ ⎤ ⎢⎣ ⎡ − − − ⎥⎦ ⎤ ⎢⎣ ⎡ − − + − − = 1 0 cos cos sin sin n n n n n n n b n n n n a

a π π π π π π

(

)

(

)

(

)

∑

∞ = − − − + = 1

0 0 0 0 0

2 n n n b a a π 0 2πa

=

Sehingga didapatkan

∫

( )

−

= π

π

π f x dx

a 2

1

0 . ...(2)

Langkah II

Langkah kedua yaitu menentukan pada persamaan (1) dengan cara mengalikan kedua ruas pada persamaan (1) dengan (m adalah bilangan bulat positif) dan kemudian mengintegralkan persamaan tersebut dari

K , , , _{2 3} 1 a a a

mx cos

π

− sampai

( )

x mxdx a

(

a nx b nx

)

mxdx f

n

n

ncos sin cos

cos 1 0

∫

∑

∫

− ∞ = − ⎥⎦ ⎤ ⎢ ⎣ ⎡ _{+ +} = π π π π

Kemudian dilakukan pengintegralan suku demi suku, didapat:

( )

∫

∑

∫

∫

∫

∞₌ − − − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = 1

0 cos cos cos sin cos

cos

n

n

n nx mxdx b nx mxdx

a mxdx a mxdx x f π π π π π π π π

∑

∞₌

∫

∫

− − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⎥⎦ ⎤ ⎢⎣ ⎡ = 1

0 cos cos sin cos

sin

n

n

n nx mxdx b nx mxdx

a m mx a π π π π π π

(

)

⎥⎦ ⎤ ⎢⎣ ⎡ − − = m m m m

a₀ sin π sin π

∑

∞₌

∫

∫

− − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + 1 cos sin cos cos n n

n nx mxdx b nx mxdx

a π π π π

[

]

∑

∞

∫

∫

= _{− −} ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + − = 1

0 0 0 cos cos sin cos

n

n

n nx mxdx b nx mxdx

a a π π π π

∑

∞

∫

∫

= − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = 1 cos sin cos cos 0 n n

n nx mxdx b nx mxdx

a

π

π π

π

Penjabaran tiap bagian:

(

)

∫

(

)

∫

∫

− − − − + + = π π π π π π xdx m n xdx m n mxdx nx cos 2 1 cos 2 1 cos cos

(

)

(

)

π π π π − − ⎥⎦ ⎤ ⎢⎣ ⎡ − − + ⎥⎦ ⎤ ⎢⎣ ⎡ + + = m n x m n m n x m n sin 2 1 sin 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = m n m n m n m

n π sin π

sin 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − + m n m n m n m

n π sin π

karena sin

(

)

sin

(

(

)

)

=0 + + − = + + m n m n m n m

n π π

(untuk semua nilai n dan m) dan

(

)

(

(

)

)

0 sin sin ₌ − − − = − − m n m n m n m

n π π

(untuk semua nilai n dan m dan n≠m).

(

)

∫

(

)

∫

∫

− − − − + + = π π π π π π xdx m n xdx m n mxdx nx sin 2 1 sin 2 1 cos sin

(

)

(

)

π π π π − − ⎥⎦ ⎤ ⎢⎣ ⎡ − − − + ⎥⎦ ⎤ ⎢⎣ ⎡ + + − = m n x m n m n x m n cos 2 1 cos 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − = m n m n m n m

n π cos π

cos 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − m n m n m n m

n π cos π

cos 2 1 0 =

karena

(

)

(

(

)

)

m n m n m n m n + + − = +

+ π cos π

cos

(untuk semua nilai n dan m) dan

(

)

(

(

)

)

m n m n m n m n − − − = −

− π cos π

cos

(untuk semua nilai n dan m dan n≠m).

Pengintegralan dari keempat bagian di atas sama dengan nol, kecuali untuk

(

)

π π π = −

∫

− xdx m n cos 2 1

jika n=m. Dengan demikian jika ,

maka .

m n=

( )

x mxdx am

f π π π =

∫

− cos

Jadi didapatkan a_m 1

∫

f

( )

x cosmxdx

−

= π

π

Langkah III

Langkah ketiga yaitu menentukan pada persamaan (1) dengan cara mengalikan kedua ruas pada persamaan (1) dengan

K , , , _{2 3} 1 b b b

mx

sin

(

m>0

)

dan kemudian mengintegralkan persamaan tersebut dari −π sampai π.

( )

x mxdx a

(

a nx b nx

)

mxdx

f

n

n

ncos sin sin

sin 1 0

∫

∑

∫

− ∞ = − ⎥⎦ ⎤ ⎢ ⎣ ⎡ + + = π π π π

Kemudian dilakukan pengintegralan suku demi suku, didapat:

( )

∫

∑

∫

∫

∫

∞₌ − − − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = 1

0 sin cos sin sin sin

sin

n

n

n nx mxdx b nx mxdx

a mxdx a mxdx x f π π π π π π π π

∑

∞

∫

∫

= − − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⎥⎦ ⎤ ⎢⎣ ⎡− = 1

0 cos sin sin sin

cos

n

n

n nx mxdx b nx mxdx

a m mx a π π π π π π

(

)

⎥⎦ ⎤ ⎢⎣ ⎡ ₋ − − = m m m m

a₀ cos π cos π

∑

∞

∫

∫

= − − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + 1 sin sin sin cos n n

n nx mxdx b nx mxdx

a π π π π

∑

∞₌

∫

∫

− − ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = 1 sin sin sin cos 0 n n

n nx mxdx b nx mxdx

a

π

π π

π

karena

(

)

m m m

mπ − π

= cos cos

untuk semua nilai m.

Penjabaran tiap bagian:

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − = m n m n m n m

n π cos π

cos 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − + m n m n m n m

n π cos π

cos 2 1

0

=

karena

(

)

(

(

)

)

m n m n m n m n + + − = +

+ π cos π

cos

(untuk semua nilai n dan m) dan

(

)

(

(

)

)

m n m n m n m n − − − = −

− π cos π

cos

(untuk semua nilai n dan m dan n≠m).

(

)

∫

(

)

∫

∫

− − − + − − = π π π π π π xdx m n xdx m n mxdx nx cos 2 1 cos 2 1 sin sin

(

)

(

)

π π π π − − ⎥⎦ ⎤ ⎢⎣ ⎡ + + − ⎥⎦ ⎤ ⎢⎣ ⎡ − − = m n x m n m n x m n sin 2 1 sin 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = m n m n m n m

n π sin π

sin 2 1

(

)

(

(

)

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − m n m n m n m

n π sin π

sin 2 1

0

=

karena sin

(

)

sin

(

(

)

)

=0 + + − = + + m n m n m n m

n π π

(untuk semua nilai n dan m) dan

(

)

(

(

)

)

0 sin sin ₌ − − − = − − m n m n m n m

n π π

(untuk semua nilai n dan m dan n≠m).

Pengintegralan dari keempat bagian di atas sama dengan nol, kecuali untuk

(

)

π π π = −

∫

− xdx m n cos 2 1

Dengan demikian jika n=m, maka f

( )

x mxdx πb_m. π

π

=

∫

−

sin

Jadi didapatkan b_m 1

∫

f

( )

x sinmxdx

−

= π

π

π , m = 1, 2, 3, ... ...(5)

Dengan mengganti m dengan n pada persamaan (2), (3), dan (4), diperoleh rumus-rumus Euler sebagai berikut:

( )

xdx f

a

∫

−

= π

π

π

2 1 0

( )

x nxdx f

a_n 1

∫

cos

−

= π

π

π n=1, 2, 3, ... ....(6)

( )

x nxdx f

b_n 1

∫

sin

−

= π

π

π

Deret trigonometri dengan koefisien-koefisien yang

ditentukan oleh (6) dinamakan deret Fourier untuk

(

∑

∞

=

+ +

1

0 cos sin

n

n

n nx b nx

a

a

)

( )

x f .

Di dalam penerapan, fungsi periodik kadang tidak mempunyai periode 2π melainkan mempunyai periode lain yaitu 2L. Jika didefinisikan pada interval , periodik dengan periode

) (x f

(

−L,L

)

2L, dan kontinu sepotong-sepotong

dalam interval tersebut, maka deret Fourier dari didefinisikan sebagai berikut:

) (x f

∑

∞ =

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₊

+ 1

0 cos sin

n

n

n x

L n b x L n a

a π π

dengan harga-harga koefisien Fourier , dan ditentukan oleh rumus-rumus Euler sebagai berikut:

0

( )

xdx f L a L L

∫

− = 2 1

0 ,

( )

dx

L x n x f L a L L n π cos 1

∫

−

= , dan

( )

dx

L x n x f L b L L n π sin 1

∫

− =

untuk n adalah bilangan bulat positif.

A. Ekspansi Fungsi Menjadi Deret Fourier

Contoh 2.9 : Tentukan koefisien Euler dan deret Fourier dari f(x) bila

( )

dan f

(

x

)

f

( )

x

x x k

k x

f + =

< < < < − ⎩ ⎨ ⎧− = π π π 2 0 0 , , Jawab:

Fungsi tersebut periodik dengan periode 2 dan dapat digambarkan sebagai π berikut

Koefisien Euler dari f(x) ditentukan sebagai berikut:

( )

xdx kdx kdx

f

a =

∫

=

∫

− +

∫

− − π π π π π π π ₀ 0 0 2 1 2 1 2 1 0 2 2 2 2 0

0 _{+ =} − _{+ =}

−

= k x_−π k xπ k k

π π

( )

( )

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − = =

∫

∫

∫

− − dx nx k dx nx k dx nx x f a_n π π π π π π ₀ 0 cos cos 1 cos 1

( )

sin sin 0

(karena sinnx=0 untuk x=−π, 0 dan π dan untuk semua nilai n)

( )

( )

⎥

⎦ ⎤ ⎢

⎣ ⎡

+ −

=

=

∫

∫

∫

− −

dx nx k dx nx k dx

nx x f b_n

π

π π

π π

π ₀

0

sin sin

1 sin

1

⎥ ⎦ ⎤ ⎢

⎣ ⎡

−

= ₋ π

π

π 0

0 cos cos

1

n nx k n

nx k

( )

[

cos0−cos − −cos +cos0

]

= π π

π n n

n k

[

]

(

π

)

π π

π n n

k n

n k

cos 1 2 cos

2

2− = −

=

Karena 1−cosnπ =2 untuk ganjil dan n 1−cosnπ =0 untuk genap, maka n K

, 5

4 ,

0 , 3 4 , 0 , 4

5 4

3 2

1 _{π π π}

k b b

k b b

k

b = = = = = .

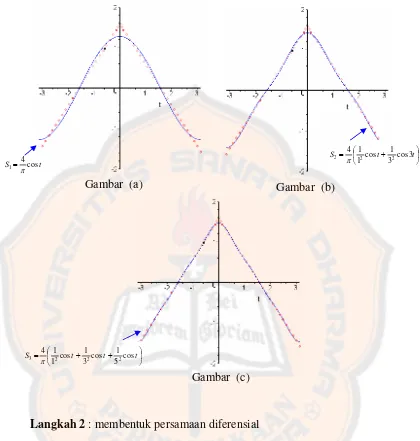
Deret Fourier untuk f

( )

x adalah :

(

)

⎟

⎠ ⎞ ⎜

⎝

⎛ _{+ + +}

= −

∑

∞ =

K

x x

x k nx n

n k

n

5 sin 5 1 3 sin 3 1 sin 4 sin

cos 1 2

1 π

π

π .

Ketiga gambar tersebut menunjukkan tiga jumlah parsial yang pertama dari deret Fourier yang dihasilkan.

Contoh 2.10: Tentukan koefisien Euler dan deret Fourier dari f(t) bila

( )

t t t f

(

t

)

f

( )

t

f = ,−π < <π dan +2π = . Jawab:

Fungsi tersebut periodik dengan periode 2 dan dapat digambarkan sebagai π berikut

f(t)

π π

−

t

Koefisien Euler dari f(t) ditentukan sebagai berikut:

( )

0

4 2

1 2

1 2

0 ⎥ =

⎦ ⎤ ⎢ ⎣ ⎡ = =

=

− −

−

∫

∫

π

π π

π π

π π π

π

t dt t dt

( )

t nt dt t nt dt f

a_n

∫

∫

− − = = π π π π π π cos 1 cos 1 ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − ⎥⎦ ⎤ ⎢⎣ ⎡ =

∫

− − π π π π

π n nt n ntdt

t sin 1 sin 1 π π π ⎥⎦₋ ⎤ ⎢⎣ ⎡ ₊ = nt n nt n t cos 1 sin 1 2

(

)

⎩ ⎨ ⎧ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋− ₋ = π π π π

π nsinn n sin n

1

(

)

⎭ ⎬ ⎫ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{π − − π} n n n n cos 1 cos 1 2 2

(

) ( )

{

0 0 0

}

0

1 = + − = π

(

)

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{π − − π = π = − π} n n n n n

n cos 0karenacos cos

1 cos

1

2 2

( )

t ntdt t nt dt

f

bn

∫

∫

− − = = π π π π π π sin 1 sin 1 ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − − ⎥⎦ ⎤ ⎢⎣ ⎡− =

∫

− − π π π π

π n nt n ntdt

t cos 1 cos 1 π π π ⎥⎦₋ ⎤ ⎢⎣ ⎡_{− +} = nt n nt n t sin 1 cos 1 2

(

)

⎩ ⎨ ⎧ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− +}− ₋ = π π π π

π ncosn n cos n

(

)

π π

π

π n n ncosn

2 0

0 cos

2

1 ₌₋

⎭ ⎬ ⎫ ⎩

⎨

⎧ _{+ −}

⎟ ⎠ ⎞ ⎜

⎝ ⎛− =

Deret Fourier untuk f

( )

t adalah :

∑

∞ =

⎟ ⎠ ⎞ ⎜

⎝ ⎛− 1

sin cos 2 n

nt n

n π

A. Fungsi Genap dan Fungsi Ganjil

Definisi 2.3 (fungsi genap dan fungsi ganjil) : Fungsi disebut fungsi genap bila berlaku

) (x f

( )

x f x

f(− )= untuk semua x dalam daerah asal dan disebut fungsi ganjil bila berlaku

) (x

f f(−x)=−f

( )

x untuk semua x dalam

daerah asal.

Sifat-sifat fungsi genap dan fungsi ganjil yaitu sebagai berikut:

1. Grafik fungsi genap y= f(x) simetris terhadap sumbu y dan grafik fungsi ganjil y= f(x) simetris terhadap titik pusat salib sumbu.

f(t)

Fungsi genap f(t)

t t

Fungsi ganjil

f(t)

2. Hasil kali dua fungsi genap dan hasil kali dua fungsi ganjil merupakan fungsi genap, sedangkan hasil kali antara fungsi ganjil dan fungsi genap adalah fungsi ganjil.

Bukti:

a. Misalkan adalah hasil kali antara fungsi genap dan fungsi genap , maka

) (x

f g(x)

) (x

h f(x)= g

( ) ( )

x h x

Fungsi ganjil Fungsi genap

t

f(t)

( ) ( )

x h x g

x

f(− )= − − = g

( ) ( )

x h x = f

( )

x

Jadi hasil kali dua fungsi genap adalah fungsi genap.

b. Misalkan adalah hasil kali antara fungsi ganjil dan fungsi ganjil , maka

) (x

f g(x)

) (x

h f(x)= g

( ) ( )

x h x

( ) ( )

x h x

g x

f(− )= − − =

(

−g

( )

x

) ( )

(

−h x

)

= f

( )

x

Jadi hasil kali dua fungsi ganjil adalah fungsi genap.

c. Misalkan adalah hasil kali antara fungsi genap dan fungsi ganjil , maka

) (x

f g(x)

) (x

h f(x)= g

( ) ( )

x h x

( ) ( )

x h x

g x

f(− )= − − = g

( ) ( )

x

(

−h x

)

=−

(

g

( ) ( )

x h x

)

= f

( )

x

Jadi hasil kali antara fungsi ganjil dan fungsi genap adalah fungsi ganjil.

3. Bila fungsi genap, maka . Bila fungsi

ganjil, maka .

) (x

f

∫

=

∫

−

L L

L

dx x f dx x f

0 ) ( 2 )

( f(x)

0 )

( =

∫

−

L

L

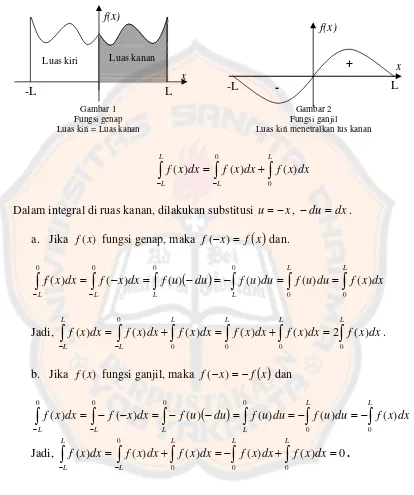
dx x f

Tafsiran geometri dari sifat ini diperlihatkan dalam gambar 1 dan 2 sebagai berikut:

Gambar 1 Fungsi genap Luas kiri = Luas kanan

-L L

f(x)

x Luas kiri Luas kanan

Gambar 2 Fungsi ganjil

Luas kiri menetralkan lus kanan

-+ L -L f(x) x

∫

∫

∫

= + − − L L L L dx x f dx x f dx x f 0 0 ) ( ) ( ) (

Dalam integral di ruas kanan, dilakukan substitusi u=−x, −du =dx. a. Jika f(x) fungsi genap, maka f(−x)= f

( )

x dan.

(

)

∫

∫

∫

∫

∫

∫

= − = − =− = = − − L L L L L L dx x f du u f du u f du u f dx x f dx x f 0 0 0 0 0 0 ) ( ) ( ) ( ) ( ) ( ) (

Jadi,

∫

=

∫

+

∫

=

∫

+

∫

=

∫

.

− − L L L L L L L dx x f dx x f dx x f dx x f dx x f dx x f 0 0 0 0 0 ) ( 2 ) ( ) ( ) ( ) ( ) (

b. Jika f(x) fungsi ganjil, maka f(−x)=−f

( )

x dan

(

)

∫

∫

∫

∫

∫

∫

= − − = − − = =− =− − − L L L L L L dx x f du u f du u f du u f dx x f dx x f 0 0 0 0 0 0 ) ( ) ( ) ( ) ( ) ( ) (

Jadi, ( ) ( ) ( ) ( ) ( ) 0.

Catatan: x adalah variabel dummy dalam lambang , yaitu

dimaksudkan bahwa x dapat diganti oleh huruf sebarang lain (diganti di setiap

kemunculannya). Jadi, .

( )

xdx f b

a

∫

( )

xdx f

( )

tdt f

( )

udu f

b

a b

a b

a

∫

∫

∫

= =

Deret Fourier untuk fungsi genap yang terdefinisi pada suatu interval , kontinu sepotong-sepotong dan periodik dengan periode 2L disebut juga Deret Kosinus Fourier dengan bentuk

) (x f

(

−L,L

)

∑

∞ =

+ 1

0 cos

n n

L x n a

a π

dengan koefisien-koefisien

( )

xdx f L a

L

∫

=

0 0

1

,

( )

dx

L x n x f L a

L n =

∫

0

cos

2 π

, ……(7) _{n=1, 2, 3, ...}

Deret Fourier untuk fungsi ganjil yang terdefinisi pada suatu interval , kontinu sepotong-sepotong dan periodik dengan periode 2L disebut juga Deret Sinus Fourier dengan bentuk

) (x f

(

−L,L

)

∑

∞ =1

sin n

n

L x n

b π

dengan koefisien-koefisien

( )

dx

L x n x f L b

L n =

∫

0

sin

2 π

Contoh 2.11:

Selidiki apakah fungsi berikut genap, ganjil, atau tidak kedua-duanya! a.

( )

= 2 +1

x x f

b.

( )

2 2 ₊ =

x x x

h

c. f

( )

t =t+1 Jawab:

a.

( )

= 2 +1 x x

f adalah fungsi genap karena

( )

x

( )

x x f

( )

x f − = − 2 +1= 2 +1= .

b.

( )

2 2 + =

x x x

h adalah fungsi ganjil karena

( )

( )

h

( )

x

x x x

x x

h =−

+ − = + −

− = −

2

2 2

2 .

c. f

( )

t =t+1 bukan fungsi genap maupun fungsi ganjil karena f

( )

−t =−t+1 bukan fungsi f

( )

t maupun − f

( )

t .

Contoh 2.12:

Klasifikasikan masing-masing fungsi-fungsi berikut apakah fungsi genap, ganjil, atau tidak genap dan tidak ganjil!

a. f

( ) (

x = x8−x

)

, 0< x<8, periode = 8

b.

( )

, periode =

0 3

3 0

, 2

, 2

< < −

< < ⎩

⎨ ⎧ − =

x x x

Jawab:

a. dengan periode = 8 merupakan fungsi genap

karena

( ) (

x = x8−x

)

, 0< x<8 f

( ) (

−x = x8−x

)

, −8<x<0 f

= f

( )

x .

Secara geometri dapat diperlihatkan dalam gambar sebagai berikut:

x

0 ₈

f(x)

16

b. dengan periode = 6 merupakan fungsi ganjil

karena

( )

0 3

3 0

, 2

, 2

< < −

< < ⎩

⎨ ⎧ − =

x x x

f

( )

f

(

x

x x x

f =−

< <

< < − ⎩

⎨ ⎧− = −

3 0

0 3

, 2

, 2

.

)

Secara geometri dapat diperlihatkan dalam gambar sebagai berikut:

-6 -3 3 6

-2 2

x

f(x)

Contoh 2.13: Tentukan deret Fourier dari fungsi f

( )

x yang periodik dengan periode 2, bila fungsi f

( )

x = x,−1<x<1.

Jawab:

Fungsi tersebut merupakan fungsi genap, sehingga . Dengan demikian, koefisien Fourier dapat ditentukan sebagai berikut:

( )

x

f b₀ =0

1 -1

f(t)

t

2 1 2

2

1 1

0 2 1

0 1

1

0 ⎥ =

⎦ ⎤ ⎢ ⎣ ⎡ = =

=

∫

∫

−

x xdx dx

x

a ,

0 1 cos 1 sin

2 cos

2 cos

1

0 1

1 ⎥⎦

⎤ ⎢⎣

⎡ ₊

= =

=

∫

∫

−

x n n

x n x n xdx n x x xdx n x

a_n π

π π π

π π

(

cos 1

)

4 ( )

2

2 2 2

2 n ganjil

n n

n π π π

− = −

= .

Jadi didapatkan deret Fourier dari f

( )

x = x , yaitu

(

)

⎟

⎠ ⎞ ⎜

⎝

⎛ _{+ + +}

− = −

+

∑

∞

=

K

x x

x x

n n

n

n

π π

π π

π π

π 5 cos5

1 3 cos 3

1 cos 4 2 1 cos

1 cos 2 2

1

2 2

2 1

2

2 .

A. Penguraian Setengah-Kisaran

Di dalam berbagai masalah penerapan, akan banyak dijumpai penggunaan deret Fourier bagi fungsi f

( )

x yang didefinisikan pada suatu selang terhingga tertentu. Dalam hal ini, f

( )

x didefinisikan dalam selang 0≤x≤L, dan pada selang ini f

( )

x akan direpresentasikan oleh deret Fourier. Untuk memperoleh deret Fourier dari fungsi tersebut dapat menggunakan L sebagai selang keperiodikan, namun akan lebih baik jika mengambil periode 2L. Hal ini disebabkan karena dengan mengambil periode 2L, maka akan diperoleh suatu deret kosinus Fourier untuk f

( )

x yang merupakan perluasan genap ke kisaran penuh , atau dapat diperoleh suatu deret sinus Fourier untuk

yang merupakan perluasan ganjil

( )

x f L

x L≤ ≤

−

( )

x

f f

( )

x ke kisaran penuh .

Masing-masing deret itu dinamakan penguraian setengah-kisaran fungsi , yang diberikan hanya pada setengah kisarannya (setengah selang keperiodikan deret tersebut).

L x L≤ ≤

−

Perluasan genap dan perluasan ganjil f

( )

x ke kisaran penuh diperlihatkan dalam gambar sebagai berikut:

L x L≤ ≤

−

(a) Fungsi f

( )

x yang diberikan L

( )

x f

x

( )

x f1

-L L x

(b) Fungsi f

( )

x diperluas sebagai suatu fungsi genap dengan periode 2L

( )

x

f₂

-L L x

(c) Fungsi f

( )

x diperluas sebagai suatu fungsi ganjil dengan periode 2L

Keterangan gambar:

(a) Fungsi f

( )

x diberikan pada selang 0≤x≤L,

(b) perluasan genap fungsi f

( )

x ke kisaran penuh −L≤ x≤L dan perluasan periodik periode 2L pada sumbu-x,

Penguraian setengah kisaran kosinus fungsi f

( )

x adalah

∑

∞ =

+ 1

0 cos

n n

L x n a

a π

dengan koefisien-koefisien

( )

xdx f L a

L

∫

=

0 0

1

,

( )

dx

L x n x f L a

L n =

∫

0

cos

2 π

, n=1, 2, 3, .... ...(9) Penguraian setengah kisaran sinus fungsi f

( )

x adalah

∑

∞ =1

sin n

n

L x n

b π

dengan koefisien-koefisien

( )

dx

L x n x f L b

L n =

∫

0

sin

2 π

, n=1, 2, 3, .... ...(10)

Contoh 2.14: Tentukan kedua penguraian setengah kisaran bagi fungsi

( )

⎪ ⎩ ⎪ ⎨ ⎧

< < −

< < =

L x L x

L

L x x

x f

2 jika

2 0

jika

Jawab:

a. Penguraian setengah kisaran kosinus untuk f

( )

x adalah

0

a f

( )

xdx L

L

∫

=

0 1

(

)

⎪⎭ ⎪ ⎬ ⎫

⎪⎩ ⎪ ⎨ ⎧

− +

=

∫

∫

L

L L

dx x L dx x L

2 2

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ + ⎥⎦ ⎤ ⎢⎣ ⎡ = L L L x Lx x L 2 2 2 0 2 2 1 2 1 1 ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⋅ = 8 2 2 4 2 1

1 2 ₂ L2 L2 L2

L L L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + = 8 8 1 L2 L2

L 4

L

=

n

a

( )

dx

L x n x f L L

∫

= 0 cos 2 π

(

)

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − + =

∫

∫

L L L dx L x n x L dx L x