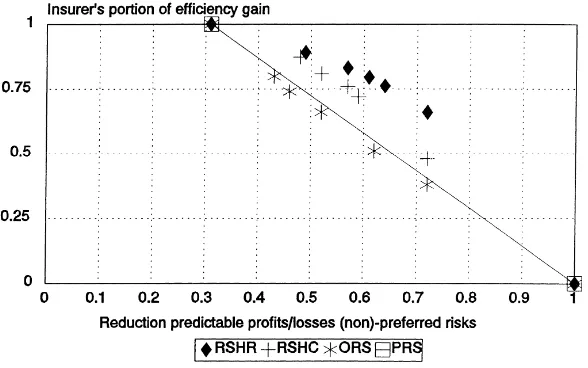
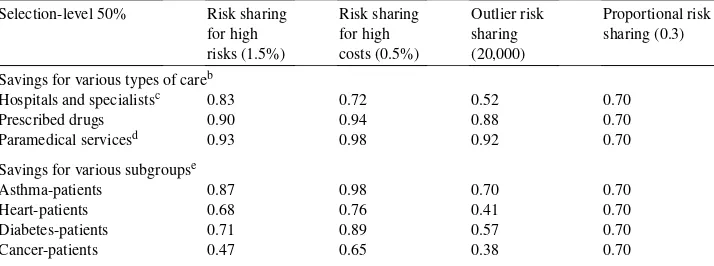
Directory UMM :Journals:Journal of Health Economics:Vol20.Issue2.Mar2001:
Teks penuh
Gambar

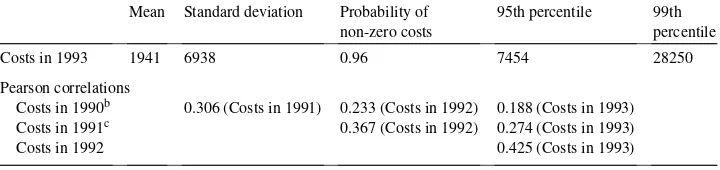

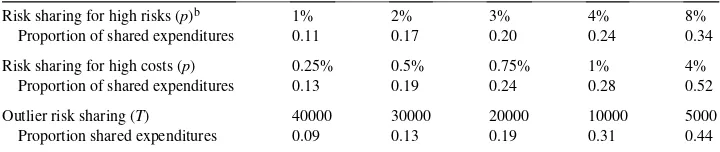
Dokumen terkait
Berdasarkan hasil mean komitmen organisasional yang sudah dilakukan dalam penelitian ini dapat dilihat bahwa nilai mean komitmen afektif memiliki nilai yang lebih besar yaitu 3,8183
Mahasiswa Melanjutkan memahami perkuliahan tentang Aplikasi Teknologi secara teoritik.
Ji ka selama masa Keadaan Kahar PPK memer intahkan secar a tertulis kepada Penyedi a untuk mener uskan peker jaan sedapat mungkin maka Penyedia ber hak untuk
i) Fot o copy surat pengakuan/ penghargaan minim al dari lembaga yang kredibel t ingkat nasional unt uk pirant i lunak (soft w are) kont en pembelajaran. j) memiliki
Sehubungan dengan tahapan proses pembuktian kualifikasi dokumen penawaran pemilihan langsung pada Dinas Pendidikan dan Kebudayaan Kota Serang, Pekerjaan Belanja Modal Pembangunan
(Pembangunan Kantor Dinas Kesehatan dan Dinas Pasar Kota Ternate), maka bersama ini POKJA Konsultansi Unit Layanan Pengadaan akan mengadakan Verifikasi/Pembuktian terhadap semua
ia Jasa Konsultansi untuk paket pekerjaan Pengawa eliharaan Jalan Paket A Pokja 1 Pengadaan Baran.. n
Pengadaan barang/jasa dilaksanakan secara elektronik dengan mengakses aplikasi Sistem Pengadaan Secara Elektronik (aplikasi SPSE) pada alamat website LPSE