Informasi Dokumen
- Penulis:
- Barnett Rich
- Christopher Thomas
- Mata Pelajaran: Geometry
- Topik: Geometry
- Tipe: Textbook
- Tahun: 2018
Ringkasan Dokumen
I. Lines, Angles, and Triangles
This chapter lays the foundational geometric concepts. It starts with a historical overview, emphasizing geometry's practical origins and its subsequent formalization by the Greeks, culminating in Euclid's Elements. The chapter then introduces undefined terms—point, line, and plane—providing descriptive explanations rather than formal definitions. This sets the stage for defining line segments, circles, angles, and triangles, all crucial building blocks for subsequent chapters. The pedagogical approach focuses on visual representation through diagrams, alongside clear textual explanations of properties and relationships.
1.1 Historical Background of Geometry
This section traces the development of geometry from its practical applications in ancient civilizations to its theoretical advancements in ancient Greece. The significance of Euclid's Elements as a foundational text is highlighted, emphasizing its enduring impact on the teaching and understanding of geometry. This historical context provides students with a broader perspective on the subject's evolution and its relevance to human civilization.
1.2 Undefined Terms of Geometry: Point, Line, and Plane
This section introduces the fundamental undefined terms of geometry: point, line, and plane. The text acknowledges that these terms cannot be formally defined but are instead explained descriptively, relying on intuitive understanding and visual representation. The concept of a plane as a flat surface is established, setting the stage for plane geometry. This approach emphasizes the building-block nature of these concepts in geometric reasoning.
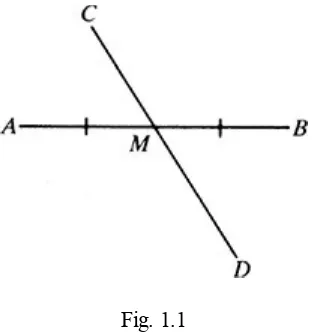
1.3 Line Segments
The concept of a line segment is introduced, including its properties and how it can be divided into parts, particularly the concept of a midpoint and a bisector. The introduction of congruent segments provides a basis for later geometric proofs and applications. The use of diagrams is crucial in visualizing these properties and relationships, making abstract concepts more concrete for students.
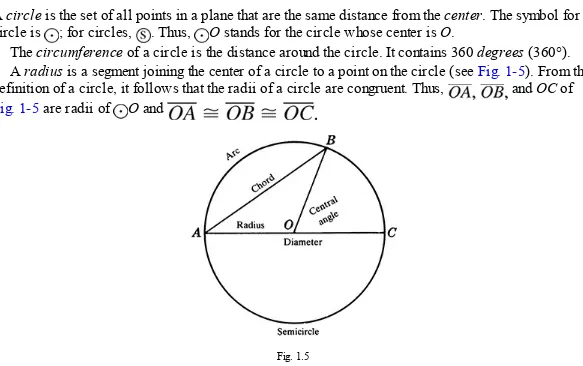
1.4 Circles
This section defines circles, radii, chords, diameters, arcs, and central angles, emphasizing their properties and relationships. The concept of congruent circles is introduced, providing the groundwork for later chapters involving circular geometry. The inclusion of diagrams illustrating these concepts helps to visualize and grasp the definitions.
1.5 Angles
Different types of angles (acute, right, obtuse, straight, reflex) are defined and illustrated with diagrams, emphasizing their measurements in degrees. The concepts of congruent angles, angle bisectors, and perpendicular lines are introduced, along with their properties. This section builds upon the previous sections' foundation, introducing concepts crucial for understanding geometric proofs and relationships.
1.6 Triangles
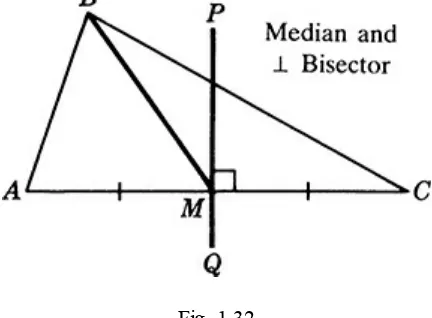
This section defines triangles and classifies them by side lengths (scalene, isosceles, equilateral) and angles (right, obtuse, acute), using diagrams to visually represent each type. Special lines in a triangle (angle bisectors, medians, altitudes, perpendicular bisectors) are introduced and illustrated. This section introduces a key geometric figure and its various properties, important for understanding advanced concepts in geometry.
1.7 Pairs of Angles
This section defines and illustrates various pairs of angles: adjacent, vertical, complementary, and supplementary angles. The principles governing the relationships between these angle pairs are presented, laying the groundwork for proofs involving angle relationships. The clear distinction between adjacent and vertical angles, and the use of diagrams, is vital for student comprehension.
II. Methods of Proof
This chapter introduces deductive reasoning as the cornerstone of geometric proof. It emphasizes the distinction between proof and methods like observation, measurement, and experimentation, highlighting the limitations of the latter in establishing absolute truth. The chapter introduces postulates (both algebraic and geometric), which serve as the foundational assumptions upon which geometric proofs are built. The chapter explains the structure of a syllogism and demonstrates how to construct and apply proofs.
2.1 Proof By Deductive Reasoning
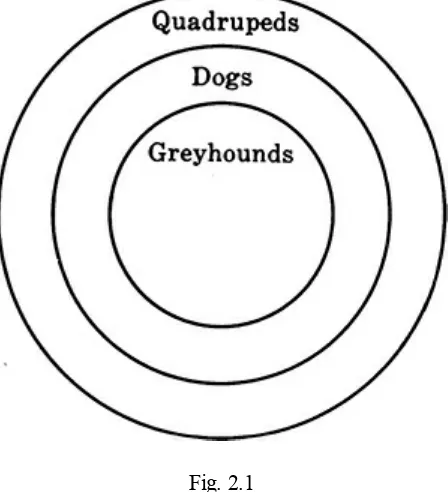
This section explains deductive reasoning as a method of proof. The three steps of a syllogism (major premise, minor premise, conclusion) are explained and illustrated using examples. The use of Venn diagrams is introduced as a visual aid to understand the relationships between sets and to derive logical conclusions. The focus is on clarifying the process of deductive reasoning and its application in geometric proofs.
2.2 Postulates (Assumptions)
This section presents the algebraic and geometric postulates that form the basis for all geometric proofs. The postulates are stated clearly, and their application is illustrated with examples. This section is crucial for understanding the underlying assumptions upon which geometric reasoning rests. The distinction between algebraic and geometric postulates is clearly articulated.
III. Congruent Triangles
This chapter delves into congruent triangles. It defines congruence and introduces different methods for proving the congruence of triangles. This knowledge is crucial for solving geometric problems and constructing formal proofs. The chapter builds upon the foundational concepts of lines, angles, and triangles established earlier.
3.1 Congruent Triangles
This section introduces the concept of congruent triangles, which are triangles that have the same size and shape. It provides methods for proving triangle congruence, such as using corresponding sides and angles. The emphasis is on understanding the conditions that guarantee triangle congruence, which will be applied to solve various geometry problems.
3.2 Isosceles and Equilateral Triangles
This section focuses on the properties of isosceles and equilateral triangles. It explores the relationships between their sides and angles, including the base angles theorem for isosceles triangles. These properties are frequently used in geometric proofs and problem-solving. The connection between isosceles and equilateral triangles is clearly stated.