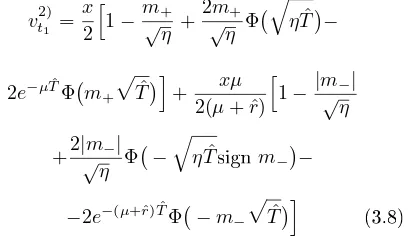Sociedad de Estadística e Investigación Operativa
Boletín de la SEIO Volumen 24, número 3
OCTUBRE 2008
REDACCIÓN
Editor: Jesús López Fidalgo [email protected]
Universidad de Castilla-La Mancha
Editores Asociados: Estadística:
M. del Carmen Pardo Llorente [email protected]
Universidad Complutense de Madrid
Investigación Operativa: Ana Meca Martínez
Universidad Miguel Hernández de Elche
Estadística Ocial: Félix Aparicio Pérez [email protected]
Instituto Nacional de Estadística
Historia y Enseñanza: Gabriel Ruiz Garzón [email protected] Universidad de Cádiz
Editor Técnico:
Fco. Javier Toledo Melero [email protected]
Universidad Miguel Hernández de Elche
Normas para los envíos de colaboracio-nes:
Los artículos se enviarán por correo electróni-co al editor asociado electróni-correspondiente o al edi-tor del Boletín. Se escribirán en estilo article de LateX. Cada artículo ha de contener el tí-tulo, el resumen y las palabras clave en inglés sin traducción al castellano. Desde la página Web de la SEIO, www.seio.es, pueden descar-garse varios modelos editados con WinEdt y con Scientic WorkPlace, tanto en español co-mo en inglés, que los autores pueden utilizar, si lo desean, como plantillas para la elabora-ción de sus artículos.
SEIO:
Facultad de CC. Matemáticas, Despacho 502 Universidad Complutense de Madrid
Plaza de Ciencias, 3
28040 Madrid (Ciudad Universitaria) [email protected], http://www.seio.es Tel: (+34) 91 544 91 02
Imprime SEROTEL Po de la Castellana, 87. Dep. Legal: M-13647-1995 ISSN: 1699-8871
ÍNDICE
ÍNDICE
Editorial . . . 3
El rincón del presidente . . . 5
1. Artículos de Estadística 6
◮ Probabilistic Valuation of Certain Unit-linked Contracts, Javier Villarroel . . . . 6
2. Artículos de Investigación Operativa 11
◮ Mechanism Design in School Choice: Some Lessons in a Nutshell, Flip Klijn . . . . 11
3. Estadística Ocial 23
◮ Time-Reversion of VARMA Processes by Polynomial Methods, Félix Aparicio Pérez y Victor Gómez Enríquez . . . 23
4. Historia y Enseñanza 27
◮ Smallpox and the Memory of D. Bernoulli. An Early Example of Applied Statistics, José Antonio Camúñez Ruiz y Francisco Javier Ortega Irizo . . . 27
5. Opiniones sobre la profesión 35
EDITORIAL
EDITORIAL
Jesús López Fidalgo∗
Instituto de Matemática Aplicada a la Ciencia y a la Ingeniería Universidad de Castilla-La Mancha
Han pasado ya cuatro años desde que se me en-comendó la dirección del Boletín. Quisiera hacer un poco de historia y aprovechar la ocasión para men-cionar y agradecer a los que han colaborado de ma-nera activa en este proyecto. En el momento en que Domingo Morales asumió la presidencia de la SEIO tenía un proyecto muy claro y atractivo de actua-lización del Boletín. Cuando me propuso llevarlo a cabo como editor no lo pensé demasiado. El reto me resultaba muy interesante y a la vez realista. Así y todo, pienso que en aquél momento ninguno de los dos imaginábamos que el Boletín se acabaría con-virtiendo en lo que es hoy día. Hace un año el nuevo presidente de la SEIO, Ignacio García Jurado, de-positó en mi su conanza de nuevo y me animó a continuar como editor al menos hasta que se asen-tara este proceso de evolución del Boletín, que no podemos decir que haya concluido ya, entre otras cosas porque debería seguir evolucionando con los tiempos.
Recientemente me he visto forzado a pedir mi relevo en la dirección del Boletín al haber asumi-do en mi universidad compromisos que me exigen una dedicación signicativa de tiempo y esfuerzo. Además pienso que hemos llegado a un momento de cierta madurez del Boletín que permite hacer un cambio no traumático en la dirección. Por otro lado se ha encontrado una persona muy adecuada pa-ra continuar con la dirección del Boletín, como es María del Carmen Pardo Llorente, a la que he de agradecer que haya aceptado tomar el testigo.
Al comienzo se hizo un esfuerzo importante por formar un equipo amplio de corresponsales repre-sentando el mapa estadístico nacional. En estos años han pasado por este puesto unas cincuenta personas. Se establecieron unas secciones del boletín claramente delimitadas, una de ellas de información general y el resto de artículos de divulgación dentro del ámbito de la Estadística y de la Investigación Operativa. Al frente de estas últimas secciones se nombraron editores asociados, que han sido piezas clave en este proceso de transformación. Quiero
ha-cer especial mención a todos ellos, que han dedicado un tiempo del que no disponían para sacar adelante este proyecto en su primera fase. Pienso que toda la SEIO debe especial gratitud a Félix Aparicio Pérez, Miguel Ángel Gómez Villegas, Montserrat Herra-dor Cansado, Ana Meca Martínez, Manuel Molina Fernández, María del Carmen Pardo Llorente, Jus-to PuerJus-to Albandoz, Gabriel Ruiz Garzón y Mayte Santos Martín. Gracias también a los que han si-do editores técnicos, María Tocasi-do y Javier Tolesi-do Melero. Un reconocimiento especial para María Je-sús Rios, que aunque nunca gura explícitamente en los ejemplares del Boletín, tiene una parte muy signicativa en la edición.
Se ha buscado que el editorial contara con una gran variedad de opiniones y puntos de vista me-diante la colaboración de personas de reconocido prestigio nacional e internacional. Buscar un autor para el editorial ha sido una de las tareas más in-teresantes para mi. Las respuestas han sido muy variadas y en muchos casos sorprendentes. Junto a la no respuesta de algunos potenciales autores, no necesariamente los de más alta reputación, he te-nido respuestas muy graticantes, en muchos casos de personas de gran prestigio, a los que no ha sido necesario insistir y presionar para que enviaran su editorial a tiempo. A todos ellos, gracias. Muy en particular desearía agradecer al numeroso cuadro de corresponsales, cuya colaboración ha sido funda-mental.
EDITORIAL
de InfoSEIO, que tiene un editor independiente del editor del Boletín y cuya periodicidad es mayor. A partir de ahora el Boletín propiamente dicho reco-gerá solamente artículos y se editará tres veces al año en lugar de las cuatro que se venía editando. De este modo se espera contribuir a una mejora en la calidad y revisión de los artículos. Además se ha incorporado una nueva sección de Historia y Ense-ñanza. Aprovecho para agradecer a la actual editora de InfoSEIO, Mayte Santos Martín, su ayuda y co-laboración en este proceso.
Se ha hecho también un esfuerzo importante de difusión del Boletín, tanto a nivel nacional como en la comunidad cientíca internacional. Durante es-tos años hemos procurado hacer llegar el Boletín a aquellas instituciones y personas que pudieran reci-birlo con interés. También se ha procurado buscar publicidad que ayudara a costear la edición en pa-pel a la vez que sirve como un medio más de difu-sión. A día de hoy el Boletín está referenciado en
MathScinet, Zentralblatt MATH, Current Index to Statistics y estamos a la espera de la evaluación a que está sometido en SCOPUS. En un futuro pró-ximo se incluirá en la Biblioteca Digital Española de Matemáticas.
Para concluir los agradecimientos, quisiera aña-dir a todos los autores de artículos, cuyo esfuerzo tiene doble mérito. Por una parte, el tiempo y es-fuerzo dedicados a componer un artículo adapta-do a los requerimientos del Boletín, que no son los habituales de las revistas en las que estamos acos-tumbrados a publicar, no es nada despreciable. Por otro lado tiene especial reconocimiento por el esca-so valor que en proceesca-sos de evaluación de la calidad se da a este tipo de publicaciones. He de acabar agradeciendo a los socios que de una manera u otra han valorado el trabajo que hemos realizado y con frecuencia así me lo han transmitido.
EL RINCÓN DEL PRESIDENTE
EL RINCÓN DEL PRESIDENTE
Ignacio García Jurado
Departamento de Estadística e Investigación Operativa Universidad de Santiago de Compostela
Este número del boletín será el último en el que Jesús López Fidalgo actúe como editor y, con tal motivo, quiero agradecerle desde este rincón, que él mismo inventó, su excelente trabajo. Jesús puso en marcha un proceso de renovación que ha hecho evo-lucionar al boletín en la dirección correcta y lo ha transformado en la revista de alta divulgación que es hoy en día. Este proceso lo retomará la nueva editora, María del Carmen Pardo, a la que deseo el mayor de los éxitos en esta nueva etapa y a la que agradezco su entusiasmo y disposición.
También quiero recordar al profesor Sixto Ríos, que ha fallecido recientemente. Aunque casi no lo traté, conozco bien la enorme importancia que su gura ha tenido en el desarrollo de la estadística y la investigación operativa en España. Así pues, de-seo reconocer desde aquí su labor, y mandarle un fuerte abrazo a toda su familia, especialmente a su
hija María Jesús, con la que he colaborado en mu-chas ocasiones en los últimos años y que lleva tanto tiempo trabajando por la SEIO.
ARTÍCULOS DE ESTADÍSTICA
1. ARTÍCULOS DE ESTADÍSTICA
PROBABILISTIC VALUATION OF CERTAIN UNIT-LINKED
CONTRACTS
Javier Villarroel∗
Facultad de Ciencias, Plaza Merced, 37008 Salamanca Universidad de Salamanca, Spain
Abstract
We consider the fair prize of insurance contracts with benet received either at the insurer's demise or at maturity. Explicit formulas are given for a Brennan&Schwartz contract with benet
contingent on decease.
Keywords: Risk-neutral fair-price, unit-linked insurance contracts, martingale probability.
1.
Introduction
A unit-linked insurance contract is a life insur-ance product where the benet depends upon the value of some reference stock which is traded in some associated market. Valuation of these prod-ucts is a natural area for probabilistic and statisti-cal applications. Even though not so widespread as that of pricing purely nancial products, this topic is becoming a classical one in the actuarial litera-ture; it was rst discussed by Brennan &Schwartz
(1976) and Boyle & Schwartz (1977). See also
Bacinello & Ortu (1993), Aase & Persson(1994),
Ekern & Persson (1996), Boyle & Hardy (1997),
Moeller (2001) and Bacinello (2005). We remark that the interplay between probability theory on the one hand, and insurance theory on the other, has been recognized for a long time (see for example Li and Ma, 2008). However, the problem of prizing in-surance contracts linked to stocks considered here goes a step beyond, requiring new ideas and tech-niques as it involves actuarial considerations as well as nancial ones.
Two sources of randomness are intrinsically as-sociated to any probabilistic model that aims to de-scribe these products. The rst stems from the un-certainty in mortality. To model this, letτ: ¯Ω→R
be the random time at which decease occurs for a given individual aged dat time 0. Mathematically,
τ is dened on a probability space ( ¯Ω,G¯,P¯). Under
natural assumptions the "life" conditional
distri-bution function (the survival function Tˆpt1+d) and conditional densityhread
ˆ
Tpt1+d≡P¯
³
τ > T|τ > t1
´
=e−
RT
t1µ(s+d;s)ds
(1.1) and
h(T) =Tˆ pt1+d µ(T+d;T) (1.2) where µ(t1 +d, t) is the mortality intensity and
ˆ
T ≡T−t1>0.
The second source of uncertainty arises from the random nature of the stock markets. Here we con-sider a simple model of nancial market consist-ing of two securities: a "savconsist-ings account" whose valueBt at timet evolves via Bt=B0ert, wherer
is the (constant) instantaneous interest rate of the market. The second instrument in the market, to which the insurance policy is linked, is a given stock whose price at time t, Xt, varies according to a
denite stochastic dynamics. The prototype model for stocks-price evolution after the seminal work of Black and Scholes (1973) and Merton (1973) as-sumes that Xt evolves via the Itô's stochastic
dif-ferential equation
dXt=κXtdt+σXtdWt (1.3)
Hereκis the mean return rate,σthe stock's
volatil-ity whileWtis a Brownian motion on a probability
space (Ω,G,P), the "real world" probability. Note
that we assume thatr, κandσare constants.
ARTÍCULOS DE ESTADÍSTICA
We suppose that the contract considered here is "written" at a certain time t1 and will expire
or "mature" at a time T > t1. At maturity T
the contract holder is entitled to a benet denoted by Ψ1)T where Ψ1)T = Ψ1)(T;X
s, t1 ≤ s ≤ T) is
a functional of the future evolution of the stock up to maturity time. However, if the insurer's demise happens at a time τ before maturity, then
the policy entitles the beneciaries to a payment
Ψ2)τ at the decease time. (This situation
corre-sponds to "endowment insurance contracts"-see sec-tion 3.2 below- By contrast, for "pure endowment contracts", benet is received only at maturity). Let ∆ be the demise time or maturity, whichever
comes rst: ∆ = min{T, τ}. Given the benet
functionΨ∆ ≡Ψ1)T1{τ≥T}+ Ψ2)τ 1{t1≤τ <T}, we de-termine in this paper explicit formulas for the fair priceυt1 required by the insurance rm at time t1 to hedge the exposure to the evolution of the risky asset i.e., we determine the mapΨ∆→υt1.
2.
Contract characteristics and
valuation
In a unit-linked contract the premium vt1 paid at time t1 is invested in a stock. LetXt,0≤t≤T
be the value at time t of an unit of the stock and
let Ft≡ σ¡Xs,0 ≤ s≤ t¢ be the ltration
gener-ated by the stock, which contains all information on past history and takeG ≡ F∞. We shall also
as-sume that our market is ecient, i.e., the existence of the Harrison and Pliska (1981) risk-neutral prob-abilityP∗ on(Ω,F∞) under which relative prices1
of all nancial productsvt′ ≡vt/Btare martingales2
with respect to the history of the process up to time
t. No further reference will be made to the
origi-nal, real world probability, so to ease notation we shall drop the symbol∗ and denote the martingale
probability P∗ simply asP≡P∗.
We assume that the risk stemming from the market has no inuence on the mortality risk. Thus, we can assume independence of the ltrations
Ft1,F¯t1 ≡σ
³
1{τ >s},0≤s≤t1
´
.
LetE ≡ EPׯP denote the expectation with
re-spect to the product measureP×P¯,EPexpectation respect to the probability measure P and so forth.
We next note that the price process must satisfy:
(i) lim
t1↑T
υt1= Ψ
1)
T. (2.1)
(ii) υ′t1 =E
³ υ′t
¯ ¯
¯Ft1∨F¯t1
´
or
υt1e
−rt1 =e−rtE
³ υt
¯ ¯
¯Ft1∨F¯t1
´
Ft1≤t≤T. (2.2)
(i) states that we "pay just what we receive" if contract matures right after it is written. (ii) is the martingale property, alluded to above. Using Doob's optional stopping theorem it can be ex-tended to random times3. We also require property (i) to hold if T is replaced by the random timeτ.
Hence
υt′1 =E
³ υ∆′
¯ ¯
¯Ft1∨F¯t1
´
=E³Ψ′∆
¯ ¯
¯Ft1∨F¯t1
´
=
E³Ψ′T1)1{τ≥T}+ Ψ′τ2)1{t1≤τ <T}
¯ ¯
¯Ft1∨F¯t1
´
=
e−rTE³Ψ1)T1{τ≥T}
¯ ¯
¯Ft1∨F¯t1
´
+
E³Ψ2)
τe−rτ1{t1≤τ <T}
¯ ¯
¯Ft1∨F¯t1
´
(2.3)
Recalling that Ft1,F¯t1 are independent σ− elds we have
E³Ψ1)T1{τ≥T}
¯ ¯
¯Ft1∨F¯t1
´
=
E¯P³1{τ≥T}
¯ ¯ ¯F¯t1
´
EP³Ψ1)T¯¯ ¯Ft1
´
=
ˆ
Tpt1+d E P³Ψ1)
T
¯ ¯ ¯Ft1
´
. (2.4)
Similarly, using the tower property for tional expectations we have in terms of the condi-tional densityhofτ (see eq. (1.1))
E³1{t1≤τ <T}Ψ
2)
τe−rτ
¯ ¯
¯Ft1∨F¯t1
´
=
EhE³1{t1≤τ <T}Ψ
2)
τe−rτ
¯ ¯
¯Ft1∨F¯t1, τ
´¯ ¯
¯Ft1∨F¯t1
i
=
E³ Z T
t1
h(s)e−rsΨ2)sds
¯ ¯
¯Ft1∨F¯t1
´
=
EP³ Z T
t1
h(s)e−rsΨ2)sds
¯ ¯ ¯Ft1
´
. (2.5)
1similarly, the relative benetΨ′
t≡Ψt/Btcompares our benet with that investing the money in a savings account.
2It implies that one can not expect a better deal by delaying the "signature" of the contract to the future. 3Note that the optional stopping theorem can be applied since¯P(∆<∞) = 1,EP
³
sup
0≤s≤T
Ψis)
´
ARTÍCULOS DE ESTADÍSTICA
Thus the risk-neutral fair-price at time t1 is
made up of two terms, in correspondence with the benets at maturity or at decease:
vt1 ≡v(T|t1, x) =v
1)
t1 +v
2)
t1 (2.6)
where
vt1)1 =Tˆpt1+de
−r(T−t1)EP
³
Ψ1)T¯¯ ¯Ft1
´
, (2.7)
vt2)1 ≡E P³
Z T
t1
h(s)e−r(s−t1)Ψ2)
sds
¯ ¯ ¯Ft1
´
. (2.8)
We shall nd it convenient to use the notation
v(T|t1, Xt1) ≡ vt1 to stress that vt1 depends not only on the "starting" values of time and of stock (t1andXt1) but also on the maturity timeT.
In a generic case, explicit evaluation ofvt1)1 and, mainly, ofv2)t1 given by (2.8) can be a dicult mat-ter. The case when Ψ2)τ can be represented as
Ψ2)τ = Ψ2(Xτ)in terms of a given increasing
func-tion Ψ2 : R → R is of particular interest in
ap-plications; further, in this case Eq. (2.8) can be simplied further since the Markovian nature ofXt
yields
v2)t1 =
hZ Tˆ
0
h(s+t1)
Bs E
P
x
¡
Ψ2)s
¢ dsi
x=Xt1
. (2.9)
For guaranteed unit-linked contracts the bene-t abene-t mabene-turibene-ty depends on bene-the value of bene-the asso-ciated stock but there is a minimum guaranteed amount if the stock price falls below a xed level; this can be taken to correspond to the capital ac-crued at a xed interest rateδ, the "technical rate".
The simplest example corresponds to a linear de-pendence on X in the benet: suppose that both
Ψ1∆,2) = X∆+Xt1
¡
eδ(∆−t1)−1¢, say; here, con-tingent on an insurance event happening (maturity
∆ = T or death ∆ = τ) the insured receives the
stock plus the interest accrued with rateδ. By
sub-stitution in eqs. (2.7) and (2.8) and using thatX′ t
is also a martingale the fair price is found in explicit way as
v1)t1 =Tˆpt1+d Xt1
³
1 +Bt1
BT
¡
eδTˆ−1¢´ ,
vt2)1 = Xt1
³
1−Tˆpt1+d+
Z T
t1
h(s)Bt1
Bs
¡ eδ(s−t1)
−1¢
ds´. (2.10)
When the mortality rateµis constant one recovers
the result of Shen & Xu (2005). A case of more
interest, non-linear inXT, is considered in the next
section.
3.
Valuation of endowment insurance
contracts of Brennan
&
Schwartz
type
We rst review the case considered by Brennan
& Schwartz (1976) and Boyle & Schwartz (1977)
whereΨ1)T = max{XT, Xt1e
δTˆ
},Ψ2)τ = 0. Here, the
insured receives at maturity the value of the associ-ated stock; further, the initial capital, accrued at a xed interest rateδ, is guaranteed, in case the stock
price does not reach this level. In case of decease before maturity, beneciaries are not entitled to any extra benet.
3.1. Pure endowment case
Evaluation of the premium involves determining the corresponding expectation given by eq. (2.7); it can be obtained in closed form, as follows. Recall rst that Girsanov's theorem implies that the evolu-tion ofXtunder the martingale probability is given
by Eq. (1.1) where the drift κ is replaced by the
instantaneous interest rate r of the market. The
solution that att1equals Xt1 is
Xt=Xt1e
σ(Wt−Wt
1)+
³
r−σ2
2
´
(t−t1)Law
=
Xt1e
σWtˆ+qtˆ, t
1≤t≤T
where we use that independence of Brownian in-crements implies that Wt−Wt1
Law
∼ Wtˆ and
de-ne q ≡ r− σ2
2,ˆt ≡ t−t1. Say Xt1 = x. Using the Markovian nature of the benet and the well known Gaussian distribution of Brownian motion
Wt∼ N(0,√t)we obtain
EP³Ψ1)T
¯ ¯ ¯Ft1
´
=
EP³Xt1max{e
σWTˆ+qtˆ, eδTˆ}|X
t1 =x
´
=
Z x
p
2πTˆ
e−y2/(2 ˆT) max{eqTˆ+σy, eδTˆ}dy=
x³erTˆΦ¡ m+
p
ˆ
T) +eδTˆΦ(−m−
p
ˆ
ARTÍCULOS DE ESTADÍSTICA
where
m± ≡σrˆ±σ2, rˆ≡r−δ, Tˆ≡T−t (3.2)
andΦis the standard normal distribution function
Φ(x) =
Z x
−∞
e−z2/2√dz
2π. (3.3)
Hencevt1)1 ≡v
1)(T
|t1, x) =
ˆ
Tpt1+dx
³
Φ¡ m+
p
ˆ
T) +e−rˆTˆΦ(−m−pTˆ)´. (3.4)
The limit behavior for long values of Tˆ is
interest-ing; depending on whether ˆr >0, ˆr = 0 or r <ˆ 0
three dierent possibilities are found: v1)(T |t1, x)
tends, respectively, to eitherTˆpt1+dx≡v
1)(T |T, x),
to 2Tˆpt1+dxor to ∞. The result is easy to under-stand. The higher the guaranteed rate the more interesting the contract becomes. Further, when δ
is higher than the market rate r, the relative
bene-t bene-tends bene-to∞asymptotically in time and so it does the fair price.
3.2. Endowment insurance contract
In the sequel we study valuation for a case that generalizes the result of Brennan & Schwartz to
a contract paying Ψ1)T = max{XT, Xt1e
δ(T−t1)} at expiry or Ψ2)τ = max{Xτ, Xt1e
δ(τ−t1)
} should
de-cease occur before maturity. It turns out that with this demise benet an analytical, exact formula for the fair price can be also derived if an exponen-tial distribution is assumed for the decease rate:
h(t) = µe−µ(t−t1) where the parameter µ−1 is the mean life. In this case, using (2.8) and (3.1) we nd
vt2)1 ≡v
2)(T
|t1, x) =
xµ Z Tˆ
0
³
e−µsΦ(m+√s) +e−(µ+ˆr)sΦ(−m−√s)
´ ds
(3.5) and hence it involves the integral
I≡ Z Tˆ
0
e−αsΦ(m√s)ds (3.6)
By interchanging integrals we nd
I= 1
2α h
1−√ |m|
m2+ 2α+
2|m| √
m2+ 2αΦ
¡|m| m
q
(m2+ 2α) ˆT¢
−
2e−αTˆΦ¡
mpTˆ¢i
. (3.7)
Thus, the demise contribution to the price is
vt2)1 =
x
2
h
1−m√+
η +
2m+ √η Φ¡
q ηTˆ¢
−
2e−µTˆΦ¡ m+
p
ˆ
T¢i
+ xµ 2(µ+ ˆr)
h
1−|m√−η|
+2|√m−|
η Φ
¡
−
q
ηTˆsignm−¢−
−2e−(µ+ˆr) ˆTΦ¡
−m−pTˆ¢i (3.8)
whereη≡m2
++2µandm±are dened in Eq. (3.2).
The premium simplies when the insurance com-pany is committed to pay a technical interest rateδ
satisfyingδ=r. In this casem±=±σ2, η=
σ2
4 +2µ
and the full pricevt1≡v
1)
t1+v
2)
t1 for such a contract reads
vt1=x
h
1 +√σ
η ³
Φ¡q ηTˆ¢
−12´i. (3.9)
In Fig. 1 we plotvt1 ≡v(T|t1, x) =v(T−t1|0, x) as a function ofT −t1. Notice how it starts from
vt1 =xwhen T −t1 = 0 and then it increases to-wardsx³1 + σ
2√η
´ . 5 5.5 6 6.5 7 7.5
0 10 20 30 40 50 60 70
[image:11.595.326.530.185.304.2]z
Figure 1: Fair price as a function of time to ma-turity given in years corresponding to a constant annual interest rate r = 4.5%. Other parameters
ARTÍCULOS DE ESTADÍSTICA
Acknowledgement
We acknowledge support from MEC under con-tract No. FIS2005-01375.
References
[1] Aase, K. &Persson, S.A. (1994). Pricing
unit-linked life insurance policies. Scand. Act. J., 1, 26-52.
[2] Bacinello, A.R. & Ortu, F. (1993). Pricing of
unit-linked life insurance with endogenous mini-mum guarantees. Ins. Math. Econ., 12, 245-257.
[3] Bacinello, A.R. (2005). Endogenous model of surrender conditions in equity-linked life insur-ance, Ins. Math. Econ., 37, 270- 296.
[4] Black, F. &Scholes, M. (1973). The pricing of
options and corporate liabilities, J. Polit. Econ., 81, 637-659.
[5] Boyle, P.P. & Schwartz, E.S. (1977).
Equilib-rium Prices of Guarantees under Equity-Linked Contracts, J. Risk Ins., 44, 639-660.
[6] Boyle, P.P. & Hardy, M.R. (1997). Reserving
for maturity guarantees: two approaches. Ins. Math. Econ., 21, 113-127.
[7] Brennan, M.J. & Schwartz, E.S. (1976). The
Pricing of Equity-Linked Life Insurance Policies with an Asset Value Guarantee, J. Fin. Econ., 3, 195-213.
[8] Ekern, S. & Persson, S.A. (1996). Exotic
unit-linked life insurance contracts. Geneva Papers Risk Ins. Th. 21, 35-63.
[9] Harrison, J.M.&Pliska, S. (1981). Stoch. Proc.
Appl. 11 215260.
[10] Merton, R.C. (1973). J. Econ. Manag. Sci., 4, 141-183.
[11] Moeller, T. (2001). Hedging equity-linked life insurance contracts, North Amer. Act. J., 5(2), 79-95.
[12] Shen, W. & Xu, H. (2005). The valuation of
unit-linked policies with or without surrender options, Ins. Math. Econ., 36, 79- 92.
[13] Li, J.&Ma, S. (2008). Some Probability
Appli-cations to the Risk Analysis in Insurance The-ory, Boletín SEIO, 24 (1), 20-24
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
2. ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
MECHANISM DESIGN IN SCHOOL CHOICE:
SOME LESSONS IN A NUTSHELL
Flip Klijn∗
Institute for Economic Analysis (CSIC) Campus UAB, Bellaterra (Barcelona)
Abstract
This paper deals with school choice as an application of matching theory. Although the use of matching theory for the design and study of school choice mechanisms is rather recent, some of its tools were already successfully employed in several other markets, the most noticeable being the labor market for medical doctors in the US. I rst briey describe the problems that some US school districts had, and why and how economic engineering has contributed a lot to the improvement of school choice programs. Then, I will review and interpret a selection of the most recent developments and results.
Keywords: school choice, matching, stability, eciency, strategy-proofness, preference revela-tion, indierences
1.
Introduction
A common feature of many markets is their bi-lateral structure and the need to match agents from one side of the market to the other side of the mar-ket. An important instance is the assignment of students to colleges, or workers to rms.
When David Gale and Lloyd Shapley published their elegant paper back in 1962 they probably did not imagine the stream of literature that would fol-low.1 They described a model in which students have to be matched to colleges, and where each student and each college has preferences over the other side of the market. They proposed an al-gorithm that always produces a matching (assign-ment) that is stable in the following sense: each agent obtains an acceptable mate, and no pair of agents who are not matched to one another would prefer to be. Their algorithm is referred to as the
deferred acceptance algorithm, the reason being that (loosely speaking) its two key elements are the proposals from either side of the market and the deferred acceptance by the other side of the mar-ket.
Gale and Shapley's deferred acceptance algo-rithm has turned out to be key in the design of many markets. In fact, even before Gale and Shap-ley's paper appeared in the American Mathematical Monthly very similar ideas were already incorpo-rated in the design of the rst centralized market for medical doctors in the US. More recently, vari-ants of the deferred acceptance algorithms were im-plemented after the redesign of school choice sys-tems in Boston and New York.2 Every now and then variants of the deferred acceptance algorithm are independently rediscovered and implemented to solve market failures.3
In their pioneering paper, Abdulkadiro§lu and ∗Corresponding Author. E-mail: [email protected]. I thank Bettina Klaus and Ana Meca for their comments on an earlier version of this paper. Any remaining errors are mine. Financial support through Plan Nacional I+D+I (SEJ2005-01690), the Consolider-Ingenio 2010 (CSD2006-00016) program, and the Barcelona Economics Program of XREA is grate-fully acknowledged.
1For an overview until 1989, see Guseld and Irving (1989) and Roth and Sotomayor (1990). Al Roth's game theory, experimental economics, and market design page has an updated bibliography.
2See Abdulkadiro§lu, Pathak, and Roth (2005) and Abdulkadiro§lu, Pathak, Roth, and Sönmez (2005) for reports on the redesign of the New York and Boston school matches, respectively.
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
Sönmez (2003) discussed some of the problems that several US school districts were experiencing and proposed two student assignment mechanisms. One mechanism they proposed is directly based on Gale and Shapley's deferred acceptance algorithm. The other mechanism is based on Gale's Top Trading Cycles algorithm, which is rst described by Shap-ley and Scarf (1974) in the context of so-called hous-ing markets. Each of the two mechanisms has a desirable feature that the other mechanism fails to satisfy. The Gale-Shapley mechanism is stable, but not (Pareto-)ecient, i.e., there are situations in which the mechanism yields a matching that can be improved upon for some students without hurt-ing the others. The Top Tradhurt-ing Cycles mechanism on the other hand is ecient, but not stable.
A rst question of course is why certain school choice districts were experiencing problems until very recently. This is what I discuss in Section 2. In Section 3, I recall Abdulkadiro§lu and Sönmez's (2003) model of school choice and give a descrip-tion of the mechanisms involved. Next, in Secdescrip-tion 4, I address some important questions and compli-cations for the full application of the theory to real school choice problems. I review and interpret a selection of the most recent developments and re-sults.4 Section 5 concludes.
2.
Why mechanism design in school
choice?
The key issue of school choice is providing the parents of a child the possibility to have a say in the assignment of their child to a public school. In their study of school choice plans in the US, Ab-dulkadiro§lu and Sönmez (2003) mentioned two ba-sic shortcomings of several school choice programs until recently. First, it turned out that many school districts simply did not have rigorous procedures. (In fact, until a decade ago children were assigned to public schools without taking into account the preferences of the parents at all.) This very of-ten led to evasive action by the students and their parents that took its ultimate form in court cases, which were very often won by the parents, making the procedure even more vulnerable to future at-tacks. Second, the school choice programs that did have explicit procedures suered from serious
short-comings. A representative case is the mechanism that was used in the Boston school district. Since seats in schools are a scarce resource it is generally not possible to assign each student to his most pre-ferred school. Therefore, apart from the students' preferences the Boston (and other) school district authorities took into account the priorities of stu-dents for schools. The priority of a student for a particular school typically is determined by factors as living in the walk zone of the school, siblings already attending the school, etc.
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
latter two mechanisms over the Boston mechanism. Their data shows that the Boston mechanism in-duces massive preference manipulation, and, as a consequence, signicant welfare loss.
Abdulkadiro§lu, Pathak, Roth, and Sönmez (2006) provided empirical evidence that under the Boston mechanism there are dierent levels of so-phistication of play. On the one hand, there are parents groups that discuss how to submit prefer-ences strategically. On the other hand, there is also a large number of parents that do not strategize (well). As a consequence, the rst groups of par-ents systematically obtain better results than the latter. This evidence was one of the reasons why the Boston school district authorities replaced the Boston mechanism by the Gale-Shapley mechanism. Abdulkadiro§lu, Pathak, Roth, and Sönmez (2005) report on some further design considerations.
Around the same time, Atila Abdulkadiro§lu, Parag Pathak, Alvin Roth, and Tayfun Sönmez as-sisted the New York City department in the design of a new student assignment mechanism. New York City has the largest public school system in the US and each year there are about 90,000 entering stu-dents. Abdulkadiro§lu, Pathak, and Roth (2005) pointed out that the matching system that was in use suered from three problems. First, there were not enough rounds to allocate all students, and as a consequence, about 30,000 students were assigned to a school that was not on their list. Second, the parents had to strategize (very much for the same reason as in Boston). Third, schools acted as strate-gic agents by withholding some of their capacity. This last point already hints at what was concluded after the initial discussions in the redesign process: the New York City schools are a two-sided mar-ket. The experience and the success of the redesign of a very similar two-sided market, where Amer-ican physicians are assigned to hospitals through the Gale-Shapley mechanism, became very useful (see Roth and Peranson, 1999 and Roth, 2002 for details). It was decided to adapt the Gale-Shapley mechanism to the particular needs and characteris-tics of the New York City school match. Abdulka-diro§lu, Pathak, and Roth (2005) report on the rst year of operation of the new mechanism. In con-trast to the previous mechanism, only about 3,000 were assigned to schools they did not list. One (but not the only) reason is that in the new mechanism
students are allowed to rank 12 schools (instead of the previous maximum of 5). In Section 4.2, I will discuss this restriction on the length of submittable preference lists in more detail.
Further theoretical, experimental, and empirical studies have disentangled some of the open prob-lems and have provided additional insights in the design of student assignment mechanisms. In the next session I will rst recall the basic model and give a description of the three mechanisms. Subse-quently I will focus on some concerns that mostly deal with the gap between the simplications in-herent to the modeling and real-life school choice procedures.
3.
The model
Following Abdulkadiro§lu and Sönmez (2003), a school choice problem is dened by a set of schools and a set of students, each of which has to be as-signed a seat at not more than one of the schools. Each student is assumed to have strict preferences over the schools and the option of remaining unas-signed. Each school is endowed with a strict priority ordering over the students and a xed capacity of seats. Formally, a school choice problem is a 5-tuple
(I, S, q, P, f)that consists of
1. a set of students I={i1, . . . , in},
2. a set of schools S={s1, . . . , sm},
3. a capacity vectorq= (qs1, . . . , qsm),
4. a prole of strict student preferences P = (Pi1, . . . , Pin), and
5. a strict priority structure of the schools over the studentsf = (fs1, . . . , fsm).
We denote byiandsa generic student and a generic
school, respectively.
The preference relationPi of student i is a
lin-ear order overS∪ {i}, wherei denotes his outside
option (e.g., enrolling in a private school). Student
i prefers school s to school s′ if sP
is′. School s
is acceptable to i if sPii. Let Ri denote the weak
preference relation associated with the preference relationPi.
The priority ordering fs of school s assigns
ranks to students according to their priority for schools. The rank of studentifor schoolsisfs(i).
Then,fs(i)< fs(j)means that studentihas higher
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
Throughout the paper the set of studentsIand
the set of schools S do not vary. Hence, a school
choice problem is given by a triple(P, f, q), or
sim-ply by P when no confusion is possible.
School choice is closely related to the college admissions model (Gale and Shapley, 1962). The only but key dierence between the two models is that in school choice schools are mere objects to be consumed by students, whereas in the college admissions model (or more generally, in two-sided matching) both sides of the market are agents with preferences over the other side. In other words, a college admissions problem is given by 14 above and 5' below:
5'. a prole of strict school preferences PS =
(Ps1, . . . , Psm),
where Ps denotes the strict preference relation of
schools∈S over the students.
Priority orderings in school choice can be rein-terpreted as school preferences in the college admis-sions model. Therefore, many results or concepts for the college admissions model have their natu-ral counterpart for school choice.5 In particular, an outcome of a school choice or college admissions problem is a matching µ:I∪S→2I
∪Ssuch that
for any i∈I and anys∈S,
• µ(i)∈S∪ {i},
• µ(s)∈2I,
• µ(i) =sif and only if i∈µ(s), and
• |µ(s)| ≤qs.
Fori∈I, ifµ(i) =s∈S then studentiis assigned
a seat at schoolsunderµ. Ifµ(i) =ithen student i is unassigned underµ.
A key property of matchings in the two-sided matching literature that does not lose its impor-tance in school choice is stability. Informally, a matching is stable if, for any student, all the schools he prefers to the one he is assigned to have ex-hausted their capacity with students that have higher priority. Formally, let P be a school choice
problem. A matching µis stable if
• it is individually rational, i.e., for alli∈I, µ(i)Rii,
• it is non wasteful (Balinski and
Sön-mez, 1999), i.e., for all i ∈ I and all s ∈ S, sPiµ(i)implies|µ(s)|=qs, and
• there is no justied envy, i.e., for alli, j∈I
with µ(j) = s ∈ S, sPiµ(i) implies fs(j) <
fs(i).
The set of stable matchings is denoted byS(P).
Another desirable property for a matching is Pareto-eciency. In the context of school choice, the schools are mere objects. Therefore, to deter-mine whether a matching is Pareto-ecient we only take into account students' welfare. A matching µ′
Pareto dominates a matchingµif all students
pre-fer µ′ to µ and there is at least one student that
strictly prefersµ′ to µ. Formally, µ′ Pareto
domi-natesµifµ′(i)R
iµ(i)for alli∈I, andµ′(i′)Pi′µ(i′)
for some i′ ∈ I. A matching is Pareto-ecient if
it is not Pareto dominated by any other matching. We denote the set of Pareto-ecient matchings by
P E(P).
A (student assignment) mechanism systemati-cally selects a matching for each school choice prob-lem. A mechanism is stable (or Pareto-ecient) if it always selects a stable (or Pareto-ecient) match-ing. A mechanismϕis manipulable by studentiat
problem P if there exists a preference relation P′ i
such thatϕ(P−i, Pi′)(i)Piϕ(P)(i). A mechanism is
strategy-proof if no student can ever manipulate it. In other words, a mechanism is strategy-proof if no student can ever benet by unilaterally misrepre-senting his preferences.6
3.1. The three mechanisms
The following concise description, which is taken from Calsamiglia et al. (2007), integrates the three student assignment mechanisms that I discussed earlier. It distinguishes between the students' and the schools' point of view. The reason is that in the eventual computations the three mechanisms only dier in the way a student is rejected by a school.
The Boston (β, BOS), Gale-Shapley (γ, GS),
and Top Trading Cycles (τ, TTC)
mecha-nisms:
Step 1: For each school, a priority ordering of students is determined (based on state and local laws/policies, etc.).
Step 2: Each student submits a preference ranking of the schools.
5See, for instance, Balinski and Sönmez (1999).
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
Step 3: The assignment of seats is obtained through an algorithm, as follows.
Round k, k ≥ 1 [students]: Each student that
has not been removed yet but is rejected in the previous round7 points to the next highest ranked school in his submitted list that has not been re-moved yet (if there is no such school then the stu-dent points to himself).
Roundk,k≥1 [schools, BOS]: Each school
as-signs seats one at a time to the students that point to it following its priority order. If the school capac-ity is or was attained, the school rejects any remain-ing students that point to it. If a student points to himself, he is assigned to himself. Any student that is assigned is removed.
The Boston algorithm terminates when all students have been removed.
Roundk,k≥1 [schools, GS]: Each school ten-tatively assigns seats one at a time to the students that point to it following its priority order. When the school capacity is attained the school rejects any remaining students that point to it. If a stu-dent points to himself, he is tentatively assigned to himself.
The Gale-Shapley algorithm terminates when no student is rejected. The tentative matching becomes nal.
Round k, k ≥ 1 [schools, TTC]: Each school
that has not been removed yet points to the stu-dent with highest priority among the stustu-dents that have not been removed yet. There is at least one cycle. If a student is in a cycle he is assigned a seat at the school he points to (or to himself if he is in a self-cycle). Students that are assigned a seat are removed. If a school is in a cycle then its number of vacant seats is decreased by 1. If a school has no longer vacant seats then it is removed.
The Top Trading Cycles algorithm terminates when all students or schools have been removed.
The Gale-Shapley and Top Trading Cycles mech-anisms are strategy-proof, but the Boston mecha-nism is not. The Gale-Shapley mechamecha-nism is also stable. In fact, it always generates the best stable matching for the students. However, it is not Pareto
ecient. In contrast, the Top Trading Cycles mech-anism is Pareto ecient but not stable. In fact, it is well-known that stability and eciency are in-compatible. That is, there is no mechanism that is both stable and ecient. The Boston mechanism is Pareto ecient, but since it is not strategy-proof, Pareto eciency is likely to be distorted in practice.
4.
Issues in the design of student
assignment mechanisms
Below I will discuss, in no particular order, some of the key issues that played a role in the design of student assignment mechanisms or that possibly will be relevant in future redesigns.
4.1. Indierence classes in the priority structure
An important question in the application of the-ory of school choice to real-life situations is the pres-ence of indierpres-ences in the priority structuref. In
practical situations there is only a limited number of relevant criteria that determine the priority of each student for a given school. Thus, it may happen that some students have exactly the same priority, i.e., there are distinct students i, j and a school s
such that fs(i) = fs(j). Then, instead of having
a strict priority list, a school's priority list typi-cally contains several indierence classes. From the school's point of view, all students in the same in-dierence class are indistinguishable. Clearly, this complication is relevant if (and only if) some stu-dents of the same indierence class compete for the same school seat.
A rst idea is to break the ties in order to get rid of the indierence classes and obtain a strict prior-ity structure. Next, one can apply either the Gale-Shapley or Top Trading Cycles mechanism. Re-garding the Top Trading Cycles mechanism, Pathak (2007) shows that it is insensitive to how ties are broken. The Gale-Shapley mechanism, however, is very much aected by the way the ties are broken. Erdil and Ergin (2008) show by means of an exam-ple that if we break ties in an arbitrary way, then it is possible that the stable matching induced by the Gale-Shapley mechanism is Pareto dominated by another stable matching. Gale and Shapley (1962) showed that this is never the case in their original setting without indierences.
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
Erdil and Ergin (2008) propose the following procedure to obtain a stable matching that is not Pareto dominated by any other stable matching. They rst introduce the concept of a stable im-provement cycle.
Denition 4.1. (Erdil and Ergin, 2008)
A matching µ admits a stable improvement
cy-cle if there is a cycy-cle of distinct students
hi1, . . . , in =: i0i (n ≥ 2) such that for any l =
0, . . . , n−1, µ(il+1)Pilµ(il) ∈ S and fµ(il+1)(il)
= min{fµ(il+1)(j) :j∈Iandµ(il+1)Pjµ(j)}. △ Loosely speaking, each studentiin a stable
im-provement cycle desires the school s to which the
next student in the cycle is assigned atµ, and in
ad-dition studentihas the highest priority (i.e., lowest
rank order) among all students that desire schools.
Given a stable improvement cyclehi1, . . . , in=:
i0i for a matching µ, one can construct a new
matching µ′ as follows,
µ′(j) :=
µ(j) ifj6∈ {i1, . . . , in},
µ(il+1) ifj=il for
some l= 0, . . . , n−1.
One easily veries that if µ is stable, then the
matchingµ′that results from satisfying the stable
improvement cycle is again a stable matching.
Theorem 4.1. (Erdil and Ergin, 2008)
Let µ be a stable matching. If µ is Pareto
domi-nated by another stable matching, then µ admits a
stable improvement cycle.
This result induces a simple algorithm to nd a matching µ∗ that is stable and constrained
e-cient. Here, constrained ecient means that there is no other stable matching that Pareto dominates
µ∗. (Of course, this does not discard the existence
of an unstable matching that Pareto dominatesµ∗.)
First, break the ties of the priority structure in an arbitrary way and apply the deferred acceptance algorithm to obtain a stable matching. Next, sat-isfy iteratively stable improvement cycles. Clearly, this algorithm terminates in a nite number of steps and by Theorem 4.1 the resulting matching is sta-ble and constrained ecient. In fact, Erdil and Ergin (2008) show that their algorithm has a re-markably small computational complexity.
Moover, Abdulkadiro§lu, Pathak, and Roth (2008) re-port that if the algorithm would have been applied to the preference data of the 2003-2004 New York City school match, then more than10%of the about 64.000 students involved would have been assigned
to a strictly preferred school, without hurting the other students.
Given that in practice the priority structure is not strict, why not immediately replace the Gale-Shapley mechanism by the algorithm proposed by Erdil and Ergin (2008)? A problem of the latter algorithm is that it cannot induce a strategy-proof mechanism. (Note that there is range of possibil-ities for such mechanism since the nal matching crucially depends on the tie-breaking.) In other words, unlike the Gale-Shapley mechanism, it does not make it a (weakly) dominant strategy to state one's true preferences. In fact, Erdil and Ergin (2008) proved the following impossibility result.
Theorem 4.2. (Erdil and Ergin, 2008)
There is no mechanism that is both strategy-proof and constrained ecient.
Abdulkadiro§lu, Pathak, and Roth (2008) fur-ther analyzed the impact of the presence of ties in the priority structure. A tie-breaker is a bijection
r : I → {1, . . . , n} and can be used to break ties at a school s by replacing its priority fs by fs′ as
follows: f′
s(i)< fs′(j)if and only if [fs(i)< fs(j)or
[fs(i) = fs(j) and rs(i) < rs(j)]]. A tie-breaking
rule is a collection of tie-breakers, one for each school. A single-tie breaking rule uses the same tie-breaker for all schools, a multiple-tie breaking rule may use dierent tie-breakers for dierent schools. Letγrdenote the mechanism that yields the
match-ing from the deferred acceptance algorithm, after breaking possible ties according tor.
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
Theorem 4.3. (Abdulkadiro§lu, Pathak, and Roth, 2008)
For any priority structure f and any school choice
problemP, ifµis constrained ecient then there is
a single-tie breaking rule rsuch that γr(P) =µ.
As has been pointed out before, if we use a tie-breaking rule and apply the deferred accep-tance algorithm then the resulting matchings need not be constrained ecient. Theorem 4.2 im-plies that Pareto improving upon these matchings comes at the price of losing strategy-proofness. Abdulkadiro§lu, Pathak, and Roth (2008) further strengthen this result as follows. A mechanism dominates another mechanism if the rst mecha-nism always gives a weakly better match to all stu-dents than the second mechanism, and for some school choice problem and for some student the rst mechanism gives a strictly better match than the second mechanism.
Theorem 4.4. (Abdulkadiro§lu, Pathak, and Roth, 2008)
For any tie-breaking rule r, there is no
strategy-proof mechanism that dominates γr.
4.2. Constrained school choice
Real-life school choice situations typically in-volve a large number of participants and a rela-tively small number of school programs. Parents are often asked to submit a preference list contain-ing only a limited number of schools.8 In other words, there is a constraint or quota on the number of schools that can be listed. This restriction is rea-son for concern: true preference revelation is (typ-ically) no longer an option. As a consequence, the Gale-Shapley and Top Trading Cycles mechanisms are no longer strategy-proof. Since the (desirable) properties of the two mechanisms are relative to the revealed preferences, it is far from clear what these properties mean in case the revealed preferences are not the true preferences. In the setting of con-strained school choice (i.e., school choice with a restriction on the length of submittable preference lists), it is likely that participants adopt strategic behavior. For instance, if a participant fears re-jection by his most preferred programs, it can be advantageous not to apply to these programs and
use instead its allowed application slots for less pre-ferred programs.
Manipulability
Pathak and Sönmez (2008b) develop a notion to compare mechanisms that are not strategy-proof based on the degree to which they encourage manip-ulation. Subsequently, they use their notion to com-pare several well-known mechanisms in the match-ing and auction literature. One specic case is the setting of constrained school choice where the Gale-Shapley and Top Trading Cycles mechanisms are not strategy-proof.
Pathak and Sönmez (2008b) call a mechanism
ψ weakly more manipulable than mechanism ϕ if
wheneverϕis manipulable, ψ is also manipulable,
even though the converse does not hold. Equiv-alently, ψ is weakly more manipulable than ϕ if
whenever truthtelling is a Nash equilibrium under
ψtruthtelling is a Nash equilibrium underϕas well.
Theorem 4.5. (Pathak and Sönmez, 2008b) The stronger the restriction on the length of submit-table preferences lists (i.e., the smaller the quota) the weakly more manipulable becomes the Gale-Shapley mechanism.
Theorem 4.6. (Pathak and Sönmez, 2008b) Let 1 ≤ k < m. If students can list at most k
schools, then the Boston mechanism is weakly more manipulable than the Gale-Shapley mechanism.
Pathak and Sönmez (2008b) consider also a sec-ond notion to compare manipulability of dierent mechanisms: a mechanismψ is strongly more
ma-nipulable than mechanism ϕ if at any prole R,
any student that can manipulateϕcan also
manip-ulate ψ, even though the converse does not hold.
Next, they show by means of an example that The-orem 4.6 cannot be strengthened through replace-ment of the rst notion by the second notion.
An interesting open problem is how the Top Trading Cycles mechanisms compares to the other two mechanisms and whether it becomes more ma-nipulable as the restriction on the length of submit-table preferences becomes more stringent.
Stability and eciency
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
ducing a preference revelation game where students can only declare up to a xed number (the quota) of schools to be acceptable. Each possible quota, from 1 up to the total number of schools, together with a student assignment mechanism induces a strategic quota-game. Since the presence of the quota elim-inates the existence of a dominant strategy when the mechanism at hand is the Gale-Shapley and Top Trading Cycles mechanisms, we focus on the Nash equilibria of the quota-games.
Fix the priority orderingf and the capacitiesq.
Given a prole of preferences P = (Pi1, . . . , Pin),
a quota k with 1 ≤ k ≤ m, and a mechanism ϕ, the induced quota-game Γϕ(P, k) is a triple
hI,Q(k)I, P
i. The strategy set of each player
(stu-dent) is the set of preference lists with at most k
acceptable schools which is denoted byQ(k).
Out-comes of the game are evaluated through the true preferences P. Let Eϕ(P, k) and
Oϕ(P, k) denote
the set of Nash equilibria and Nash equilibrium outcomes, respectively. Haeringer and Klijn (2007) show that for all three mechanisms discussed above there are Nash equilibria in pure strategies.
Below I summarize the results regarding the stability of the equilibrium outcomes, and sub-sequently comment on eciency. The following benchmark is, given the negative empirical evidence regarding the Boston mechanism, quite surprising.
Theorem 4.7. (Ergin and Sönmez, 2006 and Haeringer and Klijn, 2007)9
For any quota k and any school choice problem P,
the game Γβ(P, k) implementsS(P) in Nash
equi-libria, i.e., Oβ(P, k) =S(P).
Whenk= 1 the deferred acceptance algorithm
consists of only one step, which moreover coincides with the (then also unique step) of the Boston al-gorithm, i.e., Γγ(P,1) = Γβ(P,1) =S(P). In case
k6= 1, it is easy to see that under the Gale-Shapley
mechanism each stable matching can still be ob-tained as an equilibrium outcome. However, as Ex-ample 3 in Sotomayor (1998) already showed, not all equilibrium outcomes need to be stable. There-fore, an important question is to nd out whether and when we can guarantee a stable outcome. One possible interpretation of when is to nd necessary and sucient conditions on the priority structure.
Fors∈S andi∈I, we denote byUf
s(i)the set
of students that have higher priority than studenti
for schools, i.e.,Uf
s(i) ={j∈I:fs(j)< fs(i)}.
Denition 4.2. Ergin-Acyclicity (Ergin, 2002) Given a priority structuref, an Ergin-cycle is
con-stituted of distincts, s′ ∈Sandi, j, l∈Isuch that
the following two conditions are satised:
Ergin-cycle condition: fs(i) < fs(j) < fs(l) and
fs′(l)< fs′(i)and
ec-scarcity condition: there exist (possibly empty and) disjoint setsIs, Is′ ⊆I\{i, j, l}such thatIs⊆ Uf
s(j),Is′ ⊆Usf′(i),|Is|=qs−1, and|Is′|=qs′−1.
A priority structure is acyclic if no
Ergin-cycles exist. △
Theorem 4.8. (Haeringer and Klijn, 2007) Let k 6= 1. Then, f is an Ergin-acyclic priority
structure if and only if for any school choice prob-lemP,Oγ(P, k) =S(P).
Denition 4.3. Kesten-Acyclicity (Kesten, 2006) Given a priority structuref, a Kesten-cycle is
con-stituted of distincts, s′ ∈Sandi, j, l∈Isuch that
the following two conditions are satised:
Kesten-cycle condition fs(i)< fs(j)< fs(l) and
fs′(l)< fs′(i), fs′(j)and
kc-scarcity condition there exists a (possibly empty) set Is ⊆ I\{i, j, l} with Is ⊆ Usf(i) ∪
h Uf
s(j)\U f s′(l)
i
and|Is|=qs−1.
A priority structure is acyclic if no
Kesten-cycles exist. △
Kesten-acyclicity implies Ergin-acyclicity (Lemma 1, Kesten, 2006). It is easy to check that the reverse holds if all schools have one seat.
Theorem 4.9. (Haeringer and Klijn, 2007) Let 1 ≤ k ≤ m. Then, f is a Kesten-acyclic
pri-ority structure if and only if for any school choice problemP,Oτ(P, k) =S(P).
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
the supposedly superior mechanisms may yield un-fair assignments in the sense that there are stu-dents that prefer a seat that is occupied by a lower priority student.
Regarding eciency, Haeringer and Klijn (2007) identify similar (but new) acyclicity conditions and show that they are necessary and sucient to guar-antee the eciency of the three mechanisms. Qual-itatively, the two (main) dierences are that (i) the Boston and Gale-Shapley mechanisms perform equally well (or bad), and (ii) the Top Trading Cy-cles mechanism performs better than the other two mechanisms.
As a closing remark, the acyclicity conditions that guarantee stability or Pareto-eciency are very limiting, and unlikely to hold in practice. This is a clear call for unrestricting preference revelation, i.e., setting k =m. Of course the negative results
above still apply for k = m but it is likely that
in this case students use their (weakly) dominant strategy, namely submitting their true preferences. Recall that in the unconstrained setting the Gale-Shapley and Top Trading Cycles mechanisms yield a stable and ecient matching, respectively. The choice for either of the two mechanisms then de-pends on whatever has the highest priority for the policy makers: stability or eciency.
4.3. Manipulation by schools
The formal model of school choice only allows the students to act strategically. More precisely, the priorities and capacities of the schools are de-termined by law and there is no room for strate-gizing. Nevertheless, Abdulkadiro§lu, Pathak, and Roth (2005) noted that in the New York City school match schools acted as strategic agents by withhold-ing some of their capacity (Sönmez, 1997). An-other possibility of manipulation is through pre-arranged matches (Sönmez, 1999): a student-school pair commit to a mutually benecial agreement prior to the centralized procedure, according to which (i) the student does not participate in the procedure and (ii) he is rewarded with a seat at the school. Here, mutually benecial means that at least the student or the school obtains a strictly bet-ter match (and the other agent does not get hurt). Sönmez (1997, 1999) showed that any stable mech-anism can be manipulated through capacity with-holding and also through pre-arranged matches.
In many school districts, each school is required to admit a minimum number of students. In other words, in this extended model each school s
can-not declare less than say qs seats. To formalize
the rst type of manipulation we need the follow-ing piece of notation. Let Ps denotes the strict
preference relation of school s ∈ S over the
(in-dividual) students (see item 5' in Section 3). More precisely, fs(i) < fs(j) if and only if iPsj for all
i, j ∈ I. With a slight abuse of notation, let Ps
also denote the preferences of schoolsover sets of
students. A usual assumption in the literature is that for each school s ∈ S the preferences Ps are
responsive (Roth, 1985), i.e.,
• ifi 6∈ I′ and |I′| < q
s, then (I′∪ {i})PsI′ if
and only ifiPs∅, and
• ifi6∈I′ andj ∈I′, then ((I′\{j})∪ {i})P sI′
if and only if iPsj.
LetPS = (Ps1, . . . , Psm).
Denition 4.4. (Sönmez, 1997)
A mechanism ϕ is non-manipulable via capacities
if for all (PS, q), all s ∈ S, and all qs < q′s < qs,
ϕ(PS, q)(s)Rsϕ(PS, q′s, q−s)(s). △
Theorem 4.10. (Kesten, 2008b)
The Boston and Top Trading Cycles mechanisms are non-manipulable via capacities. The Gale-Shapley mechanism is non-manipulable via capac-ities if and only if f is an Ergin-acyclic priority
structure.
The second type of manipulation by schools is formalized as follows.
Denition 4.5. (Sönmez, 1999)
A mechanismϕis non-manipulable via pre-arranged
matches at (I, PI, PS, q)if there is a student i∈I
and a school s ∈ S such thatsRiϕ(I, PI, PS, q)(i)
and ³{i} ∪ϕ(I\{i}, PI\{i}, P I\{i}
S , q−s, qs−1)(s)
´
Rsϕ(I, PI, PS, q)(s) with at least one of the
rela-tions holding strictly. △
Here, PSI\{i} denotes the preferences of the schools
over the set of students I\{i}. As the following result shows, it is virtually impossible to avoid ma-nipulation via pre-arranged matches.
Theorem 4.11. (Kesten, 2008b)
Suppose that at(I, PI, PS, q)for some schools∈S,
qs < n. Then, any mechanism is manipulable via
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
Kojima (2007) studies the same two kinds of ma-nipulation. As Kojima (2007) points out, there are two dierences between his and Kesten's (2008b) paper. First, Kojima (2007) follows the litera-ture on school choice by assuming that the schools' priorities (or preferences) are publicly known. Kesten (2008b) assumes that the priorities are pri-vate information. Second, Kojima (2007) obtains conditions in terms of preferences of an individual school under which that particular school cannot manipulate. Clearly, Kesten's results (Theorems 4.10 and 4.11) deal with conditions on the entire priority structure such that no school can manipu-late.
Denition 4.6. (Konishi and Ünver, 2006) Preference relation Psis strongly monotone in
pop-ulation if, ifqs>|I′|>|I′′|and each studenti∈I′
is acceptable (i.e., iPs∅), thenI′PsI′′. △
The following two results show that the class of strongly monotone preferences in population is a maximal domain for non-manipulability via capac-ities of the Gale-Shapley mechanism.
Theorem 4.12. (Konishi and Ünver, 2006) If Ps is strongly monotone in population, then s
cannot manipulate the Gale-Shapley mechanism via capacities.
Theorem 4.13. (Kojima, 2007)
Fix I, S, s ∈ S, Ps, and qs. If Ps is not strongly
monotone in population, then there exist preferences of students and other schools (PI, P−s)such that s
can manipulate the Gale-Shapley mechanism via ca-pacities. The preferences of the other schools can be taken as strongly monotone in population.
Kojima (2007) also identies a maximal domain for the second type of manipulation.
Denition 4.7. (Kojima, 2007)
Preference relation Ps is weakly maximin if [qs =
|I′| = |I′′|, each student i ∈ I′ is acceptable, and
the least preferred student inI′is strictly preferred
to the least preferred student inI′′] impliesI′P sI′′.△
Theorem 4.14. (Kojima, 2007)
(i) If Ps is weakly maximin, thens cannot
manip-ulate the Gale-Shapley mechanism via pre-arranged matches.
(ii) Fix I, S, s∈S, Ps, andqs. If Ps is not weakly
maximin, then there exist preferences of students and other schools(PI, P−s)such thats can
manip-ulate the Gale-Shapley mechanism via pre-arranged matches. The preferences of the other schools can be taken as weakly maximin.
4.4. Further issues
There are many other important issues and new developments in the eld. I just mention three. Ab-dulkadiro§lu and Ehlers (2006) study how in prac-tice one can assign students to school while main-taining racial and ethnic balance. They introduce a notion of fairness and show that there is always a constrained non-wasteful matching that satises it. On the other hand, they prove that there is no such mechanism that is also strategy-proof.
Kesten (2008a) provides theoretical and compu-tational evidence that the Gale-Shapley mechanism may suer large welfare losses. He proposes an ad-justment such that a student's waiving his priority for a particular school leads to a Pareto improve-ment. He further shows that the adjustment prac-tically does not disrupt strategy-proofness.
Abdulkadiro§lu, Che, and Yasuda (2008) ex-pand the set of strategies by allowing students to signal a school (in addition to a preference list). They introduce a new mechanism and show that it improves upon the Gale-Shapley mechanism.
5.
Concluding remarks
It has become clear that matching theory and mechanism design can provide a better understand-ing of several real-life markets and help to improve their working.10 The case of school choice is a clear example. The assistance of economists in the de-sign of school choice programs has led to student assignment mechanisms that are considered fair or ecient. Addtionally, the new mechanisms have also taken away concerns of the parents since they no longer have to strategize and can simply submit their true preferences. As an illustration, the Insti-tute for Innovation in Public School Choice, which 10See, for instance, Roth, 2008b.
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
is a nonprot organization in the US, makes use of the know-how of economists in the eld of market design.11
On the other hand, recent literature shows there is still room for further improvements in student as-signment mechanisms. I mentioned for instance the presence of a cap on the length of submittable pref-erence lists is harmful, and there is no clear rea-son to not remove it. It is also necessary to take care of the ties in the priority structure. All of this could lead to additional social welfare. An impor-tant but dicult task for economic engineers is to convince authorities how one should deal with these and other market failures. One diculty is that authorities or clearinghouses may not always be eager to share information about the exact pro-cedures or cannot reveal the (submitted) prefer-ences of the participants. Finally, groups of in-terest may be resistant against redesign. For the case of school choice, Pathak and Sönmez (2008a) identied groups of parents that invested in learn-ing about the Boston mechanism. These parents obtained a clear advantage over the other partici-pants, and opposed changing the mechanism.
The interaction between practical problems and theory leads also to new interesting theoretical problems. One challenge is to model, study, and compare dierent informational environments (that correspond to more realistic settings). Another challenge is to nd out how well the mechanisms perform. For instance, if a mechanism is manipula-ble, inecient, or unstamanipula-ble, how manipulamanipula-ble, inef-cient, or unstable is it really?
References
[1] Abdulkadiro§lu, A. Y.-K. Che, and Y. Yasuda (2008) Expanding Choice in School Choice, Mimeo, Duke University.
[2] Abdulkadiro§lu, A. and L. Ehlers (2006) Con-trolled School Choice, Mimeo, CIREQ, Univer-sité de Montréal.
[3] Abdulkadiro§lu, A., P.A. Pathak, and A.E. Roth (2005) The New York City High School Match, American Economic Review, Papers and Proceedings, 95, 364367.
[4] Abdulkadiro§lu, A., P.A. Pathak, and A.E. Roth (2008) Strategy-proofness versus
E-ciency in Matching with Indierences: Re-designing the NYC High School Match, Mimeo, Harvard University.
[5] Abdulkadiro§lu, A., P.A. Pathak, A.E. Roth, and T. Sönmez (2005) The Boston Public Schools Match, American Economic Review, Papers and Proceedings, 95, 368371.
[6] Abdulkadiro§lu, A., P.A. Pathak, A.E. Roth, and T. Sönmez (2006) Changing the Boston School Choice Mechanism: Strategy-Proofness as Equal Access, Mimeo, Boston College and Harvard University.
[7] Abdulkadiro§lu, A. and T. Sönmez (2003) School Choice: A Mechanism Design Ap-proach, American Economic Review, 93, 729 747.
[8] Balinski, M. and T. Sönmez (1999) A Tale of Two Mechanisms: Student Placement, Journal of Economic Theory, 84, 7394.
[9] Biró, P. (2008) Higher Education Admission in Hungary by a Score-limit Algorithm, Mimeo, University of Glasgow.
[10] Calsamiglia, C. G. Haeringer, and F. Klijn (2007) Constrained School Choice: An Exper-imental Study, Mimeo, Universitat Autònoma de Barcelona.
[11] Chen, Y. and T. Sönmez (2006) School Choice: An Experimental Study, Journal of Economic Theory, 127, 202231.
[12] Erdil, A. and H. . Ergin (2008) What's the Matter with Tie-Breaking? (Improving E-ciency in School Choice), American Economic Review, 98, 669-689.
[13] Ergin, H. . (2002) Ecient Resource Alloca-tion on the Basis of Priorities, Econometrica, 70, 24892497.
[14] Ergin, H. . and T. Sönmez (2006) Games of School Choice under the Boston Mechanism, Journal of Public Economics, 90, 215237.
ARTÍCULOS DE INVESTIGACIÓN OPERATIVA
[16] Guseld, D. and R.W. Irving (1989) The Sta-ble Marriage ProSta-blem: Structure and Algo-rithms. MIT Press, Cambridge.
[17] Haeringer, G. and F. Klijn (2007) Constrained School Choice, Barcelona Economics Working Paper 294.
[18] Kesten, O. (2006) On Two Competing Mecha-nisms for Priority-Based Allocation Problems, Journal of Economic Theory, 127, 155171.
[19] Kesten, O. (2008a) An Alternative Mechanism Design Approach to School Choice in the US, Mimeo, Tepper School of Business, Carnegie Mellon University.
[20] Kesten, O. (2008b) On Two Kinds of Manip-ulation for School Choice Problems, Mimeo, Tepper School of Business, Carnegie Mellon Un