Mathematica

M athematica 

Mathematica Nedir? 

Mathematica, her türlü sembolik ve nümerik hesaplamalar yapabilen, 2 ve 3 boyutlu grafikler  çizebilen  etkin  bir  programlama  dilidir.  İşlevsel  ve  kural  temelli  bir  programlama  dili  olan  Mathematica’da ilk başta biraz güçlük çıkabilmekte ancak kısa bir süre sonra global yapısının  yöntemsel programlamadan çok daha kolay anlaşılır olduğu görülecektir. 

Basit  bir  işlemden  büyük  ölçekteki  programlamaya,  bilimsel  araştırmalardan,  mühendislik  analizi  ve  modellemelerine,  lise’den  üniversiteye  kadar  teknik  eğitimde,  kısaca  sayısal  yöntemlerin kullanıldığı her alanda Mathematica temel bir araçtır.

Mathematica Programının Kullanımı ve Menüler 

Bu  bölümde  sizlere  Mathematica  menülerinin  ve  program  yazma  penceresinin  nasıl  kullanıldığı anlatılacaktır. Öncelikle programımızı Şekil 1’deki gibi çalıştıralım. 

Şekil 1 

Şekil  2’deki  beyaz  zeminli  Untitled­1  adlı  pencere  programlarımızı  yazıp  sonuçları  göreceğimiz  yerdir. Hemen  yanındaki  sembolik  yardımcılar  ise File/Palettes/Basic Input’dan  açılabilir. Benzer şekilde File/Palettes altındaki diğer yardımcı menüleri de inceleyebilirsiniz.

Şekil 2 

Eğer  yazı  tipi  ile  ilgili  özellikleri  değiştirmek  istiyorsanız  Edit/Preferences  menüsünden  Formatting Options/Font Options’tan istediğiniz değişikliği yapabilirsiniz 

Komutlarımızı  yazdığımız  satırlar  Mathematica  tarafından  In  (Input)  ismi  ile  adlandırılacak  ve  yanında  işlem  numarası  yazılacaktır. Çıktı satırları  ise Out (Output)  ile adlandırılacaktır.

Örneğin, In[12]:= ve Out[12]= gibi. Komutunuzun çalışmasını sağlamak için imleciniz satırın  herhangi bir yerinde iken Shift+Enter tuşlarına birlikte basmalısınız. 

Eğer komutun birden fazla satırdan oluşuyorsa her satırın (ya da alt komutun) sonunda Enter  tuşuna  basıp  en  sonda  Shift+Enter  tuşlarına  basmanız  gerekir.  In  ve  Out  satırlarının  her  biri  için  sağ tarafta  birer  mavi köşeli  parantez oluşur. Böylece In  ve Out satırlarını  biri  birinden  kolayca ayırabilirsiniz. 

Dosyalarınızı kaydetmek için File/Save veya File/Save As menülerini kullanabilirsiniz. Şimdi  aritmetik bir dört işlem örneği verelim ve yukarıdaki açıklamalarımızı Şekil 3’te görelim.

Şekil 3 

İki  farklı  işlemi tek  bir  satırda  nasıl  yapacağımıza ait  bir örneği de Şekil 4’te görebilirsiniz.  Burada ikinci dereceden bir denklemin kökleri bulunup bu denklemin grafiği çiziliyor.

Mathematica Yardım Menüsü 

Mathematica, tüm komutların kullanım şekli ve örneklerin bulunduğu oldukça gelişmiş bir  yardım menüsüne sahiptir. Buna Help/Master Index yolu ile ulaşabilir ve aradığınız kelimeyi  yazarak Go ile arama yaptırabilirsiniz. 

Temel Bilgiler 

Dört İşlem ve Parantezler 

+ toplama, ­ çıkarma, * çarpma ve / bölme için kullanılır. Ayrıca ^ üs almak için kullanılır.  Mathematica’da  (  ),  [  ]  ve  {  }  şeklinde  üç  değişik  parantez  farklı  amaçlar  için  kullanılmaktadır.

·  (  )  normal  parantez,  aritmetik  işlemlerde  ve  fonksiyon  yazımlarında  gruplandırma  amacıyla kullanılır.  Örnek  In[1]:=  1+(2­4)*3+2/7  Out[1]= - 33 7 ·  [ ] köşeli parantez, fonksiyon argümanları ve tüm komutlar için kullanılır.

Örnek  In[2]:=  Sin[Pi/2]  Out[2]=  1  Örnek  In[3]:=  Solve[2*x­6Š7­3*x,x]  Out[3]=

::x® 13  5 >> ·  { } süslü parantez, aralık tanımlamaları, listeler ve sayaçlar için kullanılır.  Örnek  In[4]:=  A={a,b,c,d}  Out[4]=  {a,b,c,d}

Örnek  In[5]:=  M={{1,2},{3,5}}//MatrixForm  Out[5]= J 1  2  3  5 N  Örnek  In[6]:=  Plot[x^3,{x,­4,4}];

­4  ­2  2  4  ­1.5  ­1  ­0.5  0.5  1  1.5 

Açıklama Satırları, Nümerik Çözüm Bulma ve Önceki Sonuçlara 

Başvurma 

Mathematica’da  açıklama  satırları  için  (*  ….  *)  kullanabiliriz.  Eğer  işlem  sonucunu  sayısal  istersek  satır  sonuna  //N  ifadesini  koymamız  yeterlidir.  Eğer  virgülden  sonra  belirli  bir

basamağa kadar ondalık sayıyı göstermesini istersek N[ifade,basamak sayısı] şeklinde komutu  kullanabiliriz.  Eğer  N[  ]  veya  //N  kullanılmazsa  Matematica  tüm  sonuçları  default  olarak  kesirli gösterir. 

Eğer  In[  ]  satırının  sonucunun  görünmesi  istenmiyorsa  satır  sonuna  ;  (noktalı  virgül)  konulabilir. Eğer birden fazla atama aynı anda yapılacaksa araya birer boşluk konularak aynı  satırda yazılabilir. Örneğin x=14; y=15; z=­4; gibi. Grafik çiziminde kullanılırsa grafik çizilir  ama Out[ ]: …Graphics… satırı görünmez. 

Mathematica’da  bir  oturum  boyunca  %  sembolü  ile  son  elde  edilen  değer  bellekten  çağrılabilir. Her yeni işlem ile bu % değeri de güncellenmiş olur. %% ile de iki işlem önceki  sonuç kullanılabilir.

Örnek  In[7]:=  Solve[2*x^3­5*x^2+10Š0,x]//N  Out[7]=  {{x®­1.1676},{x®1.8338 +0.958888 ä},{x®1.8338 ­0.958888 ä}}  Örnek  In[8]:=  N[Pi,20]  Out[8]=  3.1415926535897932385

Eşit İşaretleri 

Mathematica’da  =,  =  =,  =  =  =  ve  :=  şeklinde  dört  değişik  eşit  işareti  farklı  amaçlar  için  kullanılmaktadır.

·  =  işareti,  atama  yapmak  için  kullanılır.  Bu  atama  sonrası  Mathematica  programı  kapanana  kadar  bu  atama  geçerli  olur.  Bunu  kaldırmak  için  Clear[  ]  komutu  kullanılmalıdır.  Eğer  anlık  atama  yapılmak  isteniyorsa  “/.”  şeklindeki  ikili  sembol  kullanılabilir.  Ancak  bu  atama  sadece  o  an  içindir,  bir  sonraki  satırdan  itibaren  bu  atama Mathematica tarafından dikkate alınmaz. 

Örnek 

In[9]:=  a=5;

Örnek  In[10]:=  2*x^2+5*y/.x­>2  Out[10]=  8+5 y  Örnek  In[11]:=  Clear[a]

·  =  =  işareti,  bir  eşitliği  (denklemi)  göstermek  amacıyla  kullanılır.  Ayrıca  If  kontrol  komutunda da kullanılır.  Örnek  In[12]:=  Solve[x^3­5*x^2+xŠ0,x]  Out[12]= :8x® 0<, :x® 1  2 I5- •!!!!!! 21M>, :x® 1  2 I5+ •!!!!!! 21M>>

·  = = = işareti, If kontrol komutunda kullanılır.  Örnek  In[13]:=  y[x_]:=x^4­3*x^2+5  If[y[x]= = =y[­x],Print["simetrik"],Print["simetrik değil"]]  Out[13]=  Simetrik ·  := işareti, fonksiyon tanımlamalarında kullanılır.

Örnek 1.14  In[14]:=  f[x_]:=Sin[2*x]­Cos[x]  f[Pi]  Out[14]=  1

Sabitler ve Sayı Türleri 

Mathematica’da p  için  Pi,  e  (doğal  logaritmik  taban)  için  E  ve  i  (kompleks  sayılar)  için  I  sabitleri kullanılmaktadır. Ayrıca C, D, N ve O harfleri de başka anlamları ve komut oldukları  için değişken ismi olarak kullanılmamalıdır. 

Ondalıklı sayılar . (nokta) ile yazılmalıdır. Örneğin; ­2.34. 

Bazı Matematiksel  İşlemler ve Rastgele Sayı Üretimi 

Mathematica’da  faktöriyel  işlemi  için  !  sembolü  kullanılabilir.  Mutlak  değer  için  Abs  [  ]  komutu, modüler aritmetik için Mod [n,m] komutu kullanılır. Burada n’nin m ile bölümünden  kalan bulunacaktır. En büyük ve en küçük elemanlar için ise Max [ ] ve Min [ ] kullanılabilir.

Logaritmik  işlemler  için  Log[b,n]  komutu  kullanılır.  Burada  b  tabanı  göstermektedir.  Eğer  doğal logaritma (ln) söz konusu ise Log[n] kullanılabilir.  Örnek  In[15]:=  Mod[11,2]+Log[E^3]  Out[15]=  4  Random [ ] komutu ile 0 ve 1 arasında rastgele ondalıklı bir sayı üretilir.

Örnek  In[16]:=  Table[Random[Integer,{1,10}],{15}](*1 ile 10 arasında 15 tane  rastgele tamsayı seçmek için*)  Out[16]=  {5,7,7,3,9,3,10,10,4,2,2,5,6,3,2}

Liste İşlemleri 

Mathematica’da  nesnelerin  bir  kümesini  Liste  yöntemiyle  oluşturabiliriz.  Bunun  için  {  }  parantezlerini  içindeki  her  elemandan  sonra  ,  (virgül)  koyarak  kullanabiliriz.  Bu  listeler  üzerinde her türlü aritmetik işlem yapılabilir. Eğer listenin bir elemanını öğrenmek istiyorsak  [[n]] yardımcı komutunu kullanmalıyız. Örneğin;  L adlı bir listenin 5­inci elemanı L[[5]] ile  bulunabilir.  Bu  L  listesinin  3­üncü  elamanını  v  ile  değiştirmek  istiyorsak  L[[3]]=v  şeklinde  tanımlama yapmalıyız. 

Örnek 

In[17]:= 

Örnek  In[18]:=  B={0,4,1,9,7,­4};  B+4  3*B  Out[18]=  {4,8,5,13,11,0}  {0,12,3,27,21,­12}

Matematiksel İfadeleri Açma, Çarpanlarına Ayırma ve Sadeleştirme 

Mathematica’da bir ifadenin en açık hali Expand[ ] (yerli olmazsa ExpandAll[ ] kullanılmalı),  çarpanlarına  ayrılmış  hali  ise  Factor  [  ]  ile  bulunur.Sadeleştirme  için  Simplify[  ]  komutunu  kullanabiliriz.  Eğer  logaritmik,  üstel  veya  trigonometrik  ifadeler  var  ise  FullSimplify[  ]  komutunu  kullanmamız  gerekir.  İstediğimiz  değişkene  göre  ifadeyi  gruplandırmak  için  Collect[ifade,değişken] komutunu kullanabiliriz.  Bunların dışında trigonometrik  ifadeler  için  TrigExpand[  ],  TrigFactor[  ],  TrigReduce[  ],  kompleks  ifadeler  için  ComplexExpand[  ]  ve  üslü ifadeler için de PowerExpand[ ] komutları kullanılabilir. Bir çok terimli ifadede istenilen  değişkenin  katsayısını  Coefficient[ifade,değişken]  komutu  ile  bulabiliriz.  Eğer  istenilen  değişkene  ait  en  büyük  kuvveti  bulmak  istersek  Exponent[ifade,değişken]  komutunu  kullanmamız  gerekir.  Part[ifade,n]  ile  verilen  ifadenin  n­inci  terimi,  Denominator[kesirli  ifade] ile kesrin paydası bulunabilir.

Simplify[ ] komutu bazı durumlarda sadeleştirme yapamaz. Böyle ifadelerde değişkenin değer  aralığını vermemiz gerekir.  Örnek  In[19]:=  FullSimplify[Sqrt[x^2],x>0]  Out[19]=  X

Örnek  In[20]:=  Simplify[Sqrt[x^2],Element[x,Reals]]  Out[20]=  Abs[x]  Örnek  In[21]:=  Factor[x^2+2*x+1]

Out[21]=

H1+ xL 2 

Mantıksal ve İlişkisel Operatörler 

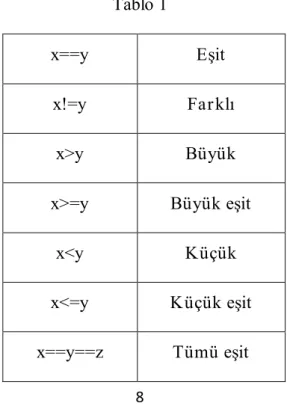
Mathematica’da && bağlacı VE anlamında, || bağlacı ise VEYA anlamında kullanılır. Tablo  1’de operatörleri görebilirsiniz.

Tablo 1  x==y  Eşit  x!=y  Far klı  x>y  Büyük  x>=y  Büyük eşit  x<y  Küçük  x<=y  Küçük eşit  x==y==z  Tümü eşit

x!=y!=z  Tümü far klı  x>y>z  Sır alı artan  Örnek  In[22]:=  7>4&&2!=3  Out[22]=  True

Mathematica’da Analiz 

Denklem Çözümü 

Mathematica’da denklem çözümü için Solve[ ] komutu kullanılır.  Örnek  In[23]:=  Solve[x^2+5*x+6Š0,x]  Out[23]=  {{x®­3},{x®­2}}

Bu  örnekte  x 2 +  x 5  + 6 = 0  denkleminin  çözümü  bulunmuştur.  Çok  bilinmeyenli  denklem  sistemlerinin çözümlerini de Mathematica’da bulmak mümkündür.  Örnek  In[24]:=  Solve[{x+5*yŠ­3,2*x­4*yŠ5},{x,y}]  Out[24]= ::x® 13  14 , y® - 11  14 >>  Bu örnekte ise x+5y=­3 ve 2x­4y=5 şeklindeki iki bilinmeyenli denklem sistemi çözülmüştür.  Trigonometrik denklemleri de Solve[ ] komutu ile çözmek mümkündür.

Örnek  In[25]:=  Solve[Cos[x]Š0,x]  Out[25]= ::x® - p 2 >, :x® p 2 >> 

Verilen  ifadelerde  çözümü  bulurken  istenilen  değişken  yok  edilerek  sonuç  isteniyorsa  Eliminate[  ]  komutu  kullanılabilir.  Reduce[  ]  komutu  da  kullanılabilecek  bir  diğer  komut  olarak verilebilir. 

Trigonometrik  denklemlerin  kökünü  bulmak  için  FindRoot[denklem,{değişken,civar  noktası}]  komutunu  kullanmak  gerekmektedir.  Örneğin;  3sin(2x)=ln(x)  denkleminin  x=1

civarındaki  çözümü  için  FindRoot[3*Sin[2*x]=Log[x],{x,1}]  şeklinde  bir  Mathematica  komutu yazmamız gerekir.  Örnek  In[26]:=  Eliminate[{a*x+yŠ0,2*x+(1+a)*yŠ1},y]  Out[26]= H-2+ a+a 2 L xŠ -1  Örnek  In[27]:=  Reduce[{a*x­bŠ0},x]

Out[27]=

HbŠ 0 && a Š 0L ÈÈ Ja¹ 0 && x Š b 

a N

Eşitsizlik Çözümü 

Mathematica’da  eşitsizleri  çözmek  için  öncelikle  kütüphane  çağırmak  gerekmektedir.  Kütüphane  çağrımı  <<konu_adı`komut`  şeklinde  olmaktadır.  Burada  kullanılan  tek  tırnak  işaretleri  klavyeden  Alt  Gr+Virgül  tuş  kombinasyonu  ile  yazılmaktadır.  Kütüphane  komut  kullanılmadan önceki ilk In[ ] satırında tek başına yazılıp çalıştırılmalıdır. Eğer  yazım doğru  ise herhangi  bir Out[ ] satırı oluşmaz.  Kütüphane Mathematica programı açık kaldığı sürece  hafızada  hazır  bekler. Her  komut kullanımında tekrar  kütüphane çağırılmasına gerek  yoktur.  Bir Mathematica oturumunda bir kez ilgili kütüphaneyi çağırmak yeterlidir.

Örnek  In[28.1]:=  <<Algebra`InequalitySolve`  In[28.2]:=  InequalitySolve[(x­3)*(2*x+5)<=6,x]  Out[28]= -3 £ x £ 7  2  Bu örnekte (x­3)(2x+5)£6 eşitsizliği çözülmüştür.

Örnek  In[29]:=  InequalitySolve[Abs[x­1]*(x^2­3)>3,x]//N  Out[29]=  x<­2.||x>2.30278 

Mathematica’da Programlama 

Ekrana yazı yazma ve bilgi girişi 

Mathematica’da ekrana bilgi yazma işlemini Print[ ] ile yapabiliriz. Ancak yazının içeriğinde  değişken kısımlar var ise o zaman StringForm[ ] komutunu da birlikte kullanmamız gerekir.

Kulanıcan değer alma işlemini Input[ ] komutu ile yapabiliriz. Örneğin; kullanıcıdan bir sayı  isteyip  bunu  “b”  adı  ile  kullanmak  istersek  b=Input[“b  sayısını  giriniz:”];    komutu  yeterli  olacaktır.  Örnek  In[57]:=  a=4;  Print[StringForm["`` sayısının karesi `` dır.",a,a^2]]  Out[57]=  4 sayısının karesi 16 dır.

Do döngüsü 

Mathematica’da  bir  işlemi  tekrar  tekrar  yazmak  yerine  Do[  ]  döngüsi  yardımıyla  bir  defada  tanımlayıp işlemleri arka arkaya yaptırabiliriz.  Örnek  In[58]:=  Do[Print[a!],{a,2,4}]  Out[58]=  2  6  24

While ve For komutları 

Mathematica’da  program  yazmak  isteyenlerin  mutlaka  ihtiyaç  duyacağı  komutlardan  ikisi  olan While[ ] ve For[ ] komutları ile ilgili örnekler aşağıda verilmiştir.  Örnek  In[59]:=  For[i=1,i<4,i++,Print[i]]  Out[59]=  1  2  3

Örnek  In[60]:=  n=17;  While[(n=Floor[n/2])!=0,Print[n]] (*Floor ondalıklı sayıların kesir  kısmını atıp tam kısmını alır*)  Out[60]=  8  4  2  1

İndis kullanımı 

Mathematica’da  Do[  ]  komutu  yarımıyla  indisleri  çok  daha  verimli  kullanmak  mümkündür.  Bu konu ile ilgili bir kısmi türev uygulaması Örnek 1.60’da verilmiştir. 

Örnek 

In[61]:= 

X@u1, u2D:= 8a*Cos@u1D*Sin@u2D, a*Sin@u1D*Sin@u2D, a*Cos@u2D<

Do@X_ut = D@X@u1, u2D, utD,8t, 2<D

Do@g@i, kD= Simplify@X_ui .X_uk D,8i, 2<,8k, 2<D

Do@Print@StringForm@"g````=``", i, k, g@i, kDDD,8i, 2<,8k, 2<D

g11=a 2 Sin@u2D 2 

g12=0 

g21=0 

Bazı Yardımcı Mathematica Komutları

 

Örnek  In[69]:=  Series[Sin[x],{x,0,10}](*fonksiyonların seri açılımı için  kullanılır*)  Out[69]=  x- x  3 6 + x 5  120 - x 7  5040 + x 9  362880 + O@xD 11

Örnek  In[70.1]:=  <<Graphics`Graphics`  In[70.2]:=  PieChart[{{35,"A"},{25,"B"},{40,"C"}}];  BarChart[{{35,"A"},{25,"B"},{40,"C"}}];  A  B  C

A  B  C  10  20  30  40  Örnek  In[71]:=  Sin[30*Degree]+Cos[Pi/4]  Out[71]=  1  2 + 1 •!!!! ₂

Örnek  In[72.1]:=  <<Graphics`Animation`  In[72.2]:=  MoviePlot3D[Sin[x*y],{x,0,t/2},{y,0,t},{t,1,6,3/4}]  0  0.1  0.2  0.3  0.4  0.5 0  0.2  0.4  0.6  0.8  1  0  0.2  0.4  0  0.1  0.2  0.3  0.4  0  0.2  0.4  0.6  0.8  0  0.5  1  1.5  0  0.25  0.5  0.75  1  0  0.2  0.4  0.6  0.8  0  0.25  0.5  0.75  1  1.25 0  0.5  1  1.5  2  2.5  0  0.25  0.5  0.75  1  0  0.25  0.5  0.75  1  0  0.5  1  1.5  0  1  2  3  ­1  ­0.5  0  0.5  1  0  0.5  1  1.5

0  0.5  1  1.5  2 0  1  2  3  4  ­1  ­0.5  0  0.5  1  0  0.5  1  1.5  0  0.5  1  1.5  2  0  1  2  3  4  ­1  ­0.5  0  0.5  1  0  0.5  1  1.5  2  0  1  2  0  2  4  ­1  ­0.5  0  0.5  1  0  1  2  Örnek  In[73]:=  pascal[n_]:=Table[Binomial[n,i],{i,0,n}]  ColumnForm[Table[pascal[m],{m,0,5}],Center]  Out[73]=

81< 81, 1< 81, 2, 1< 81, 3, 3, 1< 81, 4, 6, 4, 1< 81, 5, 10, 10, 5, 1<  Örnek  In[74]:=  TreeForm[3+a+Sin[2*Pi*x^y]]  Out[74]=

PlusB3, a, È SinB È TimesB2, p, È Power@x, yD F F F  Örnek  In[75]:=  ContourPlot[Sin[x*y],{x,0,3},{y,0,4}];

0  0.5  1  1.5  2  2.5  3  0  1  2  3  4  Örnek  In[76]:=  Solve[{x^2+y^2Š16,x^2­4Šy},{x,y}]//TableForm

Out[76]=  y® -4  x® 0  y® -4  x® 0  y® 3  x® - •!!!! 7  y® 3  x® •!!!! 7  Örnek  In[77.1]:=  <<Graphics`Graphics`  In[77.2]:=  PolarPlot[t,{t,0,2*Pi}];

­2  2  4  6  ­4  ­3  ­2  ­1  1  Örnek 

K={­4,7,a,b,0,5,x,11,y}  şeklinde  bir  küme  (liste)  olsun.  Bu  K  kümesi  üzerinde  bazı  komut  uygulamaları yapalım.

In[78]:=  K={­4,7,a,b,0,­5,x,11,y};  Length[K]  K[[3]]  K[[­2]]  Sort[K]  Append[K,70]  Prepend[K,Z]  Insert[K,325,2]  First[K]  Last[K]

K[[Range[3,5]]]  Select[K,Positive]  Select[K,Negative]  Out[78]=  9  a  11  {­5,­4,0,3,7,11,a,x,y}  {­4,7,a,3,0,­5,x,11,y,70}  {Z,­4,7,a,3,0,­5,x,11,y}  {­4,325,7,a,3,0,­5,x,11,y}

­4  y  {a,3,0}  {7,3,11}  {­4,­5}  Örnek  In[79]:=  Together[a/b+c/d]  Collect[a*x+b*x+c*y+d*y,{x,y}]  Numerator[(x+2)/(x­1)]

Denominator[(x+2)/(x­1)]  Out[79]=  b c+ a d  b d  (a+b) x+(c+d) y  2+x  ­1+x 

Karışık Örnekler 

Örnek  A={­2,­1,0,1,2}, B={0,2,4} ve F={­1,1,3,5} ise ( A\ B ) È ( B Ç F ) kümesi nedir?

In[91]:=  A={­2,­1,0,1,2};  B={0,2,4};  F={­1,1,3,5};  Union[Complement[A,B],Intersection[B,F]]  Out[91]=  {­2,­1,1}  Örnek  4  1  , 5  1 , 8  1 - -  ve  3  1  sayılarını sıralayınız ve en büyüğünü bulunuz?

In[92]:=  A=Sort[{­1/8,1/5,­1/4,1/3}]  Max[A]  Out[92.1]= :- 1  4 , - 1  8 ,  1  5 ,  1  3> Out[92.2]=  1  3 Örnek  2  4  3  )  2  (  )  3  (  2 - - - - + -  işleminin sonucunu bulunuz.  In[93]:=  ­2^3+(­3)^4­(­2)^(­2)

Out[93]=  291  4  Örnek  3  4  2x -  ³ eşitsizliğinin çözüm kümesini bulunuz.  In[94.1]:=  <<Algebra`InequalitySolve`  In[94.2]:=  InequalitySolve[Abs[2*x­4]>=3,x]  Out[94.2]=

x£ 1  2 ÈÈx³ 7  2  Örnek  2  4 = -  x  denkleminin çözümü nedir?  In[95]:=  Solve[Abs[Abs[x]­4]Š2,x]  Out[95]=  {{x®­6},{x®­2},{x®2},{x®6}}

Örnek  20  3  3  24  1 -  işleminin sonucunu bulunuz.  In[96]:=  Sqrt[1/24]­3*Sqrt[2/40]//N  Out[96]=  ­0.466696  Örnek 

In[97.1]:=  cozum=Solve[{x­yŠ3,x*yŠ10},{x,y}]  Out[97.1]=  {{x®­2,y®­5},{x®5,y®2}}  In[97.2]:=  x=x/.cozum[[1,1]];  y=y/.cozum[[1,2]];  x^2+y^2  Out[97.2]=  29

Örnek  3  27  a-  ifadesinin özdeşini bulunuz.  In[98]:=  Factor[27­a^3]  Out[98]= -H-3+aL H9+ 3 a+a 2 L  Örnek  (x­1)+2x=3x+8 denklemini çözünüz.  In[99]:=  Solve[x­1+2*xŠ3*x+8,x]  Out[99]=

{} (*çözüm boş kümedir*)  Örnek  1  22  1  2  1  4  2 - = - + +  x  x  x  denklemini çözünüz.  In[100]:=  Solve[4/(x+1)+2/(x­1)Š22/(x^2­1),x]  Out[100]=  {{x®4}}

Karışık Örnekler 

Örnek þ ý ü = + = +  9  4  12  2  3  y  x  y  x  denklem sisteminin çözüm kümesini bulunuz.  In[101]:=  Solve[{3*x+2*yŠ12,x+4*yŠ9},{x,y}]  Out[101]= ::x® 3, y® 3  2 >>

Örnek  0  6  4  2  3 = - +  x  x  x  denkleminin çözüm kümesini bulunuz.  In[102]:=  NSolve[x^3+4*x^2­6*xŠ0,x]  Out[102]=  {{x®­5.16228},{x®0.},{x®1.16228}}  Örnek  0  )  9  )(  4  (  2 2  < - -  x  x  x  eşitsizliğinin çözüm kümesini bulunuz.  In[103.1]:=

<<Algebra`InequalitySolve`  In[103.2]:=  InequalitySolve[x*(x^2­4)*(x^2­9)<0,x]  Out[103.2]=  x<­3||­2<x<0||2<x<3  Örnek  f:R→R ve f:x→y,  2  3  2 + =  x  y  fonksiyonunun grafiğini çiziniz.  In[104]:=  y[x_]:=3/(x^2+2)  Plot[y[x],{x,­3,3}];

­3  ­2  ­1  1  2  3  0.4  0.6  0.8  1.2  1.4  Örnek 1.105  f:R→R,  f( x ) = 2 x 2 + x 4 fonksiyonu tek mi yoksa çift midir? Araştırınız.  In[105]:=  f[x_]:=2*x^2+x^4

If[f[x]===f[­x],Print["fonksiyon çift"],  If[f[­x]===­f[x],Print["fonksiyon tek"],  Print["fonksiyon ne tek ne de çift"]]]  Out[105]=  fonksiyon çift  Örnek  f:R→R,  f ( x ) = x 2 - 2 ile f:R→R, g( x ) = x 3  fonksiyonlarının gof(2) bileşke fonksiyonunun  değerini bulunuz.  In[106]:=

f[x_]:=x^2­2  g[x_]:=x^3  g[f[2]]  Out[106]=  8  Örnek  f:R\{4}→ R\{2},  4  5  2  )  ( - + =  x  x  x  f  şeklinde tanımlanıyor. f’nin tersi olan fonksiyonu bulunuz.  In[107]:=  f[x_]:=(2*x+5)/(x­4)  bul=Solve[f[x]Šy,x];

g[x_]:=x/.bul[[1]]  g[x_]=g[x]/.y­>x  Out[107]=  5+ 4 x -2+x  Örnek  1  2  )  (x  =  x - f  fonksiyonunun tersini bulup her iki fonksiyonun grafiğini çiziniz.  In[108]:=  f[x_]:=2*x­1  bul=Solve[f[x]Šy,x];

g[x_]:=x/.bul[[1]]  g[x_]=g[x]/.y®x  Plot[{f[x],g[x]},{x,­2,3}];  Out[108]=  1+ x  2  ­2  ­1  1  2  3  ­4  ­2  2  4

Örnek ï î ï í ì - < < £ - - ³ - =  1  ,  3  2  1  ,  2  2  ,  4  )  (  2  x  x  x  x  x  x  f  parçalı fonksiyonun grafiğini çiziniz.  In[109]:=  f[x_/;x>=2]:=4­x^2  f[x_/;­1<=x<2]:=x­2  f[x_/;x<­1]:=3  Plot[f[x],{x,­5,5}];

­4  ­2  2  4  ­12  ­10  ­8  ­6  ­4  ­2  2  Örnek  3  2  2  log  ifadesinin sonucunu elde ediniz.  In[110]:=  Log[2,2^(1/3)]  Out[110]=  1  3

Örnek  5  32  log_x  =  eşitliğinde x’in değerini elde ediniz.  In[111]:=  Solve[Log[x,32]Š5,x]  Out[111]=  {{x®2}}  Örnek  1  )  4  ( 3- x  2 - x = denkleminin çözümünü elde ediniz.  In[112]:=

Solve[(4^(3­x))^(2­x)Š1,x]  Out[112]=  {{x®2},{x®3}}  ALIŞTIRMALAR (Mathematica’da çözünüz)  1.  Tüm alt kümelerinin sayısı 64 olan küme kaç elemanlıdır?  ( n elemanlı bir kümenin tüm alt kümelerinin sayısı 2 n dir)  2.  A ={­1, 2, 4, 6, 8}, B = {­2, 0, 1, 2, 3} ve C = {­3, 1, 5, 7, 11, 15} ise A Ç B,  B Ç C, AÈ B, BÈ C, A \ B ve B \ A kümelerini bulunuz. 

3.  X  =  {a,  b,  c,  d}  ve  Y  =  {a,  c,  e}  kümeleri  veriliyor.  (X t  \  Y) t kümesinin  elemanları nedir?

ALIŞTIRMALAR ( Mathematica kullanmadan çözünüz)  1.  x = 1,213  sayısının rasyonel sayı olan eşitini bulunuz.  2.  A =  11  1,  2  2,  23  0,  3  4, - -  ise A kaçtır?  ALIŞTIRMALAR ( Mathematica’da çözünüz)  1.  1;  3 ; –2/3; 3; 5/2;p; –4; 4,50 ve 18/4 gerçel sayılarını sayı ekseni üzerinde  gösteriniz.  2.  –11/3, 7, –p, 8/3, –2 sayılarını sıralayınız.

ALIŞTIRMALAR ( Mathematica’da çözünüz)  1.  2 –4 , 5 2 / 125, (4.2 5 ) 3 ve (3/81) –3 işlemlerinin sonuçları nedir?  2.  7 –5 .7 –4 .7 5 .7 –8 = ?  3.  –2 6 – (–4) 5 –(–1) 8 + (–6) 2 = ?  4.  9 64 , 3  64 ,  324  -  ve 3  208  ifadelerinin sonuçlar ını bulunuz.  5.  |x + 3| £ 2 ile belir lenen kapalı aralığı bulunuz.  6.  |x + 5| = 6 denkleminde x’in değer leri nedir?

ALIŞTIRMALAR ( Mathematica kullanmadan çözünüz)  1.  | |2x| + 5| = 7 denkleminin çözümü nedir?  2.  xÎZ olmak üzere,  3  x  8-  <6 eşitsizliğinin çözüm kümesi nedir? 

3.  3 2a = m olduğuna göre 9 3a­2 ifadesinin sonucu nedir? 

4.  Bir sınıfın tüm öğrencileri futbol (F), voleybol (V) ve basketbol (B) sporundan  en  az  birisini  yapmaktadır.  Her  üç  sporu  yapanlar  3  kişi,  futbol  ve  voleybol  oynayanlar 4 kişi, voleybol ve basketbol oynayanlar 8 kişi, futbol ve basketbol  oynayanlar 6 kişidirler. Voleybol oynayanlar 14 kişi, basketbol oynayanlar 22  kişi, futbol oynayanlar 17 kişi olduğuna göre sınıfın mevcudu nedir?

ALIŞTIRMALAR ( Mathematica’da çözünüz)  1.  (x + y) 2m+3 . (x + y) –2m–3 = ?  2.  (27 –4 .81 0 .9 –2 ) / (3 –6 .27 4 ) = ?  3.  -  = ? 24  1  2  72  1  4.  | 5x ­ 1| – 11³ 0 eşitsizliğinin çözüm kümesi nedir?

Mathematica’da Çizim 

İki boyutlu grafik çizimi 

Mathematica’da iki boyutlu grafikleri çizmek için Plot[ ] komutu kullanılır. Eğer grafiğin bir  çerçeve içinde olmasını isterseniz Frame­>True, eksenlere isim vermek için AxesLabel­>{“x­  ekseni  ismi”,”y­ekseni  ismi”},  grafiğin  çizildiği  zemini  küçük  karelere  (ızgara)  bölmek  için  GridLines­>Automatic,  grafiğin  eni  ve  boyunun  oranını  eşitlemek  için  AspectRatio­>1  komutlarını kullanabiliriz. 

Ayrıca  çizgi  rengi  ve  çizgi  kalınlığı  için  de  PlotStyle­>{RGBColor[0,0,1]},  Thickness[0.015]} benzeri bir komutta Plot[ ] komutunun içinde yer alabilir. Burada RGB ile  Red,  Gren ve Blue (Kırmızı, Yeşil  ve Mavi) temsil  edilmekte ve [0,0,1] değerleri  ile  her  bir

renkten  ne  kadar  kullanılacağı  belirtilmektedir.  Değerler  0.00­1.00  arasında  olabilir.  Thickness[  ]  komutunun  içinde  yazan  değer  ise  çizgi  kalınlığıdır.  Çizgi  yerine  kesikli  çizgi  çizmek için Dashing[ ] komutuda yine PlotStyle­>{} içine yazılabilir. 

Aynı anda birden fazla fonksiyonun grafiğini de çizmek mümkündür. 

Örnek 

In[38]:= 

1  2  3  4  5  6  ­1  ­0.5  0.5  1  Örnek  In[39]:=  Plot[{Abs[x^2­6],Sign[x^2­5],0.5*Round[x]},{x,0,2*Pi},  PlotStyle->{RGBColor[0,0,1],Thickness[0.015],Dashing[{0.03}]}];

(*Bu örnekte bir mutlak değer, bir işaret fonksiyonu ve bir de  basamak değer (tam değer) fonksiyonu kullanılmıştır*)  1  2  3  4  5  6  2  4  6

Düzlemde nokta çizimi 

Mathematica’da  x­y  koordinatlarında  nokta  çizmek  için  ListPlot[  ]  komutu  kullanılır.  Eğer  nokta  büyüklüklerini  değiştirmek  isterseniz  PlotStyle­>PointSize[ebat]  komutunu,  noktaların  rengi için de PlotStyle­>RGBColor[ ] komutunu kullanabilirsiniz. 

Örnek 1.40 

In[40]:= 

­2  ­1  1  2  3  5.5 

6  6.5 

7 

Bu  örnekte  (­2,5)  ve  (3,7)  noktaları  çizilmiştir.  Nokta  sayısı  istenildiği  kadar  arttırılabilir.  Eğer  noktaları  birleştirip  üzerlerinden  geçen  bir  eğri  ya  da  doğru  çizmek  istenirse  PlotJoined­>True komutu ListPlot[ ]’un içine yazılmalıdır.

Parametrik Çizim 

Elle çizimi oldukça zor olan bu grafikler için ParametricPlot[ ] komutu komutu kullanılabilir. 

Örnek 

In[41]:= 

­1  ­0.5  0.5  1  ­1  ­0.5  0.5  1 

Kapalı Fonksiyonların Çizimi 

Eğer  fonksiyonumuz  kapalı  (implicit)  ise  o  zaman  ImplicitPlot[  ]  komutunu  kullanmamız  gerekir.  Yalnız  bu  komutta  kendisine  ait  olan  kütüphaneye  ihtiyaç  duymaktadır.  Bu  yüzden  öncelikle <<Graphics`ImplicitPlot` komutu ile kütüphane çağrılmalıdır.

Örnek 

In[42.1]:= 

<<Graphics`ImplicitPlot`  In[42.2]:= 

­10  ­5  0  5  10  ­10  ­5  0  5  10

Üç boyutlu grafik çizimleri 

3  boyutlu  çizimler  için  Mathematica’da  Plot3D[  ]  komutu  kullanılır.  Ayrıca  parametrik  denklemler  için  de  ParametricPlot3D[  ]  komutu  kullanılabilir.  Her  iki  komutta  da  grafiğe  bakış noktamızı ViewPoint­>{x,y,z} ile belirlemek mümkündür. 

Örnek 

In[43]:= 

0  1  2  3  0  0.5  1  1.5  ­1  0  1  2  3  0  1  2  3  Örnek  In[44]:=  ParametricPlot3D[{t,u,Sin[t*u]},{t,0,3},{u,0,3},

ViewPoint->{0,4,3}];  0  1  2  3  0  1  2  3  ­1  ­0.5  0  0.5  1  0  1  2

İki boyutlu çizimlerde alan boyama 

Mathematica’da  iki  eğri  arasında  kalan  alan  veya  eğri  ile  x­ekseni  arasında  kalan  alanlar  boyanabilir.  Bunun  için  FilledPlot[  ]  komutu,  öncelikle  <<Graphics`FilledPlot`  kütüphanesi  çağrıldıktan sonra kullanılabilir.  Örnek  In[45.1]:=  <<Graphics`FilledPlot`  In[45.1]:=  FilledPlot[x^2,{x,­4,4}];

­4  ­2  2  4  2.5  5  7.5  10  12.5  15  ­4  ­2  2  4  2.5  5  7.5  10  12.5  15

Grafiklerin birleştirilmesi 

Mathematica’da  farklı  tür  grafikleri  birleştirmek  için  Show[  ]  komutu  kullanılır.  Burada  dikkat edilmesi gereken tüm grafikleri  birer  isim  ataması  yapmak  ve  bunları Show[  ]  içinde  çağırmaktır.  Örnek  In[46]:=  noktalar=ListPlot[{{­2,0},{2,0}},PlotStyle->PointSize[0.035]];  f[x_]:=x^2­4  grafik=Plot[f[x],{x,­5,5},PlotStyle->{RGBColor[1,0,1]}];  Show[noktalar,grafik];

­4  ­2  2  4  5 

10  15  20

Vektör ve Matris İşlemleri 

Vektörler 

Mathematica’da  vektörler  {  }  parantezleri  içinde  her  elemandan  sonra  virgül  konulacak  şekilde  yazılır.  Örneğin;  {­1,2,4}  gibi.  Vektörlerin  3  çeşit  çarpma  işlemi  olabilmektedir.  Bunlar; Cross[ ] (iç), . (nokta, vektörel) ve * (yıldız, skaler) çarpımlarıdır. 

Örnek  In[47]:=  u={­1,3,5};  v={0,3,2};  u.v  u*v  Cross[u,v]  Out[47]=  19  {0,9,10}

{­9,2,­3}  Örnek  In[48]:=  <<Graphics`Arrow`  vektör[a_,b_]:=Graphics[{Hue[1],Arrow[b,a+b]}]  vektör[a_]:=vektör[a,{0,0}]  Show[vektör[{1,1},{2,1}],Axes->True,PlotRange->{{0,3},{0,3}}];  Show[vektör[{1,2}],vektör[{2,1}],Axes->True,  PlotRange->{{0,3},{0,3}}];

0.5  1  1.5  2  2.5  3  0.5  1  1.5  2  2.5  3

0.5  1  1.5  2  2.5  3  0.5  1  1.5  2  2.5  3 

Matrisler 

Matrisler { } parantezlerin içine her satır ayrı bir { } içinde olmak üzere yazılırlar. Örneğin;  {{2,4},{5,­1}} matrisi 2x2 ebatlarında bir matris tanımıdır. Eğer tanım sonuna //MatrixForm  yazmazsak  matrisi  tek  bir  satırda  parantezler  içinde  görürürüz.  Bu  yardımcı  komut  bize

matrisi  gerçek  haliyle  görmemizi  sağlar.  Ancak  bu  sırada  bir  atama  yapmış  ise  bu  geçersiz  kalır. Çünkü Mathematica ancak  liste ahlindeki  matris tanımını atamada uygun görmektedir.  Matrislerin  tersi  için  Inverse[  ],  transpozu  (devriği)  için  Transpose[  ]  ve  determinantını  bulmak için Det[ ] komutlarını kullanabiliriz. 

Eğer  bir denklem  sistemi  m katsayılar  matrisi,  x  bilinmeyenler  matrisi  ve  b değerler  matrisi  olmak üzere mx=b şeklinde verilmişse bu sistemi LinearSolve[m,b] komutu ile çözebiliriz. 

Örnek 

In[49]:= 

M={{2,5,6},{0,3,­2},{­5,1,­1}}//MatrixForm  Out[49]=

i k j j j j j 2  5  6  0  3 -2 -5  1 -1 y { z z z z z  Örnek  In[50]:=  M={{2,5,6},{0,3,­2},{­5,1,­1}};  Inverse[M]//MatrixForm  Transpose[M]  Det[M]  Out[50]=

i k j j j j j j j j j j j - 1 138  11  138 - 14 69  5  69  14 69  2  69  5  46 - 9  46  1  23 y { z z z z z z z z z z z {{2,0,­5},{5,3,1},{6,­2,­1}}  138 

Diğer Matematiksel İşlemler 

Mathematica’da  diferansiyel  denklemi  çözmek  için  DSolve[denklem,fonksiyon,değişken]  komutu kullanılabilir. Seri toplam için Sum[genel terim,{değişken,alt_sınır,üst_sınır}] ve seri  çarpım için Product[genel terim,{değişken,alt_sınır,üst_sınır}] komutlarını da kullanabiliriz.

Örnek  In[37]:=  Sum[1/a^2,{a,1,Infinity}]         (*Infinity, sonsuz demektir*)  Out[37]= p 2 6  Bir amaç fonksiyonun verilen kısıtlamalar içinde minimum ya da maksimum değerini bulmak  için Minimize[ ] ve Maximize[ ] komutları kullanılabilir.  Örnek  In[52]:=  Minimize[x­y+z,{y­z<3,x>7},{x,y,z}]

Out[52]=  {4,{x®7,y®3,z®0}}  Örnek 1.53  In[53]:=  Maximize[{x^2+y,x^2+y^2£1},{x,y}]  Out[53]= : 5  4 , :x® - •!!!! 3  2 , y ® 1  2 >>

Karışık Örnekler 

Örnek ï þ ï ý ü - = - = + + = + -  11  7  5  3  2  4  3  2  z  y  z  y  x  z  y  x  lineer denklem sisteminin çözümünü elde ediniz.  In[125]:=  Solve[{x­2*y+3*zŠ4,2*x+y+zŠ3,5*y­7*zŠ­11},{x,y,z}]  Out[125]=  {{x®­1,y®2,z®3}}

Örnek ú û ù ê ë é =  4  3  5  2  A  , _ú û ù ê ë é - =  1  2  3  1  B  ve _ú û ù ê ë é =  3  1  0  2  F  ise A+B­2F’nin sonucunu bulunuz.  In[126]:=  A={{2,5},{­3,4}}; B={{1,3},{2,­1}}; F={{2,0},{1,3}};  A+B­2*F//MatrixForm  Out[126]= J -1  8 -3 -3 N

Örnek ú û ù ê ë é - =  1  5  4  2  A  ve _ú û ù ê ë é =  7  4  3  0 

B  ise A T ´ B işleminin sonucunu bulunuz.  In[127]:=  A={{2,4},{5,­1}}; B={{0,3},{4,7}};  Transpose[A]*B//MatrixForm  Out[127]= J 0  15  16 -7 N

Örnek ú ú ú û ù ê ê ê ë é - =  5  0  0  0  3  0  0  0  1 

A  köşegen matrisi ve I  birim matrisi verildiğine göre A.B’yi bulunuz. ₃ 

In[128]:=  DiagonalMatrix[{1,3,5}].IdentityMatrix[3]//TraditionalForm  Out[128]= i k j j j j j j 1  0  0  0� � 3  0  0  0  5 y { z z z z z z

Örnek ú ú ú û ù ê ê ê ë é - - - =  9  8  1  3  4  4  6  4  3  A  matrisinin determinant değerini elde ediniz.  In[129]:=  Det[{{3,4,­6},{4,4,­3},{1,8,­9}}]  Out[129]=  ­72

Örnek ï þ ï ý ü = + + = + + = + +  18  4  2  22  3  2  3  25  2  3  3  z  y  x  z  y  x  z  y  x  lineer denklem sistemini matrisler yardımıyla ifade ederek çözünüz.  In[130]:=  m={{3,3,2},{3,2,3},{2,1,4}};  a={{x},{y},{z}}; b={{25},{22},{18}};  Solve[m.aŠb,{x,y,z}]  Out[130]= ::x® 1, y® 28  5 , z ® 13  5 >>

Örnek ï ï þ ï ï ý ü = + + - = + + + = + - + = + - +  4  7  6  3  5  2  3  2  2  4  3  1  4  5  t  z  y  t  z  y  x  t  z  y  x  t  z  y  x  denklem sistemini arttırılmış matris yarımıyla çözünüz.  In[131.1]:=  <<LinearAlgebra`MatrixManipulation`  In[131.2]:=  m={{1,5,­4,1},{3,4,­1,2},{3,2,1,5},{0,­6,7,1}};  b={{1},{2},{3},{4}};  AppendRows[m,b]//MatrixForm

Out[131.2]= i k j j j j j j j j j 1  5 -4  1  1  3  4 -1  2  2  3  2  1  5  3  0 -6  7  1  4 y { z z z z z z z z z  In[131.3]:=  RowReduce[%]//MatrixForm  Out[131.3]= i k j j j j j j j j j j j j j j j j j j 1  0  0  0 - 127  35  0  1  0  0  141  35  0  0  1  0  139  35  0  0  0  1  13 35 y { z z z z z z z z z z z z z z z z z z

Örnek ú ú ú û ù ê ê ê ë é -  1  2  1  2  3  2  1  1  1  matrisinin tersini bulunuz.  In[132]:=  Inverse[{{1,1,1},{2,3,­2},{1,2,1}}]//MatrixForm  Out[132]= i k j j j j j j j j j 7  4  1  4 - 5  4 -1  0  1  1  4 - 1  4  1  4 y { z z z z z z z z z

Örnek ï þ ï ý ü = + - - = + + - = +  8  3  2  30  6  4  3  6  2  z  y  x  z  y  x  z  x  lineer denklem sisteminin çözümünü ters matris yardımıyla elde ediniz.  In[133]:=  m={{1,0,2},{­3,4,6},{­1,­2,3}};  b={{6},{30},{8}};  Inverse[m].b  Out[133]= ::- 10  11 >, : 18  11 >, : 38  11 >>

Örnek  In[83]:=  A={{2,3,4},{6,3,9}};  Dimensions[A](*satır ve sütun sayısını bulur*)  Out[83]=  {2,3}  Örnek  Det[ ] komutunu kullanamadan B matrisinin determinantını dizi indeksleri kullanarak bulalım.  Burada örneğin B[[1,2]] ile ifade edilen B matrisinin 1. satır 2. sütunundaki değerdir.  In[84]:=  B={{2,3},{6,3}};

B[[1,1]]*B[[2,2]]­B[[1,2]]*B[[2,1]]  Out[84]= 

­12 

Örnek 

M  matrisinin  Inverse[  ]  komutu  ile  bulunan  tersinin  doğruluğunu  kontrol  edelim.  Buradaki  IdentityMatrix[3] ile 3x3’lük birim matris ifade edilmiştir. 

In[85]:= 

M={{2,3,4},{6,3,9},{0,­1,1}};  M.Inverse[M]ŠIdentityMatrix[3]

Out[85]=  True 

Trigonometri

 

Örnek 

In[67]:=  v={12,­57,10};  boy[v_List]:=Sqrt[v.v]  boy[v]//N  Out[67]=  59.1016  Örnek  Bir önceki örnekteki boy[ ] tanımı yarımıyla (2,4) ve (9,­13) vektörleri arasındaki açıyı derece  cinsinden bulalım.

In[68]:=  boy[v_List]:=Sqrt[v.v]  u={2,4};  v={9,­13};  N[ArcCos[u.v/(boy[u]*boy[v])]]/Degree  Out[68]=  118.74  Örnek  In[80]:=  Tan[3*Pi/2­t]

Simplify[E^(2*Pi*I)]  TrigExpand[Cos[a­b]]  TrigToExp[Tan[x]]  ExpToTrig[(E^x­E^(­x))/2]  TrigReduce[Tan[x+Pi/2]]  TrigFactor[Cos[a]+Cos[b]]  Out[80]=  Cot[t]  1

Cos[a] Cos[b]+Sin[a] Sin[b] ä Iã -ä x - ã ä x M ã -äx _{+ ã} äx  Sinh[x]  ­Cot[x]  2 CosB a  2 - b  2 F CosB a  2 + b  2 F  Örnek  In[81]:=  Do[Print[n,Switch[n,_,"derece"]," = ",n*Pi/180],{n,0,360,60}]

Out[81]=  0 derece  =  0  60derece = p 3  120derece = 2p 3  180 derece  = p 240derece = 4p 3  300derece = 5p 3  360 derece  =  2 p

Örnek  Ekrandan girilecek bir açı hakkında bilgi veren bir uygulama yapalım.  In[82]:=  a=Input["Aciyi derece olarak giriniz:"]  kat=Floor[a/360]; gercek=a­kat*360;  Print["Gercek aci:",gercek]  If[0<gercek<90,Print["Girilen aci I. bolgededir ve esas  olcusu:",gercek],  If[90<gercek<180,Print["Girilen aci II. bolgededir ve esas  olcusu:",180­gercek],  If[180<gercek<270,Print["Girilen aci III. bolgededir ve esas  olcusu:",gercek­180],

If[270<gercek<360,Print["Girilen aci IV. bolgededir ve esas  olcusu:",360­gercek],  Print["Aci eksenler uzerindedir",gercek]]]]]  Out[82]=  207  Gercek aci: 207  Girilen aci III. bolgededir ve esas olcusu: 27 

Karışık Örnekler 

Örnek

150 derecelik yayı radyan cinsinden hesaplayınız.  In[113]:=  a=150;  Solve[a/180ŠR/Pi,R]  Out[113]= ::R® 5p 6 >>  Örnek a a a  sin  1  sin  1  cos 2 + = -  olduğunu gösteriniz.

In[114]:=  FullSimplify[(Cos[a])^2/(1­Sin[a])]  Out[114]=  1+Sin[a]  Örnek  )  2  ( a  Sin  değerini elde ediniz.  In[115]:=  TrigExpand[Sin[2*a]]  Out[115]=  2 Cos[a] Sin[a]

Örnek  )  135  sin( °  ’yi hesaplayınız.  In[116]:=  Sin[135 Degree]  Out[116]=  1 •!!!! ₂  Örnek a a p  cos  )  2  sin( -  = olduğunu gösteriniz.

In[117]:=  TrigReduce[Sin[Pi/2­a]]  Out[117]=  Cos[a]  Örnek  2  sin x = x  denkleminin x=1.5 civarındaki çözümünü elde ediniz.  In[118]:=  FindRoot[Sin[x]Šx/2,{x,1.5}]  Out[118]=

{x®1.89549}  Örnek  1  2  cos  2  cos  2  2 x +  x = denkleminin çözümünü elde ediniz.  In[119]:=  Solve[2*Cos[x]^2+2*Cos[2*x]Š1,x]  Out[119]= ::x® - 3p 4 >, :x® - p 4 >, :x® p 4 >, :x ® 3p 4 >>  Örnek

Kenarları 12, 15 ve 18 birim olan bir üçgenin alanını hesaplayınız.  In[120]:=  a=12; b=15; c=18;  s=(a+b+c)/2;  Sqrt[s*(s­a)*(s­b)*(s­c)]//N  Out[120]=  89.2941  Örnek  0  ile 2 p  arasındaki  6 p 

artarak  elde  edilen  açıların  Sinüs,  Kosinüs,  Tanjant  ve  Kotanjantını  bulup tablo halinde gösteren bir Mathematica uygulaması yapalım.

In[55]:= 

TableForm[Table[{açı,Sin[açı],Cos[açı],Tan[açı],Cot[açı]},  {açı,0,2*Pi,Pi/6}],TableHeadings®{None,{"Açı","Sin","Cos",  "Tan","Cot"}}] 

Açi  Sin  Cos  Tan  Cot  0  0  1  0  ComplexInfinity p 6  1  2 " #### ₃ 2  1 "#### ₃ •!!!! ₃ p 3 " #### ₃ 2  1  2 •!!!! 3  1 "#### ₃ p 2  1  0  ComplexInfinity  0  2p 3 " #### ₃ 2 - 1  2 - •!!!! 3 - 1 "#### ₃  5p 6  1  2 - "#### ₃ 2 - 1 "#### ₃ - •!!!! 3

p 0 -1  0  ComplexInfinity  7p 6 - 1  2 - "#### ₃ 2  1 " #### ₃ •!!!! 3  4p 3 - "#### ₃ 2 - 1  2 •!!!! 3  1 "#### ₃  3p 2 -1  0  ComplexInfinity  0  5p 3 - "#### ₃ 2  1  2 - •!!!! ₃ - 1 "#### ₃  11p 6 - 1  2 "#### ₃ 2 - 1 "#### ₃ - •!!!! 3  2p 0  1  0  ComplexInfinity