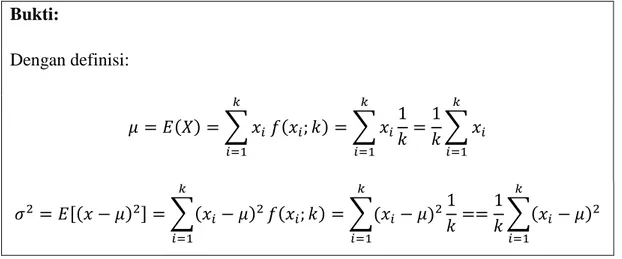STATISTIKA MATEMATIKA. Di Susun: Dr. Ahmad Yani T.,M.Pd. NIP

(1)

STATISTIKA MATEMATIKA

Di Susun:

Dr. Ahmad Yani T.,M.Pd. NIP. 196604011991021001

PROGRAM STUDI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN IPA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS TANJUNGPURA PONTIANAK

(2)

(3)

i

KATA PENGANTAR

Assalamualaikum Wr.Wb.

Alhamdulillah, Puji syukur kami ucapkan kehadirat Allah Swt karena atas rahmat dan hidayahnya lah kami dapat menyelesaikan penyusunan buku ini, sebagai prasyarat untuk menyelesaikan tugas kuliah “Statistika Matematika”

Semoga makalah ini dapat bermanfaat bagi para pembaca untuk

kedepannya.

Terima kasih kami ucapkan kepada Bapak Dr. Ahmad Yani . T .selaku dosen mata kuliah Statistika Matematika yang telah banyak membimbing dalam perkuliahan.

Kami sebagai penulis menyadari bahwa dalam penyusunan makalah ini terdapat kekurangan oleh sebab kami sangat membutuhkan kritik dan saran demi kesempurnaan makalah ini.Akhirnya saya ucapkan terima kasih atas kesediaannya membaca makalah ini.

Wassalamualaikum Wr.Wb.

Pontianak, Juni 2013 Hormat kami,

(4)

ii

DAFTAR ISI

Kata Pengantar ... ii

Daftar Isi ... ii

Bab 1 Koefisien Korelasi ... 1

Bab 2 Hubungan Harapan Dan Variansi Dari Peubah Acak Khusus (Bahasan 1) 18 Bab 3 Hubungan Harapan Dan Variansi Dari Peubah Acak Khusus (Bahasan 2) 36 Bab 4 Kebebasan Stokastik ... 54

Bab 5 Sifat-Sifat Kebebasan Stokastik Dua Peubah Acak ... 73

Bab 6 Peubah Acak Diskrit ... 82

Bab 7 Distribusi Hipergeometrik & Distribusi Poisson ... 97

Bab 8 Beberapa Model Distribusi Kontinu ... 116

Bab 9 Distribusi Normal ... 132

Bab 10 Distribusi Gamma, Eksponensial, Dan Chi-Square ... 146

Bab 11 Transformasi Peubah ... 162

Bab 12 Uji 𝑡, Distribusi 𝐹, Distribusi 𝑋 Dan Distribusi S2 ... 196

(5)

1

BAB I

KOEFISIEN KORELASI

Tujuan pembelajaran secara umumnya mempelajari materi ini adalah diharapkan mampu memahami konsep korelasi dengan baik. Adapun tujuan instruksional khususnya adalah sebagai berikut:

1. Diharapkan dapat menjelaskan makna korelasi.

2. Diharapkan dapat menjelaskan dan menghitung koefisien korelasi 

3. Diharapkan dapat menjelaskan dan menggunakan hubungan  dengan mean bersyarat E ( Y | x ) yang berupa fungsi linear dari x.

4. Diharapkan dapat menjelaskan dan menggunakan hubungan  dengan mean bersyarat E ( X | y ) yang berupa fungsi linear dari y.

5. Diharapkan dapat menjelaskan dan menggunakan  dengan variansi bersyarat dari Y diketahui X = x. Khususnya bila variansi tersebut berupa fungsi dari x yang berharga konstan.

6. Diharapkan dapat menjelaskan dan menggunakan  dengan variansi bersyarat dari X diketahui Y = y. Khususnya bila variansi tersebut berupa fungsi dari y yang berharga konstan.

A. MATERI

Apakah usia pada seseorang ada kaitan dengan berat dan tinggi. Jika ada kaitannya maka dapat dinyatakan jika usia bertambah pada seseorang maka berat badan seseorang bertambah. Pernyataan ini hanya berlaku pada seseorang yang berusia sampai 18 tahun, namun tidak berlaku lagi pada seseorang usia di atas 40 tahun.

Hubungan dan kaitan antara peubah pertama dengan peubah kedua disebut korelasi. Korelasi pada contoh-contoh di atas dapat berupa garis lurus atau disekitar garis lurus. Korelasi antara peubah yang ditunjukkan oleh contoh-contoh di atas adalah positif atau negatif atau nol. Korelasi positif menunjukan bahwa ada hubungan atau kaitan antara kedua peubah tersebut. Korelasi negatif menunjukkan bahwa kedua peubah tersebut tidak mempunyai hubungan atau kaitannya. Contoh hubungan antara jauh perjalanan kendaran bermotor dengan bahan bakar yang ada di dalam tangkinya. Korelasi nol atau hampir mendekati nol menunjukkan hubungan antara kedua peubah tidak ada atau tidak menentu (Ruseffendi, 1993:204). Berdasarkan uraian di atas, korelasi itu dapat positif, nol dan negatif. Jika dinyatakan dalam bilangan bahwa korelasi itu paling kecil -1 dan paling besar +1. Atau jika r adalah korelasi maka -1 ≤  ≤ 1.

Koefisien korelasi diperlukan untuk mendeteksi apakah suatu kasus distribusi bersama merupakan kebebasan stokastik atau tidak. Koefisien korelasi

(6)

2

juga dapat diartikan sebagai nilai yang menunjukkan kekuatan dan arah hubungan linier antara dua buah peubah acak.

Korelasi bermanfaat untuk mengukur kekuatan hubungan antara dua variabel atau lebih dengan skala-skala tertentu, misalnya Pearson data harus berskala interval atau rasio; Spearman dan Kendal menggunakan skala ordinal; Chi Square menggunakan data nominal.



1



2



E_ X- Y- _ dinamakan kovariansi X dan Y, dan ditulis Kov(X,Y). Untuk menghitung kovariansi, akan lebih mudah menggunakan teorema berikut:

Dari teorema di atas, sebelum menentukan kov(X,Y), kita harus menentukan nilai Ekspektasi X, Ekspektasi Y, dan Ekspektasi XY. Yang perlu diperhatikan dalam mencari nilai-nilai ekspektasi tersebut adalah bagaimana bentuk soal yang diberikan. Apakah bentuk kontinu atau diskrit.

Setelah mendapatkan nilai kov(X,Y) kita dapat menentukan koefisen korelasi dengan cara membagi kov(X,Y) dengan simpangan baku dari X dan simpangan baku dari Y.

Untuk lebih jelas perhatikan definisi koefisien korelasi:

𝜌 = 𝐾𝑜𝑣(𝑋, 𝑌) 𝜎_𝑥𝜎_𝑦

Dengan 𝜎_𝑥2 dan 𝜎_𝑦2masing-masing adalah variansi X dan variansi Y, dinamakan koefisien korelasi antara X dan Y (𝜎_𝑥 ≠ 0, 𝜎_𝑦 ≠ 0).

Rumus mencari koefisien korelasi juga dapat dinyatakan dalam bentuk

𝜌 = 𝑛 ∑ 𝑋𝑌 − ∑ 𝑋 ∑ 𝑌

√{𝑛 ∑ 𝑋2_{− (∑ 𝑋)}2_{}{𝑛 ∑ 𝑌}2_{− (∑ 𝑌)}2_}

Koefisien korelasi menunjukkan kekuatan hubungan linear dan arah hubungan dua variabel acak. Jika koefisien korelasi positif, maka kedua variabel mempunyai hubungan searah. Artinya jika nilai variabel X tinggi, maka nilai

(7)

3

variabel Y akan tinggi pula. Sebaliknya, jika koefisien korelasi negatif, maka kedua variabel mempunyai hubungan terbalik. Artinya jika nilai variabel X tinggi, maka nilai variabel Y akan menjadi rendah (dan sebaliknya).

Koefisien korelasi terletak antara -1 dan 1. Berikut ini adalah arti dari koefisien korelasi:

1). Jika 0,9 <𝜌< 1 atau -0,9 <𝜌< -1 , maka hubungan antara dua peubah acak sangat kuat.

2). Jika 0,7 <𝜌< 0,9 atau -0,7 <𝜌< -0,9, maka hubungan antara dua peubah acak kuat.

3). Jika 0,5 <𝜌< 0,7 atau -0,5 <𝜌< -0,7, maka hubungan antara dua peubah acak moderat.

4). Jika 0,3 <𝜌< 0,5 atau -0,3 <𝜌< -0,5, maka hubungan antara dua peubah acak lemah.

5). Jika 0 <𝜌< 0,3 atau 0 <𝜌< -0,3, maka hubungan antara dua peubah acak sangat lemah

6). Jika 𝜌 = 0, maka tidak ada hubungan antara dua peubah acak.

CONTOH 1 :

Misalnya X dan Y dua peubah acak diskrit yang memiliki f. k. p bersama sebagai berikut:

f (x) = {

1

2, 𝑢𝑛𝑡𝑢𝑘 𝑥 = 0,1

0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛 Hitunglah koefisien korelasi antara X dan Y !

Penyelesaian:

(8)

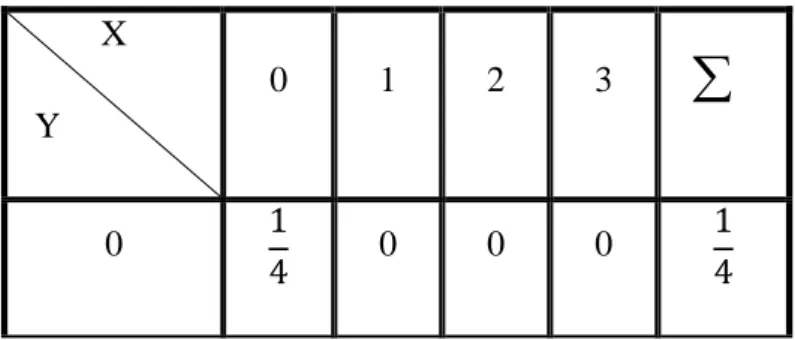
4 X Y 0 1



0 ½ 0 ½ 1 0 ½ ½



½ ½ 1

a. Jumlah ke bawah membentuk f.k.p marginal X, yaitu: f (x) = {

1

2, 𝑢𝑛𝑡𝑢𝑘 𝑥 = 0,1

0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛 Jadi, mean dan variansi X adalah E(X) = ∑1 𝑥. 𝑓1(𝑥) 𝑋=0 = 0. ( 1 2) + 1. ( 1 2) = 1 2 𝜎12 = E(X2) – (E(X))2 = 0. ( 1 2) + 1. ( 1 2) = 1 2 𝜎1 = √ 1 2

b. Jumlah ke samping membentuk f.k.p marginal Y, yaitu: f (x) = {

1

2, 𝑢𝑛𝑡𝑢𝑘 𝑥 = 0,1

0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛 Jadi, mean dan variansi Y adalah E(Y) = ∑1_𝑦=0𝑦. 𝑓2(𝑥)= 0. (1 2) + 1. ( 1 2) = 1 2 𝜎22 = E(Y2) – (E(Y))2 = 0. ( 1 2) + 1. ( 1 2) = 1 2

(9)

5 𝜎2 = √ 1 2 c. Kov(X,Y) E(XY) = ∑1_𝑋=0∑1_𝑦=0𝑥𝑦. 𝑓(𝑥, 𝑦) = 0.0.f(0,0) + 0.1.f(0,1) + 1.0.f(1,0) + 1.1.f(1,1) = 0 + 1 2

Jadi Kov(X,Y) = E(XY) – E(X).E(Y) = 1

2− 1 2 . 1 2 = 1 2 − 1 4= 1 4

Akibatnya, koefisien korelasi antara X dan Y adalah:

𝜌 = 𝐾𝑜𝑣 (𝑋, 𝑌) 𝜎x𝜎y = 1 4 √1 2. √ 1 2 = 1 4 1 2 = 1 2= 0,5

Pada contoh di atas diperoleh  = 0,5. Ini menandakan hubungan yang moderat antara X dan Y.

CONTOH 2 :

Jika X dan Y peubah acak dengan variansi 𝜎x2 = 5,𝜎y2 = 2 dan kovariansi 𝜎xy = 4

Tentukan variansi peubah acak Z = 4X – 2Y + 11 !

Penyelesaian:

𝜎z2 = 𝜎4x-2y+11 2

= 𝜎4x-2y 2

= 16 𝜎x2 - 16 𝜎xy + 4 𝜎y2

(10)

6

= 24

Jadi, variansi peubah acak Z = 4x – 2y + 11 yaitu 24

CONTOH 3 :

Berikut ini adalah data tinggi badan dan berat badan mahasiswa P. MTK 2010

Data A B C D E F G H I J

Tinggi Badan (X)

170 168 173 172 165 168 165 168 172 148

Berat Badan (Y) 50 63 80 75 45 68 62 80 85 40 Tentukanlah koefisien korelasi tinggi badan dan berat badan mahasiswa P. MTK 2010, serta berikan kesimpulan!

Penyelesaian : X 170 168 173 172 165 168 165 168 172 148 ∑ 𝑋= 1.669 Y 50 63 80 75 45 68 62 80 85 40 ∑ 𝑌= 648 𝑋2 2890 0 2822 4 2992 9 2958 4 2722 5 2822 4 2722 5 2822 4 2958 4 2190 4 ∑ 𝑋2₌ 279.0 23 𝑌2_{2500 3969 6400 5625 2025 4624 3844 6400 7225 1600 ∑ 𝑌}2₌ 44.21 2

(11)

7 X Y 8500 1058 4 1384 0 1290 0 7425 1142 4 1023 0 3440 1462 0 5920 ∑𝑋𝑌= 108.8 83

Dari tabel di atas, diperoleh : ∑𝑋= 1.669, ∑ 𝑌= 648, ∑ 𝑋2= 279.023, ∑𝑌2= 44.212, dan ∑𝑋𝑌= 108.883.

Maka, koefisien korelasinya adalah :

𝜌 = 𝑛 ∑ 𝑋𝑌 − ∑ 𝑋 ∑ 𝑌 √{𝑛 ∑ 𝑋2_{− (∑ 𝑋)}2_{}{𝑛 ∑ 𝑌}2 _{− (∑ 𝑌)}2_} 𝜌 = 10(108.883) − (1.669)(648) √{10(279.023) − (1669)2_{}{10(44.212) − (648)}2_} 𝜌 = 1.088.830 − 1.081.512 √{2.790.230 − 2.785.561}{442.120 − 419.904} 𝜌 = 7.318 √(4669)(22.216) 𝜌 = 7.318 10.184,621 𝜌 = 0,72

Karena, nilai 𝜌= 0,72 terletak di antara 0,7 dan 0,9, maka terdapat hubungan yang kuat dan berbanding lurus antara tinggi badan dan berat badan mahasiswa P.MTK 2010.

𝜌2_{= (0,72)}2_{= 0,5184 = 51,84%, artinya variasi tinggi badan yang dapat}

dijelaskan oleh variasi berat badan mahasiswa oleh persamaan regresi Ŷ = -197,23 + 1,57X adalah sebesar 51,84%. Sisanya sebesar 48,16% dijelaskan oleh faktor lain di luar variabel pada persamaan regresi tersebut.

(12)

8 Sifat-Sifat Koefisien Korelasi

Teorema 1.6.1:

Jika E ( Y | x ) berupa fungsi linier dari x maka

E ( Y | x ) ( ₁) 1 2 2         x Bukti:

Misalkan E ( Y | x ) merupakan fungsi linier dari x. Maka E ( Y | x ) = a + bx. Akan dicari nilai a dan b. Karena E ( Y | x )



    y f ( Y | x ) dy



    y x f( ) 1 f ( x , y ) dy Atau



   y x f( ) 1 f ( x , y ) dy = a + bx



   y f ( x , y ) dy = (a + bx) f(x) ……….. (1)

Kedua ruas pers (1) kita integrasikan terhadap x dari -∞ sampai ∞, maka:



  



   y f ( x , y ) dy dx =



   (a + bx) f (x) dx E ( Y ) = a + b E ( X )

(13)

9

Atau

1

2 

 ab ………(2)

Selanjutnya jika kedua ruas pers (1) dikalikan dengan x kemudian kita integrasikan terhadap x dari -∞ sampai ∞ maka:

Dari pers (2) dan (3) diperoleh

a 1 1 2 2 _       dan b 1 2     E ( Y | x ) = a + bx 1 1 2 2 _       + 1 2    x ) ( ₁ 1 2 2         x

(14)

10

Jika E ( Y | x ) berupa fungsi linier dari x maka

E ( Y | x ) = ( ₁) 1 2 2         x Terbukti. Teorema 1.6.2:

Jika E ( X | y ) berupa fungsi linier dari y maka

E ( X | y ) 1 1 2 2 (x )         Bukti:

Misalkan E ( X | y ) merupakan fungsi linier dari y. Maka E ( X | y ) = a + by. Akan dicari nilai a dan b. Karena E ( X | y ) x   



f ( X | y ) dx 1 ( ) x f y   



f ( x , y ) dx Atau 1 ( ) x f y  



f ( x , y ) dx = a + by x  



f ( x , y ) dx = (a + by) f(y) ……….. (1)

Kedua ruas pers (1) kita integrasikan terhadap y dari -∞ sampai ∞, maka:



   x  



f ( x , y ) dx dy =



   (a + by) f (y) dy

(15)

11

E ( X ) = a + b E ( Y ) Atau

1 a b 2



 



………(2)

Selanjutnya jika kedua ruas pers (1) dikalikan dengan y kemudian kita integrasikan terhadap y dari -∞ sampai ∞ maka:



  



   yx f ( x , y ) dx dy =



   y (a + by) f (y) dy Atau E ( XY ) = a E ( Y ) + b E ( 2 Y ) atau 2 2 2 1 2 1 a 2 b( 2 2)          ………(3) Ingat: ) ( ) ( ) , ( Y X Y X kov     atau Kov ( X, Y ) = (X)(Y) Kov ( X, Y ) = E ( XY ) - E ( X ) E ( Y ) Jadi E ( XY ) =

   

₂ ₁ ₂ ₁

Dari pers (2) dan (3) diperoleh

a 1 1 2 2        dan b 1 2     E ( X | y ) = a + by 1 1 2 2        + 1 2    y

(16)

12 1 1 2 2 (y )        

Jika E ( X | y ) berupa fungsi linier dari y maka

E ( X | y ) = 1 1 2 2 (y )         Terbukti. Teorema 1.6.3

Misalkan E(𝑌|x) berupa fungsi linear dari x. Jika k(x) = E [{𝑌 − 𝐸(𝑌|𝑥)}2|𝑥] maka E[𝑘(𝑥)]=𝜎₂2(1 − 𝜌2₎ Bukti : Ingat : E (𝑌|𝑥) = 𝜇₂ + 𝜌𝜎2 𝜎1(𝑥 − 𝜇1) K(x) = E [{𝑌 − 𝐸(𝑌|𝑥)}2_|𝑥] =∫ {𝑌 − 𝜇2− 𝜌 𝜎2 𝜎1(𝑥 − 𝜇1)} 2 ~ −~ 𝑓(𝑦|𝑥)𝑑𝑦 = 1 𝑓(𝑥)∫ {(𝑌 − 𝜇2) − 𝜌 𝜎2 𝜎1(𝑥 − 𝜇1)} 2 ~ −~ 𝑓(𝑦|𝑥)𝑑𝑦

Jika kedua ruas kita kalikan dengan f(x) kemudian kita integrasikan terhadap x dari −~ sampai , maka

∫ 𝑘(𝑥)𝑓(𝑥) = ~ −~ ∫ ∫ ~ −~ {𝑌 − 𝜇₂− 𝜌𝜎2 𝜎₁(𝑥 − 𝜇1)} 2 ~ −~ 𝑓(𝑦|𝑥)𝑑𝑦𝑑𝑥 = ∫ ∫ ~ −~ {(𝑌 − 𝜇₂)2_{− 2 𝜌}𝜎2 𝜎₁(𝑥 − 𝜇1)(𝑌 − 𝜇2) ~ −~ + 𝜌2𝜎2 𝜎1 (𝑥 − 𝜇1)2} 𝑓(𝑥, 𝑦)𝑑𝑦𝑑𝑥

(17)

13 = E[(𝑌 − 𝜇₂)2_{− 2 𝜌}𝜎2 𝜎1(𝑥 − 𝜇1)(𝑌 − 𝜇2) + 𝜌 2 𝜎2 𝜎1𝐸[(𝑥 − 𝜇1) 2_{] ]} =𝜎₂2_{− 2𝜌}𝜎2 𝜎1(𝜌𝜎1𝜎2) + 𝜌 2 𝜎22 𝜎₁2𝜎1 2 Ingat 𝜌 =𝐸(𝑥−𝜇1)(𝑌−𝜇2) 𝜎1𝜎2 =𝜎₂2− 2𝜌₁2𝜎₂2+ 𝜌2𝜎₂2 =𝜎₂2− 𝜌2𝜎₂2 =𝜎2(1 − 𝜌2)

Karena ∫ 𝑘(𝑥)𝑓(𝑥) = _−~~ 𝐸[𝑘(𝑥)] berarti 𝐸[𝑘(𝑥)]=𝜎2(1 − 𝜌2) (terbukti)

CONTOH 4 :

Misalkan E(𝑌|x) = 4x+3 dan E (𝑋|y) = 1

16𝑦 − 3 Hitunglah 𝜎₁ , 𝜎_{2 ,}𝑑𝑎𝑛𝜌 ! Penyelesaian : Diketahui : E (𝑌|𝑥) = 𝜇₂+ 𝜌𝜎2 𝜎1(𝑥 − 𝜇1) E (𝑌|𝑥) = 𝜇₁+ 𝜌𝜎1 𝜎2(𝑦 − 𝜇2) sehingga E (𝑌|𝜎1) = 𝜇2 E (𝑋|𝜎₁) = 𝜇1

sehingga E(𝑌|σ₁) = 4x+3 dan E (𝑋|σ₂) = 1

16𝑦 − 3

(σ₁)= 4x+3 dan E (σ₂) = 1

(18)

14

Kemudian diperoleh 𝜎₁ = −15

4 𝑑𝑎𝑛 𝜎2 = −12

Untuk menghitung 𝜌 perhatikan persamaan 1 dan 2 dengan mengalikan koefisien dari x dan koefisien dari y.

=𝜌 𝜎2 𝜎1𝜌 𝜎1 𝜎2 = 𝜌 2 Akibatnya 𝜌2 _{= 4.} 1 16= 1 4 𝑗𝑎𝑑𝑖 𝜌 = 1 2

(19)

15

LATIHAN SOAL

Misalnya X dan Y dua peubah acak diskrit yang memiliki f. k. p bersama sebagai berikut:

f(x) ={ 1

4, 𝑢𝑛𝑡𝑢𝑘 𝑥 = (0,0), (1,1), (2,2), (3,3) 0, 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛

1. Berapakah mean dari x? a. 1 2 b. 1 c. 3 2 d. 2

2. Berapakah mean dari y? a. 1 2 b. 1 c. 3 2 d. 2

3. Berapakah variansi dari x? a. 1 4 b. 3 4 c. 5 4 d. 7 4

4. Berapakah variansi dari y? a. 1 4 b. 3 4 c. 5 4 d. 7 4

5. Berapakah ekspetasi xy? a. 1

2

b. 3

(20)

16

c. 5

2

d. 7

2

6. Berapakah kovariansi x dan y? a. 1 2 b. 1 3 c. 5 4 d. 1

7. Berapakah koefisien korelasi antara x dan y? a. 1 b. 1 3 c. 1 2 d. 1 4

8. Jika X dan Y peubah acak dengan variansi 𝜎x2 = 3,𝜎y2 = 3 dan kovariansi 𝜎xy =

3.Tentukan variansi peubah acak Z = 2X – 3Y + 7! a. 1

b. 2 c. 3 d. 4

PEMBAHASAN

Tabel distribusi peluang bersama dari X dan Y X Y 0 1 2 3



0 1 4 0 0 0 1 4

(21)

16 1 0 1 4 0 0 1 4 2 0 0 1 4 0 1 4 3 0 0 0 1 4 1 4



1 4 1 4 1 4 1 4 1 1. Mean dari x E(X) = ∑3_𝑋=0𝑥. 𝑓1(𝑥)= 0. (1 4) + 1. ( 1 4) + 2. ( 1 4) + 3. ( 1 4) = 3 2 2. Mean dari y E(X) = ∑3_𝑋=0𝑥. 𝑓2(𝑦)= 0. (1 4) + 1. ( 1 4) + 2. ( 1 4) + 3. ( 1 4) = 3 2 3. Variansi dari x 𝜎x2 = E(X2) – (E(X))2 = [0. ( 1 4) + 1. ( 1 4) + 4. ( 1 4) + 9. ( 1 4)] − ( 3 2) 2 = 5 4 4. Variansi dari y 𝜎y2 = E(Y2) – (E(Y))2 = [0. ( 1 4) + 1. ( 1 4) + 4. ( 1 4) + 9. ( 1 4)] − ( 3 2) 2 = 5 4 5. Ekspetasi xy E(XY) = ∑3_𝑋=0∑3_𝑦=0𝑥𝑦. 𝑓(𝑥, 𝑦) = 0.0.f(0,0) + 0.1.f(0,1) + 0.2.f(0,2) + 0.3.f(0,3) + 1.0.f(1,0) + 1.1.f(1,1) + 1.2.f(1,2) + 1.3.f(1,3) + 2.0.f(2,0) + 2.1.f(2,1) + 2.2.f(2,2) + 2.3.f(2,3) + 3.0.f(3,0) + 3.1.f(3,1) + 3.2.f(3,2) + 3.3.f(3,3) = 0 + 0 + 0 + 0 + 0 + 1.1 4 + 0 + 0 + 0 + 0 + 4. 1 4 + 0 + 0 + 0 + 0 + 9. 1 4 = 1 4 + 4 4 + 9 4 = 7 2

(22)

17

6. Kov(X,Y) = E(XY) – E(X).E(Y) = 7

2− 3 2 . 3 2 = 14 4 − 9 4= 5 4

7. Koefisien korelasi antara X dan Y 𝜌 = 𝐾𝑜𝑣 (𝑋, 𝑌) 𝜎x𝜎y = 5 4 √5 4. √ 5 4 = 5 4 5 4 = 1 8. 𝜎z2 = 𝜎2x-3y+7 2 = 𝜎2x-3y 2 = 4𝜎x2 - 12 𝜎xy + 9𝜎y2 = 4(3) – 12(3) + 9(3) = 3

(23)

18

BAB 2

HUBUNGAN HARAPAN DAN VARIANSI DARI PEUBAH ACAK KHUSUS (bahasan 1)

1. Tujuan

Adapun tujuan dari mempelajari materi hubungan harapan dan variansi dari peubah acak adalah :

a. Mengetahui bagaimana hubungan harapan dan variansi dari peubah acak.

b. Memenuhi tugas mata kuliah statistik matematika

2. Materi

Untuk menentukan nilai variansi dari peubah acak khusus terlebih dahulu kita harus dapat mecari nilai harapannya (ekspektasi). Hubungan harapan dan variansi dari peubah acak khusus ditunjukkan oleh rumus sebagai berikut :

 𝑉𝑎𝑟 (𝑥) = 𝐸(𝑥2) − (𝐸(𝑥))2

𝜎2 = 𝐸(𝑥2) − 𝜇2

 𝐸(𝑥) = ∑ 𝑥. 𝑓(𝑥)

Disini terdapat beberapa teorema yang akan menunjukkan hubungan harapan dan variansi, beberapa teorema tersebut diataranya :

(24)

19 Teorema 1.7.1 :

Jika 𝑥 berdistribusi Bernoulli 𝑝(𝑥) = {𝑝𝑥(1 − 𝑝)1−𝑥, 𝑥 = 0, 1 0, untuk 𝑥 yang lain Maka 𝐸(𝑥) = 𝑝 dan 𝑉𝑎𝑟(𝑥) = 𝑝𝑞 Bukti : E(X) = ∑_𝑥𝑥 . 𝑝(𝑥) E (X) =



   1 0 1 ) 1 ( x x x p xp = 0 1 0 11 ) 1 ( 1 ) 1 ( 0p  p   p  p  = 0(1p)1.p = p Jadi E (X) = p. E (X2) =



   1 0 1 2 ) 1 ( x x x p p x = 2 0 1 0 2 1 1 ) 1 ( 1 ) 1 ( 0 p  p   p  p  = 0(1 p)1.p = p Jadi E (X2_{) = p.} Var (X) = E (X2) -



E

 

X



2 = p – p2

(25)

20

= p (1 – p)

= pq Ingat : q = 1 – p.

Jadi, jika X berdistribusi Bernoulli p(x) =       lain yang untuk x , 0 . 1 , 0 , ) 1 ( p 1 x px x

maka E (X) = p dan Var (X) = pq.

Teorema 1.7.2 :

Jika 𝑥 berdistribusi binomial 𝑝(𝑥) = {(

𝑛

𝑥)𝑝𝑥(1 − 𝑝)𝑛−𝑥, 𝑥 = 1, 2, 3, … , 𝑛



x n x n x p p x n x x x           



1 (1 ) 0 =





x



Jadi, jika X berdistribusi Bernoulli p(x) =              lain yang untuk x , 0 . ,..., 2 , 1 , 0 , ) 1 ( p x n p x n _x _n _x

maka E (X) = np dan Var (X) = npq. Terbukti.

Teorema 1.7.3 :

Jika 𝑥 berdistribusi poisson 𝑝(𝑥) = {𝑒−𝜆 𝜆

𝑥

𝑥!, 𝑥 = 0, 1, 2, …

0, untuk 𝑥 yang lain maka 𝐸(𝑥) = 𝜆 dan 𝑉𝑎𝑟(𝑥) = 𝜆 Bukti :

)

(

)

(

tx x

t

E

e

M



(28)

23

Jika x~p(x) maka f.p.m adalah

Jika t = 0 maka

Jadi, jika x berdistribusi poisson

)

1 (

.

~

0 )

!

)

(

.

!

.

~

0 

























t

e

t

e

t

e

x

t

e

x

e

x

tx

e



) 1 ( ) ( ) ( ' : ) 1 ( ) (     t e e t e t M akibatnya t e e t x M   











)

0 (

'

1 )

1 .

(

)

0 (

'

)

1

0 (

)

0 (

)

0 (

'

M

e

M

)

1 (

2 )

(

)

1 (

)

(

)

(

"

t



e

t

e

t





e

t

e

t



M









         2 2 2 ) 0 ( " 2 ) 2 ( 2 ) 0 ( " M x E M



Terbukti . dan maka ,... 2 , 1 , 0 , ! . lain yang untuk x , 0 ) (











     x x e x x f

(29)

24 Teorema 1.7.4 :

Jika X berdistribusi seragam f (x) =     _ _ _  lain yang untuk x , 0 c b c, x b , 1 b c maka E (X) = 2 c b dan Var (X) =





12 2 b c Bukti :



 _   c b b c x b c dx b c x X E 1 2 2 1 1 ) ( = 1 2[ 𝑐2_{− 𝑏}2 𝑐 − 𝑏 ] = 1 2 (𝑐 + 𝑏)(𝑐 − 𝑏) (𝑐 − 𝑏) =1 2(𝑐 + 𝑏) E(𝑥2_{) = ∫ 𝑥}2 1 𝑐 − 𝑏𝑑𝑥 = c b 1 3 1 𝑐 − 𝑏𝑥 3_Ι b c = 1 3 1 𝑐 − 𝑏(𝑐 3_{− 𝑏}3₎ = 1 3 1 𝑐 − 𝑏(𝑐 2_{+ 𝑏𝑐 + 𝑏}2_{)(𝑐 − 𝑏)} = 1 3(𝑐 2_{+ 𝑏𝑐 + 𝑏}2₎

(30)

25

Var (𝑥) = E[x] − [E(𝑥)]2

= 1 3(𝑐 2_{+ 𝑏𝑐 + 𝑏}2_{) − [}1 2(𝑐 + 𝑏)] 2 = 1 12(𝑐 − 𝑏) 2

Jadi, jika berdistribusi seragam 𝑓(𝑥) = {

1

𝑐−𝑏, 𝑏 ≤ 𝑥 ≤ 𝑐, 𝑏 ≠ 𝑐

0, untuk 𝑥 yang lain

Maka 𝐸(𝑥) = 𝑏+𝑐

2 dan Var (𝑥) = (𝑐−𝑏)2

(31)

26

SOAL-SOAL DAN PEMBAHASANNYA

A. Pilihan berganda

Jawablah pertanyaan di bawah ini dengan memilih jawaban yang tepat dengan memberi tanda silang pada huruf A, B, C, D, atau E.

1. Probabilitas untuk memperoleh sedikitnya 4 kali tanda gambar dalam 6 kali pelemparan sebuah koin adalah...

A. 11/32 D. 22/32

B. 11/64 E. 22/96

C. 11/96

Jawaban : A Penyelesaian :

Misalnya X menyatakan banyak tanda gambar yang muncul Dalam hal ini, 𝑥 = 4, 𝑛 = 6 dan 𝑝 = 1/2

Fungsi peluang dari X adalah : 𝑝(𝑥) = (6_𝑥) (1 2) 𝑥 (1 2) 6−𝑥 ; x = 4, 5, 6 Jadi : P(X ≥ 4) = P(X = 4, 5, 6) = P(X = 4) + P(X = 5) + P(X = 6) = (6₄) (1 2) 4 (1 2) 2 + (6₅) (1 2) 5 (1 2) 1 + (6₆) (1 2) 6 (1 2) 0 = 15 64+ 6 64+ 1 64 P(X ≥ 4) =22 64 = 11 32

(32)

27

2. Misalkan X adalah peubah acak berdistribusi poisson dengan parameter 𝜆. Jika P (X = 0) = 0,2, maka nilai P ( X = 2 ) adalah. Jawab : A. 0,2584 D. 0,2376 B. 0,3256 E. 0,4432 C. 0,3342 Jawaban : A Penyelesaian : P(X) = P(X = x) = 𝜆 𝑥_𝑒−𝜆 𝑥! ; x = 0, 1, 2, 3, … P(X = 0) = 0,2 𝜆0𝑒−𝜆 0! = 0,2 𝑒−𝜆 = 0,2 𝜆 = 1,6 Jadi : P(X= 2) =(1,6) 2_𝑒−1,6 2! = 0, 2584

3. Misalkan fungsi densitas dari X berbentuk : g (x) = 1

4 ; 0< 𝑥 < 4

= 0, x lainnya

(33)

28 Jawab : A. 2/3 C. 3/4 E. 4/5 B. 1/2 D. 3/2 Jawaban : B Penyelesaian :

Berdasarkan sifat dari fungsi densitas, maka : P( 1< 𝑥 < 3) = ∫₁31₄ dx = [1 4𝑥]₁ 3 = [1 4. 3] − [ 1 4. 1] = [3 4] − [ 1 4] = [2 4] = [1 2] P( 1< 𝑥 < 3) = 2 4 = 1 2

1. Suatu suku cadang dapat menahan uji guncangan tertentu dengan probabilitas 0.75. Hitung probabilitas bahwa tepat 2 dari 4 suku cadang yang diuji tidak akan rusak.

a. 27 128 d. 25 128 b. 27 127 e. 25 125 c. 28 127

(34)

29

Jawaban : A Penyelesaian :

Misalnya X menyatakan banyak tanda gambar yang muncul Dalam hal ini, 𝑥 = 2, 𝑛 = 4 dan 𝑝 = 0,75 = 3/4

Fungsi peluang dari X adalah : 𝑝(𝑥) = (𝑛_𝑥)(𝑝)𝑥_{(1 − 𝑝)}𝑛−𝑥_{; x = 2} 𝑝(2) = (4₂) (3 4) 2 (1 4) 4−2 ; 𝑝(2) = 4! 2! 2!( 3 4) 2 (1 4) 2 = 27 128

B. Selesaikanlah soal di bawah ini!

1. Apakah artinya Y ~ P(y, 2)? Kemudian tuliskan bentuk fungsi peluangnya. Fungsi peluang dari Y.

Penyelesaian :

Y ~ P(y, 2) artinya peubah acak Y berdistribusi poisson dengan parameter 𝜆 = 2

Fungsi peluang dari Y berbentuk : P(y) = 2

𝑦_𝑒−2

𝑦! ; y = 0, 1, 2, 3, …

2. Apakah artinya Y ~ B(y, 6, 1

4 ) kemudian tuliskan bentuk fungsi

peluangnya.

Penyelesaian :

Y ~ B(y, 6, 1

4 ) artinya peubah acak Y mengikuti distribusi binomial

dengan banyak pengulangan eksperimennya sampai 6 kali, peluang terjadinya peristiwa sukses sebesar 1

(35)

30

Fungsi peluang dari Y adalah : P(y) = (6_𝑦) (1 4) 𝑦 (3 4) 6−𝑦 ; y = 0, 1, 2, 3, 4, 5, 6, 3. Misalkan Y~ B(y, 1, 1 4 )

Tentukan fungsi distribusi dari Y.

Penyelesaian :

Fungsi peluang dari Y adalah :

P(y) = P(Y=y) = (1 4) 𝑦 (3 4) 1−𝑦 ; y = 0,1 Jadi : p(0) = 3 4 P(1) = 1 4

Distribusi peluang dari Y adalah :

Y 0 1

P(y) 3

4

1 4

Fungsi distribusi dari Y adalah Untuk y < 0 F(y) = 0 Untuk 0 ≤ y < 1 F(y) = ∑1≤𝑦𝑝(𝑡) = ∑1≤0𝑝(𝑡) = p(0) F(y) = 3 4

(36)

31 Untuk y ≥ 1 F(y) = ∑1≤𝑦𝑝(𝑡) = ∑1≤1𝑝(𝑡) = p(0) + p(1) = 3 4+ 1 4 F(y) = 1 Sehingga : F(y) = 0, y < 0 = 3 4 ; 0 ≤ 𝑦 < 1 = 1 ; y ≥ 1

4. Misalkan fungsi densitas dari X berbentuk : g(x) = 1

5 , 0 <x < 6

= 0 , x lainnya Hitung P( 1< x < 4) !

Penyelesaian :

Berdasarkan sifat dari fungsi densitas , maka : P( 1 < x < 5) = ∫₁4₅1𝑑𝑥 =1 4(𝑥]𝑥=1) 4 P( 1< x < 5) =3 4

(37)

32

5. Misalkan x adalah peubah acak berdistribusi normal dengan rataan 3 dan varian 5. Jika y = 3x2-2 , maka E(y) adalah….

penyelesaian :

diketahui E(x)= 3 dan var(x)=5 maka : var(x)= E(x2_{) –(E(x))}2

5= E(x2) – 9 E(x2)= 14

Sehingga E(y) = E(2x2-1) = E(2x2) – 1 = 2(14) – 1 E(y) = 27

6. Hitunglah probabilitas peristiwa binomial! 𝑝 =1 2, 𝑞 = 1 2, 𝑟 = 2, 𝑑𝑎𝑛 𝑛 = 5 penyelesaian : Diket: 𝑝 =1 2, 𝑞 = 1 2, 𝑟 = 2, 𝑑𝑎𝑛 𝑛 = 5

Ditanyakan: 𝑃(𝑟) = probabilitas peristiwa binomial Jawab:

𝑃(𝑟) = (𝑛

(38)

33 𝑃(2) = (5 2) ( 1 2) 2 (1 2) 5−2 𝑃(2) =5.4.3! 2! .3!. ( 1 4) ( 1 8) 𝑃(2) = 5 16

Jadi, probabilitas peristiwa binomial tersebut adalah 5

16

7. Dalam pengetosan 3 buah uang logam, berapakah probabilitas untuk memperoleh 2 buah H?

Penyelesaian:

Diket: 𝑝 =1

2 Peluang satu koin muncul H

𝑟 = 2 memperoleh 2 buah H 𝑛 = 3 3 buah uang logam

Ditanyakan: 𝑃(2) = probabilitas memperoleh 2 H Jawab: 𝑃(𝑟) = (𝑛 𝑟) 𝑝𝑟(1 − 𝑝)𝑛−𝑟, 𝑑𝑒𝑛𝑔𝑎𝑛 1 − 𝑝 = 𝑞 𝑃(2) = (3 2) ( 1 2) 2 (1 2) 3−2 𝑃(2) = 3.2! 2! .1!. ( 1 4) ( 1 2) 𝑃(2) = 3 8

Jadi, probabilitas untuk memperoleh 2 buah H adalah 3

8

8. Andaikan kita memperoleh soal tipe objektif benar-salah sebanyak 10 buah. Dalam menyelesaikan soal-soal itu andaikata ada anak yang tidak belajar,

(39)

34

menjawabnya itu hanya melalui tebak-menebak, berapakah probabilitas (nilai peluang) yang memperoleh paling tidak 7 buah soal jawabannya benar.

Penyelesaian:

Diket: 𝑝 =1

2 Peluang satu soal dengan pilihan benar-salah

𝑟 = 7, 8, 9,10 paling tidak satu buah soal benar 𝑛 = 10 10 buah soal

Ditanyakan: 𝑃(𝑟) = probabilitas paling tidak 7 buah soal benar. Jawab:

Membuat tabel distribusi

𝑟 ₍𝑛 𝑟) 𝑝 𝑟 _(𝑞)𝑛−𝑟 _{𝑛𝑖𝑙𝑎𝑖 𝑝𝑒𝑙𝑢𝑎𝑛𝑔} = (𝑛 𝑟) 𝑝𝑟(𝑞)𝑛−𝑟 7 ( 10 7) = 120 (1₂) 7 (1 2) 3 120 (1 2) 10 8 ( 10 8) = 45 (1₂) 8 (1 2) 2 45 (1 2) 10 9 ( 10 9) = 10 (1₂) 9 (1 2) 1 10 (1 2) 10 10 ( 10 10) = 1 (1₂) 10 (1 2) 0 (1 2) 10 Peluang total 176 1024= 0,172

(40)

35 RANGKUMAN 1. Distribusi Bernoulli a. Fungsi peluang : 𝑝𝑥(1 − 𝑝)1−𝑥_{, 𝑥 = 0, 1} b. Notasi :X ~ B (x ; 1 , p) c. Rataan : 𝜇 = 𝑝 d. Varians : 𝜎2 = 𝑝(1 − 𝑝)

e. Fungsi pembangkit Momen :𝑀𝑥(𝑡) = (1 − 𝑝) + 𝑝. 𝑒𝑡 ; 𝑡 𝜖 𝑅

2. Distribusi Binomial a. Fungsi peluang : 𝑝(𝑥) = 𝑃(𝑋 = 𝑥) = (𝑛_𝑥)𝑝𝑥_{(1 − 𝑝)}𝑛−𝑥_{, 𝑥 =} 1, 2, 3, … , 𝑛 b. Notasi X~ B (x ; n , p) c. Rataan : 𝜇 = 𝑛𝑝 d. Variansi : 𝜎2 = 𝑛𝑝(1 − 𝑝)

e. Fungsi pembangkit Momen :𝑀_𝑥(𝑡) = [(1 − 𝑝) + 𝑝. 𝑒𝑡_]𝑛_{; 𝑡 𝜖 𝑅}

3. Distribussi Poisson a. Fungsi peluang : 𝑝(𝑥) = 𝑃(𝑋 = 𝑥) = 𝑒−𝜆 𝜆𝑥 𝑥!, 𝑥 = 0, 1, 2, … b. Notasi X ~P (𝑥 ; ℷ) c. Rataan : 𝜇 = ℷ d. Variansi : 𝜎2 _{= ℷ}

e. Fungsi pembangkit Momen :𝑀_𝑥(𝑡) = 𝑒ℷ(𝑒𝑡−1)_{; 𝑡 𝜖}

4. Distribusi Seragam a. Fungsi densitas : 𝑓(𝑥) = 1 𝛽−𝛼 ; 𝛼 < 𝑥 < 𝛽 b. Rataan ( 𝜇 ) = E(X) = (1 2) (𝛼 + 𝛽) c. Varians = 𝜎₂ = 𝑉𝑎𝑟 (𝑋) = (1 12) (𝛽 − 𝛼) 2

d. Fungsi pembangkit Momen : 𝑀_𝑥(𝑡) =𝑒𝛽𝑡−𝑒𝛼𝑡

𝑡(𝛽−𝛼) ; 𝑡 ≠ 0

(41)

36

BAB 3

HUBUNGAN HARAPAN DAN VARIANSI DARI PEUBAH ACAK KHUSUS (bahasan 2)

Tujuan

Adapun tujuan dari mempelajari materi hubungan harapan dan variansi dari peubah acak kontinu adalah

a. Mengetahui bagaimana hubungan harapan dan variansi dari peubah acak kontinu.

b. Memenuhi tugas mata kuliah statistik matematika

Materi

Ekspektasi

Jika X menyatakan suatu variabel acak kontinu yang dapat mengambil setiap nilai x yang memiliki probabilitas 𝑓(x), maka ekspektasi atau nilai harapan dinyatakan sebagai berikut:

𝐸(𝑋) = ∫ 𝑥. 𝑓(𝑥) 𝑑𝑥

Variansi

Misalkan X peubah acak kontinu dengan distribusi peluang 𝑓(𝑥) dan rataan 𝜇, maka 𝑉𝑎𝑟(𝑋) = 𝜎2 adalah 𝜎2 = 𝐸[(𝑋 − 𝜇)2]

𝑉𝑎𝑟 (𝑋) = 𝜎2 = 𝐸(𝑋 − 𝜇)2 = 𝐸(𝑋2) − 𝜇2 _{= 𝐸(𝑋}2_{) − [𝐸(𝑋)]}2

Teorema 1.7.5

Jika 𝑥 berdistribusi eksponen 𝑓(𝑥) = {

1 𝜆𝑒

−𝑥

𝜆, 0 ≤ 𝑥 ≤ ∞

0, untuk 𝑥 yang lain Maka 𝐸(𝑥) = 𝜆danVar(𝑥) = 𝜆2

(42)

37 Bukti : 𝐸(𝑥) = ∫ 𝑥₀∞ 1_𝜆𝑒−𝑥𝜆𝑑𝑥 = ∫ 𝑦𝑒∞ −𝑦_𝜆𝑑𝑦 0 = 𝜆 ∫ 𝑦𝑒∞ −𝑦_𝑑𝑦 0 = 𝜆(1!) 𝐸(𝑥) = 𝜆 𝐸(𝑥2) = ∫ 𝑥2 1 𝜆 ∞ 0 𝑒 −𝑥 𝜆𝑑𝑥 = ∫ 𝑥𝑥 𝜆𝑒 −𝑥 𝜆𝑑𝑥 ∞ 0 = ∫ 𝜆𝑥 𝜆 𝑥 𝜆𝑒 −𝑥 𝜆𝑑𝑥 ∞ 0 = ∫ 𝜆𝑦𝑦𝑒−𝑦𝜆 ∞ 0 𝑑𝑦 = 𝜆2_{∫ 𝑦}2_𝑒−𝑦_𝑑𝑦 ∞ 0 = 𝜆2(2!) = 2𝜆2 Misalkan : 𝑦 =𝑥 𝜆↔ 𝑑𝑦 = 1 𝜆𝑑𝑥 Catatan : 𝑒𝑦= ∫ 𝑦 𝑛 𝑛! 𝑑𝑦 ∞ 0 𝑒𝑦= 1 𝑛!∫ 𝑦 𝑛_𝑑𝑦 ∞ 0 𝑛! = 1 𝑒𝑦∫ 𝑦𝑛𝑑𝑦 ∞ 0 𝑛! = ∫ 𝑦 𝑛 𝑒𝑦 𝑑𝑦 ∞ 0 𝑛! = ∫ 𝑦𝑛𝑒−𝑦𝑑𝑦 ∞ 0 Karena n = 1, diperoleh : 1! = ∫ 𝑦 𝑒−𝑦𝑑𝑦 ∞ 0 Misalkan : 𝑦 =𝑥 𝜆↔ 𝑑𝑦 = 1 𝜆𝑑𝑥

(43)

38

𝑉𝑎𝑟 (𝑥) = 𝐸(𝑥2) − (𝐸(𝑥))2 𝑉𝑎𝑟 (𝑥) = 2𝜆2− (𝜆)2 𝑉𝑎𝑟 (𝑥) = 2𝜆2_{− 𝜆}2

𝑉𝑎𝑟(𝑥) = 𝜆2

Jadi, jika 𝑥 berdistribusi eksponen 𝑓(𝑥) = {

1 𝜆𝑒

−𝑥

𝜆, 0 ≤ 𝑥 ≤ ∞

0, untuk 𝑥 yang lain Maka 𝐸(𝑥) = 𝜆 dan 𝑉𝑎𝑟(𝑥) = 𝜆2 (terbukti)

Contoh :

Tentukan fungi densitas dari 𝑋~𝐸𝑥𝑝(2)! Jawab :

𝑋~𝐸𝑥𝑝(2) merupakan peubah acak X berdistribusi eksponensial dengan parameter 𝜃 = 2.

Fungsi densitas dari X berbentuk : 𝑔(𝑥) = 1 2. 𝑒 −𝑥 2 ; 𝑥 > 0 = 𝑜 ; 𝑥 𝑙𝑎𝑖𝑛𝑛𝑦𝑎 Teorema 1.7.6

Dipelajari pertama kali pd abad ke -18 Pencetus :

De Moivre (1733) Laplace (1775)

(44)

39

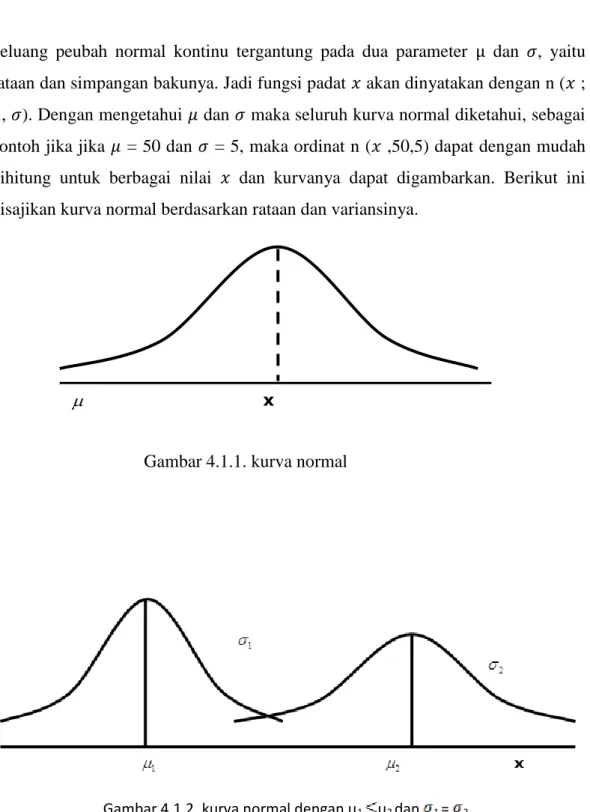
Suatu variabel random kontinu x dikatakan berdistribusi normal dgn mean  dan variansi 2 adalah jika mempunyai fungsi probabilitas yang berbentuk :

2 2( ) 2 1 2 2 1 ) (       e X X f Untuk - < x < - << 2_{> 0 dan}_{= 3,14 dan e = 2,718}

Jika X berdistribusi normal

2 2 1 2 1 ) (           



         2 2 2 1 2 y z e I dy dz

Dalam koordinat polar diketahui:  cos . r y  maka 2 2 2 cos . r y   sin . r x maka 2 2 2 sin . r x  Sehingga diperoleh : 2 2 2 2 2 2 2 sin cos . r r r z y      Kita substitusikan 2 2 2 r z y   maka diperoleh : I e r r.dr.d 2 2 1 2

 

       

Dengan menggunakan teori limit diperoleh , substitusikan



     2 2 1 y e I dy =  2 kedalam persamaan (1)

 

_

_2 x Var . Terbukti.

(47)

42

Sifat-sifat distribusi normal :

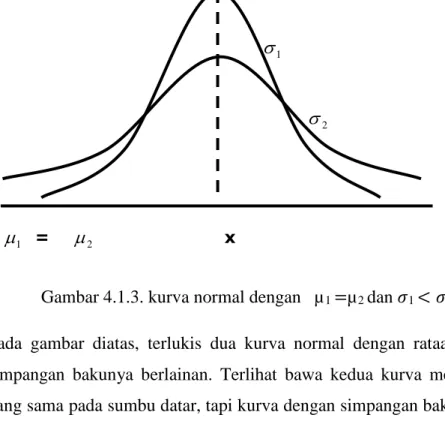
1. Harga modus, yaitu harga pada sumbu x dengan kurva maksimum terletak pada x = 

2. Kurva normal simetris terhadap sumbu vertikal melalui  3. Kurva normal mempunyai titik belok pada x = 

4. Kurva normal memotong sumbu mendatar secara asimtotis

5. Luas daerah dibawah kurva normal dan diatas sumbu mendatar sama dengan 1.

Kurva Normal

Luas bagian kurva normal antara x=a dan x=b dapat ditulis menjadi P(a≤x≤b) Nilai ini untuk distribusi normal standar telah ditabelkan  Tabel III

Distribusi normal standar adalah distribusi normal yang mempunyai mean =0 dan standar deviasi =1

Untuk distribusi normal yang bukan distribusi normal standar maka diubah dengan rumus transformasi Z :

    x z Contoh:

Misalkan peubah acak Y berdistribusi gamma dengan parameter 𝛼 = 2 𝑑𝑎𝑛𝛽 = 3. Peluang bahwa harga Y lebih dari 4 adalah….

a. 0,6151 d. 1,543 b. 1,6151 e. 0,153

x 𝜇

(48)

43

c. 0,06151 Penyelesaian :

Fungsi densitas dari Y berbentuk :ℎ(𝑦) = (𝑦

9) 𝑒 −𝑦 3_{; y > 0} = 0 ; yang lainnya Jadi : P(y>4) = ∫∞1₉𝑦. 𝑒−𝑦3 𝑑𝑦 4 = 1 9𝑏→∞lim 𝑒 −𝑦 3 𝑑𝑦

Integral di atas dapat diselesaikan denga integral parsial. Misalnya u = y , maka du = dy 𝑑𝑣 = 𝑒 −𝑦 3 𝑑𝑦, 𝑚𝑎𝑘𝑎𝑣 = −3. 𝑒 −𝑦 3 𝑝(𝑦 > 4) = 1 9𝑛→∞lim (−3𝑦. 𝑒 −𝑦 3 | +3 ∫ 𝑒 −𝑦 3𝑑𝑦 𝑏 4 𝑦=4𝑏 ) = 1 9𝑛→∞lim (−3𝑦| −9. 𝑒 −𝑦 3 ]_𝑦=4𝑏𝑑𝑦 𝑦=4𝑏 ) =1 9𝑛→∞lim (−3𝑏. 𝑒 −𝑦 3 + 12. 𝑒 −𝑦 3 . 9. 𝑒 −𝑦 3 + 9. 𝑒 −𝑦 3 ) = 1 9[ lim𝑛→∞(−3𝑏. 𝑒 −𝑦 3) + 21. 𝑒 −𝑦 3 lim 𝑛→∞(9. 𝑒 −𝑏 3 )] =1 9(0 + 21. 𝑒 −4 3 − 0) 𝑝(𝑦 > 4) = (21 9 ) e −4 3 = 0,6151 Teorema 1.7.7

(49)

44 Γ(𝑛) ≡ ∫ 𝑥𝑛−1_𝑒−𝑥_{𝑑𝑥 = 2 ∫ 𝑦}2𝑛−1_𝑒−𝑦2_𝑑𝑦 ∞ 0 ∞ 0 bukti: Γ(𝑛) ≡ ∫ 𝑥𝑛−1_𝑒−𝑥_𝑑𝑥 ∞ 0 Subtitusi 𝑥 = 𝑦2 𝑑𝑥 = 2𝑦𝑑 Sehingga ∫ 𝑥𝑛−1𝑒−𝑥𝑑𝑥 ∞ 0 = ∫(𝑦2)𝑛−1𝑒−(𝑦2)2𝑦𝑑𝑦 ∞ 0 = 2 ∫ 𝑦2𝑛−2_𝑒−𝑦2_𝑦𝑑𝑦 2 0 = 2 ∫ 𝑦2𝑛−1𝑒−𝑦2𝑑𝑦 1 0

Peubah acak X berdistribusi gamma dan dinamakan peubah acak gamma jika Fkp-nya berbentuk: 𝑓(𝑥) = { 1 √𝛼𝛽𝛼𝑥 𝑎−1_𝑒−𝑥 𝛽 , 𝑥 > 0(𝛼, 𝛽 > 0) 0, 𝑥 ≤ 0

Jika X berdistribusi Gamma G(x,, A = 0 ) maka 𝜇 = 𝐸𝑋 = 𝛼𝛽 𝜎2 _{= 𝑉𝑎𝑟(𝑋) = 𝛼𝛽}2

(50)

45 Bukti: 𝜇 = 𝐸𝑋 = ∫ 𝑥𝑓(𝑥)𝑑𝑥 𝑥 −𝑥 = ∫ 1 Γ𝛼𝛽𝛼 ∞ 0 𝑥𝛼𝑒− 𝑥 𝛽_𝑑𝑥 = 1 Γ𝛼𝛽𝛼∫ 𝑥𝛼𝑒 −_𝛽𝑥 𝑑𝑥 𝑥 0 Misalkan 𝑥

𝛽= 𝑦 maka 𝑥 = 𝛽𝑦 dan 𝑑𝑥 = 𝛽𝑑𝑦 dan karena 0 < 𝑥 < ∞, maka 0 <

𝑦 < ∞ Maka 𝜇 = 𝐸𝑋 = 1 Γ𝛼𝛽𝛼∫(𝛽𝑦)𝛼𝑒 −𝑥 𝛽_𝑑𝑥 𝑥 0 = 𝛽 Γ𝛼∫ 𝑦 𝛼_𝑒−𝑦 𝑥 𝑜 𝑑𝑦 = 𝛽 Γ𝛼Γ(𝛼 + 1) = 𝛽 Γ𝛼𝛼 − √𝛼 = 𝛼𝛽

Sehingga terbukti bahwa 𝜇 = 𝐸(𝑋) = 𝛼𝛽

Sifat fungsi Gamma : 1. (p + 1) = p (p)

(51)

46 3. (1 2) = √π Bukti: Γ(1) = ∫ 𝑥1−1_𝑒−𝑥_{𝑑𝑥 = ∫ −𝑒}−𝑥_] 0 ∞_{= 1} ∞ 0 ∞ 0 Γ(𝑛) = ∫ 𝑥𝑛−1_𝑒−𝑥_{𝑑𝑥 = −𝑥}𝑛−1_𝑒−𝑥_] 0 ∞_{+ ∫ 𝑒}−𝑥_{(𝑛 − 1)𝑥}𝑛−2_𝑑𝑥 ∞ 0 ∞ 0 Γ(𝑛) = (𝑛 − 1)Γ(𝑛 − 1)

Jadi, secara langsung dibuktikan bahwa Γ(1) = 1, dan dengan menggunakan integrasi perbagian telah diperlihatkan bahwa untuk n > 1, Γ(𝑛) = (𝑛 − 1)Γ(𝑛 − 1). Berdasarkan induksi matematika

Γ(𝑛) = (𝑛 − 1)! bila n suatu bilangan bulat positif.

Contoh:

Misalkan peubah acak x berdistribusi Gamma G(x4, 2, 3). Tentukan titik a sehingga peluangnya 50% memperoleh nilai x yang lebih kecil atau sama dengan a [P (x ≤ a) = 0,05]. (nilai a disebut median dari x juga suatu distribusi x).

Jawab: Diketahui : G(x4, 2, 3) maka  = 4  = 2 A = 3 berarti 3 ≤ x < ∞ Sehingga ∫ f(x)dx = 𝛼 −∞ ∫ 1 24+1 (4+1) 𝛼 −∞ (x − 1)4e−x−92 dx

(52)

47

a − 3

 = 4,671 Karena  = 2 maka a = 2(4,671) + 3 = 12,342 Jadi median G(x4, 2, 3) adalah 12,342 .

Teorema 1.7.8

Suatu variabel acak dikatakan memiliki distribusi Beta dengan parameter a dan b, jika fungsi kepadatanya adalah 𝑓(𝑥) = {

1 𝐵(𝑎,𝑏)𝑥

𝑎−1_{(1 − 𝑥)}𝑏−1_{0 < 𝑥 < 1}

0 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛 di mana 𝐵 (𝑎, 𝑏) merupakan fungsi Beta yang didefinisikan sebagai

𝐵(𝑎, 𝑏) = ∫ 𝑥𝑎−1(1 − 𝑥)𝑏−1 𝑎 < 0, 𝑏 < 0

1

0

Fungsi Beta dihubungkan dengan fungsi Gamma oleh

𝐵(𝑎, 𝑏) =Γ(𝑎)Γ(𝑏) Γ(a + b)

Sehingga distribusi Beta juga dapat didefinisikan oleh fungsi kepadatan

𝑓(𝑥) = {

Γ(𝑎)Γ(𝑏) Γ(a + b) 𝑥

𝑎−1_{(1 − 𝑥)}𝑏−1_{0 < 𝑥 < 1}

0 𝑢𝑛𝑡𝑢𝑘 𝑥 𝑦𝑎𝑛𝑔 𝑙𝑎𝑖𝑛

Mean dan variansi dari distribusi Beta dengan parameter a dan b masing-masing adalah 𝜇 = 𝑎 𝑎 + 𝑏 𝑑𝑎𝑛 𝜎 2 ₌ 𝑎𝑏 (𝑎 + 𝑏 + 1)(𝑎 + 𝑏)2 Bukti :

(53)

48

Menghitung momen dari distribusi Beta bisa dilakukan dengan metode sebagai berikut 𝐸𝑋𝑛 ₌ 1 𝐵(𝑎, 𝑏)∫ 𝑥 𝑛_𝑥𝑎−1 1 0 (1 − 𝑥)𝑏−1_𝑑𝑥 = 1 𝐵(𝑎,𝑏)∫ 𝑥 (𝑎+𝑛)−1 1 0 (1 − 𝑥) 𝑏−1_{𝑑𝑥 ……….(1)}

maka juga dapat diperoleh persamaan 𝐸𝑋𝑛 ₌𝐵(𝑎+𝑛,𝑏)

𝐵(𝑎,𝑏) =

Γ(𝑎+𝑛)Γ(𝑎+𝑏)

Γ(𝑎+𝑏+𝑛)Γ(𝑎) ………..(2)

Berdasarkan persamaan (1) dan persamaan (2), maka untuk memperoleh mean

(EX) dan 𝑉𝑎𝑟(𝑋) = (𝐸𝑋2_{) − [(𝐸𝑋)]}2_{adalah dengan mensubsitusikan n= 1 dan}

n= 2 ke persamaan (2), maka 𝜇 = 𝐸𝑋1 ₌Γ(𝑎 + 1)Γ(𝑎 + 𝑏) Γ(𝑎 + 𝑏 + 1)Γ(𝑎) = 𝑎Γ(𝑎)Γ(𝑎 + 𝑏) (𝑎 + 𝑏)Γ(𝑎 + 𝑏)Γ(𝑎) = 𝑎 𝑎 + 𝑏 Dan 𝑉𝑎𝑟(𝑋) = (𝐸𝑋2) − [(𝐸𝑋)]2 Karena 𝐸𝑋2 = Γ(𝑎 + 2)Γ(𝑎 + 𝑏) Γ(𝑎 + 𝑏 + 2)Γ(𝑎) Maka 𝑉𝑎𝑟(𝑋) = (𝑎 + 1)𝑎 (𝑎 + 𝑏 + 1)(𝑎 + 𝑏)− ( 𝑎 𝑎 + 𝑏) 2

(54)

49 = (𝑎 + 1)𝑎 (𝑎 + 𝑏 + 1)(𝑎 + 𝑏)− 𝑎2 (𝑎 + 𝑏)2 = (𝑎 + 𝑏)(𝑎 2_{+ 𝑎) − 𝑎}2_{(𝑎 + 𝑏 + 1)} (𝑎 + 𝑏)2_{(𝑎 + 𝑏 + 1)} = 𝑎𝑏 (𝑎 + 𝑏 + 1)(𝑎 + 𝑏)2

(55)

50

SOAL-SOAL DAN PEMBAHASANNYA

Jawablah pertanyaan di bawah ini dengan memilih jawaban yang tepat dengan memberi tanda silang pada huruf A, B, C, D, atau E.

1. Misalkan peubah acak y berdistribusi eksponensial dengan parameter 𝜃 = 3. Peluang bahwa y bernilai lebih dari 2 adalah…

a. 0,01534 d. 0,005 b. 0,1534 e. 0,511 c. 0,06

penyelesaian :

Fungsi densitas dari y adalah :ℎ(𝑦) = (1

3) . 𝑒 −𝑦

3 ; 𝑦 > 0

= 0 ;untuk yang lainnya.

𝑝(𝑦 > 2) = 1 − 𝑝(𝑦 ≤ 2) = 1 − ∫ 1 3. 𝑒 −𝑦 3𝑑𝑦 2 0 = 1 −1 3. (−3. 𝑒 −𝑦 3 ] 𝑦=02 ) = 1 + (𝑒−23 − 1) 𝑝(𝑦 > 2) = 𝑒−23 = 0,5134

(56)

51

2. Jika peubah acak X berdistribusi eksponesial dengan parameter 𝜃 = 20, dengan

𝑃(𝑋 > 40| 𝑋 > 10) adalah...

Penyelesaian :

Fungsi densitas dari y adalah :𝑔(𝑥) = (1

20) . 𝑒 −𝑥

20 ; 𝑥 > 0

= 0 ;untuk yang lainnya.

𝑝(𝑥 > 40) = 1 − 𝑝(𝑥 ≤ 40) = 1 − ∫ 1 20. 𝑒 −𝑥 20𝑑𝑥 40 0 = 1 − 1 20. [−20 . 𝑒 −𝑥 20]] 0 40 = 1 + (𝑒 −2 1 − 1) 𝑝(𝑥 > 40) = 𝑒−2 𝑝(𝑥 > 10) = 1 − 𝑝(𝑥 ≤ 10) = 1 − ∫ 1 20. 𝑒 −𝑥 20𝑑𝑥 10 0 = 1 − 1 20. [−20 . 𝑒 −𝑥 20]] 0 10 = 1 + (𝑒 −1 2 − 1) 𝑝(𝑥 > 10) = 𝑒−12

(57)

52 𝑃(𝑋 > 40| 𝑋 > 10) =𝑝(𝑥 > 40) 𝑝(𝑥 > 10) = 𝑒 −2 𝑒 −1 2 = 𝑒−2− 𝑒 −1 2 = 𝑒−2−( −1 2) = 𝑒−1,5

3. Jika peubah acak X berdistribusi umum dengan rataan 2 dan varians 0,16. Maka P(X > 2,3) adalah…

a. 0,5 d. 0,2734 b. 0,75 e. 0,2266 c. 2,3

penyelesaian:

dalam hal ini 𝜇 = 2 𝑑𝑎𝑛𝜎 = 0,4 𝑃(𝑋 > 2,3) = 𝑃 (𝑋 − 𝜇

𝜎 >

2,3 − 2

0,4 ) = 𝑃(𝑍 > 0,75)

Kurva berdistribusi normal baku untuk Z = 0,75 bisa dilihat berikut ini,

Daerah yang dicari mulai dari z= 0,75 sampai z=∞

Jadi P(X>2,3) = 0,5 – ( daerah dari Z = 0 sampai Z = 0,75 )= 0,5 – 0,2734

0,75

_∞

(58)

53

P(X>2,3) = 0,2266

4. Untuk n = 6, maka fungsi Gamma dan nilainya adalah: a. Γ(6) = ∫ x₀~ 6e−xdx dan Γ(6) = 120 b. Γ(6) = ∫ x~ 5_e−x_{dx dan Γ(6) = 720} 0 c. Γ(6) = ∫ x~ 6_e−x_{dx dan Γ(6) = 720} 0 d. Γ(6) = ∫ x₀~ 5e−xdx dan Γ(6) = 120 Jawaban: D Penyelesaian: Γ(n) = ∫ xn−1e−xdx ~ 0 Untuk n=6 Γ(6) = ∫ x6_e−x_dx ~ 0 Γ(6) = (6 − 1)! = 5! = 120

5. Jika X peubah acak berdistribusi beta dengan parameter a=1 dan b=4, maka rerata X adalah

a. 0,1 b. 0,2 c. 0,3 d. 0,4 Jawaban : B Penyelesaian: 𝜇 = 𝑎 𝑎 + 𝑏= 1 1 + 5 = 0,2

(59)

54

BAB 4

KEBEBASAN STOKASTIK

A. Proses Stokastik Berhingga Pengertian

Suatu eksperimen berupa deret berhingga di mana tiap eksperimen mempunyai sejumlah berhingga hasil yang mungkin dengan peluang tertentu.

Contoh:

Terdapat 4 buah kotak yang berisi bola merah dan bola biru pada tiap-tiap kotak. Kotak I berisi 10 bola, 3 di antaranya berwarna merah. Kotak II berisi 8 bola, 2 di berwarna merah. Kotak III berisi 5 bola, 1 di antaranya berwarna merah. Kotak IV berisi 10 bola, 4 di antaranya berwarna merah. Kita akan mengambil satu kotak secara random dan kemudian dari kotak tersebut diambil satu buah bola biru secara random. Berapakah peluang bola berwarna biru terambil?

Jawab:

Dalam soal ini kita akan melakukan dua eksperimen sebagai berikut: 1. Memilih 1 dari 4 kotak

2. Mengambil 1 buah bola yang mungkin berwarna merah atau biru Peluang mengambil 1 kotak dari 4 kotak secara random adalah 1

4.

Jadi, peluang terambil kotak I = peluang terambil kotak II = peluang terambil kotak III = peluang terambil kotak IV.

Dari kotak I yang berisi 10 bola, 3 diantaranya berwarna merah. Peluang terambil bola merah adalah 3

10 dan peluang terambil bola biru adalah 7 10.

Dari kotak II yang berisi 8 bola , 2 diantaranya berwarna merah. Peluang terambil bola merah adalah 2

8 dan peluang peluang terambil bola biru

adalah 6

(60)

55

Dari kotak III yang berisi 5 buah durian, 1 diantaranya berwarna merah. Peluang terambil bola merah adalah 1

5 dan peluang peluang terambil bola

biru adalah 4

5.

Dari kotak IV yang berisi 10 buah durian, 4 diantaranya berwarna merah. Peluang terambil bola merah adalah 4

10 dan peluang peluang terambil bola

biru adalah 6

10.

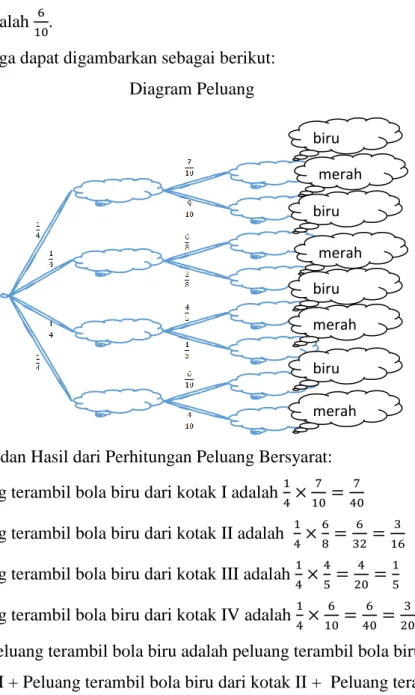
Sehingga dapat digambarkan sebagai berikut: Diagram Peluang

Proses dan Hasil dari Perhitungan Peluang Bersyarat: Peluang terambil bola biru dari kotak I adalah 1

4× 7 10=

7 40

Peluang terambil bola biru dari kotak II adalah 1

4× 6 8= 6 32= 3 16

Peluang terambil bola biru dari kotak III adalah 1

4× 4 5= 4 20= 1 5

Peluang terambil bola biru dari kotak IV adalah 1

4× 6 10= 6 40= 3 20

Jadi, peluang terambil bola biru adalah peluang terambil bola biru dari kotak I + Peluang terambil bola biru dari kotak II + Peluang terambil bola

I baik busuk II baik busuk III baik busuk IV baik busuk biru biru merah merah biru merah biru merah

(61)

56

biru dari kotak III + Peluang terambil bola biru dari kotak IV adalah 7

40+ 3 16+ 1 5+ 3 20= 51 80

B. Kebebasan Stokastik Diskrit Definisi:

Misalnya dua peubah acak diskrit X dan Y mempunyai nilai fungsi peluang gabungan di (𝑥, 𝑦), yaitu 𝑝(𝑥, 𝑦) serta masing-masing mempunyai nilai fungsi peluang marginal dari X di x, yaitu 𝑝₁(𝑥) dan nilai fungsi peluang marginal dari Y di y, yaitu 𝑝₂(𝑦).

Kedua peubah acak X dan Y dikatakan bebas stokastik, jika dan hanya jika:

𝑝(𝑥, 𝑦) = 𝑝₁(𝑥). 𝑝₂(𝑦)

Untuk semua pasangan nilai (𝑥, 𝑦)

Contoh:

Misalnya fungsi peluang gabungan dari X dan Y berbentuk: 𝑝(𝑥, 𝑦) = (1

72) (𝑥 + 2𝑦); 𝑥 = 0,1,2,3 dan 𝑦 = 0,1,2,3 Apakah X dan Y bebas stokastik?

Penyelesaian:

Fungsi marginal dari X adalah: 𝑝₁(𝑥) = ∑ (1 72) (𝑥 + 2𝑦) 3 𝑦=0 = ( 1 72) {𝑥 + (𝑥 + 2) + (𝑥 + 4) + (𝑥 + 6)} = ( 1 72) (4𝑥 + 12) = ( 1 72) . 4(𝑥 + 3) 𝑝₁(𝑥) = (1 18) (𝑥 + 3)

(62)

57

Jadi, 𝑝1(𝑥) = ( 1

18) (𝑥 + 3); 𝑥 = 0,1,2,3

Fungsi marginal dari Y adalah: 𝑝₂(𝑦) = ∑ (1 72) (𝑥 + 2𝑦) 3 𝑥=0 = (1 72) {2𝑦 + (1 + 2𝑦) + (2 + 2𝑦) + (3 + 2𝑦)} = (1 72) (8𝑦 + 6) = (1 72) . 2(4𝑦 + 3) 𝑝₂(𝑦) = (1 36) (4𝑦 + 3) Jadi, 𝑝₂(𝑦) = (1 36) (4𝑦 + 3); 𝑦 = 0,1,2,3

Misalnya pasangan nilai dari X dan Y diambil (𝑥, 𝑦) = (0,0).  𝑝(𝑥 = 0, 𝑦 = 0) = (1 72) (0 + 0) = 0  𝑝₁(𝑥 = 0) = 3 18= 1 6  𝑝2(𝑦 = 0) = 3 36= 1 12 𝑝(𝑥 = 0, 𝑦 = 0) = (1 72) (𝑥 + 2𝑦) = (1 72) (0 + 2(0)) = (1 72) (0) = 0 𝑝1(𝑥 = 0). 𝑝2(𝑦 = 0) = ( 1 18) (𝑥 + 3). ( 1 36) (4𝑦 + 3) = (1 18) (0 + 3). ( 1 36) (4(0) + 3) = (1 18) (3). ( 1 36) (3)

(63)

58 =1 6. 1 12 = 1 72

∴ karena 𝑝(𝑥 = 0, 𝑦 = 0) ≠ 𝑝₁(𝑥 = 0). 𝑝₂(𝑦 = 0), maka X dan Y dua peubah acak tidak bebas stokastik

C. Kebebasan Stokastik Kontinu Definisi :

Misalnya dua peubah acak kontinu 𝑋 dan 𝑌 mempunyai nilai fungsi densitas, gabungan di (𝑥, 𝑦), yaitu 𝑓(𝑥, 𝑦) serta masing-masing mempunyai nilai fungsi densitas marginal dari 𝑋 di 𝑥, yaitu 𝑓1(𝑥) dan nilai fungsi densitas marginal

dari 𝑌 di 𝑦, yaitu 𝑓₂(𝑦). Kedua peubah acak 𝑋 dan 𝑌 dikatakan bebas stokastik, jika dan hanya jika :

𝑓(𝑥, 𝑦) = 𝑓₁(𝑥)𝑓2(𝑦)

Dalam praktiknya, soal yang menyangkut kebebasan stokastik dua peubah acak kontinu ini ada dua kemungkinan, yaitu sebagai berikut.

1. Fungsi densitas gabungan dari kedua peubah acak diketahui bentuknya. Kita harus menentukan terlebih dahulu fungsi densitas marginal dari masing-masing peubah acaknya. Kemudian kita menggunakan persyaratan kebebasan stokastik, dan kita memperhatikan hasilnya dengan kriteria sebagai berikut.

a. Apabila ruas kiri sama dengan ruas kanan, maka kedua peubah acak itu dikatakan bebas stokastik.

b. Apabila ruas kiri tidak sama dengan ruas kanan, maka kedua peubah acak itu dikatakan tidak bebas stokastik atau bergantungan.

2. Fungsi densitas gabungan dari kedua peubah acak tidak diketahui bentuknya. Dalam hal ini fungsi densitas marginal dari masing-masing peubah acak diketahui bentuknya. Kemudian kita menggunakan pesyaratan kebebasan stokastik dan kriterianya sama dengan sebelumnya. Contoh :

Misalnya fungsi peluang gabungan dari 𝑋 dan 𝑌 berbentuk : 𝑓(𝑥, 𝑦) = 𝑥 + 𝑦 ; 0 < 𝑥 < 1, 0 < 𝑦 < 1

(64)

59

= 0 ; 𝑥 , 𝑦 lainnya. Apakah 𝑋 dan 𝑌 bebas stokastik?

Penyelesaian :

Kita harus menentukan dahulu fungsi densitas marginal masing-masing dari 𝑋 dan 𝑌.

Fungsi densitas marginal dari 𝑋 adalah : 𝑔 (𝑥) = ∫_−∞∞ 𝑓(𝑥, 𝑦) 𝑑𝑦 = ∫_−∞0 𝑓(𝑥, 𝑦) 𝑑𝑦 + ∫ 𝑓(𝑥, 𝑦)₀1 𝑑𝑦 + ∫ 𝑓(𝑥, 𝑦)₁∞ 𝑑𝑦 = ∫_−∞0 0 𝑑𝑦 + ∫ (𝑥 + 𝑦)₀1 𝑑𝑦 + ∫ 0₁∞ 𝑑𝑦 = 0 + {𝑥𝑦 + (1 2) 𝑦 2_}] 𝑦=0 1 + 0 𝑔(𝑥) = 𝑥 + 1 2 Jadi, 𝑔(𝑥) = 𝑥 + 1 2 ; 0 < 𝑥 < 1 = 0 ; 𝑥 lainnya.

Fungsi densitas marginal dari 𝑌 adalah : ℎ(𝑦) = ∫_−∞∞ 𝑓(𝑥, 𝑦) 𝑑𝑥 = ∫_−∞0 𝑓(𝑥, 𝑦) 𝑑𝑥 + ∫ 𝑓(𝑥, 𝑦)₀1 𝑑𝑥 + ∫ 𝑓(𝑥, 𝑦)₁∞ 𝑑𝑥 = ∫_−∞0 0 𝑑𝑥 + ∫ (𝑥 + 𝑦)₀1 𝑑𝑥 + ∫ 0₁∞ 𝑑𝑥 = 0 + {(1 2) 𝑥 2_{+ 𝑥𝑦}]} 𝑥=0 1 + 0 ℎ(𝑦) =1 2+ 𝑦 Jadi, ℎ(𝑦) =1 2+ 𝑦 ; 0 < 𝑦 < 1

(65)

60 = 0 ; 𝑦 lainnya. Maka 𝑔(𝑥) . ℎ(𝑦) = (𝑥 + 1 2) ( 1 2+ 𝑦) = 𝑥 2+ 𝑥𝑦 + 𝑦 2+ 1 4 Ternyata 𝑓(𝑥 , 𝑦) ≠ 𝑔(𝑥). ℎ(𝑦), karena 𝑥 + 𝑦 ≠𝑥 2+ 𝑥𝑦 + 𝑦 2+ 1 4

Sehingga 𝑋 dan 𝑌 merupakan peubah acak yang tidak bebas stokastik atau bergantungan.

Teorema 2.1.1

Misalkan f.k.p bersama dari 𝑋 dan 𝑌 adalah 𝑓(𝑥, 𝑦). Maka 𝑋 dan 𝑌 bebas stokastik jika dan hanya jika terdapat fungsi-fungsi non negatif 𝑔(𝑥) dan ℎ(𝑦) sehingga 𝑓(𝑥, 𝑦) = 𝑔(𝑥) ℎ(𝑦) dan domain dari 𝑔 tidak tergantung dari 𝑦 serta domain h tidak tergantung dari 𝑥.

Bukti:

a. Misalkan x dan y bebas stokastik. Maka 𝑓(𝑥, 𝑦) = 𝑓(𝑥) 𝑓(𝑦). Dalam hal ini cukup diambil 𝑔(𝑥) = 𝑓(𝑥) dan ℎ(𝑦) = 𝑓(𝑦). b. Misalkan 𝑓(𝑥, 𝑦) = 𝑔(𝑥)ℎ(𝑦); 𝑔(𝑥) ≥ 0 dan ℎ(𝑦) ≥ 0.

Akan dibuktikan 𝑋 dan 𝑌 bebas stokastik, untuk itu dicari 𝑓(𝑥) dan 𝑓(𝑦). 𝑓(𝑥) = ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 = ∫ 𝑔(𝑥)ℎ(𝑦)𝑑𝑦 ∞ −∞ = 𝑔(𝑥) ∞ −∞ ∫ ℎ(𝑦)𝑑𝑦 ∞ −∞

= 𝐾𝑔(𝑥)dengan K = ∫ ℎ(𝑦)𝑑𝑦 suatu konstanta

∞ −∞ 𝑓(𝑥) = ∫ 𝑓(𝑥, 𝑦) ∞ −∞ 𝑑𝑥 = ∫ 𝑔(𝑥) ∞ −∞ ℎ(𝑦)𝑑𝑥 = ℎ(𝑦) ∫ 𝑔(𝑥) 𝑑𝑥 ∞ −∞

= 𝐿ℎ (𝑦)dengan L = ∫ 𝑔(𝑥)𝑑𝑥 suatu konstanta

∞

(66)

61 Akan tetapi, KL = ∫ ℎ(𝑦)𝑑𝑦 ∫ 𝑔(𝑥) ∞ −∞ ∞ −∞ = ∫ ∫ 𝑔(𝑥)ℎ(𝑦) 𝑑𝑦 𝑑𝑥 ∞ −∞ ∞ −∞ = ∫ ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 𝑑𝑥 = 1 ∞ −∞ ∞ −∞ Akibatnya, 𝑓(𝑥 , 𝑦) = 𝑔(𝑥)ℎ(𝑦) = 𝑓(𝑥) 𝐾 . 𝑓(𝑦) 𝐿 = 𝑓(𝑥)𝑓(𝑦)

Dari persamaan (a) dan (b) berarti 𝑋 dan 𝑌 bebas stokastik.

Contoh:

Diketahui f.k.p bersama dari 𝑋 dan 𝑌 sebagai berikut:

𝑓(𝑥 , 𝑦) = {12𝑥𝑦 (1 − 𝑦); 0 < 𝑥 < 1 ; 0 < 𝑦 < 1 0 ; untuk 𝑥 yang lain

Buktikan bahwa 𝑋 dan 𝑌 bebas stokastik! Jawab:

𝑥 dan 𝑦 yang lain, yang mungkin : 𝑔(𝑥) = 12𝑥 (1 − 𝑦) 𝑔(𝑥) = 12𝑥 𝑔(𝑥) = 𝑥 𝑔(𝑥) = 𝑥 (1 − 𝑦) ℎ(𝑦) = 𝑦 ℎ(𝑦) = 𝑦 (1 − 𝑦) ℎ(𝑦) = 12𝑦 (1 − 𝑦) ℎ(𝑦) = 12𝑦 Contoh : Tulislah 𝑔(𝑥) = 12𝑥 dan ℎ(𝑦) = 𝑦(1 − 𝑦).

(67)

62

Jelas bahwa :

a. 𝑔(𝑥) > 0untuk setiap 𝑥; 0 < 𝑥 < 1 b. ℎ(𝑦) > 0untuk setiap 𝑦; 0 < 𝑦 < 1

c. 𝑓(𝑥, 𝑦) = 𝑔(𝑥)ℎ(𝑦); 0 < 𝑥 < 1 ; 0 < 𝑦 < 1 Berarti 𝑋 dan 𝑌 bebas stokastik.

(68)

63

Soal Latihan dan Jawaban

1. Suatu mata kuliah statistika matematika diikuti 50 mahasiswa angkatan 2010, 15 mahasiswa angkatan 2009 dan 10 mahasiswa angkatan 2008. Diketahui mahasiswa yang mendapatkan nilai A sebanyak 10 orang dari mahasiswa angkatan 2010, 8 orang dari mahasiswa angkatan 2009 dan 5 orang mahasiswa angkatan 2008. Bila seorang mahasiswa dipilih secara acak, berapakah peluang dia mendapat nilai A?

a.10 75 b.23 75 c.10 23 d.52 75 Penyelesain: 10 50 40 50 50 75 8 15 15 75 7 15 10 75 5 10 5 10

Peluang mahasiswa yang mendapatkan nilai A = (50

75× 10 50) + ( 15 75× 8 15) + (10 75× 5 10) 2010 2009 2008 Nilai A Nilai A Nilai A Selain A Selain A Selain A

(69)

64 = 10 75+ 8 75+ 5 75= 23 75

Jadi, peluang mahasiswa yang mendapat nilai adalah 23

75

2. Fungsi peluang gabungan dari X dan Y berbentuk:

𝑝(𝑥, 𝑦) = 𝑘𝑥𝑦; 𝑥 = 1,2,3, dan 𝑦 = 1,2,3

Dengan X dan Y merupakan peubah acak bebas stokastik. Nilai 𝑘 adalah ... a.1 36 b.1 6 c.2 36 d.2 6 Penyelesaian:

Fungsi peluang marginal dari X adalah: 𝑝₁(𝑥) = ∑(𝑘𝑥𝑦) 3 𝑦=1 𝑝1(𝑥) = 𝑘𝑥(1 + 2 + 3) 𝑝₁(𝑥) = 𝑘𝑥(6) 𝑝₁(𝑥) = 6𝑘𝑥

Fungsi peluang marginal dari Y adalah: 𝑝2(𝑦) = ∑(𝑘𝑥𝑦) 3 𝑥=1 𝑝₂(𝑦) = 𝑘(1 + 2 + 3)𝑦 𝑝₂(𝑦) = 𝑘(6)𝑦 𝑝2(𝑦) = 6𝑘𝑦

Karena peubah acak X dan Y bebas stokastik maka 𝑝(𝑥, 𝑦) =

𝑝₁(𝑥). 𝑝₂(𝑦), sehingga 𝑘𝑥𝑦 = 6𝑘𝑥. 6𝑘𝑦. jika diambil (𝑥, 𝑦) = (1,1) maka: 𝑘(1)(1) = 6𝑘(1).6𝑘(1) 𝑘 = 36𝑘2 𝑘 𝑘2 = 36 1 𝑘= 36 𝑘 = 1 36