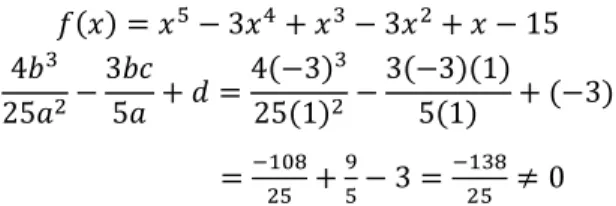Permasalahan Optimasi pada Fungsi Polinomial Berderajat Tinggi Tanpa Melibatkan Konsep Turunan

(1)

Permasalahan Optimasi pada Fungsi Polinomial Berderajat Tinggi Tanpa

Melibatkan Konsep Turunan

Cresentia Carina Ardianti Ayuningtyas __{Veni Setyarini}__{Fransiska Dian Retnosari} Mahasiswa S1 Pendidikan Matematika,

FKIP Universitas Sanata Dharma, Yogyakarta, Indonesia Email: cresentia.carina@gmail.com

Abstrak. Nilai esktrem dari fungsi polinomial pangkat 3 dan berderajat tinggi tidak hanya dapat dicari dengan menggunakan konsep turunan, tetapi dapat menggunakan teknik dasar dalam aljabar elementer. Metode yang digunakan dalam penelitian ini adalah kajian pustaka. Penelitian ini bertujuan untuk mencari nilai optimum fungsi polinomial pangkat 3, 4, dan 5 tanpa menggunakan konsep turunan. Konsep yang digunakan adalah konsep dasar dalam aljabar. Materi pokok yang digunakan pada penelitian ini adalah definisi fungsi ganjil dan transformasi fungsi. Pada fungsi polinomial pangkat tiga, dapat dicari nilai ekstremnya tanpa menggunakan konsep turunan. Pengembangan yang selanjutnya adalah pada bentuk fungsi polinomial pangkat 4 dan 5 dengan cara yang sama pada polinomial pangkat 3. Pada polinomial pangkat 4, nilai ekstrem tidak dapat dicari dengan cara yang sama seperti bentuk polinomial pangkat 3, karena polinomial pangkat 4 tidak dapat dibawa ke dalam fungsi ganjil sehingga tidak dapat ditentukan titik simetri putarnya. Pada fungsi polinomial pangkat 5, ditemukan kesulitan dalam mencari nilai optimumnya karena menghasilkan bentuk yang kompleks sehingga belum dapat dicari nilainya secara eksplisit. Kesimpulan dari penelitian adalah aljabar dan geometri mampu menjadi alternatif dalam menentukan nilai ekstrem fungsi polynomial derajat 3, namun belum mampu untuk fungsi polinomial derajat 4 dan 5.

Kata kunci. fungsi ganjil, fungsi polinomial, nilai ekstrem, titik simetri putar, translasi

1. Pengantar

Nilai ekstrem dari suatu fungsi biasanya dicari dengan menggunakan konsep turunan. Hal ini berakibat konsep turunan harus dikuasai dengan benar. Jika konsep turunan belum dikuasai atau belum dipelajari, maka akan ditemukan kesulitan dalam mencari nilai ekstrem fungsi polinomial. Penelitian ini akan menunjukkan adanya cara lain untuk mencari nilai ekstrem tanpa menggunakan konsep turunan, tetapi menggunakan konsep-konsep dasar pada aljabar. Tujuan dari penelitian ini adalah mencari nilai ekstrem polinomial pangkat 3, pangkat 4, dan pangkat 5 tanpa menggunakan konsep turunan. Penelitian ini menggunakan metode kajian pustaka dari artikel jurnal dan berbagai referensi.

2. Optimasi Fungsi Polinomal Pangkat 3 Tanpa Konsep Turunan

Nilai ekstrem dari fungsi pangkat dua maupun polinomial pangkat tiga dapat dicari dengan menggunakan konsep turunan. Namun dalam sebuah artikel “Optimization of Cubic Polynomial Functions without Calculus” menjelaskan penelitian tentang mencari nilai ekstrem dari fungsi polinomial pangkat tiga tanpa menggunakan konsep turunan. Konsep yang digunakan dalam penelitian tersebut adalah transformasi fungsi, ide akar-akar persamaan suku banyak, dan definisi dari fungsi ganjil. Secara garis besar, hal tersebut dilakukan dengan menunjukkan setiap fungsi kubik memiliki simetri putar di satu titik, kemudian langkah selanjutnya adalah menggeser atau mentranslasikan grafik fungsi asli sebanyak dua kali untuk membentuk fungsi

(2)

baru, dan langkah terakhir adalah mencari absis nilai ekstrem fungsi asli yang berhubungan dengan absis dari persamaan fungsi baru.

2.1. Solusi Kalkulus

Pencarian nilai optimum suatu fungsi bentuk polinomial dengan kalkulus, menggunakan konsep turunan. Nilai optimum dari suatu fungsi bentuk polinomial dapat dicari dengan mencari akar-akar persamaan dari turunan pertama fungsi polinomial. Misal ( ) = +

+ + , maka untuk menentukan nilai optimum dari fungsi tersebut perlu mecari turunan pertama fungsi . Turunan pertama dari adalah ′( ) = 3 + 2 + . Nilai optimum dicapai ketika ′( ) = 0 , maka dengan mencari akar-akar persamaan menggunakan metode diperoleh :

= ±√ (1) Solusi secara kalkulus ini memiliki kelebihan, yaitu lebih mudah dan ringkas. Namun, untuk mendapatkannya diperlukan pemahaman konsep turunan terlebih dahulu. Solusi tanpa menggunakan konsep turunan dapat menjadi salah satu cara dalam menentukan nilai optimum fungsi polinomial dengan menggunakan konsep-konsep dasar aljabar.

2.2. Titik Simetri Putar Fungsi Kubik

Fungsi kubik secara umum dapat dituliskan ( ) = + + + . De Villiers (2004) dalam artikelnya menunjukkan dengan teknis kalkulus bahwa setiap fungsi polinomial kubik dengan bentuk ( ) = + + + mempunyai titik simetri putar dengan absis =

. Solusi mencari nilai ekstrem secara nonkalkulus dimulai dengan hasil penemuan Villiers. Perlu diingat, fungsi kubik f(x) berlaku fungsi ganjil jika dan hanya jika − ( ) = (− ) atau ekuivalen dengan ( ) = − (− )

+ + + = (− ) + (− ) + (− ) +

= − + −

Jadi, persamaan kubik ( ) adalah fungsi ganjil jika dan hanya jika = = 0.

Fungsi memiliki titik simetri putar di ( , ) jika dan hanya jika ( ) = ( + ) −

adalah fungsi ganjil, sehingga fungsi menjadi ( ) = + (3 + ) + (3 + 2 + ) . Hal ini berakibat fungsi merupakan fungsi ganjil maka berlaku 3 + = 0

sehingga diperoleh = dan = ( ) = . Selanjutnya, nilai =

disubstitusikan ke persamaan ( ) sehingga :

( ) = + (3 + ) + (3 + 2 + )

= + 3 −_{3 +} + 3 (−_{3 )} + 2 −_{3 +}

= 3₊ 3 − 2

(3)

2.3. Akar Persamaan Baru

Pada langkah ini menggunakan akar-akar persamaan fungsi polinomial untuk mencari nilai ekstrem. Langkah pertama adalah membentuk fungsi baru dari hasil translasi fungsi . Misal titik puncak dari ( ) adalah ( , ). Fungsi ditranslasikan sedemikian sehingga menjadi akar dari fungsi baru yaitu fungsi ℎ. Fungsi ℎ didefiniskan sebagai ℎ( ) = ( ) − . Disisi lain fungsi ℎ memiliki dua akar kembar di = , dan akar lain di = maka ℎ dapat ditulis menjadi :

ℎ( ) = ( − ) ( − )

ℎ( ) = + (−2 − 2 ) + ( + 2 ) −

(3)

Namun, ℎ( ) = ( ) − sehingga persamaan (2) menjadi :

( ) − = + − (4) Dari persamaan (3) dan (4) dengan menyamakan koefisien dan diperoleh =±√ , dengan adalah salah satu akar dari ℎ( ) yaitu ( , 0) yang sekaligus menjadi titik esktrem fungsi ℎ.

2.4. Nilai Ekstrem Fungsi Kubik Semula

Langkah selanjutnya adalah mentranslasikan kembali titik ( , 0) pada ℎ ke titik ekstrem fungsi dengan jalur yang sama pada langkah sebelumnya dengan arah yang berlawanan. Fungsi ℎ ditranslasikan ke lalu ditranslasikan lagi ke .

Titik ekstrem dari dapat diperoleh dari hasil translasi fungsi ℎ ke fungsi , yaitu = + = +±√ = ±√ . Jadi titik ekstrem dari fungsi adalah ( =

±√ _{, ( ))}_{. Solusi yang didapat dari metode tanpa menggunakan konsep turunan sama} dengan solusi dengan menggunakan konsep turunan, yaitu pada persamaan (1).

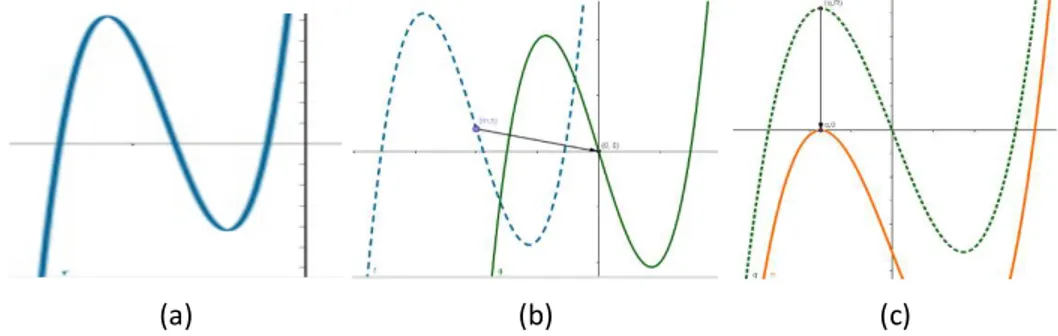
(a) (b) (c)

Gambar 1. (a) Grafik fungsi , (b) grafik fungsi dan , dan (c) grafik fungsi dan ℎ.

3. Optimasi Fungsi Polinomal Berderajat Tinggi Tanpa Kalkulus

Penelitian ini bertujuan untuk mengembangkan penelitian yang sudah dilakukan sebelumnya yaitu “Optimization of Cubic Polynomial Function without Calculus”. Jenjang yang pertama adalah mengembangkan ke bentuk polinomial pangkat 4 dengan cara yang sama seperti dalam

(4)

penelitian sebelumnya. Jenjang yang selanjutnya adalah mengembangkan ke bentuk polinomial pangkat 5. Langkah-langkah yang digunakan serupa dengan bentuk polinomial pangkat 3, yaitu dengan menggunakan konsep dasar aljabar, fungsi ganjil dan titik simetri putar grafik.

3.1. Fungsi Polinomial Pangkat 4

Pada penelitian sebelumnya, langkah pertama adalah menunjukkan titik simetri putar pada polinomial. Dengan cara yang sama, perlu ditunjukkan titik simetri putar polinomial pangkat 4 dengan cara membawa fungsi tersebut ke fungsi ganjil. Definisi fungsi ganjil adalah (− ) =

− ( ).Persamaan umum polinomial pangkat 4 adalah : ( ) = + + + + ,

maka:

(− ) = − ( )

(− ) + (− ) + (− ) + (− ) + = − + + + +

− + − + = − − − − −

Fungsi ganjil jika dan hanya jika = = = 0. Jika = 0, maka persamaan yang terbentuk bukan lagi polinomial pangkat 4. Oleh karena itu, fungsi polinomial pangkat 4 tidak dapat dicari nilai ekstremnya dengan cara kerja yang sama pada polinomial pangkat 3 di penelitian sebelumnya.

3.2. Fungsi Polinomial Pangkat 5

Setelah bentuk polinomial pangkat 4, dilanjutkan pengembangan mencari nilai ekstrem dari fungsi polinomial pangkat 5 dengan cara atau langkah-langkah yang sama dengan bentuk polinomial pangkat 3, yaitu dengan mencari titik simetri putar, kemudian mentranslasikan titik simteri putar ke titik origin (0,0), lalu mentranslasikan kembali grafik sehingga membentuk persamaan baru. Setelah bentuk polinomial pangkat 4, dilanjutkan pengembangan mencari nilai ekstrem dari fungsi polinomial pangkat 5 dengan cara atau langkah-langkah yang sama dengan bentuk polinomial pangkat 3, yaitu dengan mencari titik simetri putar, kemudian mentranslasikan titik simetri putar ke titik origin (0,0), lalu mentranslasikan kembali grafik sehingga membentuk persamaan baru.

3.2.1. Solusi Kalkulus

Pencarian nilai optimum fungsi polinomial pangkat 5 dengan kalkulus, dapat dilakukan dengan mencari akar-akar persamaan dari turunan pertama fungsi polinomial pangkat 5. Misal ( ) = + + + + + , maka untuk menentukan nilai optimum dari fungsi tersebut perlu mencari turunan pertama fungsi . Turunan pertama dari adalah ′( ) = 5 + 4 + 3 + 2 + , yang merupakan bentuk fungsi polinomial pangkat 4.

Nilai optimum dicapai ketika ′( ) = 0. Metode yang dapat digunakan untuk mencari akar-akar persamaan ′( ) adalah metode Horner. Namun, dengan menggunakan metode Horner, perlu diawali dengan langkah coba-coba semua kemungkinan faktor dari . Hal ini menjadi sulit karena tidak semua persamaan dapat dengan mudah dicari akar-akarnya menggunakan metode Horner.

(5)

3.2.2. Titik Simetri Putar

Langkah pertama yang perlu dilakukan dalam mencari nilai optimum dari fungsi polinomial pangkat 5 adalah mencari titik simetri putar. Fungsi polinomial pangkat 5 yang dapat dicari nilai ekstremnya tanpa kalkulus diduga adalah fungsi yang memiliki titik simetri putar. Sebelumnya sudah dijelaskan definisi fungsi ganjil yaitu (− ) = − ( ). Jika ditinjau secara grafis, grafik fungsi ganjil simetris di titik origin (0,0).

Goehle & Kobayashi (2013) menunjukkan bahwa untuk bentuk umum fungsi polinomial

( ) = + + ⋯ + + , jika fungsi polinomial tersebut memiliki pusat

simetris, maka absis dari pusat simetrisnya adalah = . Penemuan Goehle dan Kobayashi akan menuntun penelitian dalam mencari nilai optimum fungsi polinomial pangkat 5. Menurut penemuan Goehle dan Kobayashi, fungsi polinomial pangkat 5 yang simetris, memiliki titik simetri putar dengan absis = . Namun, peneliti ingin mencari ciri-ciri fungsi polinomial pangkat 5 yang simetris secara umum.

Bentuk umum fungsi pangkat 5: ( ) = + + + + + . Bentuk umum

( ) tersebut akan dibawa ke bentuk fungsi ganjil. (− ) = − ( )

(− ) + (− ) + (− ) + (− ) + (− ) + =−( + + + + + )

− + − + − + = − − − − − −

Bentuk umum pangkat 5 tersebut akan menjadi fungsi ganjil jika dan hanya jika = = = 0.

Selanjutnya, akan dicari titik simetri putar dari fungsi pangkat 5 dengan cara mentranslasikan fungsi tersebut menjadi fungsi , dimana fungsi merupakan fungsi ganjil. Asumsikan mempunyai titik simetri putar di (m,n), sehingga = ( ). Fungsi didefinisikan ( )= ( + ) – , maka: ( ) = ( + ) – = ( + ) + ( + ) + + ( + ) + + ( + ) + ( + ) + f – ( + + + + + f) = ( + 5 + 10 + 10 + 5 + ) + ( + 4 + 6 + 4 + ) + ( + 3 + 3 + ) + ( + 2 + ) + + + − − − − − − = + 5 + 10 + 10 + 5 + + + 4 + 6 + 4 + + + 3 + 3 + + + 2 + + + + − − − − − − = + 5 + + 10 +4 + +10 +6 +3 + + 5 + 4 + 3 + 2 + = + (5 + ) + (10 + 4 + ) + (10 + 6 + 3 + ) + (5 + 4 + 3 + 2 + )

(6)

5 + = 0

5 = 0

= (5)

dan

10 + 6 + 3 + = 0 (6)

Jika persamaan (5) disubstitusikan ke persamaan (6), maka diperoleh:

10 + 6 + 3 + = 0

+ − + = 0

− + = 0

Dari perhitungan di atas, didapat fungsi polinomial pangkat 5 memiliki titik simetri putar di

( , ) = , , jika memenuhi persamaan:

− + = 0. (7) Contoh 1: ( ) = + 10 + 35 + 50 + 24 + 4 4 25 −35 + =4(10)25(1) −3(10)(35)5(1) + 50 =4000_{25 −}1050_{5 + 50} = 160 − 210 + 50 = 0

Karena memenuhi persamaan (7), maka memiliki titik simetri putar di , =

( ), ( ) = −2, (−2) = (−2,4).

Gambar 2. Grafik fungsi polinomial pangkat 5 (fungsi pada contoh 1) yang memiliki titik simetri putar.

(7)

( ) = − 3 + − 3 + − 15 4

25 −35 + =4(−3)25(1) −3(−3)(1)5(1) + (−3)

= + − 3 = 0

Karena tidak memenuhi persamaan (7), maka tidak memiliki titik simetri putar. Hal ini mengakibatkan fungsi ini tidak dapat dicari nilai ekstremnya tanpa kalkulus dengan cara yang analog pada bentuk polinomial pangkat 3.

Gambar 3. Grafik fungsi polinomial pangkat 5 (fungsi contoh 2) yang tidak memiliki titik simetri putar.

Dari perhitungan dan contoh di atas, dapat disimpulkan tidak semua fungsi polinomial pangkat 5 memiliki titik simetri putar. Fungsi polinomial pangkat 5 yang memiliki titik simetri putar, titik simetri putarnya berada di titik , .

Jika nilai = − , maka fungsi dapat dituliskan menjadi:

( ) = + 10 + 4 + + 5 + 4 + 3 + 2 + = 5₊ 2 2 5 − 4 2 5 + 3+ −3 4 125 3+ 3 2 25 2− 2 5 +

(8)

Gambar 4. Grafik fungsi polinomial pangkat 5 fungsi dan .

3.2.3. Akar Persamaan Baru

Langkah yang selanjutnya adalah mentransformasikan fungsi ke fungsi yang baru yaitu fungsi ℎ. Pada langkah 3.2.1 diketahui fungsi ( ) = + + + + +

dengan ( , ) = , dan ( ) = ( + ) − adalah sebuah fungsi ganjil. Jika mempunyai titik relatif maksimum, maka mempunyai dua akar yang simetris terhadap titik origin (0,0). Asumsikan g mempunyai relatif maksimum di titik ( , ) dan didefinisikan:

ℎ( ) = ( ) −

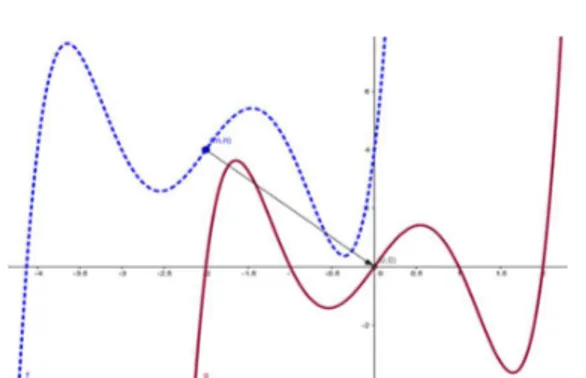
Karena mempunyai relatif maksimum di = , maka grafik h akan terlihat pada Gambar 5. Grafik ℎ mempunyai akar kembar di = , akar di = dan akar imajiner yang dimana tidak memotong sumbu .

Gambar 5. Grafik fungsi polinomial pangkat 5 fungsi dan ℎ.

Fungsi ℎ dapat dituliskan menjadi ℎ( ) = ( − ) ( − )( 2₊ _{+ ) ,}_dengan ₋

4 0, maka:

ℎ( ) = + ( − − 2 ) + ( − + 2 − 2 + ) + ( − + 2 −

) + (− + + 2 ) − . (8) Namun di sisi lain ℎ( ) = ( ) − ,

( ) − = + − + + + − + − (9)

Dengan menyamakan koefisien dan pada persamaan (8) dan (9), maka diperoleh:

( − − 2 ) = 0 (koefisien )

(9)

− + 2 − = 0 (koefisien ) ( + 2 ) − + 2( + 2 ) − = 0 substitusi persamaan (10) + 2 − + 2 + 4 − = 0 2 + 2 + 4 − = 0 2 ( + + 2 ) − = 0 = 2 ( + + 2 ) = ( ) (11)

Dengan menyamakan koefisien dan pada persamaan (8) dan (9) dan mensubstitusikan persamaan (10) dan (11) maka diperoleh:

− ( + 2 ) + 2 − 2( + 2 ) + ( )= − + (koefisien )

+ − = − + (12)

−( + 2 ) + ( ) + 2 ( )= + − + (koefisien

)

+ 8 + 8 + 3 = + − + (13)

3.2.4. Nilai Ekstrem Fungsi Polinomial Pangkat 5

Pada langkah mencari akar persamaan baru di atas, dihasilkan persamaan (12) dan (13). Kedua persamaan tersebut tidak dapat menghasilkan nilai secara eksplisit, seperti pada langkah pencarian nilai optimum pada polinomial pangkat 3. Bentuk dari kedua persamaan yang kompleks, merupakan kesulitan bagi peneliti untuk menemukan nilai ekstrem fungsi polinomial pangkat 5 secara tepat dan eskplisit dengan cara aljabar yang sederhana seperti eliminasi atau substitusi. Jadi, fungsi polinomial pangkat 5 belum dapat dicari nilai ekstremnya karena menghasilkan persamaan yang kompleks sehingga tidak didapat nilai secara eksplisit.

4. Kesimpulan dan saran

Fungsi polinomial pangkat 3 dapat dicari nilai ekstremnya tanpa kalkulus dengan menggunakan teknik dasar aljabar. Fungsi polinomial pangkat 4 tidak dapat dicari nilai ekstremnya dengan menggunakan cara yang sama pada fungsi polinomial pangkat 3, karena fungsi polinomial pangkat 4 tidak dapat dibawa ke dalam bentuk fungsi ganjil. Pada fungsi polinomial pangkat 5 belum dapat dicari nilai ekstremnya karena menghasilkan dua persamaan yang kompleks, sehingga tidak dapat dicari nilainya secara eksplisit hanya dengan menggunakan konsep dasar aljabar sederhana. Saran bagi penelitian selanjutnya adalah dapat menyelesaikan kedua persamaan (persamaan (12) dan (13)) yang kompleks sehingga didapatkan nilai secara eksplisit. Selain itu juga dapat mengembangkan optimasi fungsi bentuk polinomial dengan derajat atau pangkat yang lebih tinggi dan mampu mengembangkan cara lain tanpa konsep turunan untuk polinomial pangkat 4 dan sebagainya.

(10)

Ucapan terima kasih

Terimakasih kepada Marcellinus Andy Rudhito, selaku dosen pengampu matakuliah Kapita Selekta yang telah membimbing dalam penyusunan makalah, Febi Sanjaya dan Herry Pribawanto, selaku dosen yang sudah membantu penelitian ini, serta teman-teman yang turut mendukung penelitian ini.

Referensi

de Villiers, M. (2004). All cubic polynomial are point symmetric. Learning and Teaching Mathematics, 1, 12–15.

Goehle, G., & Kobayasi, M. (2013). Polynomial graphs and symmetry. The College Mathematics Journal, 44(1), 3–42.

Hatton, J. (2013). The “center” of polynomial graph. Diambil dari https://jrh74.wordpress.com/2013/01/11 /the-center-of-a-polynomial-graph/ diakses 11 April 2016.

Taylor, R. D., & Hansen, R. (2008). Optimization of cubic polynomial function without calculus. Journal of The Mathematics Teacher, 101(6), 408–411.