POROS A. Pendahuluan
Sebuah poros adalah bagian mesin yang berputar yang digunakan untuk memindahkan daya dari satu tempat ke tempat yang lain. Tenaga yang dipindahkan pada poros oleh sebuah gaya tangensial dan menghasilkan momen putar yang dipasang dalam tenaga yang diijinkan untuk dipindahkan pada beberapa mesin yang terhubung pada poros. Untuk memindahkan tenaga dari poros ke lainnya, berbagai komponen seperti puli, roda gigi, dan lain-lain dipasang pada poros. Komponen yang terpasang pada porong ini menyebabkan poros membengkok. Dengan kata lain kita bisa mengatakan bahwa poros digunakan untuk memindahkan putaran dan momen bengkok. Komponen yang dipasang di poros dipasang dengan menggunakan pena atau spi.
B. Bahan Poros
Bahan yang umumnya digunakan untuk poros adalah baja menengah. Ketika tegangan tinggi dibutuhkan, maka digunakan baja paduan seperti nikel, krom-nikel atau baja krom-vanadium.
Poros umumnya dibentuk dengan pengerolan panas dan difinishing untuk mendapatkan ukurannya dengan proses dingin atau pembubutan dan gerinda. Poros yang diroll dingin lebih kuat daripada poros yang diroll panas tapi dengan tegangan sisa lebih tinggi. Tegangan residual menyebabkan penyimpangan pada poros saat pemesinan, khususnya saat pembuatan lubang spi atau pena. Poros dengan diameter yang lebih besar untuk mendapatkan ukurannya digunakan mesin bubut.
C. Jenis poros
Beberapa jenis poros dilihat dari penggunaanya. 1. Poros Transmisi
2. Poros Mesin
1. Poros Transmisi
Poros ini memindahkan tenaga antara sumber dan mesin yang menyerap tenaga. Poros lurus, poros counter, poros overhead dan semua poros pabrikan adalah poro transmisi. Karena poros ini membawa bagian mesin seperti puli, roda gigi, dan lainnya, maka akan menyebabkan bengkokan yang menyebabkan putus.
2. Poros Mesin
Poros ini adalah bagian dari mesin itu sendiri. Poros engkol adalah contoh dari poros mesin.
D. Ukuran Standar Poros Transmisi
Ukuran standar dari poros transmisi adalah: 25 mm – 60 mm dengan tingkatan 5 mm 60 mm – 110 mm dengan tingkatan 10 mm
110 mm – 140 mm dengan tingkatan 15 mm; dan 140 mm – 500 mm dengan tingkatan 20 mm
Panjang standar untuk poros adalah 5 m, 6 m, dan 7 m. E. Tegangan pada Poros
Tegangan yang terjadi pada poros adalah:
1. Tegangan geser yang disebabkan pemindahan putaran (karena beban yang berputar)
2. Tegangan bengkok (tarik atau tekan) yang disebabkan gaya yang bekerja pada bagian mesin seperti roda gigi, puli dan lain-lain dan juga yang disebabkan oleh berat puli itu sendiri.
3. Gabungan tegangan puntir dan bengkok
F. Tegangan maksimum yang diijinkan pada poros transmisi
Tegangan tekan maksimum yang dijinkan bekerja pada poros transmisi dalam puntiran atau tekan diambil
(a) 1,120 kg/cm2 untuk poros tanpa kelonggaran untuk lubang pengunci
(b)8,40 kg/cm2 untuk poros dengan kelonggaran untuk lubang pengunci
Untuk poros yang dibuat dengan ukuran fisik yang ditentukan, tegangan tarik yang diijinkan dapat dipakai 60% dari batas elastisitas tarik, tapi tidak boleh lebih dari 36% kekuatan tarik maksimum.
Tegangan geser maksimum yang diijinkan dapat dipakai
(a) 560 kg/cm2 untuk poros tanpa kelonggaran untuk lubang pengunci (b) 420 kg/cm2 untuk poros dengan kelonggaran untuk lubang pengunci
Untuk poros yang dibuat dengan ukuran fisik yang ditentukan, tegangan tarik yang diijinkan dapat dipakai 30% dari batas elastisitas tarik, tapi tidak boleh lebih 18% dari kekuatan tarik maksimum.
G. Perencanaan poros
Poros mungkin direncanakan atas dasar (1)Kekuatan
(2)Kekakuan
Dalam merencanakan poros atas dasar kekuatan, beberapa faktor perlu diperhatikan
(a) Poros yang didasarkan hanya untuk momen puntir (b)Poros yang didasarkan hanya untuk momen bengkok (c) Poros yang didasarkan untuk puntiran dan bengkokan
(d)Poros yang didasarkan untuk beban axial yang ditambah gabungan puntiran dan bengkokan.
H. Poros yang didasarkan hanya untuk momen puntir
Ketika poros didasarkan hanya pada mmen puntir dan torsi saja, maka diameter poros bisa didapatkan dengan persamaan torsi. Kita tahu bahwa
r f j T = s
Dimana T = Momen Puntir atau torsi yang bekerja pada poros, kg.cm J = Momen Inersia batang berpenampang bulat, cm4.
fs = tegangan geser puntiran, kg/cm2.
r = jari-jari, cm =
2
d
; dimana d adalah diameter poros Untuk poros pejal,
4 32 d
J = π
Persamaan (i) bisa ditulis
2 4 . 16 2 32 d f T d f d T s s π π = =
Dari persamaan ini kita bisa mencari diameter poros pejal. Untuk poros berongga
) ( 32 4 4 i o d d J = π −
Dimana do dan di = Diameter luar dan diameter dalam poros.
dan
2
o
d r=
Subsitusikan nilai ini ke pers. (i), kita dapatkan
(
)
( )
( )
4 2 4 4 4 4 4 1 16 an subsitusik 1 1 16 2 32 k d f T k d d k d f d d d f d d fs d T d f d T o s o i o s o i o s i o o s − ⋅ ⋅ ⋅ = = − ⋅ ⋅ = − ⋅ ⋅ = − ⋅ ⋅ = ⋅ ⋅ = π π π π πSebagai catatan:
1. Poros berongga biasanya digunakan pada pekerjaan laut. Poros ini lebih kuat per kg dari bahannya dan dikerjakan pada sebuah mandrel, bahannya juga lebih homogen dan mungkin digunakan untuk poros pejal.
Ketika poros berongga dibuat sama kekuatannya dengan poros pejal, maka momen puntir keduanya harus sama. Dengan kata lain, dengan bahan yang sama dari kedua poros,
( )
4 3 3 4 4 1 3 1 6 1 6 d k d d f d d d f T o s o i o s = − ⋅ ⋅ = − ⋅ ⋅ = π π2. Momen puntir T bisa didapatkan sengan persamaan Daya, P= 2⋅π4500⋅N⋅T Atau N P T ⋅ ⋅ × = π 2 4500
Dimana T = momen puntir, kg.m N = Putaran, rpm
Dalam satuan SI, persamaan di bawah bisa digunakan 60
2 N T P= ⋅π⋅ ⋅
Dimana P = Daya, dalam watt T = Momen puntir, N.m N = Putaran, rpm
3. Dalam kasus sabuk pembawa, torsi (T) diberikan
(
T T)
RT = 1− 2 ⋅
Dimana T1 dan T2 = Tegangan pada sisi tegang dan sisi kendur pada
sabuk
R = jari-jari puli.
Contoh 1: Sebuah poros rata berputar pada 200 rpm memindahkan
daya 25 HP. Poros diasumsikan dibuat dari baja menengah dengan tegangan geser yang diijinkan 420 kg/cm2. tentukan diameter poros, abaikan momen bengkok pada poros.
Diketahui
N = 200 rpm P = 25 HP fs = 420 kg/cm2 Jawab:
Pertama kita cari nilai torsi (T), gunakan persamaan kg.cm 850 kg.m 5 , 89 200 2 4500 25 2 4500 = = × × = ⋅ ⋅ × = π π N P T Diameter poros 3 16 f d T = π ⋅ s⋅ cm 5 atau 77 , 4 5 , 108 420 8950 16 . 16 3 3 3 = = × × = = π π fs T d
Contoh 2: Cari diameter poros pejal yang memindahkan 25 hp pada
200 rpm. Tegangan geser maksimum diambil 3600 kg/cm2 dan faktor keamanan 8. Jika poros berongga digunakan menggantikan poros pejal, cari diameter luar dan diameter dalam jika rasio diameter luar dan dalam 0,5
Diketahui P = 25 hp N = 200 rpm
Tegangan geser maksimum = 3600 Faktor keamanan = 8
Tegangan geser yang diijinkan 2 kg/cm 450 8 3800 = = s f Jawab
Pertama kita cari nilai torsi yang dipindahkan oleh poros
kg.cm 8950 kg.m 5 , 89 200 2 4500 25 2 4500 = = × × = × = π πN P T
Diameter poros pejal
3 16 f d T = π ⋅ s⋅ cm 5 atau 66 , 4 3 , 101 450 8950 16 . 16 3 3 3 = = × × = = π π fs T d
Diameter poros berongga Jika do = diameter luar, dan
Gunakan persamaan
(
)
(
)
(
)
cm 5 , 2 5 5 , 0 5 , 0 cm 5 atau 76 , 4 108 5 , 0 1 450 8950 16 1 . . 16 1 16 3 3 4 3 4 4 2 = × = ⋅ = = = − × × ⋅ = − = − ⋅ ⋅ ⋅ = do d k f T d k d f T i s o o s π π πContoh 3: (Satuan SI). Sebuah poros memindahkan daya 1 MW
pada 240 rpm. Tentukan diameter poros jika torsi maksimum yang diijinkan tidak boleh melebihi 20% torsi rata-rata. Ambil tegangan geser yang diijinkan 60 N/mm2. Diketahui: P = 1 MW = 106 Watt N = 240 rpm Tmax = 1,2 Tmean fs = 60 N/mm2. Jawab
Pertama kita temukan rata-rata torsi yang dipindahkan oleh poros N.mm 39.788.000 . 39788 240 2 60 106 60 240 2 10 60 2 6 = = × × = × × = ⋅ ⋅ ⋅ = m N T T T N P mean mean mean π π π Tmax = 39.788.000 x 1,2 = 47.745.600 N.mm Sekarang gunakan persamaan
mm 160 atau 4 , 159 770 . 052 . 4 770 . 052 . 4 60 47745600 16 16 16 3 max 3 3 max = = = × × = ⋅ × = ⋅ = d fs T d d fs T π π π
I. Poros yang didasarkan hanya untuk momen bengkok
Ketika poros hanya menerima momen bengkok, maka tegangan maksimum (tarik dan tekan) diberikan persamaan bengkok. Kita tahu bahwa
y f I M = b
Dimana: M = Momen Bengkok, kg.cm I = Momen inersia, cm4
fb = Tegangan bengkok, kg/cm2
y = jarak dari axis netral ke luar, cm
Kita tahu bahwa momen inersia untuk poros pejal
2 64 4 d y d I = = π
Subsitusikan nilai ini ke persamaan (i), kita dapatkan
3 4 32 2 64 d f M d f d M b b ⋅ ⋅ = = π π
Dari persamaan ini diameter poros dapat diketahui. Juga kita tahu untuk poros berongga,
(
)
( )
2 d a n d im a n a 1 6 4 6 4 4 4 4 4 o o i o i o d y d d k k d d d I = = − = − = π πSubsitusikan lagi nilai ini ke persamaan (i), kita dapatkan
( )
( )
4 3 4 4 1 3 2 2 1 6 4 k d f M d f k d M o b o b o − ⋅ ⋅ = = − π πDari persamaan ini diameter luar poros kita dapatkan.
Contoh 4. Sepasang roda dari sebuah gerbong kereta api membawa
beban 5 ton tiap kotak as, bergerak sejauh 10 cm keluar dari pangkalan. Ukuran dari rel adalah 140 cm. Cari diameter as antara roda, jika tegangan tidak boleh lebih dari 1000 kg/cm2.
Diketahui:
Beban tiap kotak as, W = 5 T = 5000 kg Jarak beban dari roda, L = 10 cm
Ukuran rel = 140 cm
Tegangan, fb = 1000 kg/cm3 Jawab:
Sedikit perumpamaan ditampilkan pada gambar di bawah bahwa momen bengkok maksimum terjadi pada roda C dan D. Adapun momen bengkok maksimum
kg.cm 50000 10 5000 × = = =WL M
Gambar 4.1 Diameter as cm 8 atau 984 , 7 509 1000 50000 32 32 32 3 3 3 3 = = × × = ⋅ = ⋅ ⋅ = π π π b b f M d d f M
J. Poros yang menerima gabungan momen puntir dan momen bengkok
Ketika poros disiapkan untuk menerima gabungan momen puntir dan momen bengkok, maka poros harus dibuat berdasarkan dua momen yang simultan. Beberapa teori telah dikeluarkan untuk menghitung kesalahan elatis dari bahan ketika dia menerima bermacam jenis gabungan tegangan. 2 teori berikut penting untuk diperhatikan.
1. Teori tegangan geser maksimum atau teori Guest’s. Ini digunakan untuk bahan ulet seperti baja menengah.
2. Teori tegangan normal maksimum atau teori Rankine’s. Ini digunakan untuk bahan rapuh seperti besi cor.
Jika fs = tegangan geser yang menyebabkan momen puntir, dan
fb = tegangan bengkok (tarik dan tekan) yang menyebabkan momen
puntir.
Berdasar pada teori tegangan geser maksimum, tegangan geser maksimum pada poros,
2 2 (max) 4 2 1 c b s f f f = +
Subsitusikan nilai fb dan fs dari bagian H dan I, kita dapatkan
) ( 16 16 16 4 32 2 1 2 2 3 (m a x) 2 2 2 2 3 2 3 (m ax ) i T M d f T M d d T d M f s s + = + ⋅ = + = π π π π
Persamaan M2+T2 dikenal sebagai persamaan mmen puntir dan disebut sebagai Te. Persamaan momen puntir mungkin didefnisikan
sebagai momen puntir, jika bekerja sendiri, menghasilkan tegangan geser (fs) yang sama dengan momen puntir yang bekerja. Dengan pembatasan tegangan geser maksimum [fs (maks)] sama dengan tegangan
geser maksimum yang diijinkan (fs) untuk bahan, persamaan (i) bisa ditulis sebagai
) ( 1 6 3 2 2 ii d f T M T s e ⋅ = + = π
Dari pernyataan ini diameter poros (d) perlu evaluasi.
Sekarang berdasarkan teori tegangan normal maksimum, tegangan normal maksimum pada poros
) ( 2 1 (max) 32 atau 2 1 32 16 32 2 1 32 2 1 ) ( 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 (max) iv T M M d fb T M M d d T d M d M iii f f f fb b b s + + = + + ⋅ = ⋅ + ⋅ × + ⋅ × = + = π π π π π Persamaan + 2 + 2 2 1 M M T
dikenal dengan persamaan momen bengkok dan disebut Me. Persamaan momen bengkok bisa didefinisikan
sebagai momen yang bekerja sendiri baik tegangan tarik atau tegangan tekan (fb) sebagai momen bengkok yang terjadi. Dengan pembatasan
tegangan normal maksimum (fb maks) sama dengan tegangan bengkok
yang diijinkan, persamaan (iv) dapat ditulis
) ( 3 2 3 2 2 2 1 v d f T M M M b e π = + + =
Dari pernyataan ini, diameter poros harus dievaluasi. Catatan:
1. Dalam kasus poros berongga, diameter poros dapat ditulis
(
)
(
4)
3 32 2 2 2 1 4 3 2 2 1 1 16 k d f T M M M k d f T M T o b e o s e − ⋅ = + + = − ⋅ = + = π π2. Ini berarti bahwa diameter poros bisa didapatkan dengan menggunakan dua teori dan nilai yang lebih besar yang diambil.
Contoh 5. Sebuah poros pejal dipasangkan pada momen bengkok
30000 kg.cm dan torsi 100.000 kg.cm. poros dibuat dari bahan baja C-45 yang memiliki tegangan tarik maksimum 700 kg/cm2 dan tegangan geser maksimum 5000 kg/cm2. Asumsikan faktor keamanan 6, cari diameter poros.
Diketahui :
Momen bengkok, M = 30000 kg.cm Torsi, T = 100.000 kg.cm
Tegangan geser maksimum = 5000 kg/cm2 Faktor keamanan = 6
Tegangan tarik yang diijinkan 2 kg/cm 67 , 1166 6 7000 = = b f
dan tegangan geser yang diijinkan 2 kg/cm 33 , 833 6 5000 = = s f Jawab:
Persamaan momen puntir (berdasarkan teori tegangan geser maksimum) kg.cm 10 44 , 10 000 . 100 000 . 30 2 2 4 2 2 × = + = + = M T Te
Sekarang gunakan persamaan
cm 6 , 8 638 638 3 , 833 16 10 44 , 10 33 , 833 16 10 44 , 10 16 3 4 3 3 4 3 = = = × × × = × × = × ⋅ = d d d d f Te s π π π
Juga kita ketahu bahwa persamaan momen bending (berdasarkan teori tegangan normal)
(
30.000 10,44 10)
6,72 10 kg.cm 2 1 2 1 4 4 2 2 × = + + = + + = M M T MeSekarang gunakan persamaan
cm 37 , 8 6 , 586 6 , 586 67 , 1167 32 10 72 , 6 67 , 1167 32 10 72 , 6 32 3 4 3 3 4 3 = = = × × × = × × = × ⋅ = d d d d f Me b π π π
Ambil nilai terbesar dari 2 nilai, kita dapat d = 8,6 atau 9 cm
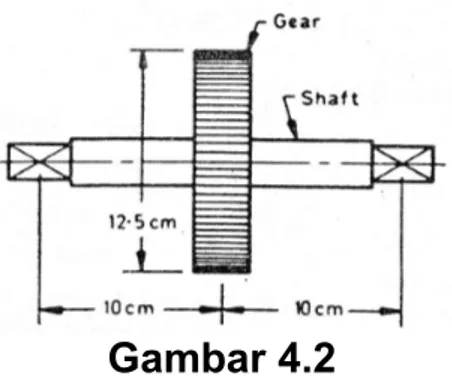
Contoh 6: Sebuah roda gigi dipasang pada poros seperti pada
gambar. Diameter roda gigi 12, cm dan 5 hp daya ditransmisikan pada putaran 120 rpm. Asumsikan tegangan geser yang diijinkan 420 kg/cm2, cari diameter poros.
Gambar 4.2
Diketahui:
Diameter roda gigi, D = 12,5 cm Daya yang ditransmisikan, P = 5 hp Putaran poros, N = 120 rpm
Tegangan geser yang diijinkan, fs = 420 kg/cm2
Jawab:
Torsi yang ditransmisikan oleh poros
kg.cm 285 kg.m 85 , 29 120 2 4500 5 2 4500 = = × × = × = π πN P T
Gaya tangensial pada gigi roda gigi, kg 5 , 477 5 , 12 2985 2 2 = × = = D T
Dan momen bending pada tengah roda gigi, kg.cm 300 2 5 , 12 480 × = = M Diameter poros, kg.cm 4232 000 . 3 29852 2 2 2 = + = + = M T Te
Sekarang gunakan persamaan
cm 4 atau 7 , 3 4 , 51 4 , 51 420 16 4232 420 16 4232 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
Contoh 7. Sebuah poros dibuat dari bahan besi menengah
dibutuhkan untuk memindahkan daya 120 HP pada 300 rpm. Panjang poros 3 meter. Poros ini membawa puli dengan berat masing-masing 150 kg dengan jarak masing-masing 1 meter dari ujung poros. Asumsikan nilai keamanan tegangan, tentukan diameter poros.
Diketahui:
Daya yang ditransmisikan, P = 120 HP Putaran poros, N = 300 rpm
Panjang poros, L = 3 meter Berat tiap-tiap puli, W = 150 kg
Jarak tiap puli dari ujung poros, = 1 m Jawab:
Torsi yang ditransmisikan
kg.m 4 , 286 300 2 4500 120 2 4500 = × × = × = π πN P T
Poros yang membawa 2 puli diperlihatkan pada gambar. Reaksi tiap tumpuan akan jadi 150 kg.
RA = RB = 150 kg
Momen bengkok maksimum akan terjadi pada tiap puli pada titik C dan D.
Momen bengkok maksimum, kg.cm 000 . 15 kg.m 150 1 150 = = × = M Gambar 4.3
Persamaan momen puntir, kg.cm 330 . 32 000 . 15 28640 2 2 2 2 = + = + = M T Te Diameter Poros Gunakan persamaan cm 5 , 6 atau 49 , 6 4 , 274 4 , 274 600 16 330 . 32 600 16 330 . 32 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
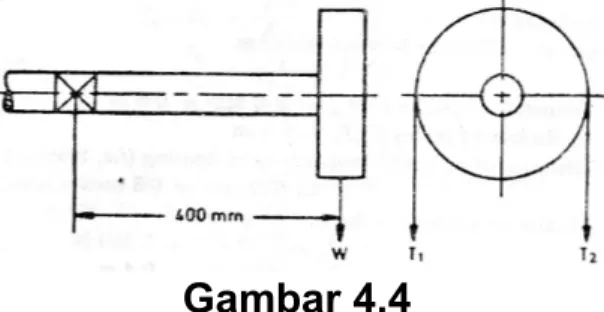
Contoh 8. (Satuan SI). Sebuah poros lurus digerakan oleh sebuah
motor yang diletakan vertical dibawahnya. Puli pada poros lurus berdiameter 1,5 meter dan tegangan pada sabuk 5,4 kN dan 1,8 kN pada sisi tegang dan sisi kendur sabuk. Kedua tegangan ini dapat diasumsikan vertical. Jika puli berada di ujung poros, jarak garis pusat puli ke garis pusat bantalan adalah 400 mm, cari diameter poros. Asumsikan tegangan geser maksimum yang diijinkan 42 N/mm2.
Diketahui: Diameter puli, D = 1,5 m Jari-jari puli, R = 0,75m 750 mm 2 5 , 1 = =
Tegangan pada sisi tegang sabuk, T1 = 5,4 kN = 5400 N
Tegangan pada sisi kendur sabuk, T2 = 1,8 kN = 1800 N
Jarak garis pusat puli ke garis pusat bantalan, L = 400 mm
Tegangan geser maksimum yang diijinkan fs = 42 N/mm2
Gambar 4.4
Jawab:
Torsi yang ditransmisikan oleh poros,
( ) (5400 1800) 750 2.700.000N.mm 2 1 = × − = − = T T R T
Mengabaikan berat dari poros, total beban vertikal yang bekerja pada puli, N 7200 1800 5400 2 1 + = + = =T T W Momen bengkok, N.mm 000 . 880 . 2 400 7200 × = = =WL M
Persamaan momen puntir,
kg.mm 10 95 , 3 000 . 700 . 2 000 . 880 . 2 8 2 2 2 2 × = + = + = M T Te Diameter Poros (d) Gunakan persamaan cm 80 atau 2 , 78 000 . 479 000 . 479 42 16 10 95 , 3 42 16 10 95 , 3 16 3 8 3 3 8 3 = = = × × × = × × = × ⋅ = d d d d f Te s π π π
Contoh 9. (Satuan SI). Sebuah poros ditumpu oleh dua bantalan
sejauh 1 meter. Sebuah puli dengan diameter 600 mm dipasang pada jarak 300 mm ke kanan dari bantalan kiri dan menggerakan sebuah puli di bawahnya dengan bantuan sabuk yang mempunyai tegangan maksimum 2,25 kN. Puli yang lain berdiameter 400 mm diletakan pada
jarak 200 mm di sebelah kiri bantalan kanan dan memutarkan motor listrik dan sabuk, yang diletakan horisontal ke kanan. Sudut kontak dari dua buah puli adalah 180o dan µ = 0,24. tentukan diameter poros yang cocok untuk poros pejal, tegangan tarik yang diijinkan 63 N/mm2 dan 42 N/mm2 pada tegangan geser untuk bahan poros. Asumsikan torsi pada setiap puli sama.
Diketahui:
Jarak antar bantalan = 1 m
Diameter puli C, D1 = 600 mm = 0,6 m Jari-jari puli C, R1 = 300 mm = 0,3 m
Jarak puli C dari bantalan kiri = 300 mm = 0,3 m Tegangan maksimum pada belt di C,
T1 = 2,25 kN = 2250 N
Diameter puli D, D2 = 400 mm = 0,4 m Jari-jari puli C, R2 = 200 mm = 0,2 m
Jarak puli C dari bantalan kiri = 200 mm = 0,2 m Sudut kontak untuk kedua puli,
rad 1080 π
θ= =
Koefisien gesek, µ = 0,24
Tegangan tarik yang bekerja, fb = 63 N/mm2
Tegangan geser yang bekerja, fs = 42 N/mm2
Jawab:
Jika T2 = Tegangan pada sisi kendur puli C
N 1060 126 , 2 2250 126 , 2 dan 126 , 2 3275 , 0 3 , 2 24 , 0 log atau 24 , 0 log 3 , 2 1 2 2 1 2 1 2 1 = = = = = × = × = = T T T T T T T T π π µ θ
Beban vertikal yang bekerja pada poros di C, N 3310 1060 2250 2 1+ = + = =T T WC
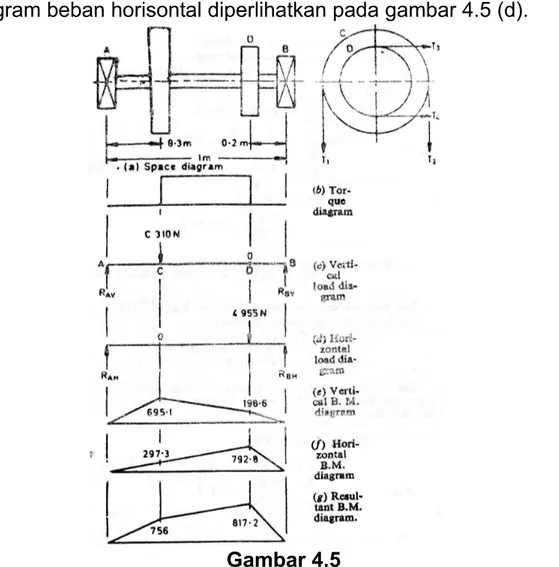
Diagram beban vertikal diperlihatkan pada gambar 4.5 (c) Kita tahu bahwa torsi pada puli C,
( ) ( ) N.mm 357 3 , 0 1060 2250 1 2 1 = × − = − = T T R T
Jika T3 dan T4 adalah tegangan pada sisi tegang dan sisi kendur
( ) ) ( 1 2 6 , 2 1 2 6 , 2 ju g a ) ( N 1 7 8 5 2 , 0 3 5 7 3 5 7 3 5 7 4 3 2 1 4 3 2 4 3 2 4 3 ii T T T T T T i R T T R T T = = = = = = − = −
Subsitusikan nilai T3 pada persamaan (i), kita dapatkan
N 3370 1585 1785 N 1585 126 , 1 1785 1785 126 , 2 3 4 4 4 = + = = = = − T T T T
Beban horisontal yang terjadi pada poros di D,
N 4955 1585 3370 4 3 = + = + =T T WD
Diagram beban horisontal diperlihatkan pada gambar 4.5 (d).
Gambar 4.5
Sekarang kita cari momen bengkok maksimum untuk pembebanan horisontal dan vertikal.
Pertama, berdasarkan pembebanan vertikal. Jika RAV dan RBV adalah
reaksi pada bantalan A dan B. N
3310
R RAV + BV =
N.m 198,6 0,5 3310 -0,8 2317 D, di Bending Momen N.m 695,1 0,3 2317 3 0 C, di Bending Momen 0 B, dan A di Bending Momen N 2317 993 3310 dan N 993 3 , 0 3310 = × × = = × = × = = = = = = × = × DV AV CV V B AV AV BV BV M , R M M M -R R l R
Diagram momen bending untuk pembebanan vertikal diperlihatkan pada gambar 4.5 (e).
Sekarang berdasarkan pembebanan horisontal. Jika RAH dan RBH
adalah reaksi pada bantalan A dan B. N
4955
R
RAH + BH =
Ambil momen di titik A,
N.m ,8 792 0,8 991 8 , 0 D, di Bending Mmen N.m 3 , 297 0,3 991 3 0 C, di Bending Momen 0 B, dan A di Bending Momen N 991 3964 4955 dan N 3964 8 , 0 4955 = × = × = = × = × = = = = − = = × = × AH DH AH CH BH AH AH BH BH R M , R M M M R R l R
Diagram momen bending untuk pembebanan vertikal diperlihatkan pada gambar 4.5 (f)
Resultan momen bending di C, N.m 756 3 , 297 1 , 695 2 + 2 = = + = CV CH C M M M
Dan Resultan momen bending di D, N.m 2 , 817 8 , 792 6 , 198 2+ 2 = = + = DV DH D M M M
Resultan diagram momen bending untuk pembebanan vertikal diperlihatkan pada gambar 4.5 (g)
Kita lihat bahwa momen bending maksimum terjadi di D. Momen bending maksimum,
N.m 2 , 817 = =MD M Diameter poros (d),
Kita ketahui persamaan momen puntir,
N.mm 10 892 N.mm 892 2 , 817 357 2 2 2 2 2 × = = + = + = T M Te
mm 6 , 47 10 108 10 108 42 16 10 892 42 16 10 892 16 3 2 2 2 3 3 2 3 = × = × = × × × = × × = × ⋅ = d d d d f Te s π π π
Kita ketahui juga bahwa persamaan momen bending,
(
)
N.mm 10 854,6 N.m 6 , 854 892 2 , 817 3 2 1 2 2 2 1 × = = + = + + = M T M MeSekarang gunakan persamaan
mm 7 , 51 10 1 , 138 10 1 , 138 63 32 10 854,6 63 32 10 854,6 32 3 3 3 3 3 3 3 3 = × = × = × × × = × × = × ⋅ = d d d d f Me b π π π
Ambil nilai yang terbesar, kita dapatkan mm 55 atau 7 , 51 = d
Contoh 10. Sebuah poros ditumpu oleh bantalan A dan B, 80 cm
tengah-tengah. Sebuah gigi penahan roda gigi lurus 200 dengan diameter pitch 60 cm, terletak di 20 cm sebelah kanan bantalan A, dan sebuah puli diameter 70 cm dipasang 25 cm sebelah kiri bantalan B. Roda gigi digerakan oleh pinion dengan gaya tangensial ke bawah sementara puli digerakan oleh sabuk horisontal yang mempunyai sudut wrap 1800. puli juga melayani sebagai flywheel dan berat 200 kg. Tegangan maksimum sabuk adalah 300 kg dan rato tegangan 3:1. Tentukan momen bengkok maksimum dan diameter poros yang dibutuhkan jika tegangan geser yang diijinkan dari bahan adalah 400 kg/cm2.
Diketahui
Jarak antara bantalan A dan B, = 80 cm
Sudut tekanan pada roda gigi C,
α = 200
Diameter pitch roda gigi C, D1 = 60 cm Jari-jari pitch roda gigi C, R1=602 =30 cm Jarak roda gigi C dari bantalan A,
Diameter pitch puli D, D2 = 70 cm Jari-jari puli D, R1=702 =35 cm Jarak puli D dari bantalan B,
= 25 cm
Sudut kontak dari sabuk pada puli D, rad 180 0 π θ= = Berat puli, 200 = W kg
Tegangan maksimum pada sabuk, T1 = 300 kg Rasio tegangan 3 2 1 = T T
Tegangan geser yang diijinkan, fs = 400 kg/cm2
Jawab:
Kita ketahui bahwa torsi yang bekerja pada poros di D,
(
)
( )
N.mm 357 kg.cm 7000 35 1 300 1 3 1 2 2 1 1 2 2 1 = = × − = − = − = R T T T R T T TGaya tangensial yang bekerja pada roda gigi C kg 3 , 233 30 7000 1 = = = R T
(Asumsi torsi pada D sama dengan torsi di C)
Dan beban normal yang bekerja pada gigi roda gigi,
kg 3 , 248 9397 , 0 3 , 233 20 cos 3 , 233 cos l tangensia gaya 0 = = = = α C W
Beban normal yang bekerja pada 200 pada arah vertikal diperlihatkan pada gambar. Menyelesaikan beban normal horisontal dan vertikal, kita dapatkan
Komponen vertikal dari WC, beban vertikal yang bekerja pada poros di C, kg 3 , 233 9397 , 0 3 , 248 20 cos 0 = × = = C CV W W Gambar 4.6
Komponen horisontal dari WC, beban vertikal yang bekerja pada poros di C,
kg 9 , 84 342 , 0 3 , 248 20 sin 0 = × = = C CH W W Karena 3 2 1 = T T dan T1 = 300 kg, maka kg 100 3 300 3 1 2 = = = T T
Beban horizontal yang bekerja pada poros di titik D, kg 400 100 300 2 1+ = + = =T T WDH
Dan beban vertikal yang bekerja pada poros di titik D, kg
200
= =W WDV
Diagram beban vertikal dan horisontal pada titik C dan D diperlihatkan pada gambar (c) dan (d).
Sekarang kita cari momen bengkok maksimum untuk pembebanan horisontal dan vertikal.
Berdasarkan pembebanan vertikal. Jika RAV dan RBV adalah reaksi pada
bantalan A dan B. N 3 , 433 200 3 , 233 R RAV + BV = + = Ambil momen di titik A,
kg.cm 4895 25 5 , 237 25 D, di Bending Mmen kg.cm 4750 20 5 , 237 20 C, di Bending M omen 0 B, dan A di Bending M omen kg 5 , 237 8 , 195 3 , 433 dan kg 8 , 195 20 3 , 233 55 200 80 = × = × = = × = × = = = = − = = × + × = × AV DV AV CV BV AV AV BV BV R M R M M M R R R
Diagram momen bengkok untuk pembebanan vertikal diperlihatkan pada gambar 4.7 (e). Sekarang berdasar pembebanan horisontal. Sekarang berdasarkan pembebanan horisontal. Jika RAH dan RBH adalah reaksi
pada bantalan A dan B.
N 9 , 484 400 9 , 84 R RAH + BH = + = Ambil momen di titik A,
kg.cm 7405 25 2 , 296 25 D, di Bending Mmen kg.cm 3772 20 6 , 188 20 C, di Bending M omen 0 B, dan A di Bending Momen kg 6 , 188 3 , 296 9 , 484 dan k 3 , 296 20 9 , 84 55 400 80 = × = × = = × = × = = = = − = = × + × = × BH DH AH CH BH AH AH BH BH R M R M M M R g R R
Momen bengkok untuk pembebanan horisontal diperlihatkan pada gambar 4.7 (f).
kg.cm 6064 3772 47502 2 = + = + = CV CH C M M M
Dan Resultan momen bending di D,
kg.cm 8876 7405 48952 2 = + = + = DV DH D M M M
Resultan diagram momen bending untuk pembebanan vertikal diperlihatkan pada gambar 4.7 (g)
Kita lihat bahwa momen bending maksimum terjadi di D. Momen bending maksimum,
kg.cm 8076 = =MD M Diameter poros (d),
Kita ketahui persamaan momen puntir,
kg.mm 11300 8876 70002 2 2 2 = + = + = T M Te
Sekarang gunakan persamaan,
cm 5 , 5 atau 24 , 5 8 , 143 8 , 143 400 16 11300 400 16 11300 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
K. Poros dengan Beban yang Berubah-ubah
Dalam pembahasan sebelumnya kita mempunyai asumsi bahwa poros diberikan torsi dan momen bengkok yang konstan. Tapi pada kenyataannya, poros diberikan torsi dan momen bengkok yang berubah-ubah. Untuk merancang poros yang seperti itu seperti poros lurus dan poros Counter, gabungan kejutan dan faktor kelelahan harus diambil untuk menghitung momen puntir yang diperhitungkan (T) dan momen bengkok (M). Ini untuk poros yang diberikan gabungan bengkokkan dan torsi, persamaan momen puntir,
( ) (2 )2 T K M K Te = m× + t×
Dan persamaan momen bengkok,
( ) ( ) × + × + × = 2 2 2 1 T K M K M K Me m m t
Dimana Km = gabungan faktor kejutan dan faktor kelelahan untuk
bengkokan, dan
Kt = gabungan faktor kejutan dan faktor kelelahan untuk puntiran
Tabel berikut memperlihatkan nilai yang dianjurkan untuk Km dan Kt
Jenis Beban Km Km
1. Poros Diam
(b) Beban kejut
2. Poros Berputar (a) Beban Bertahap
(b) Beban kejut dengan hentakan kecil
(c) Beban kejut dengan hentakan besar 1.5 to 2.0 1.5 1.5 to 2.0 2.0 to 3.0 1.5 to 2.0 1.0 1.5 to 2.0 1.5 to 3.0
Contoh 11. Sebuah poros baja menengah memindahkan 25 hp pada
200 rpm. Poros ini membawa beban pusat 90 kg dan ditumpu sederhana antara bantalan yang berjarak 2,5 m. Tentukan ukuran dari poros, jika tegangan geser yang diijinkan adalah 420 kg/cm2 dan tegangan tarik dan tekan tidak boleh lebih dari 560 kg/cm2. Berapa ukuran poros yang dibutuhkan jika dipasang pada beban bertahap?
Diketahui
Daya yang ditransmisikan, P = 25 hp
Putaran poros, N = 200 rpm
Beban pusat yang dibawa oleh poros, W = 90 kg
Jarak poros antar bantalan, L = 2,5 m = 250 cm
Tegangan geser yang diijinkan, fs = 420 kg/cm2
tegangan tekan atau tarik maksimum, fb = 560 kg/cm2
Jawab
Jika T dan M = Torsi dan momen bengkok ditransmisikan oleh poros. Gunakan persamaan kg.cm 950 . 8 kg.m 5 , 89 200 2 500 . 4 25 2 500 . 4 = = × × = × = π πN P T
Kita tahu untuk poros yang ditumpu sederhana membawa sebuah beban sentral, momen bengkok maksimum,
kg.cm 625 . 5 4 250 90 4 = × = =WL M Ukuran poros
Jika d = Diameter poros, dalam cm.
kg.cm 571 . 10 8950 56252 2 2 2 = + = + = T M Te
Sekarang gunakan persamaan,
cm 04 , 5 18 . 128 18 . 128 420 16 571 . 10 420 16 571 . 10 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
Juga kita ketahui bahwa persamaan momen bengkok,
(
5.625 10.571)
8.098k .cm 2 1 2 2 2 1 g T M M Me = + = + + =Sekarang gunakan persamaan
cm 28 , 5 29 , 147 29 , 147 560 32 098 . 8 560 32 098 . 8 32 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Me b π π π
Ambil nilai yang terbesar, kita dapatkan cm 5,5 atau 28 , 5 = d
Ukuran poros ketika didasarkan kepada Beban bertahap Jika d = Diameter poros, dalam cm
Dari tabel, untuk putaran poros dengan Beban bertahap, Km = 1,5 dan Kt = 1
Persamaan momen puntir atau torsi ,
( ) ( ) ( ) ( ) kg.cm 300 . 12 8950 1 5625 5 , 1 2 2 2 2 = × + × = × + × = K M K T Te m t Menggunakan persamaan cm 5 , 5 atau 3 , 5 149 149 420 16 300 . 12 420 16 300 . 12 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
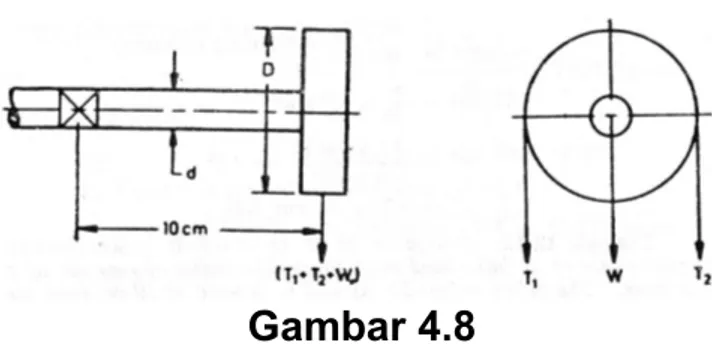
Contoh 12. Rancang sebuah poros untuk memindahkan daya dari
puli dengan perantara sabuk. Berat puli 20 kg dan terletak 10 cm dari tengah bantalan. Jika diameter puli adalah 20 cm dan daya yang ditransmisikan maksimum adalah 1,5 hp pada 120 rpm. Sudut putar sabuk 180o dan koefisien gesek antara sabuk dan puli 0,3. faktor kejutan dan faktor kelelahan untuk bengkok dan puntiran adalah 1,5 dan 2,0. tegangan geser yang diijinkan pada poros diambil 350 kg/cm2.
Diketahui: Berat puli, W = 20 kg
Jarak puli dari pusat bantalan, L = 10 cm
Diameter puli D = 20 cm Jari-jari puli R =10 cm
Daya maksimum yang ditransmisikan, P = 1,5 hp
Putaran, N = 120 rpm Sudut putar sabuk,
rad 180 0 π
θ= =
Koefisien gesek antara sabuk dan puli,
µ = 0,3
Tegangan geser yang diijinkan pada poros, fs = 350 kg/cm2
Faktor kejutan dan kelelahan untuk bengkokan, Km = 1,5
Faktor kejutan dan kelelahan untuk puntiran, Kt = 2,0
Gambar 4.8
Jawab:
Kita tahu bahwa torsi yang dipindahkan oleh poros,
kg.cm 895 kg.m 95 , 8 120 2 500 . 4 5 , 1 2 500 . 4 = = × × = × = π πN P T
Jika T1 dan T2 = tegangan pada sisi tegang dan sisi kendur sabuk. Kita
(
)
(
)
(i) k g 5, 8 9 1 0 8 9 5 2 1 2 1 2 1 = − × − = − = T T T T R T T TKita juga tahu bahwa
2 1 2 1 2 1 2 1 57 , 2 dan 57 , 2 4098 , 0 3 , 2 3 , 0 log atau 3 , 0 log 3 , 2 T T T T T T T T = = = × = × = = π π µ θ
Subsitusikan nilai T1 pada persamaan, kita dapatkan
kg 146,5 57 2,57 2,57 dan kg 57 57 , 1 5 , 89 5 , 89 57 , 1 5 , 89 57 , 2 2 1 2 2 2 2 = × = = = = = = − T T T T T T
Dan total beban vertikal yang bekerja pada puli kg 5 , 223 20 57 5 , 146 2 1+ + = + + = =T T W
Momen bengkok yang bekerja pada poros,
(
1+ 2 +)
=223,5×10 =2325kg.cm= T T W L
M
Persamaan momen puntiran,
( ) ( ) ( ) ( ) kg.cm 800 . 3 895 0 , 2 235 . 2 5 , 1 2 2 2 2 = × + × = × + × = K M K T Te m t Ukuran poros
Jika d = Diameter poros, dalam cm. Gunakan persamaan, cm 4 atau 8 , 3 3 , 55 3 , 55 350 16 3800 350 16 3800 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
Contoh 13. Sebuah poros baja nikel horizontal diletakan pada dua
bantalan, A di kiri dan B di kanan dan membawa 2 roda gigi C dan D yang terletak pada jarak 25 cm dam 40 cm dari garis tengah bantalan kiri dan kanan. Diameter pitch roda gigi C 60 cm dan roda gigi D 20 cm. Jarak antara garis tengah bantalan 240 cm. Poros memindahkan daya 25 hp pada putaran 120 rpm. Gaya yang dihantarkan pada poros oleh
roda gigi C dan dikeluarkan pada roda gigi D dengan cara menekan gigi PtC dari roda gigi C dan roda gigi D secara vertikal ke arah bawah.
Cari diameter poros, jika tegangan yang bekerja 1000 kg/cm2 pada tarikan dan 560 kg/cm2 pada geseran. Berat roda gigi C dan D 95 kg dan 35 kg. Gabungan faktor kejutan dan kelelahan untuk bengkok dan torsi diambil 1,5 dan 1,2.
Diketahui:
Diameter pitch roda gigi C, DC = 60 cm
Jari-jari roda gigi C, RC = 30 cm
Diameter pitch roda gigi D, DD = 20 cm
Jari-jari roda gigi C, RD = 10 cm
Daya yang ditransmisikan, P = 25 hp
Putaran, N = 120 rpm
Tegangan tarik yang bekerja, ft = 1000 kg/cm2
Tegangan geser yang bekerja, fs = 560 kg/cm2
Berat roda gigi C, WC = 95 kg
Berat roda gigi D, WD = 35 kg
Faktor kejutan dan kelelahan untuk bengkokan, Km = 1,5
Faktor kejutan dan kelelahan untuk puntiran, Kt = 1,2
Gambar 4.9
Jawab:
Torsi yang ditransmisikan oleh poros. Gunakan persamaan
kg.cm 920 . 14 kg.m 2 , 149 120 2 500 . 4 25 2 500 . 4 = = × × = × = π πN P T
kg 3 , 497 30 920 . 14 = = = C tC R T P
Total beban yang bekerja ke arah bawah pada poros di titik C, kg 3 , 592 95 3 , 497 + = = + C tC W P
Hal yang sama, gaya tangensial yang bekerja pada roda gigi D, kg 1492 10 920 . 14 = = = D tD R T P
Total beban yang bekerja ke arah bawah pada poros di titik D, kg 527 . 1 35 492 . 1 + = = + D tD W P
Sekarang kita asumsikan poros ditumpu, momen bengkok maksimum bisa didapatkan dengan pemecahan di bawah:
Jika RA dan RB = Reaksi pada A dan B
RA + RB = Total beban yang bekerja ke arah bawah pada C dan D
= 592,3 + 1.527 = 2.119,3 kg Ambil momen di titik A,
kg 1 , 785 2 , 334 . 1 3 , 119 . 2 2 , 334 . 1 25 3 , 592 200 527 . 1 240 = + = = × + × = × A B B R kg R R
Sebuah pertimbangan mengatakan bahwa momen bengkok maksimum akan terjadi di titik C atau D.
Momen bending di titik C,
kg.cm 5 , 627 . 19 25 1 , 785 25= × = × = A C R M
Momen bengkok pada titik D,
kg.cm 5 , 367 . 53 175 3 , 592 200 1 , 785 175 C) titik pada total (Beban 200 = × − × = × − × = A D R M
Momen bengkok maksimum yang dipindahkan oleh poros, kg.cm 5 , 567 . 53 = =MD M
Persamaan momen bengkok,
( ) ( ) ( ) ( ) kg.cm 040 . 81 920 . 14 2 , 1 5 , 367 . 53 5 , 1 5 , 367 . 53 5 , 1 2 2 2 1 2 2 2 1 = × + × + × = × + × + × = T K M K M K Me m m t
Persamaan momen puntir atau torsi,
( ) ( ) ( ) ( ) kg.cm 029 . 82 920 . 14 2 , 1 5 , 367 . 53 5 , 1 2 2 2 2 = × + × = × + × = K M K T Te m t Ukuran poros
Jika d = Diameter poros, dalam cm. Gunakan persamaan,
mm 38 , 9 47 , 825 47 , 825 000 . 1 32 81.040 ) (ambil 000 . 1 32 040 . 81 32 3 3 t 3 3 = = = × × = = × × = ⋅ = d d f f d d f M b b e π π π
Gunakan juga persamaan
cm 07 , 9 746 746 560 16 029 . 82 560 16 029 . 82 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
Ambil nilai terbesar, kita dapatkan cm 10 atau 38 , 9 = d
Contoh 14. Sebuah tromol kerek diameter 50 cm dikunci pada poros
yang ditumpu dua buah bantalan dan diputarkan melalui rasio pengurangan 12:1 oleh sebuah motor listrik. Tentukan daya yang memutarkan motor jika beban maksimum 800 kg diangkat pada putaran 50 m/mnit dan efisiensi pemutar 80%. Juga tentukan torsi pada poros tromol dan putaran motor dalam rpm. Tentukan juga diameter poros yang dibuat dari baja pemesinan, tegangan tarik yang bekerja adalah 1150 kg/cm2 dan tegangan gesr 500 kg/cm2. Roda gigi pembawa berdiameter 45 cm dipasang pada ujung poros dan tergantung 15 cm dekat bantalan. Gabungan faktor kejutan dan kelelahan untuk bengkokan dan torsi masing-masing diambil 2 dan 1,5.
Diketahui:
Diameter dari tromol, D = 50 cm Jari-jari tromol, R = 25 cm = 0,25 m Rasio pengurangan = 12 : 1
Beban maksimum, W = 800 kg Kecepatan, v = 50 m/min
Tegangan tarik yang bekerja, ft atau fb = 1.150 kg/cm2
Tegangan geser yang bekerja, fs = 500 kg/cm2
Diameter roda gigi pembawa, D1 = 45 cm
Jari-jari roda gigi pembawa, cm 5 , 22 2 45 1 = = R Jarak menggantung, = 15 cm
Gabungan faktor kejutan dan kelelahan untuk bengkokan, Km = 2
Kt = 1,5
Jawab:
Daya Motor
Kita tahu bahwa energi yang diberikan pada tromol lift per menit kg.m/min 000 . 40 50 800 × = = =Wv
Daya pada tromol lift
hp 9 , 8 4500 000 . 40 4500 diberikan yang energi = = =
Karena efisiensi pembawa adalah ,8, maka daya motor pembawa hp 1 , 11 8 , 0 9 , 8 = =
Torsi pada Poros Tromol
Kita tahu bahwa torsi pada poros tromol, kg.cm 000 . 20 25 800 × = = × =W R T Putaran Motor rad/min 200 25 , 0 50 drum jari -jari linear putaran = = = = R v
Karena rasio pengurangan 12 : 1, maka kecepatan sudut dari motor listrik adalah rad/min 400 . 2 12 200× = = ω
Putaran motor dalam rpm rpm 382 2 2400 2 = = = π π ω N Diameter Poros
Torsi pada poros tromol adalah 20.000 kg.cm, maka beban gigi tangensial pada gigi pembawa
kg 890 5 , 22 000 . 20 1 = = = R T
Asumsikan bahwa sudut tekan dari roda ggi pembawa adalah 20o, maka beban bengkok maksimum pada poros karena beban gigi
kg 947 9397 , 0 890 20 cos 890 o = = =
Momen bengkok pada bantalan, kg.cm 205 . 14 15 947 × = = M
Kita tahu bahwa persamaan momen puntir,
( ) ( ) ( ) ( ) kg.cm 320 . 41 000 . 20 5 , 1 205 . 14 2 2 2 2 2 = × + × = × + × = K M K T Te m t Gunakan persamaan
cm 49 , 7 421 421 500 16 320 . 41 500 16 320 . 41 16 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Te s π π π
Kita ketahui juga bahwa persamaan momen bengkok,
(
) (
)
kg.cm 865 . 34 320 . 41 205 . 14 2 2 1 2 2 2 1 = + × = × + × + × = T K M K M K Me m m tGunakan persamaan tegangan
cm 75 , 6 309 309 150 . 1 32 34865 ) (ambil 150 . 1 32 865 . 34 32 3 3 t 3 3 = = = × × = = × × = ⋅ = d d f f d d f M b b e π π π
Ambil nilai yang terbesar, kita dapatkan cm 5 , 7 atau 49 , 7 = d
Contoh 15. Sebuah poros pejal ditumpu oleh dua bantalan yang
berjarak 180 cm berputar pada 250 rpm. Sebuah roda gigi miring D 20o dengan diameter 30 cm dipasang pada poros denan jarak 15 cm ke kiri dari bantalan sebelah kanan. Dua buah puli B dan C berdiameter 75 cm dan 60 cm diletakan pada poros dengan jarak masing-masing 60 cm dan 135 cm di sebelah kanan bantalan sebelah kiri. Sebuah tenaga memberikan 40 hp ke roda gigi dan pemesinan mengambil 25 hp dari puli C dan 15 hp dari B. Arah dari B adalah vertikal ke arah bawah sementara arah dari C adalah ke bawah dengan sudut 60o ke horisontal. Dalam kedua kasus, rasio tegangan pada sabuk 2 dan sudut kontak 1800. gabungan faktor kejutan dan kelelahan untuk torsi dan bengkokan masing-masing 1,5 dan 2,0. rancang sebuah poros yang sesuai, ambil tegangan yang bekerja 840 kg/cm2 pada tarikan dan 420 kg/cm2 pada geseran.
Diketahui:
Jarak antara 2 bantalan P dan Q, = 180 cm
Putaran poros, N = 250 rpm Sudut penekan roda gigi D,
α = 20o
Diameter pitch roda gigi D = 30 cm Jari-jari pitch roda gigi D, RD = 15 cm
Diameter puli B = 75 cm Jari-jari puli B, RB = 37,5 cm
Diameter puli C = 60 cm Jari-jari puli C,
RC = 30 cm
Daya yang dipasok ke roda gigi D, PD = 40 hp
Daya yang dikirim oleh puli C, PC = 25 hp
Daya yang dikirim oleh puli B, PB = 15 hp
Rasio tegangan antara puli B dan C 2 2 1 2 1 = = C C B B T T T T
Sudut kontak, θ=1800 =πrad
Gabungan faktor kejutan dan kelelahan untuk bengkokan, Km = 2
Gabungan faktor kejutan dan kelelahan untuk puntiran, Kt = 1,5
Tegangan tarik yang bekerja, fb = 840 kg/cm2
Tegangan geser yang bekerja, fs = 420 kg/cm2
Jawab:
Pertama kita cari total beban yang bekerja pada roda gigi D dan masing-masing pada puli C dan B.
Roda Gigi D
Torsi yang ditransmisikan oleh roda gigi D,
kg.cm 460 . 11 kg.m 6 , 114 250 2 500 . 4 40 2 500 . 4 = = × × = × = π πN P TD
Gaya tangensial yang bekerja pada roda gigi D kg 764 15 460 . 11 = = = D D R T
Dan beban normal yang bekerja pada gigi roda gigi,
kg 813 9397 , 0 764 20 cos 764 cos l tangensia gaya 0 = = = = α D W
Beban normal bekerja pada sudut 200 arah vertikal diperlihatkan pada gambar. Pemecahan dari gaya normal vertkal dan horisontal, kita dapatkan
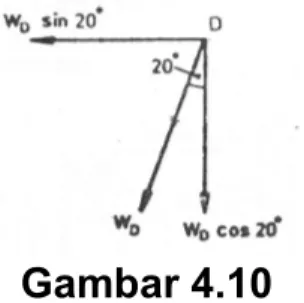
Gambar 4.10 Komponen vertikal WD kg 764 9397 , 0 813 20 cos 0 = × = =WD Komponen horisontal WD kg 278 312 , 0 813 20 sin 0 = × = =WD Puli C
Torsi yang ditransmisikan oleh puli C,
kg.cm 160 . 7 kg.m 6 , 71 250 2 500 . 4 25 2 500 . 4 = = × × = × = π πN P TC
Jika TC1 dan TC2 = Tegangan pada sisi tegang dan sisi kendur pada
sabuk untuk puli C Torsi yang ditransmisikan oleh puli C
( ) ( ) k g 4 , 4 7 7 k g 7 , 2 3 8 2 b a h w a ju g a ta h u K ita k g 7 , 2 3 8 3 0 1 6 0 .7 3 0 1 6 0 .7 1 2 2 1 2 1 2 1 2 1 = = = = = − × − = − = C C C C C C C C C C C T T T T T T T T R T T
Total beban yang bekerja pada puli C,
kg 1 , 716 7 , 238 4 , 477 C) puli berat (abaikan 2 1 = + = + = C C C T T W
Beban ini bekerja pada sudut 600 arah horisontal, ditunjukan pada gambar. 1.11 Pemecahan dari gaya normal vertkal dan horisontal, kita dapatkan
Gambar 4.11
kg 620 866 , 0 1 , 716 60 sin 0 = × = =WC Komponen horisontal WC kg 358 5 , 0 1 , 716 60 cos 0 = × = =WC Puli B
Torsi yang ditransmisikan oleh puli B,
kg.cm 300 . 4 kg.m 43 250 2 500 . 4 15 2 500 . 4 = = × × = × = π πN P TB
Jika TB1 dan TB2 = Tegangan pada sisi tegang dan sisi kendur pada
sabuk untuk puli B Torsi yang ditransmisikan oleh puli B
( ) ( ) k g 4 , 2 2 9 k g 7 , 1 1 4 2 b a h w a ju g a ta h u K ita k g 7 , 1 1 4 5, 3 7 3 0 0 . 4 5, 3 7 3 0 0 . 4 1 2 2 1 2 1 2 1 2 1 = = = = = − × − = − = B B B B B B B B B B B T T T T T T T T R T T
Total beban yang bekerja pada puli B, kg 1 , 344 4 , 229 7 , 114 2 1 = + = + = B B B T T W
Gambar 4.12
Dari perhitungan di atas, kita bisa katakan bahwa poros menerima beban horisontal dan vertikal sebagai berikut:
Jenis Beban
Beban in kg
Pada D Pada C Pada B
Vertikal 754 620 344,1
horisontal 278 358 0
Diagram beban vertikal dan horisontal diperlihatkan pada gambar 4.12 (c) dan (d).
Pembebanan Vertikal
Jika RPV dan RQV adalah reaksi pada bantalan P dan Q untuk
pembebanan vertikal. kg 1 , 728 . 1 1 , 344 620 764 + + = = + QV PV R R
0 P pada bending momen kg.cm 26.880 75 620 -105 764 -120 1.280 B pada bending momen kg.cm 34.680 30 764 -45 1.280 C pada bending momen kg.cm 19.200 15 1.280 D pada bending momen 0 Q pada Bending momen kg 448,1 1.280 -1.728,1 kg 280 . 1 180 406 . 230 406 . 230 60 1 , 344 135 620 165 764 180 = = × × × = = × × = = × = = = = = = = × + × + × = × PV QV QV R R R
Grafik momen bending untuk pembebanan vertikal diperlihatkan pada gambar 4.12 (e).
Pembebanan Horisontal
Jika RPH dan RQH adalah reaksi pada bantalan P dan Q untuk
pembebanan vertikal. kg 636 358 278+ = = + QH PH R R
Ambil momen P, kita dapatkan
0 P pada bending momen kg.cm 6.765 75 75 , 112 B pada bending momen kg.cm .208 15 30 278 -45 3 , 523 C pada bending momen kg.cm 5 , 849 . 7 15 3 , 523 D pada bending momen 0 Q pada Bending momen kg 7 , 112 3 , 523 636 kg 3 , 523 180 200 . 94 200 . 94 135 358 165 278 180 = = × = = × × = = × = = = − = = = = × + × = × PH QV QH R R R
Grafik momen bending untuk pembebanan vertikal diperlihatkan pada gambar 4.12 (f).
Resultan momen bengkok untuk titik D, C, dan B:
kg.cm 720 . 27 765 . 6 26.880 B pada Bending Momen Resultan kg.cm 870 . 37 5 , 208 . 15 680 . 34 C pada Bending Momen Resultan kg.cm 740 . 20 5 , 849 . 7 19.200 D pada Bending Momen Resultan 2 2 2 2 2 2 = + = = + = = + =
Dari resultan momen bengkok, kita lihat bahwa momen bengkok maksimum adalah pada titik C,
kg.cm 870 . 37 = M
Dan torsi maksimum pada titik C, kg.cm 460 . 11 hp 40 ke berhubung Torsi = = = TD T Diameter Poros
Kita tahu bahwa persamaan momen puntir,
( ) ( ) ( ) ( ) kg.cm 10 7 , 7 460 . 11 5 , 1 870 . 37 2 4 2 2 2 2 × = × + × = × + × = K M K T Te m t Gunakan persamaan
cm 8 , 9 2 , 945 2 , 945 420 16 10 7 , 7 420 16 10 7 , 7 16 3 4 3 3 4 3 = = = × × × = × × = × ⋅ = d d d d f Te s π π π
Kita ketahui juga bahwa persamaan momen bengkok,
(
) (
)
kg.cm 720 . 76 10 7 , 7 870 . 37 2 4 2 1 2 2 2 1 = × + × = × + × + × = T K M K M K Me m m tGunakan persamaan tegangan
cm 76 , 9 3 , 930 3 , 930 840 32 720 . 76 840 32 720 . 76 32 3 3 3 3 = = = × × = × × = ⋅ = d d d d f Me b π π π
Ambil nilai yang terbesar, kita dapatkan cm 10 atau 8 , 9 = d
L. Poros yang Menerima Beban Axial dengan Pembebanan Gabungan Torsi dan Bengkokan
Ketika poros menerima sebuah beban axial (F) dengan pembebanan gabungan torsi dan bengkokan seperti pada poros baling-baling kapal dan poros penggerak roda gigi cacing, maka tegangan yang disebabkan beban axial harus dtambahkan pada tegangan bengkok fb. Kita tahu
persamaan bengkokan 2 4 64 32 2 / d M d d M I My f y f I M b b π π = × = = =
Tegangan pada beban axial
(
)
( )
− ∴ = = − = − = = = o i o i o i o d d k k d F d d F d d F d F d F 1 4 berongga) poros (untuk 4 pejal) poros (untuk 4 2 2 2 2 2 2 4 2 2 4 π π π π π + = = + = + = 8 1 an subsitusik 32 8 32 4 32 2 1 2 2 2 1 d F M M d M F M d d F d M f d π π π π
Untuk poros berongga, reultan tegangan,
(
)
(
)
(
)
(
)
(
)
( )
− = + − − = − + − = − + = 8 2 1 2 1 berongga, poros untuk an subsitusik 4 2 1 2 2 4 2 2 2 4 2 1 1 32 8 1 1 32 1 4 1 32 k o Fd M M o o o o o k d M k Fd M k d k d F k d M f π π π πUntuk poros yang panjang (poros langsing) pemberian beban tekan, faktor kolom (α ) harus dimasukan ke dalam perhitungan.
Tegangan yang disebabkan beban tekan,
(
)
(untuk poros berongga) 1 4 pejal) poros (untuk 4 4 2 2 k d F d F f o e − × = × = π α π αNilai faktor kolom (α ) untuk *beban tekan bisa didapat dari persamaan berikut: > = < − = 115 jika * * * 115 jika * * 0044 , 0 1 1 kolom, faktor 2 2 K L K L E C f K L K L y π α
Dimana L = Panjang poros antaran bantalan, dalam cm K = Radius terkecil dari putaran, dalam cm
fy = Titik yield tegangan tekan bahan poros, dalam kg/cm2
C = Koefisien dalam formula Euler berdasarkan kondisi ujung. Nilai C berdasarkan kondisi ujung.
bantalan dengan ujung untuk 1,6 tetap ujung untuk 2,25 berengsel ujung untuk 1, = = = C Keterangan:
* Nilai faktor kolom (α ) untuk kesatuan beban tarik ** Rasio K
L
dikenal sebagai rasio kelangsingan *** Formula Euler’s untuk kolom yang panjang Catatan:
Pada umumnya, untuk poros yang berongga yang diberikan beban bengkok dan torsi yang berubah-ubah dengan beban axial, persamaan momen puntir (Te) dan persamaan momen bengkok (Me), bisa ditulis
( )
(
)
( )(
4)
3 2 2 4 3 2 2 1 32 8 8 2 1 1 16 8 k d f T K d F M K d F M K M k d f T K d F M K T o s t o m o m e o s t o m e − = + + + + = − = + + = π α α π αDapat ditulis bahwa,
axial tarik pembebanan dengan 1 axial beban tanpa 0 pejal poros untuk dan 0 = = = = α F d d k o
Contoh 16. Sebuah poros berongga bekerja pada sebuah torsi
maksimum 15.00 kg.cm dan momen bengkok maksimum 30.000 kg.cm. Pada saat yang sama, sebuah beban axial 1.000 kg bekerja padanya. Asumsikan bahwa beban dipasang bertahap dan rasio diameter dalam dan diameter luar adalah 0,5. Jika diameter dalam poros adalah 8 cm, cari tegangan geser yang terjadi pada poros.
Diketahui:
Torsi maksimum yang ditransmisikan, T = 15.000 kg.cm
Momen bengkok maksimum, M = 30.000 kg.cm Beban axial, F = 1.000 kg 5 , 0 , luar diemeter dalam diameter = k Diameter luar, do = 8 cm Jawab:
Tegangan Geser yang Terjadi pada Poros Karena beban dipasang gradually, dari tabel
Km = 1,5 dan Kt = 1,0
(
)
( )(
)
(
)
( ) 2 4 4 2 2 2 2 4 2 2 2 4 3 kg/cm 8 , 515 22 , 94 10 86 , 4 10 86 , 4 000 . 15 250 . 46 22 , 94 000 . 15 1 8 5 , 0 1 000 . 1 000 . 30 5 , 1 5 , 0 1 8 16 8 1 16 = × = × = + = × + × + × + = − × × + + = − s s s t o m o s f f f T K d F M K k d f π α πContoh 17. Sebuah poros berongga diameter luar 50 cm dan
diameter dalam 30 cm digunakan untuk menggerakan baling-baling sebuah kapal laut. Poros dipasang pada bantalan sejauh 8 m dan mentransmisikan 7.500 hp pada 150 rpm. Gaya axial maksimum 50.000 kg dan berat poros 7.000 kg. Tentukan
(a) Tegangan geser maksimum yang diberikan pada poros (b) Puntiran antar bantalan
Diketahui:
Diameter luar poros, do = 50 cm
Diameter dalam poros, di = 30 cm
Panjang poros antara bantalan, l = 6 m = 600 cm
Daya yang ditransmisikan P = 7.500 hp
Kecepatan, N = 150 rpm Gaya axial maksimum, F = 50.000 kg
Berat poros, W = 7.000 kg Jawab:
Torsi yang ditransmisikan poros,
kg.cm 10 581 . 3 kg.m 810 . 35 150 2 500 . 4 5000 . 7 2 500 . 4 2 × = = × × = × = π πN P T
Momen bengkok maksimum,
kg.cm 10 525 8 600 7000 8 3 × = × = =ML M
(
)
(
4 4)
4 4 4 64 i o i o d d d d A I K − − = = ππ(
)(
)
(
)
(
)
2 , 1 18 , 0 1 1 15 , 41 0044 , 0 1 1 115 K L 0044 , 0 1 1 kolom, faktor 15 , 41 58 , 14 600 K L cm 58 , 14 30 50 16 2 2 4 1 2 2 4 1 2 2 2 2 2 2 = − = × − = < − = = = = + = + = − − + = K L d d d d d d d d i o i o i o i o α(a) Tegangan Geser yang terjadi pada Poros Gunakan persamaan
(
)
( )2 2 4 3 8 1 16 K T d F M K k d f o t m o s + + = − α πAsumsikan bahwa beban terpasang gradually, maka Km = 1,5 dan Kt = 1,0 Juga 0,6 50 30 = = = o i d d k
(
)
(
)
500 . 518 8 6 , 0 1 50 000 . 50 22 , 1 8 1 dan 2 2 = + × × = +k Fdo αSubsitusikan niai ke persamaan di atas, kita dapatkan
(
) (
) (
)
( )(
)
2 2 2 2 2 2 2 2 4 2 kg/cm 5 , 176 353 . 21 760 . 768 . 3 760 . 768 . 3 10 581 . 3 500 . 518 250 . 656 353 . 21 10 581 . 3 1 500 . 518 10 525 5 , 1 6 , 0 1 50 16 = = = × + + = × × + + × × = − s s s f f f π(b) Sudut Puntiran antara Bantalan Gunakan persamaan
(
)
0 2 5 4 4 5 2 274 , 0 180 00478 , 0 ) kg/cm 10 8,4 G (ambil rad 00478 , 0 30 50 32 10 4 , 8 600 10 581 . 3 = = × = = − × × × × = × × = = π π θ θ J G L T L G J TM. Perancanaan Poros atas Dasar Kekakuan
Kadang poros dirancang atas dasar kekakuan. Kita harus memperhatikan 2 jenis kekakuan berikut:
1. Kekakuan Puntiran
2. Kekakuan Lateral
1. Kekakuan Puntiran
Kekakuan Puntiran sangat penting dalam kasus poros engkol dari sebuah mesin, dimana waktu pengatupan akan sangat diefektifkan. Jumlah puntiran yang diijinkan tidak lebih dari 0,250 per meter panjang pada poros. Untuk poros lurus atau poros transmisi, penyimpangan 2,5 sampai 3 derajat pe meter panjang bisa digunakan sebagai nilai batas. Penyimpangan lebar pada poros terbatas sampai 1 derajat pada panjang sama dengan 12x diameter poros.
Penyimpangan kekakuan puntiran bisa didapat dengan persamaan torsi,
JG TL L G J T = = θ θ atau
Dimana: θ = Penyimpangan puntiran atau sudut puntiran, dalam rad T = Momen puntir atau torsi pada poros, dalam kg.cm
J = Momen inersia polar, dalam cm4
d
32 π
= (untuk poros pejal)
(
4 4)
32 do −di
= π (untuk poros berongga)
G = Modulus kekakuan untuk bahan poros, dalam kg/cm2 L = Panjang poros, dalam cm.
2. Kekakuan Lateral
Kekakuan lateral sangat penting dalam kasus poros transmisi dan poros yang berputar dengan kecepatan tinggi, dimana penyimpangan lateral kecil akan menyebabkan tegangan di luar kontrol yang besar. Kekakuan lateral juga penting untuk memelihara kelonggaran bantalan yang tepat dan untuk penempatan mata roda gigi secara benar. Jika
poros memiliki penampang melintang yang seragam, maka penyimpangan lateral bisa dicari menggunakan formula penyimpangan dalam kekuatan bahan. Tapi jika poros memiliki penampang melintang yang berbeda, maka penyimpangan dapat dicari dari persamaan dasar untuk kurva elastis dari balok.
EI M dx y d = 2 2
Contoh 18. Sebuah spindle baja memindahkan 5 hp pada 800 rpm.
Penyimpangan kekakuan tidak boleh lebih dari 0,250 per meter. Jika modulus kekakuan dari bahan adalah 0,84 x 105 kg/cm2, cari diameter spindle dan tegangan geser yang terjadi pada spindle.
Diketahui:
Daya yang ditransmisikan, P = 5 hp Kecepatan spindle, N = 800 rpm Sudut penyimpangan θ=0,250 =0,25×180π = 0,00436 rad Panjang spindle, L = 1 m = 100 cm Modulus kekakuan, G = 0,84 x 105 kg/cm2 Jawab:
Torsi yang ditransmisikan oleh spindle
kg.cm 6 , 447 kg.m 476 , 4 800 2 500 . 4 5 2 500 . 4 = = × × = × = π πN P T Diameter Poros cm 5 , 3 atau 34 , 3 5 , 124 5 , 124 6 , 36 32 6 , 447 6 , 36 100 00436 , 0 10 x 0,84 32 6 , 447 4 4 5 4 = = = × × = = × = = d d d L G J T π π θ
2 3 3 3 kg/cm 17 , 53 5 , 3 16 6 , 447 5 , 3 16 6 , 447 16 = × × = × × = ⋅ = π π π s s s f f d f T
Contoh 19. Bandingkan berat, kekuatan dan kekakuan dari sebuah
poros berongga yang memiliki diameter luar sama dengan poros pejal. Diameter dalam poros berongga adalah setengah dari diameter luranya. Kedua poros memiliki bahan dan panjang yang sama.
Diketahui:
Diameter dalam poros berongga,
o i
d
d
=
21d ia m e te r
lu ar
=
12 Rasio dari ,k = 21 =0,5 d d o iDiameter poros pejal, d =do Jawab:
Perbandingan Berat Berat poros berongga,
(
)
panjang berat jenis 4 jenis berat panjang Permukaan Luas 2 2 − × × = × × = i o H d d W πDan berat poros pejal,
jenis berat panjang 4 2× × = d WS π
Karena kedua poros memiliki bahan dan panjang yang sama, maka
(
)
( ) ( )
75 , 0 5 , 0 1 1 1 4 4 2 2 2 2 2 2 2 2 2 2 2 2 2 2 = − = − = − = − = − = − = k d k d d d d d d d d d d W W o o o i o i o i o S H π π Perbandingan Kekuatan Kekuatan poros berongga(
4)
3 1 16 f d kDan kekuatan pada poros pejal
(
)
(
)
9375 , 0 5 , 0 1 1 1 16 1 16 16 4 4 3 4 3 3 4 3 3 = − = − = − = ⋅ − ⋅ = ⋅ = k d k d d f k d f T T d f T o o s o s S H s S π π π Perbandingan Kekakuan Kekakuan l J C T = × = θUntuk poros berongga,
(
4 4)
32 o i
H l d d
C
S = ×π −
Dan untuk poros pejal