BAB II
LANDASAN TEORI
2.1. Optimasi Produksi
Optimasi adalah tindakan untuk memperoleh hasil yang terbaik dengan keadaan yang diberikan.Dalam pelaksanaannya harus diambil keputusan manajerial dalam beberapa tahap.Tujuan akhir dari semua keputusan seperti itu adalah meminimalkan upaya yang diperlukan atau untuk memaksimalkan manfaat yang diinginkan.Usaha yang diperlukan atau manfaat uang yang diinginkan dalam prakteknya dapat dinyatakan sebagai fungsi dari variabel keputusan tertentu. Optimasi dapat didefinisikan sebagai proses untuk mendapatkan keadaan yang memberikan nilai maksimum atau minimum dari suatu fungsi.
Optimasi produksi adalah penggunaan faktor-faktor produksi yang terbatas seefisien mungkin. Faktor-faktor produksi tersebut adalah modal, mesin, bahan baku, bahan pembantu, tenaga kerja, dan lain sebagainya. Optimasi produksi diperlukan perusahaan dalam rangka mengoptimalkan sumber daya yang digunakan agar suatu produksi dapat menghasilkan produk. Optimasi merupakan pendekatan normatif dengan mengidentifikasi penyelesaian terbaik dari suatu permasalahan yang diarahkan pada titik maksimum atau minimum suatu fungsi tujuan dalam kuantitas dan kualitas yang diharapkan, sehingga perusahaan dapat mencapai tujuannya.
2.1.1 Perencanaan Produksi
sebuah rencana produksi. Tanpa adanya rencana produksi yang baik, maka tujuan tidak akan dapat dicapai dengan efektif dan efisien, sehingga faktor-faktor produksi yang ada akan dipergunakan secara boros. Oleh karena itu, perencanaan produksi merupakan spesifikasi tujuan perusahaan yang ingin dicapai serta cara-cara yang akan ditempuh untuk mencapai tujuan tersebut.
Kegunaan atau pentingnya diadakan produksi adalah sebagai berikut : 1. Suatu perencanaan meliputi usaha untuk menetapkan tujuan atau
memformulasikan tujuan yang dipilih untuk dicapai, maka dengan adanya perencanaan produksi, dapat membedakan arah bagi setiap kegiatan produksi yang jelas.
2. Dengan perencanaan yang memberikan formulasi tujuan yang hendak dicapai, maka akan memungkinkan untuk mengetahui apakah tujuan-tujuan tersebut telah tercapai atau tidak.
3. Memudahkan pelaksanaan kegiatan untuk mengidentifikasikan hambatan-hambatan yang mungkin timbul dalam usaha tujuan tersebut. Dengan memperhitungkan hambatan-hambatan tersebut, persiapan untuk mengatasinya menjadi lebih terarah.
4. Menghindarkan pertumbuhan dan perkembangan yang tidak terkendali.
2.2Peramalan
2.2.1 Metode Deret Waktu (Time-Series)
Ada empat komponen utama yang mempengaruhi analisis ini, yaitu : a. Pola Siklis (Cycle)
Penjualan produk dapat memiliki siklus yang berulang secara periodik.Banyak produk dipengaruhi pola pergerakan aktivitas ekonomi yang terkadang memiliki kecenderungan periodik.Komponen siklis ini sangat berguna dalam peramalan jangka menengah.
Pola data ini terjadi bila data memiliki kecenderungan untuk naik atau turun terus-menerus. Pola data bentuk ini digambarkan sebagai berikut :
Gambar 2.1 Pola Siklis
b. Pola Musiman (Season)
Perkataan musim menggambarkan pola penjualan yang berulang setiap periode.Komponen musim dapat dijabarkan ke dalam vektor cuaca, libur, atau kecenderungan perdagangan.Pola musiman berguna meramalkan penjualan dalam jangka pendek.Pola data musiman dapat digambarkan sebagai berikut :
Gambar 2.2 Pola Musiman
c. Pola kecenderungan (trend)
Pola data ini terjadi bila data memiliki kecenderungan untuk naik atau turun terus menerus. Pola data dalam bentuk ini dapat digambarkan sebagai berikut :
d. Pola Acak
Pola data ini menggambarkan pola penjualan yang setiap periodenya memiliki kondisi yang beragam dan acak. Pola data dalam bentuk ini dapat digambarkan sebagai berikut :
Gambar 2.4 Pola Acak
Peramalan deret waktu (time-series) memiliki beberapa metode yang dapat digunakan untuk meramalkan kondisi pada periode yang akan datang, yaitu : a. Metode Penghalusan (Smoothing)
Metode smoothing digunakan untuk mengurangi ketidak-teraturan musiman dari data yang lalu, dengan membuat rata-rata tertimbang dari sederetan data masa lalu. Ketetapan peramalan dengan metode ini akan terdapat pada peramalan jangka pendek, sedangkan untuk peramalan jangka panjang kurang akurat.
Metode smoothing terdiri dari beberapa jenis, antara lain : 1. Metode rata-rata bergerak (Moving Average)
a. Single Moving Average
Moving Average pada suatu periode merupakan peramalan untuk satu periode ke depan dari periode rata-rata tersebut. Persoalan yang timbul dalam penggunaan metode ini adalah dalam menentukan nilai t (periode perata-rata). Semakin besar nilai t maka peramalan yang dihasilkan akan semakin menjauhi pola data.
Secara matematis, rumus fungsi peramalan metode ini adalah :
+ = −�+ + ⋯ + + +
Dimana : = Data pengamatan periode ke-i
N = Jumlah deret waktu yang digunakan
b. Linear Moving average (LMA)
Dasar dari metode ini adalah penggunaan Moving Average kedua untuk memperoleh penyesuaian bentuk pola trend. Prosedur Linear Moving Averageadalah :
- Penggunaan rata-rata bergerak tunggal pada waktu t (ditulis )
- Penyesuaian yang merupakan perbedaan antara rata-rata bergerak tunggal dan ganda pada waktu t (ditulis ′ − ′′)
- Penyesuaian untuk kecenderungan dari periode ke t+1 (atau ke periode t+m jika ingin meramalkan m periode ke muka)
Secara umum persamaan prosedur rata-rata bergerak linier dapat diterangkan melalui persamaan sebagai berikut :
′= + − + − + ⋯ + − −
′′ = + − + − + ⋯ + − −
= ′+ ′− ′′ = ′− ′′
= − ′− ′′
+ = + ∙
Kesalahan negatif atau positif yang mungkin terjadi dapat dihilangkan atau dikeluarkan.Rata-rata dapat dilakukan terhadap seluruh angka konstanta dari data pengamatan. Sesuai dengan tujuan di atas, maka teknik ini dapat menghilangkan trend dan musiman (seasonality). Harga yang diramalkan dalam Single Moving Average dihitung berdasarkan rumus :
+ = | − |⋯ | − −
+ = + − −
Dimana : = nilai data
c. Weigted Moving Average
Pada meode rata-rata sederhana, jumlah data pada kelompok inisialisasi makin lama semakin bertambah dengan naiknya harga i. Tetapi pada metode rata-rata bergerak tunggal jumlah data kelompok inisialisasi adalah konstan, bilamana harga i bertambah satu, maka data baru yang akan menggeser/menggantikan data yang paling tua. Untuk waktu (t+1), (t+2), nilai ramalannya adalah :
+ = ∑=
+ = ∑
= =
+
2. Metode Exponensial Smoothing, terdiri atas
a. Pemulusan Eksponensial Tunggal (Single Exponensial Smoothing)
Metode pemulusan eksponensial tunggal (single exponensial smoothing) menambahkan parameter α dalam modelnya untuk mengurangi faktor kerandoman. Nilai peramalan dapat dicari dengan menggunakan rumus berikut ini :
+ = ∙ + − ∙
Dimana :
= data permintaan pada periode t = faktor/konstan pemulusan
+ = peramalan untuk periode t
Istilah eksponensial dalam metode ini berasal dari pembobotan (faktor pemulusan) dari periode sebelumnya yang berbentuk eksponensial, sebagaimana dijabarkan berikut ini :
+ = ∙ + − ∙
= ∙ + − ∙ − + − ∙ −
= ∙ + − ∙ − + − ∙ − + ⋯
+ − ∙ − �−
Di sini terlihat bahwa koefisien X dari waktu ke waktu membentuk hubungan eksponensial. Misalnya, untuk α = 0,2 maka koefisien dari , − , − , ⋯ , −�+ berturut-turut adalah 0,2; 0,2(0,8); 0,2(0,8)2; …
; 0,2(0,8)N+1.
b. Pemulusan Eksponensial Linier (Linear Exponential Smoothing/Double Exponential Smoothing)
Metode pemulusan eksponensial tunggal hanya akan efektif apabila serial data yang diamati memiliki pola horizontal (stasioner). Jika metode itu digunakan untuk serial data yang memiliki unsur trend (kecenderungan) yang konsisten, nilai-nilai peramalannya akan selalu berada di belakang nilai aktualnya (terjadi lagging yang terus menerus). Metode yang tepat untuk melakukan peramalan serial data yang memiliki unsur trend adalah metode pemulusan eksponensial linier. Salah satu metode yang digunakan adalah metode pemulusan eksponensial linier dari Holt, yang menggunakan persamaan sebagai berikut :
= ∙ + − − + −
= ∙ − − + − ∙ −
+ = + ∙
dengan 1. Kedua parameter itu dapat mempunyai nilai yang sama atau berbeda besarnya.
Proses inisialisasi untuk pemulusan eksponensial linier dari Holt memerlukan dua taksiran, yaitu untuk nilai dan . Nilai dapat disamakan dengan nilai aktual (pengamatan) atau rata-rata dari beberapa nilai pengamatan pada periode awal, sedangkan nilai menggunakan taksiran kemiringan dari serial data tersebut (menggunakan persamaan regresi linier, akan dibahas kemudian) atau menggunakan rata-rata kenaikan dari beberapa periode, misalnya :
= − + − + −
c. Pemulusan Eksponensial Musiman
Sebagaimana halnya dengan persamaan pemulusan eksponensial linier yang dapat digunakan untuk meramalkan serial data yang memiliki pola trend, bentuk persamaan yang lebih tinggi dapat digunakan jika pola dasar serial datanya musiman. Salah satu metode peramalan yang khusus untuk data yang berpola musiman adalah metode pemulusan eksponensial linier dan musiman dari Winter. Metode ini didasarkan atas tiga persamaan, yaitu unsur stasioner, trend dan musiman, yang dirumuskan sebagai berikut :
= (
− ) + − − + −
= + − + − −
= ( ) + − −
+ = + ∙ − +
Dimana :
Sebagaimana dalam perhitungan pemulusan eksponensial tunggal, nilai inisial dapat disamakan dengan nilai aktualnya atau berupa rata-rata dari beberapa nilai pada musim yang sama, sedangkan nilai inisial T dicari dengan menggunakan rumus sebagai berikut :
= { + − + + − + ⋯ + − − }
2.2.2Ketelitian Peramalan
Bila adalah data yang sebenarnya pada periode i dan adalah hasil peramalan pada periode yang sama maka penyimpangan yang terjadi dapat didefinisikan sebagai berikut :
= −
Sehingga bila terdapat n periode pengamatan, maka akan terdapat sejumlah n penyimpangan.Berikut ini akan diberikan beberapa rumus yang dapat digunakan untuk mengukur ketelitian peramalan :
1. Mean Error
= ∑
=
2. Mean Absolute Error
= ∑| |
=
3. Sum of Squared Errors
= ∑
=
4. Mean Squared Error
= ∑
=
5. Standard Deviation Errors
2.2.3 Pengujian Pola Peramalan
Setelah dipilih metode peramalan sesuai dengan pola data dan faktor-faktor lainnya, maka hasil ramalan yang diperoleh perlu diuji apakah penyimpangan yang terdapat dalam peramalan tersebut bersifat random atau tidak.Metode peramalan yang baik adalah bila penyimpangan yang terjadi bersifat random.
Metode yang digunakan untuk pengujian ini adalah metode Box-Pierce Test dengan rumus sebagai berikut :
= ∑ �
=
� = ∑=− [∑ − ̅ + − ̅ ] −
−
Dimana :
� = koefisien autokorelasi pada time lag ke-k = penyimpangan periode ke-i
̅ = rata-rata penyimpangan = banyaknya data
Setelah harga Q diperoleh, kemudian dibandingkan dengan nilai . Jika < � berarti penyimpangan yang terjadi bersifat random.
2.3. Goal Programming
yang ada yaitu sumber daya yang tersedia, teknologi yang ada, kendala tujuan, dan sebagainya. (Nasendi, 1985)
Goal Programming pertama kali diperkenalkan oleh Charnes dan Coopers (1961). Charnes dan coopers mencoba menyelesaikan persoalan program linier dengan banyak kendala dengan waktu yang bersamaan. Gagasan itu berawal dari adanya program linier yang tidak bisa diselesaikan karena memiliki tujuan ganda. Charnes dan coopers mengatakan bahwa jika di dalam persamaan linier tersebut terdapat slack variabel dan surplus variabel di dalam persamaan kendalanya, maka fungsi tujuan dari persamaan tersebut bisa dikendalikan yaitu dengan mengendalikan nilai ruas kiri dari persamaan tersebut agar sama dengan nilai ruas kanannya. Inilah yang menjadi dasar Charnes dan coopers mengembangkan metode Goal Programming.
2.3.1. Konsep Goal Programming
Goal Programming pada umumnya digunakan pada masalah-masalah linier dengan memasukkan berbagai tujuan dalam formulasi modelnya.Tujuan-tujuan yang ingin dicapai dinyatakan sebagai goal dan dipresentasikan secara numerik.Namun kenyataannya goal yang ingin dicapai tidak selalu dapat diselesaikan secara bersamaan karena terdapat penyimpangan-penyimpangan atau sering disebut dengan deviasi.Oleh Karena itu dalam Goal Programming, tujuan yang telah dinyatakan dalam goal tersebut harus ditetapkan terlebih dahulu.
Solusi yang ingin dicapai adalah meminimumkan penyimpangan tujuan-tujuan yang terdapat pada masing-masing goal.Fungsi tujuan-tujuan dalam Goal Programming dinyatakan sebagai minimasi penyimpangan dari fungsi pencapaian goal.
Adapaun bentuk umum dari Goal Programming (tanpa faktor prioritas di dalam strukturnya) adalah sebagai berikut :
= ∑ + ++ − −
+ = Variabel deviasi yang mempresentasikan tingkat pencapaian
diatas target (over achievement).
− = Variabel deviasi yang mempresentasikan tingkat pencapaian
dibawah target (under achievement). = Koefisien fungsi kendala tujuan
= Variabel keputusan atau oeubah pengambilan keputusan
= Tujuan atau target yang ingin dicapai = Koefisien fungsi kendala biasa
= Jumlah sumber daya k yang tersedia
= Macam batasan sumber atau fasilitas yang tersedia
Model tersebut hanya menyatakan persoalan pengoptimuman dari suatu permalahan yang hanya meminimumkan jumlah agregat dari semua deviasi positif dan negatif yang individual dari tujuan yang ditetapkan.
Namun pada kenyataannya seringkali pada proses pengambilan keputusan terdapat kendala pada kondisi dimana satu tujuan saling bertentangan dengan tujuan lainnya (multiple and conflicting goals). Maka untuk menyelesaikannya diperlukan penentuan prioritas atau tujuan mana yang terlebih dahulu diutamakan atau diprioritaskan.
Model untuk persoalan tujuan ganda dengan struktur pengutamaan (preemptive weights) adalah sebagai berikut :
= ∑( + +, + − −, ) =
∑ − ++ − = =
∑
=
= , , , ⋯ , = , , , ⋯ , = , , , ⋯ , �
, +, −
Keterangan :
, = Faktor-faktor prioritas
,
+ = Bobot relatif dari + dalam urutan (rangking) ke-y
,
2.3.2. Terminologi Goal Programming
Adapun istilah-istilah yang digunakan dalam Goal Programming menurut budiman (2009) adalah :
a. Variabel deviasi
Variabel deviasi atau jarak antara merupakan perbedaan yang khusus membedakan antara program linier dengan Goal Programming. Andaikan d adalah variabel yang bertanda sembarang, maka dapat dinyatakan sebagai:
= ++ −.
Dengan:
+ = {+ ,
, <
− = { ,
− , < Dengan + = komponen positif dari d
− = komponen negatif dari d
Variabel deviasi mempunyai fungsi sebagai penampung terhadap tujuan-tujuan yang dikehendaki yang dibedakan menjadi dua bagian yaitu :
1. Deviasi positif ( +)
Vaiabel deviasi positif berfungsi untuk menampung deviasi yang berada diatas tujuan yang dikehendaki. Notasi untuk deviasi positif adalah + dan
+ akan selalu berkoefisien -1 pada setiap kendala tujuan sehingga bentuk
kendalanya adalah :
∑ − + =
=
Atau dapat ditulis juga dengan :
∑ = + +
=
Dimana : = , , , ⋯ ,
2. Deviasi negatif −
Variabel deviasi negatif berfungsi untuk menampung deviasi yang berada dibawah tujuan yang dikehendaki. Notasi untuk deviasi negatif adalah − dan − akan selalu berkoefisien +1 pada setiap kendalan tujuan sehingga bentuk kendalanya adalah :
∑ + − =
=
Atau dapat ditulis juga dengan :
∑ = − −
=
Dimana : = , , , ⋯ ,
= , , , ⋯ ,
Dengan demikian jelas bahwa kedua jenis variabel mendekati sebuah garis kendala dari dua arah yang berlawanan. Dapat ditulis secara matematika yaitu : dari kendala tujuan diatas dapat disimpulkan sebagai berikut ;
i. + = − = , sehingga
∑
=
>
iii. + = dan − > , sehingga
∑ =
=
− −
Artinya tujuan tidak tercapai karena
∑
=
<
Jadi jelas bahwa kondisi dimana + > dan − > pada sebuah kendala tujuan tidak akan mungkin terjadi.
b. Variabel keputusan
Seperangkat variabel yang tidak diketahui (dalam model Goal Programming dilambangkan dengan , dimana j=1, 2, 3, …, n). Biasanya disebut juga
decision variables.
c. Nilai ruas kanan
Nilai-nilai yang biasanya menunjukkan ketersediaan sumber daya (dilambangkan dengan , dimana i=1, 2, 3, …, n) yang akan ditentukan kekurangan atau kelebihan penggunaannya. Biasanya disebut juga Right Handside Values (RHS).
d. Goal
Keinginan yang ingin dicapai yaitu meminimumkan angka penyimpangan dari suatu nilai RHS pada suatu kendala tujuan tertentu.
e. Kendala tujuan
f. Prioritas (preemptive priority factor)
Pengambil keputusan menghadapi suatu persoalan dengan tujuan ganda, tapi satu tujuan saling bertentangan dengan tujuan yang lainnya (multiple and conflicting goals).Dalam memecahkan persoalan tersebut, maka pengambil keputusan harus menentukan mana dari antara berbagai tujuan tersebut yang diutamakan atau diprioritaskan.
Tujuan yang paling penting ditentukan sebagai prioritas ke-1, sementara tujuan yang kurang begitu penting ditentukan sebagai prioritas ke-2 demikian seterusnya.Pembagian prioritas tersebut dikatakan sebagai pengutamaan (preemptive), yaitu mendahulukan tercapainya tujuan yang telah diberikan prioritas utama sebelum menuju kepada tujuan-tujuan atau prioritas-prioritas berikutnya.Jadi, harus disusun dalam suatu urutan (ranking) menurut prioritasnya.
Dalam perumusan model Goal Programming faktor prioritas tersebut dinyatakan sebagai , dimana x=1, 2, 3, …, m. Sistem urutan itu menempatkan tujuan-tujuan dalam susunan dengan hubungan seperti berikut :
> > ⋯ > Dimana : merupakan tujuan paling penting
merupakan tujuan yang kurang penting dan seterusnya
g. Bobot (Differential Weight)
Prioritas sebagai ukuran dari variabel-variabel deviasi yang diminalkan sering mempunyai ukuran yang berbeda-beda.Untuk mengatasi hal itu maka dalam fungsi tujuan masing-masing variabel deviasi yang ada dalam satu prioritas diberi bobot.
Bobot adalah besaran numerik yang diberikan pada variabel-variabel yang diminimumkan pada fungsi tujuan Goal Programming (dilambangkan dengan
2.3.3. Komponen Goal Programming
Dalam metode Goal Programming terdapat beberapa komponen yang umum dijumpai dalam pemecahan masalah dengan Goal Programming, yaitu fungsi tujuan, kendala tujuan, kendala struktural, dan kendala non negatif.
a. Fungsi Tujuan
Berbeda dengan program linier yang fungsi tujuannya dapat memaksimumkan atau meminimumkan, tetapi fungsi tujuan dalam Goal Programming adalah meminimumkan deviasi.Hal ini merupakan konsekuensi logis dari kehadiran variabel deviasi dalam fungsi kendala tujuan.
Dalam model Goal Programming hanya terdapat empat jenis fungsi tuuan jika dihubungkan dengan prioritas dan bobot, yaitu :
1. Menimimumkan = ∑= ++ −
Fungsi tujuan ini digunakan apabila variabel deviasi dalam suatu masalah tidak dibedakan menurut prioritas atau bobot.
2. Meminimumkan = ∑= ++ − untuk k=1, 2, …, n
Fungsi tujuan ini digunakan apabila urutan atau prioritas dan setiap tujuan diperlukan.
3. Meminimumkan = ∑= , ++ − untuk x=1, 2, …, n
Fungsi tujuan ini digunakan apabila tujuan-tujuan diurutkan dan variabel deviasi dibedakan dengan diberikan bobot yang berlainan.
4. Menimimumkan = ∑= . ++ − untuk k=1,2, …, n dan x=1,2, …,n
Fungsi tujuan ini digunakan apabila tujuan-tujuan diurutkan berdasar prioritas dan bobot.
b. Kendala tujuan
kendala sedapat mungkin mendekati nilai ruas kanannya maka variabel deviasi ini harus diminimumkan dalam fungsi tujuan.
Kendala tujuan merupakan kendala-kendala yang dihadapi dalam mencapai tujuan.Charnes dan cooper telah memanipulasi program linier sehingga pada program linier kendala-kendala fungsional yang menjadi pembatas bagi usaha pemaksimuman atau peminimuman fungsi tujuan, maka di Goal Programming kendala-kendala merupakan sarana untuk mewujudkan tujuan yang hendak dicapai.
Bentuk persamaan kendala tujuan secara umum adalah : , =,
Dan secara umum dituliskan menjadi :
∑ − ++ − =
=
c. Kendala struktural
Kendala fungsional atau struktural adalah kendala-kendala lingkungan yang tidak berhubungan langsung dengan tujuan-tujuan masalah yang dihadapi.Variabel deviasi tidak dimasukkan kedalam kendala struktural, karena hal ini tidak merupakan fungsi tujuan.
d. Kendala non-negatif
2.3.4. Asumsi dalam Goal Programming
Dalam memodelkan suatu masalah tertentu ke dalam Goal Programming diperlukan sejumlah asumsi yang jika tidak dapat terpenuhi maka Goal Programming bukan merupakan model yang cocok untuk permasalah tersebut.Jadi asumsi model membatasi penggunaan metode Goal Programming.
Asumsi-asumsi dalam Goal Programming : 1. Additivitas dan Linieritas
Diasumsikan bahwa proporsi penggunaan yang ditentukan oleh harus
tetap benar tanpa memperhatikan nilai solusi yang dihasilkan. Hal ini
berarti bahwa ruas kiri dari kendala tujuan harus sama dengan nilai ruas kanan.
2. Divisibilitas
Diasumsikan bahwa nilai-nilai , +, dan − yang dihasilkan dapat dipecah.
Hal ini berarti jumlah pecahan nilai dapat diselesaikan dan digunakan
dalam solusi. 3. Terbatas
2.3.5. Penyelesaian Metode Goal Programming
Terdapat beberapa metode yang dapat digunakan untuk menyelesaikan model Goal Programming, yaitu :
1. Metode Grafik
Metode grafik digunakan untuk menyelesaikan masalah Goal Programming dengan dua variabel. Langkah-langkah penyelesaiannya adalah :
a. Menggambarkan fungsi kendala pada bidang kerja sehingga diperoleh daerah yang memenuhi kendala
2. Metode Algoritma Simpleks
Algoritma simpleks digunakan untuk menyelesaikan masalah Goal Programming dengan menggunakan variabel keputusan yang lebih dari dua. Langkah-langkah penyelesaian Goal Programming dengan metode algoritma simpleks adalah ;
a. Membentuk tabel simpleks awal
b. Pilih kolom kunci (kolom pivot) dimana − memiliki nilai negatif
terbesar
c. Pilih baris (baris pivot) yang berpedoman pada / dengan rasio
terkecil dimana adalah nilai sisi kanan dari setiap persamaan
d. Mencari nilai elemen pivot yang bernilai 1 dan elemen lain bernilai nol dengan cara mengalikan baris pivot dengan -1 lalu menambahkannya dengan semua elemen di baris pertama. Dengan demikian diperoleh tabel simpleks iterasi I.
e. Pemeriksaan optimalitas, yaitu melihat apakah solusi sudah layak atau tidak. Solusi dikatakan layak bila variabel adalah positif atau nol.
Berikut akan diberikan contoh kasus penggunaan Goal Programming. Sebuah Perusahaan memproduksi 2 jenis produk yang berbeda, yaitu A dan B. Produk tersebut dikerjakan melalui 2 proses pengerjaan yang berbeda, yaitu proses 1 dan proses 2. Proses 1 mampu menghasilkan 8 unit produk A dan 5 unit produk B sedangkan untuk proses 2 hanya mampu menghasilkan 2 unit produk A dan 3 unit produk B. Kapasitas maksimum proses 1 dan 2 masing-masing adalah 40 dan 20.
Dalam hal ini perusahaan mendapatkan 4 macam sasaran yaitu : 1. Kapasitas yang tersedia pada proses 1 dimanfaatkan secara maksimum 2. Kapasitas yang tersedia pada proses 2 dimanfaatkan secara maksimum 3. Produk A paling sedikit 15 unit
4. Produk B paling sedikit 8 unit Penyelesaian :
B = Jumlah produk B yang akan diproduksi Yang menjadi fungsi kendala adalah : 8A + 5B ≤ 40
2A + 3B ≤ 20 A ≥ 15 B ≥ 8
Sesuai dengan sasaran yang akan dicapai, maka model goal programming untuk permasalahan diatas adalah :
= ++ − + ++ − + −+ −
+ + −− + =
+ + −− + =
+ −− + =
+ −− + =
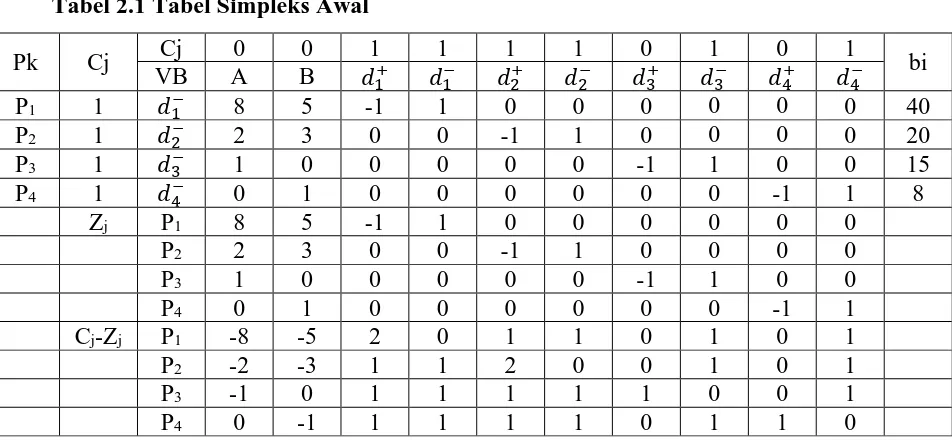
Penyelesaian model ini dimulai dengan membuat tabel simpleks awal seperti pada tabel 2.1 sebagai berikut :
Tabel 2.1 Tabel Simpleks Awal
Pk Cj Cj 0 0 1 1 1 1 0 1 0 1 bi
Yang menjadi kolom kunci adalah kolom ke-1 dimana − memiliki nilai
memiliki nilai bi/aij terkecil yaitu 5.Pemilihan kolom kunci dapat dilihat pada tabel 2.2.
Tabel 2.2 Tabel Simpleks Awal (Pemilihan Kolom Kunci)
Pk Cj Cj 0 0 1 1 1 1 0 1 0 1 bi
Langkah selanjutnya adalah mencari sistem kanonikal yaitu sistem dimana nilai elemen pivot bernilai 1 dan elemen lain bernilai nol dengan cara mengalikan baris pivot dengan -1 lalu menambahkannya dengan semua elemen di baris lainnya.
Tabel 2.3 Tabel Simpleks Iterasi I
Pk Cj Cj 0 0 1 1 1 1 0 1 0 1 bi
Tabel 2.4 Tabel Simpleks Iterasi II
Pk Cj Cj 0 0 1 1 1 1 0 1 0 1 bi
VB A B + − + − + − + −
0 A 1 0 -3/14 3/14 5/14 -5/14 0 0 0 0 10/7
P3 1 − 0 0 3/14 -3/14 -5/14 5/14 -1 1 0 0 95/7
P4 1 − 0 0 -1/7 1/7 4/7 -4/7 0 0 -1 1 16/7
Zj P3 0 0 3/14 -3/14 -5/14 5/14 -1 1 0 0
P4 0 0 -1/7 1/7 4/7 -4/7 0 0 -1 1
Cj-Zj P3 0 0 11/4 17/14 19.14 9/14 1 0 0 1
P4 0 0 8/7 6/7 3/7 11/7 0 1 1 0
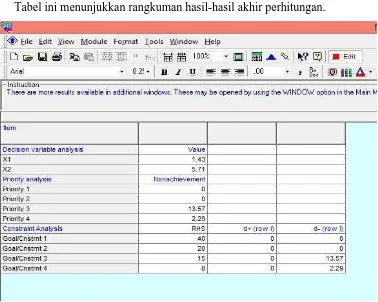
Pada iterasi II diperoleh solusi optimal karena seluruh − . Dengan demikian, solusi optimal untuk produk yang diproduksi adalah A=1,43≈1 unit
dan B=5,71≈6 unit dengan penyimpangan −=13,57≈14 dan −=2,28≈2.
3. Penyelesaian dengan bantuan software QM
QM singkatan dari Quality Method adalah sebuah program yang dirancang untuk menyelesaikan persoalan-persoalan metode kuantitatif, manajemen sains atau operasi riset.Sebuah permasalahan harus diubah dahulu ke dalam sebuah model matematis pemrograman linier, kemudian diinput ke dalam software QM.
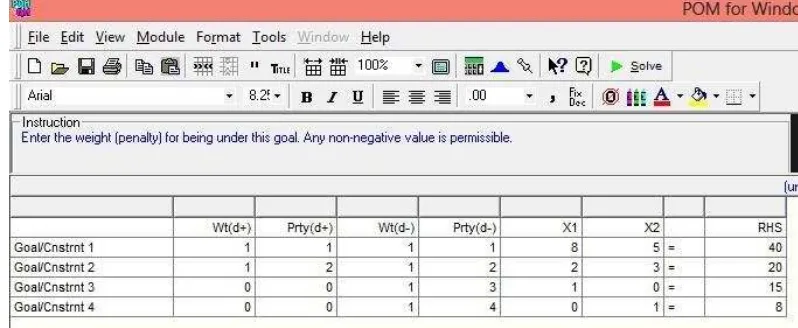
Program ini memiliki beberapa modul untuk menyelesaikan beragam persoalam matematika dan yang menjadi input adalah model matematika yang telah dirancang berdasarkan permasalahn yang ada. Dalam penelitian ini digunakan modul goal programming.Misalnya contoh diatas, bentuk inputnya adalah :
Setelah data diinput, segera perintahkan program untuk mengola data tersebut
melalui fasilitas “solve”. Sesaat kemudian program akan menayangkan
hasilnya dalam 3 bentuk yaitu : - Final Table
Tabel ini menunjukkan hasil perhitungan pada iterasi terakhir metode simpleks.
Gambar 2.6 Hasil Akhir Pada Perhitungan Metode Simpleks
- Summary
Tabel ini menunjukkan rangkuman hasil-hasil akhir perhitungan.
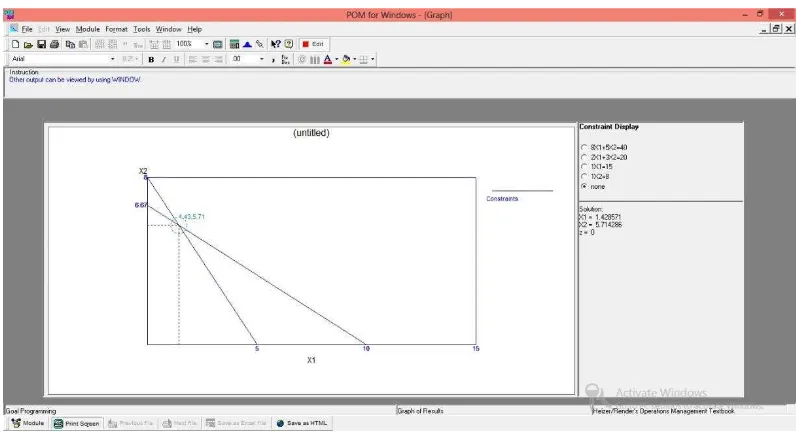
- Graph
Grafik yang menunjukkan solusi optimal atas model matematika dari suatu permasalahan.