OPTIMASI PEMROGRAMAN KUADRATIK KONVEKS DENGAN MENGGUNAKAN METODE PRIMAL-DUAL PATH-FOLLOWING

(1)

OPTIMASI PEMROGRAMAN KUADRATIK KONVEKS DENGAN

MENGGUNAKAN METODE PRIMAL-DUAL PATH-FOLLOWING

Raras Tyasnurita1)_{, Wiwik Anggraeni}2)_{, Rully Soelaiman}3)

1)_{Jurusan Sistem Informasi} 3)_{Jurusan Teknik Informatika}

Fakultas Teknologi Informasi, Institut Teknologi Sepuluh Nopember, Kampus Keputih, Sukolilo, Surabaya 60111, Indonesia E-mail : raras@its-sby.edu1)_{, wiwik@its-sby.edu}2)_{, rully@si.its.ac.id}3)

Abstrak

Metode Interior Point dapat digunakan sebagai alternatif penyelesaian permasalahan optimasi pemrograman kuadratik konveks. Metode ini melakukan pemotongan pencarian dari bagian interior daerah solusi menuju solusi optimal. Akan tetapi cara tersebut belum tentu bisa memberikan perkiraan jumlah iterasi yang dihasilkan.

Pada penelitian ini diimplementasikan metode Interior Point dengan Primal-Dual Path-Following untuk menyelesaikan permasalahan pemrograman kuadratik konveks. Pencarian solusi melalui beberapa tahap, yaitu pemberian sembarang titik awal yang memenuhi kondisi Interior Point, menghitung move direction untuk titik x,y,z sebagai titik solusi, dan perubahan (update) terhadap titik x,y,z.

Uji coba dilakukan dengan menggunakan 10 contoh permasalahan pemrograman kuadratik konveks dengan nilai titik awal yang berbeda untuk setiap permasalahan. Berdasarkan hasil uji coba didapatkan bahwa grafik trayektori yang dihasilkan konvergen pada satu titik kesetimbangan antara bentuk primal dan dual, yang mana nilainya setara dengan penyelesaian menggunakan toolbox optimasi “fmincon” di MATLAB.

Pada makalah ini berhasil ditentukan rumusan untuk pencapaian kondisi optimal. Kata kunci : Pemrograman kuadratik konveks, metode Interior Point, metode Primal-Dual

Path-Following

1. PENDAHULUAN

Pendekatan optimasi saat ini semakin banyak diperlukan dalam penyelesaian permasalahan pada kehidupan sehari-hari. Permasalahan nonlinier sebagai salah satu bentuk permasalahan dalam optimasi memberikan area yang luas bagi kegiatan penelitian yang bertujuan untuk merancang konsep atau metode penyelesaian yang lebih efisien. Hal ini mengingat model-model nonlinier seringkali memiliki bentuk yang lebih kompleks dan dinamis. Pemrograman kuadratik merupakan salah satu subklas atau bagian khusus dari pemrograman nonlinier. Adapun pemrograman kuadratik konveks memiliki fungsi tujuan yang bersifat kuadratik dan konveks.

Metode optimasi yang digunakan pada pemrograman kuadratik pada umumnya dilakukan dengan modifikasi pada metode Simpleks. Walaupun dalam praktiknya metode Simpleks dapat menyelesaikan permasalahan skala besar, namun secara teoretis jumlah iterasi

yang dibutuhkan untuk mencapai solusi optimal akan meningkat secara eksponensial sehingga akan menghabiskan banyak waktu perhitungan. Hal ini dikarenakan pencarian solusi optimal pada metode Simpleks sangat bergantung pada pencarian extreme point dari ruang solusi. Berbeda dengan metode Simpleks, penggunaan metode Interior Point dalam pencarian solusi optimal tidak bergantung pada pencarian

extreme point. Dengan demikian untuk

persamaan yang besar, waktu pencarian solusi optimal dengan metode Interior Point membutuhkan waktu yang lebih sedikit daripada dengan menggunakan metode Simpleks. Umumnya penggunaan metode Interior Point diterapkan untuk menyelesaikan permasalahan linier, namun dilihat dari performanya maka diharapkan dapat juga diterapkan untuk menyelesaikan permasalahan kuadratik.

Metode Primal-Dual Path-Following digunakan dalam pencarian arah pergerakan titik dalam

(2)

daerah layak menuju solusi optimal. Pencarian arah merupakan salah satu tahap dalam metode Interior Point. Nilai tambah dari metode Primal-Dual Path-Following adalah kemampuannya untuk memperkirakan jumlah iterasi yang dibutuhkan dalam mencapai kondisi optimal sebelum perhitungan.

Oleh karena itu, tujuan dari riset ini adalah melakukan optimasi pemrograman kuadratik konveks dengan menggunakan metode Primal-Dual Path-Following serta melakukan pengujian aspek kebenaran dari algoritma yang dikembangkan pada berbagai contoh permasalahan yang berbeda. Adapun permasalahan yang diangkat yaitu bagaimana implementasi dan uji kebenaran dari metode Primal-Dual Path-Following sebagai solusi pada berbagai contoh permasalahan pemrograman kuadratik konveks.

2. OPTIMASI PEMROGRAMAN

KUADRATIK KONVEKS

Optimasi ialah suatu proses untuk mencapai hasil yang ideal atau optimal (nilai efektif yang dapat dicapai). Dalam permasalahan optimasi, terdapat tiga komponen dasar yang bermanfaat dalam pembuatan formula permasalahan maupun pencarian penyelesaian (Taha, 2003). Tiga komponen dasar tersebut adalah:

1) Variabel Keputusan, yaitu variabel yang akan dicari untuk mencapai nilai fungsi tujuan (solusi) yang optimal.

2) Fungsi Tujuan (objective function), yaitu fungsi tujuan (solusi optimal) yang hendak dicapai dalam suatu permasalahan optimasi. 3) Pembatas/batasan (constraint), yaitu

persamaan/ pertidaksamaan yang dijadikan syarat atau batasan untuk mencapai fungsi tujuan.

Permasalahan optimasi dapat digolongkan menjadi dua jenis, yaitu permasalahan linier dan permasalahan nonlinier. Pemrograman kuadratik merupakan bagian khusus dari pemrograman nonlinear. Adapun pemrograman kuadratik konveks, fungsi tujuannya selain bersifat kuadratik, juga bersifat konveks. Pemrograman kuadratik ini mempunyai matriks Hessian (matriks turunan kedua dari fungsi tujuan) yang semidefinit positif sehingga permasalahan memiliki bentuk fungsi konveks (mempunyai solusi yang unik).

Bentuk umum Pemrograman Kuadratik adalah sebagai berikut (Achache, 2006):

Bentuk Primal:

Minimize:

x

T

Qx

₊

c

T

x

2

1

(1)

Subject to:

Ax

=

b

dan

x

≥

0

nXn n m mXn

_b

_R

_c

_R

_dan

_Q

_R

R

A

∈

,

∈

,

∈

Bentuk Dual: Maximize:

₋

x

T

Qx

₊

b

T

y

2

1

(2) Subject to:

₋

Qx

₊

A

T

y

₊

z

₌

c

z

≥

0

Matriks A pada kondisi full rank (m

≤

n). Kondisi optimal dari penyelesaian permasalahan pemrograman kuadratik akan tercapai apabila memenuhi kondisi Karush Kuhn Tucker (KKT). Kondisi KKT menjadi sebuah syarat perlu (necessary requirement) untuk mendapatkan jaminan adanya solusi global optima bagi pemecahan semua permasalahan optimasi nonlinier, dan menjadi syarat kecukupan (sufficient requirement) bagi penyelesaian permasalahan pemrograman kuadratik.

3. PRIMAL-DUAL PATH-FOLLOWING

Prinsip pada metode Interior Point adalah mengunjungi titik-titik "interior" (tidak ekstrim) di dalam daerah yang "feasible" atau layak (Winarti, 2007). Beberapa ide dasar dari metode ini berasal dari pemikiran Karmarkar (Hillier, 1994) yaitu:

1) Bergeraklah melalui daerah layak menuju suatu penyelesaian optimal (pemilihan titik awal).

2) Bergeraklah dalam arah yang meningkatkan nilai fungsi tujuan dengan tingkat kecepatan yang paling tinggi (pencarian nilai move

direction oleh proses search direction).

3) Ubahlah daerah layak untuk menempatkan penyelesaian percobaan yang sekarang sedekat mungkin pada titik pusatnya, dengan demikian memungkinkan peningkatan yang besar bilamana melaksanakan konsep dua (update nilai solusi).

Salah satu kelas utama dalam metode Interior Point adalah metode Path-Following (Nash, 1996). Adapun metode Primal-Dual Path-Following adalah metode dimana titik awalan akan mendekati central path, sehingga titik solusi

(3)

juga akan tetap dekat dengan central path dan mengurangi perbedaan antara nilai fungsi tujuan primal dan dual pada tiap iterasi (Wright, 1997). Ini dilakukan guna memenuhi konsep dualitas yaitu strong duality, di mana primal optimal adalah dual optimalnya.

Central path menstabilkan algoritma primal-dual

dengan menyediakan rute yang dapat diikuti sampai ke set solusi. Metode Path-Following secara tegas membatasi iterasi pada daerah sekitar

central path dan mengikutinya ke arah solusi.

Bahan kunci dari algoritma optimasi manapun adalah ukuran keinginan tiap titik dalam ruang pencarian. Pada metode Path-Following, yang memegang peran ini adalah parameter path (mu), sehingga iterasi semakin mendekati pemenuhan kondisi KKT. Nilai mu akan semakin mendekati nol dalam pergerakan titik solusi menuju titik optimal.

Optimasi pemrograman kuadratik konveks dengan metode Primal-Dual Path-Following terdiri dari beberapa langkah yaitu:

1) Pemilihan titik awal pencarian solusi. Titik tersebut harus berada di daerah

interior pada ruang solusi yang layak dan memenuhi batasan (memenuhi kondisi Interior Point). Selain itu dalam pergerakannya, diasumsikan titik solusi tetap dekat dengan central path. Asumsi diwujudkan dengan ukuran kedekatan pada central path yang nilainya kurang dari parameter kedekatan yang sudah ditentukan di awal, didefinisikan dengan:

||

2 ||

||

)

,

(

XZe

µ

=

p

=

e

−

v

δ

τ

µ

δ

(

X

0

Z

0

e

,

)

<

(3) 2) Pemberian nilai awal parameter path. Parameter path berfungsi untuk

menyusutkan gap, yaitu selisih antara nilai fungsi tujuan primal dan dual. Nilai awal sebesar :

(x0_{'* z}0_)/n.

3) Set indeks iterasi i ← 1.

4) Kondisi optimal: Jika nilai selisih dari fungsi tujuan bentuk primal dan dual sudah cukup kecil maka iterasi dihentikan, dikarenakan solusi yang didapatkan sudah cukup optimal.

5) Perubahan nilai Parameter path:

µ

θ

µ

=

( −

1 )

(4) Dimana

_θ

= 1 / (2

_n

).

6) Menentukan move direction:

V

X

d

x

₌

_x

_/

−1

Δ

V

Z

d

z

_z

_/

−1

=

Δ

(5) y

d

y =

Δ

7) Update terhadap nilai solusi untuk

pencarian titik solusi yang baru:

x

+

←

+

Δ

y

+

←

+

Δ

(6)

z

+

←

+

Δ

8) Set indeks iterasi i ← i + 1

Kemudian kembali ke langkah 4, diulangi hingga iterasi dihentikan.

4. UJI COBA

Contoh uji coba yang dilakukan adalah sebagai berikut : • Bentuk awal: min

_{( )}

2 ₂1 ₂2 1 2 1

_x

x

f

=

+

Subject to

0 ,

3

2 1 1

≥

=

x

• Bentuk standar: min

_{( )}

2 ₂1 ₂2 1 2 1

_x

x

f

=

+

Subject to

0 ,

3

2 1 1

≥

=

x

• Bentuk Matriks:

(

1 0

)

= A ; ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 0 c ; b=

_{( )}

3 ; ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 1 0 0 1 Q

• Nilai Titik Awal:

(

)

(

)

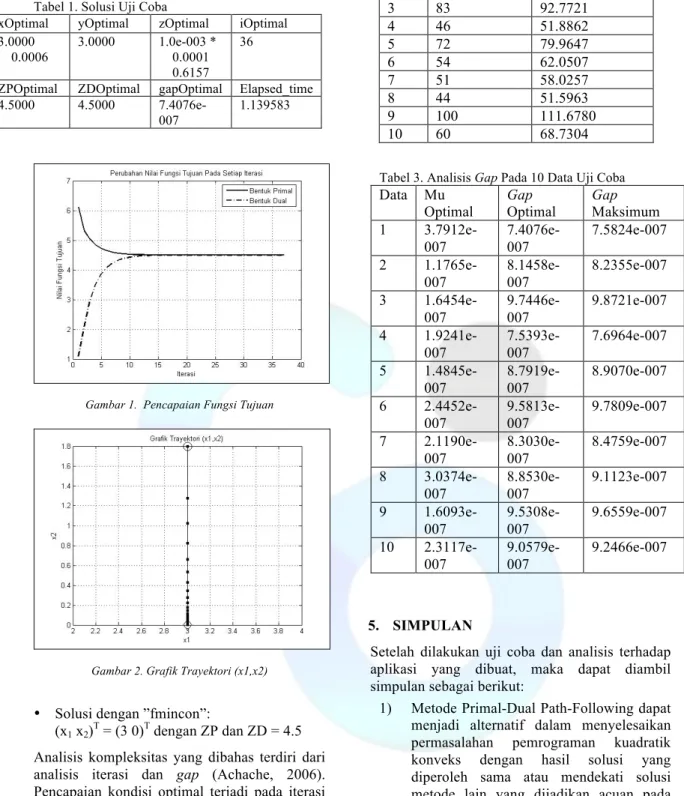
T T z x 070618 1.79781425 377127 0.59566857 0 070618 1.79781425 000000 3.00000000 0 = =

Tabel 1 menunjukkan solusi akhir yang diperoleh. Selanjutnya pada gambar 1 didapatkan bahwa kondisi optimal didapatkan setelah dilakukan iterasi sebanyak 36 kali, dengan nilai fungsi tujuan bentuk primal dan dual adalah sebesar 4,5. Pada gambar 2 didapatkan bahwa titik optimal yang dicapai adalah: x1 = 3 dan x2 = 0.

(4)

Tabel 1. Solusi Uji Coba

xOptimal yOptimal zOptimal iOptimal

3.0000

0.0006 3.0000 1.0e-003 * 0.0001 0.6157

36

ZPOptimal ZDOptimal gapOptimal Elapsed_time

4.5000 4.5000

7.4076e-007

1.139583

Gambar 1. Pencapaian Fungsi Tujuan

Gambar 2. Grafik Trayektori (x1,x2)

• Solusi dengan ”fmincon”:

(x1 x2)T = (3 0)T dengan ZP dan ZD = 4.5 Analisis kompleksitas yang dibahas terdiri dari analisis iterasi dan gap (Achache, 2006). Pencapaian kondisi optimal terjadi pada iterasi

paling banyak sejumlah

_⎥

⎦

⎤

⎢

⎣

⎡

ε

0 0

₎

(

log

2 n

x

z

T

dan pada gap paling banyak sejumlah

_µ

n

. Hal ini dibuktikan dalam hasil perhitungan pada tabel 2 untuk analisis jumlah iterasi dan tabel 3 untuk analisis nilai gap.

Tabel 2. Analisis Iterasi Pada 10 Data Uji Coba

Data Iterasi Optimal Iterasi Maksimum 1 36 43.6392 2 83 90.9688 3 83 92.7721 4 46 51.8862 5 72 79.9647 6 54 62.0507 7 51 58.0257 8 44 51.5963 9 100 111.6780 10 60 68.7304

Tabel 3. Analisis Gap Pada 10 Data Uji Coba

Data Mu Optimal Gap Optimal Gap Maksimum 1 3.7912e-007 7.4076e-007 7.5824e-007 2 1.1765e-007 8.1458e-007 8.2355e-007 3 1.6454e-007 9.7446e-007 9.8721e-007 4 1.9241e-007 7.5393e-007 7.6964e-007 5 1.4845e-007 8.7919e-007 8.9070e-007 6 2.4452e-007 9.5813e-007 9.7809e-007 7 2.1190e-007 8.3030e-007 8.4759e-007 8 3.0374e-007 8.8530e-007 9.1123e-007 9 1.6093e-007 9.5308e-007 9.6559e-007 10 2.3117e-007 9.0579e-007 9.2466e-007 5. SIMPULAN

Setelah dilakukan uji coba dan analisis terhadap aplikasi yang dibuat, maka dapat diambil simpulan sebagai berikut:

1) Metode Primal-Dual Path-Following dapat menjadi alternatif dalam menyelesaikan permasalahan pemrograman kuadratik konveks dengan hasil solusi yang diperoleh sama atau mendekati solusi metode lain yang dijadikan acuan pada penelitian ini.

2) Pemberian nilai titik awal (starting point) diberikan secara manual oleh pengguna, yang nilainya harus memenuhi batasan dan syarat yang ditentukan. Apabila nilai titik awal tidak memenuhi batasan dan syarat yang ada, maka tidak dapat dihasilkan nilai solusi optimal. Hal ini memunculkan kesulitan tersendiri dan menjadi kelemahan dari aplikasi ini.

3) Titik awal yang berada di interior akan menuju ke daerah batasan (boundary)

(5)

yaitu ke titik solusi optimal. Pada kondisi optimal, diperoleh nilai selisih yang cukup kecil untuk fungsi tujuan permasalahan bentuk primal dan dual.

4) Pencarian solusi optimal pemrograman kuadratik konveks dengan metode Primal-Dual Path-Following melalui beberapa tahap, yaitu pemberian titik awal yang berada di interior daerah batasan, menghitung move direction untuk titik x,y,z dan perubahan (update) terhadap titik x,y,z. Proses terus diulang hingga dicapai kondisi optimal.

5) Metode Primal-Dual Path-Following mengarahkan titik solusi mendekati central

path sehingga dapat memenuhi asumsi

ukuran kedekatan central path pada sebagian besar iterasi.

6) Pemenuhan kondisi Interior Point (IPC) dapat membantu proses optimasi dalam mencapai kondisi optimal, namun tetap memperhatikan ketepatan titik awal yang dipilih.

7) Jumlah iterasi pada kondisi optimal dapat diperkirakan sebelum perhitungan, yaitu pada iterasi maksimum sebesar

⎥

⎦

⎤

⎢

⎣

⎡

ε

0 0

₎

(

log

2 n

x

z

T

dengan nilai gap maksimum sebesar

µ

n

.

6. DAFTAR PUSTAKA

Achache, M, 2006. A New Primal-Dual

Path-Following Method for Convex Quadratic Programming. Algeria : Departement de

Mathematiques, Faculte des Sciences, University Ferhat Abbas.

Hillier, Frederick S., Lieberman, Gerald J., 1994.

Introduction to Operation Research. Singapore :

McGraw-Hill.

Nash, Stephen G., Sofer, Ariela, 1996. Linear

and Nonlinear Programming. Singapore :

McGraw Hill.

Taha, Hamdy A. 2003. Operation research: An

Introduction 7th_{.New Jersey : Prentice Hall.} Venkataraman, P, 2002. Applied Optimization

with MATLAB Programming. John Wiley &

Sons.

Winarti, Nike D, 2007. Optimasi Pemrograman

Kuadratik Dengan Menggunakan Algoritma Primal-Dual Interior Point. Surabaya : FTIF-ITS.

Wright, S. J., 1997. Primal Dual Interior Point