PENGANTAR SIMUTATED ANNEATING DAN APLII(ASINYA

(1)

PENGANTAR

SIMUTATED

ANNEATING

(2)

PENGANTAR

SIMULATED ANNEALING

DAN APLIKASINYA

Dr. Suparman, M.Si., DEA

FST UTY Press

Yogyakarta

(3)

PENGANTAR SIMULATED ANNEALING DAN APLIKASINYA

Oleh : Dr. Suparman, M.Si., DEA Hak Cipta @ 2010 pada Penulis

Penerbit : FST UTY Press

Jl. Ringroad Utara, Jombor Sleman

Hak cipta dilindungi undang-undang. Dilarang memperbanyak buku ini sebagian atau seluruhnya, dalam bentuk dan dengan cara apa pun juga, baik secara mekanis maupun elektronis, termasuk fotokopi, rekaman, dan lain-lain tanpa izin tertulis dari penulis.

Edisi pertama

Cetakan pertama, 2010

Editor : Sugiyarto, M.Si., Ph.D

Desain Cover : Magistera Laningratum Setting : Ayudea Az Zahra Zulfa

Dr. Suparman, M.Si., DEA

Pengantar Simulated Annealing dan Aplikasinya, ________ Yogyakarta : FST UTY Press, 2010

vi+52 hlm; 18,5 x 26,5 cm ISBN : 978-979-1334-30-3 Statistika : Buku Referensi

Kutipan Pasal 44 : Sangsi pelanggaran undang-undang hak cipta 1987

1. Barang siapa dengan sengaja dan tanpa hak mengumumkan atau memperbanyak suatu ciptaan atau memberi ijin untuk itu, dipidana dengan pidana penjara paling lama 7 (tujuh) tahun dan/atau denda paling banyak Rp 100.000.000,- (seratus juta rupiah).

2. Barang siapa dengan sengaja menyiarkan, memamerkan,

mengedarkan, atau menjual kepada umum suatu ciptaan atau barang hasil pelanggaran hak cipta sebagaimana dimaksud ayat 1 (satu), dipidana dengan pidana penjara paling lama 5 (lima) tahun dan/atau denda paling banyak Rp 50.000.000,- (lima puluh juta rupiah).

(4)

Kata Pengantar

KATA PENGANTAR

Buku ini disusun berdasarkan penelitian dan pengajaran yang penulis lakukan selama lima tahun. Di samping itu, penulis juga telah mengkaji berbagai literatur dan hasil penelitian. Buku ini ditulis sebagai buku referensi untuk para peneliti, para pengajar di Perguruan Tinggi dan para mahasiswa dalam memahami Metode Simulated Annealing. Dalam buku ini disertakan beberapa aplikasinya sehingga membuat buku ini cocok juga untuk para praktisi yang ingin memahami Metode Simulated Annealing dan permasalahan yang bisa diselesaikan dengan metode ini.

Dalam buku ini dibahas berbagai hal, yaitu : 1) Simulated Annealing; 2) Estimasi Model Runtun Waktu Autoregresif; 3) Estimasi Model Runtun Waktu Subset Autoregresif; 4) Estimasi Model Runtun Waktu Moving Average; 5) Estimasi Model Runtun Waktu Subset Moving Average; 6) Estimasi Model Subset Autoregresif Moving Average; dan 7) Segmentasi Model Synthetic Aperture Radar.

Karena saya tidak mungkin menyelesaikan buku ini sendirian, daya ingin mengucapkan banyak terima kasih pada berbagai pihak yang telah mendukung kelancaran penulisan buku ini. Akhirnya penulis tetap mengharapkan berbagai masukan, kritik dan saran demi perbaikan karya di masa yang akan datang.

Yogyakarta, Juni 2010 Penulis

(5)

Kata Pengantar

Pengantar Simulated Annealing dan Aplikasinya | Dr. Suparman, M.Si., DEA

(6)

Daftar Isi

DAFTAR ISI

KATA PENGANTAR iii

DAFTAR ISI v

BAB 1 SIMULATED ANNEALING 1

1.1 Pendahuluan 1

1.2 Pembentukan Ukuran 4

1.3 Perhitungan Fungsi Kepadatan 6

1.4 Simulated Annealing 8

BAB 2 ESTIMASI MODEL RUNTUN WAKTU AUTOGRESIF 11

2.1 Rumusan Masalah 11 2.2 Bayesian Hirarki 12 2.3 Metode MCMC 13 2.4 Algoritma SA 14 2.5 Aplikasi 14 2.6 Kesimpulan 18

BAB 3 ESTIMASI MODEL RUNTUN WAKTU SUBSET AUTOGRESIF 19 3.1 Rumusan Masalah 19 3.2 Bayesian Hirarki 19 3.3 Metode MCMC 21 3.4 Algoritma SA 21 3.5 Kesimpulan 22

BAB 4 ESTIMASI MODEL RUNTUN MOVING AVERAGE 23

4.1 Rumusan Masalah 23 4.2 Bayesian Hirarki 24 4.3 Metode MCMC 25 4.4 Algoritma SA 26 4.5 Aplikasi 26 4.6 Kesimpulan 30

(7)

Daftar Isi

vi

BAB 5 ESTIMASI MODEL RUNTUN SUBSET MOVING AVERAGE 31 5.1 Rumusan Masalah 31 5.2 Bayesian Hirarki 31 5.3 Metode MCMC 33 5.4 Algoritma SA 33 5.5 Kesimpulan 34

BAB 6 ESTIMASI MODEL RUNTUN WAKTU SUBSET AUTOGRESIF MOVING AVERAGE

35 6.1 Rumusan Masalah 35 6.2 Bayesian Hirarki 36 6.3 Metode MCMC 37 6.4 Algoritma SA 38 6.5 Kesimpulan 38

BAB 7 SEGMENTASI MODEL SYNTHETIC APERTURE RADAR 39 7.1 Rumusan Masalah 39 7.2 Pendekatan Bayesian 40 7.3 Metode SA 41 7.4 Aplikasi 42 7.5 Kesimpulan 45 DAFTAR PUSTAKA 47

(8)

Bab 1 Simulated Annealing

BAB

1 SIMULATED ANNEALING

1.1 PENDAHULUAN

Misalkan E menyatakan himpunan keadaan dan  menyatakan probabilitas keadaan pada E. Algoritma Metropolis-Hastings ([1], [2]) menghasilkan rantai Markov pada E yang mempunyai probabilitas stasioner sama dengan . Pembentukan rantai Markov tersebut mendasarkan pada kondisi reversibilite. Probabilitas 

disebut stasioner jika untuk kernel K dari rantai Markov pada E berlaku :



    E y ) x , y ( K ) y ( ) x (

untuk semua xE. Probabilitas  disebut reversibel untuk kernel K

jika ) x , y ( K ) y ( ) y , x ( K ) x (  

untuk semua x,yE. Jelas bahwa reversibilite dari  berimplikasi

pada stasionaritas untuk kernel K. Sifat ini digunakan untuk membentuk kernel K sedemikian sehingga  merupakan distribusi stasioner. Misalkan q menyatakan kernel bantu pada E. Dimulai dari xE, penarikan sebuah titik baru y dilakukan dalam 2 tahap :

1. Titik y ditarik menurut q(x,y)

2. Titik y diterima dengan probabilitas

          ) y , x ( q ) x ( ) x , y ( q ) y ( , 1 min ) y , x (

Kernel K didefinisikan sebagai





          



x y ) y , x ( 1 ) x , x ( q ) y , x ( K y x jika ) y , x ( ) y , x ( q ) y , x ( K

Kernel K ini memenuhi persamaan reversibite. Dibawah kondisi bahwa rantai Markov adalah irreduktibel dan aperiodik maka probabilitas  juga merupakan probabilitas limit.

(9)

2

Misalkan E menyatakan ruang yang dibentuk oleh dua ruang yang berbeda dimensinya.



E



₁_xn1 

 

₂ _xn2

dengan n1 dan n2 adalah bilangan bulat yang berbeda. Untuk selanjutnya



₁_xn1 ditulis dengan n1dan

 

₂ _xn2ditulis dengan n2.

Dengan demikian himpunan E dibentuk oleh dua unsur yaitu unsur dari n1 dan unsur dari n2. Demikian pula, ukuran  dibentuk

oleh₁dibawa oleh n1 dan

2

 dibawa oleh n2.

Di dalam n1atau n2, algoritma Metropolis-Hastings dapat

berfungsi tanpa kesulitan. Sebaliknya perlu mendefinisikan tranformasi dari n1menuju n2atau sebalinya yang memenuhi

persamaan reversibilite. Idea dari Green ([3]), misalkan q menyatakan kernel instrumental dan menyatakan probabilitas penerimaan/penolakan. Maka harus dipenuhi





A (dx)



Bq(x,dx')(x,x')



B(dx')



Aq(x',dx) (x',x)

untuk semua A1 dan B2. Atau





A (dx)



Bq12(x,dx') (x,x')



B(dx')



Aq21(x',dx) (x',x)

Dimana q12 menyatakan kernel probabilitas dari n1menuju n2 dan

q12 menyatakan kernel probabilitas dari n2menuju n1.

Misalkan bahwa ukuran dan kernel mempunyai fungsi kepadatan terhadap ukuran Lebesque, maka



 AxB 1(x)q12(x,x')(x,x')dxdx'



 BxA 2(x') q21(x',x)(x',x)dx'dx 



 AxB 2(x') q21(x',x)(x',x)dxdx' Atau ) x ( 1  q12(x,x')(x,x')=2(x') q21(x',x)(x',x) Jadi

(10)

Bab 1 Simulated Annealing           ) ' x , x ( q ) x ( ) x , ' x ( q ) ' x ( , 1 min ) x , ' x ( 12 1 21 2

Selanjutnya dibentuk ukuran  dalam himpunan ExE simetris dan memenuhi (dx) q(x,dx') mempunyai fungsi kepadatan

) ' x , x (

f dan (dx')q(x',dx) mempunyai fungsi kepadatan f(x',x)

terhadap . Ingatlah bahwa ukuran  adalah simetris jika dan hanya jika untuk semua fungsi terukur positif (x,y)diatas ExE

berlaku ) dy , dx ( ) y , x ( ExE  



(y,x) (dx,dy) ExE   



Karena ukuran ini simetris, maka ) dx ( A 



q(x,dx') (x,x') B 



f(x.x') (x,x') (dx,dx') AxB   



f(x'.x) (x',x) (dx,dx') BxA   



) ' dx ( B 



q(x',dx) (x',x) A 



f(x'.x) (x',x) (dx',dx) BxA   

_

f(x.x') (x,x') (dx,dx') BxA   



Persamaan reversibilite menjadi ) ' dx , dx ( ) x , ' x ( ) x '. x ( f BxA  



f(x.x') (x,x') (dx,dx') BxA   

_

Agar supaya persamaan ini dipenuhi, cukup dipenuhi ) x , ' x ( f (x',x)f(x,x') (x,x') untuk semua (x,x')ExE. Atau

        ) ' x , x ( f ) x , ' x ( f , 1 min ) ' x , x ( .

(11)

4

Permasalahan selanjutnya adalah bagaimana membentuk ukuran 

yang simetris diatas ExE dan fungsi kepadatan f yang berkaitan dengan transformasi yang dilakukan.

1.2 PEMBENTUKAN UKURAN

Ide umum adalah melengkapi dua ruang n1dan n2 untuk berada

dalam ruang yang sama dimensinya. Misalkan m1dan m2adalah dua

bilangan positif sedemikian sehingga

2 2 1

1 m n m

n   

Selanjutnya mendefinisikan transformasi-transformasi yang bersesuaian. Misalkan         ) x , x ( g ) x , x ( : g 1 2 1 n m n 2 2 1 1 dan         ) x , ' x ( g ) x , ' x ( : g 2 1 2 n m n 1 1 2 2

Anggap bahwa ada ijektivitas dari transformasi-transformasi terhadap komponen, yaitu untuk i =1, 2 berlaku

) , u ( g ) , u ( g_i   _i  

Anggap juga bahwa ada sebuah rumus inversi yang memungkinkan untuk kembali ke belakang. Untuk semua _xn1 dan m1

1

x  , terdapat dengan tunggal m2

2

x  sedemikian sehingga



g (x,x ),x



x

g1 2 1 2  . Definisikan juga sebuah fungsi h2 dari

1

1 m

n

x

 ke

dalam m2 dengan memisalkan _x _h ₍_x_,_x ₎

1 2

2  yang memenuhi

persamaan sebelumnya.

Secara simetris, untuk semua _x_'n2dan m2

2

x  terdapat

dengan tunggal m1

1

x  sedemikian sehingga g2



g1(x',x2),x1



x'. Definisikan fungsi ha dari n2_xm2 ke dalam m1 dengan memisalkan

) x , ' x ( h

x₁  ₁ ₂ Akhirnya sifat inversi ini memungkinkan berdasarkan g1 dan g2, untuk membentuk dua aplikasi yang saling invers

(12)



g (x,x ),h (x,x )



) x , x ( x : 1 2 1 2 1 m n m n 12 2 2 1 1        dan



g (x',x ),h (x',x )



) x , ' x ( x : 2 1 2 1 2 m n m n 21 1 1 3 2       

Untuk ilustrasi, misalkan n1 1dan n2 2. Maka lengkapi ruang 

dan ambil m1 1dan m2 0. Definisikan aplikasi g1 dan g2dengan

cara berikut           ) x x , x x ( ) x , x ( g ) x , x ( : g 1 1 1 2 1 2 2 2 dan                  2 ' x ' x ) " x ( g ) ' x , ' x ( : x : g 2 1 2 2 1 2 1

Ingatlah bahwa E adalah berbentuk



₁_xn1

 

₂ _xn2 dan ukuran 

simetris diatas ExE berdasarkan aplikasi g1 dan g2. Dimulai dengan mendefinisikan pada n1_xn2 kemudian secara simetris pada

2

1 m

m

x

 dan akhirnya diperluas pada ExE. Pertimbangkan aplikasi



x,g (x,x )



) x , x ( x x : 1 2 1 m n m n₁ ₁ ₂ ₂       

Karena  adalah bayangan dari ukuran Lebesque  dari

2

1 n

n

x

 melalui aplikasi maka dapat dimisalkan d.d. Untuk

1 n A dan _Bn2 berlaku ) AxB (  



(x,x₁)n1xm1 xAdang₂(x,x₁)B



Definisi ini diperluas pada m1_xm2 melalui sifat simetris dengan

memisalkan

) BxA (

 (AxB) untuk _An1dan _Bn2.

Akhirnya ) AxB (  



_An1_xBn2







_An2_xBn1



Perhatikan bahwa 0 ) AxB (   jika _An1 dan _Bn1 Dan

(13)

6 0 ) AxB (   jika _An2 dan _Bn2

Untuk sebuah fungsi dua variabel positif (x,y)pada ExE berlaku



  ExE ) ' dx , dx ( ) ' x , x (



     1 n 1 n_x ) ' dx , dx ( ) ' x , x (



     2 n 2 n_x ) ' dx , dx ( ) ' x , x (

Karena simetris maka juga berlaku



  ExE ) ' dx , dx ( ) ' x , x (



       1 n 1 n_x ) ' dx , dx ( )) x , ' x ( ) ' x , x ( (

Akhirnya, untuk _An1dan _Bn2berlaku



  AxB ) ' dx , dx ( ) ' x , x ( 



  ExE B A(x)1 (x') (x,x') (dx,dx') 1



     2 n 1 n_x 1 1 2 1 2 B A(x)1 (g (x,x )) (x,g (x,x )) (dx,dx ) 1

1.3 PERHITUNGAN FUNGSI KEPADATAN

Misalkan _xn1. Dipilih lompatan menuju n2dengan probabilitas

j(2,x) dan tinggal di n1dengan probabilitas 1-j(2,x). Ambil secara

random titik m1

1

x  dengan distribusi bantu q1(x1) dan kemudian

dimisalkan x'g2(x,x1)

Misalkan ₁(x) dan ₂(x)adalah fungsi-fungsi kepadatan terhadap ukuran Lebesque dari n1dan n2. Maka

) dx ( A 



q(x,dx') (x,x') B 





    2 n 1 n_x 1 2 B 1 A(x) (x)1 (g (x,x ))) 1 j(2,x)(x,g₂(x,x₁)) q₁(x₁)dxdx₁ dengan _An1dan _Bn2.

(14)

Bab 1 Simulated Annealing Menurut kondisi inversi, untuk x dan x' yang diberikan terdapat

dengan tunggal x1 sedemikian sehingga x'g₂(x,x₁). Dengan demikian q₁(x₁)dinyatakan dengan q₁(x,x').

) dx ( A 



q(x,dx') (x,x') B 







  AxB 1(x)j(2,x) (x,x')q1(x,x')(dx,dx')

Sehingga fungsi kepadatan terhadap ukuran  dapat ditulis sebagai ) ' x , x ( q ) x , 2 ( j ) x ( ) ' x , x ( f ₁ ₁

Dengan cara yang sama diperoleh ) ' dx ( B 



q(x',dx) (x',x) A 





    1 m 1 n_x 2 1 A 2 B(x') (x')1 (g (x',x )) 1 j(1,x')(x',g1(x',x2)) q2(x2)dxdx2

Untuk menyatakan integral ini terhadap ukuran , lakukan perubahan variabel      ) x , x ( h x ) x , x ( g ' x 1 2 2 1 2

Jika integral di ruas kanan dinyatakan sebagai fungsi dari x dan x1 maka akan muncul jacobian

) x , x ( ) x , ' x ( 1 2   Sehingga ) ' dx ( B 



q(x',dx) (x',x) A 



(15)

8 



 AxB A 2 B(x') (x')1 (x) 1 j(1,x')(x',x) (dx,dx') ) x , x ( ) x , ' x ( ) x , ' x ( q 1 2 2    Maka diperoleh ) x , ' x ( q ) ' x , 1 ( j ) ' x ( ) x , ' x ( f 2 2 ) x , x ( ) x , ' x ( 1 2  

Probabilitas penerimaan menjadi

            ) x , x ( ) x , ' x ( ) ' x , x ( q ) x , 2 ( j ) x ( ) x , ' x ( q ) ' x , 1 ( j ) ' x ( , 1 min ) ' x , x ( 1 1 1 2 2 . 1.4 SIMULATED ANNEALING

Algoritma reversibel jump Markov chain Monte Carlo yang diuraikan dalam bagian sebelumnya menghasilkan pengamatan

 

i

x dalam ruang keadaan E menurut distribusi .

Dalam bagian ini, diuraikan versi simulated annealing dari algoritma reversible jupm Markov chain Monte Carlo. Algoritma Simulated Annealing (lihat sebagai contoh [4]) menggunakan skema penurunan temperatur

 

Ti dan menghasilkan

 

i x menurut distribusi          i T T ) x ( h ) x (

dimana h(x)log(x). Dengan menurunkan temperatur Ti menuju

0, nilai yang disimulasikan berada disekitar dekat sekali dengan minimum global dari fungsi h(x).

Bartoli dan Del Moral memberikan kondisi sangat umum dari kekonvergenan algoritma simulated annealing dalam ruang terukur sembarang. Kondisi reversibilitas dari kernel otomatis dipenuhi untuk kernel Metropolis-Hasting. Di sini, skema penurunan

(16)

Bab 1 Simulated Annealing temperatur Ti dicari secara empiris. Probabilitas penerimaan/penolakan (x,x*) menjadi        ) u , x ( ) u , x ( f ) u ( g ) x ( j ) u ( h ) x ( j , 1 min ) x , x ( 12 12 * * 21 * T            (x,x ) T 1 exp * i dengan               ) x ( log ) x ( h ) x ( log ) x ( h ) x ( h ) x ( h ) x , x ( * * * *

(17)

(18)

Bab 2 Estimasi Model Runtun Waktu Autoregresif

BAB

2 ESTIMASI MODEL RUNTUN WAKTU

AUTOREGRESIF

2.1 RUMUSAN MASALAH

Misalkan (Xt)tZ adalah suatu runtun waktu berharga riil.

Runtun waktu (Xt)tZ dikatakan memiliki model AR dengan orde p,

dinotasikan sebagai AR(p), jika (Xt)tZ memenuhi persamaan

stokhastik berikut :

_

     p 1 i t i t ) p ( i t X E X tZ (2.1)

di mana orde _p__N_{, vektor koefisien}



p



P p p p p  ( ) ( )  2 ) ( 1 ) (  _, _, _,  

dan (Et)tZ merupakan suatu barisan peubah acak berharga riil

yang saling bebas dan masing-masing berdistribusi normal dengan rata-rata 0 dan variansi 2 ([5]). Data jumlah pembangkit tenaga

listrik oleh industri listrik, jumlah pendaftaran mobil di suatu negara, jumlah penumpang pesawat udara dan data jumlah penjualan industri merupakan beberapa contoh data riil yang dapat dimodelkan oleh model AR.

Selanjutnya model AR (Xt)tZ disebut stasioner jika dan hanya

jika persamaan suku banyak



     p 1 i i ) p ( i a 1 ) a (

bernilai nol untuk nilai a di luar lingkaran dengan jari-jari sama dengan satu ([6]).

Berdasarkan data xt (t = 1, 2, …, n), selanjutnya kita akan berusaha untuk menaksir harga

p, (p), dan 2.

Untuk melakukan itu, kita akan menggunakan pendekatan Bayesian hierarki, yang akan diuraikan dalam bagian berikut ini.

(19)

12

2.2 BAYESIAN HIERARKI

Andaikan s



xp1,xp2,,xn



adalah suatu realisasi dari model

AR(p). Jika nilai s0 



x1,x2,,xp



diketahui, maka fungsi

kemungkinan dari s dapat ditulis kurang lebih sebagai berikut :







_

_ _







            n 1 q t ) p ( 2 2 2 / ) p n ( 2 2 ) p ( , p , t g 2 1 exp 2 1 , , p s  (2.2) di mana







  pi1 ti ) p ( i t ) p ( x x , p , t g

untuk t = p+1, p+2, …, n dengan nilai awal xˆ1 xˆ2  xˆp 0 ([7]).

Misalkan Sp adalah daerah stabilitas. Dengan menggunakan transformasi





p ) p ( p ) p ( 2 ) p ( 1 ) p ( S , , , : G        

_

_

p p 2 1 ) p ( ) 1 , 1 ( r , , r , r r     (2.3) maka model AR (Xt)tZ stasioner jika dan hanya jika





p

p _r _r

r( )  1,, (1,1) ([8]). Selanjutnya fungsi kemungkinan dapat

ditulis kembali sebagai :







_

_ _



 _



           n 1 p t ) p ( 1 2 2 2 / ) p n ( 2 2 ) r ( ) ( G , p , t g 2 1 exp 2 1 , r , p s  (2.4)

Penentukan distribusi prior untuk parameter-parameter tersebut di atas adalah sebagai berikut :

a) Orde p berdistribusikan Binomial dengan parameter λ :

p p p p p max max (1 ) C ) p (      

b) Untuk orde q ditentukan terlebih dahulu, vektor koefisien _r(p)

berdistribusikan seragam pada interval (-1, 1)q_.

c) Variansi 2 berdistribusikan invers gamma dengan parameter

α/2 dan β/2 : ) 2 /( exp ) ( ) 2 / ( ) 2 / ( ) , ( 2 (1 /2) 2 2 / 2              

Di sini parameter λ diasumsikan berdistribusi seragam pada interval (0,1), nilai α diambil sama dengan 2 dan parameter β diasumsikan berdistribusi Jeffrey. Sehingga distribusi prior untuk parameter

) , ,

( ( ) 2

1 p r p 

H  dan H2 (,) dapat dinyatakan sebagai : _₍_H _,_H ₎_ 2 1 



p 







r p

 

 ,



2 ) p ( ) (  () (2.5)

(20)

Bab 2 Estimasi Model Runtun Waktu Autoregresif Menurut Teorema Bayes, maka distribusi a posteriori untuk parameter H1 dan H2 dapat dinyatakan sebagai :

_₍_H _,_H _s₎_

2

1 



s H1



(H1,H2) (2.6)

Distribusi a posteriori merupakan gabungan dari fungsi kemungkinan dan distribusi prior yang kita asumsikan sebelum sampel diambil. Fungsi kemungkinan bersifat obyektif sementara distribusi prior ini bersifat subyektif. Dalam kasus ini, distribusi a posteriori 



H1,H2s



mempunyai bentuk yang sangat rumit sehingga

tidak dapat diselesaikan secara analitis. Untuk mengatasi masalah tersebut, diusulkan metode MCMC.

2.3 METODE MCMC

Misalkan M = (H1, H2). Secara umum, metode Markov Chain Monte Carlo (MCMC) merupakan suatu metode sampling, yaitu dengan cara membuat rantai Markov homogen M1,...,Mm yang memenuhi sifat aperiodik dan irreduktibel ([9]) sedemikian hingga M1,...,Mm dapat dipertimbangkan sebagai variabel acak yang mengikuti distribusi 



H1,H2s



. Dengan demikian M1,...,Mm dapat

digunakan sebagai sarana untuk menaksir parameter M. Untuk merealisasikan itu diadopsi algoritma Gibbs Hibrida ([9]) yang terdiri dari dua tahap :

1. Simulasi distribusi 



H2s





H1,H2s



Algoritma Gibbs digunakan untuk mensimulasikan distribusi



H2s



 dan algoritma hibrida, yang mengabungkan algoritma Reversible Jump Markov Chain Monte Carlo (RJMCMC) ([3]) untuk mensimulasikan parameter (_p,_r(p)) dengan algoritma Gibbs untuk mensimulasikan parameter σ2_{, digunakan untuk mensimulasikan} distribusi 



H1,H2s



. Algoritma RJMCMC merupakan rampatan dari

algoritma Metroppolis-Hastings ([1], [9]).

Estimator yang dihasilkan oleh metode MCMC dalam dua tahap. Tahap pertama adalah estimator dari orde q. Tahap kedua adalah estimator dari parameter model AR dan variansi σ2_yang bersesuaian dengan orde q yang diperoleh pada tahap pertama.

(21)

14

Untuk mendapatkan kecepatan dan efisiensi diperlukan suatu algoritma untuk menentukan estimator orde q, parameter model AR dan variansi σ2_{secara bersamaan. Untuk keperluan itu, diusulkan} algoritma Simulated Annealing (SA).

2.4 ALGORTIMA SA

Algoritma SA ([10]) diperoleh dengan menambahkan barisan temperatur T1,...,Tm dalam metode MCMC di atas. Selanjutnya algoritma SA akan memproduksi suatu rantai Markov M(T1),...,M(Tm) yang tidak lagi homogen. Dengan suatu hipotesis tertentu pada T1,...,Tm ([11]) maka M(Tm) akan konvergen menuju suatu nilai yang memaksimumkan distribusi posteriori 



H1,H2s



.

2.5 APLIKASI

Sebagai ilustrasi, kita akan menerapkan metode ini untuk mengidentifikasi orde dan menaksir parameter data AR sintesis dan data riil. Studi simulasi ditempuh untuk mengkonfirmasi kinerja dari algoritma SA apakah dapat berkerja dengan baik. Sedangkan studi kasus diberikan untuk memberikan contoh penerapan penelitian dalam memecahkan permasalahan dalam kehidupan sehari-hari.

Baik untuk data AR sintesis maupun data AR riil ini, kita akan menggunakan algoritma SA untuk mengidentifikasi orde dan mengestimasi parameter model AR yang bersesuaiaan. Untuk keperluan itu, algoritma SA dimplementasikan sebanyak 70000 iterasi dengan nilai awal temperatur T0 = 10 kemudian temperatur diturunkan dengan faktor 0,995 hingga mencapai temperatur akhir T1400 = 0,01. Nilai orde q dibatasi maksimum 10 sehingga qmaks = 10.

Data AR Sintesis

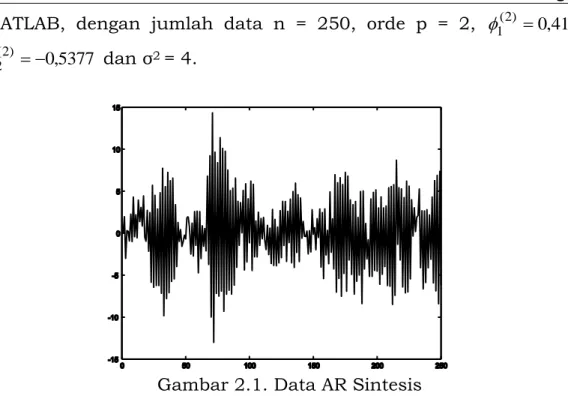
Gambar 2.1 merupakan data AR sintesis yang dibuat menurut persamaan (2.1) di atas dengan menggunakan bahasa pemograman

(22)

Bab 2 Estimasi Model Runtun Waktu Autoregresif MATLAB, dengan jumlah data n = 250, orde p = 2, ₁(2) 0,4162,

5377 , 0 ) 2 ( 2   dan σ2 _{= 4.}

Gambar 2.1. Data AR Sintesis

Selanjutnya berdasarkan data dalam Gambar 2.1 orde p, parameter model AR, variansi σ2_{akan ditentukan atau lebih tepat akan ditaksir} dengan menggunakan algoritma SA. Penaksir orde, parameter model AR dan variansi σ2_{yang dihasilkan oleh algoritma SA adalah} _p_ˆ _₂_,

4073 , 0 ˆ(2) 1   , ˆ₂(2) 0,5430 dan ˆ2= 3,5239. Data AR Riil

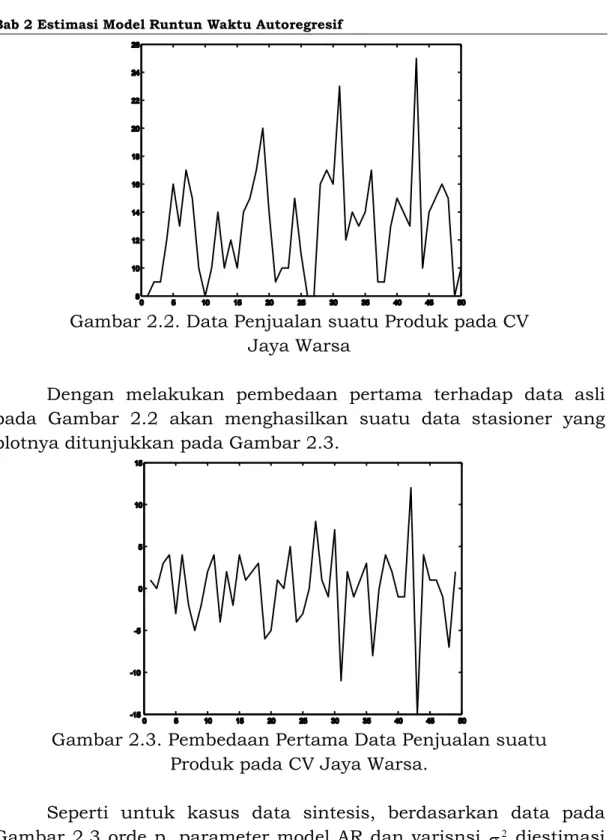
Gambar 2.2 menyajikan data penjualan suatu produk pada CV Jaya Warsa Klaten untuk 50 periode yaitu dari Januari 2002 sampai Pebruari 2006 ([12]). Dari plot data dapat kita lihat bahwa bahwa data tidak stasioner. Untuk mendapatkan menstasionerkan data, dibuat data baru yang terdiri dari pembedaan data asli antara periode yang berturut-turut.

(23)

16

Gambar 2.2. Data Penjualan suatu Produk pada CV Jaya Warsa

Dengan melakukan pembedaan pertama terhadap data asli pada Gambar 2.2 akan menghasilkan suatu data stasioner yang plotnya ditunjukkan pada Gambar 2.3.

Gambar 2.3. Pembedaan Pertama Data Penjualan suatu Produk pada CV Jaya Warsa.

Seperti untuk kasus data sintesis, berdasarkan data pada Gambar 2.3 orde p, parameter model AR dan varisnsi _2 diestimasi

dengan menggunakan algoritma SA. Hasilnya adalah pˆ 4, 5105 , 0 ˆ(4) 1   , ˆ₂(4) 0,3414, ˆ₃(4) 0,2809, ˆ₄(4) 0,2250 dan ˆ2= 16,6262.

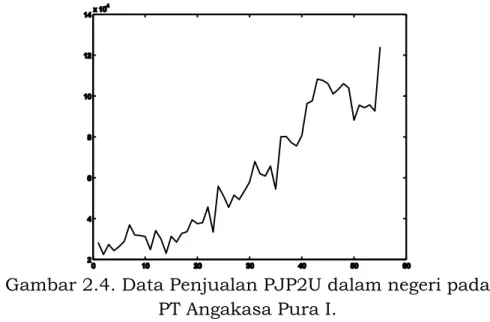
Data riil kedua disajikan pada Gambar 2.4. Data tersebut merupakan data penjualan Penjualan Jasa Penumpang Pesawat

(24)

Bab 2 Estimasi Model Runtun Waktu Autoregresif Udara (PJP2U) dalam negeri pada PT Angakasa Pura I Bandar Udara Internasional Adisutjipto Yogyakarta untuk 55 periode yaitu Januari 2001 sampai Juli 2005 ([13]). Terlihat jelas pada Gambar 4 bahwa data inipun tidak stasioner.

Gambar 2.4. Data Penjualan PJP2U dalam negeri pada PT Angakasa Pura I.

Untuk mendapakan data yang stasioner dilakukan pembedaan pertama dan hasilnya ditunjukkan pada Gambar 2.5.

Gambar 2.5. Pembedaan Pertama Data Penjualan PJP2U dalam Negeri pada PT Angakasa Pura I.

Berdasarkan data pada Gambar 2.5 selanjutnya orde p, parameter model AR dan variansi σ2_{ditaksir dengan menggunakan}

(25)

18

algoritma SA. Hasilnya adalah pˆ 1, ˆ₁(1) 0,3926 dan ˆ2= 6,8499 x

107_.

2.6 KESIMPULAN

Uraian di atas, merupakan kajian teori tentang algoritma SA dan penerapannya pada identifikasi orde p, penaksiran vektor koefisien _(p)_{, dan penaksiran variansi σ}₂_{dari model AR. Dari hasil}

simulasi menunjukkan bahwa algoritma SA dapat menaksir parameter-parameter itu dengan baik.

Sebagai implementasi algoritma SA, diambil dua data riil pada CV Jaya Warsa dan PT Angkasa Pura I. Hasilnya adalah data penjualan suatu produk pada CV Jaya Warsa Klaten dapat dimodelkan dengan model ARI(4) dan data penjualan PJP2U dalam negeri pada PT Angakasa Pura I Bandar Udara Internasional Adisutjipto Yogyakarta dapat dimodelkan dengan model ARI(1). Selanjutnya model-model yang diperoleh dapat digunakan untuk memprediksi jumlah penjualan pada CV Jaya Warsa dan juga jumlah penjualan PJP2U dalam negeri pada PT Angakasa Pura I Bandar Udara Internasional Adisutjipto pada periode berikutnya.

(26)

Bab 3 Estimasi Model Runtun Waktu Subset Autoregresif

BAB

3 ESTIMASI MODEL RUNTUN WAKTU

SUBSET AUTOREGRESIF

Runtun waktu (Xt)tZ dikatakan memiliki model Subset

AutoRegresif dengan orde p, dinotasikan sebagai SAR(p), jika (Xt)tZ

memenuhi persamaan stokhastik berikut :

Z t E X Xt _ip _mp_i tmi  t,  ) ( 1  (3.1)

di mana orde _p__N_{dan vektor koefisien}



p



p m p m p p   ( ) ( ) ) ( _, _, 1     .

Di sini, (Et)tZ merupakan suatu barisan peubah acak berharga riil

yang saling bebas dan masing-masing berdistribusi normal dengan mean 0 dan variansi σ2_{. Data kurs mata uang rupiah terhadap euro,} jumlah pendaftaran mobil di suatu negara, jumlah penumpang pesawat udara dan data jumlah penjualan industri merupakan beberapa contoh data riil yang dapat dimodelkan oleh model SAR.

p, (p) dan σ2.

Andaikan s



xp1,xp2,,xn



SAR(p). Jika nilai s0 



x1,x2,,xp



(27)

20 ) , , ( 2 1 exp 2 1 ) , , ( 2 ( ) 1 2 2 / ) ( 2 2 ) ( n p p t p n p _g _t _p p s               _ _   (3.2) di mana ) , , , , (_t _p _q (p) (q) g   _i t mi p m p i t x x _   ( ) 1 

untuk t = p+1, p+2, …, n dengan nilai awal xˆ1 xˆ2  xˆp 0.

p p p p p max max (1 ) C ) p (      

b) Untuk orde p ditentukan terlebih dahulu, vektor koefisien (p)

berdistribusikan normal dengan mean 0 dan variansi 1.

c) Variansi σ2_{berdistribusikan invers gamma dengan parameter α/2} dan β/2 : ) 2 /( exp ) ( ) 2 / ( ) 2 / ( ) , ( 2 (1 /2) 2 2 / 2              

Di sini parameter λ diasumsikan berdistribusi seragam pada interval (0,1), nilai α diambil sama dengan 2 dan parameter β diasumsikan berdistribusi Jeffrey. Sehingga distribusi prior untuk parameter

) , ,

( ( ) 2

1 p  p 

H  dan H2 (,) dapat dinyatakan sebagai : ) , (H1 H2  (H1 H2)(H2) (_p )((p) _p)₍2 _,₎₍₎₍₎₍₎ (3.3)

Menurut Teorema Bayes, maka distribusi a posteriori untuk parameter H1 dan H2 dapat dinyatakan sebagai :

_₍_H _,_H _s₎_

2

1 



s H1



(H1,H2) (3.4)



H1,H2s



tidak dapat diselesaikan secara analitis. Untuk mengatasi masalah tersebut, diusulkan metode Markov Chain Monte Carlo (MCMC).

(28)

Bab 3 Estimasi Model Runtun Waktu Subset Autoregresif 3.3 METODE MCMC



H1,H2s





H2 H1,s





H1H2,s



Untuk mensimulasikan distribusi 



H2 H1,s



dipergunakan

algoritma hibrida. Algoritma hibrida merupakan penggabungan algoritma Reversible Jump Markov Chain Monte Carlo (RJMCMC) ([3]) dan algoritma Gibbs. Algoritma RJMCMC dipergunakan untuk mensimulasikan distribusi 



H1H2,s



. Sedangkan algoritma Gibbs

dipergunakan untuk mensimulasikan distribusi 



H1H2,s



.

Algoritma RJMCMC merupakan rampatan dari algoritma Metropolis-Hastings ([1], [2]).

Estimator yang dihasilkan oleh algoritma RJMCMC dalam dua tahap. Tahap pertama algoritma RJMCMC menghasilkan estimator untuk orde p. Tahap kedua algoritma RJMCMC menghasilkan estimator untuk parameter model SAR dan variansi σ2_yang bersesuaian dengan orde p yang diperoleh pada tahap pertama. Untuk mendapatkan kecepatan dan efisiensi diperlukan suatu algoritma yang dapat menentukan estimator orde p, parameter model SAR dan variansi σ2_{secara bersamaan. Untuk keperluan itu,} diusulkan algoritma Simulated Annealing (SA).

Algoritma SA ([10]) diperoleh dengan menambahkan barisan temperatur T1,...,Tm dalam metode MCMC di atas. Selanjutnya

(29)

22

M(T1),...,M(Tm) yang tidak lagi homogen. Dengan suatu hipotesis tertentu pada T1,...,Tm ([11]) maka M(Tm) akan konvergen menuju suatu nilai yang memaksimumkan distribusi posteriori 



H1,H2s



.

3.5 KESIMPULAN

Uraian di atas, merupakan kajian teori tentang algoritma SA untuk pengidentifikasi orde p, penaksiran vektor koefisien _(p)_dan

(30)

Bab 4 Estimasi Model Runtun Waktu Moving Average

BAB

4 ESTIMASI MODEL RUNTUN WAKTU

MOVING AVERAGE

Runtun waktu (Xt)tZ dikatakan memiliki model MA dengan orde q,

dinotasikan sebagai MA(q), jika (Xt)tZ memenuhi persamaan

stokhastik berikut :

Xt q_j_₁ (_jq)Etj Et, _t_Z (4.1)

di mana orde _p__N_{, vektor koefisien}



q



q q q q  ( ) ( )  1 ) (  _, _,  

dan (Et)tZ merupakan suatu barisan peubah acak berharga riil

yang saling bebas dan masing-masing berdistribusi normal dengan rata-rata 0 dan variansi 2 ([5]). Data jumlah pembangkit tenaga

listrik oleh industri listrik, jumlah pendaftaran mobil di suatu negara, jumlah penumpang pesawat udara dan data jumlah penjualan industri merupakan beberapa contoh data riil yang dapat dimodelkan oleh model MA.

Selanjutnya model MA (Xt)tZ disebut inversibel jika dan

hanya jika persamaan suku banyak



     q 1 j j ) q ( j a 1 ) a (

bernilai nol untuk nilai a di luar lingkaran dengan jari-jari sama dengan satu ([6]).

q, (q), dan 2.

(31)

24

Andaikan s



xq1,xq2,,xn



MA(q). Jika nilai s0 



x1,x2,,xq



kemungkinan dari s dapat ditulis kurang lebih sebagai berikut :







_

_ _







            n 1 q t ) q ( 2 2 2 / ) q n ( 2 2 ) q ( , q , t g 2 1 exp 2 1 , , q s  (4.2) di mana







 

_

_   q 1 j t j ) q ( j t ) q ( eˆ x , q , t g dan



     q 1 j t j ) q ( j t t x eˆ eˆ

untuk t = q+1, q+2, …, n dengan nilai awal eˆ1eˆ2 eˆq 0 ([7]).

Misalkan Iq adalah daerah inversilibite. Dengan menggunakan transformasi





q ) q ( q ) q ( 2 ) q ( 1 ) q ( I , , , : F        

_

_

q q 2 1 ) q ( ) 1 , 1 ( , , ,        (4.3) maka model MA (Xt)tZ inversibel jika dan hanya jika



_q



q

q) ₁_, _, ₍ ₁_,₁₎

(     

  ([14]). Selanjutnya fungsi kemungkinan

dapat ditulis kembali sebagai :







_

_ _



 _



            n 1 q t ) q ( 1 2 2 2 / ) q n ( 2 2 ) q ( ) ( F , q , t g 2 1 exp 2 1 , , q s  (4.4) Penentukan distribusi prior untuk parameter-parameter tersebut di atas adalah sebagai berikut :

a) Orde q berdistribusikan Binomial dengan parameter λ :

q q q q q max max (1 ) C ) q (      

b) Untuk orde q ditentukan terlebih dahulu, vektor koefisien (q)

berdistribusikan seragam pada interval (-1, 1)q_.

c) Variansi 2 berdistribusikan invers gamma dengan parameter

α/2 dan β/2 : ) 2 /( exp ) ( ) 2 / ( ) 2 / ( ) , ( 2 (1 /2) 2 2 / 2              

Di sini parameter λ diasumsikan berdistribusi seragam pada interval (0,1), nilai α diambil sama dengan 2 dan parameter β diasumsikan

(32)

Bab 4 Estimasi Model Runtun Waktu Moving Average berdistribusi Jeffrey. Sehingga distribusi prior untuk parameter

) , ,

( ( ) 2

1 q  q 

H  dan H2 (,) dapat dinyatakan sebagai : _₍_H _,_H ₎_ 2 1 

 

q  



 q

 

 ,



2 ) q ( ₍₎₍₎ (4.5)

_₍_H _,_H _s₎_

2

1 



s H1



(H1,H2) (4.6)



H1,H2s



tidak dapat diselesaikan secara analitis. Untuk mengatasi masalah tersebut, diusulkan metode MCMC.

4.3 METODE MCMC



H1,H2s





H2s





H1,H2s



Algoritma Gibbs digunakan untuk mensimulasikan distribusi



H2s



 dan algoritma hibrida, yang mengabungkan algoritma Reversible Jump Markov Chain Monte Carlo (RJMCMC) ([3]) untuk mensimulasikan parameter (_p,_r(p)) dengan algoritma Gibbs untuk mensimulasikan parameter σ2_{, digunakan untuk mensimulasikan} distribusi 



H1,H2s



. Algoritma RJMCMC merupakan rampatan dari

(33)

26

Estimator yang dihasilkan oleh metode MCMC dalam dua tahap. Tahap pertama adalah estimator dari orde q. Tahap kedua adalah estimator dari parameter model MA dan variansi σ2_yang bersesuaian dengan orde q yang diperoleh pada tahap pertama. Oleh karena itu diusulkan suatu algoritma untuk menentukan estimator orde q, parameter model MA dan variansi σ2_{secara simultan. Untuk} keperluan itu, diadopsi algoritma Simulated Annealing (SA).



H1,H2s



.

4.5 APLIKASI

Sebagai ilustrasi, kita akan menerapkan metode ini untuk mengidentifikasi orde dan menaksir parameter data MA sintesis dan data riil. Studi simulasi ditempuh untuk mengkonfirmasi kinerja dari algoritma SA apakah dapat berkerja dengan baik. Sedangkan studi kasus diberikan untuk memberikan contoh penerapan penelitian dalam memecahkan permasalahan dalam kehidupan sehari-hari.

Baik untuk data MA sintesis maupun data MA riil ini, kita akan menggunakan algoritma SA untuk mengidentifikasi orde dan mengestimasi parameter model MA yang bersesuaiaan. Untuk keperluan itu, algoritma SA dimplementasikan sebanyak 70000 iterasi dengan nilai awal temperatur T0 = 10 kemudian temperatur diturunkan dengan faktor 0,995 hingga mencapai temperatur akhir T1400 = 0,01. Nilai orde q dibatasi maksimum 10 sehingga qmaks = 10.

(34)

Bab 4 Estimasi Model Runtun Waktu Moving Average Data MA Sintesis

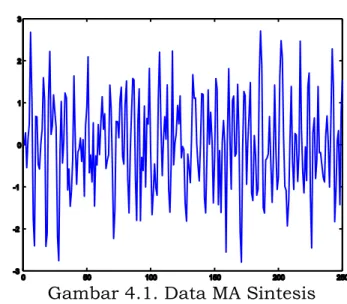
Gambar 4.1 merupakan data MA sintesis yang dibuat menurut persamaan (4.1) di atas dengan menggunakan bahasa pemograman MATLAB, dengan jumlah data n = 250, orde q = 3, ₁(3) 0,5900,

3616 , 0 ) 3 ( 2   , ₃(3) 0,8936 dan σ2 = 0,49.

Gambar 4.1. Data MA Sintesis

Selanjutnya berdasarkan data dalam Gambar 4.1 orde q, parameter model MA, variansi σ2_{akan ditentukan atau lebih tepat akan} ditaksir dengan menggunakan algoritma SA. Penaksir orde, parameter model MA dan variansi σ2_{yang dihasilkan oleh algoritma} SA adalah qˆ3, ˆ₁(3) 0,5700, ˆ₂(3) 0,3623, ˆ₃(3) 0,8811 dan ˆ2=

0,5655.

Data MA Riil

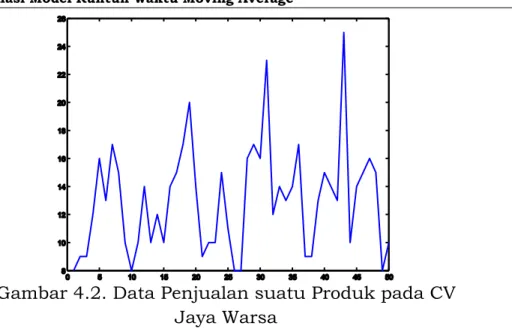
Gambar 4.2 menyajikan data penjualan suatu produk pada CV Jaya Warsa Klaten untuk 50 periode yaitu dari Januari 2002 sampai Pebruari 2006. Dari plot data dapat kita lihat bahwa bahwa data tidak stasioner. Untuk mendapatkan menstasionerkan data, dibuat data baru yang terdiri dari pembedaan data asli antara periode yang berturut-turut.

(35)

28

Gambar 4.2. Data Penjualan suatu Produk pada CV Jaya Warsa

Dengan melakukan pembedaan pertama terhadap data asli pada Gambar 4.2 akan menghasilkan suatu data stasioner yang plotnya ditunjukkan pada Gambar 4.3.

Gambar 4.3. Pembedaan Pertama Data Penjualan suatu Produk pada CV Jaya Warsa.

Seperti untuk kasus data sintesis, berdasarkan data pada Gambar 4.3 orde q, parameter model MA dan varisnsi 2 diestimasi

dengan menggunakan algoritma SA. Hasilnya adalah qˆ2, 6285 , 0 ˆ(2) 1   , ˆ₂(2) 0,2025, dan σ2 = 15,4388.

Data riil kedua disajikan pada Gambar 4.4. Data tersebut merupakan data penjualan Penjualan Jasa Penumpang Pesawat

(36)

Bab 4 Estimasi Model Runtun Waktu Moving Average Udara (PJP2U) dalam negeri pada PT Angakasa Pura I Bandar Udara Internasional Adisutjipto Yogyakarta untuk 55 periode yaitu Januari 2001 sampai Juli 2005. Terlihat jelas pada Gambar 4 bahwa data inipun tidak stasioner.

Gambar 4.4. Data Penjualan PJP2U dalam negeri pada PT Angakasa Pura I.

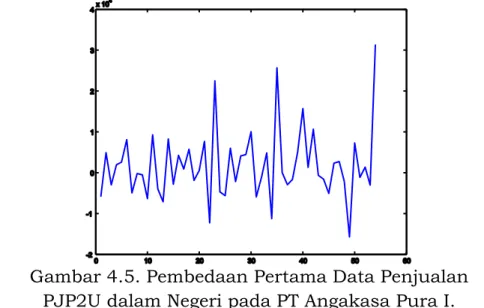
Untuk mendapakan data yang stasioner dilakukan pembedaan pertama dan hasilnya ditunjukkan pada Gambar 4.5.

Gambar 4.5. Pembedaan Pertama Data Penjualan PJP2U dalam Negeri pada PT Angakasa Pura I.

Berdasarkan data pada Gambar 4.5 selanjutnya orde q, parameter model MA dan variansi 2 ditaksir dengan menggunakan

(37)

30

algoritma SA. Hasilnya adalah qˆ1, ˆ₁(1) 0,3301 dan σ2 = 7,0977 x

107_.

4.6 KESIMPULAN

Uraian di atas, merupakan kajian teori tentang algoritma SA dan penerapannya pada identifikasi orde q, penaksiran vektor koefisien (q), dan penaksiran variansi σ2 dari model MA. Dari hasil

simulasi menunjukkan bahwa algoritma SA dapat menaksir parameter-parameter itu dengan baik.

Sebagai implementasi algoritma SA pada dua data riil yang diambil dari CV Jaya Warsa dan PT Angkasa Pura I. Hasilnya adalah data penjualan suatu produk pada CV Jaya Warsa Klaten dapat dimodelkan dengan model IMA(2) dan data penjualan PJP2U dalam negeri pada PT Angakasa Pura I Bandar Udara Internasional Adisutjipto Yogyakarta dapat dimodelkan dengan model IMA(1). Selanjutnya model-model yang diperoleh dapat digunakan untuk memprediksi jumlah penjualan pada CV Jaya Warsa dan juga jumlah penjualan PJP2U dalam negeri pada PT Angakasa Pura I Bandar Udara Internasional Adisutjipto pada periode berikutnya.

(38)

Bab 5 Estimasi Model Runtun Waktu Subset Moving Average

BAB

5 ESTIMASI MODEL RUNTUN WAKTU

SUBSET MOVING AVERAGE

Runtun waktu (Xt)tZ dikatakan memiliki model Subset Moving

Average dengan orde q, dinotasikan sebagai SMA(p,q), jika (Xt)tZ

memenuhi persamaan stokhastik berikut :

Z t E E X _j t kj q k q j t t   _₁ ( )  ,  (5.1)

di mana orde _q__N_{, vektor koefisien dan}



q



q k q k q q   ( ) ( ) ) ( _, _, 1     .

yang saling bebas dan masing-masing berdistribusi normal dengan mean 0 dan variansi σ2_{([5]). Data kurs mata uang rupiah terhadap} euro, jumlah pendaftaran mobil di suatu negara, jumlah penumpang pesawat udara dan data jumlah penjualan industri merupakan beberapa contoh data riil yang dapat dimodelkan oleh model SMA.

q,(q) dan σ2_.

Andaikan s



xq1,xq2,,xn



SARMA(p,q). Jika nilai s0 



x1,x2,,xq



(39)

32 ) , , ( 2 1 exp 2 1 ) , , ( 2 ( ) 1 2 2 / ) ( 2 2 ) ( n q p t q n q _g _t _q q s               _ _   (5.2) di mana ) , , , , (_t _p _q (p) (q) g   _j t kj q k q j t z x  _   ( ) 1 

untuk t = q+1, q+2, …, n dengan nilai awal eˆ1eˆ2 eˆq 0.

a) Orde q berdistribusikan Binomial dengan parameter μ :

q q q q Q max max (1 ) C ) q (      

b) Untuk orde q ditentukan terlebih dahulu, vektor koefisien (q)

c) Variansi σ2_{berdistribusikan invers gamma dengan parameter α/2} dan β/2 : ) 2 /( exp ) ( ) 2 / ( ) 2 / ( ) , ( 2 (1 /2) 2 2 / 2              

Di sini parameter μ diasumsikan berdistribusi seragam pada interval (0,1), nilai α diambil sama dengan 2 dan parameter β diasumsikan berdistribusi Jeffrey. Sehingga distribusi prior untuk parameter

) , ,

( ( ) 2

1 q q 

H  dan H2 (,) dapat dinyatakan sebagai : ) , (H1 H2  (H1 H2)(H2) (_q )((q) _q)₍2 _,₎₍₎₍₎ (5.3)

_₍_H _,_H _s₎_

2

1 



s H1



(H1,H2) (5.4)



H1,H2s



tidak dapat diselesaikan secara analitis. Untuk mengatasi masalah tersebut, diusulkan metode Markov Chain Monte Carlo (MCMC).

(40)

Bab 5 Estimasi Model Runtun Waktu Subset Moving Average 5.3 METODE MCMC



H1,H2s





H2 H1,s





H1H2,s





H2 H1,s



dipergunakan



H1H2,s





H1H2,s



.

Estimator yang dihasilkan oleh algoritma RJMCMC dalam dua tahap. Tahap pertama algoritma RJMCMC menghasilkan estimator untuk orde q. Tahap kedua algoritma RJMCMC menghasilkan estimator untuk parameter model SMA dan variansi σ2_yang bersesuaian dengan orde q yang diperoleh pada tahap pertama. Untuk mendapatkan kecepatan dan efisiensi diperlukan suatu algoritma yang dapat menentukan estimator orde q, parameter model SMA dan variansi σ2_{secara bersamaan. Untuk keperluan itu,} diusulkan algoritma Simulated Annealing (SA).

Algoritma SA ([10]) diperoleh dengan menambahkan barisan temperatur T1,...,Tm dalam metode MCMC di atas. Selanjutnya

(41)

34

M(T1),...,M(Tm) yang tidak lagi homogen. Dengan suatu hipotesis tertentu pada T1,...,Tm ([11]) maka M(Tm) akan konvergen menuju suatu nilai yang memaksimumkan distribusi posteriori 



H1,H2s



.

5.5 KESIMPULAN

Uraian di atas, merupakan kajian teori tentang algoritma SA untuk pengidentifikasi orde q, penaksiran vektor koefisien (q), dan

(42)

Bab 6 Estimasi Model Runtun Waktu Subset Autoregresif Moving Average

BAB

6 ESTIMASI MODEL RUNTUN WAKTU

SUBSET AUTOREGRESIF MOVING

AVERAGE

Runtun waktu (Xt)tZ dikatakan memiliki model Subset

AutoRegresif Moving Average dengan orde p dan q, dinotasikan sebagai SARMA(p,q), jika (Xt)tZ memenuhi persamaan stokhastik

berikut : Z t E E X X j j i i t k q k q j t m t p m p i t _₁ ( )    _₁ ( )  ,  (6.1)

di mana orde _p_,_q__N_{, vektor koefisien}



p



p m p m p p   ( ) ( ) ) ( _, _, 1     , dan



q



q k q k q q   ( ) ( ) ) ( _, _, 1     .

yang saling bebas dan masing-masing berdistribusi normal dengan mean 0 dan variansi σ2_{([5]). Data kurs mata uang rupiah terhadap} euro, jumlah pendaftaran mobil di suatu negara, jumlah penumpang pesawat udara dan data jumlah penjualan industri merupakan beberapa contoh data riil yang dapat dimodelkan oleh model SARMA. Berdasarkan data xt (t = 1, 2, …, n), selanjutnya kita akan berusaha untuk menaksir harga

p, q, (p),(q) dan σ2_.

(43)

36

Andaikan s



xpq1,xpq2,,xn



adalah suatu realisasi dari

model SARMA(p,q). Jika nilai s0 



x1,x2,,xpq



diketahui, maka

fungsi kemungkinan dari s dapat ditulis kurang lebih sebagai berikut :







_

___



 



             n 1 q p t ) q ( ) p ( 2 2 2 / ) p n ( 2 2 ) Q ( ) p ( _g _t_,_p_,_q_, _, 2 1 exp 2 1 , , , q , p s  (6.2) di mana ) , , , , (_t _p _q (p) (q) g   _i i _j t kj q k q j m t p m p i t x z x _   _   ( ) 1 ) ( 1  

untuk t = p+q+1, p+q+2, …, n dengan nilai awal xˆ1 xˆ2  xˆpq 0

(Shaarawy et al. [16]).

p p p p p max max (1 ) C ) p (      

b) Orde q berdistribusikan Binomial dengan parameter μ :

q q q q Q max max (1 ) C ) q (      

c) Untuk orde p ditentukan terlebih dahulu, vektor koefisien (p)

d) Untuk orde q ditentukan terlebih dahulu, vektor koefisien (q)

e) Variansi σ2_{berdistribusikan invers gamma dengan parameter α/2} dan β/2 : ) 2 /( exp ) ( ) 2 / ( ) 2 / ( ) , ( 2 (1 /2) 2 2 / 2 _ __ _           

Di sini parameter λ dan μ diasumsikan berdistribusi seragam pada interval (0,1), nilai α diambil sama dengan 2 dan parameter β diasumsikan berdistribusi Jeffrey. Sehingga distribusi prior untuk parameter ( , , ( ), ( ), 2)

1 p q p  q 

H  dan H2 (,,) dapat dinyatakan sebagai : ) , (H1 H2  (H1 H2)(H2)

(44)

Bab 6 Estimasi Model Runtun Waktu Subset Autoregresif Moving Average (_p )(_q )((p) _p)((q) _q)₍2 _,₎₍₎₍₎₍₎ (6.3)

_₍_H _,_H _s₎_

2

1 



s H1



(H1,H2) (6.4)



H1,H2s



tidak dapat diselesaikan secara analitis. Untuk mengatasi masalah tersebut, diusulkan metode Markov Chain Monte Carlo (MCMC). 6.3 METODE MCMC



H1,H2s





H2 H1,s





H1H2,s





H2 H1,s



dipergunakan



H1H2,s





H1H2,s



.

Estimator yang dihasilkan oleh algoritma RJMCMC dalam dua tahap. Tahap pertama algoritma RJMCMC menghasilkan estimator untuk orde p dan q. Tahap kedua algoritma RJMCMC menghasilkan

(45)

38

estimator untuk parameter model SARMA dan variansi σ2_yang bersesuaian dengan orde p dan q yang diperoleh pada tahap pertama. Untuk mendapatkan kecepatan dan efisiensi diperlukan suatu algoritma yang dapat menentukan estimator orde p dan q, parameter model SARMA dan variansi σ2_{secara bersamaan. Untuk} keperluan itu, diusulkan algoritma Simulated Annealing (SA).



H1,H2s



.

6.5 KESIMPULAN

Uraian di atas, merupakan kajian teori tentang algoritma SA untuk pengidentifikasi orde p dan q, penaksiran vektor koefisien

) (p