Lucio Canoica MSc. CE ETHZ Lucio Canoica MSc. CE ETHZ
Memahmi
Memahmi
ME
Nl
ME
Nl
TEKNIK 1
TEKNIK 1
EdisiEdisi Ke-1,Ke-1, TahunTahun 19911991
.., , .. ��
..
..-
-.
. �··
�·· ..
��
··.. :_:_
\�:\�:�·�·(
(
penerbitpenerbit
AGK
AGK
bandungbandungJAN MERDEK NO.
JAN MERDEK NO. 66 TELP 43913TELP 43913
--
447575 OO BOX 353BOX 353/80 B/80 BANDUANDUNG NG INDONESIAINDONESIA
=
=..]
]·
· �;:a-
�;:a-0
0
l
Lucio Canoica MSc. CE ETHZ Lucio Canoica MSc. CE ETHZ
Memahmi
Memahmi
ME
Nl
ME
Nl
TEKNIK 1
TEKNIK 1
EdisiEdisi Ke-1,Ke-1, TahunTahun 19911991
.., , .. ��
..
..-
-.
. �··
�·· ..
��
··.. :_:_
\�:\�:�·�·(
(
penerbitpenerbit
AGK
AGK
bandungbandungJAN MERDEK NO.
JAN MERDEK NO. 66 TELP 43913TELP 43913
--
447575 OO BOX 353BOX 353/80 B/80 BANDUANDUNG NG INDONESIAINDONESIA
=
=..]
]·
· �;:a-
�;:a-0
0
l
Hak cipta
Hak cipta
©©
dlndung Undang-undangdlndung Undang-undang Hak Penerbtan pada Penerbt ANGKASA Hak Penerbtan pada Penerbt ANGKASAAnggota IKAP Anggota IKAP
Cetakan ke (angk erkhr) Cetakan ke (angk erkhr)
ISBN
ISBN
99
99
99 44 -964 -
99 44 -964 -
44 -96 -
44 -96 -
ilarang memperbanak penerbtan ni dan/atau menebarkan
ilarang memperbanak penerbtan ni dan/atau menebarkan
berupa etakan fotokopi, mkrofim atau dalam bentuk
berupa etakan fotokopi, mkrofim atau dalam bentuk
apa pun, tanpa izn tertui dari penerbit
apa pun, tanpa izn tertui dari penerbit
M typesetting, Lay-out Flm Pencetakan M typesetting, Lay-out Flm Pencetakan
oleh Percetakan Ofset AGKASA oleh Percetakan Ofset AGKASA
Jl Kiaraondong o. Jl Kiaraondong o.
Telp
ENGN
Buku ini meupakan hasil pengalaman saya sbagai insinyu knsulan dan pengaa selama ahun. Akan eapi dngan unuk menulisnya munul dai kegiaan saya yang eakhi seagai enaa ahli pada Pyek Pendidikan Plieknik di Indnesia Sasaan pyek ini adalah menyiakan paa pesinal yang ea kaiannya dengan pakek pembangunan aena alasanalasan inilah saya elah memilih bidangidang yang dibuuhan leh paa insiny dalam kegiaannya sehaihai dan bukan halhal yang lebih ehubungan dengan peneliian dan pengemangan ilmu
Penekanan uku ini dileakkan pada pemahaman aas apa yang eadi dalam pakek dan agai mana kenyaaan esebu dapa isedehanakan leh seang insinyu ag ia dapa bekea dengan aaaa yang sedehana aman dan eknmis Pendekaan yang menyangku pemahaman dasa gealageala isika ini dipelukan uga agi pekeaanpekeaan yang lebih anggih yang daa inpu unuk ehiungan kmpuenya haus dipilih leh endein edakan medemede yang sedehana namun ukup elii Hasil ehiunganpehiungan dipelukan uga aga ia daa meme iksa keluaan pehiungan kmue leh kaena kemungkinan adanya kekuanga emunyi pada peangka lunaknya. Pada akhinya yang eanggung awa aas hasilhasilnya adaah pen desain ukan kmpue!
Di saming iu pses penguasaan pengeahuan bau dalam pendidik hauslah eak ada apa yang elah dikeahui leh paa siswa dan pengenaan unsuunsu bau haus nng dengan menghuungkannya dengan masalah dan lambanglamang yang sedehana la
pening agi siswa aena iulah anyak digunakan gamba unuk menelaskan ei sa gama mengandung inmasi yang huungannya u dengan yang lain dapa epa dipahamiHaaan saya adalah melalui pemahaman yang elas aas suau geala keeayaan dii paa siswa akan meningka sehingga ia akan eani menghadai apa yang eadi dan dapa memeahkan masah masalahnya seaa mandii dan eanggung awab
Saya sanga beeima kasih kepada
nny Sewandi Pemimin yek Pendidikan Pliek nik yang elah menyeuui naskah ini dieikan Hal ini membukikan adanya usaha pengembangan di bidang pendidikan eknik yang dialankan leh yek yang sellu diingkakan dan disemu nakanSaya pun menguakan eima kasih aas segala nasiha dan saansan yang dieikan sehingga naskah ini dapa sealan dengan uuan pyek esebu
Selain iu saya ehuang bdi kepada
Ds Aan Eendi yang elah membanu seaa sak sama pesiapan penyusunan naskah ii sea aas sumangannya sehingga isi uku ini sesai dengan ukuanukuan dan kelaiman yang belaku saa ini di Indnesia aena naskah ini disusun dalam waku yang singka dan ebaas dapa a eadi kekuangankekuangan Saya akan eeima kasih kepada paa pemaa yang dapa menunukkannya keada syaI ui annia Via emm 3
AASA STRUTUR
se mmSuku ialah himpua elemeeleme baha uuk meeska bebabeba ke aah a a ma
Sebaang phon adalah sbah kr aam
i mudah utuk meealiya
Sba <ga aaah :.;1J
ika beba lebih besa kia memluka suau suku ya lebih kua.
b
Kayika bahaya lebih kua kia memlu ka eleme suku ya lebih keil.
ika kia ii lebih am kia meme luka lebih bayak baha
eau ai beuk elemeeleme ya hus diua ka meu eilaku sifasifa bahayasmbngn
tergantung dari bentuk sambungan di tara elemenelemen.
tergantung dari maam tumpuan g dipakaimua hal di atas harus dipertimbangkan untuk mengirangirakan bahwa struktur tersebut aman Ada beberapa ara untuk menghimpun elemenlemen pemikul beban
Contoh
;
bentuk embatan ang berbedabeda ang mentasi sungaiadi, struktur ng berbeda dapat digunakan ika pemindahan/penerusan beban lebih langsung maka struktur akan lebih ekonomis bahan ang digunakn sedikit).
ngsng ngsng
Persoalanpersoalan sebelum kita menelesaikan penganalisisan suatu struktur
•
Ben harus iseerhanakan sesuai dengan peraturanContoh Bean berguna untuk orang dan perkakas rumah tangga p
=
200 kg/m •
Struktur harus disederhanakan dengan menghilangkan/mengabaikan ior ffcs kemungkinanperubahan/deformasi harus diperhitungkan sejauh mngkn )
Smbngn p/jpi ( ppn p mpn) Smbngn Pin/ps (bbs bp p mpn = ban smbngn ps eban F=
•
Peilaku ahan haus disedehanakan seagai ontoh pengandaianpekiaan ahwa deomasi/ peuahan entuk adalah seanding dengan enn
pnndn
/
nny- beban yang di jinkan
pa ya pr dipriksa
?
Bedasakan penedehanan in enginee menelesaikan pehitunganna, dan memeiksa ahwa
•
Stuktu dalam keseimangan tidak egeak) Hal ini tejadi ketika ean total ang ekeja diimangi oleh gaa eaksi pada tumpuan•
Stuktu stabilHal ini tejadi jika bebanbean ang bekeja menghasilkan peubahan bentukdeomasi ang tidak menebabkan stuktu untuh
•
Stuktu mempunai kekuatan ang ukup untuk memikul eban tanpa patah•
Stuktu mempunai kekakun ang ukup begitu juga bahwa deomasi tidak membuat stuktu tak begunabagai ontoh kosenkosen pintu sepeti gamba di samping.
12
Bean yang berja pada suatu strukturBo , And dp mnp pin mn S id il Tl mdh dinon And dp mnp pin
Tedapat bebeapa maam be yg eeda ang ekea pada suatu stuktu
•
Bean mati dead los sepeti eat sendii stuktu dan beat bagagian stuktu g
G) yng tetap sepeti lantai dan seagaina. Bean ini besiat•
Beba hdup (lie loads) p P)•
Beba ag (wid loads) (w
•
Beba gempa (eahquake loads)•
Beba khusus (speial loads)Besifa idak eap da dapa begeak sepei oag; pe kakas umah agga dalam suau uaga
Beba ii adalah peedehaaa ag ama dai keaaa sebea.
Beba ii juga hasil peedehaaa dai keaaa ag sebeaa.
Hasil suau gempa (damik) digai oleh suau gaa khusus (kodisi/keadaa sais ).
sepei peuua (selemes), eek hemal susu (shi kage)
Semua beba ii meupaka peedehaaa keaaa sehaihai
Beba dapa epusa (G P da F aau beba ebagi meaa (g, p; q) iap mee pajag aau mee
pesegi
Kia dapa mejumlahka bebabeba ag bebeda ke dalam suau kombiasi, ialah Pembebaa eap g p
=
Pembebaa semeaa g +
w Pembebaa khususSebagai beba kombiasi ia mempuai kemugkia ag bebeda uuk ejadi Peauapeau meghedaki fako keamaa ag bebeda uuk kombiasi ag bebeda pula.
Kombiasi ag seig eadi
ako keamaa omal/biasa.•
Komb iasi ag jaag eadi
fako keamaa dipekeiluk keeaga lebih laju eag pembebaa, liha Peaua Pembebaa doesia uuk Gedug 198'
II AYAAYA (K) DAN RAKSIRAKSI (R)
2.1
Gy-gy Aksi, Reksi dn MomenSbah gaa ang bka pada sa bnda disb ks dan mnbabkan bnda bgak.
ika kia ingin bnda/obk sb idak bgak dalam kadaan simbang) kia has mmpnai sa gaa pnahan ang disb y rks ang bka pada bnda sb ang mnahn bnda rsb ap pada posisina
Bsaa gaa aksi sama dngan gaa ang bkja aksi) api blawanan ah Kia bikan anda + dan - nk ang lainna
Kia dapa mngaakan gaagaa ng bkja
pada sa bnda dalam k sb jk:
K
=
R aaK + R
=
aam bnk mm dinaakan
gaagaa
=
ni bai idak ada pbahan posisi displamn)
¢
'
Gy
c
K
Pbahn lak/mpa/posisi displamn) sa bnda ang disbabkan olh sa gaa disb rss
Sah gaa digambakan saa gafis bpa spoong gas ls bjng anda panah. ang nnjkkan aah kja gaa
Panjang gais sb mlkiskan bsa gaa. Gaa ang bkja ada sa bnda pada sa iik disb kp.
Gais ang diaik mlali iik angkap ini arahna sama dngan arah gaa dan disb rs k rj y
Sa bsaan ng digamakan bsa dan aana disb vk or
Sbah gaa dapa dipindahkan spanjang gais kjana anpa mmpngahi ksimbangan bn da vo
KN
Gy n')
jbuah benda tida hanya dapat meneruan ebuah gaya ia dapat uga berputar
ita ebut Momen M) yg merupaan hail peraian gaya dan ara
d
=
DefiniiGaya yang beera 2 tetapi aranya d, e hingga hailnya 2). d)
=
MHailnya ama dengan M
Jia in gin benda tida berputar, maa aibat total dari momen yang beea pada benda ter ebut aru nol eeimbangan momenmomen) Dalam bentu umum digambaran
M
=
0 ini berarti tida ada perputaranContoh baut
pptaan
Conoh piulan
K
M d 0 2d
=
0buah momen dtandai berupa uatu gari lengung dengan uungnya berupa ana panah
yang menunuan arah perputaran dan bearnya M
M Dua gaya eaar, ama bear tetapi arahnya berlawanan dengan ara
z =
2d diebut momen opel couple).edua gaya terebut bila dimomenan terhadap titi P aan menghailan M = d
d=
K Momen opel mempunai ifat yang huu Momen opel tetap ama ber dan arah putarannya) ia ita pindah titi acuannya dari P e P
K
L
2.2.
Ksmbngn Sutu BndJa t mengngnan uatu benda tda bergera, in berart bahwa benda terbut dalam eembangan.
ta dapat mengataannya bahwa
•
Ia haru tda bergera epanjang dua arah yang berbeda
emngnn pgn
•
Ia haru tda berputar ta dapat menyataan yaratyarat n dengan ada mmnya 1 2 0 0 M
0Cotoh
ontrol eembanganarah horzontal arah ertal
eadaan embang a V = 0
�
dengan V
+1
RA + R8 50
0 1 ) = 0
�
tdak ada gaya horzontal
M
0 � denganM
+RA· 4 5 0 2 0
dar 2)
�
RA 25 1)�
Rs 25Ja RA = R8 = 25 trtu dalam eadaan embang ta dapat uga mengetahu bahwa :
. . . 2 )
g g Dua onep daar ini lebih bai digambaran dengan ebuah peroban ang dibua dengan a li mlalui ereanerean pada mana bebanbeban diiaan
E=6 agian R=6 agian 1 agan agian 2 ia ebu : , = Gaya omponen R Gayareulan E Gaya penyeimbang
ia liha di perobaan bahwa = 2 dan a dapa mengaaan
•
Dua buah gaya d K2 dapa digaioeh ebuah gaya R yang beera pada i yang ama (= gaya ra).ia dapa memeria bahwa gaya R ni adalah diagona dari aaran genang gaya yang dibenu oeh gayagaya dan K2 ebaga ii aaran genang gaya
Ini diebu h jajara gjag gaya
Yang memperhaan hubungan diara dua buah gaya dan reulan nya
•
Sebuah Gaya E dapa ibagi oleh gayagaya dan yang beera pada i yangama
ia dapa melha bahwa emua gayagaa ini membenu uau poygon eruup diebu
poygo gaya
gr Jia ia ingin menggani ebuah gay dengan dua buah gaa x dan yang beera dalam arah
x
dan y dan aing ega luru au dengan lainnya, ia dapa meneleaiannya dengan aar genang gaya pallelogram law)G ataa besya da daam arah
K
l
(
K
aa d atas dsebut graa sebuah gaya menad dua buah gaya komponen
os som
etap a ta mempun gayagaya x dan y ta dapat enggantnya dengan satu gaya penggat
atau gaya resultan
ara d atas dsebut ys ebuah gaya dar dua buah komponen gaya
aa
serng dpakai untuk menggnt sebuah gaya dengan gayagaya omponen x dan y enga cara d atas kta dapat menyelesaan salsoal dengan lebh mudah2
suta r gay yg ra a st erhatan, bahwa gaya dapat dpndahan sepanang gars keranya, tanpa mempengaruh ese mbangan benda dmana gaya tersebut beera
engan sfat d atas kta dapa menyelesakan beberapa persoalan mencar resultan beberapa gaya
Cooh 1
Ddg paha aah ronong)entuan besarnya resultan R k a gaya yang beera
erat sendr GTenan tanah E
a) Pysaa scara grafs Gambar dengan sala gaya dan skala panang)
eyelesaan dengan cara aaran genang gaya
oygon gy
langahlagah enyelesaan
G + E � R
R + G � R
Reultan R ecaa lengap dnyataan dengan
beya gaya da polygon gaya
ga ea gaya da enampang 1 bPysaia cara aaiisGaya rsa a i sa ayaaya vrika da ayaaya horisoa ya b k rja pada sa bda RH H = Et + E2
}
R =
R � = Gl + G2 tg +R
R
R
4,
H
Mo ya bka akiba aya Rsa dapa ai o ya bkrja pada sa bda akiba ayaaya G da
Momen abat R MA
MA
Momen abat dan H
MAV + �MAH MA + � M tandaMt
+ MA=R
A MA = GX1 + G2
- EY1 - E2 Y2 lanutnya . . )
R
n untu mnntuan leta gaya eultant.Coh Bbabba koo pada podasi tntuan leta dan beya gaya eultant R a
gaya yang bea P
P2 danP 3•Mabat + dan H �MAV + � MAH
= 0
MRA
Tt A dpih embaang 2a Pysaia cara aaiis
R = P1 + P2 +P3 RH � H= 0
a etak R dapat detahui dengan
R . X =
Mf
= P X PX P.X2.b .Pysa scara af untuk anda yang tertarik
esaya gaya resultant didapat dengan menumlahkan ektorektor gaya.
tak gaya resultan dapat dicari dengan menggunakan cara aaran genang gaya.
Gayagaya P , P dan adalah seaar dan garis keranya tidak saing berpotongan, maka diperlukan perubahan pada cara di atas.
ita ganti tiaptiap gaya P dengan dua buah gaya komponen yang bertemu di titik
titik kutub yan dipiih sembarang Pengaruh yang ditimbul kannya terhadap benda akan sama.Gayagaya komponen
ihimpun dalam sebuahpolygon gaya
s bayak
bata
Gaya komponen 2 dari P
dan P serta gaya komponen dari P dan P dalam keseimbangan
Hanya gaya komponen dan 4 tidak dalam keseimbangan.
ita dapat mengganti dua komponen gaya tersebut dengan
R.
R mempunyai pengaruh yang sama pada benda sebagai halnya
+ P + P•
Catata Untuk menentukan R kita memerlukan gambar polygon gaya dan segi banyak batang
Penggambaran harus dengan skala gaya dan skala pang
a pnjn
eda dengan skala gaya.III . DUA PANDANGAN TERHADAP STRUKTUR
31 Stkt Seaga Sat esata a Bagaga Sea Stkt
ita harus selau epertibangkan suatu struktur dari dua sudut panang ini Kita anggap bahwa struktur adalahkaku (tidak epunyai deforasi internal
Dala kenyataannya, kita lhat sebuah struktur mepunyai deforasi inteal tetapi angat kecil dibandingkan dengan diensi/ukur struktur. cara uu deforasi in tidak ep1a ruhi dala keseibangan sebuah struktur
32 Stktr Seaga Sat esata
Mengingat sruktur sebagai sebuah benda kaku (rigid body), maka ia daam k eseimba ngan jika struk tur ditahan tetap di tempatnya dengan tumpuan-tumpuan
Struktur harus dapa enahan gerakan ataupun perputaran Kita dapat memilih bentukbentuk tumpuan yang berbeda untuk sebuah struktur Karenanya pergerakan/perputaran dapat ditahan, dan struktur tetap dalam keeimbangan.
Gerakangerakn dari sebuah benda kaku dapat berupa
Pegeseran vertikal S Pergeseran horisontal S Putaran ' erputar pada suatu titik P
* ala rangka enahan gerakan-gerakan ni, kita perlukan gayagaya reaktif seaga berikut:
Rv menghaangi S RH me nghaangi Sh
* Dalam praktek kita ketahu ini acamaca tumpuan
Simbo: Nama: Tumpuan sendi/ sederhana (simple supot) M P . '0 M menghaangi ' Haanganhangan SA 0 SAH = 0
Ry
Tumpuan r
Tumpuan kabe
Tumpuan jep i
8
BV 8
BV 8
V 8
<
Seaang ia haus melengapi suu yang dipeimbangan sebagai benda au - dengan umpuanumpuan sehingga ia ida dapa begea ( seimbangSebagai cn
nda dengan mudah dapa memeisa bahwa benda au ini ida dapa begea ia dalam
eseimbangan.
ai hal di aas ia dapaan
dapa uga diulisan sebagai dapa ua diulisan sebagai dapa uga diulisan sebagai
seimbang =
H = M=
elah ia eahui bahwa dengan syaasyaa esembangan in dimungnan menghiung gaya aya easi dai suau suu
Jia unu suau suu mempunya cukup gayagaya perawanan yang dihasilan oleh
umpuanumpuan dalam eadaan seimbang maa ia bebiaa masalah sisem sais er enu.
iga onoh yang elah dibiaaan di aas ialah sisemsisem sais eenu
engan peolongan iga syaa eseimbangan di aas dimunginan menghiung 3 (iga gaya
gaya easi yang belum dieah
a unu seah benda au ia dapaan ebi banyak gayagaya perawanan daripada
juma minimumnya 3 yang dpeluan dalam eadaan seimbang maa ia bebiaa
masalahsisem sais ak enu
tRv
Rv
Cono
(P)
*
Sais eenu Benda au Tiga gaya easi*
*
Sais eenuBenda a au abel
Contocono iung gayagaya easi yang dipeluan dengan menggunaan syaasyaa
eseimbangan di bawah
V =
=
M =
Pilihan +
+
Cn:Peama ali ia pilih aah posiip unu
RA; RA RB
dan unuM).
Jia seelah pehiungan dlauan didapa hasil dengan da+
maa aah yang dpilih bena Jia andya beaiR
beeja dengan aah yang belawanan dengan aah yang dipilih adi haus diba aahnyaConto no 1
V =
RA + RB ' =
1 )
=
RA =
)
MA =
RB 4 =
3a aauRA· 4 =
MB =
3b ) ai 3b ai )
RA
ai
)
aau 3aRB =
Cono n
V = +
V =
V =
= +
=
=
,
MA =
o(
+M =
M =
aau MB =
(
+
M V =
M = K )
2 •t
reebdy (dgram benda bebas
Feeod alah ebuah benda kaku dengan gayagaya yang bekerja padanya dan dengan gaygaya yang dperlukan untuk mendapatkan kesembangan.
onoh
ayagaya luar
feebod
Gaagaa ang beeja pada uau uu, emau gaagaa ea pda umpuan debu gaagaa lua Ka dapa mengaaan bahwa gayagaya luar yang bekerja pada truktur terebut arus dalam k esemb angan
33 Bagaagan Seah S
elah mendapaan emua gaagaa lua eaang a ngn mengeahu bagamana gaagaa ddstrbuskan le mereka sendr e dalam baganbagan g bebeda aau elemenelemen ebua
uu
Ka pembangan uu dbag dalam baganbagan aau elemenelemen unu menenuan gaagaa ang beeja d bagan dalam uu pada elemen ee bu
ayagaya dalam
Gaagaa ang beeja d bagan dalam sebua struktur atau pada elemenelemen ersebut d sebut gayagaya dalam
Elemenlemen ebuah uu au cuup ua unu menahan gaagaa dalam ang beeja ehngga uu aman
nsp dasar untuk mengtungmenentukan gayagaya dalam
ka sebua benda kaku dalam kesembangan maka taptap bagan darpadana arus dala kesembangan uga ja ebuah benda au da begea maa apap bagan hau da
beea juga
Unu menjaga uau bagan da ebuah benda au eap pada pona a hau memauan bebeapa gaa
M
, N ang ecaa naa dbean ole bagan lanna ha cono d bawa Gaagaa ndsebut gayagaya dalam.Freebd erluasan onep
Satu bagan da sebua benda kaku dengan gaagaa ang beeja padana an gaagaa daam ang dpeluan unu mendapaan eembangan debu ebua feebod Kadangadang a bemanfaa unu mengambl ebua feebod ang elampau ecl/pende panjangna ehngga dapa dbaangan
Cnt
Sebuah eebod dapa beupa eluuh benda ebagan aau ebuah dapadana
Struktur dalam
Mx
Gaya dala peluan unu eseimbangan bagan - X Gaya dalam dpeluan unu esembangan X - BL
Gaya gese gaya
ang dalamN
Gaya nomal dalam M Momen lenu dalam erjanjian andaUnu gayagaya dalam sepei yang dipeihaan dalam gamba d aas ia bei anda
Peanian n uga belau unu gayagaya lua sepei dalam gambaPehaan bahwa gayagaya daam ada bagian kiri dan ada bagian kanan bekerja daam ara yang berawanan. Karenanya masingmasing ing mengiangkan membua seimbang) sau sama ain. (onoh M sembang dengan M anan
Jia ia eapan syaasyaa eseimbangan maa ia dapaan
*
Unu feebody X sebeah
0
5 = 0
= 5
0
N x - 5 0
N
5
Mx
0
M51
0
M
5
Unu feebody X B sebelah ananV
0
105
0
L
5
2 H 0
N 5
0
N
5
Mx= O
M 10153
M
5
Maa gayagaya dalam elah didapaanKia dapa menenuan gayagaya dalam pada i yang lain dengan membua gamba aan feebody lannya sesua aa yang elah diuaan
Gaya gese dalamgaya lnang L menaan gerakan uncuran bagan reaifehadap bagian anan
Gaya ema bagan
Momen dalam menaan eru aan bagan i ehadap bagan anan
!0
i5
nomal dalamN me naan erindaan elaif ehadap bagian anan
Perjanjian tanda poitip untuk gayagaya yang bekea pada Freebody
Kita perkenalkan gaya-gaya dalam dengan perjanian tanda positip.
Jika setelah perhitungan kita dapatkan suatu nilai negatif (tanda ) ini berarti gaya dalam yang benar mempunyai arah yang berlawanan.
ika setelh perhitungan kita dapatkan suatu nilai positip (tanda +) maka arah gaya dalam adalah ama seperti anggapan semula.
Ditribui gayagaa dalam
Variasi gaya-gaya dalam, dalam s ebuah struk tur dapat k ita temui dengan me mba struktur erebut menjadi freebodyfree body.
Conth : No 1
langkah pertama: Tentukan besarnya gayagaya reaksi dengan meninjau eebody.
RAH A 3 Dari 3) - R sv 5 2) RAH 0 1) RAv 5 B t + RAv + R sv-10 + RAH 0 l
M
= 0 � + R8v 6 -103 0 . 1) 0 2) 0 .... 3)* langkah kedua Tentukan distribusi gayagaya dalam denganmeninjau freebody yang berbeda
Freebody Freebody
{Lx
-5Mx
0 0 0 Lx = 5 M x = 0 �E = li
3 3 lV 0 lH= 0 1 Iaa x x a au a ta
Lx 5 Mx 5 3 0 0{
Lx - 5 = 0 Mx 5 . 3 = 0
Lx 5 + 10 M x 1 5 0 0
Lx + 10 5 = 0 Mx 5 3 0
Lx + 5 = 0 Mx 5 3 = 0 5 15 5 15 5 15 -5 15 -5 1 5{
Lx + 5 Mx + 0 0 0 5= RB v 0* langkah ketiga : Penggambaan diagram distribusi gaya geser(gaya lntang dan Momen
Diagam Lx
Diaam Mx
Contoh no. 2
Sisim dan pembebanan
* langka h pertama Dapatkan eaksi-eaksi tumpuan dengan meninjau fee body V = 0 + A v + RB v 106 H = 0 - + RA + 0 MA = 0
J
+ RB v·6 06 dai 3 RB v 30 1) RA v 3C 2 ) RA H 0 0 0 0 . . 1 . . . . . 2 ) . . . . . 3 )�c
_-ls jt
j
\1
*
aa a: Hitung distribusi gay-gaya dalam dengan mennjau freebody yang berbeda
�cao.z :
{
Lx
3
Mx
11 3
=
1.1
3.1
=
1.2 3
�
Mx
1.
3.2
Lx
1.33
Mx
1.3.
i
3.3
=
Lx =
Mx=
Lx =
Mx=
Lx =
Mx=
Lx =
Mx=
*
angk a k tga :Peggban dsbus gaya gesegy itag d Moen.
*
Dagam Lx
*
Dagm Mx
3
2
2
1
4
45Berbentuk parabola berderajat dua
RA
dengan cr yg sma
Untu bgan sebeah an daat dhtung sendr
l
\·) :
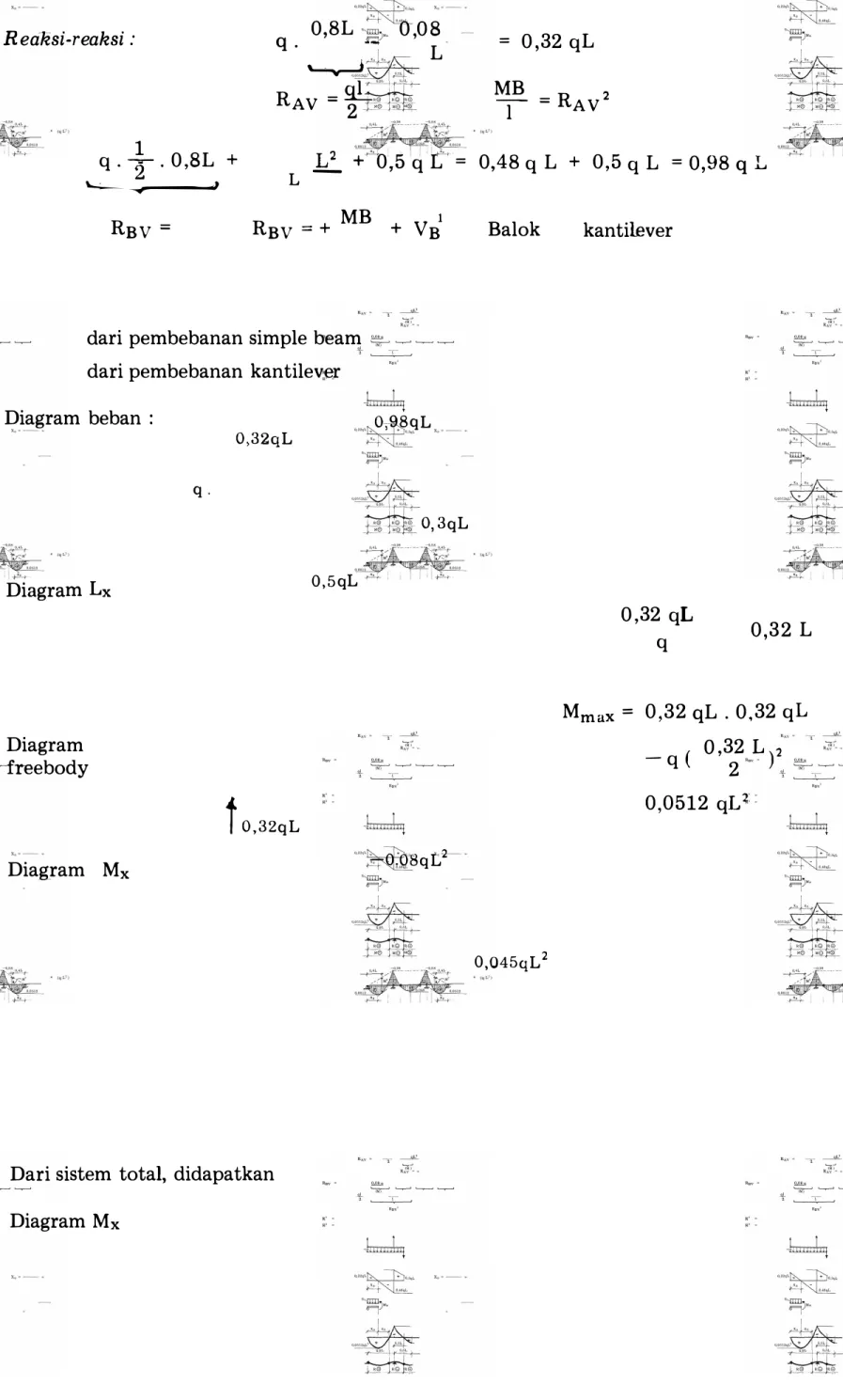
Huug tr e, g litg d mome etur di dm struktur.ri ooh biku ii kia aka myimpuka hubuga rsbu Kia iau f body dai bagia balok di bawah ii
Sisim da b ba
F body
Gaya dalam pada po x adalah sama dga gaya dalam pada po x diambah �
Jika kia umuska kadaa simbag dai f body sbu kia aka mmpoh
H (L x + �L) + q .� -L " 0 - �L = -q � - �Q (N
�N ) N �N = . . . 1 �X�
(M- + �M) M- L.�x+
q
.�x."
�M L q
da dga p 1 L .+
�
da ika kia ijau diagam gaya iag, kia iha bawa
+ , bada poip
L.
�
ua 12 x)�X
�L.
= ua 1,2,3 bada gaipmaka
+ +
api uas dai apsum yag sama uga dapa dipolh dai
Lratarata �x u 1, 3, x) , maka dapa kia ulika
�M Lratarata �X
=
uas L . . . . . 2 ) Hubungn 1Pubaha gaya iag/gsr �L spaag �x adaah sama dga bba
q �
bka spaag�
yag sama*
Jika idak ada bba spaag�
L kosa kaa �L = *
Jika bba rpusa P dikaka di aas L bubah saa mdadak , �L =q .�
*
Jika bba maaq
dikraka di aas�
L bupa gais luus , �L q .�
H
Hbaba 22
L
L
XX
==uas
uas L
L bat
bat bahwa
bahwa
ubahan
ubahan momn
momn AM sanjang
AM sanjang A
A adaah
adaah sama dngan
sama dngan uas
uas dagam Ls
dagam Lsanjang
anjang
yang sama
yang sama
**
**
**
Ja
Ja L onstan
L onstan sanjang
sanjang
M muaan gas uus
M muaan gas uus
(ana
(ana uas
uas L,
L, , bubah
, bubah scaa
scaa n)
n)
Ja
Ja L
L n
n sanjang
sanjang
M muaan gas ngung ngung aaboa)
M muaan gas ngung ngung aaboa)
(n
(na
a uas
uas L,
L, ,
, bubah
bubah tda
tda scaa
scaa n
n ))
Ja L
Ja L
bubah scaa mndada
bubah scaa mndada , AL
, AL
==
M muaan gas atah
M muaan gas atah
Da hubungan
Da hubungan
22ta
ta juga
juga daat
daat mhat
mhat bahwa,
bahwa, ja
ja LL
= = 00
ma
maa AM
a AM
= = 00omn tda mngaam
omn tda mngaam ubahan ana tah mnca
nyataan
ubahan ana tah mncaa haga masmum dan bh
a haga masmum dan bh ba ta
ba ta
nyataan sbaga
sbaga
Hba
Hba 33 = = 00
MM
==MM
Hubu
Hubunganhubungan
nganhubungan
Stah mnghtung gayagaya as
Stah mnghtung gayagaya as
RA
RA
dan
dan
RR
ta daat mnggamba dagam bban
ta daat mnggamba dagam bban
iagram bban : iagram bban :**
Gambaan bbanbban
Gambaan bbanbban
d atas gas
d atas gas
**
Gambaan bban-bban
Gambaan bban-bban
d bawah gas
d bawah gas
iaram Liaram L
Dmua d
Dmua d
kiri k kaa mmbtkkiri k kaa mmbtkdagam ssua hu
dagam ssua hu
bungan bb dan L
bungan bb dan L
AL
AL
==
q. =q. =
AQ
AQ
Da ta daat
Da ta daat gambaan ag
gambaan ag
iaram L· iaram L·
**
Ttaan
Ttaan
bntkbntkdagam
dagam
L
L dan
dan M
M
AM
AM
==uas
uas L L
AA
L
L
ssua
ssua dngan hubungan
dngan hubungan
enyeesaan prakts dar baok sederana (smpe beams)enyeesaan prakts dar baok sederana (smpe beams)Dngan
Dngan mnggunaan
htungan da sstm bao sdhana dngan angahangah sbaga bu
htungan da sstm bao sdhana dngan angahangah sbaga butt
mnggunaan tga
tga hubungan yang tah ta oh,
hubungan yang tah ta oh, ta daat mnydhanaan
ta daat mnydhanaan
aka
aka 1 1
Tntuan as taannya
Tntuan as taannya
AAy y AAHH
,,
BB
, dng
, dngan mnggunaan tga syaat
an mnggunaan tga syaat s
s
mbann
mbann ada
ada
body
body bao
bao da
da sstm
sstm dan
dan mbbanannya
mbbanannya
dmana L
dmana L
tsbut d
tsbut d
atas sangat ntng, ana bdasaan haha tsbut
atas sangat ntng, ana bdasaan
haha tsbut mmungn
mmungn
an nysaan dagam M,N,L sca cat untu sstm bao
an nysaan dagam M,N,L sca cat untu sstm bao sdha (sm
sdha (smbams)
bams)
turanaturan prakts penggambaran Dagram Mx dan Lx turanaturan prakts penggambaran Dagram Mx dan Lx
\
\
3of
3of
X
X
••
ngka ngka ngka ngka 33 onto onto 11
Tuka gayagaya dalam
Tuka gayagaya dalam LxLx ,, MxMx dga lagkahlagkah sbagai bdga lagkahlagkah sbagai b 22 .. 1 1 Gamb Gamb diadiagragram m dardari i pmbbaa.pmbbaa.
2222 . . Gambar Gambar didiagagraramm LxLx dga mgiga bahwadga mgiga bahwa ALxALx
AAQQ**
Jika idaJika idak ada bbk ada bba bkraa bkra
LxLx kosa.kosa.**
JikJika bba a bba P bkaP bka
LxLx brubah sara mdadakbrubah sara mdadak ALx-ALx- PP**
Jika bba mraaJika bba mraa
bkrabkra
LxLx brupa garis urusbrupa garis urus 23. ari diaam23. ari diaam LxLx uka iikuka iik
xx
yag brarakyag brarakxx
dari suau praka rdari suau praka r u, dimaau, dimaa LxLx
0
0
Pada iik rsbu
Pada iik rsbu MxMx MmaMmax.x.
Lx
Lx
0
0
MxMx
MmaxMmax22 TiTiau frau frbody, body, dari saldari salahsau prakahsau praka saa sampai mpai iikiik
xx
rsbu di aas,rsbu di aas, dga mgguadga mgguaka ksimbaga momka ksimbaga mom
xx
0,
0,
MMmamaxx diprohdiproh5.
5.
Gambar buk dari diagramGambar buk dari diagram MxMx dga mgiga bahwa prubaha momdga mgiga bahwa prubaha momAMx
AMx sama dsama dgaga uas dari diagram uas dari diagram LxLx
**
JikaJika LxLx kosakosa
MxMx brupa garis brupa garis lurus.lurus.**
JikaJika LxLx liirliir MxMx brupa gkuga parabolabrupa gkuga parabola**
JikaJikaL
L
brubah sara mdadakbrubah sara mdadak ALxALx
PP
MMxx brua garis paahbrua garis paah Jika bba horisoa PJika bba horisoa P dikrjaka, bba rsbudikrjaka, bba rsbu.. aka bkra dari iik krayaaka bkra dari iik kraya sampai prlaka
sampai prlaka yag diam yag diam $bagai $bagai gaya Norma Ngaya Norma N
Sisim da bbabba Sisim da bbabba
33
frfrbodybody
akak:VO
:VO
Av
Av1B
1Bvv
00
::
0
0
AH
AH 0
0
0 0
AA
00
33
Langka Langka AxAx AA
00
33
MgMg00
B610
B610 3 3
00
BBvv
55
dari
dari
11 A-1050
A-1050
AAvv
55
**
iagramb aiagramb a**
iiagagraramm
00
XX
3 3
L:L:
ngka
ngka 1 1 babaloklok
00
33 44 onto onto ..
**
itim dn bbnbbn itim dn bbnbbn **
II
Lngk Lngk 1 1 600 600 II ((QQ==1100.6.6))
600 600**
LngkLngk **
**
Fr Fr bdbdyy : : MM xx = = 00 M Mmm aaxx 5.35.3 00 �� M M mm aa xx.. = = 1515 iagram iagramMMxx balk balk ffrrbdybdy �� raksiraksi
vv
00 ++ Av- Av- 106106++ Bv =Bv = o o A AHH ++ 0 0 = = 00 �� By6603 = By6603 = 00 �� ByBy 3 300 dari dari 11 30 = 30 = 3030 A Avv==33ooff
ff
ssvv=30=30U·
U·
**
iagrambbaiagrambba0 0 L L xx==OO xx mamaxx 3 30000
tt
300 300 44**
iiagagraramm LLxx LLxx = = 00
**
Fr bdyFr bdy**
iaiagrgramam MMxx � � X X == 66 33 22 MM xx 00 M Mmm aaxx++ ((1100,,33)).. 2233303303 M Mmm aaxx 4545 0 0�
�
rr
XX
r� r� A Av = 60v = 60 HtL HtL x x
ono
*
isim an bbanbban *
Langka 1 *
Langka 2:H
20 20 209
0
X
_
-17
rboao feeod
raksi�v
� H
0
t+0
Av-
10 352
Bv
1 AH + 0 0
AH = 0Bv6
7 10
Av
17 8 9
*
Daaea
*
*
Daa
Lx0
XFeeod
�
M x 0
2
Mm ax- 9.2 0 Mmx 18
0 �32) 35'
ll l
' Contoh 4:
* Sistim dan bebanbeban
A B A 0 Q * Langkah 1 * Langkah 2
A,-95p£
Av=05p£
Contoh 5:* Sitem dan beban-beban :
Bv05p£
A G B 0 ba okfreebody reaksi � v 0 t+ Av - p.l + Bv = o � H 0 + AH + 0 = 0 AH 0 By l pl 2 0 Bv = dari@
Av - p + p o Av * * Dia grambeban Dia gram L t x = Av - px x = 0 : 05 p px 0,5 p - pX 0 X = 05 Free body � M X= 0 1 Mm + p 2 .4-2
p . 2= 0' � •
.,05p£
p
Ot/ x.
*
ana 1 ( 0.6 t)H
4.00 600*
ana 0t lOt 0t/m=pmax lQ _
1 -p 346577t/m xmax 101
ono
*
im an bban
B
balok - freeboy � rai
� v
0
+
Ay- 10,6 + By= 0 2AH +
0=
0 �A =
0 ar 1 By 6 - . 4= 0 - By= 20 �Ay=
10.
. 2x
=
3, 6 0 3,46 :1,45
--- _J
L 1:
·P�Ay-
30 + 20=
*
Da rambeban*
*
Da ram �Q
Lx Ay-p. 2 = 10 10 6 Lx 0 : 10 10
0 12 X e oy
=
120=
12 10 Mmax+
998115 103,6=
Mma= 2 3,12 Da ram MxPy= P
sn PH= P
os *
Lagka 1 AH1
PH
Av Q/ 2*
Lagka 2 P Contoh 7: Ms A B Qbalok-freebody
rakik v
0
+
H= 0+
+
A-P+B=O
AH PH 0
1 dari
1
By .1-Py =0E
2
- By=- 2 Ay Py+ 0 Av �*
Diagrambeban
*
Dagram-L
Lx =0
X 2*
Free body
= 0
LX
- =0
2 Lx=
2O
H= 0
Nx+PH= 0
Nx=-H
k
MX= 0
Mmax-2· = 0
P
Mmax=
*
Dagram-
Mx*
Dagram-
Nx*
Sstim dan beban
Q/ 2 Bv v ma _!
4 -4* angkah 1 balok freebo dy reaksi
�V= 0 t Av +Bv=o· 1
) B
�H = 0 � + AH+0 = o HAv
Qr
Bv
� M g 0 t By .Q MBy= = 0 M Q
dari 1 Ay-
a
M 0 �Q Av -Bv = M * angkah 2: * Diagrambeban
a
* Diagram-L x L x = 0 X 0 X = Q * Free body X = 0E?
Mx
�V=O Lx -ya
M 0 � L x =a
M Q ok a
Tl
x � M = 0 M x 0 0 � M x= 0 ok * Freebody x= Q Ma
Ma
�V= 0 L x = 0 � L x = ok aj
Q Q Q xQa
M � M = 0 M x -Q=0 - M =a
M ok X * Diagram-M x * A
M A > aM=
a
Qt
Cntoh 8:
Sistim dan bebanbeban
C
*
angkah 1 balok freebody
� reaksi* Freebody
X
= 0 �v
= 0+
� H = 0�
�M
0)+
dari
1A B
0
AH
0 = 0 = 0BQ-MM
0* Dagram beban
*
Dagram
L xX
0X
�V= 0 +
L x+MA - MB Q �M=
0+ Mx
M
A
M
* Freebody
Q
�V=O �M
= 0+
*
0ok
Dagram Mx
Ms
AH
£=5 * angkah
AH
=
---A - MB �
Q
x
{+
ontoh
p
Lngkh 1
Lngkh 2 £�
+
2p
sm
sin
+
p
cos
Sm da bba-bba Pb"
Psn
balokfbody�
k 0 t+ yP+By = 0 1 H 0 + H +0 = 0�
P£ M 0 t+ By£
dai 1 y P+ 2
iagam bba
iagam Vx Vx= 0*
F body M; 0
iagam Mx 0�
�
2�
By= _ 2 P y x
V xO+Hxi Nx
xo VxiO £ 2
£ Mmax 0 Mmax
iagam Nx N
X
Hx oO V x i
iagam x x VxoO+Hxi
�p
=== x
max-
Contoh 1 0 :
Ih
* Lah 1 * Langkah 2 H Q / Mx=M max + +* Sistim dan hehan
w �w,
Wv=WH = Ww
cos� sin�H
haok - freehody � reaksi
L V= 0
t+
LH= 0 �+ LMA= 0 t+ �
= Av Wv +BvC
AH +WH=
0 � AH = -WH Q h ByQ-Wy 2-WH 2
0 Q By .2+ Q h WH ·2 Wv2 + (2·£)
WH h dariC
- =Wv - Wv.
+
WH
-
(
)
* Behan Horisontal * Diagram Hx * Behan veria * Dagram Vx * * * * Freehody LM 0 Vx= 0 X Q 2 Q M m ax.- Ay .
0 Wy.Q WH . h � M =- m a x. 4 4 Diagram Mx Diagram NxDiagram Lx Vx cos�+ Hx sin �
Bv
Wv
Contoh 1 1 : \.'� * *
Q * Langkah 2 : * *�
/ * *�
xmax. *•7&
�
* .Q = -4 * 4Sistim da beban/Freeody
Langkah 1 � reaksi � N 0 AN - PN + BN = 0 � T = 0 AT - PT = 0 � = PT � MA= 0 BN Q PN· :- Q dari 1 AN PN
+ �
2 Beban angensial Diagram - Nx Beba orma Diagram - LxL
= 0 � X Free body = 0 Q 2 0 � M = 0 Mma x PN Q - 2 · B = AN= 0 Diagram Mx�
m ax = P. {OS 0 Q = Q cos0 P Q = max. = Diagram Mx 1 PN 2 PN 2 ATContoh 1 2 : * Langkah 2 p 2 + Mx=Mmx. Q
t �
2 p . . sm 1 p p .cos (l 2 2 B* Sisim dan eanFreedy
* Langkah 1 : reaksi r v 0 Av - P + Bv = 0 ' H 0 A + 0 = 0 - AH P . Q ' M 0 Bv . Q - = 0 - Bv = dari 1 Av - P + = 0 -
T
* Bean hosnal/ Diagram Hx* * * Bean etal Dagam - Vx Freedy M = 0 0,5Q p Q Mm ax 2 2 * Diagam - Mx ,o
* Dagram Nx Nx = Hxos - Vxsin e
,o
* Diagram - L Vx cse + Hxsin e
�
-