METODE RUNGE-KUTTA ORDE 4 PADA SOLUSI NUMERIK MODEL PENYEBARAN PENYAKIT TUBERKULOSIS SKRIPSI ENDA SURANY BARUS

(1)

METODE RUNGE-KUTTA ORDE 4 PADA SOLUSI NUMERIK MODEL PENYEBARAN PENYAKIT TUBERKULOSIS

SKRIPSI

ENDA SURANY BARUS 170803061

PROGRAM STUDI S1 MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

2021

(2)

METODE RUNGE-KUTTA ORDE 4 PADA SOLUSI NUMERIK MODEL PENYEBARAN PENYAKIT TUBERKULOSIS

SKRIPSI

DIAJUKAN UNTUK MELENGKAPI TUGAS DAN MEMENUHI SYARAT MENCAPAI GELAR SARJANA SAINS

ENDA SURANY BARUS 170803061

PROGRAM STUDI S1 MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

2021

(3)

PERNYATAAN ORISINALITAS

Metode Runge-Kutta Orde 4 pada Solusi Numerik Model Penyebaran Penyakit Tuberkulosis

SKRIPSI

Saya menyatakan bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Agustus 2021

Enda Surany Barus 170803061

(4)

(5)

ii

METODE RUNGE-KUTTA ORDE 4 PADA SOLUSI NUMERIK MODEL PENYEBARAN PENYAKIT TUBERKULOSIS

ABSTRAK

Penelitian ini bertujuan untuk menyelesaikan masalah model epidemi matematika dengan penyelesaian numerik, sebagai salah satu upaya pencegahan penyebaran penyakit Tuberkulosis. Model epidemi matematika yang akan diselesaikan dalam penelitian ini adalah model model SIR, SITR, dan SEIR pada penyebaran penyakit Tuberkulosis. Model epidemi tersebut dapat diselesaikan dengan metode numerik. Metode numerik yang dipandang cukup baik dalam mencari solusi numerik model epidemi matematika yakni Metode Runge-Kutta Orde 4. Dikarenakan metode ini memiliki ketelitian yang cukup tinggi, tidak membutuhkan lebih banyak nilai awal untuk dapat diiterasikan dalam penyelesaian numerik, dan tidak memerlukan turunan fungsi dalam penyelesaiannya.

Kata Kunci : Metode Runge-Kutta, Metode Runge-Kutta Orde 4, Tuberkulosis, SIR, SITR, SEIR.

(6)

iii

METODE RUNGE-KUTTA ORDE 4 PADA SOLUSI NUMERIK MODEL PENYEBARAN PENYAKIT TUBERKULOSIS

ABSTRACT

This research aims to solve the problem of a mathematical epidemic model woth numerical solutions, as an effort to prevent the spread of Tuberculosis. The

mathematical epidemic models that completed in this research are SIR, SITR, and SEIR models on the spread of Tubeculosis. The epidemic models can be solved by numerical method. The numerical methos that is considered quite good in finding a numerical solution to the mathematical epidemic model is the Runge-Kutta Method of Order 4.

Because this method has a fairly high accuracy. It does not require more initial values to be iterated in numerical solutions, and does not require a derivative function in its solution.

Keywords : Runge-Kutta Method, Runge-Kutta Method Fourth Order, Tuberculosis, SIR model, SITR model, SEIR model

(7)

iv

PENGHARGAAN

Puji dan syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa atas berkat dan kasih-Nya kepada penulis, sehingga penulis dapat menyelesaikan skripsi ini tepat pada waktunya. Skripsi dengan judul “METODE RUNGE-KUTTA ORDE 4 PADA SOLUSI NUMERIK MODEL PENYEBARAN PENYAKIT TUBERKULOSIS”.

Dalam menyelesaikan skripsi ini, banyak pihak yang telah membantu penulis. Untuk itu, penulis menyampaikan ucapan terima kasih yang sebesar-besarnya dan penghargaan yang setinggi-tingginya kepada:

1. Bapak Dr. Sutarman, M.Sc. selaku dosen pembimbing yang senantiasa membantu dan mengarahkan saya dalam menyelesaikan skripsi ini

2. Bapak Dr. Syahriol Sitorus, M.IT selaku dosen pembanding 1, dan Dr. Suyanto, M.Kom. selaku dosen pembanding 2 yang memberikan kritik dan saran yang membangun dalam menyelesaikan skripsi penulis

3. Ibu Dr. Nursahara Pasaribu, M.Sc. selaku Dekan FMIPA USU serta seluruh Staf pegawai di Fakultas Matematika Dan Ilmu Pengetahuan Alam USU

4. Bapak Dr. Suyanto, M.Kom selaku Ketua jurusan Matematika dan Bapak Drs.

Rosman Siregar, M.Si selaku Sekretaris jurusan Matematika serta seluruh Bapak dan Ibu dosen yang telah mendidik penulis selama menjalani pendidikan di Fakultas Matematika Dan Ilmu Pengetahuan Alam USU.

5. Teristimewa dan yang paling utama penulis ucapkan terimakasih kepada kedua orangtua tersayang yaitu Ayahanda Agen Barus dan Ibunda Samaria br.Tarigan, saudari penulis yaitu Ariany Ema Dila Barus, Saudara penulis Melvin Dev Kiano Barus serta keluarga besar Barus Siberas dan Tarigan Tua yang sangat penulis sayangi dan banggakan.

(8)

v 6. Tak terlupakan seluruh rekan-rekan kuliah Matematika stambuk 2017 dan HMM FMIPA USU, terkhusus kepada teman-teman penulis yaitu Miralda, Elsadday, Thresya, Uli, dan Priskila yang telah berjuang bersama-sama dan memberikan dukungan dan semangat kepada penulis. Semoga Tuhan Yang Maha Esa memberikan balasan yang tak terhingga. Amin.

Terima kasih penulis ucapkan kepada seluruh pihak yang telah membantu dalam proses pembuatan skripsi.

Medan, Agustus 2021

Enda Surany Barus

170803061

(9)

vi

DAFTAR ISI

Halaman

PENGESAHAN SKRIPSI i

ABSTRAK ⁱⁱ

ABSTRACT ⁱⁱⁱ

PENGHARGAAN ^iv

DAFTAR ISI ^vi

DAFTAR TABEL ^viii

DAFTAR GAMBAR ^ix

DAFTAR LAMPIRAN ^xi

DAFTAR SINGKATAN ^xii

BAB 1 PENDAHULUAN ¹

1.1 Latar Belakang ¹

1.2 Rumusan Masalah ³

1.3 Batasan Masalah ³

1.4 Tujuan Penelitian ⁴

1.5 Manfaat Penelitian ⁴

BAB 2 TINJAUAN PUSTAKA ⁵

2.1 Persamaan Diferensial Biasa ⁵

(10)

vii

2.1.1 Persamaan Diferensial Biasa Linier ⁶ 2.1.2 Persamaan Diferensial Biasa Nonlinier 6

2.2 Sistem Persamaan Diferensial ⁶

2.3 Masalah Nilai Awal ⁷

2.4 Metode Numerik ⁹

2.5 Metode Runge-Kutta ⁹

2.5.1 Metode Runge-Kutta Orde 2 11

2.5.2 Metode Runge-Kutta Orde 3 ¹¹ 2.5.3 Metode Runge-Kutta Orde 4 ¹²

2.6 Model Epidemi SIR ¹²

2.6.1 Model Epidemi SIR Pada Penyebaran Penyakit Tuberkulosis

13

2.7 Model Epidemi SITR ¹⁶

2.7.1 Model Epidemi SITR Pada Penyebaran Penyakit Tuberkulosis

17

2.7.2 Model Epidemi SEIR ¹⁹

2.7.3 Model Epidemi SEIR Pada Penyebaran Penyakit Tuberkulosis

19

BAB 3 METODE RUNGE-KUTTA ORDE 4 ²³

BAB 4 METODE PENELITIAN ³⁷

4.1 Desain Penelitian ³⁷

4.2 Metode Penyelesaian ³⁷

(11)

viii

4.3 Langkah-Langkah Penelitian ³⁹

BAB 5 SOLUSI NUMERIK DAN PENENTUAN SYARAT AWAL MODEL EPIDEMI

40

5.1 Solusi Numerik Model Epidemi SIR Pada Penyebaran Penyakit Tuberkulosis dengan Metode Runge-Kutta Orde 4.

40

5.2 Penentuan Syarat Awal Model Epidemi SIR Pada Penyebaran Penyakit Tuberkulosis

41

5.3 Simulasi Program dengan menggunakan MATLAB

44

5.3.1 Plot Suspectible model epidemi SIR pada penyebaran penyakit Tuberkulosis dengan MATLAB

44

5.3.2 Plot Infectious model epidemi SIR pada penyebaran penyakit Tuberkulosis dengan MATLAB

45

5.3.3 Plot Recovered model epidemi SIR pada penyebaran penyakit Tuberkulosis dengan MATLAB

46

5.4 Solusi Numerik Model Epidemi SITR Pada Penyebaran Penyakit Tuberkulosis dengan Metode Runge-Kutta Orde 4

46

5.5 Penentuan Syarat Awal Model Epidemi SITR Pada Penyebaran Penyakit Tuberkulosis

48

51

(12)

ix 5.6.1 Plot Suspectible model epidemi SITR pada

penyebaran penyakit Tuberkulosis dengan MATLAB

51

5.6.2 Plot Infectious model epidemi SITR pada penyebaran penyakit Tuberkulosis dengan MATLAB

52

5.6.3 Plot Treatment model epidemi SITR pada penyebaran penyakit Tuberkulosis dengan MATLAB

53

5.6.4 Plot Recovered model epidemi SITR pada penyebaran penyakit Tuberkulosis dengan MATLAB

54

5.7 Solusi Numerik Model Epidemi SEIR Pada Penyebaran Penyakit Tuberkulosis dengan Metode Runge-Kutta Orde 4

54

5.8 Penentuan Syarat Awal Model Epidemi SEIR Pada Penyebaran Penyakit Tuberkulosis

56

59

5.9.1 Plot Suspectible model epidemi SEIR pada penyebaran penyakit Tuberkulosis dengan MATLAB

59

5.9.2 Plot Exposed model epidemi SEIR pada penyebaran penyakit Tuberkulosis dengan MATLAB

60

5.9.3 Plot Infectious model epidemi SEIR pada penyebaran penyakit Tuberkulosis dengan MATLAB

61

(13)

x 5.9.4 Plot Recovered model epidemi SEIR pada

penyebaran penyakit Tuberkulosis dengan MATLAB

62

BAB 6 KESIMPULAN DAN SARAN ⁶³

6.1 Kesimpulan ⁶³

6.2 Saran ⁶⁵

DAFTAR PUSTAKA ⁶⁶

LAMPIRAN ⁶⁸

(14)

xi

DAFTAR TABEL

Nomor Tabel Judul Halaman

2.1 Penjelasan variabel yang digunakan pada model SIR

15

2.2 Penjelasan parameter yang digunakan pada model SIR

15

2.3 Penjelasan variabel yang digunakan pada model SITR

18

2.4 Tabel penjelasan parameter yang digunakan pada model SITR

18

2.5 Penjelasan variabel yang digunakan pada model SEIR

21

2.6 Penjelasan parameter yang digunakan pada model SEIR

21

5.1 Syarat Awal yang digunakan pada Model Epidemi SIR pada Penyebaran Penyakit Tuberkulosis

42

5.2 Syarat Awal yang digunakan pada Model Epidemi SITR pada Penyebaran Penyakit Tuberkulosis

49

5.3 Syarat Awal yang digunakan pada Model Epidemi SEIR pada Penyebaran Penyakit Tuberkulosis

57

(15)

xii

DAFTAR GAMBAR

Nomor Gambar Judul Halaman

2.1 Diagram kompartemen SIR 14

2.2 Diagram kompartemen SITR 17

2.3 Diagram kompartemen SEIR 20

5.1 Plot Suspectible model epidemi SIR pada penyebaran penyakit Tuberkulosis

44

5.2 Plot Infectious model epidemi SIR pada penyebaran penyakit Tuberkulosis

45

5.3 Plot Recovered model epidemi SIR pada penyebaran penyakit Tuberkulosis

46

5.4 Plot Suspectible model epidemi SITR pada penyebaran penyakit Tuberkulosis

51

5.5 Plot Infectious model epidemi SITR pada penyebaran penyakit Tuberkulosis

52

5.6 Plot Treatment model epidemi SITR pada penyebaran penyakit Tuberkulosis

53

5.7 Plot Recovered model epidemi SITR pada penyebaran penyakit Tuberkulosis

54

5.8 Plot Suspectible model epidemi SEIR pada penyebaran penyakit Tuberkulosis

59

5.9 Plot Exposed model epidemi SEIR pada penyebaran penyakit Tuberkulosis

60

(16)

xiii

5.10 Plot Infectious model epidemi SEIR pada penyebaran penyakit Tuberkulosis

61

5.11 Plot Recovered model epidemi SEIR pada penyebaran penyakit Tuberkulosis

62

(17)

xiv

DAFTAR LAMPIRAN

Nomor Lampiran Judul Halaman

1. Kode program solusi numerik model epidemi SIR pada penyebaran penyakit Tuberkulosis dengan Metode-Runge Kutta Orde 4, pada software MATLAB

68

2. Kode program solusi numerik model epidemi SITR pada penyebaran penyakit Tuberkulosis dengan Metode-Runge Kutta Orde 4, pada software MATLAB

70

3. Kode program solusi numerik model epidemi SITR pada penyebaran penyakit Tuberkulosis dengan Metode-Runge Kutta Orde 4, pada software MATLAB

72

(18)

xv

DAFTAR SINGKATAN

TB = Tuberkulosis

SI = Susceptible Infectious

SIR = Susceptible Infectious Recovered

SITR = Susceptible Infectious Treatment Recovered SEIR = Susceptible Exposed Infectious Recovered BPS = Badan Pusat Statistik

(19)

BAB I PENDAHULUAN

1.1 Latar Belakang

Metode Runge-Kutta merupakan salah satu metode numerik yang dapat digunakan untuk menyelesaikan persamaan differensial biasa yang menyangkut nilai awal dengan ukuran langkah waktu yang bervariasi. Penyelesaian persamaan differensial biasa dengan Metode Runge-Kutta Orde 4 adalah proses mencari nilai fungsi 𝑦(𝑥) pada titik 𝑥 tertentu dari persamaan differensial biasa 𝑓(𝑥, 𝑦) yang diketahui. Persamaan differensial biasa sering kali diterapkan pada berbagai model matematika yang menggambarkan masalah dalam kehidupan nyata, salah satunya dalam model epidemi matematika sebagai upaya pencegahan penyebaran penyakit menular Tuberkulosis.

Metode Runge-Kutta Orde 4 ini dipandang cukup baik dalam mencari solusi numerik model epidemi matematika dikarenakan memiliki ketelitian yang cukup tinggi dibandingkan dengan metode numerik lainnya (Triatmodjo, 2002), sehingga nantinya nilai hampiran yang diperoleh memiliki galat yang lebih kecil. Metode Runge-Kutta Orde 4 ini juga tidak membutuhkan lebih banyak nilai awal untuk dapat diiterasikan dalam penyelesaian numerik, dan keunggulan lain dari Metode Runge-Kutta Orde 4 adalah tidak memerlukan turunan fungsi dalam penyelesaiannya (Munir, 2015).

Model epidemi matematika kerap sekali digunakan dalam pemodelan penyakit menular Tuberkulosis (TB). Model epidemi SIR (Susceptible, Infected, Recovered) dan SEIR (Susceptible, Exposed, Infected, Recovered), yang telah dibahas dalam Global Stability of SIR and SEIR Model for Tuberculosis Disease Transmission with Lyapunov Function Method (Side et al., 2016).

Model epidemi matematika dapat diselesaikan secara analitik dan numerik.

Terdapat beberapa penelitian terdahulu mengenai penyelesaian model epidemi matematika secara analitik. Yong dan Owen (2017) yang telah membahas tentang formulasi metode analisis homotofi dalam menentukan hampiran solusi analitik dari beberapa model epidemi seperti model SI, SIR, dan SEIR.

Christyanti dan Syahdan (2019) yang membahas tentang metode dekomposisi

(20)

adomian yang digunakan untuk menyelesaikan sistem persamaan model SEIR pada penyakit Tuberkulosis, dan setelah itu akan diamati perilakunya melalui simulasi numerik berdasarkan parameter-parameter tertentu yang diberikan. Namun, penyelesaian model epidemi secara analitik memiliki kelemahan, yaitu penyelesaian persamaan differensial biasa secara analitik biasanya menghasilkan solusi dalam bentuk fungsi matematika yang selanjutnya fungsi tersebut dapat dievaluasi untuk menghasilkan nilai dalam bentuk angka. Hal tersebut membuat penyelesaian analitik sulit untuk diselesaikan mengingat tidak semua fungsi mudah dihitung turunannya (Triatmodjo, 2002).

Karena hal itu, beberapa penelitian terdahulu juga membahas mengenai penyelesain model epidemi matematika secara numerik, yakni (Kuzairi et al., 2016) yang membahas mengenai aplikasi metode Adams Bashforth-Moulthon pada model epidemi matematika namun dikarenakan metode Adams Bashforth-Moulthon ini merupakan metode banyak langkah, sehingga pada penelitian (Kuzairi et al., 2016) ini digunakan metode Runge-Kutta untuk mencari nilai awalnya.

Penelitian terdahulu juga telah dilakukan oleh Nur dan Abdal (2016) yang membahas mengenai solusi numerik dengan menggunakan metode milne-simpson.

Namun, dikarenakan metode ini membutuhkan nilai awal yang lebih banyak sebelum diiterasikan dengan metode milne-simpson, maka pada penelitian tersebut penulis menggunakan metode Runge-Kutta untuk mencari nilai awalnya, sehingga pada penelitian tersebut metode yang digunakan disebut dengan metode modified milne- simpson.

1.2 Rumusan Masalah

Berdasarkan uraian dari latar belakang, didapati bahwa penyelesaian model epidemi matematika secara analitik sulit untuk diselesaikan, dikarenakan solusi yang dihasilkan berupa fungsi matematika. Oleh karena itu, pendekatan numerik dapat digunakan dalam menyelesaikan model epidemi matematika. Metode pendekatan numerik yang dianggap cukup baik dalam menyelesaikan model epidemi matematika adalah Metode Runge-Kutta Orde 4. Metode Runge-Kutta Orde 4 memiliki ketelitian yang cukup

(21)

3

tinggi dibandingkan dengan metode pendekatan numerik lainnya. Selain itu, Metode Runge-Kutta Orde 4 juga tidak membutuhkan lebih banyak nilai awal untuk dapat diiterasikan dalam penyelesaian numerik, dan keunggulan lain dari Metode Runge-Kutta Orde 4 adalah tidak memerlukan turunan fungsi dalam penyelesaiannya.

1.3 Batasan Masalah

Agar penelitian yang dilakukan dapat menghasilkan penelitian yang fokus dan akurat, maka penulis memberikan batasan masalah dalam penelitian ini yaitu :

1. Persamaan yang digunakan adalah hasil pemodelan penyebaran penyakit Tuberkulosis dengan model SIR (Susceptible, Infectious, dan Recovered) yang telah dibahas oleh (Fredlina et al., 2012), model epidemi SITR (Susceptible, Infectious, Treatment, Recovered) untuk penyebaran penyakit Tuberkulosis yang telah dibahas oleh (Side et al., 2016), dan model epidemi SEIR (Susceptible, Exposed, Infectious, Recovered) untuk penyebaran penyakit Tuberkulosis yang dipakai oleh (Christyanti dan Syahdan, 2019) dalam mencari solusi analitik dengan metode dekomposisi adomian.

2. Populasi yang digunakan pada penelitian ini adalah populasi penduduk Sumatera Utara tahun 2018.

1.4 Tujuan Penelitian

Adapun tujuan dari penelitian ini adalah untuk mendapatkan penyelesaian numerik dari model penyebaran penyakit Tuberkulosis. Kemudian, sebagai salah satu upaya pencegahan penularan penyakit Tuberkulosis tersebut, maka perlu diamati perlakuan dari penyakit Tuberkulosis tersebut. Oleh karena itu, dilakukan simulasi numerik berdasarkan syarat awal yang telah diberikan pada model epidemi SIR, SITR, dan SEIR yang dimana syarat awal tersebut ditetapkan berdasarkan data yang telah diperoleh.

(22)

1.5 Manfaat Penelitian

Manfaat yang diperoleh dari penelitian ini adalah untuk menambah wawasan mengenai penerapan ilmu matematika dalam dunia nyata, salah satunya yaitu dengan penerapan metode Runge-Kutta Orde 4 dalam mencari solusi numerik model epidemi SIR, SITR, dan SEIR pada penyebaran penyakit Tuberkulosis. Mengetahui syarat awal yakni nilai-nilai parameter dan nilai awal yang digunakan dalam model SIR, SITR, dan SEIR penyebaran penyakit Tuberkulosis berdasarkan data yang diperoleh. Kemudian, untuk memahami hasil simulasi dari solusi numerik model SIR, SITR, dan SEIR pada penyebaran penyakit Tuberkulosis dengan Metode Runge-Kutta Orde 4.

(23)

BAB 2

TINJAUAN PUSTAKA

Pada bab ini akan diuraikan teori dan konsep dasar yang berhubungan dengan Metode Runge-Kutta Orde 4 pada Model Penyebaran Penyakit Tuberkulosis, yakni Persamaan Differensial Biasa (Kartono, 2012), Sistem Persamaan Differensial (Neuhauser, 2004), Masalah Nilai Awal (Oktaviani et al., 2014), Metode Numerik (Triatmodjo, 2002), Metode Runge-Kutta (Gerald dan Wheatley, 1985), Model epidemi SIR (Fredlina et al., 2012), Model epidemi SITR (Side et al., 2016), dan Model epidemi SEIR (Christyanti dan Syahdan, 2019). Materi yang dijelaskan berguna untuk menyelesaikan Model Penyebaran Penyakit Tuberkulosis.

2.1 Persamaan Diferensial Biasa

Persamaan Diferensial Biasa merupakan persamaan diferensial yang hanya mempunyai satu variabel bebas. Variabel bebas biasanya disimbolkan dengan 𝑡. Jika 𝑥 adalah fungsi dari 𝑡, menurut Kartono (2012), bentuk umum dari persamaan differensial biasa dituliskan seperti pada persamaan berikut persamaan (2.1) dan persamaan (2.2) berikut :

𝐹 (𝑡, 𝑥, 𝑥^′, 𝑥^′′, 𝑥^′′′, , … , 𝑥^(𝑛)) = 0 (2.1) 𝐹 (𝑡, 𝑥,^𝑑𝑥

𝑑𝑡,^𝑑²^𝑥

𝑑𝑡² ,^𝑑³^𝑥

𝑑𝑡³, … ,^𝑑^𝑛^𝑥

𝑑𝑡^𝑛) = 0 (2.2)

Maka contoh persamaan differensial biasa adalah

𝑑𝑥

𝑑𝑡 = 𝑡²cos 𝑥 (2.3)

Dimana persamaan tersebut memiliki orde satu. Orde dari persamaan differensial adalah turunan tertinggi pada fungsi tak diketahui (variabel terikat) yang muncul dalam persamaan differensial.

Berdasarkan sifat ke linieran dari variabel terikatnya, persamaan diferensial biasa dapat dibedakan menjadi persamaan diferensial biasa linier dan persamaan diferensial biasa nonlinier.

(24)

2.1.1 Persamaan Diferensial Biasa Linier

Persamaan diferensial biasa linier memiliki bentuk umum : 𝑎_𝑛(𝑡)^𝑑^𝑛^𝑥

𝑑𝑡^𝑛+ 𝑎_𝑛−1(𝑡)^𝑑^𝑛−1^𝑥

𝑑𝑡^𝑛−1+ ⋯ + 𝑎₁(𝑡)^𝑑𝑥

𝑑𝑡+ 𝑎₀(𝑡)𝑥 = 𝑓(𝑡) (2.4) Dengan 𝑎 ≠ 0, 𝑎, 𝑎₁, … , 𝑎_𝑛 disebut koefisien persamaan diferensial. Fungsi 𝑓(𝑡) disebut input atau unsur nonhomogen. Jika 𝑓(𝑡) disebut input, maka solusi dari persamaan diferensial 𝑥(𝑡) biasanya disebut output. Jika ruas sebelah kanan 𝑓(𝑡) Bernilai nol untuk semua nilai 𝑡 dalam interval yang ditinjau, maka persamaan ini dikatakan homogen, jika sebaliknya maka dikatakan nonhomogen. Contoh persamaan diferensial linier adalah :

𝑑𝑥

𝑑𝑡 = 𝑎𝑥 + 𝑏𝑡 (2.5)

Yang merupakan persamaan differensial biasa linier nonhomogen orde satu.

2.1.2 Persamaan Diferensial Biasa nonlinier

Jika persamaan diferensial biasa tidak dapat dinyatakan dalam bentuk umum persamaan diferensial biasa linier, yaitu pada persamaan (2.4), maka persamaan diferensial tersebut adalah persamaan diferensial biasa nonlinier. Contoh persamaan diferensial biasa nonlinier adalah :

𝑑²𝑥

𝑑𝑡² + 4𝑥² = sin 𝑡 (2.6)

Yang merupakan persamaan diferensial biasa nonlinier nonhomogen orde dua.

2.2 Sistem Persamaan Differensial

Sistem persamaan differensial adalah suatu sistem yang memuat 𝑛 buah persamaan diferensial, dengan 𝑛 buah fungsi yang tidak diketahui, dimana 𝑛 merupakan bilangan bulat positif lebih besar sama dengan dua. Antara persamaan differensial yang satu dengan yang lain saling keterkaitan dan konsisten.

Bentuk umum dari suatu sistem 𝑛 persamaan orde pertama mempunyai bentuk sebagaimana pada persamaan (2.7) berikut :

(25)

7

𝑑𝑥₁

𝑑𝑡 = 𝑓₁(𝑡, 𝑥₁, 𝑥₂, … , 𝑥_𝑛) 𝑑𝑥₂

𝑑𝑡 = 𝑓₂(𝑡, 𝑥₁, 𝑥₂, … , 𝑥_𝑛)

⋮ (2.7)

𝑑𝑥_𝑛

𝑑𝑡 = 𝑓_𝑛(𝑡, 𝑥₁, 𝑥₂, … , 𝑥_𝑛)

dengan 𝑥₁, 𝑥₂, … , 𝑥_𝑛 adalah variabel bebas dan 𝑡 adalah variabel terikat, sehingga 𝑥₁ = 𝑥₁(𝑡), 𝑥₂ = 𝑥₂(𝑡), … , 𝑥_𝑛 = 𝑥_𝑛(𝑡), dalam hal ini ^𝑑𝑥^𝑛

𝑑𝑡 merupakan turunan fungsi 𝑥_𝑛 terhadap 𝑡, dan 𝑓 adalah fungsi yang bergantung pada variabel 𝑥₁, 𝑥₂, … , 𝑥_𝑛 dan 𝑡 (Neuhauser, 2004).

2.3 Masalah Nilai Awal

Masalah nilai awal merupakan masalah penyelesaian suatu persamaan diferensial dengan syarat awal yang telah diketahui (Oktaviani et al., 2014). Suatu persamaan differensial orde 𝑛 memiliki 𝑛 syarat bantu untuk nilai awal yang sama dari variabel bebasnya, dimana nilai awal tersebut merupakan syarat batas disuatu titik. Masalah nilai awal memainkan peranan penting dalam teori dan terapan dari persamaan differensial.

Singkatnya, masalah nilai awal merupakan nilai bantu awal yang dibutuhkan sebagai acuan awal untuk menentukan langkah selanjutnya dari penyelesaian suatu persamaan differensial. Misalnya saja dalam kasus menentukan solusi numerik model penyebaran penyakit Tuberkulosis, nilai awal merupakan nilai bantu yang dibutuhkan untuk melihat perlakuan selanjutnya dari penyebaran penyakit Tuberkulosis, melalui penyelesaian model epidemi terkait. Secara umum, misalkan suatu persamaan diferensial yang dapat ditulis dalam bentuk :

𝑦^𝑛 = 𝑓(𝑥, 𝑦, 𝑦^′, … , 𝑦^(𝑛−1).

Kemudian, masalah nilai awal untuk persamaan diferensial orde 𝑛 tersebut dapat dituliskan seperti persamaan (2.8) berikut :

(26)

𝑠𝑒𝑙𝑒𝑠𝑎𝑖𝑘𝑎𝑛

𝑑^𝑛𝑥

𝑑𝑥^𝑛 = 𝑓(𝑥, 𝑦, 𝑦^′, … , 𝑦^(𝑛−1)) 𝑠𝑦𝑎𝑟𝑎𝑡

𝑦(𝑥₀) = 𝑦₀, 𝑦^′(𝑥₀) = 𝑦₁, … , 𝑦^(𝑛−1)(𝑥₀) = 𝑦_𝑛−1

(2.8)

dengan 𝑦₀, 𝑦₁, 𝑦₂, … , 𝑦_𝑛−1 adalah nilai – nilai yang diketahui.

Berikut ini diberikan satu contoh penyelesaian masalah nilai awal dari persamaan diferensial orde 𝑛.

Tentukan solusi khusus dari persamaan ^𝑑

2𝑦

𝑑𝑥² = 𝑒^−𝑥. Dengan titik nilai 𝑦(0) = 1, 𝑦^′(0) = 4.

Penyelesaian : Persamaan ^𝑑²^𝑦

𝑑𝑥² = 𝑒^−𝑥 dapat juga dituliskan menjadi 𝑑²𝑦 = 𝑒^−𝑥𝑑𝑥². Sehingga

∫ 𝑑²𝑦 = ∫ 𝑒^−𝑥𝑑𝑥²

𝑑𝑦 = (−𝑒^−𝑥+ 𝑐₁)𝑑𝑥, sehingga

∫ 𝑑𝑦 = ∫ (−𝑒^−𝑥+ 𝑐₁)𝑑𝑥 𝑦 = 𝑒^−𝑥+ 𝑐₁+ 𝑐₂

𝑦(0) = 1, sehingga 1 = 𝑒⁻⁽⁰⁾+ 𝑐₁(0) + 𝑐₂ 1 = 1 + 𝑐₂

𝑐₂ = 0

𝑦^′(0) = 4, sehingga 4 = 𝑒⁻⁽⁰⁾+ 𝑐₁

4 = −1 + 𝑐₁ 𝑐₁ = 5

Sehingga diperoleh 𝑦 = 𝑒^−𝑥+ 5𝑥 Jadi, solusi khusus persamaan ^𝑑²^𝑦

𝑑𝑥² = 𝑒^−𝑥. Dengan titik nilai 𝑦(0) = 1, 𝑦^′(0) = 4 adalah

(27)

9

𝑦 = 𝑒^−𝑥+ 5𝑥.

2.4 Metode Numerik

Metode Numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematik sehingga dapat dipecahkan dengan operasi hitung atau aritmetika biasa.

Metode artinya cara, sedangkan numerik artinya angka. Jadi, metode numerik secara harfiah berarti cara berhitung dengan menggunakan angka-angka.

Metode numerik digunakan untuk mencari penyelesaian numerik suatu model matematika dan digunakan apabila dengan metode analitik penyelesaiannya sulit dicari dan memerlukan waktu yang lama, karena modelnya berukuran besar, dalam hal ini dilakukan dengan menggunakan metode yang lebih efisien.

Metode numerik memiliki perbedaan mendasar dengan metode analitik dalam dua hal, yaitu :

1. Solusi dengan metode numerik selalu berbentuk angka dibandingkan dengan metode analitik yang biasanya menghasilkan solusi dalam bentuk fungsi matematika yang selanjutnya fungsi tersebut dapat dievaluasi untuk menghasilkan nilai dalam bentuk angka.

2. Dengan metode numerik, solusi yang diperoleh hanya solusi yang menghampiri atau mendekati eksak sehingga solusi numerik dinamakan juga solusi hampiran atau solusi pendekatan, namun solusi hampiran dapat dibuat seteliti yang diinginkan, meskipun solusi tersebut jelas tidak tepat samadengan solusi eksak, sehingga ada selisih antara keduanya. Selisih inilah yang disebut dengan galat (error).

2.5 Metode Runge-Kutta

Metode Runge-Kutta ini ditemukan oleh matematikawan asal Jerman, Carl Runge (1856-1927) dan Wilhelm Kutta (1867-1944). Dasar pemikiran dari metode ini adalah untuk mempertahankan hampiran Taylor, tetapi didalam penyelesaian persamaan diferensial biasa dengan metode Taylor tidak praktis karena metode tersebut membutuhkan perhitungan turunan 𝑓(𝑥, 𝑦). Lagipula tidak semua fungsi dapat dihitung

(28)

turunannya dengan mudah, terutama bagi fungsi yang bentuknya rumit. Semakin tinggi orde metode deret Taylor, semakin tinggi pula turunan fungsi yang harus dihitung.

Metode Runge-Kutta merupakan metode yang memberikan ketelitian hasil yang lebih besar dan metode Runge-Kutta juga tidak memerlukan turunan dari fungsi. Bentuk umum dari metode Runge-Kutta adalah :

𝑥_𝑖+1= 𝑥_𝑖+ 𝜙(𝑡_𝑖, 𝑥_𝑖, ℎ)ℎ (2.23) dengan 𝜙(𝑡_𝑖, 𝑥_𝑖, ℎ) adalah fungsi penambahan yang merupakan kemiringan rata-rata pada interval dan digunakan untuk mengekstrapolasi dari nilai lama 𝑥_𝑖 ke nilai baru 𝑥_𝑖+1sepanjang interval ℎ. Fungsi pertambahan dapat ditulis dalam bentuk umum :

𝜙 = 𝑎₁𝑘₁+ 𝑎₂𝑘₂+ ⋯ + 𝑎_𝑛𝑘_𝑛 (2.24) dengan 𝑎₁, 𝑎₂, … , 𝑎_𝑛 adalah konstanta dan merupakan tetapan dan 𝑘 adalah :

𝑘₁ = 𝑓 (𝑡_𝑖, 𝑥_𝑖)

𝑘₂ = 𝑓 (𝑡_𝑖+ 𝑝_𝑖ℎ , 𝑥_𝑖+ 𝑞₁₁𝑘₁ℎ)

𝑘₃ = 𝑓 (𝑡_𝑖+ 𝑝_𝑖ℎ , 𝑥_𝑖+ 𝑞₂₁𝑘₁ℎ + 𝑞₂₂𝑘₂ℎ )

⋮ (2.25)

𝑘_𝑛 = 𝑓 (𝑡_𝑖+ 𝑝_𝑛−1ℎ , 𝑥_𝑖+ 𝑞_𝑛−1,1𝑘₁ℎ + 𝑞_𝑛−1,2𝑘₂ℎ + ⋯ + 𝑞_{𝑛−1,𝑛−1}𝑘_𝑛−1ℎ ) dengan 𝑝 dan 𝑞 adalah konstanta. Nilai 𝑘 menunjukkan hubungan berurutan. Nilai 𝑘₁muncul dalam persamaan 𝑘₂, yang keduanya juga muncul dalam persamaan 𝑘₃, dan seterusnya. Hubungan yang berurutan ini membuat metode Runge-Kutta efisien untuk perhitungan dengan komputer.

Ada beberapa metode Runge-Kutta yang bergantung pada nilai 𝑛 (orde) yang digunakan. Misalnya, untuk 𝑛 = 1 disebut metode Runge-Kutta Orde 1 atau disebut juga dengan metode Euler, yang diperoleh dari 𝑘₁ = 𝑓 (𝑡_𝑖, 𝑥_𝑖)dan persamaan (2.24).

𝜙 = 𝑎₁𝑘₁ = 𝑎₁ 𝑓 (𝑡_𝑖, 𝑥_𝑖) Untuk 𝑎₁ = 1 maka persamaan menjadi :

𝑥_𝑖+1= 𝑥_𝑖+ 𝑓 (𝑡_𝑖, 𝑥_𝑖)ℎ

Didalam metode Runge-Kutta, setelah itu nilai 𝑛 ditetapkan, kemudian nilai 𝑎, 𝑝, 𝑞 dicari dengan menyamakan persamaan (2.23) dengan suku-suku dari deret Taylor.

(29)

11

2.5.1 Metode Runge-Kutta Orde 2

Metode Runge-Kutta Orde 2 mempunyai bentuk sebagai berikut :

𝑥_𝑖+1= 𝑥_𝑖+ (𝑎₁𝑘₁+ 𝑎₂𝑘₂)ℎ (2.25) dengan nilai 𝑘₁dan 𝑘₂ seperti pada persamaan (2.24) serta untuk nilai 𝑎₁, 𝑎₂, 𝑝₁ dan 𝑞₁₁ dievaluasi dengan menyamakan persamaan (2.25) dengan deret Taylor Orde 2, sehingga didapatkan nilai sebagai berikut :

𝑎₁+ 𝑎₂ = 1 𝑎₂𝑝₁= 𝑎₂𝑞₁₁ = 1

2 Dengan memilih nilai 𝑎₁ = ¹

2 , maka diperoleh 𝑎₂ = ¹

2 dan 𝑝₁ = 𝑞₁₁ = 1. Selanjutnya substitusikan nilai-nilai tersebut pada persamaan (2.25), sehingga didapatkan rumus metode Runge-Kutta Orde 2 sebagai berikut :

𝑥_𝑖+1= 𝑥_𝑖+1

2(𝑘₁+ 𝑘₂)ℎ Dalam hal ini 𝑘 adalah :

𝑘₁ = 𝑓 (𝑡_𝑖, 𝑥_𝑖)

𝑘₂ = 𝑓 (𝑡_𝑖+ ℎ , 𝑥_𝑖+ 𝑘₁ℎ)

Metode Runge-Kutta Orde 3 diturunkan dengan cara yang sama seperti Runge- Kutta Orde 2 untuk nilai 𝑛 = 3. Hasil dari turunan ini adalah enam persamaan dengan delapan bilangan tidak diketahui. Oleh karena itu, dua bilangan tidak diketahui tersebut harus ditetapkan terlebih dahulu untuk mendapatkan enam bilangan tak diketahui lainnya.

Metode Runge-Kutta Orde 3 mempunyai bentuk sebagai berikut : 𝑥_𝑖+1= 𝑥_𝑖+¹

6(𝑘₁+ 4𝑘₂+ 𝑘₃)ℎ (2.27) Dalam hal ini 𝑘 adalah :

𝑘₁ = 𝑓 (𝑡_𝑖, 𝑥_𝑖)

𝑘₂ = 𝑓 (𝑡_𝑖+ ℎ , 𝑥_𝑖+ 𝑘₁ℎ)

𝑘₃ = 𝑓 (𝑡_𝑖+ ℎ , 𝑥_𝑖− 𝑘₁ℎ + 2𝑘₂ℎ )

(30)

Metode Runge-Kutta Orde 4 merupakan metode yang lebih teliti dibandingkan dengan metode Runge-Kutta Orde 2 dan metode Runge-Kutta Orde 3. Oleh karena itu, metode Runge-Kutta Orde 4 sering digunakan untuk menyelesaikan persamaan diferensial. Metode Runge-Kutta orde empat diturunkan dengan cara yang sama seperti metode Runge-Kutta Orde 2 untuk nilai 𝑛 = 4. Metode Runge-Kutta Orde 4 mempunyai bentuk persamaan sebagai berikut :

𝑥_𝑖+1= 𝑥_𝑖+¹

6(𝑘₁+ 2𝑘₂+ 2𝑘₃+ 𝑘₄)ℎ (2.28) Dalam hal ini 𝑘 adalah :

𝑘₁ = 𝑓 (𝑡_𝑖, 𝑥_𝑖) 𝑘₂ = 𝑓 (𝑡_𝑖+1

2ℎ , 𝑥_𝑖+1 2𝑘₁ℎ) 𝑘₃ = 𝑓 (𝑡_𝑖+1

2ℎ , 𝑥_𝑖+1 2𝑘₂ℎ ) 𝑘₄ = 𝑓 (𝑡_𝑖+ ℎ , 𝑥_𝑖+ 𝑘₃ℎ)

2.6 Model Epidemi SIR

Model epidemi SIR pertama kali dikenalkan oleh Kermack dan Mc. Kendrick pada tahun 1927. Model tersebut terdiri dari tiga kategori, yaitu Susceptible (S) atau kelompok yang memiliki potensi untuk terinfeksi penyakit. Infectious (I) atau kelompok yang telah terinfeksi dan dapat menyebarkan penyakit tersebut kepada individu yang rentan.

Recovered (R) atau kelompok yang telah sembuh atau kekebalan tubuhnya telah kembali normal sehingga kebal terhadap penyakit Tuberkulosis tersebut. Model SIR pertama kali dikembangkan untuk mengetahui laju penyebaran dan kepunahan suatu wabah penyakit dalam suatu populasi tertutup dan bersifat epidemi.

Menurut Yau dan Nweze (2011), model SIR dibangun berdasarkan asumsi-asumsi sebagai berikut :

1. Populasi adalah tetap (konstan).

2. Satu-satunya cara individu dapat meninggalkan kelompok rentan yaitu dengan cara terinfeksi penyakit. Satu-satunya cara individu yang terinfeksi ingin sembuh,

(31)

13

yaitu dengan proses pemulihan. Setelah itu, individu dapat sembuh, dan memiliki kekebalan tubuh.

3. Usia, seks dan ras tidak memengaruhi seseorang terinfeksi.

4. Tidak ada kekebalan tubuh yang diwariskan.

5. Anggota dari populasi campuran memiliki interaksi yang sama dengan satu sama lain pada tingkat yang sama.

Total populasi (N) diasumsikan konstan karena kelahiran dan kematian diasumsikan memiliki laju yang sama dan pengaruh luar tidak diperhatikan. Maka persamaannya adalah

𝑁 = 𝑆 + 𝐼 + 𝑅

Dengan N merupakan jumlah populasi total dari suatu kelompok masyarakat. Model SIR diawali dengan beberapa notasi yaitu sebagai berikut :

𝑑𝑆

𝑑𝑡 = −𝑟𝑆𝐼 (2.9)

𝑑𝐼

𝑑𝑡= 𝑟𝑆𝐼 − 𝑎𝐼 (2.10)

𝑑𝑅

𝑑𝑡 = 𝑎𝐼 (2.11)

Keterangan :

𝑆 = Jumlah individu rentan dalam populasi pada waktu 𝑡 𝐼 = Jumlah individu terinfeksi dalam populasi pada waktu 𝑡 R = Jumlah individu sembuh dalam populasi pada waktu 𝑡 𝑎 = Laju kesembuhan dari Infectious (I) menjadi Recovered (R) 𝑟 = Laju kesembuhan dari Susceptible (S) menjadi Infectious (I)

2.6.1 Model Epidemi SIR Pada Penyebaran Penyakit Tuberkulosis

Dalam pembentukan model matematika penyebaran penyakit Tuberkulosis (Fredlina et al., 2012), populasi (𝑁) dibagi menjadi 3 sub populasi, yaitu Susceptible (𝑆), Infectious (𝐼) dan Recovered (𝑅).

Jumlah populasi 𝑆 akan bertambah karena kelahiran sebesar 𝜋, dengan 𝜋 adalah konstan. 𝑆 akan berkurang karena kematian dengan laju 𝜇. Kontak langsung individu

(32)

rentan dengan individu yang terinfeksi akan menyebabkan individu pada populasi rentan ikut terinfeksi dan akan masuk menjadi populasi 𝐼. Hal ini menyebabkan berkurangnya populasi 𝑆. Laju penularan penyakit Tuberkulosis adalah 𝑏.

Kelas 𝐼 menyatakan individu yang terinfeksi dan dapat menularkan Tuberkulosis kepada oranglain. Berkurangnya populasi ini disebabkan oleh kematian karena faktor lain dengan laju 𝜇 dan kematian karena penyakit Tuberkulosis dengan laju 𝜇_𝑡. Individu yang terinfeksi Tuberkulosis dapat sembuh secara spontan dengan laju 𝑐 dan masuk dalam populasi 𝑅. Hal ini juga menyebabkan berkurangnya populasi 𝐼. Individu dalam kelas 𝑅 diasumsikan tidak akan kambuh kembali menjadi penderita Tuberkulosis. Berkurangnya populasi ini disebabkan oleh kematian dengan laju 𝜇.

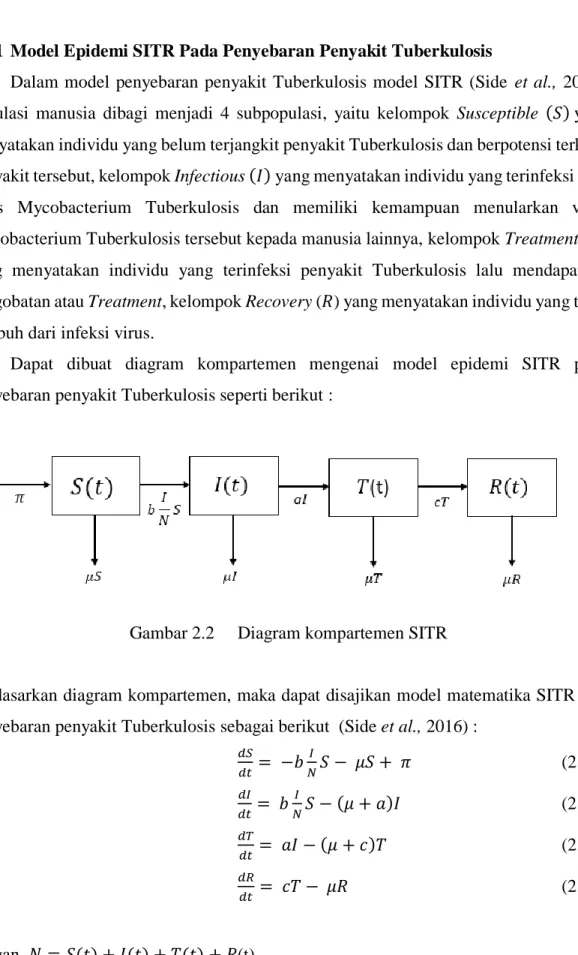
Dapat dibuat diagram kompartemen mengenai model epidemi SIR pada penyebaran penyakit Tuberkulosis seperti berikut :

Gambar 2.1 Diagram kompartemen SIR

Berdasarkan diagram kompartemen, maka dapat disajikan model matematika SIR dari penyebaran penyakit Tuberkulosis sebagai berikut (Fredlina et al., 2012) :

𝑑𝑆

𝑑𝑡 = −𝑏_𝑁^𝐼𝑆 − 𝜇𝑆 + 𝜋 (2.12)

𝑑𝐼 𝑑𝑡= 𝑏 ^𝐼

𝑁𝑆 − (𝜇 + 𝜇_𝑡+ 𝑐)𝐼 = 𝑏 ^𝐼

𝑁𝑆 − (𝜇 + 𝑐)𝐼 (2.13)

𝑑𝑅

𝑑𝑡 = 𝑐𝐼 − 𝜇𝑅 (2.14)

dengan, 𝑁 = 𝑆(𝑡) + 𝐼(𝑡) + 𝑅(𝑡).

(33)

15

Tabel 2.1 Penjelasan variabel yang digunakan pada model SIR

No Variabel Definisi Syarat

1. 𝑆(𝑡) Jumlah individu yang rentan dalam populasi pada waktu ke-𝑡

𝑆(𝑡) > 0

2. 𝐼(𝑡) Jumlah individu yang terinfeksi dalam populasi pada waktu ke-𝑡

𝐼(𝑡) ≥ 0

3. 𝑅(𝑡) Jumlah individu yang sembuh dalam populasi pada waktu ke-𝑡

𝑅(𝑡) ≥ 0

Tabel 2.2 Penjelasan parameter yang digunakan pada model SIR

No Parameter Definisi Nilai

1. 𝜋 Laju kelahiran manusia (konstan) 𝜋 > 0

2. 𝑏 Laju Penularan Penyakit

Tuberkulosis

[0,∞]

3. 𝑐 Laju Kesembuhan Individu yang Terinfeksi

[0,∞]

4. 𝜇 Laju Kematian manusia karena faktor lain

[0,∞]

(34)

Tabel 2.2 Penjelasan parameter yang digunakan pada model SIR (Lanjutan) 5. 𝜇_𝑡 Laju Kematian manusia karena

Tuberkulosis

[0,∞]

2.7 Model Epidemi SITR

Model epidemi SITR merupakan model penyebaran penyakit yang membagi populasi menjadi empat subpopulasi, yaitu Susceptible (S) atau kelompok yang memiliki potensi untuk terinfeksi penyakit. Infectious (I) atau kelompok yang telah terinfeksi dan dapat menyebarkan penyakit tersebut kepada individu yang rentan. Treatment (T) atau kelompok yang melakukan pengobatan. Recovered (R) atau kelompok yang telah sembuh atau kekebalan tubuhnya telah kembali normal sehingga kebal terhadap penyakit Tuberkulosis tersebut. Model epidemi SITR merupakan suatu pengembangan dari model SIR. Namun yang membedakannya adalah model epidemi SIR mengasumsikan bahwa individu yang terinfeksi penyakit akan sembuh, sedangkan model SITR mewakili suatu situasi ketika individu yang terinfeksi harus melakukan pengobatan untuk sembuh.

Ada beberapa asumsi yang digunakan dalam pembentukan model SITR, yaitu:

1. Terdapat kelahiran dan kematian dalam suatu populasi (N) 2. Setiap individu yang lahir akan menjadi bagian populasi rentan

3. Termasuk penyakit yang berbahaya, jika terinfeksi dapat menimbulkan kematian 4. Individu yang telah terinfeksi, jika diberikan Treatment (pengobatan) akan kebal terhadap penyakit Tuberkulosis dan tidak menjadi rentan kembali

5. Populasi konstan (tertutup), Artinya 𝑁 = 𝑆(𝑡) + 𝐼(𝑡) + 𝑇(𝑡) + R(t) atau jumlah populasi dalam waktu 𝑡 sama dengan jumlah individu rentan, terinfeksi, terobati dan sembuh.

(35)

17

2.7.1 Model Epidemi SITR Pada Penyebaran Penyakit Tuberkulosis

Dalam model penyebaran penyakit Tuberkulosis model SITR (Side et al., 2016), populasi manusia dibagi menjadi 4 subpopulasi, yaitu kelompok Susceptible (𝑆) yang menyatakan individu yang belum terjangkit penyakit Tuberkulosis dan berpotensi terkena penyakit tersebut, kelompok Infectious (𝐼) yang menyatakan individu yang terinfeksi oleh virus Mycobacterium Tuberkulosis dan memiliki kemampuan menularkan virus Mycobacterium Tuberkulosis tersebut kepada manusia lainnya, kelompok Treatment (𝑇) yang menyatakan individu yang terinfeksi penyakit Tuberkulosis lalu mendapatkan pengobatan atau Treatment, kelompok Recovery (𝑅) yang menyatakan individu yang telah sembuh dari infeksi virus.

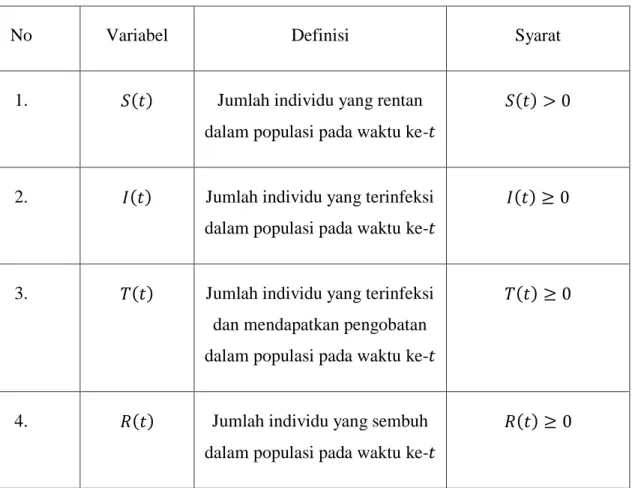
Dapat dibuat diagram kompartemen mengenai model epidemi SITR pada penyebaran penyakit Tuberkulosis seperti berikut :

Gambar 2.2 Diagram kompartemen SITR

Berdasarkan diagram kompartemen, maka dapat disajikan model matematika SITR dari penyebaran penyakit Tuberkulosis sebagai berikut (Side et al., 2016) :

𝑑𝑆

𝑑𝑡 = −𝑏^𝐼

𝑁𝑆 − 𝜇𝑆 + 𝜋 (2.15)

𝑑𝐼 𝑑𝑡= 𝑏 ^𝐼

𝑁𝑆 − (𝜇 + 𝑎)𝐼 (2.16)

𝑑𝑇

𝑑𝑡 = 𝑎𝐼 − (𝜇 + 𝑐)𝑇 (2.17)

𝑑𝑅

𝑑𝑡 = 𝑐𝑇 − 𝜇𝑅 (2.18) dengan, 𝑁 = 𝑆(𝑡) + 𝐼(𝑡) + 𝑇(𝑡) + 𝑅(t).

(36)

Tabel 2.3 Penjelasan variabel yang digunakan pada model SITR

𝑆(𝑡) > 0

𝐼(𝑡) ≥ 0

3. 𝑇(𝑡) Jumlah individu yang terinfeksi dan mendapatkan pengobatan dalam populasi pada waktu ke-𝑡

𝑇(𝑡) ≥ 0

𝑅(𝑡) ≥ 0

Tabel 2.4 Tabel penjelasan parameter yang digunakan pada model SITR

No Parameter Definisi Nilai

1. 𝜋 Laju kelahiran manusia

(konstan)

𝜋 > 0

Tuberkulosis

[0,∞]

3. 𝑐 Laju Kesembuhan Individu [0,∞]

(37)

19

Tabel 2.4 Tabel penjelasan parameter yang digunakan pada model SITR (Lanjutan)

4. 𝜇 Laju Kematian manusia [0,∞]

5. 𝑎 Pemberian treatment

(pengobatan)

[0,∞]

2.8 Model Epidemi SEIR

Model epidemi SEIR merupakan suatu pengembangan dari model SIR, hanya mengalami penambahan sebuah variabel Exposed (𝐸), yaitu individu yang telah terpapar oleh penyakit namun belum sepenuhnya terinfeksi. Model epidemi SEIR merupakan model penyebaran penyakit yang membagi populasi menjadi empat subpopulasi, yaitu susceptible (𝑆) atau kelompok yang memiliki potensi untuk terinfeksi penyakit, Exposed (𝐸) atau kelompok yang telah terpapar namun belum sepenuhnya terinfeksi, Infectious (𝐼) atau kelompok yang telah terinfeksi dan dapat menyebarkan penyakit tersebut kepada individu yang rentan, dan Recovered (𝑅) atau kelompok yang telah sembuh atau kekebalan tubuhnya telah kembali normal sehingga kebal terhadap penyakit.

2.8.1 Model Epidemi SEIR Pada Penyebaran Penyakit Tuberkulosis

Dalam model penyebaran penyakit Tuberkulosis model SEIR (Christyanti dan Syahdan, 2019), dan pada model SEIR oleh (Side et al., 2016) populasi manusia dibagi menjadi 4 subpopulasi, yaitu kelompok Susceptible (𝑆) yang menyatakan individu yang belum terjangkit penyakit Tuberkulosis dan berpotensi terkena penyakit tersebut, kelompok Exposed (𝐸) atau kelompok yang telah terpapar namun belum sepenuhnya terinfeksi, kelompok Infectious (𝐼) yang menyatakan individu yang terinfeksi oleh virus Mycobacterium Tuberkulosis dan memiliki kemampuan menularkan virus Mycobacterium Tuberkulosis tersebut kepada manusia lainnya, dan kelompok Recovery (𝑅) yang menyatakan individu yang telah sembuh dari infeksi virus.

(38)

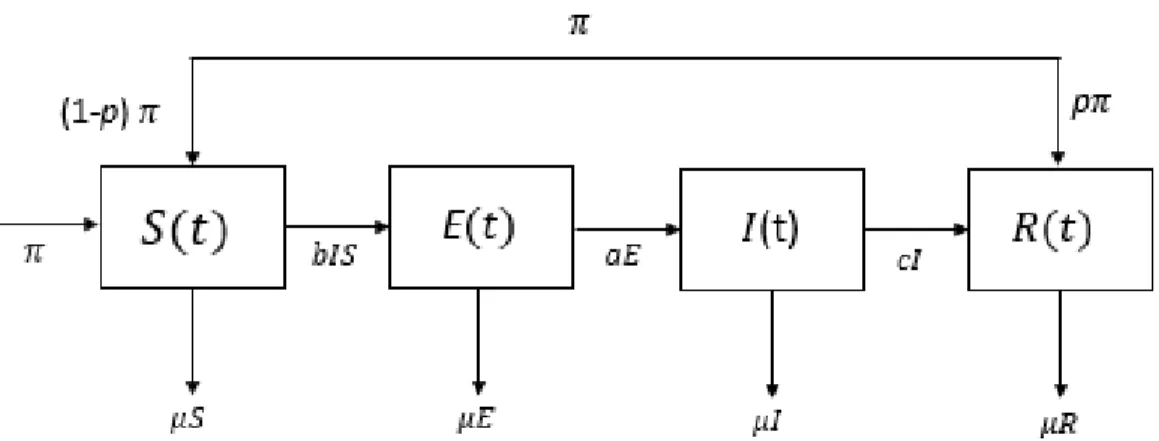
Dapat dibuat diagram kompartemen mengenai model epidemi SEIR pada penyebaran penyakit Tuberkulosis seperti berikut :

Gambar 2.3 Diagram kompartemen SEIR

Berdasarkan diagram kompartemen, maka dapat disajikan model matematika SEIR dari penyebaran penyakit Tuberkulosis sebagai berikut (Christyanti dan Syahdan, 2019) :

^𝑑𝑆

𝑑𝑡 = −𝑏𝑆𝐼 − 𝜇𝑆 + (1 − 𝑝)𝜋 (2.19)

𝑑𝐸

𝑑𝑡 = 𝑏𝑆𝐼 − (𝜇 + 𝑎)𝐸 (2.20)

𝑑𝐼

𝑑𝑡= 𝑎𝐸 − (𝜇 + 𝑐)𝐼 (2.21)

^𝑑𝑅

𝑑𝑡 = 𝜋𝑝 + 𝑐𝐼 − 𝜇𝑅 (2.22)

dengan, 𝑁 = 𝑆(𝑡) + 𝐸(𝑡) + 𝐼(𝑡) + 𝑅(t).

(39)

21

Tabel 2.5 Penjelasan variabel yang digunakan pada model SEIR

𝑆(𝑡) > 0

2. 𝐸(𝑡) Jumlah individu yang laten dalam populasi pada waktu ke-𝑡

𝐸(𝑡) ≥ 0

𝐼(𝑡) ≥ 0

𝑅(𝑡) ≥ 0

Tabel 2.6 Penjelasan parameter yang digunakan pada model SEIR

No Parameter Defenisi Nilai

1. 𝜋 Laju kelahiran manusia

(konstan)

𝜋 ≥ 0

Tuberkulosis

[0,∞]

3. 𝑐 Laju Kesembuhan Individu

yang Terinfeksi

[0,∞]

(40)

Tabel 2.6 Penjelasan parameter yang digunakan pada model SEIR (Lanjutan) 4. 𝑎 Laju transfer dari kelas laten

menjadi terinfeksi

[0,∞]

5. 𝜇 Laju Kematian manusia [0,∞]

6. 𝑝 Proporsi vaksinasi 0 ≤ 𝑝 ≤ 1

(41)

23

BAB 3

METODE RUNGE-KUTTA ORDE 4

Pada bab ini akan diuraikan cara mendapatkan koefisien yang digunakan pada rumus Runge-Kutta Orde 4 (Carnahan et al. 1976; Kandasamy et al. 2006).

Bentuk umum dari Metode Runge-Kutta Orde 4 dapat dilihat pada persamaan (3.1) berikut :

𝑥_𝑖+1 = 𝑥_𝑖+ (𝑎₁𝑘₁+ 𝑎₂𝑘₂+ 𝑎₃𝑘₃+ 𝑎₄𝑘₄)ℎ (3.1)

Dalam hal ini 𝑘 adalah :

𝑘₁ = 𝑓 (𝑡_𝑖, 𝑥_𝑖) (3.2)

𝑘₂ = 𝑓 (𝑡_𝑖+ 𝑝₁ℎ , 𝑥_𝑖+ 𝑞₁₁𝑘₁ℎ) (3.3) 𝑘₃ = 𝑓 (𝑡_𝑖+ 𝑝₂ℎ , 𝑥_𝑖+ 𝑞₂₁𝑘₁ℎ + 𝑞₂₂𝑘₂ℎ ) (3.4) 𝑘₄ = 𝑓 (𝑡_𝑖+ 𝑝₃ℎ , 𝑥_𝑖+ 𝑞₃₁𝑘₁ℎ + 𝑞₃₂𝑘₂ℎ + 𝑞₃₃𝑘₃ℎ) (3.5)

Untuk mendapatkan hasil penurunan dari Metode Runge-Kutta Orde 4 maka dibutuhkan persamaan deret Taylor orde 4 seperti pada persamaan (3.2) berikut :

𝑥_𝑖+1 = 𝑥_𝑖+ 𝑓(𝑡_𝑖, 𝑥_𝑖)ℎ + 𝑓^′(𝑡_𝑖, 𝑥_𝑖)^ℎ²

2!+𝑓^′′(𝑡_𝑖, 𝑥_𝑖)^ℎ³

3! + 𝑓^′′′(𝑡_𝑖, 𝑥_𝑖)^ℎ⁴

4! + 0(ℎ⁵) (3.6)

Selanjutnya, mencari turunan pertama dari deret Taylor 𝑓(𝑡, 𝑥) =^𝑑𝑥

𝑑𝑡 dengan 𝑦 merupakan fungsi implisit dari 𝑡, sehingga diperoleh :

𝑓^′ = 𝑓_𝑡+ 𝑓_𝑥𝑓 (3.7)

Kemudian, mencari turunan kedua dari deret Taylor 𝑓(𝑡, 𝑥) = ^𝑑𝑥

𝑓^′′ = ^𝜕

𝜕𝑡(𝑓^′) + ^𝜕

𝜕𝑥(𝑓^′)𝑓 = ^𝜕

𝜕𝑡(𝑓_𝑡+ 𝑓_𝑥𝑓) + ^𝜕

𝜕𝑥(𝑓_𝑡+ 𝑓_𝑥𝑓)𝑓

(42)

= 𝑓_𝑡𝑡+ ^𝜕

𝜕𝑡(𝑓_𝑥𝑓) + 𝑓_𝑡𝑥𝑓 + ^𝜕

𝜕𝑥(𝑓_𝑥𝑓)𝑓

= 𝑓_𝑡𝑡+ 𝑓_𝑥𝑓_𝑡+ 𝑓_𝑡𝑥𝑓 + 𝑓_𝑥𝑡𝑓 + ^𝜕

𝜕𝑥(𝑓_𝑥𝑓)𝑓

= 𝑓_𝑡𝑡+ 𝑓_𝑥𝑓_𝑡+ 2𝑓_𝑥𝑡𝑓 + 𝑓_𝑡²𝑓 + 𝑓_𝑥𝑥𝑓² (3.8) Kemudian, mencari turunan ketiga dari deret Taylor 𝑓(𝑡, 𝑥) =^𝑑𝑥

𝑓^′′′ = ^𝜕

𝜕𝑡(𝑓^′′) + ^𝜕

𝜕𝑥(𝑓^′′)𝑓

= ^𝜕

𝜕𝑡(𝑓_𝑡𝑡+ 𝑓_𝑡𝑓_𝑥+ 2𝑓𝑓_𝑡𝑥 + 𝑓_𝑥²𝑓 + 𝑓_𝑥𝑥𝑓²) + ^𝜕

𝜕𝑥(𝑓_𝑡𝑡 + 𝑓_𝑡𝑓_𝑥+ 2𝑓𝑓_𝑡𝑥+ 𝑓_𝑥²𝑓 + 𝑓_𝑥𝑥𝑓²)𝑓

= 𝑓_𝑡𝑡𝑡+ 𝑓_𝑡𝑥𝑓_𝑡+ 𝑓_𝑥𝑓_𝑡𝑡+ 2𝑓_𝑡𝑡𝑥𝑓 + 2𝑓_𝑡𝑥𝑓_𝑡+ 2𝑓_𝑡𝑥𝑓_𝑥𝑓 + 𝑓_𝑥²𝑓_𝑡+ 𝑓_𝑡𝑥𝑥𝑓²+ 2𝑓_𝑥𝑥𝑓_𝑡𝑓 + (𝑓_𝑥𝑡𝑡+ 𝑓_𝑥𝑥𝑓_𝑡+ 𝑓_𝑥𝑓_𝑥𝑡+ 2𝑓_𝑥𝑥𝑡𝑓 + 2𝑓_𝑡𝑥𝑓_𝑥+ 2𝑓_𝑥𝑥𝑓_𝑥𝑓 + 𝑓_𝑥³+ 𝑓_𝑥𝑥𝑥𝑓²+ 2𝑓_𝑥𝑥𝑓_𝑥𝑓)𝑓

= 𝑓_𝑡𝑡𝑡+ 𝑓_𝑡𝑥𝑓_𝑡+ 𝑓_𝑥𝑓_𝑡𝑡+ 2𝑓_𝑡𝑡𝑥𝑓 + 2𝑓_𝑡𝑥𝑓_𝑡+ 2𝑓_𝑡𝑥𝑓_𝑥𝑓 + 𝑓_𝑥²𝑓_𝑡+ 𝑓_𝑡𝑥𝑥𝑓²+ 2𝑓_𝑥𝑥𝑓_𝑡𝑓 + 𝑓_𝑥𝑡𝑡𝑓 + 𝑓_𝑥𝑥𝑓_𝑡𝑓 + 𝑓_𝑥𝑓_𝑥𝑡𝑓 + 2𝑓_𝑥𝑥𝑡𝑓²+ 2𝑓_𝑡𝑥𝑓_𝑥𝑓 + 2𝑓_𝑥𝑥𝑓_𝑥𝑓²+ 𝑓_𝑥³𝑓 + 𝑓_𝑥𝑥𝑥𝑓³+ 2𝑓_𝑥𝑥𝑓_𝑥𝑓²