Algoritma Particle Swarm Optimization dan terapannya dalam menyelesaikan masalah pemotongan rol kertas

(1)

ALGORITMA PARTICLE SWARM OPTIMIZATION DAN TERAPANNYA DALAM MENYELESAIKAN MASALAH PEMOTONGAN ROL KERTAS

MAKALAH

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh:

Helvetika Amperiana

NIM: 123114009

PROGRAM STUDI MATEMATIKA

JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(2)

i

ALGORITMA PARTICLE SWARM OPTIMIZATION DAN TERAPANNYA DALAM MENYELESAIKAN MASALAH PEMOTONGAN ROL KERTAS

MAKALAH

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh:

NIM: 123114009

PROGRAM STUDI MATEMATIKA

JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(3)

ii

PARTICLE SWARM OPTIMIZATION ALGORITHM AND ITS APPLICATION IN SOLVING CUTTING PAPER ROLL PROBLEM

A PAPER

Presented as a Partial Fulfillment of the

Requirements to Obtain the Degree of Sarjana Sains

Mathematics Study Program

Written by:

Student ID: 123114009

MATHEMATICS STUDY PROGRAM

DEPARTMENT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

(4)

(5)

(6)

v

HALAMAN PERSEMBAHAN

Ma ka..

Inga t s e la lu ba hwa b e rka t da n ka ru n ia be rba nding lurus de nga n ta n g g u n g ja wa b

da n itu s e mua ha nya da pa t dis e mpurna ka n ole h Ka s ih .

Tuga s a khir ini s a ya pe rs e mba hka n untuk ora ng tua s a ya te rcinta , Ir. Yugianto dan Ho’ing Buddy

(7)

(8)

vii

ABSTRAK

Algoritma Particle Swarm Optimization (PSO) merupakan salah satu algo-ritma optimasi dengan teknik pendekatan heuristik. Pendekatan haeuristik yaitu pendekatan komputasi untuk mencari suatu penyelesaian optimal atau mendekati optimal dari suatu masalah optimasi dengan cara mencoba secara iteratif untuk memperbaiki kandidat solusi dengan memperhatikan batasan kualitas solusi yang diinginkan. Algoritma PSO terinspirasi dari perilaku sekawanan burung atau sekumpulan ikan yang dapat menjelajah ruang solusi secara efektif sehingga mempunyai keefektifan yang baik dalam menyelesaikan masalah.

Makalah ini mengimplementasikan algoritma PSO untuk menyelesaikan masalah pemotongan persediaan kertas, yaitu pada rol kertas jumbo yang akan dipotong untuk mendapatkan rol kertas kecil. Lebar rol kertas kecil ditentukan oleh permintaan pelanggan dan jumlah rol yang dipesan juga berbeda-beda. Tujuannya adalah mencari dan menyusun pola pemotongan dari sebuah rol jumbo menjadi rol kecil sedemikian hingga diperoleh hasil yang optimum. Berdasarkan hasil penelitian ini, diperoleh solusi optimal yaitu jumlah rol jumbo dan sisa yang minimum untuk beberapa kasus pesanan yang masuk. Selanjutnya dibuat suatu program tampilan dengan MATLAB berdasarkan algoritma PSO. Dibandingkan dengan perhitungan software Quantitative Method (QM), yaitu software yang populer digunakan untuk memproses data kuantitatif, hasilnya cukup mendekati.

(9)

viii

ABSTRACT

Particle Swarm Optimization (PSO) algorithm is an optimization algorithm classified as a heuristic approach technique. It seeks an optimal solution or almost optimal in iterative manner. The candidate for solutions are improved iteratively with regards to the quality of the desired solution. PSO algorithm is inspired by the behavior of a flock of birds or school of fish that can explore the solution space effectively so have a good effectiveness in solving the problems.

This paper implements the PSO algorithm to solve the problem of cutting paper supplies. Jumbo paper rolls are cut in to smaller paper rolls which widths are determined by customer demand. The number of rolls are also varied. The goal is to find and develop cutting pattern of jumbo rolls into small rolls so that optimum results are obtained. Based on PSO algorithms written in MATLAB, the optimal solution is obtained which minimizes the use of the number of jumbo rolls for some cases of incoming orders. Compared to the results produced by optimization software QM (Quantitative Methods), the result is quite accurate.

Paper industry produces jumbo paper rolls by using a paper machine. The

(10)

(11)

(12)

xi

DAFTAR ISI

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ...vi

ABSTRAK ... vii

ABSTRACT ... viii

LEMBAR PERNYATAAN PERSETUJUAN ... vii

KATA PENGANTAR ... x

G. Sistematika Penulisan ... 7

BAB II LANDASAN TEORI ... 10

A. Program Linear... 10

B. Program Linear Bilangan Bulat ... 11

C. Masalah Knapsack ... 16

D. Algoritma Particle Swarm Optimization (PSO) ... 29

BAB III MASALAH PEMOTONGAN PERSEDIAAN ... 54

A. Masalah Pemotongan Persediaan (Cutting Stock Problem) ... 54

B. Algoritma PSO Sebagai Pendekatan untuk Pencarian Solusi Optimal CSP 60 BAB IV PENERAPAN ALGORITMA PARTICLE SWARM OPTIMIZATION UNTUK MASALAH PEMOTONGAN ROL KERTAS ... 69

BAB V PENUTUP ... 76

A. Kesimpulan ... 76

B. Saran ... 77

(13)

xii

(14)

1

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Metode heuristik adalah suatu teknik aproksimasi atau pendekatan yang didesain untuk memecahkan masalah optimasi dengan cara mencoba secara iteratif sebagai upaya memperbaiki kandidat solusi dengan memperhatikan batasan kualitas solusi yang diinginkan dengan mengutamakan waktu komputasi dan biasanya menghasilkan solusi yang cukup baik, dalam arti optimal atau mendekati optimal. Metode ini dapat mencari solusi dalam ruang pencarian (search space) yang besar dengan cara memadukan interaksi antara prosedur pencarian lokal dan melakukan pencarian di ruang solusi untuk menemukan solusi global. Selain itu, ada prosedur yang memanfaatkan satu atau lebih titik-titik tetangga (neighborhood structures) sebagai acuan menuju solusi lain. Karena metode ini dapat

menghasilkan solusi yang cukup baik dalam memecahkan permasalahan kombinatorial dengan skala yang cukup besar dan waktu komputasi yang relatif cepat, maka metode ini muncul sebagai alternatif yang dapat beradaptasi dengan baik untuk kasus-kasus sulit dalam konteks industri dan telah mencatatkan sejarah sukses.

(15)

Cat Swarm Optimization (CSO), dan lain-lain. Akan tetapi, yang akan dibahas disini adalah Algoritma Particle Swarm Optimization (PSO) sebagaimana diterapkan dalam penelitian ini dengan tujuan untuk mencapai solusi yang optimal bagi masalah pemotongan kertas.

Particle Swarm Optimization (PSO) diperkenalkan pertama kali oleh James

Kennedy (seorang psikolog sosial) dan Russell Eberhart (seorang insinyur elektro) pada tahun 1995, PSO berasal dari simulasi perilaku kawanan burung. Meskipun sejumlah ilmuwan telah menciptakan simulasi komputer tentang berbagai penafsiran dari gerakan organisme pada kawanan burung atau gerombolan ikan, Kennedy dan Eberhart hanya tertarik pada model yang dikembangkan oleh Heppner (ahli zoologi). Dalam model Heppner ini, burung akan mulai dengan beterbangan di sekitar tanpa tujuan tertentu dan membentuk kawanan secara spontan sampai salah satu burung terbang di atas wilayah yang akan dijadikan tempat bersarang. Bagi Eberhart dan Kennedy, menemukan sebuah tempat bersarang analog dengan menemukan solusi yang baik pada bidang penyelesaian yang memungkinkan. Mereka juga merevisi metodologi Heppner sehingga partikel (individu) akan terbang di atas ruang solusi dan mencoba untuk menemukan solusi terbaik menurut penemuan mereka sendiri dan pengalaman masa lalu dari tetangga mereka. Kita bisa mengutip beberapa karya yang berhasil menggunakan metode ini seperti masalah pemotongan berdasarkan pola oleh Ghassen Ben Lagha dan Xianjun Shen dkk.

(16)

hendak melakukan proses pemotongan kertas dalam rangka untuk memenuhi semua pesanan dari konsumen.

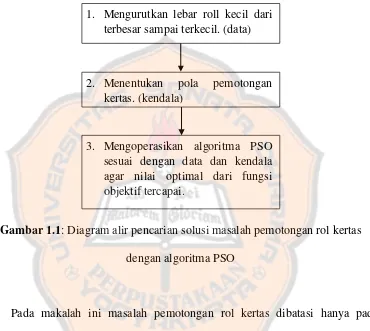
Berikut diagram alir dari pencarian solusi masalah pemotongan rol kertas dengan algoritma PSO.

Gambar 1.1: Diagram alir pencarian solusi masalah pemotongan rol kertas dengan algoritma PSO

Pada makalah ini masalah pemotongan rol kertas dibatasi hanya pada pemotongan dari rol ke rol yang berarti hanya untuk pemotongan dari rol jumbo menjadi rol-rol kecil dan dengan pola pemotongan satu dimensi.

Selebihnya makalah ini mengandung bagian-bagian sebagai berikut: Bagian pertama menyatakan formulasi matematis dan menjelaskan bagaimana mengatasi masalahnya. Bagian kedua yaitu pendekatan dengan algoritma PSO dan fitur-fiturnya. Bagian ketiga akan melaporkan penyelidikan eksperimental. Bagian keempat menyajikan penerapan algoritma PSO yang dapat digunakan secara

1. Mengurutkan lebar roll kecil dari terbesar sampai terkecil. (data)

2. Menentukan pola pemotongan kertas. (kendala)

(17)

langsung untuk menyelesaikan masalah pemotongan kertas satu dimensi (dari rol ke rol) menggunakan GUI yang dibuat dengan menggunakan MATLAB. Dan bagian terakhir berisi kesimpulan dan saran.

Seperti yang sudah disinggung sebelumnya, akan dibahas algoritma PSO sebagai salah satu metode heuristik yang dapat memecahkan permasalahan kombinatorial dengan skala yang cukup besar. Salah satu masalah kombinatorial yang dihadapi sejak masa revolusi industri yang berjaya pada abad terakhir, adalah masalah pemotongan persediaan atau Cutting Stock Problem (CSP) maupun masalah pengurangan sisa atau Trim Loss Problem (TLP). Masalah pemotongan persediaan atau Cutting Stock Problem (CSP) biasanya berkaitan dengan meminimumkan biaya produksi untuk mencapai pemakaian bahan baku yang optimal. Salah satu cara yang ditempuh untuk dapat meminimumkan biaya produksi adalah dengan memproduksi jumlah rol yang sesuai dengan pesanan.

(18)

Sebelum rol jumbo dipotong menjadi potongan kertas atau rol kecil, maka harus diperhitungan berbagai macam kemungkinan pola pemotongan dari rol jumbo tersebut yang kemudian akan dipilih yang paling optimal. Pola tersebut berupa gabungan dari beberapa ukuran kertas atau rol yang diinginkan konsumen. Pembentukan pola tersebut juga harus memperhatikan beberapa kendala agar didapat hasil yang optimal. Dalam 1 rol jumbo yang akan dipotong menjadi rol-rol kecil haruslah memuat pesanan dengan diameter rol, panjang rol, jenis kertas, warna kertas, dan berat yang sama.

Terdapat banyak metode untuk menyelesaikan masalah tersebut salah satunya dengan program linear. Secara umum, masalah program linear dapat dirumuskan sebagai berikut:

Maksimumkan atau minimumkan

� =

Dengan kendala

� {=}

�

dengan = , , … , ₊ � , = , , … , ₊ , � = [

, +

⋱

, +

],

(19)

Dalam mencari penyelesaian program linear, metode yang sering digunakan adalah metode simpleks. Ketika masalah tersebut diaplikasikan dalam dunia industri, dapat dipastikan bahwa akan dilibatkan data dalam jumlah besar sebagai masukan. Semakin besar masalah ukuran ini, semakin banyak penyelesaian dan proses mengoptimumkan menjadi lebih sulit. Oleh karena itu, selain metode simpleks, terdapat metode yang juga dapat digunakan untuk menyelesaikan masalah di atas yaitu metode heuristik.

B. Rumusan Masalah

Berdasarkan latar belakang tersebut, secara garis besar uraian rumusan masalah yang dibahas dalam makalah ini adalah:

a. Bagaimana memodelkan masalah pemotongan kertas agar didapat solusi yang optimal?

b. Bagaimana menyelesaikan masalah pemotongan kertas dengan menggunakan algoritma PSO?

c. Bagaimana menyelesaikan masalah pemotongan kertas dengan menggunakan MATLAB?

C. Pembatasan Masalah

(20)

D. Tujuan Penulisan

Tujuan yang ingin dicapai penulis dalam penulisan makalah ini selain untuk memenuhi syarat makalah dalam program studi Matematika Universitas Sanata Dharma, yaitu sebagai berikut.

a. Memodelkan masalah pemotongan kertas.

b. Menyelesaikan masalah pemotongan kertas dengan algoritma PSO. c. Menyelesaikan masalah pemotongan kertas dengan aplikasi MATLAB.

E. Manfaat Penulisan

Manfaat penulisan dari makalah ini adalah:

a. Dapat memodelkan dan mengaplikasikan program linear dalam masalah pemotongan kertas.

b. Dapat membantu berbagai pihak untuk menentukan pola pemotongan kertas yang optimal.

F. Metode Penulisan

Metode yang digunakan penulis dalam penyusunan makalah yaitu studi pustaka, yaitu dengan mempelajari buku atau jurnal yang berkaitan dengan masalah pemotongan persediaan (cutting stock problem).

G. Sistematika Penulisan

(21)

B. Perumusan Masalah C. Pembatasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan

BAB II. PROGRAM LINEAR DAN METODE HEURISTIK A. Program Linear

B. Program Linear Bilangan Bulat C. Masalah Knapsack

D. Algoritma Particle Swarm Optimization (PSO)

BAB III. MASALAH PEMOTONGAN PERSEDIAAN

A. Masalah Pemotongan Persediaan (Cutting Stock Problem) B. Pencarian Solusi Optimal dengan Algoritma PSO

BAB IV. PENERAPAN ALGORITMA PSO UNTUK MENYELESAIKAN MASALAH PEMOTONGAN ROL KERTAS

(22)

(23)

10

BAB II

LANDASAN TEORI

A. Program Linear

Program linear adalah sebuah metode matematis yang berkarakteristik linear untuk menemukan suatu penyelesaian optimal dengan cara memaksimumkan atau meminimumkan fungsi obyektif atau tujuan terhadap suatu susunan kendala. Istilah program linear secara eksplisit telah menunjukkan karakteristiknya. Model matematika harus berupa fungsi linear dan penyelesaian optimal diturunkan melalui teknik optimasi linear.

Bentuk baku model matematis program linear dapat dilihat: Fungsi obyektif/tujuan:

Maksimumkan/minimumkan = ∑ ₌ Terhadap fungsi kendala-kendala

∑ {=}

=

(2.1)

dengan : Variabel keputusan ke-j : Parameter fungsi tujuan ke-j : Kapasitas kendala ke-i

: Parameter fungsi tujuan ke-i untuk variabel keputusan ke-j

∶ , , … ,

(24)

dengan setiap pertidaksamaan yang memiliki simbol, , , =, hanya dipilih salah satu. Fungsi obyektif atau fungsi tujuan disebut juga fungsi linear. Dengan disebut koefisien teknis, disebut koefisien ongkos, dan disebut suku tetap di

ruas kanan disingkat “suku tetap” atau “ruas kanan”. Jika , = , … , memenuhi

semua kendala, maka disebut penyelesaian layak. Penyelesaian layak yang juga mengoptimumkan disebut penyelesaian optimum.

Setiap masalah minimum dapat dilihat seperti masalah maksimum dan sebaliknya. Ini dapat terlihat dari pengamatan berikut

∑

=

= − ⁡ − ∑

=

(2.2)

Itu berarti untuk meminimumkan fungsi tujuan kita dapat memaksimumkan negatif dari fungsi tujuannya kemudian menegatifkan lagi hasil maksimumnya.

Solusi yang digunakan untuk menyelesaikan masalah program linear yaitu dengan metode grafik dan metode simpleks. Metode grafik digunakan untuk memecahkan persoalan model program linear dua variabel. Lalu pada tahun 1947 G. Dantzig mengembangkan metode yang dapat memecahkan persoalan model program linear dengan lebih dari dua variabel yang disebut metode simpleks. Namun kedua metode tersebut tidak akan dibahas di sini.

B. Program Linear Bilangan Bulat

(25)

mewakili item yang utuh dan tidak dapat dipecah seperti pada: masalah Knapsack dan masalah pemotongan persediaan. Program linear bilangan bulat adalah sebuah model penyelesaian matematis yang memungkinkan solusi masalah program linear yang berupa bilangan pecahan diubah menjadi bilangan bulat tanpa meninggalkan optimalitas penyelesaian. Program linear bilangan bulat secara umum terbagi menjadi 3 jenis yaitu program linear bilangan bulat murni (pure), program linear bilangan bulat campuran (mixed), dan program linear bilangan bulat 0-1 (binary). Program linear bilangan bulat murni terjadi apabila semua variabel dalam solusi optimal merupakan bilangan bulat. Sedangkan program linear bilangan bulat campuran terjadi apabila variabelnya ada yang bukan bilangan bulat. Selanjutnya untuk program linear bilangan bulat 0-1 (biner) secara khusus mensyaratkan agar semua variabel dalam solusi optimal harus merupakan bilangan bulat bernilai 0 atau 1.

Untuk masalah program linear bilangan bulat yang kasusnya besar, metode yang biasa digunakan yaitu metode pemotongan bidang (Cutting Plane), dan metode cabang dan batas (Branch and Bound). Namun disini hanya akan dibahas metode cabang dan batas untuk penyelesaian masalah program linear bilangan bulat.

Metode Pencabangan dan Pembatasan (Branch and Bound Method)

(26)

(integer). Metode ini diusulkan pertama kali oleh A. H. Land dan A. G. Doig pada tahun 1960.

Metode ini secara umum dimulai dengan mencari solusi masalah program linear tanpa menambahkan syarat bahwa penyelesaian optimalnya harus berupa bilangan bulat.

1. Jika secara kebetulan penyelesaian optimal yang didapat berupa bilangan bulat, maka penyelesaian ini juga merupakan penyelesaian masalah program linear bulatnya.

2. Jika penyelesaian yang didapat bukan bilangan bulat, maka selanjutnya kendala baru yang membatasi nilai salah satu variabel yang tidak bulat ditambahkan.

3. Penambahan ini mengakibatkan terbaginya daerah layak menjadi 2 bagian sehingga terbentuklah 2 sub-masalah baru yang kemudian harus diselesaikan. Dengan kata lain, terjadi pencabangan dari masalah aslinya menjadi 2 sub-masalah baru.

4. Batas untuk nilai fungsi obyektif atau fungsi tujuan kemudian dapat ditentukan. Batas ini dapat digunakan untuk mengeliminasi sub-masalah yang tidak diperlukan dan menentukan apakah penyelesaian optimalnya sudah tercapai.

5. Jika penyelesaian yang didapat belum optimal, maka sub-masalah baru dipilih dan proses pencabangan berlanjut.

(27)

syarat bahwa nilai dari variabel-variabelnya harus berupa bilangan bulat diabaikan untuk sementara. Apabila dalam penyelesaian ini diperoleh variabel-variabel yang tidak bulat, katakanlah maka pasti dapat ditemukan dua bilangan bulat tak negatif dan + sehingga ⁡ < ⁡ < ⁡ + . Selanjutnya, masalah program linear bulat di atas dicabangkan menjadi dua masalah program linear bulat baru dengan menambahkan kendala



⁡ dan ⁡



⁡ + .

Proses pencabangan ini bertujuan untuk mempersempit daerah layak sehingga dapat dilakukan eliminasi terhadap penyelesaian yang tak bulat bagi dari tinjauan selanjutnya, tetapi masih tetap mempertahankan semua penyelesaian bilangan bulat yang mungkin terhadap masalah semula. Kemudian, proses pencabangan ini terus dilakukan hingga diperoleh suatu penyelesaian bilangan bulat yang pertama.

Contoh 2.1

Minimumkan = + Dengan kendala

{ ++

, ⁡dan⁡bilan�an⁡bulat

Penyelesaian:

(28)

Selanjutnya, masalah program linear bulat di atas dicabangkan menjadi dua masalah program linear bulat baru dengan menambahkan kendala



⁡ dan



. Sehingga didapatkan dua sub-masalah baru yang harus diselesaikan sebagai berikut.

Batas untuk nilai tujuan belum dapat ditentukan karena belum mendapatkan penyelesaian bilangan bulat.

Dari submasalah 1 diperoleh penyelesaian = , = , , dan = , . Penyelesaian tidak berbentuk bilangan bulat maka lanjut ke langkah 2.

Langkah 2: Sub-masalah program linear dicabangkan menjadi dua masalah program linear bulat baru dengan menambahkan kendala



dan



.

(29)

Dari sub-masalah 2 diperoleh penyelesaian = , = − , , dan = , . Penyelesaian tidak berbentuk bilangan bulat maka lanjut ke langkah 2.

Langkah 2: Sub-masalah program linear dicabangkan menjadi dua masalah program linear bulat baru dengan menambahkan kendala



dan



.

Karena



tidak berada dalam daerah layak maka kita memilih



sehingga

= . Jadi, diperoleh solusi optimal yaitu = , = , dan = .

C. Masalah Knapsack

Masalah Knapsack adalah masalah program linear bilangan bulat yang hanya memiliki satu kendala dan penyelesaian berupa bilangan bulat. Masalah Knapsack biasanya digunakan untuk menyusun barang ke dalam karung yang besar yang tidak dapat memuat semua barang. Permasalahan Knapsack ini mencari solusi terbaik dari semua kemungkinan susunan barang yang akan dimasukkan ke dalam karung. Masalah Knapsack dapat dituliskan sebagai berikut.

Maksimumkan = ∑₌

dengan kendala

∑

=

(2.3)

(30)

dapat segera dihapus). Perbandingan ⁄ merupakan nilai per satuan ukuran dari barang ke-i atau sebagai efisiensi variabel . Kita asumsikan lagi efisiensi variabel diurutkan secara menurun menurut nilai yang dikandungnya:

⁄ ⁄ ⁄ (2.4)

Untuk setiap solusi optimal dari masalah Knapsack memenuhi:

− ∑

=

< (2.5)

Pertidaksamaan (2.5) artinya sisa ukuran dari karung haruslah kurang dari barang ke-m.

Masalah Knapsack memiliki dua jenis berdasarkan penyelesaiannya yaitu Knapsack (0-1) dan Knapsack bilangan bulat. Pada makalah ini akan menggunakan

Knapsack bilangan bulat yang akan diselesaikan menggunakan metode cabang dan

batas.

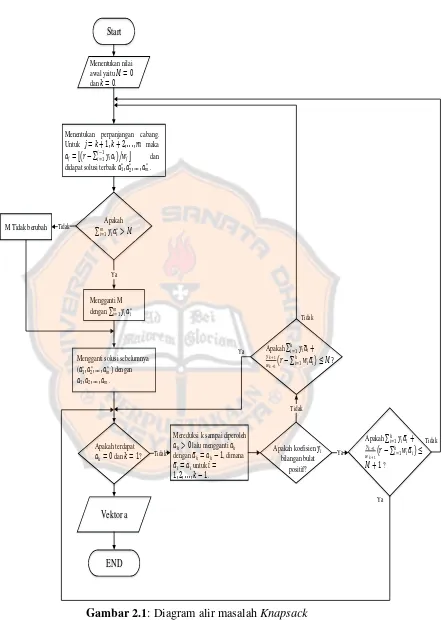
Berikut adalah tahapan untuk menyelesaikan masalah Knapsack dengan metode cabang dan batas.

1. Menentukan nilai awal yaitu = dan = .

2. Menemukan perpanjangan cabang. Untuk = + , + , . . . , maka =

⌊( − ∑₌− )⁄ ⌋. Biasanya untuk = ⁄ . Maka didapat solusi

terbaik ∗, ∗, … , ∗ .

(31)

4. Menemukan cabang selanjutnya.

Menemukan k terbesar sedemikian hingga − dimana > . Kita dapat tuliskan ̅ = untuk = , , . . . , − .

a. Jika k=1 maka berhenti; selain itu ganti k dengan k-1.

b. Jika = , maka kembali ke 4a, selain itu ganti dengan = − . c. Pencarian cabang yang lebih baik.

Jika ∑₌ ̅ + �+1

�+1( − ∑= ̅) (untuk koefisien bukan

bilang-an bulat positif) atau ∑₌ ̅ + �+1

�+1( − ∑= ̅ ) + (untuk

(32)

Start

Mereduksi k sampai diperoleh

> 0 lalu mengganti dengan ̅ = −1, dimana

̅= untuk = 1, 2, . . . , −1.

Tidak Apakah koefisien

bilangan bulat positif? Menentukan perpanjangan cabang.

Untuk = + 1, + 2, . . . , maka

(33)

Contoh 2.2 3. Menentukan apakah solusi yang diperoleh meningkat?

Karena ∑₌ = , > = , maka = , dan ∗ = , ∗ = ∗ ₌ ∗ ₌ _{diganti menjadi} _{= ,} ₌ ₌ ₌ _.

4. Didapatkan k=3 = lalu dikurangkan sampai diperoleh k=1 dimana > . Maka kita ganti = menjadi ̅ = .

(34)

Karena koefisien bukan bilangan bulat positif, maka kita uji pertidaksamaan

Karena pertidaksamaan tersebut tidak terpenuhi maka cabang layak untuk dieksplor. Kembali ke langkah 2.

2. Diketahui k=1 dan = ̅ = , maka diperoleh

(35)

5. Apakah cabang layak untuk dieksplor?

Karena koefisien bukan bilangan bulat positif, maka kita uji pertidaksamaan berikut dengan k=2 dan ̅ = , ̅ = .

Karena pertidaksamaan tersebut terpenuhi maka cabang tidak layak untuk dieksplor. Kembali ke langkah 4.

4. Didapatkan k=2 = lalu dikurangkan sampai diperoleh k=1 dimana > dan kita ganti = dengan ̅ = .

(36)

+ , = , >

2. Diketahui k=1 dan = ̅ = , maka diperoleh 5. Apakah cabang layak untuk dieksplor?

(37)

+ , = , >

2. Diketahui k=3, = ̅ = , = ̅ = , dan = ̅ = , maka diperoleh

4. Didapatkan k=3 = lalu dikurangkan sampai diperoleh k=2 dimana < , maka kita ganti = dengan ̅ = .

(38)

4. Kita peroleh k=2 dimana < , maka kita ganti = dengan ̅ = . 5. Apakah cabang layak untuk dieksplor?

(39)

= , >

2. Diketahui k=1 dan = ̅ = , maka diperoleh

(40)

( . + . ) + / ( − , . + , . )

+ , = ,

(41)

∑ ̅

(42)

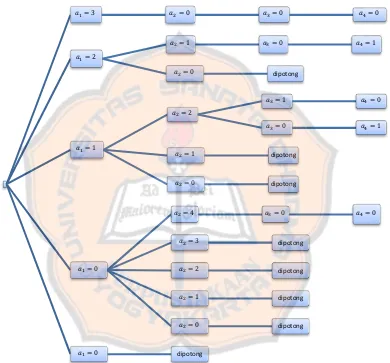
Jadi didapatkan solusi yaitu ∗ = , ∗ = , ∗ = , ∗ = dengan = , ∗ _{= ,} ∗ _{= ,} ∗ _{= ,} ∗ ₌ _dengan ₌ _{, dan} ∗ _{= ,} ∗ _{= ,} ∗ _{= ,} ∗ ₌

dengan = . Berikut pohon enumerasi dari solusi-solusi yang sudah didapat diatas.

Gambar 2.3: Pohon enumerasi yang dihasilkan dari contoh 2.2

D. Algoritma Particle Swarm Optimization (PSO)

Algoritma Particle Swarm Optimization (PSO) meniru perilaku sosial organisme (burung atau ikan), dimana perilaku sosial terdiri dari tindakan individu dan pengaruh dari individu-individu lain dalam suatu kelompok. Tiap-tiap makhluk

(43)

hidup (selanjutnya disebut partikel) akan disebar di ruang pencarian solusi (search space) yang seragam secara acak. Kemudian setiap partikel akan berusaha

berpindah posisi untuk mencari posisi lain yang dapat menghasilkan fungsi obyektif atau tujuan yang lebih baik. Setiap pergerakan partikel akan dipandu oleh dua hal, posisi terbaik yang pernah ditempati partikel tersebut dan posisi terbaik yang pernah ditemui oleh seluruh partikel. Sehingga, partikel-partikel tersebut akan bekerja sama dalam mencari solusi optimal.

Kata partikel menunjukkan, misalnya, seekor burung dalam kawanan burung. Setiap individu atau partikel berperilaku secara terdistribusi dengan cara menggunakan kecerdasannya (intelligence) sendiri dan juga dipengaruhi perilaku kelompok kolektifnya. Dengan demikian, jika satu partikel atau seekor burung menemukan jalan yang tepat atau pendek menuju ke sumber makanan, sisa kelompok yang lain juga akan dapat segera mengikuti jalan tersebut meskipun lokasi mereka jauh di kelompok tersebut.

Dalam algoritma PSO, kawanan diasumsikan mempunyai ukuran tertentu dengan setiap partikel posisi awalnya terletak di suatu lokasi yang acak dalam ruang multidimensi. Setiap partikel diasumsikan memiliki dua karakteristik: posisi dan kecepatan. Setiap partikel bergerak dalam ruang berdasarkan informasi yang diterima mengenai posisi yang baik tersebut. Sebagai contoh, misalnya perilaku burung-burung dalam kawanan burung. Meskipun setiap burung mempunyai keterbatasan dalam hal kecerdasan, biasanya ia akan mengikuti kebiasaan (rule) seperti berikut:

(44)

2. Burung tersebut akan mengarahkan terbangnya ke arah rata-rata keseluruhan burung.

3. Burung akan memposisikan diri dengan rata-rata posisi burung yang lain dengan menjaga jarak sehingga jarak antar burung dalam kawanan itu tidak terlalu jauh.

Dengan demikian, perilaku kawanan burung akan didasarkan pada kombinasi dari 3 faktor simpel berikut:

1. Kohesi – terbang bersama 2. Separasi – jangan terlalu dekat

3. Penyesuaian (alignment) – mengikuti arah bersama Jadi PSO dikembangkan dengan berdasarkan pada model berikut :

1. Ketika seekor burung mendekati target atau makanan (atau bisa minimum atau maksimum dari nilai suatu fungsi tujuan) secara cepat mengirim informasi kepada burung-burung yang lain dalam kawanan tersebut.

2. Burung yang lain akan mengikuti arah menuju ke makanan tetapi tidak secara langsung.

3. Ada komponen yang tergantung pada pikiran setiap burung, yaitu memorinya tentang apa yang sudah dilewati pada waktu sebelumnya.

(45)

solusi dari permasalahan yang dihadapi. Setiap partikel melakukan pencarian solusi yang optimal dengan melintasi ruang pencarian (search space). Hal ini dilakukan dengan cara setiap partikel melakukan penyesuaian terhadap posisi partikel terbaik dari partikel tersebut (local best) dan penyesuaian terhadap posisi partikel terbaik dari seluruh kawanan (global best) selama melintasi ruang pencarian. Jadi, penyebaran pengalaman atau informasi terjadi di dalam partikel itu sendiri dan antara suatu partikel dengan partikel terbaik dari seluruh kawanan selama proses pencarian solusi. Setelah itu, dilakukan proses pencarian untuk mencari posisi terbaik setiap partikel dalam sejumlah iterasi tertentu sampai didapatkan posisi yang relatif tetap (steady) dengan kata lain nilai fungsi mulai konvergen atau iterasi telah mencapai batas yang telah ditetapkan. Pada setiap iterasi, setiap solusi yang direpresentasikan oleh posisi partikel dievaluasi performanya dengan cara memasukkan solusi tersebut ke dalam fungsi kesesuaian (fitness function).

Setiap partikel diperlakukan seperti sebuah titik pada suatu dimensi ruang tertentu. Kemudian terdapat dua faktor yang memberikan karakter terhadap status partikel pada ruang pencarian, yaitu posisi partikel dan kecepatan partikel. Berikut ini merupakan formulasi matematis yang menggambarkan posisi dan kecepatan partikel pada suatu dimensi ruang tertentu:

� = , , ..., _� (2.6)

� = , , ..., _� (2.7)

(46)

menggambarkan mekanisme pembaruan status partikel kecepatan maupun posisi (updating velocity and position), adalah sebagai berikut:

� = � − + . . ��− � − + . . ��− � − (2.8)

� = � + � − (2.9)

dengan �_� = _� , _� , ..., _�� merepresentasikan local best dari partikel ke-i (yang selanjutnya akan dke-isebut sebagake-i partke-icle best). Sedangkan �_� = _� , _� ,

..., _�� merepresentasikan global best dari seluruh kawanan. Sedangkan dan adalah suatu konstanta yang bernilai positif yang biasanya disebut faktor pembelajaran (learning factor) atau faktor percepatan (acceleration factor). Kemudian dan adalah suatu bilangan acak (random) yang bernilai antara 0 sampai 1. Persamaan (2.8) digunakan untuk menghitung kecepatan partikel yang baru berdasarkan kecepatan sebelumnya, jarak antara posisi saat ini dengan posisi terbaik partikel (particle best), dan jarak antara posisi saat ini dengan posisi terbaik kawanan (global best). Kemudian partikel terbang menuju posisi yang baru berdasarkan persamaan (2.9). Setelah algoritma PSO ini dijalankan dengan sejumlah iterasi tertentu hingga mencapai kriteria pemberhentian, maka akan didapatkan solusi yang terletak pada posisi terbaik kawanan (global best).

(47)

Proses untuk mencari nilai minimum menggunakan algoritma PSO yaitu sebagai berikut :

1. Inisialisasi sekumpulan partikel secara acak atau random (setiap partikel merepresentasikan solusi yang mungkin untuk masalah optimasi). 2. Inisialisasi posisi dari setiap partikel (� ) dan kecepatan dari setiap

partikel (� ).

3. Hitung nilai kesesuaian dari setiap partikel berdasarkan formula dan model yang telah ditentukan sesuai dengan masalah optimasinya. 4. Untuk setiap partikel, bandingkan nilai kesesuaian dengan nilai

terbaiknya yang telah dicapai �_� (particle best), jika < �_�, maka �_� diganti dengan .

5. Untuk setiap partikel, bandingkan nilai kesesuaian dengan nilai terbaik yang dicapai dalam populasi �_�(global best), jika < �_�, maka

�� diganti dengan .

6. Berdasarkan bagian 4 dan 5, kecepatan (� ) dan posisi dari partikel (� ) diubah.

Rumus pembaruan kecepatan (� ) :

� = � − + . . ��− � − + . . �� − � −

Adapun rumus pembaruan posisi (� ) adalah � = � − + � . 7. Jika telah mencapai kondisi akhir (mencapai nilai iterasi optimum atau

(48)

minimum) maka perulangan berhenti dan nilai optimumnya didapatkan namun jika belum maka diulangi pada nomor 3.

Berikut Pseudo code dari algoritma PSO :

For setiap partikel Inisialisasi partikel

End

Repeat

For setiap partikel

Hitung nilai kesesuaian

If nilai kesesuaian baru lebih baik daripada nilai kesesuian lama Perbarui nilai kesesuian dari partikel tersebut

End

Pilih partikel dengan nilai kesesuaian terbaik diantara semua partikel tetangganya dan simpan nilai kesesuaian terbaik tersebut

For setiap partikel

Hitung kecepatan partikel menggunakan rumus pertama di atas Perbarui posisi pertikel menggunakan rumus kedua di atas

End

(49)

Berikut ini adalah diagram alir dari algoritma PSO:

Tidak

Ya

Mulai

Bangkitkan parameter dari PSO

Inisialisasi posisi, kecepatan, dan ruang setiap partikel

Evaluasi nilai kesesuianterbaik dari tiap partikel, dan pilih Pbest dan Gbest

Hitung kembali nilai kesesuaian tiap partikel dan perbarui Pbest dan Gbest

Apakah kriteria terpenuhi?

Cetak nilai optimal dari variabel Bangkitkan iterasi dari t = 1

(50)

Cara Kerja Algoritma Particle Swarm Optimization

Misalkan kita mempunyai fungsi berikut: min f(x) dimana

Prosedur PSO dapat dijabarkan dengan langkah-langkah sebagai berikut: 1. Asumsikan bahwa ukuran kelompok atau kawanan (jumlah partikel)

adalah N. Untuk mengurangi jumlah evaluasi fungsi yang diperlukan untuk menemukan solusi, sebaiknya ukuran N tidak terlalu besar, tetapi juga tidak terlalu kecil, agar ada banyak kemungkinan posisi menuju solusi terbaik atau optimal. Jika terlalu kecil, sedikit kemungkinan menemukan posisi partikel yang baik. Terlalu besar juga akan membuat perhitungan jadi panjang. Biasanya digunakan ukuran kawanan adalah 20 sampai 30 partikel.

2. Bangkitkan populasi awal dengan rentang dan secara random sehingga didapat , , . . . , _�. Setelah itu, untuk mudahnya, posisi partikel j dan kecepatannya pada iterasi i dinotasikan sebagai dan . Sehingga partikel-partikel awal ini dinotasikan , , ..., _� dan kecepatan-kecepatan awal ini dinotasikan , , ..., _�. Vektor ,

= , , … , disebut vektor koordinat dari partikel dan vektor ,

(51)

3. Hitung kecepatan dari semua partikel. Semua partikel bergerak menuju titik optimal dengan suatu kecepatan. Awalnya semua kecepatan dari partikel diasumsikan sama dengan nol. Set iterasi = .

4. Pada iterasi ke-i, temukan 2 parameter penting untuk setiap partikel j, yaitu:

a. Nilai terbaik sejauh ini dari (koordinat partikel j pada iterasi i) dan untuk memudahkan penulisan, nyatakan saja sebagai Pbest,j, dengan nilai fungsi obyektif paling rendah (kasus minimasi), f[ ], yang ditemui sebuah partikel j pada semua iterasi sebelumnya. Nilai terbaik untuk semua partikel yang ditemukan sampai iterasi ke-i, kita tuliskan saja sebagai Gbest, dengan nilai fungsi tujuan paling kecil atau minimum diantara semua partikel untuk semua iterasi sebelumnya, f[ ].

b. Hitung kecepatan partikel j pada iterasi ke-i dengan rumus sebagai berikut:

= − + . . Pbest,j⁡–⁡ − + . . Gbest⁡–⁡ − ,⁡dengan

= , , … ,

(52)

adalah 2 sehingga partikel-partikel akan mendekati target sekitar setengah selisihnya.

c. Hitung posisi atau koordinat partikel j pada iterasi ke-i dengan cara = − + ; j = 1, 2, ..., N

Evaluasi nilai fungsi tujuan untuk setiap partikel dan nyatakan sebagai f[ ], f[ ], ..., f[ _�].

5. Cek apakah solusi yang sekarang sudah konvergen. Jika posisi semua partikel menuju ke satu nilai yang sama, maka ini disebut konvergen. Jika belum konvergen maka langkah 4 diulang dengan memperbarui iterasi ⁡ = ⁡ ⁡ + ⁡ , dengan cara menghitung nilai baru dari Pbest,j dan Gbest. Proses iterasi ini dilanjutkan sampai semua partikel menuju ke satu titik solusi yang sama. Biasanya akan ditentukan dengan kriteria penghentian (stopping criteria), misalnya jumlah selisih solusi sekarang dengan solusi sebelumnya sudah sangat kecil.

Contoh 2.3

Kerjakan soal berikut:

min = ⁡– ⁡

dengan

60 ≤ x ≤ 120

(53)

variabel yang akan dicari nilainya. Kemudian tentukan jumlah partikel yang digunakan dalam perhitungan. Diasumsikan dalam kasus ini, jumlah partikel yang digunakan adalah 4 partikel. Tentukan jumlah iterasi yang digunakan oleh setiap partikel untuk melakukan proses. Diasumsikan dalam kasus ini, jumlah iterasi yang digunakan adalah 3 kali. Tentukan total posisi yang harus dicapai. Semua solusi yang ditemukan oleh masing-masing individu harus berjumlah sebanyak variabel ini. Diasumsikan dalam kasus ini, total nilai yang harus dicapai adalah sesuai fungsi obyektif atau fungsi tujuan dan memenuhi batasan nilai yang diberikan yaitu bernilai antara 60 dan 120. Tentukan kecepatan awal untuk perpindahan posisi partikel dalam setiap proses. Diasumsikan dalam kasus ini nilai kecepatan awal adalah 0. Kemudian bobot sosial dalam contoh soal ini diasumsikan = = .

Langkah-langkah penggunaan algoritma ini adalah

1. Inisialisasi data, dengan jumlah partikel = seperti yang sudah ditentukan sebelumnya, didapat populasi awal secara acak (random) misalkan:

= ,

= .

2. Hitung nilai fungsi untuk setiap partikel ⁡ untuk = , , , dan nyatakan dengan:

(54)

= = ,

= = .

3. Seperti yang sudah dipaparkan di atas, ditentukan kecepatan awal =

⁡ = = = dan tetapkan iterasi pertama yaitu = .

4. Selanjutnya ditemukan nilai terbaik lokal sejauh ini yang merupakan posisi partikel terbaik dari partikel tersebut alias � _{� ,} serta nilai terbaik global yang merupakan posisi partikel terbaik dari seluruh kawanan ( _� ).

� � , = ,

� = .

5. Hitung dengan = = dan misalkan nilai bilangan acak (random) yang didapat = . dan = . dengan rumus:

= − + . . Pbest,j⁡–⁡ − + . . Gbest⁡–⁡ −

diperoleh:

= + . . Pbest,1⁡–⁡ + . . Gbest⁡–⁡ = + . − +

. − =

= + . . Pbest,2⁡–⁡ + . . Gbest⁡–⁡ = + . − +

(55)

= + . . Pbest,3⁡–⁡ + . . Gbest⁡–⁡ = + . −

+ . − = −

= + . . Pbest,4⁡–⁡ + . . Gbest⁡–⁡ = + . − +

. − = .

Sehingga nilai sebagai posisi partikel yang baru adalah:

= + = ,

= − = ,

= + . = .

6. Hitung nilai fungsi sekarang pada partikel ⁡ untuk = , , ,

= = ,

= . = .

Sedangkan pada iterasi sebelumnya kita dapatkan

= = ,

= =

7. Nilai ( ) dari iterasi sebelumnya tidak ada yang lebih baik sehingga

� � , baru untuk masing-masing partikel sama dengan nilai nya.

(56)

� � , = ,

� � , = . ,

� = .

Apakah solusi sudah konvergen, dimana nilai dari masing-masing nya sudah dekat? Belum. Maka, lanjutkan ke iterasi berikutnya yaitu = . 8. Hitung kecepatan baru dan misalkan nilai bilangan acak (random)

selanjutnya yang didapat adalah = . dan = . maka diperoleh:

= + . . Pbest,1⁡–⁡ + . . Gbest⁡–⁡ = + . − +

. − =

= + . . Pbest,2⁡–⁡ + . . Gbest⁡–⁡ = + . − +

. − =

= + . . Pbest,3⁡–⁡ + . . Gbest⁡–⁡ = − + . −

+ . − = −

= + . . Pbest,4⁡–⁡ + . . Gbest⁡–⁡ = . + . . −

. + . − . =

Sehingga nilai sebagai posisi partikel yang baru adalah:

= + = ,

= − = ,

= . + = .

(57)

= = ,

Cek kembali, apakah solusi sudah konvergen? Jika belum konvergen, set

= , masuk ke iterasi berikutnya.lanjutkan ke langkah berikutnya dengan

menghitung kecepatan baru dimana = ⁡; ⁡ = , , , dan ulangi langkah-langkah selanjutnya sampai mencapai suatu nilai yang konvergen.

Hasil dari langkah-langkah di atas dapat disajikan dalam bentuk tabel:

(58)

=

Tabel 2.1: Tabel hasil perhitungan PSO secara manual untuk contoh 2.3

(59)

Iteration Best particle Objective fun

1 4 0.0000

2 4 0.0000

3 4 0.0000

4 4 0.0000

---

*********************************************************

Final Results---

bestfun =

0

bestrun =

2

best_variables =

100

*********************************************************

(60)

Berikut adalah grafik konvergensi yang ditampilkan dari best run:

Gambar 2.3: Gambar grafik konvergensi PSO pada run ke 2

Dalam implementasinya, ditemukan bahwa kecepatan partikel dalam PSO standar diperbarui (update) terlalu cepat dan nilai minimum fungsi tujuan yang dicari sering terlewati. Oleh karena itu, kemudian dilakukan modifikasi atau perbaikan terhadap algoritma PSO standar. Perbaikan itu berupa penambahan suatu bobot inersia untuk mengurangi kecepatan pada formula pembaruan (update) kecepatan seperti yang telah disinggung sebelumnya.

(61)

algoritma aslinya yaitu algoritma PSO standar. Biasanya nilai bobot inersia dibuat sedemikian hingga semakin besar iterasi yang dilalui, semakin mengecil kecepatan partikelnya. Nilai ini bervariasi secara linear dalam rentang 0.4 hingga 0.9. Secara matematis perbaikan PSO ini dapat dituliskan sebagai berikut:

= . − + . . Pbest,j⁡–⁡ − + . . Gbest⁡–⁡ − ,⁡dengan = , , … ,

Formula tersebut adalah modifikasi terhadap formula sebelumnya, yaitu:

= − + . . Pbest,j⁡–⁡ − + . . Gbest⁡–⁡ − ,⁡dengan = , , … ,

Perlu diketahui bahwa nilai bobot inersia ( ) yang tinggi menambah posisi pencarian global (global exploration), sedangkan nilai bobot inersia ( ) yang rendah menambah posisi pencarian lokal (local search). Oleh karena itu, supaya tidak terlalu menitikberatkan pada salah satu bagian dan tetap mencari area pencarian yang baru dalam ruang berdimensi tertentu, maka perlu dicari nilai bobot inersia ( ) yang secara imbang menjaga pencarian global dan lokal. Untuk mencapai itu dan mempercepat konvergensi, suatu bobot inersia yang mengecil nilainya dengan bertambahnya iterasi dapat dirumuskan:

= − ( − ) (2.10)

(62)

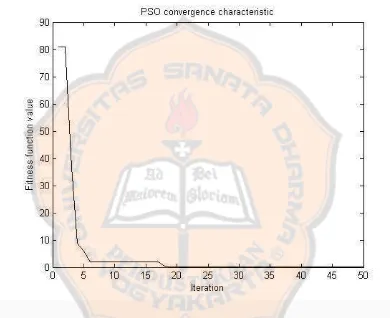
⁡– ⁡ setelah dilakukan modifikasi terhadap PSO (dengan menyertakan bobot inersia) untuk 50 iterasi ditunjukkan dalam gambar 2.3. Terlihat bahwa dengan adanya modifikasi, pergerakan akan lebih cepat konvergen.

Berikut ini diberikan hasil implementasi grafik konvergensi dua jenis PSO:

(63)

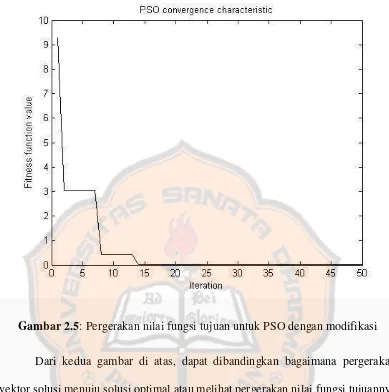
Gambar 2.5:Pergerakan nilai fungsi tujuan untuk PSO dengan modifikasi

Dari kedua gambar di atas, dapat dibandingkan bagaimana pergerakan vektor solusi menuju solusi optimal atau melihat pergerakan nilai fungsi tujuannya dari PSO asli (PSO standar) maupun PSO yang sudah dimodifikasi (disertai bobot inersia).

Contoh 2.4

Contoh berikutnya yaitu bagaimana meminimalkan fungsi tujuan berdimensi lebih dari satu dan memiliki kendala (constraint).

Fungsi obyektif : min = − + − dengan kendala

(64)

Langsung saja kita proses dengan bantuan MATLAB dan didapatkan hasilnya sebagai berikut:

********************************************************* Final Results---

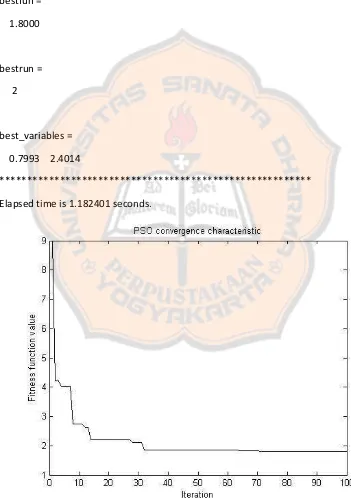
bestfun = 1.8000

bestrun = 2

best_variables = 0.7993 2.4014

********************************************************* Elapsed time is 1.182401 seconds.

(65)

Untuk mendapatkan hasil tersebut, diperlukan dua script program MATLAB yang telah dimodifikasi dari script program asli yang telah dituliskan oleh Nabab Alam. File pertama mendefinisikan fungsi obyektif atau fungsi tujuan, dan file kedua dibangun program utama yang akan memecahkan masalah dengan menggunakan algoritma PSO. Script kode program terlampir. Untuk file pertama diberi nama ofun2.m. Kemudian file ke2 merupakan file program utama.

Setelah script program tersebut dijalankan, diketahui nilai fungsi obyektif (fungsi tujuan) terbaik yang dihasilkan setelah 10 kali independent run adalah 1.8000 dan menghasilkan nilai variabel-variabel terbaik antara lain: x(1) = 0.7993 dan x(2) = 2.4014. Dari 10 run yang dilakukan, diketahui run yang memberikan hasil terbaik adalah run ke-2. Simulasi ini memerlukan waktu 1.182401 detik. Kita juga dapat melakukan perhitungan tanpa kendala dengan mengganti fungsi objektif pada file pertama. Sebagai contoh, kita akan kerjakan lagi contoh yang tadi tetapi tanpa kendala dan mengubah nama script ofun2.m menjadi ofun.m Kita juga harus mengubah kata ofun2 menjadi ofun pada baris 32 dan baris 73 pada file kedua (program PSO utama). Script utuh dapat diperiksa pada lampiran.

Hasilnya adalah sebagai berikut:

********************************************************* Final Results---

(66)

best_variables = 2 3

********************************************************* Elapsed time is 0.501870 seconds.

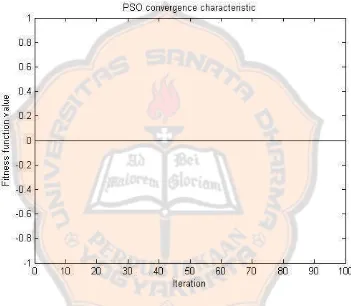
Tampilan grafik konvergensi pada best run adalah:

(67)

54

BAB III

MASALAH PEMOTONGAN PERSEDIAAN

A. Masalah Pemotongan Persediaan (Cutting Stock Problem)

Masalah pemotongan persediaan pertama kali dijelaskan di awal era pemrograman linear. Gilmore dan Gomory (1961) adalah yang pertama merumuskan masalah pemotongan persediaan. Masalah dalam bentuk yang paling sederhana dapat digambarkan sebagai berikut: materi yang diberikan yang tersedia dalam berbagai bentuk dan ukuran tertentu, dipotong agar bisa menghasilkan bentuk dan ukuran tertentu yang diinginkan, sehingga dapat meminimalkan beberapa tujuan seperti biaya. Tergantung pada jenis bahan dan pola pemotongan berdasarkan pertimbangan, kita membedakan masalah pemotongan diantaranya satu, dua, dan tiga dimensi. Sebagai contoh, pemotongan kertas koran untuk panjang yang berbeda adalah masalah pemotongan satu dimensi. Karena lebar koran tetap sama, sementara hanya panjangnya yang bervariasi atau beragam. Pada makalah ini, hanya akan dibahas masalah pemotongan persediaan satu dimensi.

Dalam suatu industri kertas, mesin kertas (paper machine) memproduksi rol kertas jumbo, dengan lebar maksimum yang sudah ditetapkan yang disebut dengan deckle. Kemudian rol jumbo melewati beberapa proses proses produksi dalam

(68)

Masalah pemotongan persediaan satu dimensi yang akan dibahas adalah tentang pemotongan rol jumbo menjadi potongan rol kecil dengan ukuran yang bervariasi. Berikut gambar pemotongan satu dimensi dari rol jumbo menjadi rol kecil.

Gambar 3.1:Pemotongan rol jumbo menjadi beberapa bagian (rol kecil). Misalkan terdapat n kemungkinan pola pemotongan untuk rol jumbo dengan lebar , rol kecil memiliki lebar untuk = , … , , dan � adalah banyaknya rol kecil dengan lebar (� bilangan bulat non negatif) sehingga ∑₌ � . Maka masalah pemotongan ini dapat diselesaikan dalam program linier sebagai berikut.

Minimumkan

= ∑

=

(3.1)

Dengan kendala

∑ �

=

(69)

dan � adalah banyaknya rol kecil dengan lebar dalam pola pemotongan ke-j, adalah banyaknya permintaan rol kecil dengan lebar , variabel menunjukkan banyaknya rol jumbo yang dipotong pada jenis pemotongan ke- , variabel mewakili banyaknya variasi lebar kertas potongan (rol kecil), variabel menunjukkan banyaknya kemungkinan pemotongan yang dapat dilakukan sesuai dengan variasi lebar kertas sesuai pesanan (pola pemotongan).

Contoh 3.1

Sebuah industri kertas menghasilkan rol jumbo dengan lebar 3 meter. Pelanggan menginginkan rol dengan lebar yang lebih kecil. Dari rol jumbo dapat dipotong ke dalam 2 rol dengan lebar 93 cm, 1 rol dengan lebar 108 cm, dan menyisakan rol dengan lebar 6 cm.

Misalkan pesanan yang diterima adalah sebagai berikut. Banyak rol Lebar rol (cm)

97 135

610 108

395 93

211 42

Tabel 3.1: Tabel pesanan yang diterima

(70)

Ada 12 kemungkinan cara memotong rol jumbo ke dalam rol kecil sesuai pesanan (dengan sisa pemotongan kurang dari 42 cm) yaitu:

Kemungkinan Lebar rol

135 108 93 42

1 2 0 0 0

2 1 1 0 1

3 1 0 1 1

4 1 0 0 3

5 0 2 0 2

6 0 1 2 0

7 0 1 1 2

8 0 1 0 4

9 0 0 3 0

10 0 0 2 2

11 0 0 1 4

12 0 0 0 7

(71)

Pola 1 dari tabel di atas berarti 1 rol jumbo dengan lebar 3 meter akan dipotong menjadi 2 rol kecil dengan lebar 135 cm. Pola 2 berarti 1 rol jumbo akan dipotong menjadi 1 rol kecil dengan lebar 135, 1 rol kecil dengan lebar 108 dan 1 rol kecil dengan lebar 42 cm. Demikian seterusnya berlaku cara membaca data yang sama untuk pola-pola pemotongan yang lain.

Untuk setiap kemungkinan pola � di atas, kita memperkenalkan variabel yang menunjukkan banyaknya rol jumbo yang harus dipotong menurut pola

�. Dengan demikian, fungsi tujuan adalah meminimumkan jumlah rol jumbo yang

dipotong yaitu ∑ ₌ . Agar pesanan terpenuhi maka untuk setiap ukuran lebar yang dipesan ditambahkan 1 kendala. Sebagai contoh, untuk pesanan 395 rol dengan lebar 93 cm, maka fungsi kendala dapat dituliskan

+ + + + +

yang berarti jumlah rol kecil dengan lebar 93 cm yang dihasilkan dengan memotong rol jumbo menurut berbagai pola pemotongan tidak boleh kurang dari 395 rol (jumlah rol pesanan). Demikian seterusnya sehingga diperoleh masalah program linier berikut.

Minimumkan

∑

=

Dengan kendala

(72)

+ + +

+ + + +

+ + + + + + + +

Masalah tersebut dapat diselesaikan dengan program QM for Windows yang merupakan perangkat lunak digunakan untuk membantu proses perhitungan secara teknis pengambilan keputusan secara kuantitatif. Program ini menyediakan modul-modul dalam area pengambilan keputusan bisnis seperti assignment, forecasting, integer programming, linear programming, quality control, inventory, dan

lain-lain.

Berikut adalah hasil yang didapat menggunakan QM.

(73)

Dari gambar di atas, didapatkan solusi optimal yaitu = , , = , ,

= , , dan selainnya bernilai 0. Itu berarti untuk memenuhi pesanan diperlukan rol sebanyak 48,5 untuk pola pemotongan pertama, 206,25 rol untuk pola pemotongan kelima, dan 197,5 rol untuk pola pemotongan keenam. Dengan demikian, banyaknya rol jumbo yang digunakan sebanyak 452,25 rol.

Ketika kita melibatkan masalah pemotongan persediaan dalam dunia industri kertas, tentu saja penyelesaian kasus pada masalah ini adalah dengan menyertakan data sebagai input. Secara umum, masalah-masalah ini sangat luas dan kompleks untuk diselesaikan sampai mendapat solusi eksak. Oleh karena itu, metode heuristik menjadi salah satu algoritma yang diharapakan dapat berjalan dengan baik untuk menemukan solusi yang optimal.

B. Algoritma PSO Sebagai Pendekatan untuk Pencarian Solusi Optimal

CSP

Seperti yang sudah dibahas sebelumnya, algoritma Particle Swarm Optimization (PSO) adalah algoritma evolusioner berbasis populasi yang

(74)

Potongan partikel A. Pengkodean Partikel

Pengkodean untuk partikel ini didesain sebagai vektor berukuran m (setara dengan jumlah potongan yang diminta). Posisi j pada partikel menandai persediaan kertas di mana bagian j tersebut dipotong pada saat iterasi ke-i.

Contoh:

Misal: � = , , ,

kita dapat mencatat bahwa solusi ini sesuai dengan ekstraksi 4 potongan dari 3 jenis panjang kertas. Sesuai dengan contoh ini, solusi atau partikel diilustrasikan sebagai berikut:

Gambar 3.2 : Ilustrasi partikel B. Fungsi Fitness

Fungsi Fitness pada masalah pemotongan persediaan ini merupakan fungsi obyektif yang bertujuan untuk mengevaluasi setiap partikel dan menemukan banyaknya kertas yang digunakan. Nilai fitness dihitung sebagai penjumlahan semua nilai fungsi obyektif dari masing-masing variabel (partikel).

C. Populasi Awal

(75)

D. Pergerakan Partikel

Setelah pembangkitan populasi awal, sebuah seleksi dilakukan untuk memilih partikel pemimpin atau solusi terbaik global. Operasi perhitungan dilakukan pada setiap iterasi untuk memilih antara Terbaik Global (Gbest) dan partikel acak untuk membawanya lebih dekat ke solusi yang optimal. Pada saat itu, kawanan tumbuh dan merangkak dengan optimal sampai tercapai kriteria penghentiannya.

Pada setiap iterasi dalam algoritma, setiap partikel xj memodifikasi kecepatan -nya dan posisi tergantung pada dua elemen penting: Sebuah lokal utama yaitu

� dan yang kedua yang mewakili perilaku sosial dari kawanan yaitu .

Kecepatan yang mengontrol pergerakan partikel ini dirancang sebagai berikut:

= − + × (� − − ) + × ( − − )

= − ₊

Selanjutnya, kita mendefinisikan operator yang dipakai persamaan di atas: 1. Operator Pengurangan: Operator (−) merupakan pengurangan untuk

mendapatkan selisih nilai antara posisi saat ini dengan partikel ke-j pada iterasi sebelumnya, − dan posisi yang diinginkan sebagai � − maupun dapat disajikan oleh vektor dari n elemen di mana, setiap elemen menunjukkan bahwa apakah isi dari elemen yang berkoresponden dalam − memenuhi kondisi yang diinginkan atau tidak. Jika ya, elemen akan mendapat nilai dari � − atau .

(76)

operator ini, partikel memiliki peluang untuk melakukan penyimpangan posisi.

3. Operator Penambahan: Hasil operator (+) ini sebenarnya memiliki misi pertukaran informasi struktural yang dikembangkan selama pencarian.

Berikut adalah hasil penyelesaian masalah pemotongan persediaan kertas sesuai contoh yang dapat ditampilkan setelah dieksekusi dengan algoritma PSO dengan bantuan MATLAB:

********************************************************* Final Results---

bestfun = 452.2747

bestrun = 5

best_variables = Columns 1 through 9

48.5080 0 0 0 206.2667 197.5001 0 0 0 Columns 10 through 12

0 0 0

>> Elapsed time is 15.217224 seconds.

(77)

Hasil perhitungan dengan algoritma PSO yang dijalankan pada program MATLAB tidak berbeda jauh dengan hasil perhitungan yang dilakukan oleh software QM, didapatkan solusi optimal yaitu = . , = . ,

= . , dan selainnya bernilai 0. Itu berarti untuk memenuhi pesanan diperlukan rol sebanyak 48.5080 untuk pola pemotongan pertama, 206.2667 rol untuk pola pemotongan kelima, dan 197.5001 rol untuk pola pemotongan keenam. Dengan demikian, banyaknya rol jumbo yang digunakan sebanyak 452.2747 rol.

(78)

Metode First-Fit Decreasing

Pada iterasi ke-j dari metode ini yaitu menemukan pola pemotongan rol jumbo ke-j. Iterasi dimulai dengan sisa permintaan setelah jumlah rol dibulatkan ke bawah yaitu ′, ′, … , ′ . Pola pemotongan yang dihasilkan untuk setiap iterasi

Mencari solusi bilangan bulat untuk contoh 3.1 didapatkan hasil Pola

(79)

Karena solusi belum bernilai bilangan bulat, maka dengan menggunakan metode first-fit decreasing solusi diubah menjadi bilangan bulat.

Pertama, semua solusi yang diperoleh dibulatkan ke bawah. Sehingga untuk pola 1 memerlukan 48 rol, pola 2 memerlukan 206 rol, dan pola 3 memerlukan 197 rol. Karena semua solusi dibulatkan ke bawah, maka jumlah produksi rol pesanan kurang atau sama dengan permintaan rol.

Lebar Rol ( ) Permintaan ( ) Produksi ( ∗ ) Sisa ( ′)

135 cm 97 rol 96 rol 1 rol

108 cm 610 rol 609 rol 1 rol

Tabel 3.5: Tabel nilai solusi yang sudah dibulatkan ke bawah dan sisa produksinya

Iterasi 1

Diketahui ′ = , ′ = , ′ = , ′ = .

= { _⁄′ = { _⁄ = { =

= {

′

⌊( − ∑

=

(80)

(81)

Sehingga didapatkan ′ = , ′ = , ′ = , ′ = . Proses iterasi diberhentikan karena semua pesanan sudah terpenuhi. Jadi, didapatkan 2 rol tambahan dengan 2 pola yang berbeda.

Pola

Lebar rol pesanan

Jumlah rol

135 108 93 42

1 2 0 0 0 48

2 0 2 0 2 206

3 0 1 2 0 197

4 1 1 0 0 1

5 0 0 1 0 1

TOTAL 453

(82)

69

BAB IV

PENERAPAN ALGORITMA PARTICLE SWARM OPTIMIZATION

UNTUK MASALAH PEMOTONGAN ROL KERTAS

Pada bab ini akan dijelaskan mengenai cara menggunakan aplikasi yang sudah dibuat berdasarkan algoritma Particle Swarm Optimization. Aplikasi ini dibuat dengan Graphical User Interface (GUI) MATLAB. Dengan adanya aplikasi ini dapat memudahkan perhitungan. Berikut penjelasan dan cara tentang aplikasi ini.

Buka aplikasi GUI MATLAB yang sudah dibuat maka akan terlihat tampilan seperti berikut ini.

(83)

Kemudian kita dapat menentukan banyak jenis rol yang dipesan berdasarkan lebarnya dengan cara mengetikkannya pada kolom yang tersedia.

(84)

Jika dipilih tombol tambah data, maka akan muncul tampilan seperti di bawah.

Gambar 4.3: Tampilan program ketika data tabel ditambah

(85)

mengetikkannya pada kolom yang tersedia. Input data ini juga akan digunakan dalam proses perhitungan.

(86)

Setelah itu, tekan tombol ‘Lakukan Proses Perhitungan’ maka akan muncul

wait baryang menunjukkan proses running dan iterasi.

(87)

Tunggu beberapa saat, maka penyelesaian optimal akan muncul pada field yang telah tersedia.

(88)

Proses diberhentikan setelah maximum run terpenuhi. Dari tampilan GUI dapat diketahui bahwa semua pesananan sudah terpenuhi serta hasil dari best fun adalah 452.2502 dan nilainya masih belum bulat karena nilai tersebut hanya merupakan suatu output dari pendekatan algoritma PSO yang akan berguna untuk mencari best variable yang akan digunakan sebagai input untuk diproses menggunakan algoritma First-fit decreasing (FFD) agar bernilai bulat. Setelah itu, kita akan mendapatkan pola secara utuh dimana pola-pola awal yang didapatkan dari best variable hasil perhitungan algoritma PSO sudah disesuaikan dan ditambahkan dengan pola-pola baru yang didapatkan dari algoritma FFD. Jadi, didapatkan 2 rol tambahan dengan 2 pola yang berbeda.

Pola

Lebar rol pesanan

Jumlah rol

135 108 93 42

1 1 1 0 1 97

2 0 2 0 2 157

3 0 1 2 0 197

4 0 2 0 0 1

5 0 0 1 0 1

TOTAL 453

(89)

76

BAB V

PENUTUP

A. Kesimpulan

Masalah pemotongan kertas merupakan masalah penting pada proses produksi selain untuk mendapatkan hasil pemotongan yang baik juga untuk meminimumkan produksi jumlah rol. Sehingga biaya produksi bahan baku juga menjadi minimum. Masalah ini juga memiliki berbagai kendala yang harus dipertimbangkan sehingga tidak mudah diselesaikan secara manual. Namun, pada makalah ini masalah ini diselesaikan dengan 2 metode yang berbeda. Pertama, memodelkan dan menyelesaikan masalah pemotongan kertas satu dimensi dengan metode program linear. Cara memodelkan masalah ini yaitu membuat suatu pola pemotongan dengan syarat sisa pemotongan kurang dari panjang pesanan minimum kemudian menyelesaikan model ini dengan program linear sehingga diperoleh kombinasi pola yang paling optimal. Dari penyelesaian yang didapat, solusi masih berupa pecahan, untuk membuat kemungkinan pola pemotongan sangat banyak, dan menghasilkan rol yang melebihi pesanan sehingga diperlukan suatu metode yang lebih efektif dalam menyelesaikan permasalahan ini. Dalam makalah ini, masalah diselesaikan dengan menggunakan perangkat lunak QM terlebih dahulu.

(90)

bentuk bilangan bulat. Hasil perhitungan dengan PSO cukup akurat sehingga dapat dipergunakan untuk menyelesaikan masalah pemotongan persediaan kertas.

Pada makalah ini juga terdapat aplikasi yang dibuat dengan GUI MATLAB untuk menyelesaikan masalah pemotongan kertas berdasarkan metode tersebut dimana hasil berupa jumlah rol. Aplikasi ini dibuat agar saat memasukkan data atau menampilkan data menjadi lebih mudah. Aplikasi ini dapat memproses data yang sudah dimasukkan sehingga perhitungan menjadi lebih cepat dan relatif mudah.

B. Saran

(91)

78

DAFTAR PUSTAKA

Anton, Howard dan Chris Rorres. (2010). Elementary Linear Algebra: Applications version. Hoboken: John Wiley & Sons.

Alam, Mahamad Nabab. (2016). ResearchGate. Codes in MATLAB for Particle Swarm Optimization. 1-4.

Alam, Mahamad Nabab. (2016). ResearchGate. Particle Swarm Optimization: Algorithm and It’s Codes in MATLAB. 1-11.

Bisschop, Johannes. (2016). AIMMS Optimization Modeling. AIIMS B.V.

Chvatal, Vasek. (1983). Linear programming. New York: W. H. Freeman and Company.

Eiselt, H.A. dan C.L. Sandblom. (2007). Linear Programming and its Applications. Verlag: Springer.

Gilat, Amos. (2011). MATLAB An Introduction. Fourth Edition. Ohio: John Wiley and Sons, Inc.

Ignizio, J. P. dan Cavalier T. M. (1994). Linear Programming. Mac Graw Hill Book Company, Inc.

Lagha, Ghassen B. dkk. (2014). Particle Swarm Optimization Approach for Resolving Cutting Stock Problem: International Conference on Advanced Logistic and Transport.

(92)

Matousek, Jiri dan Bernd Gartner. (2007). Understanding and Using Linear Programming. Verlag: Springer.

Parmar, Kashyap B. dkk. (2014). Cutting Stock Problem: A Survey of Evolutionary Computing Based Solution in 2014 International Conference on Green

Computing Communication and Electrical Engineering.

Putra, Antonius Rianditya. (2015). Penjadwalan Mata Kuliah Menggunakan Algoritma Particle Swarm Optimization. Yogyakarta: Jurusan Teknik

Informatika USD.

Sahyar. (2016). Algoritma & Pemrograman Menggunakan MATLAB (Matrix Laboratory). Jakarta: Kencana.

Santosa, Budi dan Paul Willy. (2011). Metoda Metaheuristik Konsep dan Implementasi. Surabaya: Guna Widya.

Shen, Xianjun dkk. (2007). A Heuristic Particle Swarm Optimization for Cutting Stock Problem Based on Cutting Pattern: ICCS.

Siswanto. (2007). Operations Research Jilid 1. Jakarta: Erlangga. Susanta. (1996). Program Linear. Jakarta: Depdikbud.

Suyanto. (2010). Algoritma Optimasi Deterministik atau Probabilistik. Yogyakarta: Graha Ilmu.

Taha, Hamdy A. (2011). Operations Reasearch An Introduction. Ninth Edition. New Jersey: Prentice Hall.