METODE BRANCH AND CUT UNTUK MENYELESAIKAN
MULTI-OBJECTIVE INTEGER PROGRAMMING
SKRIPSI
RIZKIKA AMALIA
100803037
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
METODE BRANCH AND CUT UNTUK MENYELESAIKAN
MULTI-OBJECTIVE INTEGER PROGRAMMING
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat untuk
mencapai gelar sarjana sains
RIZKIKA AMALIA
100803037
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Metode Branch and Cut Untuk Menyelesaikan Multi-Objective Integer Programming
Kategori : Skripsi
Nama : Rizkika Amalia
Nomor Induk Mahasiswa : 100803037
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2014
Komisi Pembimbing
Pembimbing 2, Pembimbing 1,
Drs. Gim Tarigan, M.Si Drs. Sawaluddin, M.IT
NIP. 195502021986011001 NIP. 195912311998021001
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
METODE BRANCH AND CUT UNTUK MENYELESAIKAN
MULTI-OBJECTIVE INTEGER PROGRAMMING
SKRIPSI
Saya mengaku bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2014
PENGHARGAAN
Asslamu’alaikum Wr. Wb.
Puji dan syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat dan karunianya sehingga penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Metode Branch and Cut untuk Menyelesaikan Multi-Objective Integer Programming.
Terimakasih penulis sampaikan kepada Drs. Sawaluddin, M.IT selaku pembimbing 1 dan Drs. Gim Tarigan, M.Si selaku pembimbing 2 yang telah meluangkan waktunya selama penyusunan skripsi ini. Terimakasih kepada Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si selaku Ketua Departemen dan Sekretaris Departemen Matematika FMIPA USU Medan, Dekan dan Pembantu Dekan FMIPA USU, seluruh Staff dan Dosen Matematika FMIPA USU, serta rekan-rekan kuliah. Akhirnya tidak terlupakan kepada Ayah, Ibu, dan keluarga yang selama ini memberikan bantuan dan dorongan yang penulis perlukan. Semoga Allah SWT senantiasa membalasnya dengan hal yang lebih baik.
Akhir kata penulis mengharapkan saran dan kritik yang membangun demi penyempurnaan skripsi ini dan berharap semoga skripsi ini dapat bermanfaat bagi para pembaca.
Medan, Juli 2014
METODE BRANCH AND CUT UNTUK MENYELESAIKAN
MULTI-OBJECTIVE INTEGER PROGRAMMING
ABSTRAK
Metode Branch and Cut merupakan salah satu metode yang digunakan untuk menyelesaikan masalah linear programming yang menghendaki penyelesaian dalam bentuk bilangan bulat (integer), tetapi biasanya digunakan pada masalah linear programming yang memiliki tujuan tunggal. Permasalahan tersebut disebut juga sebagai Single Objective Integer Programming. Dalam tulisan ini akan ditunjukkan bagaimana metode Branch and Cut menyelesaikan masalah linear programming yang memiliki banyak tujuan. Permasalahan tersebut disebut Multi-Objective Integer Programming atau biasa disebut goal programming. Dalam penyelesaiannya penulis menggunakan software LINDO (Linear Discrete Optimization).
BRANCH AND CUT METHOD FOR SOLVING
MULTI-OBJECTIVE INTEGER PROGRAMMING
ABSTRACT
Branch and Cut method is a kind of technique for solving linear programming problem which expect integer for its decision variable, but it usually use to solve a single objective integer programming form. In this paper, the author will show how Branch and Cut method can solve a multi-objective integer programming or so-called goal programming. The author also used LINDO (Linear Discrete Optimization).
DAFTAR ISI
Daftar Tabel viii
Daftar Gambar ix
Bab 1. Pendahuluan 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Batasan Masalah 2
1.4 Tinjauan Pustaka 2
1.5 Tujuan Penelitian 5
1.6 Kontribusi Penelitian 5
1.7 Metode Penelitian 5
Bab 2. Landasan Teori 6
2.1 Linear Programming 6
2.1.1 Karakteristik Linear Programming 7
2.1.2 Asumsi dalam LinearProgramming 7
2.2 Integer Programming (IP) 9
2.2.1 Pemrograman Bilangan Bulat Murni 9
(Pure Integer Programming)
2.2.2 Pemrograman Bilangan Bulat Campuran 10
(Mixed Integer Programming)
2.2.3 Pemrograman Bilangan Bulat Biner
(Binary Integer Programming) 10
2.3 Metode Penyelesaian Masalah Integer Programming 11
2.3.1 Metode Pendekatan Pembulatan 11
2.3.2 Metode Pendekatan Grafik 14
2.3.3 Metode Cutting Plane (Pendekatan Gomory) 15
2.3.4 Metode Branch and Bound 21
Bab 3. Pembahasan 27
3.1Goal Programming 27
3.2Bentuk Umum Goal Programming 30
3.3Perumusan Masalah Goal Programming 31
3.5Penyelesaian Multi-Objective Integer Programming 32 dengan Metode Branch and Cut
3.6Perbandingan Metode Branch and Bound, 41
Cutting Plane, dan Branch and Cut
Bab 4. Kesimpulan dan Saran 45
4.1 Kesimpulan 45
4.2 Saran 45
DAFTAR TABEL
Nomor Judul Halaman
Tabel
2.1 Perbandingan Solusi dengan Metode Pendekatan Pembulatan 13
Dengan Bulat Optimum Sesungguhnya
2.2 Solusi Optimum Masalah Linear Programming 16
2.3 Penambahan Kendala Gomory 17
2.4 Solusi Optimal Contoh 2.3 (Iterasi 0) 18
2.5 Penambahan Kendala Gomory Contoh 2.3 (Iterasi 0) 19
2.6 Solusi Optimal Contoh 2.3 (Iterasi 1) 19
2.7 Penambahan Kendala Gomory Contoh 2.3 (Iterasi 1) 20
2.8 Solusi Optimal Contoh 2.3 (Iterasi 2) 20
3.1 Iterasi 0 Simpleks 33
3.2 Iterasi 0 Simpleks Baru 33
3.3 Iterasi 1 Simpleks 34
3.4 Iterasi 2 Simpleks 34
3.5 Iterasi 3 Simpleks 35
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
2.1 Penyelesaian dengan Pendekatan Grafik 15
2.2 Grafik Pencabangan pada Metode Branch and Bound 26
3.1 Penyelesian Goal Programming dengan LINDO 36
3.2 Penyelesaian Sub Masalah 1 dengan LINDO 37
3.3 Penyelesaian Sub Masalah 2 dengan LINDO 38
3.4 Penyelesaian Sub Masalah 1 Baru dengan LINDO 39
METODE BRANCH AND CUT UNTUK MENYELESAIKAN
MULTI-OBJECTIVE INTEGER PROGRAMMING
ABSTRAK
Metode Branch and Cut merupakan salah satu metode yang digunakan untuk menyelesaikan masalah linear programming yang menghendaki penyelesaian dalam bentuk bilangan bulat (integer), tetapi biasanya digunakan pada masalah linear programming yang memiliki tujuan tunggal. Permasalahan tersebut disebut juga sebagai Single Objective Integer Programming. Dalam tulisan ini akan ditunjukkan bagaimana metode Branch and Cut menyelesaikan masalah linear programming yang memiliki banyak tujuan. Permasalahan tersebut disebut Multi-Objective Integer Programming atau biasa disebut goal programming. Dalam penyelesaiannya penulis menggunakan software LINDO (Linear Discrete Optimization).
BRANCH AND CUT METHOD FOR SOLVING
MULTI-OBJECTIVE INTEGER PROGRAMMING
ABSTRACT
Branch and Cut method is a kind of technique for solving linear programming problem which expect integer for its decision variable, but it usually use to solve a single objective integer programming form. In this paper, the author will show how Branch and Cut method can solve a multi-objective integer programming or so-called goal programming. The author also used LINDO (Linear Discrete Optimization).
Bab 1
PENDAHULUAN
1.1Latar Belakang
Dewasa ini, manusia sering dihadapi oleh permasalahan melibatkan optimasi tujuan ganda (multi-objective), contohnya dalam hal perencanaan atau peramalan pasar yang biasanya pihak manajemen perusahaan akan melakukan survey terhadap produk yang digemari oleh konsumen, yang selanjutnya akan memproduksi produk tersebut semaksimal mungkin sesuai dengan selera konsumen sekaligus meminimumkan biaya produksi sesuai dengan batasan-batasan yang ada. Dalam beberapa permasalahan, terkadang pihak manajemen membutuhkan hasil atau solusi yang merupakan bilangan bulat. Permasalahan ini disebut juga dengan multi-objective integer programming atau juga dikenal dengan istilah goal programming.
Multi-Objective Integer Programming (MOIP) dapat dilihat sebagai bentuk pengembangan dari Integer Programming (IP) yang dapat digunakan dalam pengambilan keputusan di dalam kehidupan sehari-hari, misalnya perencanaan, logistik, alokasi barang, penjadwalan, routing, dan sebagainya. Multi-objective Integer Programming memungkinkan si pembuat keputusan untuk mempertimbangkan tidak hanya satu tujuan (single-objective) melainkan beberapa tujuan (multi-objective)secara bersamaan, seperti biaya pengeluaran, keuntungan, kerusakan mesin, waktu kerja, dan sebagainya.
Berdasarkan uraian yang dikemukakan di atas maka penulis tertarik untuk
membahas masalah MOLP dengan judul “Metode Branch and Cut Untuk
Menyelesaikan Multi–Objective Integer Programming”.
1.2Perumusan Masalah
Permasalahan yang akan dibahas adalah apakah metode branch and cut dapat digunakan untuk menyelesaikan persoalan multi-objective integer programming.
1.3Batasan Masalah
Dalam penulisan ini, penulis hanya membatasi pada persoalan multi-objective integer programming dengan menggunakan metode branch and cut. Dalam hal ini masalah yang diangkat adalah masalah goal programming dan pure integer programming.
1.4Tinjauan Pustaka
Matthias Ehrgott dan Xavier Gandibleux dalam bukunya yang berjudul “Multiple Criteria Optimization: “State Of The Art Annotated Bibliographic Surveys” menjelaskan bahwa masalah optimasi banyak fungsi objektif yang berlawanan sekaligus dengan kendala-kendala yang diberikan disebut masalah multiobjective programming dan dapat diformulasikan sebagai vektor minimasi sebagai berikut:
Minimumkan ≜ , , …
Kendala ∈ ≜ ∈ | , , … ,
di mana , , … , adalah k fungsi objektif berbeda dari vektor
keputusan , , … , adalah m pertidaksamaan kendala-kendala dan X
Thomas Vincent dalam makalahnya yang berjudul “Multi-objective Branch and Bound for Mixed 0-1 Linear Programming: Corrections and Improvements for the Biobjective Case” menjelaskan bahwa multiple objective linear program (MOLP) dan diformulasikan sebagai berikut:
Min
Kendala ∈
Dalam hal ini, , … , dengan baris , … , merupakan sebuah
matriks linear p x n, ∈ merupakan vektor dari variable-variabel, dan
≔ ∈ ∶ ,
adalah himpunan yang mungkin dalam ruang keputusan . A adalah matriks m x n dari kendala-kendala dan ∈ adalah vektor sisi sebelah kanan. Kita tunjukkan
≔ ≔ ≔ ∈ : ∈
sebagai outcome set di ruang objective .
Melih Ozlen dan Benjamin A. Burton (2009) dalam makalahnya yang
berjudul “Multi-Objective Integer Programming: An Improved recursive
algorithm” menerangkan bahwa bentuk umum dari MOIP didefinisikan sebagai berikut :
Min , , … ,
Kendala
di mana X adalah himpunan titik-titik layak yang didefinisikan oleh
masing-masing fungsi objektifnya didefinisikan
, dan ∈ untuk semua ∈ , , … , . Masing–masing fungsi
objektifnya didefinisikan oleh
∑ , ∑ , … , ∑ dimana ∈
Sebuah titik ′∈ disebut -objektif yang efisien jika dan hanya jika
tidak ada ′∈ yang mengakibatkan ′ untuk setiap ∈
, , , … , dan ′ untuk sedikitnya satu . Hasil vector objektif
′ , ′ , … , ′ dikatakan -objektif yang tidak terdominasi.
John E. Mitchell dalam makalahnya yang berjudul ”Branch and Cut Algorithms for Combinatorial Optimization Problems” menjelaskan bahwa algoritma branch and cut
memodifikasi strategi dasar branch and bound dengan mencoba menguatkan linear programming relaxation (LPR) dari permasalah integer programming (IP) dengan
pertidaksaman baru sebelum melakukan mencabangan solusi bagian. Branch and bound murni dapat dipercepat dengan menggunakan cutting planes baik di awal diagram pohon branch and bound maupun di tiap-tiap nodenya, karena cutting planes mampu
mengurangi banyak diagram pohon tersebut. Branch and cut dapat digunakan dalam penyambungan dengan heuristic untuk memperoleh batas yang lebih rendah pada nilai optimal dengan menggunakan algoritma branch and bound.
Shon Albert dalam makalahnya yang berjudul “Solving Mixed Integer Linear Programs Using Branch and Cut Algorithm” menerangkan bahwa metode branch and cut menggabungkan keuntungan dari skema branch and bound murni dan skema gomory cutting plane. Menyelesaikan masalah dengan metode branch and cut akan lebih cepat dibandingkan dengan branch and bound saja.
Gomory cutting plane cepat, tetapi tidak dapat diandalkan. Branch and bound dapat diandalkan, tetapi lambat. Akibatnya kedua metode dapat digabung menjadi satu yaitu dinamakan branch and cut. Pertama ditambahkan beberapa cut
dari menggunakan skema gomory kemudian mengaplikasikan sisanya
menggunakan branch and bound. Algoritma tersebut tidak hanya dapat
1.5Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk mendapatkan penyelesaian multi-objective integer programming dengan menggunakan metode branch and cut.
1.6Kontribusi Penelitian
Manfaat dari penelitian ini adalah sebagai berikut :
1. Membantu penulis menerapkan ilmu yang telah diperoleh dari perkuliahan ke dunia nyata.
2. Menambah wawasan penulis dan pembaca tulisan ini tentang penyelesaian multi-objective integer programming dengan menggunakan metode branch and cut.
1.7Metode Penelitian
Penelitian ini adalah penelitian literatur yang disusun dengan langkah-langkah sebagai berikut:
1. Mencari literatur dari beberapa buku dan jurnal tentang metode branch and cut serta pemrograman bilangan bulat (integer programming).
2. Menjelaskan definisi dari linear programming dan klasifikasinya. 3. Menjelaskan definisi dari integer linear programming.
4. Menjelaskan beberapa metode yang dapat digunakan untuk menyelesaikan permasalahan integer linear programming.
5. Memberikan contoh penyelesaian single-objective integer programming dengan menggunakan metode pendekatan, metode grafik, gomory (cutting plane)dan metode branch and bound.
6. Menjelaskan bagaimana penyelesaian multi-objective integer programming dengan menggunakan simpleks.
7. Mengambil contoh soal untuk diselesaikan dengan metode branch and cut. 8. Mengambil contoh soal untuk diselesaikan dengan metode branch and bound,
Bab 2
LANDASAN TEORI
2.1 Linear Programming
Linear Programming (LP) merupakan metode yang digunakan untuk mencapai hasil terbaik (optimal) seperti keuntungan maksimum atau biaya minimum dalam model matematika yang melibatkan variable-variabel linear. Linear programming juga dapat dikatakan sebagai teknik untuk mengoptimasi sebuah fungsi objective linear, dengan kendala berbentuk persamaan linear maupun pertidaksamaan linear. Secara umum, linear programming dapat dinyatakan sebagai:
Optimalkan , ∈ ⊆ dengan adalah himpunan semua vektor real
komponen dan merupakan fungsi objektif yang didefinisikan dalam atau juga disebut sebagai himpunan kendala. Setiap ∈ disebut sebagai solusi layak (feasible solution), sedangkan ∈ yang memenuhi ∞, ∀ ∈ disebut sebagai solusi optimal (optimal solution).
2.1.1 Karakteristik Linear Programming
Karakteristik-karakteristik dalam linear programming yang biasa digunakan untuk memodelkan suatu masalah dan memformulasikannya secara matematik yaitu:
a. Variabel Keputusan
Variabel keputusan adalah variabel yang secara lengkap menguraikan keputusan-keputusan yang akan dibuat.
b. Fungsi Tujuan
Fungsi tujuan merupakan suatu hubungan linier dari variabel keputusan yang berupa fungsi maksimum atau minimum.
c. Kendala
Kendala merupakan batasan-batasan dalam penyelesaian linear
programming yang harus diperhatikan. Kendala diekspresikan dalam persamaan dan pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumberdaya dalam suatu masalah.
2.1.2 Asumsi dalam Linear Programming
Model linear programming mengandung asumsi-asumsi implisit tertentu yang harus
a. Linieritas (Linearity)
Fungsi tujuan (objective function) dan kendala – kendalanya (constraints) dibuat dalam fungsi linier. Sifat linearitas suatu kasus dapat ditentukan dengan menggunakan beberapa cara, misalnya dengan menggunakan grafik atau menggunakan uji hipotesa.
b. Kesetaraan (Proportionality)
i. Kontribusi setiap variabel keputusan terhadap fungsi tujuan adalah sebanding dengan nilai variabel keputusan.
ii. Kontribusi suatu variabel keputusan terhadap ruas kiri dari setiap pembatas juga sebanding dengan nilai variabel keputusan itu.
c. Penambahan (Addivity)
Sifat penambahan mengasumsikan bahwa tidak terdapat bentuk perkalian silang pada model, baik bagi fungsi tujuan maupun kendala.
d. Pembagian (Divisibility)
Solusi dapat berupa bilangan bulat (integer) atau bilangan pecahan.
e. Ketidaknegatifan (Nonnegativity)
Nilai variabel keputusan harus lebih besar atau sama dengan nol.
f. Kepastian (Certainty)
Asumsi-asumsi di atas harus dipenuhi apabila ingin menyelesaikan masalah model linear programming. Jika asumsi-asumsi tersebut tidak dapat terpenuhi, persoalan dapt diselesaikan dengan program matematik
lain seperti; integer programming, nonlinear programming, goal
programming, atau dynamic programming.
2.2 Integer Programming (IP)
Program bilangan bulat (integer programming) merupakan bentuk perluasan dari linear programming. Persoalan IP menginginkan solusi yang didapat berupa bilangan bulat, bukan berupa bilangan pecahan. Contoh persoalan yang sering ditemui misalnya menentukan banyaknya barang elektronik yang harus diproduksi, banyaknya unit rumah yang akan dibangun pada suatu proyek perumahan, banyaknya orang yang diperlukan untuk mengerjakan suatu proyek, dan sebagainya. Integer programming memiliki model matematis yang sama dengan model linear programming pada umumnya, tetapi ditambah batasan bahwa variabelnya harus bilangan bulat.
Berdasarkan jenis keputusan yang akan diperoleh, persoalan integer programming dapat dibedakan atas tiga jenis, yaitu:
1. Pemrograman Bilangan Bulat Murni (Pure Integer Programming) 2. Pemrograman Bilangan Bulat Campuran (Mixed Integer Programming) 3. Pemrograman Bilangan Bulat Biner (Binary Integer Programming)
2.2.1 Pemrograman Bilangan Bulat Murni (Pure Integer Programming)
Pure Integer Programming (PIR) merupakan pemrograman bilangan bulat di mana semua nilai variabel keputusan haruslah bilangan bulat. Bentuk umum pure integer programming yaitu:
Optimalkan : ∑
, , … , , , … ,
,
2.2.2 Pemrograman Bilangan Bulat Campuran (Mixed Integer Programming)
Mixed Integer Programming (PIR) merupakan pemrograman bilangan bulat di mana nilai variabel keputusannya berupa campuran antara bilangan bulat dan bilangan desimal atau pecahan. Bentuk umum mixed nteger programming yaitu:
Optimalkan : ∑ ∑
Kendala : ∑ ∑ , ,
, , … , , , … , , , … ,
,
2.2.3 Pemrograman Bilangan Bulat Biner (Binary Integer Programming)
Bentuk lain dari masalah integer programming adalah binary integer
programming (BIP). Dalam persoalan binary integer programming nilai variabel keputusannya berupa bilangan biner (0 atau 1). Dalam aplikasi sehari-hari,
masalah binary integer programming menyangkut masalah pengambilan
Bentuk umum dari binary integer programming yaitu:
2.3 Metode Penyelesaian Masalah Integer Programming
Tampaknya cukup untuk mendapatkan solusi bulat dari masalah linear
programming, dengan menggunakan metode simpleks biasa dan kemudian membulatkan nilai-nilai pecah solusi optimum. Bukan tugas mudah untuk membulatkan nilai-nilai pecah variabel basis yang menjamin tetap memenuhi semua kendala dan tidak menyimpang cukup jauh dari solusi bulat yang tepat. Akibatnya diperlukan prosedur yang sistematis untuk mendapatkan solusi bulat optimum terhadap masalah itu. Beberapa metode yang dapat digunakan untuk menyelesaikan masalah integer programming antara lain:
1. Metode Pendekatan Pembulatan 2. Metode Pendekatan Grafik 3. Metode Branch and Bound 4. Metode Cutting Plane
2.3.1 Metode Pendekatan Pembulatan
Suatu pendekatan yang sederhana dalam menyelesaikan masalah integer
Namun demikian sebab utama kegagalan pendekatan ini adalah bahwa solusi yang diperoleh mungkin bukan solusi integer optimum yang sesungguhnya. Dengan kata lain, solusi pembulatab dapat lebih jelek dibandingkan solusi integer optimum yang sesungguhnya atau mungkin merupakan solusi tak layak.
Tiga masalah berikut disajikan untuk mengilustrasikan prosedur pembulatan:
Contoh 2.1:
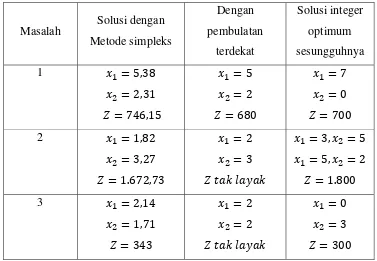
Tabel 2.1 Perbandingan solusi dengan metode pendekatan pembulatan dengan bulat optimum sesungguhnya.
Masalah Solusi dengan
Metode simpleks
Masalah pertama adalah masalah maksimasi, di mana solusi pembulatan menghasilkan keuntungan 680, hanya lebih kecil 20 dibanding yang dihasilkan solusi bulat optimum 700. Masalah kedua adalah masalah minimasi di mana solusi pembulatan adalah tak layak. Ini menunjukkan bahwa meskipun pendekatan adalah sederhana, namun kadang-kadang menyebabkan solusi tak layak. Untuk mencegah ketidaklayakan, nilai solusi simpleks dalam masalah minimasi harus dibulatkan ke atas. Sebaliknya, pada masalah maksimasi nilai solusi simpleks semestinya dibulatkan ke bawah. Contohnya, pada masalah kedua jika solusi simpleksnya dibulatkan ke atas akan diperoleh dan dan merupakan solusi layak. Juga pada masalah ketiga, jika solusi simpleksnya
dibulatkan ke bawah akan diperoleh dan dan merupakan solusi
Nilai fungsi tujuan melalui simpleks tanpa pembatasan bilangan bulat akan selalu lebih baik dibanding solusi integer optimum karena terletak pada titik pojok luar dari batas ruang solusi layak. Suatu metode yang serupa dengan pendekatan pembulatan adalah prosedur coba-coba (trial and error). Dengan menggunakan cara ini, pengambil keputusan mengamati solusi integer dan memilih solusi yang mengoptimumkan nilai fungsi tujuan. Cara ini sangat tidak efektif jika masalahnya melibatkan sejumlah besar kendala dan variabel. Terlebih lagi, memeriksa kelayakan setiap solusi yang dibulatkan akan banyak memakan waktu.
2.3.2 Metode Pendekatan Grafik
Masalah integer programming yang melibatkan dua variabel dapat diselesaikan dengan metode pendekatan grafik. Metode ini identik dengan metode grafik yang biasa digunakan dalam linear programming. Metode grafik relatif lebih mudah untuk menyelesaikan masalah integer programming dua variabel yaitu dengan menggambar grafik di atas kertas grafik kemudian menggambarkan sekumpulan titik-titik integer dalam ruang solusi layak. Masalah berikut akan diselesaikan dengan pendekatan grafik.
Model ini serupa dengan model linear programming biasa. Perbedaannya terletak pada kendala terakhir yang menginginkan solusi bernilai non negatif integer.
Solusi grafik untuk masalah ini ditunjukkan pada gambar di bawah. Ruang
solusi layak adalah OABC. Solusi optimum masalah linear programming
2. Periksa solusi optimum. Jika semua variabel basis memiliki nilai integer, maka solusi optimum telah diperoleh dan proses berakhir. Jika masih ada satu atau lebih variabel basis memiliki nilai pecah, teruskan ke tahap 3.
3. Buatlah suatu skala Gomory (suatu bidang pemotong atau cutting plane) dan cari solusi optimum melalui proses dual simpleks. Kembali ke tahap 2.
Kendala Gomory dalam Pure Integer Programming
Tabel optimum masalah linear programming berikut merupakan solusi optimum kontinu.
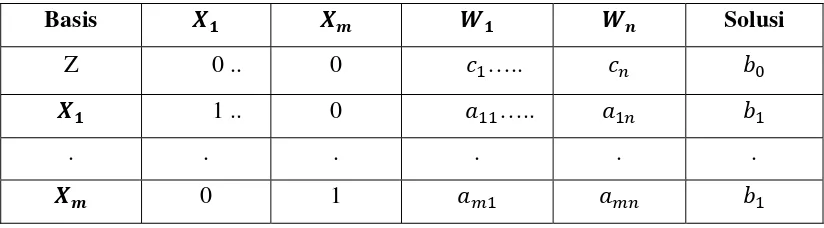
Tabel 2.2 Solusi optimum masalah linear programming
Basis Solusi
Z 0 .. 0 …..
1 .. 0 …..
. . . . . . 0 1
Di mana variabel , … , menunjukkan variabel basis dan variabel , … , adalah non basis.
Perhatikan persamaan ke di mana variabel diasumsikan bernilai non integer.
∑ di mana non integer.
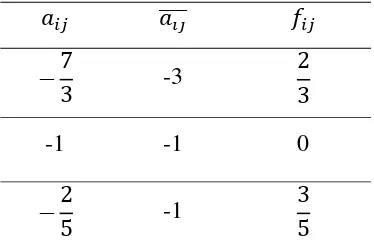
Kemudian pisahkan dan menjadi bagian yang bulat dan bagian pecah non negatif seperti berikut:
jadi , di mana
Contoh:
Kendala Gomory yang diinginkan yaitu:
, adalah variabel slack Gomory ke .
Pada umumnya, persamaan kendala yang berhubungan dengan solusi pecah dipilih untuk menghasilkan suatu kendala Gomory. Namun, sebagai aturan main biasanya dipilih persamaan yang memiliki maksimum.
Tabel baru setelah penambahan kendala Gomory disajikan pada tabel berikut:
Tabel 2.3 Penambahan kendala Gomory
Basis Solusi
Karena diperoleh solusi primal optimum tetapi tidak layak maka digunakan metode dual simpleks. Proses pembentukan kendala Gomory berakhir jika solusi baru semua berupa bilangan bulat. Jika tidak, suatu kendala Gomory baru dibuat
lagi dari tabel yang dihasilkan dan metode dual simpleks digunakan lagi untuk mengatasi ketidaklayakan. Jika pada setiap iterasi metode dual simpleks menunjukkan bahwa tidak ada solusi layak, berarti masalah itu tidak memiliki solusi integer yang layak.
Berikut ini terdapat persoalan integer programming:
Contoh 2.3:
Maksimumkan Kendala
,
Solusi kontinu optimumnya diperoleh dalam tabel berikut:
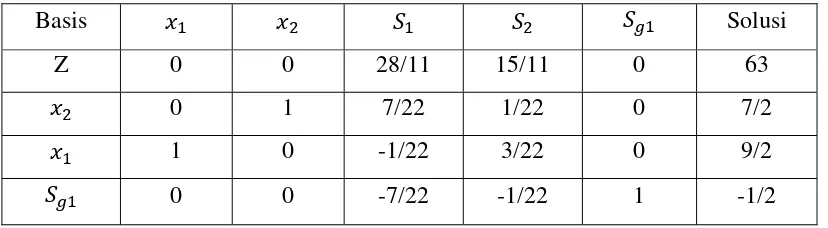
Tabel 2.4 Solusi optimal contoh 2.3 (iterasi 0)
Basis Solusi
Z 0 0 28/11 15/11 63
0 1 7/22 1/22 7/2
1 0 -1/22 3/22 9/2
Karena solusi tidak bulat, suatu kendala Gomory ditambahkan pada tabel itu. Kedua persamaan ( dan ) pada masalah ini memiliki nilai yang sama, yaitu
, sehingga salah satu dapat digunakan, misalkan digunakan persamaan
, ini menghasilkan
Sehingga kendala Gomory menjadi:
Tabel baru setelah penambahan kendala Gomory menjadi:
Tabel 2.5 Penambahan kendala Gomory contoh 2.3 (iterasi 0)
Basis Solusi
Z 0 0 28/11 15/11 0 63
0 1 7/22 1/22 0 7/2
1 0 -1/22 3/22 0 9/2
0 0 -7/22 -1/22 1 -1/2
Dengan memakai metode dual simpleks diperoleh tabel baru yaitu:
Tabel 2.6 Solusi optimal contoh 2.3 (iterasi 1)
Basis Solusi
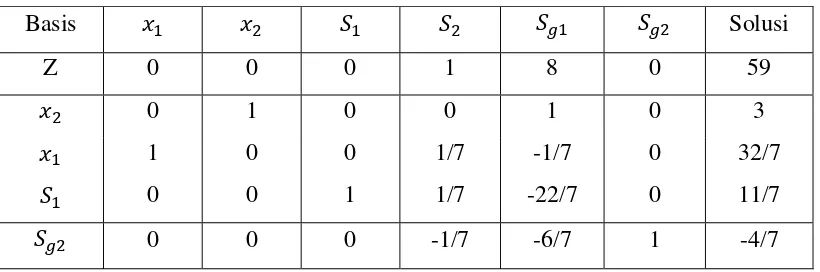
Z 0 0 0 1 8 59 0 1 0 0 1 3
1 0 0 1/7 -1/7 32/7
0 0 1 1/7 -22/7 11/7
Solusi baru yang didapat masih belum bilangan bulat, akibatnya suatu kendala Gomory baru ditambahkan. Dapat dilihat bahwa persamaan memiliki (
), maka ditulis dalam berikut:
Kemudian ditambahkan pada tabel 2.7 berikut:
Tabel 2.7 Penambahan kendala Gomory contoh 2.3 (iterasi 1)
Basis Solusi
Z 0 0 0 1 8 0 59 0 1 0 0 1 0 3
1 0 0 1/7 -1/7 0 32/7
0 0 1 1/7 -22/7 0 11/7
0 0 0 -1/7 -6/7 1 -4/7
Dengan menggunakan dual simpleks diperoleh hasil:
Tabel 2.8 Solusi optimal contoh 2.3 (iterasi 2)
Basis Solusi
Z 0 0 0 0 2 7 55 0 1 0 0 1 0 3 1 0 0 0 -1 1 4 0 0 1 0 -4 1 1 0 0 0 1 6 -7 4
2.3.4 Metode Branch and Bound
Metode branch and boundadalah salah satu metode untuk mendapatkan
penyelesaian optimal program linier yang menghasilkan variable-variable keputusan bilangan bulat. Metode ini membatasi penyelesaian optimum yang akan menghasilkan bilangan pecahan dengan cara membuat cabang atas dan bawah bagi masing-masing variable keputusan yang bernilai pecahan agar bernilai bulat sehingga setiap pembatasan akan menghasilkan cabang baru.
Metode branch and bound telah menjadi kode computer standar untuk integer programming, dan penerapan-penerapan dalam praktek tampaknya menyarankan bahwa metode ini lebih efisien dibanding dengan metode cutting plane. Metode branch and bound dapat digunakan untuk menyelesaikan masalah pure maupun mixed integer programming.
Berikut ini adalah langkah-langkah penyelesaian masalah maksimasi dengan metode branch and bound:
1. Selesaikan masalah LP biasa tanpa pembatasan bilangan bulat dengan metode simpleks biasa.
2. Teliti solusi optimalnya. Jika semua variabel basis telah bernilai bulat, maka solusi optimum telah tercapai dan proses berakhir. Jika satu atau lebih variabel basis belum bernilai bulat, lanjut ke tahap 3.
3. Jadikan solusi pada penyelesaian tahap 1 (relaxed solution) menjadi batas atas dan sebagai batas bawahnya digunakan solusi yang variabel basisnya telah dibulatkan ke bawah (rounded-down).
4. Pilih variabel yang mempunyai nilai pecahan yang terbesar untuk dijadikan pencabangan ke dalam sub-sub masalah. Tujuannya adalah untuk menghilangkan solusi kontinu yang tidak memenuhi persyaratan bulat dalam masalah itu. Pencabangan dilakukan secara mutually exclusive untuk memenuhi persyaratan bulat dengan jaminan tidak ada solusi bulat layak yang tidak diikut sertakan.
awalnya, ini adalah solusi kontinu yang dibulatkan ke bawah). Sub – sub masalah yang memiliki batas atas kurang dari batas bawah yang ada, tidak diikut sertakan pada analisa selanjutnya. Suatu solusi bulat layak adalah sama baik atau lebih baik dari batas atas untuk setiap sub masalah yang dicari. Jika solusi yang demikian terjadi, suatu sub masalah dengan batas atas terbaik dipilih untuk dicabangkan. Kembali ke langkah 4.
Untuk masalah minimasi, solusi yang menjadi batas atas dibulatkan keatas, atau dengan kata lain batas atas dan bawah pada kasus minimasi berlawanan pada kasus maksimasi.
Untuk memperoleh gambaran yang lebih jelas tentang metode Branch dan Bound, perhatikan contoh 2.4 berikut:
Contoh 2.4:
Maksimumkan Kendala
,
Solusi optimum kontinu masalah tersebut adalah , , dan
, .
Solusi tersebut merupakan batas awal. Batas bawah merupakan solusi
yang dibulatkan ke bawah, yaitu , dan 34. Pada metode branch
dan 3 yang selanjutnya akan diuraikan sebagai bagian A dan bagian B. Kendala-kendala baru tersebut secara efektif menghilangkan semua nilai pecah yang mungkin .
Bagian A dan bagian B diselesaikan dengan metode simpleks tanpa pembatasan bilangan bulat. Solusi simpleksnya yaitu:
Bagian A: 8, 2, dan 34
Bagian B: 6,5, 3, dan 34,5
Selanjutnya bagian B dicabangkan ke dalam dua sub bagian, yaitu B1 dan B2. Pada sub bagian B1 ditambah kendala baru yaitu 6, sedangkan pada sub
bagian B2 ditambah kendala 7. Kedua sub-masalah tersebut dinyatakan
sebagai berikut:
Solusi simpleks kedua sub masalah tersebut yaitu: Sub bagian B1: 6, 3,25, dan 34,25 Sub bagian B2: tidak layak.
Sub bagian B1a:
Solusi optimum dengan metode simpleks adalah: Sub bagian B1a: 6, 3, dan 33. Sub bagian B1b: 4,25, 4, dan 33,5.
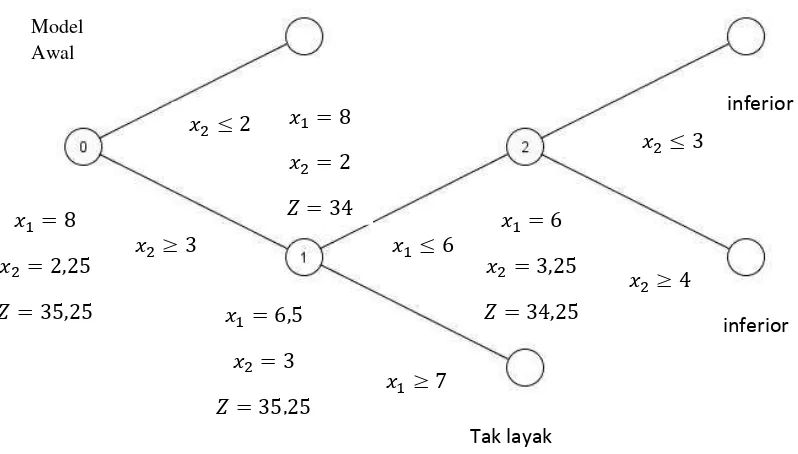
Seluruh prosedur branch and bound untuk masalah ini ditunjukkan pada gambar berikut:
Gambar 2.2 Grafik pencabangan pada metode Branch and Bound Model
Awal
,
,
,
,
, ,
Tak layak
inferior
Bab 3
PEMBAHASAN
3.1 Goal Programming
Pada bab sebelumnya telah dibahas bahwa model linear programming biasa hanya bisa menyelesaikan masalah dengan fungsi tujuan tunggal, tidak dapat menyelesaikan masalah yang melibatkan fungsi tujuan ganda. Misalnya, politisi berjanji untuk mengurangi hutang negara sekaligus menawarkan keringanan pajak penghasilan. Dalam situasi seperti itu, mustahil untuk menemukan solusi tunggal yang dapat mengoptimasi dua tujuan yang bertentangan tersebut.
Memperhatikan hal tersebut, A. Charnes dan W. M. Cooper mengembangkan
model linear programming agar mampu menyelesaikan masalah tersebut yang
kemudia dikenal dengan program tujuan ganda (multi-objective programming). Selain
itu dalam kenyataannya linear programming tidak selalu tepat dan layak bagi suatu
permasalahan terterntu, misalnya:
1. Pertentangan tujuan. Manajemen mungkin menghadapi pertentangan
tujuan antara meminimumkan biaya atau memaksimumkan pelayanan kepada pelanggan. Padahal tingginya tingkat pelayanan akan menjadikan biaya pelayanan semakin tinggi.
2. Perbedaan fungsi tujuan. Misalnya, tujuannya adalah menentukan jumlah unit produksi yang akan memaksimumkan keuntungan atau memaksimumkan market share.
3. Kesulitan mengukur tujuan. Misalnya, tujuannya adalah memaksimumkan tingkat pelayanan kepada pelanggan. Hal tersebut tentunya sulit diukur.
Adapun program tujuan ganda, yang biasa dikenal dengan multi-objective programming atau goal programming, merupakan kelanjutan dari linear programming yang digunakan untuk menyelesaikan program linier yang memiliki fungsi tujuan lebih dari satu. Selanjutnya tiap fungsi tujuan dinyatakan sebagai goal. Tujuan dari goal programming sendiri adalah meminimumkan penyimpangan dalam mencapai tujuan suatu masalah.
Berdasarkan fungsinya, goal programming dapat dibedakan atas dua macam, yakni :
a. Variabel Deviasional Atas
Variabel ini berada di atas sasaran yang dikehendaki. Dengan kata lain variabel ini berfungsi menampung deviasi positif. Oleh karena itu ia akan selalu mempunyai koefisien -1 pada setiap kendala sasaran. Variabel deviasional atas selanjutnya ditulis sebagai .
b. Variabel Deviasional Bawah
Variabel ini berada di bawah sasaran yang dikehendaki, dengan kata lain variabel ini berfungsi menampung deviasi negatif. Oleh karena itu ia akan selalu mempunyai koefisien +1 pada setiap kendala sasaran. Variabel deviasional bawah selanjutnya ditulis sebagai .
Dengan demikian, jelas bahwa variabel deviasional tersebut mempunyai fungsi yang berbeda. Bila variabel deviasional atas menampung penyimpangan nilai di atas sasaran, maka variabel deviasional atas menampung penyimpangan nilai di bawah sasaran. Sehingga dapat dipahami bahwa nilai penyimpangan minimum di atas maupun sasaran adalah nol dan tidak mungkin negatif.
atau
(3.1)
Berdasarkan (3.1) dapat diketahui bahwa kedua variabel deviasional tersebut mendekati garis kendala dari arah yang berlawanan. Dalam hal ini, ada 3 kemungkinan yang akan terjadi, yaitu:
1. dan , maka diperoleh:
(3.2)
atau dapat dikatakan hasil di atas sasaran.
2. dan , maka diperoleh:
(3.3) atau dapat dikatakan hasil di bawah sasaran.
3. dan , maka diperoleh:
Berdasarkan 3 jenis kemungkinan di atas, dapat diketahui bahwa sasaran akan tercapai apabila kedua jenis variabel deviasional bernilai 0. Oleh karena itu, pada model goal programming kedua jenis variabel deviasional dan pada fungsi tujuan menjadi:
Minimumkan:
(3.2)
3.2 Bentuk Umum Goal Programming
Secara umum model goal programming dinyatakan sebagai berikut:
Minimumkan: d d
:
3.3Perumusan Masalah Goal Programming
Perumusan masalah goal programming hampir sama dengan perumusan masalah linear programming. Perbedaannya terletak dalam penentuan fungsi tujuan. Dalam linear programming yang digunakan adalah variabel simpangannya, sementara pada goal programming adalah variabel keputusannya. Berikut ini beberapa langkah dalam perumusan masalah goal programming.
1. Tentukanlah target goal yang akan dicapai.
2. Dalam setiap kendala goal programming, terdapat variabel deviasi dan di mana:
adalah goal di atas target adalah goal di bawah target
3. Buatlah fungsi tujuan dalam bentuk minimum dan hanya meliputi variabel deviasi (bukan variabel keputusan aslinya).
4. Tulislah semua kendala termasuk kendala linear programming yang akan menjadi kendala dalam goal programming.
3.4Metode Penyelesaian Masalah
Ada dua macam metode yang digunakan untuk menyelesaikan masalah goal programming, yaitu:
1. Metode Grafik
Metode grafik digunakan untuk menyelesaikan masalah goal
programming dengan dua variabel. Langkah-langkah penyelesaian dengan metode grafik adalah:
a. Menggambar fungsi kendala pada bidang kerja sehingga diperoleh daerah yang memenuhi kendala.
b. Meminimumkan variabel deviasional agar sasaran-sasaran yang
2. Metode Simpleks
Metode simpleks digunakan untuk menyelesaikan masalah goal
programming dengan menggunakan variabel keputusan lebih dari dua. Langkah-langkah penyelesaian goal programming dengan menggunakan metode simpleks adalah:
a. Membentuk tabel simpleks awal.
b. Pilih kolom kunci dengan cara menentukan nilai terbesar kemudian bagikan dengan tiap-tiap nilai variabel pada baris tersebut. Kolom dengan rasio terkecil disebut baris pivot.
c. Pilih baris kunci yang berpedoman pada dengan rasio terkecil di
mana adalah nilai sisi kanan dari setiap persamaan. Baris kunci ini disebut baris pivot.
d. Mencari sistem kanonikal yaitu sistem di mana nilai elemen pivot bernilai 1 dan elemen lain bernilai 0. Dengan demikian diperoleh tabel simpleks iterasi .
e. Mencari variabel masuk dan variabel keluar basis. Variabel yang menjadi kolom pivot akan masuk ke dalam basis. Variabel yang menjadi baris pivot akan keluar dari basis.
f. Pemeriksaan optimalitas, yaitu melihat apakah solusi sudah layak atau tidak. Solusi dikatakan layak bila variabel adalah positif atau nol.
3.5Penyelesaian Multi-Objective Integer Programming dengan Metode Branch and Cut
Pada contoh berikut akan diberikan contoh permasalahan goal programming yang
membutuhkan penyelesaian dalam bilangan bulat murni (pure integer
programming). Penyelesaian akan dilakukan dengan metode branch and cut.
Minimum
Kendala
, , , , , , , , , , , dan bulat
Penyelesaian dengan Metode Simpleks:
Tabel 3.1 Iterasi 0 simpleks
B
Tabel 3.2 Iterasi 0 simpleks baru
Tabel 3.3 Tabel Iterasi 1 simpleks
B
P1 -1 0
P2 -1 0
P3 1 -1 7
P4 -1 0
1 2 -1 1
1
1 -1 1 7
1 1 -1 1 18
masuk ke dalam basis dan keluar dari basis
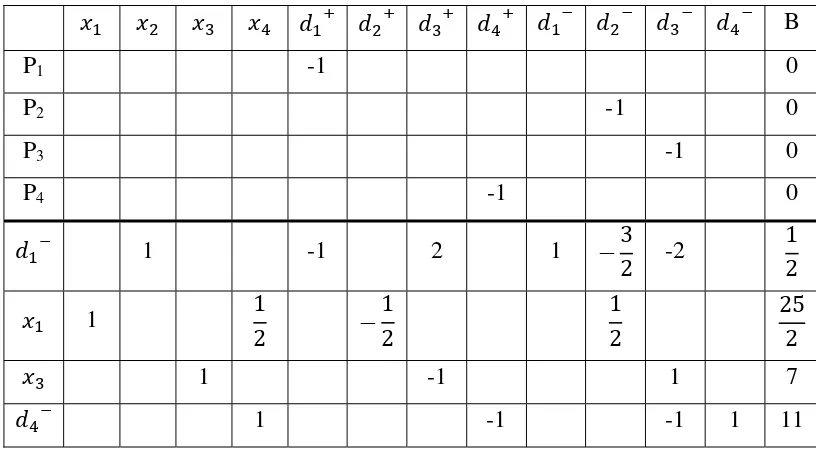
Tabel 3.4 Tabel Iterasi 2 simpleks
B
P1 -1 0
P2 -1 0
P3 -1 0
P4 -1 0
1 -1 2 1 -2
1
Tabel 3.5 Tabel Iterasi 3 simpleks
B
P1 -1 0
P2 1 -1 2 1 -2
P3 1 -1 2 1
P4 -1 0
1 -1 2 1 -2
1
1 -1 1 7 1 -1 -1 1 11
masuk ke dalam basis dan keluar dari basis
Tabel 3.6 Tabel Iterasi 4 simpleks
B
P1 -1 0
P2
P3 2 0
P4 -1 0
1 -1 2 1 -2
1
Tabel telah optimal dan didapat penyelesaian , , , dan
serta nilai fungsi tujuan = 0.
Dengan menggunakan bantuan software Lindo, didapat hasil sebagai berikut:
Gambar 3.1. Penyelesaian goal programming dengan LINDO
Dapat dilihat bahwa hasil yang didapat melalui metode simpleks sama dengan hasil yang didapat dengan menggunakan bantuan LINDO. Untuk selanjutnya, penyelesaian akan dilakukan dengan LINDO.
Berdasarkan penyelesaian optimum, penyelesaian yang didapat belum sepenuhnya bulat. Oleh karena itu masalah akan dilakukan pencabangan (branch) pada salah
satu variabel yang belum bulat, maka dicabangkan, sehingga masalah
keseluruhan tidak dihentikan dan algoritma tersebut dilanjutkan. Masalah selanjutnya dibagi atas dua sub masalah yang masing-masing ditambahkan kendala
Sub masalah 1:
Minimum Kendala
, , , , , , , , , , , dan bulat
Sub masalah 2:
Minimum Kendala
, , , , , , , , , , , dan bulat
Gambar 3.3. Penyelesaian sub masalah 2 dengan LINDO
atau
Sehingga cut yang digunakan yaitu dan ditambahkan ke dalam
masing-masing sub masalah. Berikut sub-sub masalah baru setelah ditambahkan sebuah cut.
Sub masalah 1:
Minimum Kendala
, , , , , , , , , , , dan bulat
Penyelesaian sudah seluruhnya bulat, dengan , , , dan serta nilai fungsi tujuan = 1.
Sub masalah 2:
Minimum Kendala
, , , , , , , , , , , dan bulat
Gambar 3.5. Penyelesaian sub masalah 2 baru dengan LINDO
Solusi sudah seluruhnya bulat dengan , , , dan serta
Pada sub masalah 1 dan sub masalah 2 yang baru, keduanya telah mendapat solusi yang bulat dan dengan nilai fungsi tujuan yang sama. Akan tetapi, penyelesaian pada sub masalah 2 lebih dianggap optimal karena memiliki nilai yang lebih kecil dari penyelesaian pada sub masalah 1.
3.6Perbandingan Metode Branch and Bound, Cutting Plane, dan Branch and Cut
Metode branch and cut merupakan kombinasi dari metode branch and bound dan metode cutting plane. Untuk mengetahui perbandingan ketiganya, maka diambil satu contoh masalah integer linear programming. Contoh permasalahan yang akan diambil antara lain adalah contoh 2.3 yang pada bab sebelumnya telah dikerjakan dengan metode cutting plane.
Contoh 2.3
Maksimumkan Kendala
, dan integer
Telah diketahui pada tabel 2.4 bahwa solusi kontinu optimum yang diperoleh yaitu sebagai berikut:
Tabel 2.4 Solusi optimal contoh 2.3 (iterasi 0)
Basis Solusi
Z 0 0 28/11 15/11 63
0 1 7/22 1/22 7/2
1 0 -1/22 3/22 9/2
Pada tabel di atas diketahui solusi optimalnya yaitu , , dan .
3.6.1 Metode Branch and Bound
Dalam masalah ini, dipilih untuk dicabangkan. Kendala baru yang diperoleh yaitu dan . Selanjutnya akan diuraikan sebagai bagian A dan bagian B.
Bagian A dan bagian B diselesaikan dengan metode simpleks tanpa pembatasan bilangan bulat. Solusi simpleksnya yaitu:
Bagian A: , , , dan .
Bagian B: , , dan .
Bagian B diperoleh solusi yang semuanya bulat. Sehingga pencabangan pada bagian tersebut tidak perlu dilanjutkan. Bagian A belum semuanya bulat, yaitu pada sehingga bagian A dicabangkan ke dalam dua sub bagian dan
Sub bagian A1 dan sub bagian A2 diselesaikan dengan metode simpleks tanpa pembatasan bilangan bulat. Solusi simpleksnya yaitu:
Sub bagian A1: , , dan .
Sub bagian A2: tidak layak.
Seluruh solusi dari pencabangan sudah bulat sehingga proses dihentikan
dengan solusi optimal , , dan .
3.6.2 Metode Cutting Plane
Bisa dilihat pada bab sebelumnya proses penyelesaian yang dilakukan dengan metode cutting plane. Penyelesaian optimal yang didapat yaitu , ,
dan .
3.6.3 Metode Branch and Cut Berdasarkan soal, didapat:
dan
Sama halnya dengan metode branch and bound pada 3.6.1, variabel yang
dicabangkan yaitu , sehingga melalui baris pada tabel 2.4 dibentuk
Selanjutnya dan disubstitusikan menjadi:
Diperoleh cut:
Dapat dilihat pada Bagian A pada penyelesaian dengan metode branch and bound pada 3.6.1 belum semuanya bulat. Sehingga cut yang telah diperoleh ditambahkan ke dalam masalah pada Bagian A. Kemudian diselesaikan
dengan metode simpleks dan didapat penyelesaian , , dan .
Penyelesaian yang diperoleh melalui tiga metode penyelesaian di atas
menghasilkan solusi optimal yang sama, yaitu , , dan .
Bab 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan hasil analisis dari penelitian ini, maka dapat diambil kesimpulan sebagai berikut:
1. Metode branch and cut dapat digunakan untuk menyelesaikan masalah multi-objective integer programming.
2. Cara penyelesaiannya sama dengan single-objective integer programming. 3. Penyelesaian masalah dengan metode branch and cut lebih efisien dari
metode branch and bound dan cutting plane karena adanya bidang pemotongan atau cut.
4.2 Saran
DAFTAR PUSTAKA
Albert, Shon. 2006. Solving Mixed Integer Linear Programs Using Branch and Cut Algorithm. North Carolina: Faculty of North Carolina State University in Partial Fulfillment of the Requirements for the Degree of Master OF Mathematics.
Ehrgott, Matthias and Gandibleux, Xavier. 2003. Multiple Criteria Optimization: “State Of The Art Annotated Bibliographic Surveys”. United State of America: Kluwer Academic Publishers.
Mitchell, John E. 1999. Branch and Cut Algorithms for Combinatorial
Optimization Problems. New York: Mathematical Sciences Rensselaer Polytechnic Institute
Ozlen, Mehli and Burton, Benjamin A. 2009. Multi-objective integer programming: “An improved recursive algorithm”. Melbourne, Australia: School of Mathematical and Geospatial Science, RMIT University.
Syahputra, Muhammad Romi. 2012. Metode Branch and Bound Untuk
Menyelesaikan Multi-Objective Integer Programming. Medan: Universitas Sumatera Utara
Sinurat, Rista Rida. 2008. Studi Penyelesaian Problema Mixed Integer Linier Programming Dengan Menggunakan Metode Branch and Cut. Medan: Universitas Sumatera Utara