Bab 2
LANDASAN TEORI
2.1 Linear Programming
Linear Programming (LP) merupakan metode yang digunakan untuk mencapai hasil terbaik (optimal) seperti keuntungan maksimum atau biaya minimum dalam model matematika yang melibatkan variable-variabel linear. Linear programming juga dapat dikatakan sebagai teknik untuk mengoptimasi sebuah fungsi objective linear, dengan kendala berbentuk persamaan linear maupun pertidaksamaan linear. Secara umum, linear programming dapat dinyatakan sebagai:
Optimalkan , ∈ ⊆ dengan adalah himpunan semua vektor real komponen dan merupakan fungsi objektif yang didefinisikan dalam atau juga disebut sebagai himpunan kendala. Setiap ∈ disebut sebagai solusi layak (feasible solution), sedangkan ∈ yang memenuhi ∞, ∀ ∈ disebut sebagai solusi optimal (optimal solution).
2.1.1 Karakteristik Linear Programming
Karakteristik-karakteristik dalam linear programming yang biasa digunakan untuk memodelkan suatu masalah dan memformulasikannya secara matematik yaitu:
a. Variabel Keputusan
Variabel keputusan adalah variabel yang secara lengkap menguraikan keputusan-keputusan yang akan dibuat.
b. Fungsi Tujuan
Fungsi tujuan merupakan suatu hubungan linier dari variabel keputusan yang berupa fungsi maksimum atau minimum.
c. Kendala
Kendala merupakan batasan-batasan dalam penyelesaian linear programming yang harus diperhatikan. Kendala diekspresikan dalam persamaan dan pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumberdaya dalam suatu masalah.
2.1.2 Asumsi dalam Linear Programming
Model linear programming mengandung asumsi-asumsi implisit tertentu yang harus
a. Linieritas (Linearity)
Fungsi tujuan (objective function) dan kendala – kendalanya (constraints) dibuat dalam fungsi linier. Sifat linearitas suatu kasus dapat ditentukan dengan menggunakan beberapa cara, misalnya dengan menggunakan grafik atau menggunakan uji hipotesa.
b. Kesetaraan (Proportionality)
i. Kontribusi setiap variabel keputusan terhadap fungsi tujuan adalah sebanding dengan nilai variabel keputusan.
ii. Kontribusi suatu variabel keputusan terhadap ruas kiri dari setiap pembatas juga sebanding dengan nilai variabel keputusan itu.
c. Penambahan (Addivity)
Sifat penambahan mengasumsikan bahwa tidak terdapat bentuk perkalian silang pada model, baik bagi fungsi tujuan maupun kendala.
d. Pembagian (Divisibility)
Solusi dapat berupa bilangan bulat (integer) atau bilangan pecahan.
e. Ketidaknegatifan (Nonnegativity)
Nilai variabel keputusan harus lebih besar atau sama dengan nol.
f. Kepastian (Certainty)
Asumsi-asumsi di atas harus dipenuhi apabila ingin menyelesaikan masalah model linear programming. Jika asumsi-asumsi tersebut tidak dapat terpenuhi, persoalan dapt diselesaikan dengan program matematik lain seperti; integer programming, nonlinear programming, goal programming, atau dynamic programming.
2.2 Integer Programming (IP)
Program bilangan bulat (integer programming) merupakan bentuk perluasan dari linear programming. Persoalan IP menginginkan solusi yang didapat berupa bilangan bulat, bukan berupa bilangan pecahan. Contoh persoalan yang sering ditemui misalnya menentukan banyaknya barang elektronik yang harus diproduksi, banyaknya unit rumah yang akan dibangun pada suatu proyek perumahan, banyaknya orang yang diperlukan untuk mengerjakan suatu proyek, dan sebagainya. Integer programming memiliki model matematis yang sama dengan model linear programming pada umumnya, tetapi ditambah batasan bahwa variabelnya harus bilangan bulat.
Berdasarkan jenis keputusan yang akan diperoleh, persoalan integer programming dapat dibedakan atas tiga jenis, yaitu:
1. Pemrograman Bilangan Bulat Murni (Pure Integer Programming) 2. Pemrograman Bilangan Bulat Campuran (Mixed Integer Programming) 3. Pemrograman Bilangan Bulat Biner (Binary Integer Programming)
2.2.1 Pemrograman Bilangan Bulat Murni (Pure Integer Programming)
Pure Integer Programming (PIR) merupakan pemrograman bilangan bulat di mana semua nilai variabel keputusan haruslah bilangan bulat. Bentuk umum pure integer programming yaitu:
Optimalkan : ∑
1, 2, … , 1, 2, … ,
0,
2.2.2 Pemrograman Bilangan Bulat Campuran (Mixed Integer Programming)
Mixed Integer Programming (PIR) merupakan pemrograman bilangan bulat di mana nilai variabel keputusannya berupa campuran antara bilangan bulat dan bilangan desimal atau pecahan. Bentuk umum mixed nteger programming yaitu:
Optimalkan : ∑ ∑
Kendala : ∑ ∑ , ,
1, 2, … , 1, 2, … , 1, 2, … ,
0, 0
2.2.3 Pemrograman Bilangan Bulat Biner (Binary Integer Programming)
Bentuk umum dari binary integer programming yaitu:
Optimalkan : ∑
Kendala : ∑ , ,
1, 2, … , 1, 2, … ,
0 atau 1
2.3 Metode Penyelesaian Masalah Integer Programming
Tampaknya cukup untuk mendapatkan solusi bulat dari masalah linear programming, dengan menggunakan metode simpleks biasa dan kemudian membulatkan nilai-nilai pecah solusi optimum. Bukan tugas mudah untuk membulatkan nilai-nilai pecah variabel basis yang menjamin tetap memenuhi semua kendala dan tidak menyimpang cukup jauh dari solusi bulat yang tepat. Akibatnya diperlukan prosedur yang sistematis untuk mendapatkan solusi bulat optimum terhadap masalah itu. Beberapa metode yang dapat digunakan untuk menyelesaikan masalah integer programming antara lain:
1. Metode Pendekatan Pembulatan 2. Metode Pendekatan Grafik 3. Metode Branch and Bound 4. Metode Cutting Plane
2.3.1 Metode Pendekatan Pembulatan
Namun demikian sebab utama kegagalan pendekatan ini adalah bahwa solusi yang diperoleh mungkin bukan solusi integer optimum yang sesungguhnya. Dengan kata lain, solusi pembulatab dapat lebih jelek dibandingkan solusi integer optimum yang sesungguhnya atau mungkin merupakan solusi tak layak.
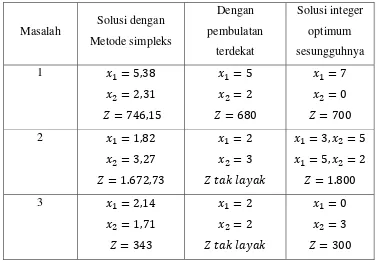
Tiga masalah berikut disajikan untuk mengilustrasikan prosedur pembulatan:
Contoh 2.1: Masalah 1:
Maksimumkan 100 90
Kendala 10 7 70
5 10 50
0
Masalah 2:
Minimumkan 200 400
Kendala 10 25 100 3 2 12
0 Masalah 3:
Maksimumkan 80 100
Kendala 4 2 12 5 15 0
Tabel 2.1 Perbandingan solusi dengan metode pendekatan pembulatan dengan bulat optimum sesungguhnya.
Masalah Solusi dengan Metode simpleks
Nilai fungsi tujuan melalui simpleks tanpa pembatasan bilangan bulat akan selalu lebih baik dibanding solusi integer optimum karena terletak pada titik pojok luar dari batas ruang solusi layak. Suatu metode yang serupa dengan pendekatan pembulatan adalah prosedur coba-coba (trial and error). Dengan menggunakan cara ini, pengambil keputusan mengamati solusi integer dan memilih solusi yang mengoptimumkan nilai fungsi tujuan. Cara ini sangat tidak efektif jika masalahnya melibatkan sejumlah besar kendala dan variabel. Terlebih lagi, memeriksa kelayakan setiap solusi yang dibulatkan akan banyak memakan waktu.
2.3.2 Metode Pendekatan Grafik
Masalah integer programming yang melibatkan dua variabel dapat diselesaikan dengan metode pendekatan grafik. Metode ini identik dengan metode grafik yang biasa digunakan dalam linear programming. Metode grafik relatif lebih mudah untuk menyelesaikan masalah integer programming dua variabel yaitu dengan menggambar grafik di atas kertas grafik kemudian menggambarkan sekumpulan titik-titik integer dalam ruang solusi layak. Masalah berikut akan diselesaikan dengan pendekatan grafik.
Contoh 2.2:
Maksimumkan 100 90
Kendala 10 7 70
5 10 50 ,
Model ini serupa dengan model linear programming biasa. Perbedaannya terletak pada kendala terakhir yang menginginkan solusi bernilai non negatif integer.
2. Periksa solusi optimum. Jika semua variabel basis memiliki nilai integer, maka solusi optimum telah diperoleh dan proses berakhir. Jika masih ada satu atau lebih variabel basis memiliki nilai pecah, teruskan ke tahap 3.
3. Buatlah suatu skala Gomory (suatu bidang pemotong atau cutting plane) dan cari solusi optimum melalui proses dual simpleks. Kembali ke tahap 2.
Kendala Gomory dalam Pure Integer Programming
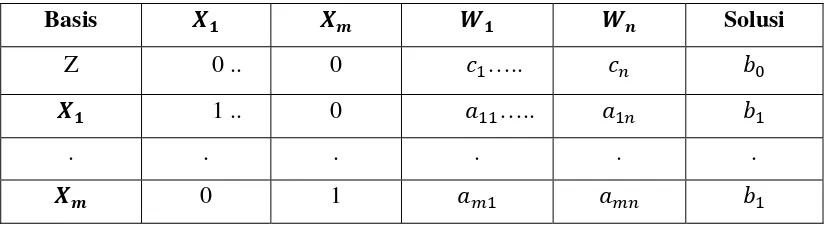
Tabel optimum masalah linear programming berikut merupakan solusi optimum kontinu.
Tabel 2.2 Solusi optimum masalah linear programming
Basis Solusi
Z 0 .. 0 …..
1 .. 0 …..
. . . . . . 0 1
Di mana variabel 1, … , menunjukkan variabel basis dan variabel 1, … , adalah non basis.
Perhatikan persamaan ke di mana variabel diasumsikan bernilai non integer. ∑ di mana non integer.
Kemudian pisahkan dan menjadi bagian yang bulat dan bagian pecah non
negatif seperti berikut:
jadi , di mana 0 1
Contoh:
Kendala Gomory yang diinginkan yaitu:
, adalah variabel slack Gomory ke .
Pada umumnya, persamaan kendala yang berhubungan dengan solusi pecah dipilih untuk menghasilkan suatu kendala Gomory. Namun, sebagai aturan main biasanya dipilih persamaan yang memiliki maksimum.
Tabel baru setelah penambahan kendala Gomory disajikan pada tabel berikut:
Tabel 2.3 Penambahan kendala Gomory
Basis Solusi
Karena diperoleh solusi primal optimum tetapi tidak layak maka digunakan metode dual simpleks. Proses pembentukan kendala Gomory berakhir jika solusi baru semua berupa bilangan bulat. Jika tidak, suatu kendala Gomory baru dibuat
lagi dari tabel yang dihasilkan dan metode dual simpleks digunakan lagi untuk mengatasi ketidaklayakan. Jika pada setiap iterasi metode dual simpleks menunjukkan bahwa tidak ada solusi layak, berarti masalah itu tidak memiliki solusi integer yang layak.
Berikut ini terdapat persoalan integer programming:
Contoh 2.3:
Maksimumkan 7 9
Kendala 3 6
7 35
,
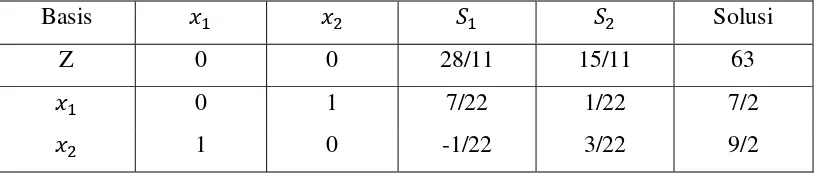
Solusi kontinu optimumnya diperoleh dalam tabel berikut:
Tabel 2.4 Solusi optimal contoh 2.3 (iterasi 0)
Basis Solusi
Z 0 0 28/11 15/11 63
0 1 7/22 1/22 7/2
1 0 -1/22 3/22 9/2
Karena solusi tidak bulat, suatu kendala Gomory ditambahkan pada tabel itu. Kedua persamaan ( dan ) pada masalah ini memiliki nilai yang sama, yaitu
, sehingga salah satu dapat digunakan, misalkan digunakan persamaan
, ini menghasilkan
atau
0 7
22 0
1
22 3
Sehingga kendala Gomory menjadi:
Tabel baru setelah penambahan kendala Gomory menjadi:
Tabel 2.5 Penambahan kendala Gomory contoh 2.3 (iterasi 0)
Basis Solusi
Z 0 0 28/11 15/11 0 63
0 1 7/22 1/22 0 7/2
1 0 -1/22 3/22 0 9/2
0 0 -7/22 -1/22 1 -1/2
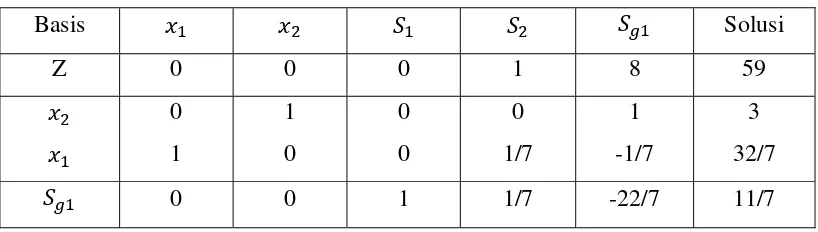
Dengan memakai metode dual simpleks diperoleh tabel baru yaitu:
Tabel 2.6 Solusi optimal contoh 2.3 (iterasi 1)
Basis Solusi
Z 0 0 0 1 8 59 0 1 0 0 1 3
1 0 0 1/7 -1/7 32/7
0 0 1 1/7 -22/7 11/7
Solusi baru yang didapat masih belum bilangan bulat, akibatnya suatu kendala Gomory baru ditambahkan. Dapat dilihat bahwa persamaan memiliki ( 47), maka ditulis dalam berikut:
0 17 0 67 4 47
Kemudian ditambahkan pada tabel 2.7 berikut:
Tabel 2.7 Penambahan kendala Gomory contoh 2.3 (iterasi 1)
Basis Solusi
Z 0 0 0 1 8 0 59 0 1 0 0 1 0 3
1 0 0 1/7 -1/7 0 32/7
0 0 1 1/7 -22/7 0 11/7
0 0 0 -1/7 -6/7 1 -4/7
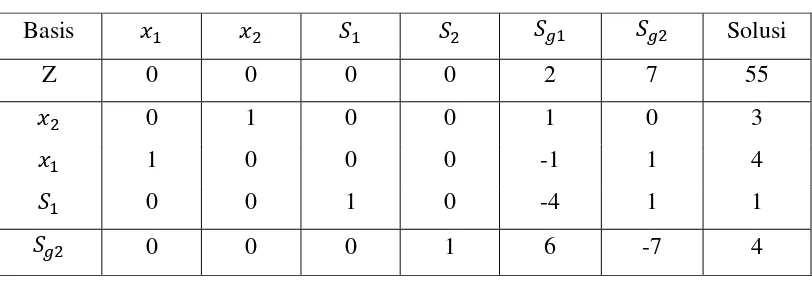
Dengan menggunakan dual simpleks diperoleh hasil:
Tabel 2.8 Solusi optimal contoh 2.3 (iterasi 2)
Basis Solusi
Z 0 0 0 0 2 7 55 0 1 0 0 1 0 3 1 0 0 0 -1 1 4 0 0 1 0 -4 1 1
0 0 0 1 6 -7 4
2.3.4 Metode Branch and Bound
Metode branch and bound adalah salah satu metode untuk mendapatkan penyelesaian optimal program linier yang menghasilkan variable-variable keputusan bilangan bulat. Metode ini membatasi penyelesaian optimum yang akan menghasilkan bilangan pecahan dengan cara membuat cabang atas dan bawah bagi masing-masing variable keputusan yang bernilai pecahan agar bernilai bulat sehingga setiap pembatasan akan menghasilkan cabang baru.
Metode branch and bound telah menjadi kode computer standar untuk integer programming, dan penerapan-penerapan dalam praktek tampaknya menyarankan bahwa metode ini lebih efisien dibanding dengan metode cutting plane. Metode branch and bound dapat digunakan untuk menyelesaikan masalah pure maupun mixed integer programming.
Berikut ini adalah langkah-langkah penyelesaian masalah maksimasi dengan metode branch and bound:
1. Selesaikan masalah LP biasa tanpa pembatasan bilangan bulat dengan metode simpleks biasa.
2. Teliti solusi optimalnya. Jika semua variabel basis telah bernilai bulat, maka solusi optimum telah tercapai dan proses berakhir. Jika satu atau lebih variabel basis belum bernilai bulat, lanjut ke tahap 3.
3. Jadikan solusi pada penyelesaian tahap 1 (relaxed solution) menjadi batas atas dan sebagai batas bawahnya digunakan solusi yang variabel basisnya telah dibulatkan ke bawah (rounded-down).
4. Pilih variabel yang mempunyai nilai pecahan yang terbesar untuk dijadikan pencabangan ke dalam sub-sub masalah. Tujuannya adalah untuk menghilangkan solusi kontinu yang tidak memenuhi persyaratan bulat dalam masalah itu. Pencabangan dilakukan secara mutually exclusive untuk memenuhi persyaratan bulat dengan jaminan tidak ada solusi bulat layak yang tidak diikut sertakan.
awalnya, ini adalah solusi kontinu yang dibulatkan ke bawah). Sub – sub masalah yang memiliki batas atas kurang dari batas bawah yang ada, tidak diikut sertakan pada analisa selanjutnya. Suatu solusi bulat layak adalah sama baik atau lebih baik dari batas atas untuk setiap sub masalah yang dicari. Jika solusi yang demikian terjadi, suatu sub masalah dengan batas atas terbaik dipilih untuk dicabangkan. Kembali ke langkah 4.
Untuk masalah minimasi, solusi yang menjadi batas atas dibulatkan keatas, atau dengan kata lain batas atas dan bawah pada kasus minimasi berlawanan pada kasus maksimasi.
Untuk memperoleh gambaran yang lebih jelas tentang metode Branch dan Bound, perhatikan contoh 2.4 berikut:
Contoh 2.4:
Maksimumkan 3 5
Kendala 2 4 25
8
2 10
,
Solusi optimum kontinu masalah tersebut adalah 8, 2,25 dan 35,25.
dan 3 yang selanjutnya akan diuraikan sebagai bagian A dan bagian B. Kendala-kendala baru tersebut secara efektif menghilangkan semua nilai pecah yang mungkin .
Bagian A:
Maksimumkan 3 5
Kendala 2 45 25
8 2 10
2
, 0
Bagian B:
Maksimumkan 3 5
Kendala 2 4 25
8 2 10
3
, 0
Bagian A dan bagian B diselesaikan dengan metode simpleks tanpa pembatasan bilangan bulat. Solusi simpleksnya yaitu:
Bagian A: 8, 2, dan 34 Bagian B: 6,5, 3, dan 34,5
Selanjutnya bagian B dicabangkan ke dalam dua sub bagian, yaitu B1 dan
B2. Pada sub bagian B1 ditambah kendala baru yaitu 6, sedangkan pada sub
bagian B2 ditambah kendala 7. Kedua sub-masalah tersebut dinyatakan
sebagai berikut:
Sub bagian B1:
Maksimumkan 3 5
Kendala 2 4 25
8 2 10
3
6
, 0
Sub bagian B2:
Maksimumkan 3 5
Kendala 2 4 25
8 2 10
3
7
, 0
Solusi simpleks kedua sub masalah tersebut yaitu: Sub bagian B1: 6, 3,25, dan 34,25
Sub bagian B2: tidak layak.
Sub-bagian B1 menghasilkan nilai fungsi tujuan yang lebih besar dari 34
Sub bagian B1a:
Maksimumkan 3 5
Kendala 2 4 25
8 2 10
3 6 3
, 0
Sub bagian B1b:
Maksimumkan 3 5
Kendala 2 4 25
8 2 10
3
6 4
, 0
Solusi optimum dengan metode simpleks adalah: Sub bagian B1a: 6, 3, dan 33.
Sub bagian B1b: 4,25, 4, dan 33,5.
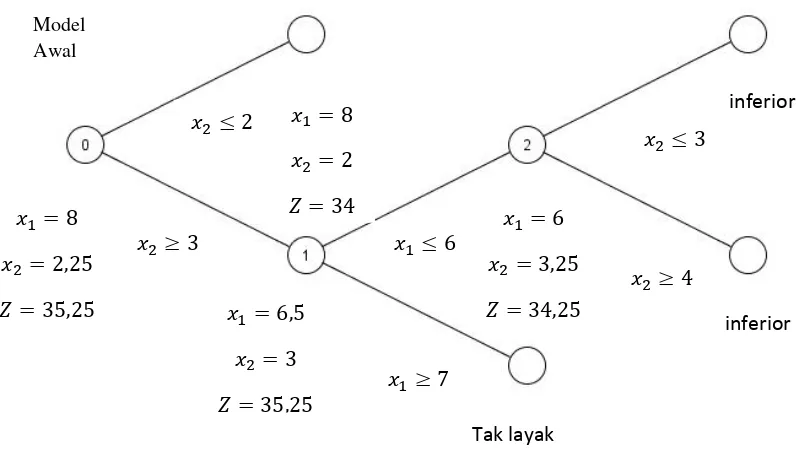
Seluruh prosedur branch and bound untuk masalah ini ditunjukkan pada gambar berikut:
Gambar 2.2 Grafik pencabangan pada metode Branch and Bound
Model Awal
8 2,25 35,25
2
3
8 2 34
6,5 3 35,25
6
7
6 3,25 34,25
3
4
Tak layak
inferior