BAB 2
LANDASAN TEORI
Pada bagian ini diberikan beberapa konsep dasar yang menjadi landasan berpikir dalam penelitian ini, seperti fungsi nonlinier, fungsi smooth, fungsi nonsmooth, turunan fungsi smooth, turunan fungsi nonsmooth, dan metode Subgradien pada fungsi
nonsmooth.
2.1 Fungsi Nonlinier
Definisi 2.1.1.
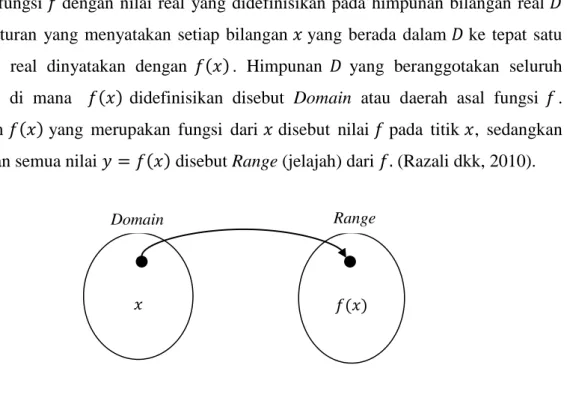
Sebuah fungsi dengan nilai real yang didefinisikan pada himpunan bilangan real adalah aturan yang menyatakan setiap bilangan yang berada dalam ke tepat satu bilangan real dinyatakan dengan ( ) . Himpunan yang beranggotakan seluruh bilangan di mana ( ) didefinisikan disebut Domain atau daerah asal fungsi . Bilangan ( ) yang merupakan fungsi dari disebut nilai pada titik , sedangkan himpunan semua nilai ( ) disebut Range (jelajah) dari (Razali dkk, 2010).
Gambar 2.1.1. Ilustrasi fungsi ( )
Fungsi nonlinier merupakan fungsi yang tidak linier, yakni grafiknya bukan berupa garis lurus melainkan berupa kurva atau garis zig-zag.
Bentuk umum dari fungsi nonlinier
( )
di mana dan merupakan koefisien.
Beberapa bentuk dari fungsi nonlinier adalah
1. Fungsi kuadrat
Fungsi kuadrat adalah fungsi yang mempunyai pangkat tertinggi dari variabelnya adalah pangkat dua. Gambar fungsi kuadrat bisa berupa lingkaran, elips, parabola, dan hiperbola.
Bentuk umum dari fungsi kuadrat adalah
di mana dan .
Diberikan beberapa ciri-ciri dari suatu fungsi kuadrat yaitu:
1
1.. Jika dan maka bentuk kurvanya lingkaran.
2
2.. dan mempunyai tanda yang sama maka bentuk
kurvanya elips.
3
3.. berlawanan tanda maka bentuk kurvanya hiperbola.
4
4.. dan jika salah satu atau maka bentuk kurvanya
parabola.
2. Fungsi kubik
Fungsi kubik adalah fungsi yang pangkat tertinggi dari variabelnya adalah pangkat tiga.
Bentuk umum dari fungsi kubik adalah
. di mana .
Sebuah fungsi kubik setidak-tidaknya mempunyai sebuah titik belok
(inflextion point), yaitu titik peralihan bentuk kurva dari cekung menjadi
cembung atau sebaliknya. Selain titik belok, fungsi kubik memungkinkan mempunyai sebuah titik ekstrim (maksimum atau minimum) atau kedua titik ekstrim (maksimum dan minimum). Ada tidaknya titik ekstrim pada fungsi kubik bergantung dari besarnya nilai di dalam persamaan.
Gambar 2.1.3. Fungsi kubik untuk
Gambar 2.1.4. Fungsi kubik untuk
3. Fungsi eksponensial
Pada fungsi eksponensial kurvanya berada di kuadran I dan II pada sistem koordinat.
Bentuk sederhana dari fungsi eksponensial di mana
Bentuk umum dari fungsi eksponensial
di mana dan adalah konstanta
Kurva fungsi eksponensial asimtotik terhadap garis Titik potong kurva eksponensial
G Gaammbbaarr22..11..5.5.FFuunnggssiieekkssppoonneennssiiaalluunnttuukk G Gaammbbaarr22..11..6.6.FFuunnggssiieekkssppoonneennssiiaalluunnttuukk
4. Fungsi logaritmik
Fungsi logaritmik merupakan kebalikan dari fungsi eksponensial yang variabel bebasnya merupakan bilangan logaritma.
B Beennttuukksseeddeerrhhaannaaddaarriiffuunnggssiillooggaarriittmmiikk d diimmaannaa B Beennttuukkuummuummddaarriiffuunnggssiillooggaarriittmmiikk yy d diimmaannaa K Kuurrvvaaffuunnggssiillooggaarriittmmiikkaaddaaddiisseebbeellaahhkkaannaannddaannaassiimmttoottiikktteerrhhaaddaappggaarriiss T Tiittiikkppoottoonnggddeennggaannssuummbbuu–– ** ++ T Tiittiikkppoottoonnggddeennggaannssuummbbuu–– ** ++ G Gaammbbaarr22..11..7 7FFuunnggssiillooggaarriittmmiikk
2.1.1 Fungsi Smooth
Sebuah fungsi pada dengan
( ) { ( ⁄ ) Adalah smooth dan mempunyai turunan 0 pada .
Sebuah fungsi yang kontinu dan mempunyai turunan pada setiap titik diberikan sebagai berikut:
( ) { ( )
di mana ( ) adalah polynomial dari derajat
Bukti:
Dengan menggunakan induksi matematika, untuk semua bilangan asli termasuk 0
( ⁄ )
di mana semua adalah kontinu dan dapat didifferensialkan pada , karena ( ) ( ) ( ) ( ⁄ )
( ) ( ) ∑ ( ) ( ) ( )
Oleh karena untuk semua bilangan positif diikutsertakan, maka digunakan persamaan fungsi pada fungsi eksponensial.
( ⁄ )
( )
Akan dibuktikan rumus untuk turunan ke dengan induksi matematika. Untuk turunan pertama dari untuk semua dan ( ) adalah polynomial dari derajat 0 adalah benar. Akibatnya turunan dari adalah 0 untuk . ( ) ( ) ( ) ( ) ( ⁄ ) ( )
Tahap induksi matematika dari sampai adalah sama. Untuk diperoleh turunannya adalah
( )( ) ( ( ) ( ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( )
di mana ( ) adalah polynomial dari derajat ( ) . Maka
turunan pertama ( ) dari adalah 0 untuk semua . Turunan pada , adalah ( ) ( ) ( ) ( ⁄ ) (Wikipedia, 2013). 2.1.2 Fungsi Nonsmooth Definisi 2.1.2.1.
Istilah nonsmooth mengacu pada situasi dimana terjadi smoothness (differensiabilitas). Sebuah fungsi yang nonsmooth dapat berupa fungsi patah namun tetap kontinu. (Clarke, 1983).
Contoh 2.1.2.1.
( ) .
Fungsi di atas dapat digambarkan sebagai berikut:
0 1 x
-1
Fungsi ( ) merupakan dua buah garis yang bertemu pada satu titik, yaitu di titik . Kedua garis memiliki turunan yang berbeda. Turunan dari sebelah kiri adalah dan turunan dari sebelah kanan adalah . (Martono, 2002)
Berdasarkan contoh di atas fungsi nonsmooth dapat diartikan sebagai fungsi yang mempunyai turunan berarah.
2.2 Turunan Fungsi Nonlinier
Definisi 2.2.1
Untuk fungsi ( ) maka turunannya di titik didefinisikan oleh: ( )
( ) ( )
jika limit ini ada. Jika ( ) ada, maka dikatakan fungsi ( ) terdifferensialkan (dapat diturunkan) di titik . (Razali dkk, 2010)
Untuk menentukan turunan dari ( ), Langkah-langkah yang harus dilakukan adalah
1. Tentukan ( )
2. Tentukan selisih ( ) ( )
3. Bagilah dengan untuk mendapatkan ( ) ( )
4. Ambil limit lalu hitung ( )
Thomas, G.B (2012) memaparkan beberapa aturan pada turunan, yaitu:
Teorema 2.2.1. (Aturan Fungsi konstanta)
Jika ( ) , di mana adalah konstanta, maka untuk sebarang berlaku ( ) Bukti: ( ) ( ) ( ) ( ) ( ) ( )
Jadi, terbukti jika ( ) maka ( )
Teorema 2.2.2. (Aturan Pangkat)
Jika ( ) di mana sebarang bilangan rasional, maka turunannya adalah ( ) Bukti: Langkah 1 ( ) ( ) ( )
Langkah 2 ( ) ( ) [ ( ) ] ( ) Langkah 3 ( ) ( ) ( ) [ ( ) ] ( ) Langkah 4
Ambil limit untuk hasil akhir langkah 3 diperoleh: ( ) ( ) ( ) ( ) ( ) ( )
Teorema 2.2.3. (Aturan perkalian fungsi dengan konstanta)
Misalkan adalah sebarang bilangan real. Jika ( ) ada maka turunan dari fungsi ( ) ( ) adalah
( ) ( )
Artinya turunan dari perkalian konstanta dengan fungsi ( ) adalah sama dengan perkalian konstanta dengan turunan ( ).
Bukti: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Teorema 2.2.4. (Aturan jumlah – selisih)
Jika diberikan fungsi ( ) ( ) ( ) di mana ( ) dan ( ) terdifferensialkan, maka:
( ) ( ) ( )
Artinya turunan dari jumlah atau selisih dua fungsi adalah sama dengan jumlah atau selisih dari turunan keduanya. Aturan ini berlaku pada tiga fungsi atau lebih.
Bukti:
Ambil jumlah dua fungsi ( ) ( ) ( ). Dengan menggunakan definisi turunan ( ) ( ) ( ) Untuk ( ) ( ) ( ), maka: Langkah 1 ( ) ( ) ( ) Langkah 2 ( ) ( ) , ( ) ( )- , ( ) ( )- , ( ) ( )- , ( ) ( )- Langkah 3 ( ) ( ) , ( ) ( , ( ) ( ( ) ( ) , ( ) ( )- , ( ) ( )-Kemudian ambil limit pero eh
Langkah 4 ( ) ( ) , ( ) ( , ( ) (
)-Teorema 2.2.5. ( Aturan perkalian )
( ) ( ) ( ) di mana ( ) dan ( ) dapat diturunkan, maka turunan dari ( ) adalah ( ) ( ) ( ) ( ) ( ) Bukti: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) * ( ) ( ) ( ) ( ) ( ) ( )+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Teorema 2.2.6. (Aturan pembagian)
Jika diberikan ( ) ( ) ( ) di mana ( ) dan ( ) terdifferensialkan maka turunannya adalah
( ) ( ) ( ) ( ) ( ) , (
)-Bukti: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) * ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )+ ( ) ,* ( ) ( ) ( ) ( ) ( ) ( )+ ( ) ( ) -( ) ( ) ( ) ( ) ( ) , (
)-2.2.1 Turunan Fungsi Smooth
Beberapa interpretasi penting mengenai turunan, yaitu:
1. Turunan ditafsirkan sebagai gradien garis singgung kurva ( ) di titik .
2. Turunan ditafsirkan sebagai laju perubahan dari fungsi ( ) di titik .
3. Turunan ditafsirkan sebagai kecepatan sesaat dari sebuah persamaan gerak ( ) di titik .
Pada fungsi smooth, turunannya ditafsirkan sebagai gradien garis singgung kurva ( ) di titik .
2.2.2 Turunan fungsi Nonsmooth
Andaikan adalah sebuah fungsi dan merupakan sebuah titik di maka fungsi tersebut dikatakan Lipschitz terhadap jika terdapat sebuah skalar dan bilangan positif ɛ sehingga:
| ( ) ( )| e er di mana B adalah sebuah unit ball yang terbuka di , maka ɛ adalah open ball pada radius ɛ pada .
Andaikan adalah Lipschitz terhadap dan andaikan vektor lain pada X. Generalizad directional derivative pada di yang menuju , disimbolkan ( ), dan didefinisikan sebagai berikut:
( )
( ) ( )
di mana adalah vektor di X dan adalah sebuah skalar positif.
Proposisi 2.2.2
Andaikan adalah Lipschitz pada rank K terhadap , maka:
1. Fungsi ( ) adalah finite, positively homogeneous, dan
subadditive pada X, dan memenuhi ( ) ‖ ‖.
2. ( ) adalah upper semicontinuous sebagai fungsi dari ( ) dan hanya sebagai fungsi saja, adalah Lipschitz dari rank K pada X. 3. ( ) ( ) ( )
Bukti:
Pada kondisi Lipschitz, nilai dari ( ) pada ‖ ‖ dimana mendekati dan mendekati 0
( ) p ( ) ( )
p ( ) ( ) p ( ) ( )
Dapat disimpulkan bahwa
( ) ( ) ( )
Andaikan * + dan * + berturut-turut konvergen pada , maka terdapat dalam X dan sehingga
‖ ‖
( ) ( ) ( )
( ) ( ) ( ) ( ) Dengan mengambil limit diperoleh
p ( ) ( )
Andaikan dan berada di X, maka
( ) ( ) ( ) ( ) ‖ ‖ ( ) ( ) ‖ ‖ ( ) p ( ) ( )
p ( )( ) ( )( ) di mana ( ) ( ) (Clarke, 1983).
Sebagai sebuah fungsi dari ( ) adalah positively
homogeneous, dan subadditive, sehingga dapat didefinisikan
himpunan tak kosong ( ) adalah generalized gradien pada di , sebagai berikut:
( ) * ( ) 〈 〉 +
Dengan mempertimbangkan sifat dari , maka ( ) himpunan bagian tak kosong yang konveks pada , untuk setiap
( ) *〈 〉 ( )+ Maka sama dengan ( ).
( ) dapat dikatakan subdifferential pada analisis konveks , dan himpunan dari vektor yang berada di dapat ditulis sebagai berikut :
( ) ( ) 〈 〉 untuk semua
Yi Zhang (2013) menjelaskan bahwa sebuah vektor adalah subgradien dari pada jika
( ) ( ) ( ) ( )
Jika konveks dan terdifferensialkan maka ( ) adalah subgradien dari pada .