BAB I PENDAHULUAN
Standar Kompetensi
Mahasiswa memahami konsep sistem bilangan real (R) sebagai semesta dalam
menentukan selesaian persamaan dan pertidaksamaan dan dapat mengembangkan dalam bentuk persamaan dan pertidaksamaan yang memuat harga mutlak serta menentukan gradien dan persamaan garis lurus.
Kompetensi Dasar
Setelah mempelajari pokok bahasan ini diharapkan:
1. Mahasiswa dapat menyatakan bilangan rasional
b a
Q sebagai bentuk desimal
berulang atau sebaliknya.
2. Mahasiswa dapat menentukan selesaian persamaan. 3. Mahasiswa dapat menentukan selesaian pertidaksamaan.
4. Mahasiswa dapat menetukan selesaian persamaan dan pertidaksamaan yang memuat harga mutlak.
5. Mahasiswa dapat menyatakan letak suatu titik dengan sistem koordinat. 6. Mahasiswa dapat menentukan gradien suatu persamaan garis lurus. 7. Mahasiswa dapat menentukan persamaan garis lurus.
Bab I, dalam buku ini memuat hal-hal pokok yang berkaitan dengan sistem bilangan real (R) antara lain (1) sistem bilangan real, (2) persamaan dan
pertidaksamaan , (3) nilai mutlak sifat-sifatnya, (4) sistem koordinat , dan (5) persamaan garis lurus
1.1 Sistem Bilangan Real
Sebelum penulis menguraikan konsep sistem bilangan real (R), terlebih
mempunyai ciri-ciri, kriteria dan syarat yang tertentu serta terdefinisi dengan jelas. Objek atau unsur sesuatu himpunan A dinamakan anggota atau elemen. Anggota suatu himpunan dinyatakan dengan huruf a, b, c, d, …, atau 1, 2, 3, 4, …. , sedangkan nama himpunan dinyatakan dengan huruf kapital A, B, C, D, dan seterusnya. Misal kita mendefinisikan suatu himpunan A dengan menyatakan secara jelas anggota-anggotanya yang terdiri dari a, b, c , d, dan e, himpunan A tersebut dapat ditulis dalam bentuk
} , , , ,
{a b c d e
A dengan masing-masing anggota himpunan A dipisahkan oleh tanda
baca koma dan terdapat dua tanda kurung { }. Jika himpunan A mempunyai anggota yang banyaknya tak hingga maka unsur-unsurnya tidak ditulis semuanya akan tetapi cukup dituliskan beberapa anggotanya dan titik-titik sebanyak 3 atau 5 titik. Misalnya
,...} 5 , 4 , 3 , 2 , 1 {
B . Selanjutnya jika a anggota suatu himpunan A, maka dituliskan
A
a dan dibaca “a anggota A”. Jika a bukan anggota himpunan A, maka dituliskan
A
a dan dibaca “a bukan anggota A. Jika suatu himpunan A tidak memiliki anggota,
maka A disebut himpunan kosong. Himpunan kosong dinotasikan dengan atau { }.
Himpunan sebagai telah disebutkan di atas, dalam penulisannya dapat dilakukan dengan dua metode, yaitu metode pencirian (notasi) dan metode perincian (tabulasi). Metode pencirian dilakukan dengan cara menuliskan syarat keanggotaan yang dimiliki oleh seluruh anggota suatu himpunan akan tetapi tidak dimiliki oleh unsur-unsur yang bukan anggota himpunan tersebut. ,
Contoh:
1) A{y ybilangan primakurangdari10} 2) B {xx faktorganjildari 21}
3) C {xx2 1,xbilangan prima}
4) D {xx faktor genapdari 21} 5) E {xx2 3x 40}
6) F {xx2 3x 40}
7) G{xx42}
8) H {(x,y)x2 y2 4}
Metode perincian dilakukan dengan cara mendaftar seluruh anggota himpunan yang memenuhi syarat dan ketentuan yang diberikan dalam suatu himpunan.
1) A{1,2,3,4,5,...}
2) B{senin,selasa,rabu,kamis, jum'at,sabtu}
3) C {2,3,5,7,11,13,17,19,...}
4) D {merah,kuning,hijau}
5) E {0}
6) F {}
7) G {1,x}
8) H {(1,2),(2,3),(3,4),...}
Misal A dan B suatu himpunan, himpunan A disebut himpunan bagian
himpunan B, ditulis dengan notasi AB, jika setiap anggota A merupakan anggota B. Kiranya tidaklah sulit untuk dipahami bahwa A untuk sebarang himpunan A. Jika
setiap anggota himpunan anggota A juga merupakan anggota setiap himpuna B maka dinotasikan dengan AB
Selanjutnya untuk memudahkan para pembaca dalam memahami konsep system bilangan real berikut ini diberikan beberapa bilangan dan himpunan bilangan yang pada bab-bab selanjutnya dalam buku ini sering ditemukan. Bilangan dan himpunan bilangan tersebut adalah:
1. Himpunan bilangan Asli (Natural)
Himpunan bilangan asli dinotasikan dengan N dan anggota-anggota bilangan asli adalah 1, 2, 3, 4, 5, 6, ... sehingga N{1,2,3,4,5,6,...}
Bilangan asli tertutup terhadap operasi penjumlahan dan perkalian, artinya untuk setiap a, b bilangan asli maka (a+b) dan (a.b) bilangan asli. Oleh karena itu, himpunan semua bilangan asli membentuk suatu sistem sistem bilangan asli.
2. Bilangan cacah (whole)
Bilangan cacah dilambangkan dengan W dan anggota-anggota bilangan cacah adalah 0, 1, 2, 3, 4, 5, 6, ..., sehingga W{0,1,2,3,4,5,6,...}. Bilangan cacah
3. Sistem bilangan asli bersama-sama dengan bilangan nol dan lawan dari bilangan-bilangan asli membentuk sistem bilangan-bilangan bulat, Bilangan bulat dinotasikan dengan Z yang anggota-anggotanya adalah ...-3, -2, -,1, 0, 1, 2, 3, ..., sehingga
Z{... 3,2,2,0,1,2,3,...}.
4. Bilangan pecahan atau bilangan rasional (quotient). Bilangan rasional adalah
bilangan yang secara umum dinyatakan dengan .a,bZ,b0 b
a Q
Contoh
1)
3 1 p
2)
11 2 q
3)
7 22 r
Bilangan-bilangan rasional di atas, dapat dinyatakan dalam bilangan-bilangan desimal, yaitu
1) 0,33333333... 3
1 p
2) 0,285714285714285714... 11
2 q
3) 3,142857142857148... 7
22 r
Jika kita cermati lebih mendetail, bilangan-bilangan desimal sebagai mana tersebut di atas selalu berulang angka-angkanya, sehingga bilangan rasional juga disebut bilangan desimal berulang. Sebaliknya bilangan desimal berulang dapat dinyatakan sebagai bilangan rasional. Untuk menyatakan bentuk desimal menjadi bilangan rasioan adalah dengan cara melihat angka yang berulang pada bilangan tersrsebut. Jika terdapat
1 angka yang berulang maka kalikan bilangan dimaksud dengan 101. Jika terdapat 2
angka yang berulang maka kalikan bilangan tersebut dengan 102. dan seterusnya.
Contoh:
Ubahlah bilangan desimal berikut ini menjadi bentuk rasional .a,bZ,b0 b
a Q
1.
b a ... 1212121212 ,
0
Tentukan a dan b. Jawab
Bilangan 0,12121212... adalah bilangan desimal dengan 2 angka berulang yaitu angka 1 dan angka 2. Karena banyaknya angka berulang sebanyak 2
angka maka kalikan bilangan semula dengan 102, sehingga diperoleh: x = 0,1212121...
100 x = 12,12121212...
100x – x = (12,12121212…) – (0,12121212..) 99 x = 12
x =
99 12
Bentuk rasional 0,1212121… adalah
99 12
2.
b a ... 33 4123333333 ,
1
Tentukan a, b.
. Jawab
Bilangan 1,41233333333... adalah desimal dengan 1 angka berulang yaitu
angka 3, sehingga kalikan bilangan semula dengan101 dan diperoleh x = 1,412333333...
10 x = 14,123333333...
10x – x = (14,12333333...) – (1,412333333…) 9 x = 12,711
x = , 9
711 , 12
karena pembilang bukan bilangan bulat maka
9 711 , 12
=
9000 12711
Bentuk rasional 1,41233333333... adalah
3.
b a 0,9826273273273...
Tentukan a dan b. Jawab
Bilangan = -0,9826273273273... adalah desimal dengan 3 angka berulang yaitu angka 2, angka 7, dan angka 3, sehingga kalikan bilangan semula dengan
3
10 sehingga diperoleh: x = -0,9826273273273... 1000x = -982,6273273273...
1000x – x = (-982,6273273…) – (0,9826273273…) 999 x = -981,6447
x =
999 6447 , 981
, pembilang bukan bilangan bulat, maka:
999 6447 , 981
=
999000 9816447
Bentuk rasional -0,9826273273273... adalah
999000 9816447
4.
b a ... 432 0543254325 ,
0
Tentukan a dan b Jawab
Bilangan 0,0543254325432...adalah bilangan desimal dengan 4 angka berulang yaitu angka 5, angka 4, angka 3, dan angka 2 sehingga kalikan
bilangan semula dengan 104 sehingga x = 0,0543254325432...
10000x = 543,254325432…..
10000x – x = (543,254325432…) - (0,054325432…) 9999 x = 543,2
x =
9999 2 , 543
=
99990 5432
Bentuk rasional 0,0543254325432... adalah
5. Bilangan Irasional (Q_ ) atau disebut juga bilangan tidak rasional yaitu bilangan
yang tidak dapat dinyatakan dalam bentuk .a,bZ,b0 b
a
Q . Karena bilangan
rasional dapat dinyatakan dengan bilangan desimal yang angka-angkanya berulang, maka bilangan irasional adalah bilangan desimal yang angka-angkanya tidak ada yang berulang. Bilangan irasional juga disebut dengan bilangan bentuk akar.
Persoalan dalam kehidupan sehari-hari sering dijumpai adanya
bilangan-bilangan irasional. Contoh bilangan-bilangan irasional antara lain adalah 2 dan . Bilangan
2 adalah panjang sisi miring segitiga siku-siku dengan panjang sisi-sisi tegaknya
masing-masing adalah 1. Perhatikan gambar berikut.
Gambar 1.1
Sedangkan bilangan merupakan hasil bagi antara keliling sebarang lingkaran dengan panjang garis tengah lingkaran tersebut. Perhatikan gambar berikut ini.
Gambar 1.2
Contoh
1) 2 = 1,41421356237...
2) 3 = 1,73205080756...
d1
l1 l2
d2
2 2 1 1
d l d
l
1
2
3) 11 = 3,316625790355...
4) π = 3.14159265358979….
5) e = 2,71828 18284 59045 23536 02874 71352…
Berdasarkan contoh di atas, tampak bilangan-bilangan dalam bentuk akar umumnya adalah bilangan desimal yang angka-angkanya tidak ada yang berulang. Sehingga bilangan akar juga disebut bilangan irasional. Dengan demikian apa yang
selama ini dianggap sama yaitu
7 22
=
tidaklah selalu benar. Karena7 22
adalah
bilangan rasional, sedangkan
adalah bilangan irasional.6. Himpunan semua bilangan irasional bersama-sama dengan bilangan rasional membentuk himpunan semua bilangan real (R), sehingga RNWZQQ Seperti telah diketahui, untuk menyatakan sebarang bilangan real seringkali digunakan cara desimal.
Contoh
Bilangan-bilangan
66 7 dan , 3 5 , 4 3
masing-masing dapat dinyatakan dalam desimal
sebagai
0,75
, 1,666...
, dan 0,1060606.... Dapat ditunjukkan bahwa bentuk desimal bilangan-bilangan rasional adalah salah satu dari 2 tipe berikut:i. berhenti ( dst.
8 1 , 2 5 , 4 3
), atau
ii. berulang beraturan ( ,dst.
66 7 , 3 5
).
Sifat-sifat Sistem Bilangan Real
Untuk sebarang a,b,c, d bilangan real berlaku sifat-sifat sebagai berikut: 1) Sifat komutatif
(i). abba (ii).a.bb.a
2) Sifat asosiatif
((iii).).aa.
b
.cb c
a.b
.ac ba
.b.cc a b c
a.(bc)(a.b)(a.c)
4) (i). .1, b0 b
a b a
(ii). , 0, 0
. ) . ( ) . (
b d
d b
c b d a d c b a
(iii). , 0, 0
. .
. b d
d b
c a d c b a
5) (i). a.(b)(a).b (a.b)
(ii). (a).(b) a.b
(iii). ( a) a
6) (i). 0 0
a , untuk setiap bilangan a 0.
(ii).
0 a
tak terdefinisikan.
(iii). 1 a a
, untuk setiap bilangan a0.
7) Hukum kanselasi
(i). Jika a.cb.c dan c 0 maka ab.
(ii). Jika b,c0 maka
b a c b
c a
. .
.
8) Sifat pembagi nol
Jika a.b0 maka a 0 atau b0.
Sifat-sifat terurut bilangan Real
Prinsip adalah aturan atau sifat yang digunakan sebagai dasar atau landasan dalam uraian yang berkaitan dengan bukti sesuatu. Prinsip dapat diambil dari definisi, aksioma, atau dalil-dalil yang “dimunculkan” kembali untuk digunakan pada bagian lain suatu konsep yang memerlukan. Diantara prinsip dalam matematika adalah prinsip urutan (well ordering principle).
Definisi
Misalkan P himpunan bagian R dan P. Untuk selanjutnya P disebut bilangan real positip kuat, maka berlaku sifat-sifat berikut ini:
(1) Jika a,bP maka (ab)P
(2) Jika a,bP maka (a.b)P
(3) Jika aR, maka tepat dari salah satu yang berikut dipenuhi aP,a0,aP
Dua sifat yang pertama menjamin kesesuaian dari urutan dengan operasi penjumlahan dan perkalian secara berurutan. Sifat (3) biasanya disebut sifat trikotomi karena membagi R menjadi 3 jenis unsur yang berbeda. Dinyatakan bahwa
}
{aaP dari bilangan real negatip tidak mempunyai unsur persekutuan dengan P,
dan selanjutnya himpunan R merupakan gabungan dari tiga himpunan yang saling asing.
Definisi
1) Jika aP, kita mengatakan bahwa a adalah suatu bilangan real positip kuat (strictly positip) dan dituliskan dengan a0, Jika aP{0} , maka a disebut
bilangan real tidak negatip dan dituliskan dalam bentuk a0.
2) Jika aP, kita mengatakan bahwa a adalah suatu bilangan real negatip kuat (strictly negatip) dan dituliskan dalam bentuk a0, Jika aP{0}, maka a
disebut bilangan real tidak positip dan dituliskan dalam bentuk a0.
3) Jika a,bRdan jika a bP maka dituliskan dalam bentuk ab atau ba. 4) ika a,bRdan jika a bP{0} maka dituliskan dalam bentuk ab atau
a b .
Untuk kesepakatan bersama kita akan menuliskan abcyang berarti abdan
c
b . Demikian juga jika abc yang berarti ab maka b c dan seterusnya. Berikut ini diberikan beberapa teorema yang berkaitan dengan prinsip keterurutan
Teorema 1
Misalkan a,b,cR
1. Jika ab dan bc maka
a
c
.ab,ab,ab
3. Jika ab dan ab maka ab
Bukti
1) abmaka menurut definisi a b0atau a bP c
b maka menurut definisi b c0 atau b cP
Karena a bPdan b cPmaka menurut definisi diperoleh (a b)(b c)P
sehingga a cPatau
a
c
2) Dengan sifat trikotomi dalam definisi, maka tepat salah satu dari yang berikut mungkin terjadi
0
b
a , atau a b0atau (a b)0sehingga abatau a batau ab
3) Jika ab, maka a b0, sehingga dari bukti (b) kita dapatkan a bPatau
P c
b yakni abatau ba. Dalam kasus lainnya salah satu dari hipotesisi tersebut kontradiksi. Jadi haruslah ab
Teorema 2
1. Jika aRdan a0maka a2 0.
2. 10
3. Jika nN maka n0
Bukti
1. Dengan sifat trikotomi jika a0, maka aPatau aP. Jika aPmaka
dengan definisi kita mempunyai a2 a.a, untuk aP. Dengan cara yang sama
Jika -a
P maka dengan definisi sebelumnya diperoleh bentukP a a
a
) ( )( )
( 2 . Berdasarkan teorema sebelumnya berakibat bahwa:
( 1)
( 1)
( 1)( 1) 2) )(
(a a a a a . Akibatnya bahwa a2P. Jadi kita
simpulkan bahwa jika a P, maka a2 0.
2. Karena 1 (1)2
, menurut bukti di atas akan menyebabkan bahwa 1 > 0.
Karena 1 > 0 dan 1P, maka k1P, sehingga pernyataan di atas benar adanya dengan menggunakan definisi sebelumnya.
Teorema 3
Misalkan a,b,cR
1. Jika ab, maka acbc
2. Jika ab, dan bc maka acbd
3. Jika ab, c0 maka acbc
4. Jika ab, c0maka acbc
5. Jika a0maka 1 0 a
6. Jika a0 maka 1 0 a
Bukti teorema di atas dapat dijelaskan sebagai berikut:
1. Karena ab berarti menurut definisi sebelumnya a b0. Karena a b0 sehingga a bP.
) ( ) ( )
(a b a b c c
) ( ) ( ) ( )
(a b c c ac bc
Sehingga (ac) (bc)P. Dengan kata lain (ac) (bc)0
Karena (ac) (bc)0berarti (ac)(bc)
2. Karena ab dan cd berarti a b0dan c d 0. Hal ini berarti a bP dan c dP.
Menurut definisi bilangan real positip kuat (1) diperoleh
P d c b
a )( )
( . Dengan kata lain (a b)(c d)0, atau
0 ) ( )
(a b c d sehingga berlaku (a b)(c d)
3. Karena ab dan cd berarti a b0dan c d 0. Hal ini berarti a bP dan c dP.
Menurut definisi bilangan real positip kuat (2) diperoleh
P c b a )
( . Dengan kata lain (ac bc)P, atau
0 )
(ac bc sehingga berlaku acbc
4. Karena ab dan c0 berarti a b0dan c0atau (c)0.
Menurut definisi bilangan real positip kuat (2) diperoleh
P c b
a )( )
( . Dengan kata lain (bc ac)P, atau
P ac bc )
( sehingga berlaku bcac
5. Jika a0 maka a0(berdasarkan sifat trikotomi). Karena a0, berdasarkan
sifat sebelumnya maka berlaku 1 0,
a Jika 0
1
a , berdasarkan teorema
sebelumnya diperoleh 1 10
a
a .
Hal ini bertentangan dengan kenyataan bahwa 1 < 0. Jadi haruslah
0 1
a
6. Jika a0, maka a0 (berdasarkan sifat trikotomi). Karena a0, berdasarkan
sifat sebelumnya maka maka berlaku 1 0,
a Jika
1 0
a , berdasarkan teorema sebelumnya diperoleh 0
1
1
a a
Hal ini bertentangan dengan kenyataan bahwa 1 < 0. Jadi haruslah
1 0 a
Teorema 4
Jika a,bR, maka a
ab
b 21
Bukti.
Karena ab, maka dapat diperoleh aaabatau 2aab
Demikian pula abmaka dapat diperoleh abbbatau ab2b
Dari ketaksamaan 2aabdan ab2bdidapatkan
b b a a 2
b b b
a a
a
(2 )
2 1 ) ( 2 1 ) 2 ( 2 1
b b a a
( )
2 1
jika aR dan a0 maka a (ab)b 2
1
Soal-soal
1) Misalkana,b,c,dRbuktikan pernyataan berikut:
a) Jika ab,bcmaka adbcacbd
b) Jika ab dan cd maka acbd
c) a2b2 0jika dan hanya jika a = 0 atau b = 0
2) Carilah bilangan a,b,c,dRyang memenuhi 0ab dan ad 0 dan berlaku a) acbd
b) acbd.
3) Tentukan bilangan real x, sedemikian sehingga: a) x2 3x4
b) 1x2 4
c) x
x 1
d) 7
2 1
x
e) 3
2 1
x
Garis Bilangan
Secara geometris, sistem bilangan real (R) dapat digambarkan dengan garis lurus. Mula-mula diambil sebarang titik untuk dipasangkan dengan bilangan 0. Titik ini dinamakan titik asal (origin), ditulis dengan O. Pada kedua sisi dari O dibuat skala sama dan disepakati arah positif disebelah kanan O sedangkan arah negatif disebelah kiri O. Selanjutnya, bilangan-bilangan bulat positif 1, 2, 3, … dapat dipasangkan dengan masing-masing titik di kanan O dan bilangan-bilangan 1, 2, 3,... dengan titik-titik di sebelah kiri O. Dengan membagi setiap segmen, maka dapat ditentukan lokasi
untuk bilangan-bilangan , 2,
3 2 , 2 1
dst.
Dengan cara demikian, maka setiap bilangan real menentukan tepat satu titik pada garis lurus dan sebaliknya setiap titik pada garis lurus menentukan tepat satu bilangan real. Oleh sebab itu, garis lurus sering disebut pula garis bilangan real.
1.2 Persamaan dan Pertidaksamaan
Istilah persamaan dan pertidaksamaan umumnya berhubungan dengan peubah atau variabel. Peubah adalah lambang yang digunakan untuk menyatakan sebarang anggota suatu himpunan. Jika himpunannya real maka perubahnya disebut peubah real. Selanjutnya yang dimaksud dengan peubah dalam persamaan dan pertidaksamaan yang akan dibahas dalam buku ini adalah peubah real.
Persamaan adalah kalimat terbuka dalam matematika yang memuat satu peubah atau lebih dengan tanda sama dengan (=).
Contoh 1) 2x34
2) x32x2 7
3) x2 3x 40
4) 2 1 3 x
x
5) 2
1
x
x x
6) x4 8x0
Pertidaksamaan adalah kalimat terbuka dalam matematika yang memuat satu
peubah atau lebih dan tanda ketidaksamaan (<, >, , ).
Contoh 1) 2x34
2) x32x2 3
2 1 0 1 2 3
Gambar 1.3
3) 2x3 2x2 5
4) x2 2x2 8
5) 0
2 3
x
6) 2 13
x x
7) 2
1
x
x x
8) 4
1 1
x
Karena persamaan dan pertidaksamaan merupakan kalimat terbuka dan mempunyai peubah, maka peubah tersebut dapat ditentukan sehingga memenuhi persamaan atau pertidaksamaan dimaksud, sehingga persamaan atau pertidaksamaan mempunyai arti dan bernilai benar. Nilia peubah yang memenuhi persamaan atau pertidaksamaa disebut selesaian. Himpunan semua bilangan real yang merupakan selesaian dari suatu persamaan atau pertidaksamaan disebut himpunan selesaian. Sifat-sifat dan hukum dalam R sangat membantu dalam menentukan selesaian persamaan atau pertidaksamaan yang diberikan.
Contoh
Tentukan selesaian persamaan dan pertidaksamaan di bawah ini. 1) 2x43
Jawab 3 4 2x
2 7
) 2 (
2 7 2 2
7 2
) 4 (
4 3 4 4 2
x
dibagi bagian
kedua x
x
dikurangi bagian
kedua x
Jadi selesaian persamaan 2x43adalah x =
2) x2 3x 40 pertidaksamaan-pertidaksamaan seperti pada contoh di atas.
Beberapa contoh diberikan sebagai berikut. 1) Tentukan selesaian x2 5x60
Jawab
Dengan memfaktorkan ruas kiri pertidaksamaan, maka diperoleh:
x 2
x 3
0Telah diketahui bahwa hasil kali 2 bilangan real positif apabila ke dua faktor positif atau ke dua faktor negatif. Oleh karena itu,
Diperoleh: x2.
Jadi, selesaian persamaan x2 5x60 adalah x < 2 atau x > 3.
Selesaian pertidaksamaan di atas dapat pula diterangkan sebagai berikut: Ruas kiri pertidaksamaan bernilai nol jika x2 atau x3. Selanjutnya, ke dua bilangan ini
membagi garis bilangan menjadi 3 bagian: x2,2x3,dan x3.
Gambar 1.4
Pada bagian x2, nilai (x 2) dan (x 3) keduanya negatif, sehingga hasil kali
keduanya positif. Pada segmen 2x3, (x 2) bernilai positif sedangkan (x 3)
bernilai negatif. Akibatnya, hasil kali keduanya bernilai negatif. Terakhir, pada bagian 3
x , (x 2) dan (x 3) masing-masing bernilai positif sehingga hasil kali
keduanya juga positif. Rangkuman uraian di atas dapat dilihat pada Tabel berikut.
Tanda nilai
Kesimpulan 2
x x 3 (x 2)(x 3)
x < 2 - - + Pertidaksamaan dipenuhi
2<x<3 + - - Pertidaksamaan tidak dipenuhi
x>3 + + + Pertidaksaman dipenuhi
Jadi, selesaian pertidaksamaan adalah x < 2 atau x > 3.
Metode penyelesaian seperti pada contoh 1 di atas dapat pula diterapkan pada bentuk-bentuk pertidaksamaan yang memuat lebih dari 2 faktor maupun bentuk-bentuk pecahan.
2) x3 2x2 x11. Jawab
Apabila ke dua ruas pada pertidaksamaan di atas ditambah 1, maka diperoleh:
0 2 3 4
0
Selanjutnya, perhatikan table berikut:
Nilai-nilai peubah x = -1, x = 1, x = 2 disebut titik kritis.
x = 1 2 0 -1 0 Pertidaksamaan dipenuhi
x = 2 3 1 0 0 Pertidaksamaan dipenuhi
Jadi, selesaian pertidaksamaanx3 2x2 x11 x 1 atau 1 x2.
Cara lain untuk menentukan selesaian pertidaksamaan x3 2x2 x11. adalah dengan menggunakan garis bilangan
2
Dengan memilih satu titik sebarang disetiap interval diatas diperoleh: - - - + + + + + + + - - - + + + + + + +
0
diperhatikan tabel
berikut:
terdefinisi Pertidaksamaan tidakdipenuhi
x = 5 7 3 0 0 Pertidaksamaan
dipenuhi
Jadi, selesaian pertidaksamaan adalah 2x2 atau x5 dan ditulis dengan notasi interval [2,2)[5,)
Berdasarkan contoh di atas, bahwa tampak selesaian suatu persamaan berupa titik (diskrit), sedangkan selesaian pertidaksamaan berupa selang/interval (kontinu).
Selang
1.3 Nilai Mutlak
Misal x suatu bilangan real, nilai mutlak x dinotasikan dengan x dan didefinisikan sebagai panjang atau jarak bilangan tersebut dari bilangan 0. Definisi Misal x real maka:
Bentuk lain dari definisi di atas adalah sebagai berikut:
2
Selanjutnya, sifat-sifat nilai mutlak diterangkan sebagai berikut.
Sifat-sifat Nilai Mutlak
Secara geometris, nilai mutlak x a dapat diartikan sebagai jarak dari a ke x. Sebagai contoh, jika x 3 7 maka artinya x berjarak 7 unit di sebelah kanan atau di sebelah kiri 3 (lihat Gambar 1.15).
Dengan cara yang sama
2
Jadi selesaian pertidaksamaan adalah x 2atau x5
2) Tentukan semua nilai x yang memenuhi 3
2
maka, diperoleh: atau 6
Jawab
Jadi selesaian pertidaksamaan adalah ,2
2,6
5Tentukan selesaian dari pertidaksamaan a. x 1 2x 3
Jawab
Menurut sifat 4 di atas, maka:
3
Titik kritis pertidaksamaan adalah x = 7/3 dan x = 5 sehingga gambar garis bilangan
+++++++++++ - - - +++++++
Jadi selesaian pertidaksamaan x 1 2x 3 adalah (-,7/5) (5,)
Soal Latihan
Tentukan selesaian pertidakasamaan dibawah ini!
1. 4x52 2. 6x39x 4 3. 3x 52
4. x2 5x 140 5. x2 3x10 6. x3 2x10
5 /
7. 1
Untuk soal 22 – 24 tentukan x sehingga masing-masing pernyataan mempunyai arti.
22. 2x2 3x 5 23.
disebut rata-rata
aritmatika dari bilangan a dan b.
27. Jika 0ab maka tunjukkan bahwa a ab b. Bilangan ab disebut rata-rata geometri dari bilangan a dan b. Tunjukkan pula bahwa rata-rata geometri dari bilangan a dan b kurang dari rata-rata aritmatikanya.
28. Tunjukkan bahwa x y x y .
1.4 Sistem Koordinat
Sistem koordinat adalah suatu cara yang digunakan untuk menentukan letak
suatu titik pada garis ( 1)
R , bidang ( 2)
R atau ruang ( 3).
R Pada bidang dikenal
tabung dan koordinat bola. Pada bagian ini hanya akan dibicarakan tentang sistem koordinat kartesius dan sistem koordinat kutub pada bidang.
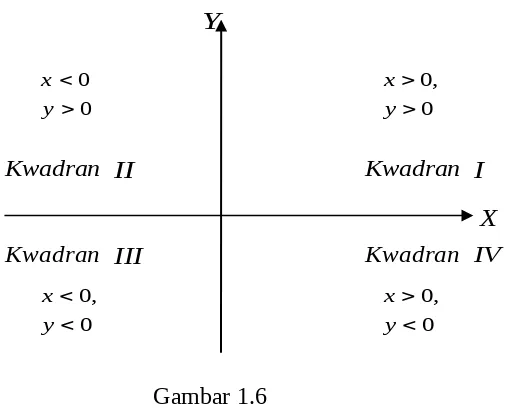
Sistem Koordinat Kartesius
Gambar 1.6
Pada gambar 1.6, terdapat 4 bidang simetris yang dibatasi oleh sumbu-sumbu koordinat (sumbu X dan Y), masing-masing bidang yang dibatasi oleh bidang dinamakan kwadran. Terdapat 4 kwadran, yaitu kuadran I (x0,y0), kwadran II
), 0 , 0
(x y kwadran III (x0,y0), dan kwadran IV(x0,y0).
Misalkan P(x,y) sebarang titik pada bidang XOY, maka titik tersebut
posisinya dapat dikwadran I, atau II, atau III, atau kwadran IV tergantung besaran x dan y. Misal P(x,y), maka x disebut absis, y disebut ordinat dan P(x,y) disebut
koordinat.
Perhatikan gambar berikut ini.
Misal P(x1,y1)dan terletak di kwadran I hal ini berarti x1 0 dan y1 0.
) , (x1 y1 P
1
y
0 , 0 y x 0
0 y x
0 , 0 y x
0 , 0 y x
X Y
Kwadran Kwadran
Kwadran Kwadran
I II
III IV
Y
Gambar 1.7
Berdasarkan gambar 1.7 di atas, terdapat segitiga yang salah satu sudutnya siku-siku dititik M (OPM). Menurut teorema Pythagoras
2 2
2 OM MP
OP
2
1 2
1 0) ( 0)
(
x y
x12 y12
2
1 2
1 y
x
OP
Bentuk ini dinamakan rumus jarak dua titik yang menghubungkan titik O(0,0) dengan titik P(x1,y1)
Jarak antara Dua Titik pada Bidang
Misal titik P(x1,y1) dan titik Q(x2,y2) terletak pada bidang, maka jarak dua titik P
dan Q dapat dinyatakan dengan rumus
2 1 2 2 1
2 ) ( )
(x x y y
PQ
Untuk membuktikan rumus tersebut dapat dilakukan dengan menggunakan teorema Pythagoras.
Selanjutnya perhatikan gambar berikut ini! 1
x ( ,0)
1 x M )
0 , 0 ( O
) , (x1 y1 P
) , (x2 y2 Q
) , (x y M
m
n
) , ( ' x y1 M
) , ( ' x2 y Q
) , (x2 y1 S
X
Gambar 1.8
Berdasarkan gambar 1.8 di atas, pandang PSQ, dengan menggunakan teorema Pythagoras
2
Pada gambar 1.8 di atas M adalah sebarang titik pada garis PQ dengan perbandingan PM:MQ = m : n
Karena PM : MQ = m : n, maka diperoleh PM’ : MQ’ = m : n dan MM’ : QQ’ = m : n Selanjutnya akan dicari koordinat M.
Karena
Dengan cara yang sama
) ( ) (
1 2
n m
ny my n
m ny my
y Q P
Jika diketahui P(x1,y1),dan Q(x2,y2),Jika M(x,y) titik tengah PQ
maka
Koordinat M dapat ditentukan dengan humus
2
2 1 x
x
xM dan
2
2 1 y
y yM
Contoh
1) Tentukan jarak titik P(3,5) dan Q(1,-6). Jawab
Untuk menentukan jarak titik P dan Q dapat digunakan rumus
PQ ( )2 ( )2
P Q p
Q x y y
x
= (1 3)2 (6 5)2
= (2)2 (11)2
= 4121
= 5 3
2) Tunjukkan bahwa titik-titik A(3,8), B(-11,3), dan (-8,-2) adalah titik-titik sudut dari segitiga sama kaki ABC.
Jawab
Dengan menggunakan rumus jarak dua titik, diperoleh AB 221
BC = 34 dan AC = 221
3) Tunjukkan bahwa titik A(-3,-2), B(5,2) dan C(9,4). Jawab
Terlebih dahulu dicari panjang AB, BC, dan AC
Dengan humus jarak dua titik diperoleh AB = 4 5, BC = 2 5 dan
AC = 6 5, sehingga AC + BC = AC, hal ini berarti titik A, B, dan C terletak pada satu garis lupus
Gradien Garis Lurus
) , (x2 y2 Q
n
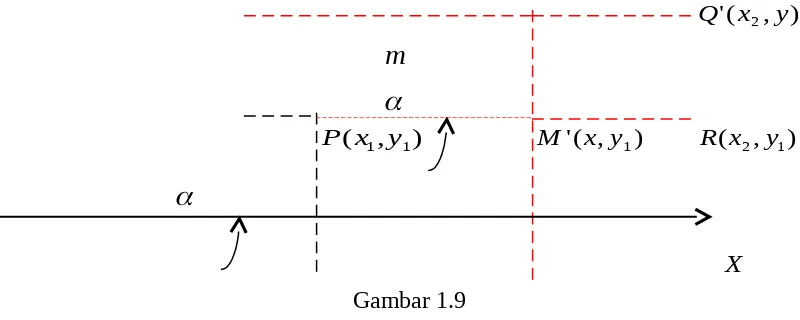
Gambar 1.9
Selanjutnya jika garis PQ pada gambar 1.9 diperpanjang, maka garis tersebut akan memotong sumbu X atau sumbu Y. Sudut yang dibentuk oleh garis PQ dengan sumb X disebut disebut inklinasi.
Selanjutnya perhatikan PQR, menurut perbandingan goniometri diperoleh
tan
=PR QR
=
1 2
1 2
x x
y y
Perbandingan goniometri tersebut selanjutnya disebut kemiringan atau gradien atau tangensial dan dinotasian dengan
1 2
1 2
tan
x x
y y m
Dengan demikian gradien garis lurus didefinisikan sebagai tangen dari sudut inklinasi.
Misal l1 dan l2 dua garis yang terletak pada sumbu koordinat, maka beberapa hal
yang mungkin adalah kedua garis sejajar, berpotongan, atau saling tegak lurus. Jika l1
dan l2 sejajar maka ml1ml2
Jika l1 dan l2tegak lurus maka, perhatikan gambar di bawah ini )
, (x1 y1 P
m
) , ( ' x y1 M
) , ( ' x2 y Q
) , (x2 y1 R
X
Y
1
l
2
l
Gambar 1.10
Misal l1 dan l2dua garis dalam bidang yang sama, maka kemungkinan kedua garis
tersebut adalah:
1) Sejajar jika dan hanya jika ml1 ml2
2) Tegak lurus jika dan hanya jika ml1.ml2 1
3) Berimpit jika dan hanya ml1ml2dan koefisien-koefisiennya yang sejenis saling berkelipatan
Luas Poligon yang Titik Sudutnya Ditentukan
Perhatikan gambar berikut!
Misal P(x1,y1), Q(x2,y2), dan Q(x3,y3). Adalah titik sudut
segitiga yang terletak pada bidang XOY seperti berikut.
X 2
1
Gambar 1.11
Pada gambar 1.11, luas PQR adalah
= (Luas trapesium PP’Q’Q + luas trapesium QQ’R’R)- luas trapesium P’R’RP
= ½ (y1+y3)(x3- x1) + ½ (y3+ y2 )(x2-x3) – ½ (y1+y2 )(x2- x1)
= ½ {(y1+y3)(x3- x1) + (y3+ y2 )(x2 -x3) – (y1+y2 )(x2 - x1)}
=½{
y
1x
3
y
1x
1
y
3x
3
y
3x
1
y
3x
2
y
3x
3
y
2x
2
y
2x
3
y
1x
2
y
1x
1
y
2x
2
y
2x
1}
)}
(
)
(
2
1
2 1 3 2 1 3 1 2 2 3 3
1
x
y
x
y
x
y
x
y
x
y
x
y
Bentuk di atas dapat dinyatakan dalam bentuk determinan matrik ordo 3 x 3
1
1
1
2
1
3
3
2
2
1
1
yx
yx
yx
A
Soal-soal
1. Buatlah ruas garis dan tentukan jarak antara pasangan titik yang diketahui berikut ini:
a. P(4,5) dan Q(-1,3) b. P(8,-2) dan Q(3,-1) c. P(-1,-2) dan Q(-3,-8) d. P(5,3) dan Q(2,-5)
) , (x1 y1 P
) , (x2 y2 R
X
'
2. Gambarlah luas suatu poligon yang titik-titik sudutnya adalah a. (-3,2), (1,5), (5,3), (1,-2)
b. (-5,0), (-3,-4), (3,-3), (7,2), (1,6)
3. Selidiki apakah segitiga yang titik-titik sudutnya di bawah ini adalah sama sisi. a. A(2,-2), B(-3,-4) dan C(1,6)
b. K(-2,2), L(6,6) dan M(2,-2) c. P(6,7), Q(-8,-1) dan R(-2,-7) d. U(2,4), V(5,1) dan W(6,5)
4. Tunjukkan bahwa segitiga berikut adalah siku-siku dan tentukan luasnya dengan menggunakan aturan yang ada.
a. A(0,9), B(-4,-1), dan C(3,2) b. P(10,5), B(3,2), dan C(6,-5) c. A(3,-2), B(-2,3), dan C(0,4) d. K(-2,8), L(-6,1), dan N(0,4)
5. Buktikan bahwa titik-titik berikut ini adalah paralelogram a. (-1,-2), (0,1), (-3,2), dan (-4,-1)
b. (-1,-5), (2,1), (1,5), dan (-2,-1) c. (2,4), (6,2), (8,6), dan (4,8)
6. Tunjukkan bahwa titik-titik berikut terletak pada satu garis lurus dengan menggunakan metode jarak.
a. (0,4), (3,-2), dan (-2,8) b. (-2,3), (-6,1), (-10,-1) c. (1,2), (-3,10), (4,-4) d. (1,3), (-2,-3), (3,7)
8. Tentukan koordinat titik P(x,y) yang membagi ruas garis dengan perbandingan diketahui:
a. A(4,-3), B(1,4) dengan AP:PB = r = 2 b. A(2,-5),B(6,3) dengan AP:PB = r = ¾ c. A(-5,2), B(1,4) dengan AP:PB = r = -5/3 d. A(0,3), B(7,4) dengan AP:PB = r = -2/7 e. A(-2,3), P(3,-2) dengan AP:PB = r = 2/5
9. Jika M (9,2) membagi ruas garis yang melalui P(6,8) dan Q(x,y) dengan perbandingan 3/7. Tentukan koordinat titik Q.
10. Tentukan titik pusat (centroid) setiap segitiga diketahui titik-titik sudutnya di bawah ini:
a. (5,7), (1,-3), (-5,1) b. (2,-1), (6,7), (-4,-3) c. (3,6), (-5,2), (7,-6) d. (7,4), (3-6), (-5,2) e. (-3,1), (2,4), (6,-2)
11. Tentukan luas poligon yang titik sudutnya adalah: a. (-3,2), (1,5), (5,3), (1,-2)
b. (-5,0), (-3,-4), (3,-3), (7,2), (1,6)
12. Tentukan koordinat titik-titik suatu segitiga, jika titik-titik tengah sisi-sisinya adalah: a. (-2,1), (5,2), (2,-3)
b. (3,2), (-1,-2), dan (5,-4)
13. Gradien dari garis lurus yang melalui titik A(3,2) adalah ¾. Lukislah titik-titik pada garis yang berjarak 5 satuan dari A.
14. Tentukan gradien suatu garis lurus yang membuat sudut 45o dengan titik (2,-1) dan
15. Garis p membentuk sudut 60o dengan garis s, Jika gradien p = 1, tentukan gradien
garis s.
16. Sudut yang dibentuk oleh garis l yang melalui titik A(-4,5), B(3,y) dan garis u yang melalui titik P(-2,4), Q(9,1). Tentukan konstanta y tersebut.
Sistem Koordinat Kutub (Polar)
Pada sistem koordinat Kartesius, letak titik pada bidang dinyatakan dengan pasangan (x,y), dengan x dan y masing-masing menyatakan jarak berarah ke sumbu-y
dan ke sumbu-x. Pada sistem koordinat kutub, letak sebarang titik P pada bidang dinyatakan dengan pasangan bilangan real
r,
, dengan r menyatakan jarak titik P ketitik O (disebut kutub) sedangkan adalah sudut antara sinar yang memancar dari titik
O melewati titik P dengan sumbu-x positif (disebut sumbu kutub)
Berbeda dengan sistem koordinat kartesius, dalam koordinat kutub letak suatu titik dapat dinyatakan dalam tak hingga banyak koordinat. Sebagai contoh, letak titik
) 3 , 3 (
P dapat digambarkan dengan cara terlebih dulu melukiskan sinar yang
memancar dari titik asal O dengan sudut sebesar
3
radian terhadap sumbu mendatar
arah positif. Kemudian titik P terletak pada sinar tadi dan berjarak 3 satuan dari titik asal O (lihat Gambar 1.2.4 (a)). Titik P dapat pula dinyatakan dalam koordinat
3, 32k
, dengan k bilangan bulat. Mudah ditunjukkan pula bahwa koordinat
3,4 3
pun juga menggambarkan titik P . Pada koordinat yang terakhir, jarakbertanda negatif. Hal ini dikarenakan titik P terletak pada bayangan sinar OP.
O
) , (r P
Secara umum, jika
r,
menyatakan koordinat kutub suatu titik makakoordinat titik tersebut dapat pula dinyatakan sebagai berikut:
r, 2k
atau
r, (2k1)
dengan k bilangan bulat.Kutub mempunyai koordinat (0,) dengan sebarang bilangan.
Hubungan antara Sistem Koordinat Kartesius dan Sistem Koordinat Kutub
Suatu titik P berkoordinat (x,y) dalam sistem koordinat Kartesius dan (r,)
dalam sistem koordinat kutub. Apabila kutub dan titik asal diimpitkan, demikian pula 3
) 3 , 3 ( P
3
(b)
3
) 2 3 , 3
( k
P
32k
(a)
Gambar 1.12 3
) 3 4 , 3 ( P
3 4
3
P
sumbu kutub dan sumbu-x positif juga diimpitkan, maka kedudukan titik dapat digambarkan sebagai berikut:
Dari rumus segitiga diperoleh hubungan sebagai berikut:
(1.1) xrcos yrsin
1) Nyatakan ke dalam system koordinat Kartesius.
a.
Dengan menggunakan persamaan (1.1):
a. 2 3
Jadi, dalam sistem koordinat Kartesius
Jadi,
Apabila x0 maka persamaan (1.2) dapat dinyatakan sebagai:
(1.3) 2 2 2 arctan , 0
Hati-hati apabila menggunakan persamaan (1.3), karena
x y arctan
akan memberikan
2 nilai yang berbeda, 0 2. Untuk menentukan nilai yang benar perlu
diperhatikan letak titik P, apakah di kwadran I atau II, ataukah dikwadran II atau IV.
Apabila dipilih nilai yang lain, maka r x2y2.
2) Nyatakan ke dalam sistem koordinat kutub: a. P
4,4
b. Q(4,4)Penyelesaian: Dari persamaan (1.3), diperoleh:
a. r 42(4)2 4 2
Selanjutnya, karena letak titik P di kwadran IV, maka:
4
Selanjutnya, karena letak titik Q di kwadran II, maka:
Jadi,
4 3 , 2
4
Q atau
4 7 , 2
4
Q .
3) Nyatakan persamaan r 2asin ke dalam sistem koordinat Kartesius. Jawab
Jika ke dua ruas persamaan di atas dikalikan dengan r maka diperoleh:
) sin ( 2
2 a r
r
Selanjutnya, karena r2 x2y2 dan rsin y maka:
, 0 2 2
2 2
2 2
ay y x
ay y
x
yaitu persamaan lingkaran dengan pusat (0,a) dan jari-jari a .
4) Nyatakan x24y2 16 ke dalam sistem koordinat kutub.
Penyelesaian: Dengan substitusi xrcos dan yrsin maka diperoleh:
16 sin
4 cos2 2 2
2 r
r
. 16 ) sin 3 1
( 2
2
r
Soal Latihan
Untuk soal 1 – 8, nyatakan masing-masing dengan dua koordinat yang lain, satu dengan 0
r dan yang lain dengan r0.
1.
6, 3
2.
3,2 5
3.
5, 4
4.
5,7 4
5.
2,5 2
6.
7, 5 6
7.
6, 7 3
8.
4,6 7
Untuk soal 9 – 16, nyatakan dalam sistem koordinat Kartesius.
9.
6,2 3
10.
4, 8
11.
5, 4
12.
6,7 4
13.
2,5 2
14.
7, 5 6
15.
6, 7 3
16.
4,7 8
Untuk soal 17 – 23, ubahlah ke dalam sistem koordinat kutub.
17.
3,3
18.
2,2
19.
2,2 3
20.
3,1
Untuk soal 24 – 29, nyatakan masing-masing persamaan ke dalam sistem koordinat Kartesius.
24. r3cos 25. r2 1sin 26.
cos 1
4 r
27. r 4 28.
4 7
29. r2
Nyatakan persamaan pada soal 30 – 32 ke dalam sistem koordinat kutub.
30. x y0 31. y2 1 4x 32. xy 1
33. Tunjukkan bahwa jarak titik P(r,) dan Q(R,) adalah:
) cos( 2
2
2
r R rR d
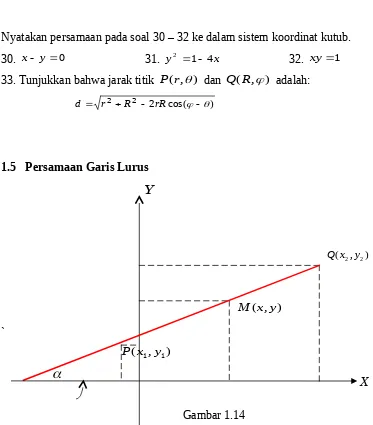
1.5 Persamaan Garis Lurus
`
Gambar 1.14
Menurut definisi kemiringan (gradien), garis PQ pada gambar diatas mempunyai kemiringan
1 2
1 2
tan
x x
y y m
,
X ) , (x2 y2 Q
Y
) , (x1 y1 P
) , (x y M
Misal M(x,y)sebarang titik pada garis lurus PQ, maka dengan cara yang sama dapat
ditentukan gradien garis lurus PM.
1 1
tan
x x
y y
1 1
tan
x x
y y m
)
( 1
1 m x x y
y
1 1 y
mx mx
y
Karenam,x1,y1R, maka persamaan tersbut dapat ditulis dalam bentuk
R c c mx
y , .
Dengan kata lain, persamaan garis lurus yang melalui dua titik dengan gradien m dapat dinyatakan dengan ymxc
Atau secara umum ditulis dalam bentuk AxByC0 dengan gradien
B A m
Soal-soal
1) Tentukan gradien dan persamaan garis lurus yang melalui titik-titik a) (1,2) dan (2,3)
b) (3,5) dan (7,-1) c) (3,0) dan (3,3) d) (3,5) dan (6,5) e) (2,-4) dan (4,9)
2) Buktikan bahwa segitiga yang titik-titik sudutnya (5,3), (-2,4), dan (10,8) adalah segitiga sama sisi.
3) Tunjukkan bahwa segitiga yang titik-titik sudutnya (2,-4), (4,0), dan (8,2) adalah segitiga siku-siku.
4) Tentukan nilai k sedemikian rupa sehingga garis 3x + ky = 5 a) melalui titik (3,1)
b) sejajar sumbu x
c) sejajar garis 2x + y = -1 d) tegak lurus garis y-2 = 3(x+3)