TINJAUAN PRIMAL-DUAL DALAM PENGAMBILAN KEPUTUSAN
Oleh : Lusi Melian
Staf Pengajar Program Studi Sistem Informasi Fakultas Teknik dan Ilmu Komputer
Universitas Komputer Indonesia
ABSTRAK
Suatu program linear dengan bentuk asli disebut sebagai primal, sedangkan bentuk kedua yang berhubungan disebut dual yang merupakan sebuah bentuk alternatif suatu program linear yang berisi informasi mengenai nilai-nilai sumber yang biasanya merupakan pembatas dari suatu model. Dual merupakan bentuk alternatif model sebagai pengembangan bentuk primal. Bentuk dual dirumuskan dan diinterpretasikan untuk mendapatkan informasi tambahan setelah menentukan solusi optimal suatu masalah program linear. Tabel simpleks yang diperoleh dari pemecahan masalah program linear primal mengandung informasi ekonomi tambahan yang tidak kalah penting daripada solusi optimum masalah tersebut, sehingga suatu solusi terhadap primal juga memberikan solusi pada bentuk dualnya. Analisis pada bentuk primal akan menghasilkan solusi-solusi dalam bentuk jumlah laba yang diperoleh, sedangkan analisis pada bentuk dual akan memberikan informasi mengenai harga dari sumber daya yang menjadi kendala tercapainya laba tersebut. .
I. HUBUNGAN PRIMAL & DUAL a. Masalah Primal-Dual Simetrik
Suatu program linear
dikatakan berbentuk simetrik jika semua konstanta ruas kanan pembatas bernilai non negatif dan semua pembatas berupa pertidaksamaan,
dimana pertidaksamaan dalam
masalah maksimasi berbentuk
, dan pertidaksamaan dalam minimasi berbentuk
.Dalam notasi matriks masalah primal-dual simetrik adalah:
Primal : Maksimasi Z = cX dengan pembatas AX ≤ b X ≥ 0 Dual : Minimasi W = Yb dengan pembatas YA ≥ c Y ≥ 0
dimana c adalah vektor baris 1xn, X adalah vektor kolom nx1, A adalah suatu matriks mxn, b adalah vektor kolom mx1, dan Y adalah vektor baris 1xm.
Atau lebih jelasnya: Primal : Maksimasi Z = c1X1 + c2X2 + …+ cnXn a11X1 + a12X2 +…+ a1nXn ≤ b1 a21X1 + a22X2 +…+ a2nXn ≤ b2 . .
am1X1 + am2X2 +…+ amnXn ≤ bn 1, X2 , … , Xn ≥ 0 Dual : Minimum W = b1Y1 + b2Y2 + … + bmYm a11Y1 + a21Y2 + … + am1Ym ≥ c1 a12Y1 + a22Y2 + … + am2Ym ≥ c2 . . a1nY1 + a2nY2 + … + amnYm ≥ cn Y1 ,Y2 , … , Ym ≥ 0
Bila masalah primal dibandingkan dengan masalah dual, terlihat beberapa hubungan sebagai berikut: 1. Koefisien fungsi tujuan masalah
primal (c) menjadi konstanta ruas kanan pembatas dual. Sebaliknya, konstanta ruas kanan pembatas dual menjadi koefisien fungsi tujuan dual.
2. Tanda pertidaksamaan pembatas dibalik (pada primal
, pada dual
)3. Tujuan berubah dari min (maks) pada primal menjadi maks (min) pada dual.
4. Setiap kolom pada primal berhubungan dengan suatu baris (kendala) dalam dual. Sehingga banyaknya pembatas dual akan sama banyaknya dengan variabel keputusan primal.
5. Setiap baris (pembatas) pada primal berhubungan dengan suatu kolom dalam dual. Sehingga setiap pembatas primal ada satu variabel keputusan dual.
6. Bentuk dual dari dual adalah primal.
Contoh dari bentuk primal-dual simetrik adalah sebagai berikut: Primal: Maks Z = 40000x1+ 50000x2 + 40000x3 4x1+ 4x2 + 6x3 ≤ 600 8x1+ 4x2 + 6x3 ≤ 800 x1 , x2 ,x3 ≥ 0 Dual:
Min W = 600y1 + 800y2 4y1 + 8y2 ≥ 40000 4y1 + 4y2 ≥ 50000 6y1 + 6y2 ≥ 40000 y1 , y2 ≥ 0
Apabila persoalan primal tersebut diselesaikan dengan metode simpleks maka diperoleh tabel simpleks optimum sebagai berikut:
VB 40000 50000 40000 0 0 RK x1 x2 x3 S1 S2 50000x2 1 1 3/2 1/4 0 150 0S2 4 0 0 -1 1 200 Zj-Cj 10000 0 35000 12500 0 7500000 Z 50000 50000 75000 12500 0
Berdasarkan tabel tersebut kita peroleh solusi optimum x1=0, x2=150 dan x3=0. Adapun nilai-nilai variabel slack adalah S1=0 dan S2=200, sedangkan nilai Z optimal adalah 7500000. Adapun tabel simpleks optimum untuk persoalan dual adalah sebagai berikut:
VB 600 800 0 0 0 M M M RK y1 y2 S1 S2 S3 R1 R2 R3 0S3 0 0 0 -3/2 1 0 3/2 -1 35000 0S1 0 -4 1 -1 0 -1 1 0 10000 600y1 1 1 0 -1/4 0 0 1/4 0 12500 Zj-Cj 0 -200 0 -150 0 -M 150-M -M 7500000 Z 600 600 0 -150 0 0 150 0
Berdasarkan tabel diatas kita peroleh solusi optimum y1 = 12500 dan y2 = 0 adapun nilai-nilai variabel slack adalah S1 = 10000, S2 = 0 dan
S3= 35000, sedangkan nilai Z optimal adalah 7500000.
Apabila kita menelaah solusi optimum primal dan solusi optimum dual terdapat hasil yang menarik yaitu:
Variabel Slack Primal S1 S2 Koef. Pers. Zj-Cj pada
optimum primal 12500 0
Variabel keputusan dual
yang berhubungan y1 y2
Kemudian perhatikan :
Variabel Slack Dual S1 S2 S3 Koef. Pers. Zj-Cj pada
optimal dual (dikalikan -1) 0 150 0 Variabel keputusan primal yang berhubungan x1 x2 x3
Terlihat bahwa solusi
optimum primal memberikan solusi terhadap permasalahan dual yang berhubungan, begitu juga sebaliknya
solusi optimum dual akan
memberikan solusi terhadap
permasalahan optimalnya. Sehingga dengan memecahkan salah satu persoalan baik primal maupun dual, kita dapat menentukan solusi
optimum dari permasalahan
kawannya.
Selain itu keterkaitan antara solusi optimum primal dan solusi optimum dual pun dapat ditunjukan oleh kedua tabel berikut:
Variabel basis awal Primal S1 S2 Koef. Pers. Zj-Cj pada
optimum primal 12500 0
Variabel keputusan dual
yang berhubungan y1 y2
Kemudian perhatikan:
Variabel basis awal
dual R1 R2 R3
Koef. Pers. Zj-Cj pada optimal dual (dengan menghilangkan M) 0 150 0 Variabel keputusan primal yang berhubungan x1 x2 x3
Kedua tabel tersebut
memberikan kesimpulan yang sama, yaitu bahwa solusi optimum primal memperlihatkan solusi optimum dual, begiru juga sebaliknya.
Hal lain yang dapat kita lihat dari tabel solusi optimum primal dan dual adalah nilai optimum fungsi tujuannya yang bernilai sama yaitu Z = W = 7500000. Hal tersebut sesuai dengan Main Duality Theorem yang menyatakan bahwa “ Jika baik masalah primal maupun dual adalah layak, maka keduanya memiliki solusi demikian hingga nilai optimum fungsi tujuannya adalah sama “.
Selain itu solusi optimum primal dan dual dapat diperoleh melaui penerapan metode Revised simpleks :
Z = W = CB.B-1.b
Dimana:
CB = matrik koefisien fungsi tujuan dari
variabel basis (VB) pada iterasi yang bersangkutan
B-1 = matriks dibawah variabel basis
awal pada iterasi yang bersangkutan
CB.B-1 = optimum simpleks multiplier.
b = vektor baris koefisien fungsi tujuan
Penerapan rumus diatas pada masalah primal-dual yang sedang dibahas adalah sebagai berikut ; pada tabel simpleks optimum primal diperoleh variabel basis optimum adalah x2 dan S2 , sedangkan variabel basis awalnya adalah S1 dan S2
sehingga optimum simpleks multipliernya adalah: x2 S2 S1 S2 cB.B-1 =
50000
0
1
4 1
1
0
y2 y1 =
12500
0
Terlihat bahwa y1 = 12500 dan y2 = 0 sesuai dengan solusi optimum dual dan nilai fungsi tujuan dual adalah W = 600(12500) + 800(0) = 7500000.Sedangkan apabila ditinjau dari tabel optimum dual diperoleh variabel basis optimum adalah S3, S1, dan y1, adapun variabel basis awalnya adalah R1, R2, dan R3, sehingga optimum simpleks multiplier-nya:
S3 S1 y1 R1 R2 R3 CB.B1=
0
4
/
1
0
0
1
1
1
2
/
3
0
600
0
0
=
0
150
0
x1 x2 x3 Terlihat bahwa x1 = 0 , x2 = 150 , dan x3 = 0 memenuhi kendala primal dan nilai fungsi tujuan primal adalah Z = 40000 (0) + 50000 (150) + 40000 (0) = 7500000.b. Masalah primal-dual asimetrik Misalkan masalah primal yang tidak simetrik adalah sebagai berikut:
Maks Z = 2x1 + 4x2+ 3x3 x1 + 3x2 + 2x3 ≤ 60 3x1 + 5x2 + 3x3 ≥ 120 x1 ,x2 ,x3 ≥ 0
Tabel di bawah ini
menyajikan hubungan primal-dual
untuk semua masalah program linear. Sehingga bentuk dual dari primal tersebut adalah:
Min W = 60y1 + 120y2 y1 + 3y2 ≥ 2 3y1 + 5y2 ≥ 4 2y1 + 3y2 ≥ 3 y1 ≥ 0 y2 ≤ 0
Apabila persoalan bentuk primal diselesaikan dengan metode simpleks maka selain variabel slack dibutuhkan juga artificial variabel R pada kendala kedua , variabel R merupakan variabel buatan dimana nilainya selalu nol, maka diperoleh tabel simpleks optimum primal sebagai berikut: VB 2 4 3 0 0 -M RK x1 x2 x3 S1 S2 R1 0S2 0 4 3 3 1 -1 60 2x1 1 3 2 1 0 0 60 Zj -Cj 0 2 1 2 0 M 120 Zj 2 6 4 2 0 0
Berdasarkan tabel optimum tersebut kita peroleh solusi optimum x 1 = 60 , x2 = 0 , dan x3 = 0, adapun nilai-nilai variabel slack S1 dan S2 berturut-turut adalah 0 dan 60 dengan nilai optimal 120.
Untuk memperlihatkan
keterkaitan antara solusi optimum primal dan solusi optimum dual pada hubungan primal-dual asimetrik, sebelumnya masalah primal yang asimetrik perlu ditransformasikan kedalam bentuk simetrik, dalam hal ini karena bentuk primal adalah maksimasi maka semua pembatas harus bertanda ≤ , maka pembatas kedua 3x1 + 5x2 + 3x3 ≥ 120 dikalikan dengan bilangan -1 agar pembatas bertanda ≤.
3x1 + 5x2 + 3x3 ≥ 120 (-1) -3x1 - 5x2 - 3x3 ≤ -120
Sehingga bentuk primal persoalan tersebut menjadi:
Maks Z = 2x1 + 4x2+ 3x3 x1 + 3x2 + 2x3 ≤ 60 -3x1 - 5x2 - 3x3 ≤ -120
x1 ,x2 ,x3 ≥ 0 Tabel Hubungan Primal-Dual
Primal Dual
A elemen matriks kendala Transpose elemen matriks
b vektor sisi kanan Koefisien fungsi tujuan
c koefisien fungsi tujuan Vektor sisi kanan
Kendala ke-i berupa persamaan Variabel dual Yi tak terbatas
Xj tak terbatas Kendala ke-j berupa persamaan
I. Maksimasi Minimasi
Kendala ke-i jenis ≤ Variabel dual Yi≥ 0
Kendala ke-i jenis ≥ Variabel dual Yi≤ 0
Xj ≥ 0 Kendala ke-j jenis ≤
Xj ≤ 0 Kendala ke-j jenis ≥
II. Minimasi Maksimasi
Kendala ke-i jenis ≤ Variabel dual Yi≤ 0
Kendala ke-i jenis ≥ Variabel dual Yi≥ 0
Xj ≥ 0 Kendala ke-j jenis ≤
Xj ≤ 0 Kendala ke-j jenis ≥
Sumber : Mulyono, Sri, Operations Research, Fakultas Ekonomi Universitas Indonesia, Jakarta, 1999
Bentuk primal yang baru ini tampaknya tidak sesuai dengan persyaratan simpleks karena terdapat nilai konstanta ruas kanan pembatas bernilai negative , padahal dalam suatu program linear simetrik semua konstanta ruas kanan pembatas bernilai non negative. Akan tetapi, nilai konstanta ruas kanan pembatas negative tersebut tidak perlu dipermasalahkan karena perubahan bentuk tersebut bukan untuk maksud diselesaikan melainkan untuk maksud perubahan kedalam bentuk dual. Nilai konstanta ruas kanan pembatas primal membentuk koefisien-koefisien fungsi tujuan dual yang nilainya boleh negative. Maka bentuk dual dari model ini diformulasikan sebagai : Min W = 60y1 - 120y2
y1 - 3y2 ≥ 2 3y1 - 5y2 ≥ 4 2y1 - 3y2 ≥ 3
y1, y2 ≥ 0
Maka tabel simpleks
optimum dari dual tersebut adalah: VB 60 -120 0 0 0 M M M RK y1 y2 S1 S2 S3 R1 R2 R3 0S3 0 -3 -2 0 1 2 0 -1 1 60 y1 1 -3 -1 0 0 1 0 0 2 0 S2 0 -4 -3 1 0 3 -1 0 2 W 0 -60 -60 0 0 60-M -M -M 120 Dari tabel tersebut solusi optimal dual y1 = 2 , y2 = 0 , nilai variabel slack S1= 0 , S2 = 2 , dan S3= 1 dan nilai W optimal 120.
Dengan cara yang sama seperti telah ditunjukan pada contoh hubungan primal-dual simetrik, hasilnya adalah:
Variabel basis awal primal S1 R1 Koef. Pers. Zj-Cj pada
optimum primal 2 M
Var. kep dual yang
bersangkutan y1 y2
Jika M diabaikan , koefisien persamaan Zj-Cj adalah 2 dan 0 yang menunjukan solusi optimum pada masalah dual, yaitu nilai y1 =2 dan y2 = 0.
Pengamatan yang sama
terhadap solusi optimum dual memberikan informasi sebagai berikut:
Variabel basis awal dual R1 R2 R3 Koef. Pers. Zj-Cj optimal
dual (dengan
mengabaikan M)
60 0 0
Var. keputusan primal
yang berhubungan x1 x2 x3
Hasil dari koefisien persamaan Zj-Cj memberikan solusi optimum primal x1 = 60 , x2 = 0 dan x3 = 0.
Melalui penerapan revised simpleks method pada contoh ini dengan cara mencari optimum simpleks multiplier seperti telah dicontohkan sebelumnya, akan memberikan kesimpulan yang sama bahwa suatu solusi optimum primal (dual) juga merupakan solusi optimum masalah dual (primal). Contoh berikut merupakan contoh lain masalah primal-dual asimetrik, dimana pada contoh berikut akan diperlihatkan suatu bentuk primal dengan pembatas bertanda =.
Maks Z = 5x1 + 2x2+ 3x3 x1 + 5x2 + 2x3 = 30 x1 - 5x2 - 6x3 ≤ 40 x1 , x2 , x3 ≥ 0
Apabila bentuk primal ini dianalogikan dengan persoalan sebelumnya , maka apabila bentuk primal ini akan diubah kedalam
bentuk dual untuk kemudian
diselesaikan dengan metode simpleks, maka langkah pertama yang perlu dilakukan adalah mengubah bentuk primal asimetrik menjadi bentuk primal simetrik. Pembatas kedua dalam contoh tersebut merupakan suatu persamaan x1 + 5x2 + 2x3 = 30 dan harus diubah kedalam bentuk ≤.
Persamaan ini ekuivalen dengan dua pembatas berikut ini:
x1 + 5x2 + 2x3 ≤ 30
x1 + 5x2 + 2x3 ≥ 30
Artinya jika nilai pembatas lebih besar atau sama dengan 30 dan kurang dari atau sama dengan 30, maka kuantitas yang memenuhi kedua pembatas tersebut adalah 30. Tetapi pada pembatas tersebut tanda ≥ masih tetap ada, dan pembatas ini dapat diubah dengan cara mengalikannya dengan (-1).
x1 + 5x2 + 2x3 ≥ 30 x(-1) -x1 - 5x2 - 2x3 ≤ -30
Sehingga model primal dalam bentuk normal adalah: Maks Z = 5x1 + 2x2+ 3x3 x1 + 5x2 + 2x3 ≤ 30 - x1 - 5x2 - 2x3 ≤ -30 x1 - 5x2 - 6x3 ≤ 40 x1 ,x2 ,x3 ≥ 0 Bentuk dual dari model ini diformulasikan sebagai:
Min W = 30y1 – 30 y2 + 40y3 y1 – y2 + y3 ≥ 5 5y1 – 5y2 – 5y3 ≥ 2 2y1 – 2y2 – 6y3 ≥ 3 y1 , y2 , y3 ≥ 0 Tetapi bentuk dual ini pun tidak sesuai dengan ketentuan hubungan primal-dual yang telah dikemukakan pada awal bagian ini. Ketidaksesuaian tersebut terletak pada jumlah pembatas primal asimetrik yang tidak sesuai dengan jumlah koefisien fungsi tujuan dual, padahal pada hubungan primal-dual setiap
pembatas pada primal berhubungan dengan satu kolom dalam dual, sehingga setiap pembatas primal terdapat satu variabel keputusan dual. Sedangkan dalam contoh ini pada bentuk primal asimetrik terdapat 2 pembatas tetapi setelah bentuk primal asimetrik ini ditransformasikan menjadi primal normal lalu kemudian dibuat bentuk dualnya, ternyata pada bentuk dual tersebut terdapat 3 variabel keputusan.
Untuk menyelesaikan
masalah tersebut, maka bentuk dual dapat dibentuk dari primal asimetrik tanpa harus mentrasnsformasikannya terlebih dahulu menjadi primal normal. Maka dengan mengikuti aturan tabel hubungan primal dual bentuk dual dari primal asimetrik itu adalah:
Min W = 30y1 + 40 y2 y1 + y2 ≥ 5 5y1 – 5y2 ≥ 2 2y1 – 6y2 ≥ 3 y1 tidak terbatas tanda
y2 ≥ 0
Karena y1 tidak terbatas tanda, maka y1 digantikan dengan y1’–y1” (y1 = y1’–y1”) dimana y1’ dan y1” ≥ 0, sehingga bentuk dualnya menjadi: Min W = 30(y1’–y1”) – 40 y2
(y1’–y1”) + y2 ≥ 5 5(y1’–y1”) – 5y2 ≥ 2 2(y1’–y1”) – 6y2 ≥ 3 (y1’–y1”) = y1 y2 ≥ 0 atau
Min W = 30y1’–30y1” – 40 y2 y1’ – y1” + y2 ≥ 5 5y1’ – 5y1” – 5y2 ≥ 2 2y1’ – 2y1” – 6y2 ≥ 3 y1’ ≥ 0 y1” ≥ 0 y2 ≥ 0
Apabila diamati bentuk dual dari primal simetrik dengan bentuk dual dari primal asimetrik memiliki bentuk yang hampir sama. Tabel solusi primal asimetrik adalah:
VB 5 2 3 0 -M RK x1 x2 x3 S1 R1 5 x1 1 5 2 0 1 30 0S1 0 -10 -8 1 -1 10 Zj -Cj 0 23 7 0 5+M 150
Sedangkan tabel solusi optimum dualnya adalah: Table 1 VB 30 -30 40 0 0 0 M M M RK y1’ y1” y2 S1 S2 S3 R1 R2 R3 0S3 0 0 8 -2 0 1 2 0 -1 7 30 y1’ 1 -1 1 -1 0 0 1 0 0 5 0 S2 0 0 10 -5 1 0 5 -1 0 23 Wj - Cj 0 0 -10 -30 0 0 30-M -M -M 150
Dari tabel solusi optimum dual tersebut didapat y1’ = 5 , y1” = 0 ( y1 = y1’- y1” = 5 – 0 = 5) dan y2 = 0 dengan nilai-nilai variabel slack berturut-turut S1= 0 , S2 = 23 , S3 = 7 dan nilai W = Z = 150.
Hasil-hasil yang menarik terungkap dengan mengamati tabel optimum pimal dan dual. Sekarang perhatikan koefisien persamaan Zj-Cj pada tabel optimum primal, hasilnya adalah:
Variabel basis awal primal R1 S1
Koef. Pers. Zj-Cj pada
optimum primal (abaikan M) 5 0
Var. keputusan dual yang
berhubungan y1 y2
Lalu perhatikan koefisien Wj-Cj pada tabel optimum dual:
Variabel basis awal dual R1 R2 R3
Koef. pers.Wj-Cj pada
optimum dual (abaikan M)
30 0 0
Var. keputusan primal
Contoh-contoh tersebut telah menunjukan bahwa setiap masalah program linear dapat diselesaikan dengan merumuskan baik bentuk primal maupun dual. Sehingga tidak perlu menyelesaikan kedua bentuk, cukup salah satunya saja karena solusi primal dapat menunjukan solusi dual begitu juga sebaliknya.
Pada umumnya suatu
program linear dengan jumlah pembatas yang lebih sedikit daripada jumlah variabel keputusan lebih mudah diselesaikan dibandingkan masalah dengan jumlah pembatas yang lebih banyak daripada variabel keputusan. Untuk itu jika akan menyelesaikan salah satu dari masalah primal atau dual, lebih mudah jika memilih dari kedua bentuk tersebut yang jumlah pembatasnya lebih sedikit dari variabel keputusan.
II. SIFAT-SIFAT PRIMAL-DUAL Untuk lebih memahami sifat-sifat primal-dual, pehatikanlah contoh primal-dual berikut ini:
Primal :
Maks Z = 2x1 + 4x2 + 3x3 x1 + 3x2 + 2x3 ≤ 60 3x1 + 5x2 + 3x3 ≥ 120 x1 , x2 , x3 ≥ 0 Bentuk standar persoalan tersebut adalah : Maks Z = 2x1 + 4x2 + 3x3 + 0S1 - 0 S2 - MR1 x1 + 3x2 + 2x3 + S1 = 60 3x1 + 5x2 + 3x3 –S2 + R1 = 120 x1 , x2 , x3 ≥ 0 Cat : Vmb = Variabel masuk basis Vkb = Variabel keluar basis
Iterasi 0 VB 2 4 3 0 0 - M RK x1 x2 x3 S1 S2 R1 0S1 1 3 2 1 0 0 60 -MR1 3 5 3 0 -1 1 120 Zj-Cj -3M-2 -5M-4 -3M-3 0 M 0 -120M Z -3M -5M -3M 0 M -M Vmb Vkb Iterasi 1 VB 2 4 3 0 0 - M RK x1 x2 x3 S1 S2 R1 4x2 1/3 1 2/3 1/3 0 0 20 -MR1 4/3 0 -1/3 -5/3 -1 1 20 Zj-Cj -4/3M-2/3 0 1/3M-1/3 5/3M+4/3 M 0 -20M+80 Z -4/3M+4/3 4 1/3M+8/3 5/3M+4/3 M -M Vmb Vkb Iterasi 2 VB 2 4 3 0 0 - M RK x1 x2 x3 S1 S2 R1 4x2 0 1 3/4 3/4 1/4 -1/4 15 2x1 1 0 -1/4 -5/4 -3/4 3/4 15 Zj-Cj 0 0 -1/2 1/2 -1/2 ½+M 90 Z 2 4 5/2 1/2 -1/2 1/2 Vkb Vmb
Iterasi 3 (solusi optimal primal)
VB 2 4 3 0 0 - M RK x1 x2 x3 S1 S2 R1 0S2 0 4 3 3 1 -1 60 2x1 1 3 2 1 0 0 60 Zj-Cj 0 2 1 2 0 M 120 Z 2 6 4 2 0 0
Solusi optimal persoalan primal adalah x1 = 60 x2 = x3 = 0 S1 = 0 S2 = 60 Z = 120.
Setelah bentuk primal ditransformasikan ke dalam bentuk normalnya, maka dual dari persoalan diatas adalah:
Dual : Min W = 60y1 – 120 y2 y1 – 3y2 ≥ 2 3y1 – 5y2 ≥ 4 2y1 – 3y2 ≥ 3 y1 , y2 ≥ 0 Bentuk standar persoalan dual tersebut adalah : Min W = 60y1 – 120 y2 – 0S1 – 0S2 – 0S3 + MR1 + MR2 + MR3 y1 – 3y2 – S1 + R1 = 2 3y1 – 5y2 – S2 + R2 = 4 2y1 – 3y2 – S3 + R3 = 3 y1 , y2 ≥ 0 Iterasi 0 VB 60 -120 0 0 0 M M M RK y1 y2 S1 S2 S3 R1 R2 R3 MR1 1 -3 -1 0 0 1 0 0 2 MR2 3 -5 0 -1 0 0 1 0 4 MR3 2 -3 0 0 -1 0 0 1 3 Wj-Cj 6M-60 -11M+120 -M -M -M 0 0 0 9M W 6M -11M -M -M -M M M M Vmb Vkb Iterasi 1 VB 60 -120 0 0 0 M M M RK y1 Y2 S1 S2 S3 R1 R2 R3 MR1 0 -4/3 -1 1/3 0 1 -1/3 0 2/3 60Y1 1 -5/3 0 -1/3 0 0 1/3 0 4/3 MR3 0 1/3 0 2/3 -1 0 -2/3 1 1/3 Wj-Cj 0 -M+20 -M M-20 -M 0 -2M+20 0 M+80 W 60 -M -M M -M M -M+20 M Vmb Vkb Iterasi 2 VB 60 -120 0 0 0 M M M RK y1 y2 S1 S2 S3 R1 R2 R3 MR1 0 -3/2 -1 0 1/2 1 0 -1/2 ½ 60Y1 1 -3/2 0 0 -1/2 0 0 1/2 3/2 0S2 0 1/2 0 1 -3/2 0 -1 3/2 1/2 Wj -Cj 0 30-3/2M -M 0 -30+1/2M 0 -M 30-3/2M 90+1/2M W 60 -90-3/2M -M 0 -30+1/2M M 0 30-1/2M Vmb Vkb
Iterasi 3 (solusi optimal dual)
VB 60 -120 0 0 0 M M M RK y1 Y2 S1 S2 S3 R1 R2 R3 0S3 0 -3 -2 0 1 2 0 -1 1 60Y1 1 -3 -1 0 0 1 0 0 2 0S2 0 -4 -3 1 0 3 -1 0 2 Wj -Cj 0 -60 -60 0 0 60-M -M -M 120 W 60 -180 -60 0 0 60 0 0
Solusi optimal persoalan dual tersebut adalah : y1 = 2 y2 = S1 = 0 S2 = 2 S3 = 1 W = 120
Contoh primal-dual diatas selanjutnya akan digunakan sebagai contoh penerapan sifat-sifat primal-dual yang akan dibahas pada bagian selanjutnya
Sifat 1:
Menentukan koefisien persamaan Zj-Cj pada variabel-variabel basis
awal pada suatu iterasi.
Pada setiap iterasi baik primal maupun dual, koefisien persamaan Zj-Cj variabel-variabel basis awal dapat dicari dengan cara:
WB = CB.B-1 - CW
dimana:
WB = matriks koefisien persamaan Zj-Cj dibawah
variabel-variabel basis awal pada iterasi yang bersangkutan. CB = matriks koefisien fungsi
tujuan dari variabel-variabel basis pada iterasi yang bersangkutan
B-1 = matriks dibawah variabel-variabel basis awal pada iterasi yang bersangkutan. CB.B-1 = simpleks multiplier
CW = matriks koefisien fungsi tujuan variabel-variabel basis awal
Sebagai contoh lihat tabel primal. Dalam persoalan tersebut variabel basis awalnya adalah S1 dan R1 dengan koefisien fungsi tujuan variabel basis awal 0 dan –M atau CW= [0 -M]
Untuk iterasi 0 : Variabel basis pada iterasi nol atau awal adalah S1 dan R1
WB = CB.B-1 - CW =
0
M
1
0
0
1
0
M
S1 R1 S1 R1 =
0
M
0
M
=
0
0
S1 R1Sekarang lihat tabel optimum dual, misalnya untuk iterasi 3, variabel basis awal bentuk dual adalah R1, R2, dan R3 dengan koefisien fungsi tujuanvariabel basis awal masing-masing adalah M atau Cw = [ M M M ] sedangkan variabel basis pada iterasi 3 adalah S3, y1 dan S2 dengan koefisien fungsi tujuan variabel basis iterasi 3 masing-masing 0, 60, dan 0 atau CB= [ 0 60 0 ] sehingga koefisien persamaan Wj – Cj pada variabel basis awal iterasi 3 adalah: WB = CB.B-1 – CW =
0
60
0
0
1
3
0
0
1
1
0
2
M
M
M
S3y
1 S2 R1 R2 R3 =
60
0
0
M
M
M
=
60
M
M
M
R1 R2 R3 Sifat 2:Menentukan koefisien persamaan Zj-Cj pada variabel-variabel non
basis awal suatu iterasi.
Pada setiap iterasi baik primal maupun dual, koefisien Zj-Cj pada variabel-variabel non basis awal dapat dicari dengan cara:
WB = SM . an- Cn
dimana:
WB = matriks koefisien persamaan Zj-Cjj dibawah variabel-variabel non basis awal pada iterasi yang bersangkutan. SM = CB.B-1 = simpleks multiplier
pada itersi yang
bersangkutan.
an = matriks dibawah variabel-variabel non basis pada iterasi awal
Cn = matriks koefisien fungsi tujuan variabel-variabel non basis awal.
Sebagai contoh, lihat optimum primal. Dalam persoalan tersebut variabel non basis awalnya adalah x1, x2, x3 dan S2 dengan koefisien fungsi tujuan masing-masing 2 , 4 , 3 dan 0 atau Cn = [ 2 4 3 0 ]
Untuk iterasi 0 : SM pada iterasi 0 adalah [ 0 –M ]
=
2
4
3
0
1
3
5
3
0
2
3
1
0
M
x1 x2 x3 S2 =
3
M
2
5
M
4
3
M
3
M
x1 x2 x3 S2 Sekarang lihat tabel optimum dual, misalkan untuk iterasi 3, variabel non basis awal bentuk dual adalah y1, y2, S1 , S2 , dan S3 dengan koefisien fungsi tujuan variabel non basis awal masing-masing adalah 60, -120, 0, 0, 0 atau Cn = [ 60 -120 0 0 0 ] sedangkan SM pada iterasi 3 adalah [ 60 0 0 ] sehingga koefisien persamaan Wj-Cj pada variabel non basis awal iterasi 3 adalah :WB = SM . an- Cn =
1 0 0 3 2 0 1 0 5 3 0 0 1 3 1 0 0 60 y1 y2 S1 S2 S3
60
120
0
0
0
=
0
60
60
0
0
y1 y2 S1 S2 S3 Sifat 3:Menentukan ruas kanan (RK) dari variabel-variabel basis suatu iterasi
Pada setiap iterasi baik primal maupun dual, nilai ruas kanan dari variabel-variabel basis suatu iterasi dapat diperoleh dengan rumus :
RK = B-1.b
Dimana:
RK = matriks ruas kanan dari variabel-variabel basis suatu iterasi.
b = matriks ruas kanan pada iterasi awal.
Sebagai contoh, lihat iterasi ke-3 solusi primal. Diketahui
sebelumnya bahwa matriks ruas kanan pada iterasi awal primal adalah
120
60
maka ruas kanan pada iterasi ke-3 : RK = B-1.b =
60
60
120
60
0
1
1
3
Untuk contoh pada dual, pandang iterasi ke-1 tabel solusi dual, diketahui bahwa matriks ruas kanan
pada iterasi awal dual adalah
3
4
2
maka ruas kanan pada iterasi ke-1 adalah : RK = B-1.RK =
0
0
1
3 2 3 1 3 1
1
0
0
3
4
2
=
3 1 3 4 3 2 Sifat 4:Menentukan koefisien pembatas variabel non basis suatu iterasi
Pada setiap iterasi baik primal maupun dual, koefisien pembatas variabel non basis suatu iterasi ditentukan menggunakan rumus:
Yi = B-1.ai
Dimana:
Yi = matriks koefisien pembatas variabel non basis awal pada iterasi yang bersangkutan. ai = matriks koefisien pembatas
variabel non basis awal pada iterasi awal.
Sebagai contoh, lihat iterasi ke-3 persoalan primal
Untuk x1 Y1 = B-1.a1 =
0
1
1
3
3
1
=
1
0
x2 Y2 = B-1.a2 =
0
1
1
3
5
3
=
3
4
hal yang sama dapat dilakukan pada variabel-variabel non basis awal yang lain baik pada iterasi ke-3 maupun iterasi sebelumnya.
Untuk contoh dual,
perhatikan iterasi ke-2 solusi persoalan dual Untuk y1 Y1 = B-1.a1 =
2
/
3
1
0
2
/
1
0
0
2
/
1
0
1
2
3
1
=
0
1
0
y2 Y2 = B-1.a2 =
2 1 2 3 2 33
5
3
2
/
3
1
0
2
/
1
0
0
2
/
1
0
1
Dengan mempelajari keempat sifat ini kita dapat menentukan nilai variabel-variabel tertentu dengan cara yang lebih mudah.
III. CONTOH KASUS
Untuk menjelaskan konsep dualitas, cara yang paling mudah adalah dengan memberikan contoh setelah teori-teori diberikan. Berikut
ini merupakan contoh yang
memperlihatkan bagaimana bentuk dual dari bentuk suatu model primal dikembangkan.
Sebuah garment PT. Bintang memproduksi dua jenis pakaian yaitu pakaian wanita dan pakaian pria. Tiap produksi 1 unit pakaian wanita memberikan keuntungan sebesar Rp 100.000,- dan tiap produksi 1 unit pakian pria memberikan keuntungan sebesar Rp. 80.000,-. Produksi pakaian pria dan wanita dihitung atas dasar harian. Tabel berikut memperlihatkan sumber-sumber daya yang terbatas beserta kebutuhan sumber-sumber berupa jumlah bahan kain, jumlah tenaga kerja dan luas
gudang penyimpanan untuk
memproduksi setiap unit pakaian wanita dan pria:
Table 2 Sumber
Daya
Kebutuhan sumber daya Jumlah yang tersedia/hari Wanita Pria Kain Tenaga Kerja Gudang Penyimpa nan 3m 4orang 12m2 3m 2orang 18m2 72m 40 orang 240m2 Keuntung an Rp 100.000,- Rp 80.000,-
Untuk mengetahui berapa banyak pakaian wanita dan pria yang
harus diproduksi untuk
memaksimalkan keuntungan, maka
diformulasikan suatu model
matematika sebagai berikut :
Maks
Z = 100.000x1 + 80.000x2 keuntungan
3x1 + 3x2 72m bahan kain
4x1 + 2x2 40orang tenaga kerja
12x1 +18x2 240m2 gudang
penyimpanan
Diketahui
x1 = Jumlah pakaian wanita yang diproduksi
x2 = Jumlah pakaian pria yang diproduksi
Model matematika tersebut merupakan model primal. Adapun model dual dari primal ini adalah:
Min
W =72y1 + 40y2 + 240y3
3y1 + 4y2 + 12y3 100.000
3y1 + 2y2 + 18y3 80.000
y1, y2, y3 0
Setelah model dual dikembangkan
dari model primal, langkah
selanjutnya adalah menentukan arti dual model tersebut.
Arti model dual dapat diinterpretasikan dengan cara mengamati solusi optimal dari bentuk primal model yang bersangkutan. Model primal diatas apabila dipecahkan dengan metode simpleks, maka solusi optimal ditunjukkan pada tabel berikut ini :
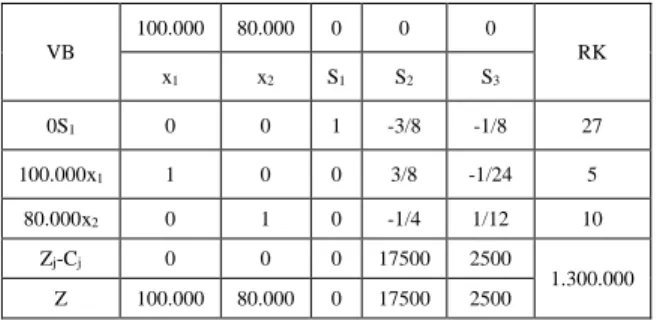
VB 100.000 80.000 0 0 0 RK x1 x2 S1 S2 S3 0S1 0 0 1 -3/8 -1/8 27 100.000x1 1 0 0 3/8 -1/24 5 80.000x2 0 1 0 -1/4 1/12 10 Zj-Cj 0 0 0 17500 2500 1.300.000 Z 100.000 80.000 0 17500 2500
Berdasarkan solusi optimal simpleks untuk model primal kita mendapatkan: x1 = 5 pakaian wanita S2 = 0 keuntungan x2 = 10 pakaian pria S3 = 0 gudang S1 = 27m kain Z = Rp 1.300.000,- keuntungan Keuntungan setiap satu buah pakaian wanita adalah Rp 100.000,-, karena diproduksi sebanyak 5 buah pakaian wanita (x1=5) maka keuntungan total dari produksi pakaian wanita adalah 5 x Rp 100.000,- = Rp 500.000,- , sedangan keuntungan setiap satu buah pakaian pria adalah Rp 80.000,- , karena diproduksi sebanyak 10
pakaian pria (x2=10) maka
keuntungan total dari produksi pakaian pria adalah 10 x Rp 80.000,-
= Rp 800.000,- sehingga keuntungan total yang diperoleh PT. Bintang sebesar Rp 500.000,- + Rp 800.000,- = Rp 1.300.000,-
Tabel optimal ini memuat
informasi mengenai primal,
sedangkan S1=27 m kain merupakan jumlah kain yang tersisa dalam
memproduksi pakaian-pakaian
tersebut, adapun S2=0 mencerminkan tenaga kerja yang tidak terpakai dan
S3=0 mencerminkan gudang
penyimpanan yang dimiliki
PT.Bintang telah habis digunakan dalam produksi pakaian wanita dan pria sehingga tidak ada kelebihan (slack) tenaga kerja maupun gudang penyimpanan yang tersisa.
Analisis lebih lanjut pada tabel optimal ini pun memuat informasi mengenai dual, nilai baris Zj-Cj sebesar 17.500 dan 2500 dibawah kolom S2 dan S3 secara berurutan merupakan nilai marginal (marginal value) dari tenaga kerja (S2) dan gudang penyimpanan (S3).
Dalam solusi tersebut S2 dan S3 bukan merupakan variabel basis sehingga keduanya sama dengan nol. Jika kita memasukkan S2 atau S3 ke dalam variabel basis maka S2 atau S3 tidak akan bernilai nol lagi. Sebagai contoh, jika satu orang tenaga kerja dimasukkan kedalam solusi (S2=1) maka satu orang tenaga kerja yang sebelumnya digunakan menjadi tidak digunakan atau tidak bekerja
(menganggur). Hal ini akan
menyebabkan penurunan keuntungan sebesar Rp 17.500,- tetapi jika tenaga kerja ini bekerja kembali (S2=0) yang berarti mengeluarkan lagi S2 dari variabel basis maka keuntungan PT.Bintang akan naik sebesar Rp 17.500,- Dengan demikian, jika kita dapat membayar 1 orang tenaga kerja, kita hanya bersedia membayar sampai setinggi Rp 17.500,- per orang karena
sebesar itulah jumlah yang dapat meningkatkan keuntungan.
Selain itu, pada tabel solusi optimal primal memperlihatkan bahwa nilai Zj-Cj pada kolom S1 adalah nol. Hal tersebut berarti bahwa bahan baku kain memiliki nilai marginal nol yaitu kita tidak akan bersedia membayar apapun untuk setiap unit kelebihan bahan baku kain. Pada tabel yang sama memperlihatkan solusi bahwa S1=27m yang berarti masih tersisa kain sebanyak 27 m setelah memproduksi 5 pakaian wanita dan 10 pakaian pria. Hal
tersebut menunjukkan bahwa
perusahaan tidak dapat menggunakan seluruh kain yang saat ini tersedia, alasan mengapa penambahan kain tidak memiliki nilai marginal karena kain bukan merupakan kendala dalam memproduksi pakaian wanita dan pria.
Nilai-nilai marginal sering dianggap sebagai shadow prices
(harga bayangan) karena
mencerminkan ongkos maksimum
yang bersedia dibayar oleh
perusahaan untuk menambah satu unit sumber-sumber daya.
Pada tabel ini pun
memperlihatkan bahwa keuntungan yang diperoleh perusahaan adalah sebesar Rp 1.300.000,-. Hal ini dapat dihubungkan dengan kontribusi
sumber-sumber daya terhadap
keuntungan sebesar Rp 1.300.000,-. Biaya yang dikeluarkan perusahaan tidak dapat melebihi keuntungan yang dihasilkan oleh sumber-sumber daya tersebut. Apabila ongkos yang dikeluarkan perusahaan untuk mendapatkan sumber-sumber daya melebihi Rp 1.300.000,- maka perusahaan akan mengalami kerugian. Nilai dari sumber-sumber daya sama dengan laba optimal.
Analisis lebih lanjut dapat dilihat sebagai berikut pandanglah pembatas tenaga kerja 4x1 + 2x2 40 orang, dari tabel primal didapat solusi optimal x1=5 pakaian wanita, x2=10 pakaian pria dan nilai satu orang tenaga kerja adalah Rp 17.500,-
Karena satu pakaian wanita memerlukan 4 tenaga kerja dan setiap tenaga kerja bernilai Rp 17.500,- maka jika memproduksi 5 pakaian wanita, biaya yang akan dikeluarkan adalah Rp 17.500,- x 5 x 4 orang = Rp 350.000,- sedangkan satu pakaian pria memerlukan 2 orang tenaga kerja dan setiap tenaga kerja bernilai Rp 17.500,- maka jika memproduksi 10 pakaian pria, biaya yang akan dikeluarkan adalah Rp 17.500,- x 10 x 2 = Rp 350.000,-
Dengan menjumlahkan biaya tenaga kerja yang digunakan untuk memproduksi pakaian wanita dan pria akan menghasilkan biaya total tenaga kerja Rp 350.000,- + Rp 350.000,- = Rp 700.000,-
Analisis yang sama dapat digunakan untuk menentukan biaya total gudang penyimpanan dalam memproduksi pakaian wanita dan pria. Pandanglah pembatas gudang penyimpanan 12x1 + 18x2 240m2 dan biaya setiap m2 gudang penyimpanan adalah Rp 2500,- Maka biaya gudang penyimpanan untuk pakaian wanita adalah : Rp 2500,- x 5 x 12 = Rp 150.000,- dan biaya gudang penyimpanan untuk pakaian pria adalah :
Rp 2500,- x 10 x 18 = Rp 450.000,- Dengan menjumlahkan biaya gudang penyimpanan untuk pakaian wanita dan pria menghasilkan biaya total gudang penyimpanan:
Rp 150.000,- + Rp 450.000,- = Rp 600.000,-
Maka dengan menjumlahkan biaya total tenaga kerja dan gudang
penyimpanan menghasilkan Rp 700.000,- (tenaga kerja) + Rp 600.000,- (gudang penyimpanan) = Rp 1.300.000,- yang sama dengan keuntungan total yang diperoleh PT. Bintang.
Adapun disini tidak
diperhitungkan mengenai biaya bahan kain karena telah dibahas sebelumnya bahwa masih tersisa bahan kain sebanyak 27 m, maka bahan kain memiliki nilai marginal nol; yaitu PT. Bintang tidak akan bersedia membayar apapun untuk satu meter ekstra dari bahan kain. Karena perusahaan masih mempunyai 27 m bahan kain yang tersisa, dalam hal ini satu meter ekstra bahan kain tidak
mempunyai nilai tambahan;
perusahaan bahkan tidak dapat menggunakan seluruh bahan kain yang saat ini tersedia.
Bentuk dual dari model ini adalah : Min W = 72y1 + 40y2 + 240y3 3y1 + 4y2 + 12y3 100.000 3y1 + 2y2 + 18y3 80.000
y1, y2, y3 0
Variabel-variabel keputusan dual mewakili nilai marginal sumber-sumber daya:
y1 = nilai marginal 1 m kain = 0 y2 = nilai marginal 1 orang tenaga kerja = Rp 17.500,-
y3 = nilai marginal 1 m2 gudang = Rp 2.500,-
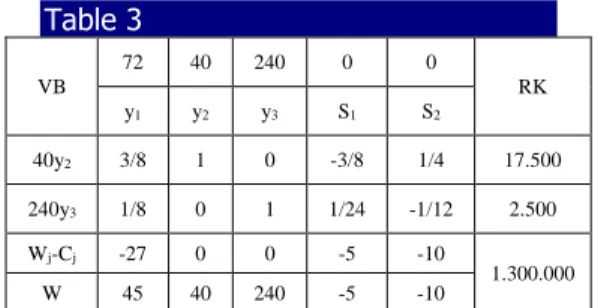
Model dual tersebut apabila dipecahkan dengan metode simpleks, maka solusi optimal dual ditunjukkan oleh tabel berikut :
Table 3 VB 72 40 240 0 0 RK y1 y2 y3 S1 S2 40y2 3/8 1 0 -3/8 1/4 17.500 240y3 1/8 0 1 1/24 -1/12 2.500 Wj-Cj -27 0 0 -5 -10 1.300.000 W 45 40 240 -5 -10 Pembahasan mengenai
batasan-batasan dual adalah sebagai berikut; pandanglah batasan dual yang pertama
3y1 + 4y2 + 12y3 100.000
Dengan mensubstitusikan nilai-nilai variabel kedalam pembatas diatas akan menghasilkan
3(0)+4(17.500)+ 12(2.500) ≥ 100.000 100.000 ≥ 100.000 Pembatas ini menunjukkan bahwa nilai dari ketiga sumber daya yang
digunakan dalam memproduksi
pakaian wanita paling sedikit harus sebesar atau sama dengan laba yang diperoleh pakaian wanita.
Dengan cara yang sama, apabila dibahas mengenai pembatas kedua: 3y1 + 2y2 + 18y3 80.000
3(0) + 2(17.500) +18(2.500) ≥ 80.000 80.000 ≥ 80.000 Dengan kata lain, Rp 80.000-, yaitu nilai sumber-sumber yang digunakan untuk memproduksi sebuah pakaian pria, sedikitnya adalah sebesar atau sama dengan Rp 80.000,- yaitu laba dari pakaian pria.
Adapun penjelasan untuk fungsi tujuan dual adalah sebagai berikut:
Min W =72y1 + 40y2 + 240y3
dimana koefisien-koefisien fungsi tujuan dual mencerminkan total kuantitas sumber yang tersedia. jadi jika nilai-nilai marginal dari satu unit sumber daya dikalikan dengan masing koefisien-koefisien tersebut, kita akan mendapatkan nilai total sumber:
W=72(0)+40(Rp17.500)+240(Rp 2.500) = Rp 1.300.000,-
Jika kita lihat ternyata nilai total sumber ini sama dengan keuntungan yang didapat dari nilai optimal Z dalam primal. Z= Rp 1.300.000,- = W Untuk itu nilai dari sumber-sumber tidak dapat melebihi keuntungan yang diperoleh dari penggunaan sumber-sumber tersebut.
IV. KESIMPULAN
Setelah model dual
didefinisikan secara lengkap, dapat
dikatakan bahwa model dual
dikembangkan dari model primal sepenuhnya. Hal tersebut dapat berarti bahwa operasi simpleks tidak perlu
dilakukan untuk mengetahui
informasi tentang dual karena solusi dual dapat ditentukan dari solusi primal.
Solusi optimum primal
memberikan informasi mengenai
banyaknya jumlah laba yang
diperoleh, sedangakan solusi optimum dual yang juga didapat dari solusi terhadap suatu masalah primal memberikan informasi yang tidak kalah penting dalam pengambilan keputusan. Bentuk dual akan memberikan informasi mengenai nilai-nilai sumber yang biasanya merupakan pembatas dari suatu model
sehingga dapat membantu
pengambilan keputusan dalam
menentukan harga dari sumber daya
yang menjadi pembatas bagi
tercapainya laba tersebut. DAFTAR PUSTAKA
Hiliier, & Lieberman,. (1990). Pengantar Riset Operasi. Jakarta : Erlangga
Mulyono, Sri. (1999). Operations Research. Jakarta : Fakultas Ekonomi Universitas Indonesia Siagian, P. (1987). Penelitian
Operasional. Jakarta : UI-Press
Tarliah, Tjutju. (2003). Operations Research. Bandung : Sinar Baru Algensindo
Taylor, Bernard. W. (2001). Sains Manajemen. Jakarta : Salemba Empat