Teknik Pengolahan Data

(1)

Universitas Gadjah Mada

Jurusan Teknik Sipil dan Lingkungan

Magister Teknik Pengelolaan Bencana Alam

Teknik Pengolahan

Data

Curve Fi)ng: Regresi dan Interpolasi

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 1

(2)

Curve Fitting

• Acuan

•  Chapra, S.C., Canale R.P., 1990, Numerical Methods for Engineers,

2nd Ed., McGraw-‐Hill Book Co., New York.

•  Chapter 11 dan 12, pp. 319-‐398. 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 2

(3)

Curve Fitting

• Mencari garis/kurva yang mewakili serangkaian ::k data

• Ada dua cara untuk melakukannya, yaitu

•  Regresi

•  Interpolasi

• Aplikasi di bidang enjiniring

•  Pola perilaku data (trend analysis)

•  Uji hipotesis (hypothesis tes;ng)

(4)

Curve Fitting

• Regresi

• Apabila data menunjukkan

:ngkat kesalahan yang

cukup signiﬁkan atau

menunjukkan adanya

noise

• Untuk mencari satu kurva

tunggal yang mewakili pola

umum perilaku data

• Kurva yang dicari :dak

perlu melewa: se:ap ::k

data

• Interpolasi

• Diketahui bahwa data

sangat akurat

• Untuk mencari satu atau

serangkaian kurva yang

melewa: se:ap ::k data

• Untuk memperkirakan

nilai-‐nilai di antara ::k-‐

::k data

(5)

Curve Fitting

• Ekstrapolasi

•  Mirip dengan interpolasi, tetapi untuk memperkirakan nilai-‐nilai di

luar kisaran ::k-‐::k data

•  Ekstrapolasi :dak disarankan

(6)

Curve Fitting

terhadap Data Pengukuran

• Analisis pola perilaku data

•  Pemanfaatan pola data (pengukuran, eksperimen) untuk melakukan

perkiraan

•  Apabila data persis (akurat): interpolasi

•  Apabila data tak persis (tak akurat): regresi

• Uji hipotesis

•  Pembandingan antara hasil teori atau hasil hitungan dengan hasil

pengukuran 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 6

(7)

Beberapa Parameter Statistik

• Rata-‐rata aritma:k,

mean

• Deviasi standar, simpangan

baku,

standard devia;on

• Varian (‘ragam’),

variance

• Coeﬃcient of varia;on

! !sy 2 = St n−1 ! !y = 1 n

∑

yi ! !sy = S_t n−1 !!St =

(

yi −y

)

2

∑

! !c.v.= s_y y 100% m er ep re se ntas ik an s eb ar an d ata 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 7

(8)

Distribusi Probabilitas

X

frek

_{Distribusi Normal}

salah satu distribusi/sebaran data yang sering dijumpai adalah distribusi normal

(9)

REGRESI

Regresi Linear 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 9

(10)

Regresi: Metode Kuadrat Terkecil

• Mencari satu kurva atau satu fungsi (pendekatan) yang sesuai

dengan pola umum yang ditunjukkan oleh data

•  Datanya menunjukkan kesalahan yang cukup signiﬁkan

•  Kurva :dak perlu memotong se:ap ::k data

• Metode

•  Regresi linear

•  Regresi persamaan-‐persamaan tak-‐linear yang dilinearkan

•  Regresi polinomial

•  Regresi linear ganda

•  Regresi tak-‐linear 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 10

(11)

Regresi: Metode Kuadrat Terkecil

• Bagaimana caranya?

•  Program komputer

•  Spreadsheet (Microsoc Excel)

• Program aplikasi gra:s, mirip MatLab

•  Octave •  Scilab •  Freemat 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 11

(12)

Regresi Linear

• Mencari suatu kurva lurus yang cocok menggambarkan pola

serangkaian ::k data: (

x

₁

,

y

₁

), (

x

₂

,

y

₂

) … (

x

_n

,

y

_n

)

• Microsoc Excel

•  INTERCEPT(y1:yn;x1:xn)

•  SLOPE(y1:yn;x1:xn) y_reg = a₀ + a₁x

a₀ : intercept a₁ : slope 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 12

(13)

Regresi Linear

• Kesalahan atau residu (

e

) adalah perbedaan antara nilai

y

sesungguhnya (data

y

) dan y nilai pendekatan (

y

_reg

) menurut

persamaan linear

a

₀

+

a

₁

x

.

• Minimumkan jumlah kuadrat residu tersebut

!

!e

=

y

−

a

0

−

a

1

x

! !min Sr ! " #$=min ei 2

∑

! " $#=min

(

yi −a0 −a1xi

)

2

∑

! "' # $( 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 13

(14)

Regresi Linear

• Bagaimana cara mencari

koeﬁsien

a

₀

dan

a

₁

?

•  Diferensialkan persamaan

tersebut dua kali, masing-‐ masing terhadap a₀ dan a₁.

•  Samakan kedua persamaan

hasil diferensiasi tersebut dengan nol.

•  Selesaikan persamaan tsb

untuk mendapatkan a₀ dan

a₁.

(

)

(

)

0 2 0 2 1 0 1 1 0 0 = − − − = ∂ ∂ = − − − = ∂ ∂

∑

i i i r i i r x x a a y a S x a a y a S 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 14 ! ! a₁ = n x

∑

iyi −

∑

xi

∑

yi n x_i2

∑

−

(

∑

x_i

)

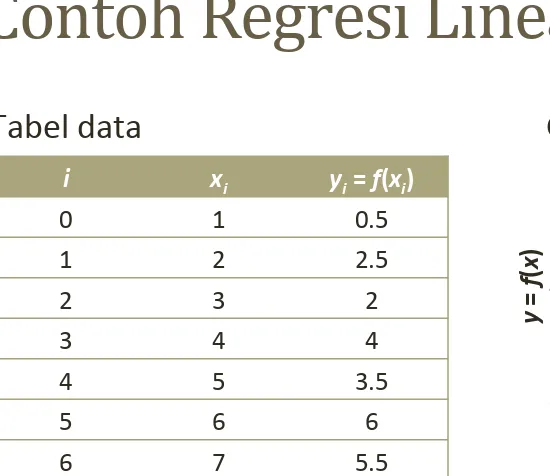
2 a₀ =y −a₁ x

(15)

Contoh Regresi Linear

i x_i y_i = f(x_i) 0 1 0.5 1 2 2.5 2 3 2 3 4 4 4 5 3.5 5 6 6 6 7 5.5 0 2 4 6 8 0 1 2 3 4 5 6 7 y = f ( x ) X

Tabel data

Graﬁk/kurva data

13-‐No

v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 15

(16)

Hitungan Regresi Linear

i x_i y_i x_i y_i x_i2 _y

reg (yi−yreg)2 (yi−ymean)2

0 1 0.5 0.5 1 0.910714 0.168686 8.576531 1 2 2.5 5 4 1.75 0.5625 0.862245 2 3 2.0 6 9 2.589286 0.347258 2.040816 3 4 4.0 16 16 3.428571 0.326531 0.326531 4 5 3.5 17.5 25 4.267857 0.589605 0.005102 5 6 6.0 36 36 5.107143 0.797194 6.612245 6 7 5.5 38.5 49 5.946429 0.199298 4.290816 ∑ = 28 24.0 119.5 140 ∑ = 2.991071 22.71429 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 16

(17)

Hitungan Regresi Linear

a₁ ₌ n

∑

xiyi −

∑

xi

∑

yi n

_∑

x_i2 ₋

(

_∑

x_i

)

2 = 7 119.5

₍

₎

₋28 24

_{( )}

7 140

₍

₎

₋

_{( )}

28 2 = 0.839286 ! ! y = 24 7 =3.4 x =28 7 = 4 a₀ =3.4−0.839286 4

( )

=0.071429 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 17

(18)

Hitungan Regresi Linear

0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 Y X data regresi 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 18

(19)

Regresi Linear

• Kuan:ﬁkasi kesalahan

•  Kesalahan standar

•  Perha:kan kemiripannya dengan simpangan baku

! !sy x = S_r n−2 ! !sy = S_t n−1 !!St =

(

yi −y

)

2

∑

! !Sr =

(

yi −a0−a1xi

)

2

∑

(20)

Regresi Linear

• Beda antara kedua kesalahan tersebut menunjukkan perbaikan

atau pengurangan kesalahan

r2 = St −Sr S_t =1− S_r S_t r ₌ n

∑

xiyi −

(

∑

xi

)

(

∑

yi

)

n

_∑

x_i2 −

(

∑

x_i

)

2 n

∑

y_i2 −

(

∑

y_i

)

2 koeﬁsien determinasi

(coefficient of determina;on) koefisien korelasi (correla;on coefficient) 13-‐No v-‐14 h8 p: // is :ar to .s taff .u gm .ac .id 20

(21)

Hitungan Regresi Linear

! ! S_r =

∑

(

y_i −a₀ −a₁x_i

)

2 =2.991071 S_t =

∑

(

y_i −y

)

2 =22.71429 ! ! r2 = St −Sr S_t =1− S_r S_t =1− 2.991071 22.71429 =0.868318 r =0.931836 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 21

(22)

REGRESI

Regresi persamaan tak-‐linear yang dilinearkan

(23)

Regresi Linear

• Linearisasi persamaan-‐persamaan tak-‐linear

•  Logaritmik menjadi linear

•  Eksponensial menjadi linear

•  Pangkat (polinomial :ngkat n > 1) menjadi linear (polinomial :ngkat

1) •  Dll. 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 23

(24)

Linearisasi Persamaan Non-‐linear

x y ln y 1 ln a !y =aebx ! !lny =lna+bx x b 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 24

(25)

Linearisasi Persamaan Non-‐linear

1 x y log y log x b !y =axb !

!logy =loga+blogx

! !logb 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 25

(26)

Linearisasi Persamaan Non-‐linear

1/y 1 !y=a x b+x 1/x y x ! ! 1 y = b+x ax = 1 a+ b a 1 x ! !1 a !b a 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 26

(27)

REGRESI

Regresi Polinomial 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 27

(28)

Regresi Polinomial

• Sebagian data bidang teknik, walaupun menunjukkan pola yang

jelas, namun pola tsb :dak dapat diwakili oleh sebuah garis lurus

•  Metode 1: transformasi koordinat (linearisasi persamaan tak-‐linear)

•  Metode 2: regresi polinomial

•  Polinomial :ngkat m

•  Jumlah residu kuadrat

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 28 ! !y =a0 +a1x+a2x 2 +...+a_mxm ! ! S_r = e_i2 i=1 n

∑

=

(

y_i −a₀−a₁x_i +a₂x_i2+...+a_mx_im

)

2 i=1 n

∑

(29)

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 29 •  Metode kuadrat

terkecil yang diperluas untuk regresi

polinomial :ngkat m

•  Persamaan-‐persamaan

di kanan ini disamakan dengan nol dan

disusun sedemikian rupa menjadi sistem persamaan linear ! ! ∂S_r ∂a₀ =−2 yi −a0−a1xi +a2xi 2 +...+a_mx_im

(

)

i=1 n

∑

∂S_r ∂a₁ =−2 xi yi −a0−a1xi +a2xi 2 +...+a_mx_im

(

)

i=1 n

∑

∂S_r ∂a₂ =−2 xi 2 _y i −a0 −a1xi +a2xi 2 +...+a_mx_im

(

)

i=1 n

∑

. . . ∂S_r ∂a_m =−2 xi m _y i −a0 −a1xi +a2xi 2 +...+a_mx_im

(

)

i=1 n

∑

(30)

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 30 ! ! a₀n+a₁ x_i i=1 n

∑

+a₂ x_i2 i=1 n

∑

+...+a_m x_im i=1 n

∑

= y_i i=1 n

∑

a₀ x_i i=1 n

∑

+a₁ x_i2 i=1 n

∑

+a₂ x_i3 i=1 n

∑

+...+a_m x_im+1 i=1 n

∑

= x_iy_i i=1 n

∑

a₀ x_i2 i=1 n

∑

+a₁ x_i3 i=1 n

∑

+a₂ x_i4 i=1 n

∑

+...+a_m x_im+2 i=1 n

∑

= x_i2y_i i=1 n

∑

. . . a₀ x_im i=1 n

∑

+a₁ x_im+1 i=1 n

∑

+a₂ x_im+2 i=1 n

∑

+...+a_m x_i2m i=1 n

∑

= x_imy_i i=1 n

∑

§

Ada m+1 persamaan linear dengan m+1 variabel tak diketahui, yaitu a₀, a₁, a₂, …, a_m

§

Persamaan-‐persamaan linear ini dapat

diselesaikan dengan metode-‐metode •  Eliminasi Gauss •  Gauss-‐Jordan •  Iterasi Jacobi •  Inversi matriks

(31)

Contoh

•  Temukanlah kurva polinomial

:ngkat 2 yang mewakili pola sebaran data pada tabel di sisi kanan ini •  Jawab 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 31 x_i y_i 0 2.1 1 7.7 2 13.6 3 27.2 4 40.9 5 61.1 ! !y =a0+a1x+a2x 2 ! ! y=2.47857+2.35929x+1.86071x2 r2 =1−Sr S_t =1− 3.74657 2513.39 =0.99851 r =0.99925

(32)

REGRESI

Regresi Linear Ganda (Mul;ple Linear Regression)

(33)

Regresi Linear Ganda

• Misal variabel

y

adalah fungsi linear dua variabel bebas

x

₁

dan

x

₂

•  Koeﬁsien a₀, a₀, a₀ pada persamaan di atas dapat ditemukan dengan

metode kuadrat terkecil kesalahan (error)

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 33 ! !y =a0+a1x1+a2x2 ! ! S_r =

(

y_i −a₀ −a₁x_1i −a₂x_2i

)

2 i=1 n

∑

(34)

Regresi Linear Ganda

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 34 ! ! ∂S_r ∂a₀ =−2_i₌₁

(

yi −a0 −a1x1i −a2x2i

)

n

∑

∂S_r ∂a₁ =−2_i₌₁ x1i

(

yi −a0−a1x1i −a2x2i

)

n

∑

∂S_r ∂a₂ =−2_i₌₁ x2i

(

yi −a0 −a1x1i −a2x2i

)

n

∑

§  Diferensial parsial persamaan

tersebut terhadap masing-‐masing koeﬁsien ! ! na₀+ x_1i a₁ i=1 n

∑

+ x_2i a₂ i=1 n

∑

= y_i i=1 n

∑

x_1i a₀ i=1 n

∑

+ x_1i2 a₁ i=1 n

∑

+ x_1ix_2i a₂ i=1 n

∑

= x_1iy_i i=1 n

∑

x_2i a₀ i=1 n

∑

+ x_1ix_2i a₁ i=1 n

∑

+ x_2i2 a₂ i=1 n

∑

= x_2iy_i i=1 n

∑

§  Samakan persamaan diferensial tsb

dengan nol dan atur suku-‐suku dalam persamaan

(35)

Regresi Linear Ganda

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 35 ! ! n x₁_i i=1 n

∑

x₂_i i=1 n

∑

x₁_i i=1 n

∑

x₁_i2 i=1 n

∑

x₁_i x₂_i i=1 n

∑

x₂_i i=1 n

∑

x₁_i x₂_i i=1 n

∑

x₂2 i=1 n

∑

" # $ $ $ $ $ $ $ $ % & ' ' ' ' ' ' ' ' a₀ a₁ a₂ ( ) ** + * * , -** . * * = y_i i=1 n

∑

x₁_i y_i i=1 n

∑

x₂_i y_i i=1 n

∑

( ) * * * * + * * * * , -* * * * . * * * *

§  Persamaan-‐persamaan linear tersebut dapat dituliskan dalam bentuk persamaan

(36)

Contoh

•  Temukanlah persamaan linear

yang mewakili pola sebaran data dalam tabel di samping ini.

•  Jawab 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 36 x₁ x₂ y 0 0 5 2 1 10 2.5 2 9 1 3 0 4 6 3 7 2 27 ! !y =5+4x1 −3x2

(37)

Regresi Linear Ganda

• Regresi linear ganda dapat dipakai pada kasus hubungan antar

variabel yang berupa persamaan pangkat (

power equa;ons

)

•  Persamaan di atas sangat bermanfaat pada kasus ﬁ)ng data

eksperimen

•  Persamaan di atas ditransformasikan menjadi persamaan linear

!

!y

=

a

0

x

1 a₁

x

₂a2

...

x

m a_m

!

(38)

REGRESI

Bentuk Umum Persamaan Regresi Linear dengan Metode Kuadrat Terkecil 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 38

(39)

Regresi Linear (Kuadrat Terkecil)

•  Tiga jenis regresi yang telah dipaparkan, yaitu regresi linear, regresi

polinomial, dan regresi linear ganda dapat dituliskan dalam bentuk umum model kuadrat terkecil

•  z₀, z₁, …, z_m adalah fungsi-‐fungsi yang berjumlah m+1

•  m+1 adalah jumlah variabel bebas

•  n+1 adalah jumlah data

•  Persamaan di atas dapat dituliskan dalam bentuk persamaan matriks

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 39 ! !y =a0z0+a1z1+a2z2+...+amzm !

{ }

Y =!"Z#$

{ }

A

(40)

Regresi Linear (Kuadrat Terkecil)

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 40 !

{ }

Y =!"Z#$

{ }

A ! ! Z ! " #$= a₀₁ a₁₁ . . . a_m₁ a₀₂ a₁₂ . . . a_m₂ . . . . . . . . . a₀_n a₁_n a_mn ! " % % % % % % % % # $ & & & & & & & &

§  {Y} adalah vektor kolom variabel tak

bebas

§  [Z] adalah matriks data nilai variabel

bebas

§  {A} adalah vektor kolom koeﬁsien

yang :dak diketahui

!!"Z#$ T Z ! " #$

{ }

A =!"Z#$ T Y

{ }

! ! S_r = y_i − a_jz_ji j=1 m

∑

# $ %% & ' (( 2 i=1 n

∑

(41)

Regresi Linear (Kuadrat Terkecil)

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 41 !!"Z#$ T Z ! " #$

{ }

A =!"Z#$ T Y

{ }

§ 

Strategi penyelesaian

•  Dekomposisi LU •  Metode Cholesky •  Inversi matriks ! !

{ }

A = Z ! " #$ T Z ! " #$ ! "% # $& −1 Z ! " #$ T Y

{ }

(42)

INTERPOLASI

Metode Newton Metode Lagrange 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 42

(43)

Interpolasi

linear kuadra:k kubik

(44)

Interpolasi

• Situasi

•  Keperluan untuk memperkirakan nilai variabel di antara data akurat

yang diketahui

•  Metode yang paling sering dipakai untuk keperluan tersebut adalah interpolasi polinomial

• Bentuk umum persamaan polinomial :ngkat

n

• Hanya ada satu polinomial :ngkat

n

atau :ngkat yang lebih kecil

yang melalui semua

n

+1 ::k data

!

f x

( )

=

a

0

+

a

1

x

+

a

2

x

2

+

...

+

a

_n

x

n

(45)

Interpolasi

• Penyelesaian persamaan polinomial :ngkat

n

membutuhkan

sejumlah

n

+ 1 ::k data

• Metode untuk mencari polinomial :ngkat

n

yang merupakan

interpolasi sejumlah

n

+ 1 ::k data:

•  Metode Newton •  Metode Lagrange 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 45

(46)

Interpolasi Linear: Metode Newton

x f(x) f(x₁) f₁(x) f(x₀) x₀ x x₁ !! f₁

_{( )}

x − f x

( )

₀ x−x₀ = f x

_{( )}

₁ − f x

( )

₀ x₁−x₀ f₁

_{( )}

x = f x

( )

₀ + f x

( )

1 − f x

( )

0 x₁ −x₀

(

x−x0

)

(47)

Interpolasi Kuadratik: Metode Newton

! ! f₂

_{( )}

x =b₀+b₁

(

x−x₀

)

+b₂

(

x−x₀

)

(

x−x₁

)

=b₀+b₁x−b₁x₀+b₂x2+b₂x₀x₁−b₂xx₀ −b₂xx₁ =

(

b₀ −b₁x₀+b₂x₀x₁

)

a₀ !###"###$+

(

b1 −b2x0 −b2x1

)

a₁ !##"##$ x+

( )

b2 a₂ %x 2 ! !f2

( )

x =a0+a1x+a2x 2 ! ! a₀ =b₀ −b₁x₀ +b₂x₀x₁ a₁ =b₁ −b₂x₀ −b₂x₁ a₂ =b₂ " # $ % $ 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 47

(48)

Interpolasi Kuadratik: Metode Newton

! ! b₂ = f x

_{( )}

₂ − f x

( )

₁ x₂ −x₁ − f x

_{( )}

₁ − f x

( )

₀ x₁−x₀ x₂−x₁ = f x2,x1,x0 " # $%= f x" ₂,x₁ # $%− f x"# 1 −x0$% x₂ −x₁ ! !b0 = f x

( )

0 ! ! b₁ = f x

( )

1 − f x

( )

0 x₁ −x₀ = f x1,x0 " # $% 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 48

(49)

Interpolasi Polinomial: Metode Newton

! !fn

( )

x =b0+b1

(

x−x0

)

+...+bn

(

x−x0

)

(

x−x1

)

...

(

x−xn−1

)

! ! b₀ = f x

( )

₀ b₁ = f x!_" ₁,x₀#_$ b₂ = f x!_" ₂,x₁,x₀#_$ . . . b_n = f x!_" _n,x_n₋₁,...,x₁,x₀#_$ 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 49

(50)

Interpolasi Polinomial: Metode Newton

! ! f x! _i,x_j " #$= f x

_{( )}

_i − f x

( )

_j x_i −x_j f x! _i,x_j,x_k " #$= f x! _i,x_j " #$− f x!" j,xk#$ x_i −x_k f x! _n,x_n₋₁,...,x₁,x₀ " #$= f x! _n,x_n₋₁,...,x₁ " $−# f x!" n−1,nn−2,...,x0#$ x_n −x₀ 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 50

( )

( ) (

)

[

]

(

)(

)

[

]

(

0

)(

1

) (

1

)

[

1 0

]

0 1 2 1 0 0 1 0 0 ,..., , ... ... , , , x x x f x x x x x x x x x f x x x x x x f x x x f x f n n n n − − − − − + + − − + − + =

(51)

Interpolasi Polinomial: Metode Newton

i x_i f(x_i) Langkah Hitungan

ke-‐1 ke-‐2 ke-‐3 0 x₀ f(x₀) f[x₁,x₀] f[x₂,x₁,x₀] f[x₃,x₂,x₁,x₀] 1 x₁ f(x₁) f[x₂,x₁] f[x₃,x₂,x₁] 2 x₂ f(x₂) f[x₃,x₂] 3 x₃ f(x₃) 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 51

(52)

Interpolasi Polinomial: Metode Lagrange

! ! f_n

_{( )}

x = L_i

( )

x f x

( )

_i i=0 n

∑

L_i

_{( )}

x = x−xj x_i −x_j j=0 j≠i n

∏

(53)

Contoh interpolasi

i x_i f(x_i) 0 1 1.5 1 4 3.1 2 5 6 3 6 2.1 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 f( x) X 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 53

(54)

SPLINE

Linear Kuadra:k Kubik 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 54

(55)

Interpolasi:

Spline

• Jumlah ::k data

n

+ 1

→

interpolasi polinomial :ngkat

n

•  Tingkat besar, n >>, mengalami kesulitan apabila ::k-‐::k data

menunjukkan adanya perubahan :ba-‐:ba di suatu ::k tertentu (perubahan gradien secara :ba-‐:ba)

•  Dalam situasi tsb, polinomial :ngkat kecil, n <<, dapat lebih

representa:f untuk mewakili pola data

•  Spline •  Cubic splines (n = 3) •  Quadra;c splines •  Linear splines 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 55

(56)

Interpolasi Polinomial vs

Spline

§ 

Polinomial :ngkat

n

n = 1 n » _n_{= 1} n » 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 56

(57)

Linear Splines

• Spline

:ngkat 1

: garis lurus

• Data urut

:

x

₀

,

x

₁

,

x

₂

, …,

x

_n

13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 57 ! ! f x

_{( )}

= f x

( )

₀ +m₀

(

x−x₀

)

x₀ ≤ x≤ x₁ f x

_{( )}

= f x

( )

₁ +m₁

(

x−x₁

)

x₁ ≤x ≤ x₂ . . . f x

_{( )}

= f x

( )

_n₋₁ +m_n₋₁

(

x−x_n₋₁

)

x_n₋₁ ≤ x ≤ x_n

(

)

( )

j i j i i x x x f x f m − − = + + 1 1 gradien:

(58)

Linear Splines

• Linear spline

•  Dengan demikian, linear spline adalah sama dengan interpolasi linear

•  Kekurangan linear spline adalah ke:dak-‐mulusan kurva interpolasi

•  Terdapat perubahan slope yang sangat tajam di ::k-‐::k data atau di

::k-‐::k pertemuan kurva spline (knot)

•  Deriva:f pertama fungsi linear spline diskon:nu di ::k-‐::k knot

•  Kelemahan linear spline tersebut diatasi dengan pemakaian

polinomial yang memiliki :ngkat lebih :nggi yang menjamin kemulusan kurva spline di knots dengan cara menyamakan nilai deriva:f di ::k-‐::k knot

(59)

Quadratic Splines

• Quadra;c splines

•  Untuk mendapatkan kurva yang memiliki diferensial/laju-‐perubahan

ke-‐m kon:nu di ::k knot, maka diperlukan kurva spline yang ber:ngkat paling kecil m + 1.

•  Yang paling banyak dipakai adalah spline :ngkat 3 (cubic spline):

diferensial pertama dan kedua kon:nu di ::k-‐::k knot.

•  Ke:dak-‐mulusan diferensial ke:ga, keempat, dst. umumnya :dak begitu

tampak secara visual

(60)

Quadratic Splines

• Tujuan: mencari polinomial :ngkat 2 untuk se:ap interval ::k-‐

::k data.

• Polinomial :ngkat 2 tsb harus memiliki diferensial pertama (laju

perubahan) yang kon:nu di ::k-‐::k data.

• Polinomial :ngkat 2:

• Untuk (

n

+1) ::k data (

i

= 0, 1, 2, …,

n

), terdapat

n

interval,

sehingga terdapat 3

n

koeﬁsien yang harus dicari (

a

_i

, b

_i

, c

_i

),

i

= 1,

2, ...,

n.

• Perlu persamaan sejumlah 3

n.

( )

x aix bix ci f = 2 + + 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 60

(61)

Quadratic Splines

• Ke-‐3

n

persamaan tsb adalah sbb.

1.  Kurva spline memotong ::k-‐::k data (knot): interval i -‐ 1 dan i bertemu di ::k data {x_i_{-‐ 1}, f(x_i_{-‐ 1})}

2.  Kurva spline di interval pertama memotong ::k data pertama (i =

1) dan kurva spline di interval terakhir memotong ::k data terakhir (i = n) i = 2, 3, …, n 2(n -‐ 1) pers. ! ! a_i−₁x_i−₁2

+b_i−1x_i−₁+c_i−₁ = f x

( )

_i−1

a_ix_i−₁2 +b_ix_i−1+c_i = f x

( )

_i−1 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 61 2 pers.

( )

n n n n n nx b x c f x a x f c x b x a = + + = + + 2 0 1 0 1 2 0 1

(62)

Quadratic Splines

• Ke-‐3

n

persamaan tsb adalah sbb.

3.  Diferensial (gradien) kurva spline di dua interval berurutan adalah

sama di ::k data yang bersangkutan

4.  Diferensial kedua (laju perubahan gradien) kurva spline di ::k data

pertama sama dengan nol

i = 2, 3, …, n (n -‐ 1) pers. 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 62 !

!f x!

( )

=2ax+b ⇒ 2ai−1xi−1+bi−1 =2aixi−1+bi

1 pers.

!

!ai =0

Konsekuensi: 2 ::k data pertama (i = 0 dan i = 1) dihubungkan dengan garis lurus

(63)

Quadratic Splines

• Dengan demikian, jumlah persamaan seluruhnya:

2(

n

– 1) + 2 + (

n

– 1) + 1 = 3

n

(64)

Cubic Splines

• Tujuan: mencari polinomial :ngkat 3 untuk se:ap interval ::k-‐

::k data.

•  Polinomial :ngkat 3 tsb harus memiliki diferensial pertama (gradien) dan diferensial kedua (laju perubahan gradien) yang kon:nu di ::k-‐::k data.

•  Polinomial orde 3:

•  Untuk (n+1) ::k data (i = 0, 1, 2, …, n), terdapat n interval, shg. terdapat 4n koeﬁsien yang harus dicari (a_i,b_i,c_i,d_i), i = 1, 2, ..., n.

•  Perlu persamaan sejumlah 4n. ! !fi

( )

x =aix 3 +b_ix2 +c_ix+d_i 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 64

(65)

Cubic Splines

• Ke-‐4

n

persamaan tsb adalah sbb.

1.  Kurva spline memotong ::k-‐::k data (knot): interval i -‐ 1 dan i bertemu di ::k data {x_i_{-‐ 1}, f(x_i_{-‐ 1})} → (2n -‐ 2) pers.

2.  Kurva spline di interval pertama memotong ::k data pertama dan kurva spline terakhir memotong ::k data terakhir → 2 pers.

3.  Diferensial pertama kurva spline di dua interval berurutan adalah sama di ::k data ybs. → (n -‐ 1) pers.

4.  Diferensial kedua kurva spline di dua interval berurutan adalah sama di ::k data ybs. → (n -‐ 1) pers.

5.  Diferensial kedua kurva spline di ::k data pertama dan terakhir sama dengan nol → 2 pers.

(66)

Cubic Splines

•  Ke-‐4n persamaan tsb.

•  Syarat kelima membawa konsekuensi sbb.

•  Kurva spline di interval pertama dan interval terakhir berupa garis lurus

•  dua ::k data pertama dihubungkan dengan sebuah garis lurus

•  dua ::k data terakhir dihubungkan dengan sebuah garis lurus

•  Ada sebuah syarat alterna:f sebagai penggan: syarat kelima tsb

•  Deriva:f kedua di ::k knot terakhir diketahui

(67)

Cubic Splines

•  Diperoleh 4n persamaan yang harus diselesaikan untuk mencari 4n

koeﬁsien, a_i, b_i, c_i, d_i

2(n – 2) + 2 + (n – 1) + (n – 1) + 2 = 4n

•  Dimungkinkan untuk melakukan manipulasi matema:s shg diperoleh

suatu teknik cubic splines yang hanya memerlukan

n – 1 penyelesaian (lihat uraian di buku acuan

•  Chapra, S.P., Canale, R.P., 1985, Numerical Methods for Engineers, McGraw-‐Hill Book Co., New York, hlm. 395-‐396).

(68)

Cubic Splines

! ! f_i

_{( )}

x = f x!!

( )

i−1 6

(

x_i −x_i₋₁

)

(

xi −x

)

3 + f x!!

( )

i−1 6

(

x_i −x_i₋₁

)

(

x−xi−1

)

3 + f x

( )

i−1 x_i−x_i₋₁

(

)

− !! f x

_{( )}

_i₋₁

(

x_i −x_i₋₁

)

6 # $ % % & ' ( (

(

xi −x

)

+ f x

( )

i x_i−x_i₋₁

(

)

− !! f x

_{( )}

_i₋₁

(

x_i −x_i₋₁

)

6 # $ % % & ' ( (

(

x−xi−1

)

! ! x_i −x_i−₁

(

)

f x""

( )

_i−₁ +2

(

x_i₊₁−x_i−1

)

f x""

( )

_i +

(

x_i₊₁−x_i

)

f x""

( )

_i₊₁ = 6 x_i₊₁−x_i

(

)

#$f x

( )

i+1 − f x

( )

i %&+ 6 x_i −x_i−1

(

)

#$f x

( )

i−1 − f x

( )

i %&

2 unknowns di se:ap interval:

! !f x!!

( )

i−1 !!dan!!f x!!

( )

i ! ! n!interval !! f x

_{( )}

₀ =0 !! f x

_{( )}

_n =0 " # $$ % $ $ ⇒

(

n−1

)

!pers. 13-‐No v-‐14 h8 p: // is :ar to .s taﬀ .u gm .ac .id 68

(69)

Teknik Pengolahan Data