iv
PERSEMBAHAN
Do the best. Be the best. But don’t think the best.
Skripsi ini kupersembahkan kepada
Kedua orang tuaku dan adikku terkasih,
Masku dan sahabat-sahabatku tersayang,
P
Saya menyatakan den
memuat karya atau ba
kutipan dan daftar pust
v
PERNYATAAN KEASLIAN KARYA
dengan sesungguhnya bahwa skripsi yang say
bagian karya orang lain, kecuali yang telah di
pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 12 Janua
Penulis
Erlina Dwi Prasekti
saya tulis ini tidak
disebutkan dalam
LEM
meminta ijin dari sa
mencantumkan nama
ARYA ILMIAH UNTUK KEPENTINGAN A
an di bawah ini, saya mahasiswa Universitas Sa
: Erlina Dwi Prasekti
: 071414052
an ilmu pengetahuan, saya memberikan kepada
Dharma sebuah karya ilmiah yang berjudul:
KOLINEASI DAN ISOMETRI
BIDANG EUCLID DAN BIDANG POINCA
saya memberikan kepada perpustakaan Uni
yimpan, mengalihkan dalam bentuk media lain,
pangkalan
data,
mendistribusikan
secara
di internet atau media lain demi kepentingan
saya maupun memberikan royalty kepada say
a saya sebagai penulis.
an ini saya buat dengan sebenarnya.
vii
ABSTRAK
Erlina Dwi Prasekti, 2012. Kolineasi dan Isometri pada Bidang Euclid dan Bidang Poincaré. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Penelitian ini membahas mengenai kolineasi dan isometri dengan pendekatan metrik. Setelah membaca penelitian ini diharapkan pembaca akan memperoleh wawasan mengenai isometri dan kolineasi.
Penelitian ini menggunakan metode studi pustaka dengan buku acuan utama adalah “Geometry: A Metric Approach with Models” karangan Millman & Parker. Kolineasi dan isometri ditulis dengan menambahkan pembuktian lemma dan teorema serta penambahan penjelasan dan contoh.
Hasil dari penelitian ini adalah: (i) Kolineasi merupakan fungsi bijektif yang mempertahankan garis (ii) Isometri adalah fungsi bijektif yang mempertahankan jarak (iii) Dalam geometri netral jika diketahui suatu fungsi merupakan isometri, maka fungsi tersebut pastilah kolineasi (iv) Dalam geometri netral, jika diketahui fungsi isometri maka akan memenuhi sifat mempertahankan keantaraan, dan mempertahankan ukuran sudut.
viii
ABSTRACT
Erlina Dwi Prasekti, 2012.Collineation and Isometry in Euclidean Plane and Poincaré Plane. Thesis. Mathematics Education Study Program, Mathematics and Science Education Department, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
This research will be talking about collineation and isometry with metric approach. After you read this research, hoping that the reader will get a new knowledge about isometry and collineation.
This research use study methods with “Geometry: A Metric Approach with Models” of Millman & Parker as a mother book. Collineation and isometry written by added the proof of lemmas and theorems with an explanation and an example.
The product of this research are: (i) Collineation is bijective that preserves lines, (ii) Isometry is bijective that preserves distance, (iii) In a neutral geometry, if a function is an isometry, the function must be collineation, (iv) In a neutral geometry, if a function is an isometry then imply preserves betweenness, and preserves angle measure.
ix
KATA PENGANTAR
Puji syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa, yang telah
senantiasa melimpahkan rahmat dan hidayah-Nya sehingga skripsi dengan judul
“Kolineasi dan Isometri pada Bidang Euclid dan Bidang Poincaré” ini dapat penulis
selesaikan.
Segala macam hambatan dan rintangan telah banyak penulis alami selama
menyelesaikan skripsi ini. Akan tetapi semua itu telah penulis lalui dengan adanya
dukungan dari banyak pihak. Untuk itu pada kesempatan ini penulis mengucapkan
terima kasih kepada beberapa pihak, di antaranya:
1. Bapak Dominikus Arif Budi Prasetyo, S.Si.,M.Si., selaku dosen pembimbing
skripsi yang dengan tekun, memberikan bimbingan dan dorongan selama
proses penyusunan skripsi.
2. Bapak Dr. M. Andy Rudhito selaku kaprodi pendidikan matematika,
Universitas Sanata Dharma.
3. Bapak Th. Sugiarto, MT selaku Dosen Pembimbing Akademik yang telah
memberikan bimbingan akademik selama penulis melaksanakan studi di
Universitas Sanata Dharma.
4. Semua dosen pendidikan matematika yang telah memberikan ilmu selama
penulis kuliah di Universitas Sanata Dharma.
6. Kedua orang t
9. Semua pihak y
Kritik dan saran
ini.
x
g tuaku, mas Anto, dan dek Wahyu yang sela
mangat.
an pendidikan matematika angkatan 2007, Dhe
Anggun yang selalu memberi semangat.
an kos, Kiki, Agnes, Ayu, Ane, Nency, Rini ya
k yang telah membantu.
ran yang membangun penulis harapkan untuk
Yogyakarta
rta, 12 januari 2012
Penulis
xi
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR SIMBOL ... xiii
DAFTAR GAMBAR ... xv
BAB I: PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 3
1.3 Batasan Masalah ... 3
1.4 Tujuan Penulisan ... 4
1.5 Manfaat Penulisan ... 4
1.6 Metode Penulisan ... 4
xii
BAB II: LANDASAN TEORI
2.1 Himpunan dan Fungsi ... 6
2.2 Bidang Euclid dan Bidang Poncaré ... 15
2.3 Geometri Abstrak dan Geometri Insidensi ... 20
2.4 Geometri Metrik ... 22
2.5 Keantaraan ... 26
2.6 Segmen Garis dan Sinar Garis ... 29
2.7 Sudut dan Segitiga ... 32
2.8 Aksioma Pembagian Bidang ... 35
2.9 Geometri Pasch ... 37
2.10 Geometri Protraktor ... 41
2.11 Geometri Netral ... 42
2.12 Euclidean Parallel Property ... 46
2.13 Kerangka Berpikir ... 47
BAB III: KOLINEASI DAN ISOMETRI 3.1 Kolineasi dan Isometri ... 48
3.2 Pengaruh Isometri terhadap Ukuran Sudut ... 72
BAB IV: PENUTUP 4.1 Kesimpulan ... 97
4.2 Saran ... 98
xiii
DAFTAR SIMBOL
P, Q, R titik-titik
k, l, m garis-garis
S himpunan titik-titik
L himpunan garis-garis
d(P,Q) jarak antara titik P dan titik Q
dE jarak Euclid
dH jarak Poincaré
int interior
La garis vertikal pada koordinat Kartesius
Lm,b garis nonvertikal pada koordinat kartesius
aL garis tipe I pada bidang Poincaré
cLr garis tipe II pada bidang Poincaré
garis AB
sinar garis AB
segmen garis AB
xiv
∠ABC sudut ABC
ΔABC segitiga ABC
□
ABCD segiempat ABCDsejajar
A Geometri Abstrak
E Bidang Euclid
I Geometri Insidensi
C Bidang Kartesius
H Bidang Poincaré
LE Garis-garis pada bidang Euclid LH Garis-garis pada bidang Poincaré
] akhir definisi
akhir pembuktian
xv
DAFTAR GAMBAR
Halaman Gambar 2.1 Koordinat Kartesius 15
Gambar 2.2 Garis Vertikal pada Bidang Euclid 16
Gambar 2.3 Garis Nonvertikal pada Bidang Euclid 16
Gambar 2.4 Garis 2 17
Gambar 2.5 Garis 2 17
Gambar 2.6 Koordinat untuk Bidang Poincaré 18
Gambar 2.7 Garis Tipe I pada Bidang Poincaré 19
Gambar 2.8 Garis Tipe II pada Bidang Poincaré 19
Gambar 2.9 (a)
Ilustrasi sinar garis dan pada bidang Euclid
Ilustrasi sinar garis dan pada bidang Poincaré
30
30
Gambar 2.13 (a) Gambar 2.13 (b)
Sudut pada Bidang Euclid Sudut pada Bidang Poincaré
33
33
Gambar 2.14 (a) Gambar 2.14 (b)
Segitiga pada Bidang Euclid Segitiga pada Bidang Poincaré
34
34
xvi
Gambar 2.15 (b) Titik pada sisi berlawanan dari garis bidang Euclid 36
Gambar 2.16 Ilustrasi definisi 2.9.1 37
Gambar 2.17 (a)
Gambar 2.19 Ilustrasi teorema 2.1.8 40
Gambar 2.20 (a) Gambar 2.20 (b)
Ilustrasi aksioma ii) dari definisi 2.10.1 Ilustrasi aksioma iii) dari definisi 2.10.1
42
42
Gambar 2.21 Ilustrasi ∆ ∆ berdasarkan definisi 2.11.1 43
Gambar 2.22 Ilustrasi ∆ ∆ berdasarkan aksioma SAS 44
Gambar 2.23 Ilustrasi ∆ ∆ berdasarkan aksioma ASA 45
Gambar 2.24 Ilustrasi ∆ ∆ berdasarkan aksioma SSS 46
Gambar 2.25 Ilustrasi definisi 2.11.6 46
Gambar 3.1 (a) Gambar 3.1 (b)
Inversi/pembalikan pada lingkaran satuan Pencerminan terhadap sumbu-y
55
Titik A, B, C pada contoh 3.1.9 pada koordinat kartesius Titik , , pada koordinat kartesius
72
72
Gambar 3.5 Ilustrasi pembuktian lemma 3.2.1 74
xvii
Gambar 3.6 (b) ∆ akibat , , terhadap A, B, C 76
Gambar 3.7 (a) Gambar 3.7 (b)
Ilustrasi pembuktian lemma 3.2.2 Ilustrasi pembuktian lemma 3.2.2
77
dengan merupakan garis bagi
dengan garis bagi
80
80
Gambar 3.10 (a) Gambar 3.10 (b)
dengan merupakan garis bagi dengan garis bagi
dengan merupakan garis bagi
dengan garis bagi
Gambar 3.13 Ilustrasi pembuktian teorema 3.2.5 86
Gambar 3.14 Ilustrasi pembuktian teorema 3.2.6 87
Gambar 3.15 (a)
Gambar 3.16 Ilustrasi lemma 3.2.8 89
Gambar 3.17 (a) Gambar 3.17 (b)
Ilustrasi pembuktian teorema 3.2.11 Ilustrasi pembuktian teorema 3.2.11
93
xviii
Gambar 3.18 Ilustrasi teorema 3.2.12 94
1
BAB I
PENDAHULUAN
1.1 LATAR BELAKANG
Geometri merupakan konsep yang mulai dikenal orang sejak tahun
3000 SM. Kata Geometri sendiri berasal dari bahasa Yunani, Geometrein ,
yaitu geo: bumi, dan metrein: mengukur (Byer,2010:1).
Studi tentang geometri diawali dengan dua konsep dasar, yaitu
pengertian tentang titik dan garis. pengertian tersebut kemudian dihubungkan
dengan kumpulan aksioma. Aksioma adalah pernyataan dari sifat yang sangat
diperlukan untuk dipelajari tetapi tidak dibuktikan. Selanjutnya ada yang
disebut sebagai model geometri. Model geometri ditentukan dengan himpunan
elemen-elemen yang disebut titik dan kumpulan himpunan bagian dari
himpunan ini yang disebut garis (Millman & Parker, 1991).
Sejak dimulainya era geometri non-Euclides, yang telah dimulai oleh
Girolomo Saccheri (1667-1733), para matematikawan semakin tertarik untuk
membuktikan kecacatan dalam geometri Euclides. Di antaranya adalah
matematikawan Rusia Nicolai Lobachevsky (1792-1856) dan matematikawan
Hungaria Janos Bolyai (1802-1860) yang menemukan geometri hiperbolik.
Kemudian pada pada tahun 1868, Beltrami membuktikan konsistensi geometri
hiperbolik tersebut. (Byer, 2010).
Seorang matematikawan Jerman, David Hilbert (1862-1943)
geometri. Tujuan Hilbert adalah memperluas sistem aksioma Euclides kepada
sesuatu yang telah lengkap dan menunjukkan logika formal yang digunakan
Euclides. Sistem geometri Hilbert merupakan geometri Euclides yang
dibangun berdasarkan kerja Moritz Pasch. Kemudian pada tahun 1932,
seorang matematikawan Amerika, George D. Birkhoff (1884-1944)
mempublikasikan aksioma Euclides dengan suatu perbedaan yang penting
dengan Euclides dan Hilbert. Aksioma Birkhoff sendiri hanya terdiri dari 4
pernyataan dan dapat membuktikan postulat kesejajaran Euclides sebagai
teorema dan dapat dibuktikan. Definisi pada sistem Birkhoff ini yaitu titik,
garis, jarak, dan sudut, dengan konsep keantaraan dibuktikan berdasarkan
konsep dasar jarak. Konsep jarak yang digunakan Birkhoff ini yang kemudian
dikenal sebagai pendekatan metrik. (Byer,2010).
Penelitian yang sudah pernah dilakukan di bidang geometri di
Universitas Sanata Dharma antara lain Geometri Hingga (berisi tentang
berbagai geometri hingga), Geometri Metrik (berisi tentang konsep geometri
metrik yang merupakan penggabungan dari bidang Euclid, bidang Poincare,
bidang Taxicab, dengan dengan fungsi jarak), Model-model Geometri Non
Euclides (berisi tentang model-model geometri non Euclides pada bidang
Euclides. Model geometri non Euclides itu adalah geometri hiperbolik dan
geometri eliptik), Geometri Euclides secara Deduktif Aksiomatis (berisi
tentang geometri Euclides sesuai dengan aksioma Hilbert), Geometri Kabur
(berisi tentang geometri kabur yang berisi titik kabur, jarak kabur, garis kabur,
Transformasi Pada Geometri Euclides (berisi tentang grup transformasi yang
terdiri dari grup dilatasi, grup isometri), dan Konsistensi pada Geometri
Hiperbolik (berisi tentang geometri hiperbolik dan konsistensinya yang
ditunjukkan dengan model konformal dari Poincare). Karena sedikitnya
penelitian di bidang geometri itu, maka penulis tertarik untuk meneliti di
bidang geometri melalui skripsi yang berjudul “KOLINEASI DAN
ISOMETRI PADA BIDANG EUCLID DAN BIDANG POINCARÉ”.
1.2 RUMUSAN MASALAH
Rumusan masalah dalam penelitian ini yaitu:
1. Apa yang dimaksud dengan kolineasi dan isometri?
2. Bagaimana pengaruh isometri terhadap besar sudut?
1.3 BATASAN MASALAH
Pembahasan mengenai kolineasi dan isometri dibatasi pada:
a) Bidang yang digunakan adalah bidang Euclid dan bidang Poincaré.
b) Menggunakan pendekatan metrik. Pendekatan metrik merupakan
pendekatan yang menggunakan konsep jarak yang ditambahkan pada
geometri insidensi.
c) Menggunakan fungsi titik.
d) Garis yang digunakan pada bidang Euclid hanya terbatas pada
1.4 TUJUAN PENULISAN
Tujuan penulisan penelitian ini yaitu:
1. Untuk mengetahui tentang kolineasi dan isometri.
2. Untuk mengetahui pengaruh isometri terhadap besar sudut.
1.5 MANFAAT PENULISAN
a) Bagi Pembaca
Dapat menambah wawasan pembaca mengenai isometri pada
bidang Euclid dan bidang Poincaré dengan pendekatan metrik.
b) Bagi Penulis
Penulis dapat menambah pengetahuan mengenai isometri pada
bidang Euclid dan bidang Poincaré dengan pendekatan metrik.
c) Bagi Universitas
Dapat menambah koleksi skripsi dalam bidang geometri.
1.6 METODE PENELITIAN
Penelitian ini menggunakan metode studi pustaka. Pembahasan tulisan
ini secara keseluruhan diambil dari buku Geometry: A Metric Approach with
Models karangan Richard Millman and Parker.
Langkah-langkah yang dilakukan dalam penelitian ini antara lain:
1) Membaca buku Geometry: A Metric Approach with Models karangan
2) Menyajikan kembali definisi-definisi pada bab Teori Isometri, subbab
Isometri dan Kolineasi.
3) Memberi contoh dari definisi-definisi.
4) Menyajikan kembali teorema-teorema, lemma-lemma, dan
akibat-akibat.
5) Melengkapi bukti teorema-teorema, lemma-lemma, dan akibat-akibat.
6) Memberi contoh dan penjelasan dari teorema-teorema, lemma-lemma,
serta akibat-akibat.
1.7 SISTEMATIKA PENULISAN
Pada bab pertama berupa pendahuluan. Pendahuluan ini berisi tentang
latar belakang masalah, rumusan masalah, batasan masalah, tujuan dan
manfaat serta metode penelitian dan sistematika penulisan.
Bab dua berisi tentang teori-teori yang digunakan dalam mendefinisikan
isometri dan kolineasi, serta definisi-definisi yang digunakan dalam
membuktikan teorema yang dibahas di bab ketiga.
Bab ketiga membahas tentang kolineasi dan isometri. Terdapat
definisi-definisi dan teorema, serta lemma dan akibat terkait dengan kolineasi dan
isometri. Diberikan juga contoh-contoh terkait dengan teorema atau definisi
menggunakan bidang Euclid maupun bidang Poncaré.
Bab keempat atau bab terakhir berisi tentang kesimpulan dari
pembahasan pada bab tiga serta saran yang diberikan penulis kepada pembaca
6
BAB II
LANDASAN TEORI
Konsep dasar dalam geometri adalah gagasan mengenai titik dan gagasan
mengenai garis yang kemudian dihubungkan satu sama lain dengan berbagai
macam aksioma. Sedangkan di sisi lain ada yang disebut sebagai model geometri.
Model geometri merupakan kesatuan matematis yang memenuhi semua aksioma
untuk geometri yang bersangkutan.
2.1 HIMPUNAN DAN FUNGSI
Konsep dasar yang harus dipahami terlebih dahulu sebelum kita
memulai pembahasan mengani geometri adalah konsep tentang himpunan.
Arti dari himpunan sendiri diberikan oleh definisi himpunan berikut.
Definisi 2.1.1 (Devlin,2003:57)
Sebuah himpunan S adalah suatu kumpulan objek yang dapat
didefinisikan secara benar. ]
Jika A merupakan sebuah himpunan, maka objek-objek pada A disebut
sebagai anggota himpunan A atau elemen A. Misalkan x adalah anggota A,
maka bisa kita tuliskan .
Berikut ini merupakan contoh dari himpunan dan anggota himpunan.
Contoh 2.1.1
himpunan semua bilangan real
, menyatakan bahwa x merupakan bilangan real. •
Di antara himpunan-himpunan sendiri terdapat relasi. Berikut
Definisi 2.1.2 (Millman & Parker,1991:4)
Himpunan T adalah himpunan bagian dari S (ditulis ) jika setiap
elemen T juga merupakan elemen S.
Himpunan T sama dengan himpunan S (ditulis ) jika setiap elemen
T di dalam S dan setiap elemen S di dalam T. (Atau jika dan hanya
jika dan ). ]
Definisi 2.1.3 (Millman & Parker,1991:4)
Himpunan kosong adalah himpunan yang tidak memiliki anggota, dan
dinotasikan dengan ∅. Catatan: ∅⊂ S untuk setiap himpunan S. ]
Definisi 2.1.2 dan definisi 2.1.3 menyatakan jika terdapat dua
himpunan maka:
a) Himpunan bagian, berarti setiap anggota himpunan pertama
merupakan anggota himpunan yang kedua, tetapi tidak sebaliknya.
b) Sama dengan, artinya untuk setiap anggota himpunan pertama
merupakan anggota himpunan himpunan yang pertama dan setiap
anggota himpunan kedua merupakan anggota himpunan yang pertama.
c) Himpunan kosong, artinya himpunan yang tidak memiliki anggota.
Sebagai contoh himpunan kosong misalnya himpunan bilangan prima
yang kurang dari dua.
Dari definisi 2.1.2 di atas diketahui juga bahwa jika T himpunan
bagian dari S dan T serta S merupakan himpunan berhingga, maka elemen
T jumlahnya kurang dari atau sama dengan elemen S.
Contoh 2.1.2
C = himpunan semua bilangan cacah antara 0 dan 5
A = himpunan semua bilangan asli yang kurang dari 5
B = himpunan semua bilangan bulat
Jika ditulis dengan cara mendaftar anggota himpunan, dapat ditulis
sebagai:
C = {1,2,3,4}
A = {1,2,3,4}
B = {…,-4,-3,-2,-1,0,1,2,3,…}
Dapat diketahui bahwa:
dan serta .
Artinya, C adalah himpunan bagian dari B, karena anggota dari C, yaitu
1,2,3,4 juga merupakan anggota dari B, atau 1,2,3,4∈B.
Himpunan A merupakan himpunan bagian dari B karena anggota A yaitu
1,2,3,4 juga merupakan anggota B, atau 1,2,3,4∈B.
Himpunan C sama dengan A karena 1,2,3,4∈C dan 1,2,3,4∈A. •
Selanjutnya akan diberikan definisi operasi dua himpunan.
Definisi 2.1.4 (Millman & Parker,1991:4)
Gabungan dari dua himpunan A dan B adalah himpunan
| .
Irisan dari dua himpunan A dan B adalah himpunan
Selisih dua himpunan A dan B dalah himpunan
| . ]
Definisi 2.1.4 mengatakan bahwa jika diketahui dua himpunan maka:
a) Gabungan dua himpunan, merupakan himpunan hasil dari
penggabungan elemen-elemen kedua himpunan.
b) Irisan dua himpunan adalah, himpunan dari elemen kedua himpunan
yang merupakan anggota himpunan pertama sekaligus anggota
himpunan kedua.
c) Selisih dua himpunan, dalam hal ini selisih himpunan pertama dan
himpunan kedua, yaitu himpunan dari elemen-elemen himpunan
pertama yang tidak merupakan elemen himpunan kedua.
Untuk lebih memahami definisi 2.1.4, perhatikan contoh 2.1.3 beikut.
Contoh 2.1.3
Diketahui A = {3,5,7} dan B = {1,2,3}
1,2,3,5,7 ; 3 ; 5,7
Gabungan himpunan A dan B adalah 1,2,3,5,7 karena 1,2,3,5,7
merupakan anggota A atau anggota B.
Irisan himpunan A dan B adalah 3 karena 3 dan 3 .
Selisih himpunan A dan B adalah 5 dan 7 karena 5,7 dan 5,7 •
Setelah pembahasan mengenai himpunan, selanjutnya akan dibahas
mengenai fungsi.
Antara dua himpunan terdapat suatu relasi khusus yang memasangkan
tiap-tiap elemen himpunan pertama tepat satu ke elemen-elemen himpunan
Definisi 2.1.5 (Giaquinta&Modica,2003:30)
Misalkan A, B adalah dua himpunan. Fungsi atau peta atau transformasi
: adalah relasi atau aturan yang memasangkan masing-masing
ke tepat satu titik pada B. ]
Diberikan : , untuk setiap kita memiliki cara untuk
memasangkan . Kita katakan bahwa adalah variabel terikat
dan adalah variabel bebas, dan kita tulis sebagai .
Untuk mendefinisikan suatu fungsi, terdapat tiga hal pokok, yaitu
domain A, codomain B, dan aturan yang memasangkan titik-titik
pada A ke titik-titik pada B.
Berikut diberikan definisi mengenai bayangan fungsi.
Definisi 2.1.6 (Millman & Parker,1991:10)
Jika : adalah fungsi, maka bayangan f adalah
| ]
Fungsi sendiri dapat diklasifikasikan menjadi tiga jenis, yaitu fungsi
surjektif, injektif, dan bijektif. Pengertian masing-masing fungsi tersebut
dapat dilihat dari definisi berikut.
Definisi 2.1.7 (Millman & Parker,1991:10)
Fungsi : disebut surjektif jika untuk setiap ada
dengan . ]
Definisi 2.1.7 mengatakan bahwa suatu fungsi dikatakan surjektif bila
setiap anggota codomain dari fungsi f pastilah memiliki kawan pada
Untuk lebih memahami definisi 2.1.7, perhatikan contoh 2.1.4 berikut.
Contoh 2.1.4
Terdapat fungsi : yang dinyatakan oleh merupakan
fungsi surjektif.
Bukti: Untuk menunjukkan bahwa f surjektif harus ditunjukkan bahwa
untuk setiap Range ada sebuah Domain dengan
. Oleh karena itu, kita harus menunjukkan bahwa persamaan
2‐1
memiliki penyelesaian untuk setiap nilai t . Karena untuk setiap bilangan
real memiliki akar kuadrat, kita dapatkan persamaan √ . Karena
kodomainnya merupakan bidlangan real positif, maka hanya digunakan
√ . Maka, √ .
Karena terdapat satu nilai Domain untuk setiap ,
maka akibatnya, f surjektif. •
Berikut diberikan definisi fungsi injektif.
Definisi 2.1.8 (Devlin,2003:32)
Fungsi : disebut injektif jika , , , sehingga
kita juga mendapatkan . Pernyataan tersebut ekuivalen dengan,
fungsi : injektif jika untuk setiap dua titik yang berbeda , ,
kita peroleh . ]
Definisi 2.1.7 menyatakan bahwa fungsi dikatakan injektif:
a) Jika dua anggota range fungsi bernilai sama, maka keduanya berasal
b) Jika dua anggota domain berbeda maka akan ada dua anggota range
yang berbeda yang merupakan hasil dari domain tersebut.
Untuk lebih memahami definisi 2.1.8, perhatikan contoh 2.1.5 berikut.
Contoh 2.1.5
Fungsi : 0 oleh 3 merupakan fungsi injektif.
Bukti:
Kita asumsikan sehingga 3 3 .
Kita selesaikan persamaan 3 3
1 2
1 2
2 2
Karena diketahui dan diperoleh , akibatnya f
injektif. •
Suatu fungsi dapat bersifat injektif atau surjektif. Namun, dapat pula
memiliki sifat keduanya, atau injektif dan surjektif sekaligus. Fungsi yang
seperti itu disebut bijektif. Berikut diberikan definisi fungsi bijektif.
Definisi 2.1.9 (Millman & Parker,1991:12)
Fungsi : disebut bijektif jika adalah injektif dan surjektif
sekaligus. ]
Definisi 2.1.9 menyatakan bahwa suatu fungsi dikatakan bijektif
apabila fungsi tersebut injektif dan juga surjektif. Untuk lebih memahami
Contoh 2.1.6
Suatu fungsi : oleh 7 12 merupakan fungsi bijektif.
Bukti:
Untuk menunjukkan bahwa h bijektif, kita harus menunjukkan bahwa h
injektif dan h surjektif.
• Untuk menunjukkan bahwa h surjektif kita harus menunjukkan bahwa
untuk setiap Range ada sebuah Domain dengan
. Oleh karena itu, kita harus menunjukkan bahwa persamaan
7 12 memiliki penyelesaian untuk setiap harga t.
7 12 . Untuk setiap bilangan real t , pastilah ada s
yang memenuhi persamaan itu, sehingga.
7 12 7 712 12
Karena setiap Range berkawan dengan tepat satu
Domain , jadi dapat disimpulkan bahwa h surjektif.
• Kita asumsikan sehingga 7 12 7 12.
Kemudian kita selesaikan persamaan tersebut.
7 12 7 12
7 12 12
7
Dari kita peroleh , akibatnya h injektif.
• Karena h surjektif dan h injektif sekaligus, maka h bijektif. •
Definisi 2.1.10 (Millman & Parker,1991:12)
Jika : , : , dan , maka komposisi dan
adalah fungsi : yang diberikan oleh . ]
Untuk memahami tentang komposisi fungsi, perhatikan contoh 2.1.7
berikut.
Contoh 2.1.7
Suatu fungsi : dan : oleh 5 dan .
Maka 5 5 25 .
Sehingga komposisi fungsi dan adalah 25 . •
Setelah memahami tentang komposisi fungsi, berikut diberikan
definisi mengenai invers fungsi.
Definisi 2.1.11 (Millman & Parker,1991:13)
Jika : adalah fungsi bijektif, maka invers f adalah fungsi :
yang didefinisikan oleh , di mana s adalah anggota tertentu
dalam S dengan . ]
Fungsi g dalam definisi 2.1.11 biasanya dinotasikan dengan f -1(notasi
invers fungsi f).
Untuk lebih memahami mengenai invers fungsi, perhatikan contoh
2.1.8 berikut ini.
Contoh 2.1.8
Diketahui fungsi : oleh 2 5. Invers dari adalah
Misalkan diambil 1 1 3 . 3 3 6 5
1 . Secara umum . . •
Definisi 2.1.11, juga mengartikan bahwa jika suatu fungsi memiliki
invers maka fungsi tersebut merupakan fungsi bijektif. Fungsi pada contoh
2.1.8 merupakan fungsi bijektif, karena memiliki invers.
2.2 BIDANG EUCLID DAN BIDANG POINCARE
Bidang Euclid atau yang biasa dikenal dengan bidang kartesius
merupakan bidang dengan koordinat x-aksis dan y-aksis. Bidang kartesius
dapat digambarkan sebagai berikut. (Byer,2010:159).
Gambar 2.1 Koordinat Kartesius
Gambar 2.1 menggambarkan mengenai koordinat kartesius.
Koordinat kartesius ini terdiri salib sumbu yaitu sumbu-x dan sumbu-y
yang berpotongan di titik O(0,0).
Terdapat empat kuadran, yaitu kuadran I, kuadran II, kuadran III, dan
kuadran IV. Kuadran I merupakan daerah yang dibatasi oleh sumbu x
positif dan y positif sehingga koordinat di kuadran I ditulis sebagai A(x,y). x
y
(x,y) (-x,y)
(-x,-y) (x,-y)
kuadran II merupakan daerah yang dibatasi oleh sumbu x negatif dan y
positif. kuadran III merupakan daerah yang dibatasi oleh sumbu x negatif
dan sumbu y negatif. Di kuaran IV yang dibatasi oleh sumbu y negatif dan
sumbu x positif.
Misalkan S = = , | , . Didefiniskan himpunan garis-garis
lurus sebagai berikut:
• La = , | , dengan a adalah bilangan real tertentu.
• Lm,b = , | , dengan m dan b adalah bilangan
real tertentu.
Himpunan semua garis pada bidang Euclid dinotasikan dengan LE.
Berikut diberikan ilustrasi garis-garis pada bidang Euclid.
Gambar 2.2 Garis vertikal Gambar 2.3 Garis non-vertikal
Model C = { , LE} disebut Bidang Kartesius. Notasi La dan Lm,b menunjukkan garis pada bidang Kartesius.
Untuk lebih memahami tentang garis-garis pada bidang Euclid,
perhatikan contoh berikut ini.
b
y = mx + b
Lm,b
Contoh 2.2.1
Titik A(2,5), B(2,-3), dan C(-2,-1) merupakan titik-titik pada bidang
Euclid. Persamaan garis yang melalui A dan B adalah 2. Garis yang
melalui A dan B ini ditunjukkan oleh gambar 2.3.
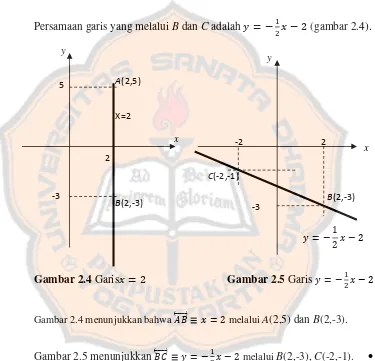
Persamaan garis yang melalui B dan C adalah 2 (gambar 2.4).
Gambar 2.4 Garis 2 Gambar 2.5 Garis 2
Gambar 2.4 menunjukkan bahwa 2 melalui A(2,5) dan B(2,-3).
Gambar 2.5 menunjukkan 2 melalui B(2,-3), C(-2,-1). •
Selain bidang kartesius, ada pula model lain yang juga digunakan
disini, yaitu bidang Poincaré. Bidang Poincaré merupakan bidang yang
dibatasi oleh sumbu x dan sumbu y positif. Bidang Poincaré ini
digambarkan oleh gambar 2.6 berikut.
Gambar 2.6 Koordinat untuk bidang Poincaré
Gambar 2.6 menunjukkan koordinat Poincaré yang dibatasi oleh sumbu x
dan sumbu y positif. terlihat bahwa sumbu x merupakan garis putus-putus,
yang menandakan bahwa koordinat dengan 0 tidak digunakan.
Misalkan S = = , | 0 . Ada dua tipe garis pada bidang
Poincaré, yaitu:
9 Garis tipe I : aL = , |
9 Garis tipe II: cLr = , | , dimana c dan
r adalah bilangan real tertentu dengan 0. Dengan,
2
dan
Himpunan semua garis pada bidang Poincaré dinotasikan dengan LH. y
Berikut merupakan ilustrasi dari garis-garis pada bidang Poincaré.
Gambar 2.7 Garis tipe I Gambar 2.8 Garis tipe II
Gambar 2.7 merupakan gambar garis tegak pada bidang Poincaré dengan
persamaan . Sedangkan gambar 2.8 merupakan gambar garis
melengkung dengan persamaan . Dalam bidang
Poincaré hanya memiliki dua jenis garis tersebut.
Selanjutnya model H = { , LH} disebut Bidang Poincaré. Notasi aL dan
cLr menunjukkan garis-garis pada H .
Untuk lebih memahami mengenai garis-garis pada bidang Poincaré,
perhatikan contoh 2.2.2 berikut ini.
Contoh 2.2.2
Misalkan titik A(2,4), B(2,1), dan C(4,3) merupakan titik-titik pada bidang
Poincaré. Terdapat garis yang melalui A dan B serta melalui B dan C.
Persamaan garis yang melalui A dan B adalah 2. Atau bisa ditulis 2L
(gambar 2.8 (a)).
aL
c r
cLr
Persamaan garis yang melalui B dan C adalah:
Gambar 2.9 (a) menunjukkan ilustrasi garis 2L yang melalui titik A(2,4)
dan B(2,1) sedangkan (b) mengilustrasikan garis 5L√10 yang melalui titik
B(2,1), dan C(4,3) pada bidang Poincare. •
Bidang Euclid dan bidang Poincaré ini yang akan dipakai dalam
pembahasan di dalam skripsi ini.
2.3 GEOMETRI ABSTRAK DAN GEOMETRI INSIDENSI
Geometri abstrak merupakan dasar dari model-model geometri lain
yang akan dibahas. Definisi dari geometri abstrak didasarkan pada titik
Definisi 2.3.1 (Millman & Parker,1991:17)
Geometri abstrak A terdiri dari himpunan S, yang anggota-anggotanya
disebut titik, himpunan L yang anggota-anggotanya berasal dari
himpunan bagian tak kosong dari S, yang disebut garis, sehingga:
i. Untuk setiap dua titik A, B ∈ S terdapat sebuah garis l ∈ L
dengan A ∈ l dan B ∈ l.
ii. Setiap garis mempunyai sekurang-kurangnya dua titik. ]
Selanjutnya, Geometri Abstrak dinotasikan dengan {S , L }.
Dari Definisi 2.2.1 dapat diketahui bahwa aksioma pertama dari
geometri abstrak mengatakan bahwa setiap sepasang titik terletak pada
sebuah garis. Tetapi harus diingat bahwa kata garis yang dimaksud disini
bukan hanya garis lurus. Garis disini adalah anggota dari himpunan L .
Sedangkan aksioma kedua merupakan kebalikan dari aksioma kedua.
Aksioma kedua ini mengatakan bahwa sebuah garis terbentuk oleh
miniman dua titik.
Setelah kita membahas mengenai Geometri Abstrak, selanjutnya kita
akan membahas mengenai Geometri Insidensi.
Definisi 2.3.2 (Millman & Parker,1991:22)
Sebuah Geometri Abstrak {S , L } adalah Geometri Insidensi jika:
(i) Setiap dua titik yang berbeda dalam S , terletak pada sebuah garis
(ii)Terdapat tiga titik A, B, C ∈ S yang tidak semuanya terletak pada
sebuah garis yang sama. ]
Selanjutnya Geometri Insidensi dinotasikan dengan {S , L }.
Aksioma pertama pada Definisi 2.3.2 merupakan aksioma yang sama
yang membentuk Definisi 2.3.1. Aksioma kedua dari geometri insidensi
mengatakan tentang jika terdapat tiga titik maka ketiga titik tersebut tidak
segaris.
2.4 GEOMETRI METRIK
Di dalam geometri metrik, konsep jarak merupakan konsep yang
natural. Secara intuitif, jarak merupakan sebuah fungsi yang dapat
dinotasikan sebagai , .
Secara formal, definisi fungsi jarak disajikan sebagai berikut.
Definisi 2.4.1 (Millman & Parker,1991:28)
Fungsi jarak pada sebuah himpunan S adalah fungsi d : S × S →
untuk semua P, Q ∈S berlaku:
(i) , 0
(ii) , 0 jika dan hanya jika
(iii) , , ]
Fungsi jarak ini yang kemudian akan menjadi dasar untuk
mendefinisikan Geometri metrik. Sebelum kita membahas mengenai
definisi geometri metrik, sebaiknya kita ketahui lebih dahulu mengenai
Definisi 2.4.2 (Fitting,1996:139)
Jarak antara titik , dan , diberikan oleh:
atau
`]
Selanjutnya, jarak pada bidang Euclid (Jarak Euclid) dilambangkan
dengan sehingga , ,
Selanjutnya juga akan didefinisikan jarak pada bidang Poincaré.
Definisi 2.4.3 (Millman & Parker,1991:28)
Jika , dan , adalah titik-titik pada bidang Poincaré
H , maka jarak Poincaré (dH) diberikan oleh
,
, jika
, jika P dan Q berada pada
]
Dari definisi 2.4.2 dan definisi 2.4.3 diketahui bahwa baik bidang
Euclid maupun bidang Poincaré pastilah memiliki fungsi jarak, artinya
setiap sepasang titik pastilah memiliki jarak.
Contoh 2.4.1
Misalkan titik P(2,5) dan Q(3,7) merupakan titik-titik pada bidang
Kartesius. Jarak kartesius antara P dan Q yaitu:
,
, 2 3 5 7
, √5
Jadi, jarak titik P dan Q pada bidang Euclid adalah , √5 satuan
jarak. •
Contoh 2.4.2 berikut merupakan contoh jarak Poincarépada definisi 2.4.3
Contoh 2.4.2
Misalkan titik-titik P(2,1) dan Q(4,3) merupakan titik-titik pada bidang
Poincaré. P dan Q berada pada cLr , dengan c = 5 dan r = √10 . Maka jarak
titik P dan titik Q adalah ,
,
2 5 √10 4 4 5 √10
3
9 3√10 4 4√10
9 3√10 4 4√10
Jadi, jarak titik P dengan titik Q pada bidang Poincaré adalah ,
9 3 10
Selanjutnya diberikan definisi mengenai sistem koordinat yang akan
berkaitan dengan pendefinisian mengenai geometri metrik.
Definisi 2.4.4 (Millman & Parker,1991:30)
Misalkan l adalah sebuah garis pada Geometri Insidensi {S , L }.
Asumsikan bahwa ada fungsi jarak d pada S . Fungsi : adalah
ruler/sistem koordinat untuk l,jika memenuhi:
i) f adalah fungsi bijektif
ii) untuk setiap pasangan titik P dan Q pada l berlaku
| | , (4-1)
Persamaan (4-1) disebut Persamaan Sistem Koordinat dan disebut
koordinat P dengan fungsi koordinat f. ]
Definisi 2.4.4 mengatakan bahwa suatu fungsi f merupakan ruler
apabila f bijektif dan terdapat fungsi jarak | | , .
Dari definisi 2.3.2 , definisi 2.4.1, dan definisi 2.4.4, dapat diperoleh
sistem geometri yang baru, yaitu geometri metrik. Berikut diberikan
definisi mengenai definisi geometri metrik.
Definisi 2.4.5 (Millman & Parker,1991:30)
Geometri Insidensi {S , L } bersama dengan fungsi jarak d memenuhi
Postulat Sistem Koordinat jika setiap garis l ∈ S memiliki sistem
koordinat. Dalam kasus ini kita katakan M = {S , L , d} adalah
Dari definisi 2.4.5, dapat ditarik kesimpulan bahwa suatu sistem
geometri disebut geometri metrik jika memenuhi syarat sebagai berikut:
1) Merupakan geometri insidensi;
2) Terdapat fungsi jarak d; dan
3) Memenuhi postulat sistem koordinat/ruler
2.5 KEANTARAAN
Konsep tentang sebuah titik yang berada di antara dua titik lainnya
merupakan konsep yang sangatlah penting. Tanpa mengetahui definisi
tentang keantaraan akan tidak mungkin untuk menghasilkan bukti. Disini
konsep mengenai fungsi jarak diperlukan untuk mendefinisikan
keantaraan.
Selanjutnya keantaraan akan membantu kita untuk mendefinisikan
bentuk-bentuk dasar seperti segmen, sinar, sudut, dan segitiga.
Definisi 2.5.1 (Millman & Parker,1991:47)
Titik B berada di antara A dan C jika A, B, C adalah jarak titik-titik yang
segaris pada geometri metrik {S , L , d} dan jika
, , , (5-1)
]
Definisi 2.5.1 mengatakan bahwa jika ada tiga titik, yaitu A, B, dan C
maka titik B dikatakan berada di antara A dan C bila memenuhi syarat:
1) Titik A, B, dan C terletak pada haris yang sama/segaris, dan
2) Jumlahan antara jarak A dan B dengan jarak B dan C sama dengan
jarak A dan C atau bisa ditulis , , , .
(i) A – B – C berarti B berada di antara A dan C
(ii) AB menyatakan jarak ,
Sehingga berdasarkan notasi di atas, persamaan (5-1) menjadi
, sehingga untuk setiap titik-titik segaris berlaku:
jika dan hanya jika
Untuk memahami tentang keantaraan, contoh 2.5.1 akan memperjelas
tentang keantaraan.
Contoh 2.5.1
Misalkan titik-titik A(1,0) , B(1,4) , C(1,8) merupakan titik-titik pada
bidang Euclid dengan .
Jarak Euclid ditentukan oleh , .
, 1 1 0 4 √16 4
, 1 1 0 8 √64 8
, 1 1 4 8 √16 4
4 4 8. Dari perhitungan diketahui bahwa 8. Karena 8 8, maka . Sehingga dapat disimpulkan bahwa
A – B – C. •
Berikut diberikan teorema tentang keantaraan. Bahwa jika terdapat 3
titik, misalnya titik A, B, dan C dan jika B terletak diantara A dan C maka
Teorema 2.5.1 (Millman & Parker,1991:51)
Titik-titik A, B, C adalah titik-titik yang segaris pada geometri metrik {S ,
L , d}. Jika maka .
Bukti:
Misalkan A, B, C adalah titik-titik tertentu dan segaris. Karena ,
maka berarti . Berdasarkan definisi 2.4.1 maka PQ = QP
untuk semua P dan Q. Sehingga kita dapatkan: . Karena
sifat komutatif dalam penjumlahan maka , sehingga
. Berdasarkan definisi 2.5.1 kita
peroleh .
Teorema 2.5.1 menyatakan bahwa bila B berada di antara A dan C
berarti juga bahwa B juga berada di antara C dan A. Artinya letak tidak
mempengaruhi, yang terpenting adalah jaraknya tetap.
(a) (b)
Gambar 2.10 Ilustrasi Pembuktian teorema 2.5.1
Gambar 2.10 (a) merupakan ilustrasi sedangkan gambar 2.10
(b) merupakan ilustrasi . Dari gambar 2.10 (a) dan (b) terlihat
bahwa B tetap terletak di antara A dan C meskipun letak A dan C berubah,
tapi jarak A dan C ke B tetap sama.
A B C
C B
2.6 SEGMEN GARIS DAN SINAR GARIS
Notasi garis merupakan bagian penting dalam geometri. Pada bagian
ini kita akan membahas mengenai bagian dari garis, yaitu segmen garis
dan sinar garis. Bagian ini penting untuk pembahasan selanjutnya
mengenai sudut dan segitiga.
Definisi 2.6.1 (Millman & Parker,1991:52)
Jika A dan B adalah titik-titik tertentu dalam geometri metrik {S , L , d},
maka segmen garis dari A ke B adalah himpunan
| ]
Definisi 2.6.1 berbicara tentang segmen garis. segmen garis
merupakan ruas garis yang ditarik dari satu titik ke titik tertentu yang lain.
Sebuah segmen garis pastilah mempunya titik-titik ujung darimana
segmen itu terbentuk. Selain itu, karena segmen terbentuk dari dua titik
yang berbeda, pastilah ia memiliki jarak. Jarak inilah yang kemudian akan
disebut sebagai panjang segmen.
Berikut diberikan definisi titik ujung dan panjang segmen.
Definisi 2.6.2 (Millman & Parker,1991:54)
Titik ujung dari segmen garis adalah A dan B. Panjang segmen garis
adalah , . ]
Dari definisi 2.6.1 dan 2.6.2 dapat disimpulkan bahwa memiliki
titik A dan titik B sebagai titik-titik ujung dan memiliki panjang.
Gambar 2.11 Segmen garis A
Gambar 2.11 menunjukkan dengan titik-titik ujungnya adalah titik A
dan titik B dengan panjang segmen , .
Selain segmen garis, bagian dari garis yang lain adalah sinar garis.
Berikut diberikan definisi tentang sinar garis.
Definisi 2.6.3 (Millman & Parker,1991:54)
Jika A dan B adalah titik-titik tertentu dalam geometri metrik {S , L , d},
maka sinar dari A menuju B adalah himpunan
| ]
Sinar garis hanya memiliki satu titik ujung, dan ujung yang lain adalah
di jauh tak hingga. Sehingga dikatakan bahwa sinar garis memiliki ujung
tapi tidak memiliki pangkal.
Berikut diberikan ilustrasi sinar garis pada bidang Euclid dan bidang
Poincaré, untuk lebih memudahkan dalam memahami tentang sinar garis.
(a) (b)
Gambar 2.12 Sinar Garis
Gambar 2.12 (a) merupakan ilustrasi dari sinar garis dan pada
bidang Euclid. Gambar 2.12 (b) merupakan ilustrasi dari sinar garis A
D
C B
D
C B
dan pada bidang Poincare. memiliki ujung di A tetapi tidak
memiliki pangkal.
Salah satu topik dalam geometri adalah kongruensi. Pembahasan
mengenai kongruensi sering dikaitkan dalam pembahasan mengenai
segitiga. Berikut diberikan definisi mengenai kongruensi.
Definisi 2.6.4 (Millman & Parker,1991:56)
Dua segmen garis dan dalam geometri metrik dikatakan kongruen
(ditulis ) jika panjang keduanya sama; atau dapat ditulis:
jika ]
Definisi 2.6.4 mengatakan bahwa jika dua segmen garis memiliki
panjang yang sama, maka kedua segmen garis tersebut kongruen. Untuk
lebih memahami definisi 2.6.4, perhatikan contoh berikut.
Contoh 2.6.1
Misalkan A(0,2), B(0,1) , P(0,4), Q(7,3), dapat ditentukan satu nilai
sehingga .
Bukti:
¾ Dalam bidang Kartesius
jika (2-1)
0 7 4 3 √49 1 √50
Karena maka kita misalkan 0,
Sehingga, 2
2 √50
2 50
2 √50
Sehingga koordinat titik C adalah (0, 2 √50)
¾ Dalam bidang Poincaré
jika
Pertama-tama harus dicari jarak P ke Q pada bidang Poincaré.
Titik P dan Q terletak pada 3L5 sehingga,
, ln 6.
Karena C = (0,y) dan A = (0,2), maka C berada pada garis tipe I
sehingga , ln .
Karena maka sehingga ln ln 6.
Akibatnya, 6 atau .
Menghasilkan 12 atau .
Karena maka kita ambil nilai sehingga 0, . •
2.7 SUDUT DAN SEGITIGA
Pada bagian ini kita akan membahas sudut dan segitiga dalam ranah
geometri metrik. Definisi mengenai sudut dan segitiga menggunakan
konsep keantaraan. Sudut memuat dua sinar garis yang tidak segaris tetapi
memiliki satu titik yang sama.
Definisi 2.7.1 (Millman & Parker,1991:59)
Jika A, B, dan C adalah titik-titik yang tidak segaris dalam geometri
metrik maka sudut merupakan himpunan
]
Definisi 2.7.1 mengatakan bahwa sudut dibentuk dari tiga titik yang
tidak segaris, dimana setiap dua titik akan membentuk satu sinar garis,
sehingga terdapat satu titik yang sama yang membentuk kedua sinar garis
itu.
Sudut pada bidang Euclid dan bidang Poincaré diilustrasikan oleh gambar
2.1.2 berikut ini.
(a) (b)
Gambar 2.13 Sudut
Gambar 2.13 (a) merupakan ilustrasi sudut pada bidang Euclid,
sedangkan (b) merupakan ilustrasi sudut pada bidang Poincaré. Dapat
dilihat bahwa baik itu pada bidang Euclid maupun bidang Poincaré,
dibentuk oleh sinar garis dan sinar garis dimana tidak segaris
dengan dan memiliki satu titik yang sama yaitu titik B. B
A
C
B
A
Setelah pembahasan mengenai sudut, selanjutnya kita akan membahas
mengenai segitiga. Berikut diberikan definisi segitiga. Definisi tentang
segitiga berikut menggunakan konsep tentang segmen garis.
Definisi 2.7.2 (Millman & Parker,1991:61)
Jika , , adalah titik-titik yang tidak segaris dalam geometri metrik
maka segitiga ABC adalah himpunan
]
Definisi 2.7.2 mengatakan bahwa segitiga dibentuk dari tiga sinar
garis dimana setiap dua sinar garis memiliki satu titik yang sama
sedemikian hingga ketiga titik tidak segaris. Segitiga pada bidang Euclid
dan bidang Poincaré ditunjukkan pada gambar 2.13 berikut.
(a) (b)
Gambar 2.14 Segitiga
Gambar 2.14 (a) menunjukkan segitiga pada bidang Euclid dan
gambar 2.14 (b) menunjukkan ilustrasi segitiga pada bidang Poincaré.
Perhatikan kedua gambar. dibentuk oleh tiga segmen garis yaitu,
memiliki satu titik yang sama, yaitu titik B. Sehingga didapat tiga titik
yang berbeda, yaitu titik A, B, dan C yang tidak segaris.
2.8 AKSIOMA PEMBAGIAN BIDANG
Aksioma Pembagian Bidang (Plane Separation Axiom/PAS)
merupakan ide yang sangat intuitif dimana setiap garis memiliki dua sisi
yang dibatasi oleh sebuah garis. Berikut ini akan dibahas mengenai PAS.
Definisi 2.8.1 (Millman & Parker,1991:63)
Misalkan {S , L , d} adalah geometri metrik dan misalkan S1⊂S . S1
disebut konveks jika untuk setiap dua titik P, Q ∈ S 1, segmen garis
adalah himpunan bagian dari S1. ]
Definisi tersebut mengungkapkan bahwa segmen garis di antara setiap
dua titik dalam S 1 juga pada S 1, tidak hanya sebagian. Untuk
menunjukkan bahwa sebuah himpunan merupakan konveks kita harus
menunjukkan bahwa untuk setiap bagian titik-titik dalam himpunan S ,
segmen yang mengikutinya juga dalam himpunan S . Untuk menunjukkan
sebuah himpunan bukan konveks, kita cukup membuktikan bahawa bagian
titik-titik bersama dengan segmen yang dihasilkan tidak seluruhnya
termuat dalam himpunan S .
Berikut ini diberikan definisi PSA yang memenuhi definisi konveks.
Definisi 2.8.2 (Millman & Parker,1991:64)
Geometri metrik {S , L , d} memenuhi aksioma pembagian bidang
(plane separation axiom/PSA) jika untuk setiap l ∈ L terdapat dua
(i) S – l = H1∪ H2
(ii) H1 dan H2 berbeda dan masing-masing merupakan konveks
(iii)Jika A ∈ H1 dan B ∈ H2 maka ]
Definisi 2.8.2 mengartikan bahwa garis l memiliki dua sisi (H1 dan
H2) dimana keduanya merupakan konveks.
Definisi 2.8.3 (Millman & Parker,1991:66)
Misalkan {S , L , d} merupakan geometri metrik yang memenuhi PSA,
misalkan l ∈L , dan misalkan H1 dan H2 adalah setengah bidang yang ditentukan oleh l. Dua titik A dan B berada pada sisi yang sama dari l jika
keduanya termasuk dalam H1 atau keduanya termasuk dalam H2. A dan B
berada pada sisi yang berlawanan terhadap l jika salah satunya termasuk
dalam H1 dan sisi yang lain termasuk dalam H2. Jika A ∈ H1, kita katakan
bahwa H1 adalah sisi l yang memuat A. ]
(a) (b)
Gambar 2.15 Ilustrasi definisi 2.8.3 A
B
A B
l
Gambar 2.15 (a) menunjukkan dua titik pada sisi yang sama dari garis
tipe II pada bidang Poincaré , sedangkan gambar 2.15 (b) menunjukkan
dua titik pada sisi berlawanan pada garis pada bidang Euclid.
2.9 GEOMETRI PASCH
Geometri Pasch dikemukakan oleh Morris Pash. Geometri Pasch
merupakan geometri metrik yang memenuhi postulat Pasch dan aksioma
pembagian bidang.
Definisi 2.9.1 (Millman & Parker,1991:75)
Geometri Metrik memenuhi Postulat Pasch (PP) jika untuk sembarang
garis l, sembarang , dan sembarang titik D ∈ l sedemikian hingga
, maka atau . ]
Untuk lebih memudahkan memahami definisi 2.9.1, perhatikan
gambar berikut yang merupakan ilustrasi definisi 2.9.1.
Gambar 2.16 Ilustrasi definisi 2.9.1
Gambar 2.1.6 merupakan dimana terdapat titik D yang terletak
diantara A dan B. D merupakan titik potong garis l dengan segmen .
Jika garis l diperpanjang sampai tak hingga, maka l akan memotong di
satu titik tertentu.
C
l
B D
Berikut ini diberikan definisi geometri Pasch. Geometri metrik yang
memenuhi aksioma pembagian bidang merupakan geometri Pasch.
Definisi 2.9.2 (Millman & Parker,1991:76)
Geometri Pasch adalah geometri metrik yang memenuhi PSA. ]
Berikut akan disajikan definisi mengenai interior dari sinar dan
segmen garis.
Definisi 2.9.3 (Millman & Parker,1991:82)
Interior dari sinar garis dalam geometri metrik adalah himpunan
Interior dari segmen garis dalam geometri metrik adalah himpunan
, ]
Untuk lebih memahami definisi 2.9.3, perhatikan gambar berikut.
(a) (b)
Gambar 2.1.7 Ilustrasi Definisi 2.9.3
Gambar 2.1.7 merupakan ilustrasi dari definisi 2.9.3. Gambar 2.1.7 (a)
merupakan ilustrasi interior sinar . Interior dari adalah tanpa
titik A. gambar 2.1.7 (b) merupakan ilustrasi segmen . Interior
adalah tanpa titik-titik A dan B. Artinya titik-titik ujung dari segmen
garis bukan merupakan anggota interior segmen garis. A
A
Setelah pembahasan mengenai interior sinar garis dan segmen garis,
berikut ini akan dibahas mengenai interior sudut. Untuk memahami
definisi interior sudut, ingat kembali definisi mengenai aksioma
pembagian bidang. Berikut definisi interior sudut.
Definisi 2.9.4 (Millman & Parker,1991:83)
Dalam geometri Pasch, interior dari (ditulis int( )), adalah
perpotongan sisi yang memuat C dengan sisi yang memuat A. ]
Definisi 2.9.4 akan mengatakan tentang interior sebuah sudut. Interior
sudut merupakan sudatu daerah yang dibatasi oleh dua sinar garis yang
membentuk sudut tersebut. Untuk memahami definisi 2.9.4, perlu diingat
kembali tentang aksioma pembagian bidang/PSA. Misalkan terdapat
, maka akan terdapat dua garis yang terkait, yaitu dan .
Misalkan D terdapat pada interior maka D, C terletak pada sisi yang
terhadap dan D, A terlatak pada sisi yang sama terhadap .
Untuk lebih memahami definisi 2.9.4, perhatikan gambar 2.1.7
berikut.
Gambar 2.18 Ilustrasi definisi 2.9.4 pada bidang E
Gambar 2.1.8 menunjukkan interior . Interior merupakan
daerah yang dibatasi oleh dan . A
B
Berikut ini diberikan teorema tentang interior sudut.
Teorema 2.9.1 (Teorema Crossbar) (Millman & Parker,1991:84)
Dalam geometri Pasch, jika P ∈ int( ) maka berpotongan
dengan di titik F dengan A – F – C.
Bukti:
Misalkan E merupakan sebuah titik sedemikian hingga E – B – C (lihat
gambar 2.16). P dan C berada pada sisi yang sama dari . C dan E pada
sisi yang berlawanan dari . . Misalkan Q adalah sebuah
titik sedemikian hingga P – B – Q. maka Q dan A berada pada sisi yang
berlawanan dari sehingga . Mengakibatkan
. Menggunakan Postulat Pasch terhadap ∆ kita lihat
bahwa . Karena A, B, C tidak segaris, untuk
F tertentu. dan . Sehingga F ∈ int( ). Akhirnya, P, A, dan
F semuanya pada sisi yang sama dari sehingga memenuhi
. Akibatnya memotong pada titik tertentu F dengan
A – F – P.
Untuk lebih memahami teorema 2.1.8, perhatikan ilustrasi berikut.
Gambar 2.19 Ilustrasi Teorema 2.1.8 A
B
C P
Gambar 2.1.9 merupakan ilustrasi teorema 2.1.8. P ∈ int( ). BP
berpotongan dengan AC di titik F sedemikian hingga A – F – C.
2.10 GEOMETRI PROTRAKTOR
Geometri protraktor merupakan sistem geometri yang merupakan
geometri Pasch dengan menambahkan satu bagian, yaitu ukuran sudut.
Sebelum dibahas mengenai definisi geometri protraktor, akan diberikan
dulu mengenai ukuran sudut, yang merupakan salah satu bagian penting
untuk dapat mendefinisikan geometri protraktor. Berikut ini diberikan
definisi ukuran sudut.
Definisi 2.10.1 (Millman & Parker,1991:90)
Misalkan ro adalah bilangan real positif. Dalam geometri Pasch, ukuran
sudut (protractor) didasarkan pada ro adalah fungsi m dari himpunan
sudut-sudut dalam A kepada himpunan bilangan real sedemikian hingga:
i) Jika ∈A maka 0
ii) Jika terletak pada sisi dari setengah bidang H1 dan jika θ adalah
bilangan real dengan 0 , maka ada sinar garis tunggal
dengan dan
iii) Jika maka ]
Aksioma pertama dari definisi 2.10.1 mengatakan bahwa ukuran sudut
dari suatu sudut terukur. Karena batas bawahnya nol, dan batas atasnya
adalah bilangan real positif, maka ukuran sudut adalah bilangan real yang
Ilustrasi untuk aksioma ii) dan iii) dapat dilihat pada gambar 2.20 berikut.
(a) (b)
Gambar 2.20 Ilustrasi aksioma ii) dan iii) dari Definisi 2.10.1 Jika 180, m disebut ukuran derajat. Jika , m disebut ukuran
radian.
Selanjutnya akan dibahas mengenai geometri protraktor yang
didefinisikan berdasarkan geometri Pasch dengan melibatkan ukuran
sudut.
Definisi 2.10.2 (Millman & Parker,1991:91)
Geometri Protraktor {S , L , d , m} merupakan geometri Pasch dengan
sebuah ukuran sudut m. ]
Selanjutnya geometri protraktor disebut dengan:
a) Pada bidang Euclid (E ) = { , LE , dE , mE} b) Pada bidang Poincaré (H ) = { , LH , dH , mH}
2.11 GEOMETRI NETRAL
Di dalam metematika, terdapat gagasan mengenai ekuivalensi. Dalam
geometri, gagasan yang sesuai dengan ekuivalensi adalah kongruensi.
Definisi 2.11.1 (Millman & Parker,1991:125)
Misalkan ∆ dan ∆ adalah dua segitiga pada Geometri
Protraktor dan misalkan : , , , , adalah fungsi bijektif di
antara titik-titik sudut segitiga tersebut. f kongruen jika:
, ,
dan
, , ]
Dua segitiga ∆ dan ∆ dikatakan kongruen jika ketiga sisi
yang bersesuaian dari kedua segitiga tersebut sama dan ketiga sudut yang
saling bersesuaian juga sama.
Untuk lebih memahami definisi 2.11.1, perhatikan ilustrasi berikut.
Selanjutnya, dalam geometri protraktor terdapat tiga aksioma
mengenai dua segitiga yang kongruen. berikut diberikan definisi mengenai
ketiga aksioma tersebut.
Definisi 2.11.2 (Millman & Parker,1991:127)
Geometri protraktor memenuhi Aksioma Sisi-Sudut-Sisi
(Side-Angle-side/SAS) jika ∆ dan ∆ adalah dua segitiga dengan ,
, , maka ∆ ∆ . ]
Berikut ini diberikan ilustrasi tentang aksioma SAS.
Gambar 2.22 ∆ ∆
Dari gambar 2.22, ∆ dan ∆ adalah dua segitiga dengan
, , . Sehingga ∆ ∆ .
Berikut ini diberikan definisi geometri netral dimana geometri netral
merupakan geometri protraktor dengan satu syarat tertentu.
Definisi 2.11.3 (Millman & Parker,1991:127)
Geometri netral adalah geometri protraktor yang memenuhi SAS. ]
Definisi 2.11.3 menyatakan bahwa geometri netral merupakan
geometri protraktor dengan syarat memenuhi definisi 2.11.2.
Aksioma SAS menyatakan bahwa sebuah segitiga dikatakan kongruen
bila tiga bagian yang saling berkorespondensi antara kedua segitiga
terukur, tiga sudut dan tiga sisi, sehingga ada kemungkinan lain yang
mungkin perbandingan yang lain.
Definisi 2.11.4 (Millman & Parker,1991:131)
Geometri protraktor memenuhi aksioma Sudut-Sisi-Sudut
(Angle-Side-Angle/ASA) jika ada ∆ dan ∆ adalah dua segitiga dengan
, , , maka ∆ ∆ . ]
Definisi 2.11.4 biasa diingat sebagai: Jika dua sudut dan sisi yang
diapitnya dalam sebuah segitiga itu kongruen dengan dua sudut dan satu
sudut dari segitiga yang lain, maka dua segitiga itu kongruen.
Gambar 2.23 ∆ ∆
Dari gambar 2.23, ada ∆ dan ∆ adalah dua segitiga dengan
, , . Sehingga ∆ ∆ .
Selain aksioma SAS dan ASA terdapat aksioma lain yang dapat
digunakan untuk membuktikan bahwa dua segitiga kongruen. aksioma
tersebut adalah aksioma sisi-sisi-sisi/SSS. Berikut diberikan definisi
mengenai aksioma SSS.
Definisi 2.11.5 (Millman & Parker,1991:132)
Geometri protraktor memenuhi aksioma Sisi-Sisi-Sisi
Definisi 2.11.5 menyatakan bahwa: Jika tiga sisi dari sebuah segitiga
kongruen dengan ketiga sisi dari segitiga yang lain, maka kedua segitiga
itu kongruen.
Gambar 2.24 ∆ ∆
Dari gambar 2.24, ∆ dan ∆ adalah dua segitiga dengan
, , . Sehingga ∆ ∆ .
2.12 EUCLIDEAN PARALLEL PROPERTY
Euclidean Parallel Property (EPP) merupakan postulat tentang
kesejajaran yang dikemukakan oleh Euclides. Postulat ini menyatakan
bahawa melalui satu titik terdapat satu garis yang sejajar terhadap suatu
garis tertentu.
Definisi 2.12.1 (Millman & Parker,1991:176)
Geometri insidensi memenuhi Euclidean Parallel Property (EPP) jika
untuk setiap garis l dan untuk setiap titik P, ada garis tertentu yang
melalui P yang sejajar l. ]
Gambar 2.25 Ilustrasi definisi 2.11.6 A
B
C
D
E
F
P
l
2.13 KERANGKA BERPIKIR
Selama ini sudah mempelajari tentang isometri terkait dengan
geometri transformasi pada Geometri Euclides. Berdasarkan teori pada
bagian 2.1 sampai 2.12, akan ditemukan bahwa sifat isometri pada
geometri Euclides juga berlaku untuk geometri lainnya terutama pada
geometri netral, karena geometri Euclides sendiri adalah geometri netral.
48
BAB III
TEORI ISOMETRI
3.1 KOLINEASI DAN ISOMETRI
Ada dua konsep dasar dalam geometri metrik, yaitu garis dan jarak.
Selain itu ada pula dua jenis fungsi yang penting. Satu fungsi (kolineasi) yang
memasangkan garis ke garis, dan fungsi yang lain (isometri) mempertahankan
jarak.
Pertama-tama akan dibahas mengenai kolineasi. Kolineasi adalah fungsi
yang mempertahankan garis. Berikut diberikan definisi mengenai kolineasi.
Definisi 3.1.1 (Millman & Parker,1991:285)
Jika I = {S , L } dan I ‘ = {S ‘ , L ‘} merupakan geometri insidensi, maka
ϕ: S → S ’ mempertahankan garis jika untuk setiap garis l anggota S ,
ϕ(l) adalah sebuah garis S ‘ ; dengan kata lain φ L ‘ jika L .
ϕ adalah sebuah kolineasi jika ϕ adalah fungsi bijektif yang
mempertahankan garis. ]
Dari definisi 3.1.1, diketahui bahwa:
a. Fungsi ϕ dalam geometri insidensi dikatakan mempertahankan garis jika l
adalah garis dalam geometri insidensi dipetakan oleh ϕ akan didapatkan
ϕ( l ) yang juga merupakan garis dalam geometri insidensi.
b. Syarat fungsi ϕ dapat disebut kolineasi yaitu:
(ii) ϕ adalah fungsi yang mempertahankan garis.
Untuk lebih memahami definisi 3.1.1, perhatikan dua contoh berikut..
Contoh 3.1.1
Misalkan I = I ‘ = { ,L E}. Fungsi : dimana ,
2 , 5 adalah sebuah kolineasi.
Bukti:
Diketahui: , 2 , 5 (3-1)
Pertama-tama harus ditunjukkan bahwa ϕ bijektif. Untuk membuktikan
bahwa ϕ bijektif, maka harus dibuktikan bahwa ϕ memiliki invers.
Invers diberikan oleh
,
,
.Karena ϕ memiliki invers, maka dapat dikatakan bahwa ϕ bijektif.
Selanjutnya harus dibuktikan bahwa ϕ mempertahankan garis.
i) Jika , berarti , sehingga persamaan (3-1) menjadi:
2 , 5 | (3-2)
Misalkan 2 (3-3)
5 (3-4)
Substitusikan persamaan (3-5) ke persamaan (3-4) sehingga
persamaan (3-2) menjadi:
, | 3 5 (3-6)
Persamaan (3-6) merupakan persamaan garis dengan m = 1 dan
3 5. Sehingga dapat ditulis sebagai:
,
ii) Jika , berarti ( )
Maka persamaan (3-1) menjadi:
2 , 5 |
2 , 1 5 |
9 Jika 2, maka .
9 Jika 2, maka , dimana dan 5 .
Dari i) dan ii) terlihat bahwa garis yang dikenai fungsi ϕ tetaplah sebuah garis
mengakibatkan ϕ mempertahankan garis.
Karena ϕ bijektif dan ϕ mempertahankan garis, maka ϕ adalah kolineasi. •
Contoh 3.1.2
Misalkan I = I ‘ ={ ,L E}. Fungsi : dimana ,
Bukti:
Diketahui: fungsi , , (3-7)
Berdasarkan definisi 3.1.1, maka pertama-tama harus dibuktikan bahwa ϕ
bijektif.
Untuk membuktikan ϕ bijektif, berdasarkan definisi 2.1.9, harus dibuktikan
bahwa ϕ memiliki invers. Invers ϕ diberikan oleh.
, 2 , 2
Karena ϕ memiliki invers, maka berarti ϕ bijektif.
Selanjutnya harus dibuktikan bahwa ϕ mempertahankan garis.
i) Jika , berarti , maka persamaan (3-7) menjadi:
, |
, | 2
,
ii) Jika , , berarti , maka persamaan (3-7) menjadi:
, |
1 , 1 |
Untuk 1, maka
Untuk 1, maka , dimana dan .