PENGARUH MODEL PEMBELAJARAN DAN GAYA KOGNITIF
TERHADAP HASIL BELAJAR MATEMATIKA
SISWA SLTP DI KOTA AMBON
Tanwey Gerson Ratumanan*
Abstrak:
Penelitian ini mengkaji perbedaan hasil belajar model pembelajaran interaktif
dengan
setting
kooperatif (model PISK) dengan model pengajaran langsung (model PL).
Dalam tiga aspek, yakni kemampuan berpikir kritis, penguasaan bahan ajar, dan sikap
terhadap matematika serta gaya kognitif dilibatkan sebagai variabel moderator. Hasil
belajar siswa SLTP Negeri 4 sebagai kelompok eksperimen, dan SLTP Negeri 6 sebagai
kelompok control dianalisis dengan menggunakan Analisis Varians Multivariat Dua Jalur
(Two Way Manova).Hasilnya menunjukkan bahwa pembelajaran matematika dengan
menggunakan model PISK lebih baik dibandingkan dengan menggunakan model PL, dan
hasil belajar matematika siswa
field independent
lebih baik pada siswa
field dependent.
Abstrak: This research aims at investigating the defferent learning results-getvees those
using Interactive leasning with cooperative setting model (PTSK) and those using Direct
Instructian (PL model). Whereas the moderatos variables consisted of three aspects, I,e;
(1) critical thinking abicity, (2) mastery of cearning material and (3) attitude and
cognitive style towarde mathematics. The learning achievemcats of students of SLTP
Negeri 4, ambon as an experimental gsorep and those SLTP Negeri 6 as a control groep
werw analysed using Two-way manova. The finding shows that the learning of
mathematics using PISK model is getter than that using PL model, and the learning
result of field independent students is getter than that of the field dependent.
Kata Kunci
: model pembelajaran, model PISK, model PL, gaya kognitif.
Akhir-akhir ini banyak model pembelajaran dikembangkan oleh para ahli, di antaranya model pembelajaran kooperatif, pembelajaran berbasis masalah, pembelajaran penemuan, dan pembelajaran interaktif. Berkaitan dengan model pembelajaran kooperatif saja, saat ini dikenal sedikitnya ada 10 tipe, yakni (1) learning together & alone, dikembangkan oleh Johnson & Johnson tahun 1960-an, (2) team games tournaments (TGT), dikembangkan oleh De Vries & Edwards awal tahun 1970-an, (3) group investigation (GI), dikembangkan oleh Sharan & Sharan pada pertengahan tahun 1970-an, (4) constructive controversy, dikembangkan oleh Johnson & Johnson student pada pertengahan tahun 1970-an, (5) Jigsaw, dikembangkan Aronson, dkk pada akhir tahun 1970-an, (6) teams achievement divisions(STAD),
______________________________
*Dosen Program Studi Pendidikan Matematika FKIP Universitas Pattimura Ambon.
dikembangkan oleh Slavin, dkk pada akhir tahun 1970-an, (7) complex instruction (CI), dikembangkan oleh Cohen pada awal tahun 1980-an, (8) team accelerated instruction (TAI), dikembangkan oleh Slavin, dkk pada awal tahun 1980-an, (9) cooperative learning structures
(CLS), dikembangkan oleh Kagan pada awal 1980-an, dan (10) cooperative integrated reading and composition (CIRC), dikembangkan oleh Stevens, Slavin, dkk pada akhir tahun 1980-an.
Berbeda dengan model pembelajaran konvensional, yang cenderung berpusat pada guru (teacher centered instruction), model-model baru di atas menempatkan siswa sebagai subjek belajar, pembelajaran lebih berpusat pada siswa (student centered learning). Model-model pembelajaran tersebut memberikan perhatian besar pada aktivitas aktif siswa, interaksi dan negosiasi makna, yang mengarahkan siswa pada konstruksi pengetahuan. Pembaharuan dalam hal pembelajaran ini memang penting untuk disadari dan diimplementasikan dalam pendidikan karena belajar bukan proses penyerapan pengetahuan, tetapi belajar haruslah merupakan upaya mengonstruksi pengetahuan. Relevan dengan hal ini, Resnik (de Lange, 1996) menegaskan bahwa Learning is not a process of passively absorbing information and storing it in easily retrievable fragments as a result of repeated practice and reinforcement. Instead, students approach each new task with some prior knowledge, assimilate new information, and construct their own meanings.
Penelitian ini selanjutnya diarahkan untuk mengkaji pengaruh penerapan model pembelajaran baru, yang dinamakan model pembelajaran interaktif dengan setting kooperatif atau model PISK (lebih jauh mengenai model ini lihat Ratumanan, 2002a dan 2002b). Pemberian nama ini didasarkan pada pertimbangan bahwa model ini dapat dipandang sebagai hasil modifikasi dari model pembelajaran interaktif (model PI) dengan cara (1) memasukkan setting kooperatif pada fase aktivitas atau pemecahan masalah dan pada fase berbagi dan diskusi (sharing and discussing, pada model PI), (2) mengganti fase berbagi dan diskusi (sharing and discussing, pada model PI) menjadi fase presentasi dan diskusi, (3) memperluas tipe-tipe interaksi, (4) memberikan peran yang jelas pada setiap anggota kelompok dan (5) memberikan kemungkinan yang lebih besar pada negosiasi dan konstruksi pengetahuan.
Dalam pembelajaran matematika, perbedaan siswa perlu mendapat perhatian guru. Setiap siswa di kelas sebenarnya merupakan pribadi yang unik. Sedekat apapun hubungan keluarganya tetap memiliki berbagai perbedaan, baik dalam hal minat, sikap, motivasi, kemampuan dalam menyerap suatu informasi, gaya belajar, dan sebagainya. Semua faktor siswa tersebut idealnya turut menjadi perhatian guru dalam perencanaan dan pelaksanaan KMB. Salah satu faktor siswa yang juga penting untuk diperhatikan guru adalah gaya kognitif. Gaya kognitif berhubungan dengan cara penerimaan dan pemrosesan informasi seseorang. Menurut Woolfolk (1998), gaya kognitif merupakan cara seseorang dalam menerima dan mengorganisasi informasi. Pendapat serupa dikemukakan oleh Messick (Lusiana, 1992), yakni gaya kognitif merupakan kecenderungan perseorangan dalam melakukan pemrosesan informasi. Menurut Lusiana (1992), gaya kognitif mempunyai peran dalam menentukan keberhasilan pembelajaran.
Gaya kognitif dapat dibedakan atas beberapa cara pengelompokan, salah satunya adalah berdasarkan kontinum global analitik dari Witkin, et al. (1977). Berdasarkan cara pengelompokan ini gaya kognitif dapat dibedakan atas (1) field independent dan (2) field dependent. Orang yang mengoperasikan efek pengecoh dengan cara analitik disebut orang yang field independent, sedangkan orang yang mengoperasikan efek pengecoh dengan cara global disebut orang yang field dependent.
Berdasarkan uraian di atas, maka masalah yang dikaji dalam penelitian ini dirumuskan sebagai berikut (1) Apakah terdapat perbedaan antara hasil belajar matematika (kemampuan berpikir kritis, penguasaan bahan ajar, dan sikap terhadap matematika) siswa yang menggunakan model PISK dan yang menggunakan model pengajaran langsung (PL), dan (2) Apakah terdapat perbedaan antara hasil belajar matematika siswa field independent (FI) dan siswa field dependent (FD).
Hipotesis yang dirumuskan dalam penelitian ini, sebagai berikut (1) hasil belajar matematika siswa yang menggunakan model PISK lebih baik daripada siswa yang menggunakan model PL, (2) hasil belajar matematika siswa FI lebih baik daripada siswa FD.
Pemilihan model PL sebagai model pembanding dalam penelitian ini didasarkan pada pertimbangkan bahwa model PL paling dekat dengan model konvensional yang saat ini banyak digunakan di sekolah-sekolah.
Metode
Penelitian ini dapat diklasifikasikan sebagai penelitian eksperimental semu (quasi experimental) dengan menggunakan kelas eksperimen dan kelas kontrol yang ekuivalen. Penelitian ini melibatkan dua variabel bebas, dua variabel moderator, dan pada pengukuran (posttest) terdapat tiga variabel terikat yang diukur. Variabel bebas adalah model pembelajaran, yang terdiri atas 2 (dua) model, yakni (1) pembelajaran interaktif dengan setting kooperatif (PISK), dan (2) pengajaran langsung (PL). Yang merupakan variabel moderator adalah gaya kognitif berdasarkan konsep Witkin, et al. Dengan demikian, gaya kognitif dibedakan atas (1) field independent, dan (2) field dependent. Sedangkan yang merupakan variabel terikat adalah hasil belajar. Hasil belajar dibedakan atas 3 (tiga) aspek, yakni (1) kemampuan berpikir kritis, (2) penguasaan bahan ajar; dan (3) sikap terhadap matematika.
Populasi dalam penelitian ini adalah siswa kelas II SLTP Negeri 4 dan SLTP Negeri 6 Ambon Tahun ajaran 2002/2003. Kedua SLTP ini memiliki level kualitas yang relatif sama. Pada kedua SLTP tersebut dipilih dua kelas pada SLTP Negeri 4 dan dua kelas pada SLTP Negeri 6 yang kemampuan siswanya relatif tidak berbeda secara signifikan. Dengan demikian, sampelnya adalah 4 (empat) kelas siswa kelas II, yakni dua kelas pada SLTP Negeri 4 Ambon (dijadikan kelas eksperimen) dan dua kelas pada SLTP Negeri 6 Ambon (dijadikan kelas kontrol).
Untuk menguji hipotesis penelitian ini digunakan Analisis Varians Multivariat Dua Jalur (Two-Way Manova). Statistik yang digunakan adalah uji statistik Wilks dengan mengambil α = 0,05. Kriteria penerimaan atau penolakan hipotesis adalah H0 ditolak jika Λ< Uα(p, k-1, N-k).
Untuk memudahkan perhitungan, digunakan bantuan program SPSS.
Hasil dan Pembahasan
Deskripsi Hasil Belajar
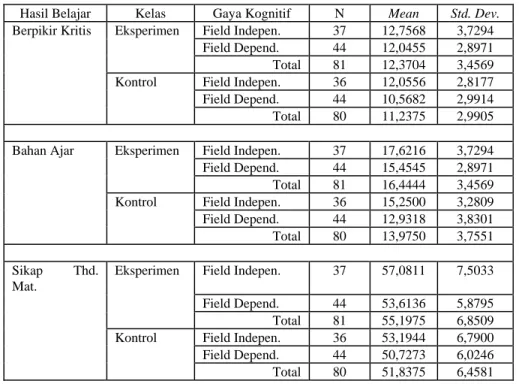
Setelah seluruh KMB yang direncanakan (12 pertemuan) dilakukan, diberikan tes dan angket pada kelas kontrol dan kelas eksperimen. Siswa kelas eksperimen (2 kelas) dan siswa kelas kontrol (2 kelas) diberikan tes kemampuan berpikir kritis (TKBK), tes penguasaan bahan ajar (TPBA), dan angket sikap terhadap matematika (ASTM), hasilnya disajikan pada Tabel 1 berikut.
Hasil Belajar Kelas Gaya Kognitif N Mean Std. Dev.
Berpikir Kritis Eksperimen Field Indepen. 37 12,7568 3,7294
Field Depend. 44 12,0455 2,8971
Total 81 12,3704 3,4569
Kontrol Field Indepen. 36 12,0556 2,8177
Field Depend. 44 10,5682 2,9914
Total 80 11,2375 2,9905
Bahan Ajar Eksperimen Field Indepen. 37 17,6216 3,7294
Field Depend. 44 15,4545 2,8971
Total 81 16,4444 3,4569
Kontrol Field Indepen. 36 15,2500 3,2809
Field Depend. 44 12,9318 3,8301
Total 80 13,9750 3,7551
Sikap Thd. Mat.
Eksperimen Field Indepen. 37 57,0811 7,5033
Field Depend. 44 53,6136 5,8795
Total 81 55,1975 6,8509
Kontrol Field Indepen. 36 53,1944 6,7900
Field Depend. 44 50,7273 6,0246
Total 80 51,8375 6,4581
Tabel 1 memperlihatkan bahwa dalam hal kemampuan berpikir kritis, diketahui bahwa (1) skor rata-rata siswa field independent lebih baik bila dibandingkan dengan siswa field dependent, baik pada kelas eksperimen (yang menggunakan model PISK) maupun pada kelas kontrol (yang menggunakan model PL), dan (2) skor rata-rata siswa kelas eksperimen lebih baik bila dari pada skor rata-rata siswa kelas kontrol.
Dalam hal penguasaan bahan ajar dan sikap terhadap matematika, Tabel 1 juga memperlihatkan hal yang sama, yakni (1) skor rata-rata (mean) siswa kelas eksperimen lebih baik daripada skor rata-rata siswa kelas kontrol, dan (2) skor rata-rata siswa Field Independent lebih baik bila dibandingkan dengan siswa Field Dependent, baik pada kelas eksperimen maupun pada kelas kontrol.
Dengan demikian, dari Tabel 1 ini dapat disimpulkan bahwa (1) hasil belajar siswa yang mengikuti kegiatan mengajar belajar matematika dengan menggunakan model PISK lebih baik bila dibandingkan dengan yang menggunakan model PL, dan (2) siswa FI memiliki hasil belajar matematika yang lebih baik daripada siswa FD.
Pengujian Hipotesis
Mengawali uji hipotesis ini, perlu dilakukan uji kesamaan matriks kovarians. Menurut Gaspersz (1992:541), analisis varians multivariat dilakukan berdasarkan asumsi kesamaan matriks kovarians.
Untuk pengujian kesamaan matriks kovarians digunakan tes Box’s. Hasil pengujian dengan menggunakan bantuan program SPSS. Kriteria yang digunakan adalah matriks kovarians homogen jika Box’s M < χ2(α, 0,5(k-1)(p)(p+1))., dengan α = 0,05. Dari hasil pengujian tersebut
diperoleh Box’s M = 46,434 dengan Sig. = 0,045. Ini berarti bahwa matriks kovarians di antara kombinasi perlakuan adalah sama. Karena asumsi kesamaan matriks kovarians dipenuhi, maka dapat dilakukan analisis varians multivariat.
1. Hipotesis B
H0 : β1 = β2 H1 : β1 ≠ β2
2. Hipotesis A
H0 : α1 = α2 H1 : α1 ≠ α2
Untuk pengujian kedua hipotesis tersebut digunakan bantuan Program SPSS. Dari hasil perhitungan dengan program tersebut, dapat dibuat tabel rata-rata sel (Cell Means), seperti terlihat pada Tabel 2 berikut.
Tabel 2. Rata-Rata Sel Hasil Belajar
B1 (PISK) B2 (PL) Rata-Rata A1 (FI) [12,7568, 17.6216, 57,0811] [12.0556, 15.2500, 53.1944] [12.4110, 16.4521, 55.1644] A2 (FD) [12.0455, 15.4545, 53.6136] [10.5682, 12.9318, 50.7273] [11.3068, 14.1932, 52.1705] Rata-Rata [12.3704, 16.4444, 55.1975] [11.2375, 13.9750, 51.8375] [11.8589, 15.3227, 53.6675]
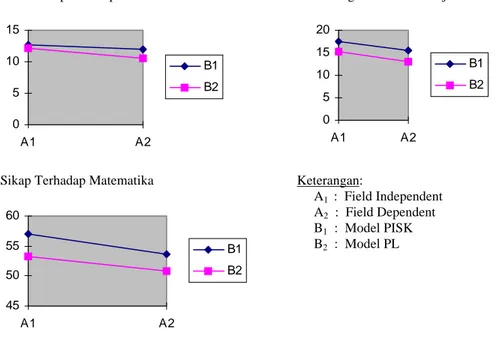
Grafik rata-rata sel tiap-tiap aspek hasil belajar pada suatu waktu dapat disajikan pada gambar berikut.
Kemampuan Berpikir Kritis
0 5 10 15 A1 A2 B1 B2
Penguasaan Bahan Ajar
0 5 10 15 20 A1 A2 B1 B2
Sikap Terhadap Matematika
45 50 55 60 A1 A2 B1 B2 Keterangan: A1 : Field Independent A2 : Field Dependent B1 : Model PISK B2 : Model PL
Gambar 1. Grafik Rata-Rata Sel Ketiga Aspek Hasil Belajar
Perhitungan dengan menggunakan SPSS juga sekaligus menampilkan hasil uji statistik Pillai (V(s)), Wilks (Λ), Lawley-Hotelling (U(s)), dan Roy (θ(s)). Keempat uji statistik tersebut
pada nilai signifikansi (Sig) yang selalu sama. Karenanya pada bagian ini hanya akan disajikan salah satu uji, yakni uji Wilks. Hasil pengujian ketiga hipotesis tersebut disajikan pada Tabel 3 berikut.
Tabel 3. Hasil Uji Statistik Wilks untuk Hipotesis Mayor
Hipotesis Wilks (Λ) U0,05(p,vh,ve) Sig.
B 0,882 0,961981 0,000
A 0,902 0,961981 0,001
Interaksi (AB) 0,993 0,961981 0,761
Data pada Tabel 3 menunjukkan bahwa untuk pengujian hipotesis B, diperoleh Sig = 0,000. Ini menunjukkan bahwa H0 ditolak, atau H1 diterima. Atau dengan memper-hatikan hasil
perhitungan statistik Wilks diperoleh Λ = 0,882, sedangkan pada tabel distribusi U, dengan α = 0,05, p = 2, vh= dbB=2-1=1, dan ve = dberror = 157, diperoleh Uα(p, vh, ve) = 0,961981. Karena Λ<
U0,05(2, 1, 156), maka H0 ditolak, atau H1 diterima Dengan demikian H0 hipotesis B yang
menyatakan bahwa tidak terdapat perbedaan yang signifikan antara hasil belajar siswa yang menggunakan model PISK dengan siswa yang menggunakan model PL, ditolak. Ini berarti bahwa pembelajaran matematika dengan menggunakan model PISK memberikan hasil yang berbeda secara signifikan dengan model PL.
Hasil di atas ternyata didukung pula oleh hasil uji F terhadap hasil belajar kelas PISK dan PL, seperti disajikan pada Tabel 4 berikut.
Tabel 4 Uji F Hasil Belajar Kelas PISK dan PL
Hasil Belajar Sum of Square Mean Difference F Sig
Berpikir Kritis 51,655 1,333 7,133 0,008
Bahan Ajar 245,441 2,469 18,853 0,000
Sikap Thd. Mat. 454,397 3,360 10,249 0,002
Dengan memperhatikan bahwa untuk ketiga aspek hasil belajar, diperoleh Sig. < 0,05, maka dapat disimpulkan bahwa perbedaan hasil belajar antara kelas kelas PISK dan PL adalah signifikan.
Dari deskripsi hasil belajar pada Tabel 1 diketahui skor rata-rata berpikir kritis, penguasaan bahan ajar, dan sikap terhadap matematika siswa kelas eksperimen masing-masing adalah 12,3704; 16,4444; dan 55,1975. Skor rata-rata ketiga aspek hasil belajar tersebut pada siswa kelas kontrol masing-masing adalah 11,2375; 13,9750; dan 51,8375. Dengan demikian, jelas bahwa pembelajaran matematika dengan menggunakan model PISK memberikan hasil belajar (berpikir kritis, penguasaan bahan ajar, dan sikap terhadap matematika) yang lebih baik bila dibandingkan dengan menggunakan model PL.
Tabel 3 di atas juga menunjukkan bahwa untuk pengujian hipotesis A, diperoleh Sig = 0,000. Ini menunjukkan bahwa H0 ditolak, atau H1 diterima. Sehingga H0 hipotesis A yang
menyatakan bahwa tidak terdapat perbedaan yang signifikan antara hasil belajar siswa FI dan FD, ditolak. Ini berarti bahwa hasil belajar matematika dari siswa FI dan FD, berbeda secara signifikan.
Hasil di atas ternyata didukung pula oleh hasil uji F terhadap hasil belajar siswa FI dan FD, seperti disajikan pada Tabel 5 berikut.
Tabel 5. Uji F Hasil Belajar Siswa FI dan FD
Hasil Belajar Sum of Square Mean Difference F Sig
Berpikir Kritis 48,644 1,104 6,700 0,011
Sikap Thd. Mat. 357,654 2,994 7,957 0,005 Dengan memperhatikan bahwa untuk ketiga aspek hasil belajar, diperoleh Sig. < 0,05, maka dapat disimpulkan bahwa perbedaan hasil belajar kedua kelompok gaya kognitif adalah signifikan.
Skor rata-rata kemampuan berpikir kritis, penguasaan bahan ajar, dan sikap terhadap matematika siswa FI masing-masing adalah 12,420; 16,4521; dan 55,1644. Sedangkan skor rata-rata masing-masing aspek hasil belajar matematika dari siswa FD adalah 11,3068; 14,1932; dan 52,1705. Dengan membandingkan masing-masing aspek hasil belajar tersebut, dapat disimpulkan bahwa hasil belajar siswa FI lebih baik dari siswa FD.
Selanjutnya perlu dilakukan pengujian apakah faktor model pembelajaran dan pengelompokan gaya kognitif tidak “berinteraksi”. Tabel 3 memperlihatkan bahwa untuk pengujian interaksi (AB), Sig = 0,761. Karena Sig >α = 0,05, maka H0 yang menyatakan bahwa
tidak terdapat pengaruh interaksi yang signifikan dari model pembelajaran dan gaya kognitif terhadap hasil belajar siswa diterima. Perhitungan dan simpulan ini relevan dengan diagram rata-rata variabel yang disajikan pada Gambar 1 di atas, yang memperlihatkan bahwa kedua garis cenderung sejajar. Kondisi ini dapat diinterpretasi sebagai ada kecenderungan tidak terdapat interaksi yang signifikan antara pengelompokan A (gaya kognitif) dan faktor B (model pembelajaran).
Terdapat tiga aspek hasil belajar matematika yang merupakan variabel terikat di dalam penelitian ini, yakni (1) kemampuan berpikir kritis, (2) penguasaan bahan ajar, dan (3) sikap terhadap matematika. Dari deskripsi tiap-tiap hasil belajar pada kelas eksperimen dan kelas kontrol, diketahui dua hal, yakni (1) untuk setiap aspek hasil belajar, perolehan siswa yang menggunakan model PISK dalam KMB matematika lebih baik bila dibandingkan dengan siswa yang menggunakan model PL, dan (2) untuk setiap aspek hasil belajar, perolehan siswa FI lebih baik daripada siswa FD.
Hasil analisis statistik deskriptif ini juga didukung oleh hasil analisis multivariat. Dari perhitungan dengan menggunakan statistik Wilks (dapat juga dengan menggunakan statistik Pillai, Lawley-Hotteling, dan Roy) diperoleh informasi yang lebih rinci, yakni (1) terdapat perbedaan yang signifikan antara hasil belajar siswa yang menggunakan model PISK dan model PL. Untuk setiap aspek hasil belajar, perolehan daripada siswa yang menggunakan model PISK lebih baik daripada siswa yang menggunakan model PL, dan (2) terdapat perbedaan yang signifikan antara hasil belajar siswa FI dan siswa FD. Setiap aspek hasil belajar, perolehan siswa FI lebih baik daripada siswa FD.
Hasil analisis yang menunjukkan bahwa model PISK memberikan hasil yang lebih baik daripada model PL (atau model konvensional) merupakan pembenaran terhadap hipotesis pertama. Pada model PL aktivitas siswa lebih didominasi oleh aktivitas mendengar penjelasan guru, membuat catatan dan mengerjakan tugas yang diberikan guru. Sedangkan dalam model PISK lebih dimungkinkan terjadinya berbagai aktivitas aktif siswa. Siswa tidak hanya menjadi pendengar, tetapi juga terlibat aktif dalam berbagai aktivitas seperti memecahkan masalah, mengajukan pertanyaan, mengemukakan pendapat, membantu memberikan penjelasan pada temannya, dan aktivitas berpikir. Keterlibatan siswa dalam berbagai aktivitas aktif tersebut memungkinkan penguasaan siswa terhadap bahan ajar menjadi lebih baik, demikian pula dengan kemampuan berpikir kritis dan sikap terhadap matematika.
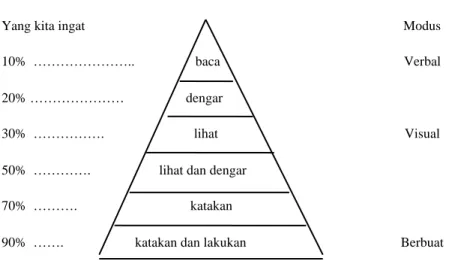
Hal ini relevan dengan penjelasan Magnesen (dalam dePorter., dkk, 2000), yang mengemukakan bahwa kita belajar 10% dari apa yang kita baca, 20% dari apa yang kita dengar, 30% dari apa yang kita lihat, 50% dari apa yang kita lihat dan dengar, 70% dari apa yang kita katakan, dan 90% dari apa yang kita katakan dan lakukan. Sheal (dalam Depdiknas, 2002) kemudian melengkapi uraian Magnesen ini dalam kerucut pengalaman belajar seperti pada Gambar 6.1 berikut.
Yang kita ingat Modus
10% ……….. baca Verbal
20% ……… dengar
30% ………. lihat Visual
50% …………. lihat dan dengar
70% ………. katakan
90% ……. katakan dan lakukan Berbuat
Gambar 2. Kerucut Pengalaman Belajar
Model PISK juga memberikan penekanan pada interaksi secara luas. Terdapat lima tipe interaksi di dalam model PISK, yakni interaksi antara (1) siswa dengan siswa (student-student = S-S), (2) siswa dengan bahan ajar (student-learning material = S-LM), (3) siswa dengan guru (student-teacher = S-T), (4) siswa-bahan ajar-siswa (student-learning material-student = S-LM-S), dan (5) siswa-bahan ajar-guru (student-learning material-teacher = S-LM-T). Interaksi ini sangat penting bagi upaya konstruksi pengetahuan, peningkatan kemampuan akademis, peningkatan kecakapan sosial, dan sebagainya. Menurut Davidson, Lappan & Schram (dalam Baroody, 1993), interaksi siswa penting untuk mengonstruksi pengetahuan matematika, mengembangkan pemecahan masalah dan kompetensi berpikir, mendorong kepercayaan, dan perolehan kecakapan sosial.
Baroody (1993) mengemukakan bahwa komunikasi (interaksi, pen.) dengan teman sebaya dapat membantu perkembangan belajar materi (bahan ajar), pemahaman, dan perolehan strategi. Baroody menjelaskan lebih jauh sebagai berikut.
a. Untuk menjadi melek secara matematis (mathematically literate), anak harus belajar aspek-aspek dasar pengetahuan matematika sedikit demi sedikit. Hasil penelitian menunjukkan bahwa kelompok belajar kooperatif dapat meningkatkan hasil belajar matematika lebih tinggi bila dibandingkan dengan pendekatan individual.
b. Untuk membantu siswa mengonstruksi pemahaman matematika, pembelajaran harus secara
teratur menantang siswa untuk berpikir. Interaksi dengan teman sebaya dapat memperbesar kesempatan untuk hal tersebut. Bekerja dalam kelompok kecil memberikan anak kesempatan untuk berbagi pertanyaan dan pemikiran (wawasan), yang lebih lanjut akan mempertinggi pemahaman.
c. Interaksi antarsiswa akan memberikan siswa kesempatan untuk berbagi strategi.
Hasil analisis yang menunjukkan bahwa hasil belajar siswa FI lebih baik bila dibandingkan dengan siswa FD merupakan pembenaran terhadap hipotesis kedua. Beberapa penelitian sebelumnya juga memberikan dukungan terhadap hipotesis ini. Di antaranya, Woolfolk
(1998) mengemukakan bahwa orang yang FI lebih baik dalam pelajaran matematika dan sains dibandingkan dengan orang yang FD. Threadgill (1979) juga melaporkan hal yang sama, yakni hasil posttes siswa FI lebih tinggi secara signifikan dari siswa FD.
Simpulan
Penelitian ini menunjukkan bahwa model PISK memberikan hasil lebih baik bila dibandingkan dengan model PL, baik dalam hal kemampuan berpikir kritis, penguasaan bahan ajar matematika, maupun sikap terhadap matematika. Karenanya model PISK dapat dijadikan sebagai model alternatif dalam pembelajaran matematika.
Hasil penelitian juga menunjukkan bahwa hasil belajar matematika siswa FI lebih baik bila dibandingkan dengan siswa FD. Hasil ini mendukung temuan sebelumnya yang menyatakan bahwa orang yang FI lebih baik dalam pelajaran matematika dan sains (lihat Woolfolk, 1998; Threadgill, 1979).
Daftar Acuan
Baroody. A.J. 1993. Problem Solving, Reasoning, and Communicating. Macmillan Publising, New York.
Crowther, David T. 1997. The Constructivist Zone, Under Construction. Http://um.edu/ homepage/jeannon/ejse/ejsev2n2ed.1
De Lange, Jan. 1996. Assesment: No Change Without Problems. In Romberg, T.A (ed.). Reform in School Mathematics and Authentic Assesment. New York: Suny Press.
Depdiknas. 2002. Pengelolaaan Kurikulum Berbasis Kompetensi. Jakarta: Pusat Kurikulum, Balitbang.
DePorter, Boby., Mark Reardon., & Sarah Singer-Nourie. 2000. Quantum Teaching. Bandung: Kaifa.
Eggen, D. Paul., & Donald P. Kauchack. 1996. Strategies for Teachers: Teaching Content and Thinking Skills. Englewood Cliffs, New Jersey: Prentice Hall.
Gaspersz, Vincent. 1992. Teknik Analisis dalam Penelitian Percobaan. Bandung: Tarsito.
Good, Thomas., & Jere E. Brophy. 1990. Educational Psychology, 4th ed. New York & London: Longman.
Holmes, Emma. E. 1995. New Directions in Elementary School Mathematics, Interactive Teaching and Learning. Englewood Cliffs, New Jersey: Prentice Hall, Inc.
Johnson, D.W., & Roger T. Johnson. 1994. Learning Together and Alone, Cooperative, Competitive and Individualistic Learning. 4th ed. Boston: Allyn and Bacon.
Johnson, D. W., Roger T. Johnson., & Mary Beth Stanne. 2002. Cooperative Learning Methods: A Meta Analysis. http://www.clcrc.com/pages/cl-methods.html.
Lusiana. 1992. Pengaruh Interaktif Antara Penggunaan Strategi Penataan Isi Mata Kuliah dan Gaya Kognitif Mahasiswa terhadap Perolehan Belajar. Tesis. Malang: PPS IKIP Malang.
Ratumanan, T. G. 2002a. Model Pembelajaran Interaktif dengan Setting Kooperatif. Surabaya: PPS Universitas Surabaya.
Ratumanan, T. G. 2002b. Pengenalan Model Pembelajaran Interaktif dengan Setting Kooperatif. Buletin Pendidikan Matematika. Vol. 4 No. 1, 27-39, Maret 2002.
Ratumanan, T. G. 2000. Pengajaran Interaktif: Arah Baru Dalam Pengajaran Matematika. Makalah. Disampaikan pada Seminar Matematika di ITS Surabaya, pada tanggal 2 Nopember 2000.
Slavin, Robert E. 1997. Educational Psychology. 5th ed.. Boston: Allyn and Bacon.
Threadgill, Judith Ann. 1979. The Relationship of Field-Independent/Dependent Cognitive Style and Two Method of Instruction in Mathematics Learning. Journal for Research in Mathematics Education. May 1979, 219-221. NCTM.
Witkin, H.A., C. A. Moore., D. R. Goodenough., & P. W. Cox. 1977. Dependent and Field-Independent Cognitive Styles and Their Educational Implications. Review of Educational Research. Winter 1977, Vol. 47, No. 1, 1-64.