Program tujuan ganda [Multiple objective programming] - USD Repository

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Christina Natalia Ika Purbawati NIM : 02 3114 013

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

Final Project

Presented As Partial Fulfillment Of The Requirements To Obtain The Sarjana Sains Degree In Mathematics

By :

Christina Natalia Ika Purbawati Student Number : 02 3114 013

STUDY PROGRAM OF MATHEMATISC SCIENSE DEPARTEMANT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

2007

Serahkanlah perbuatanmu itu kepada Tuhan,

maka terlaksanalah segala rencanamu.

Dengan penuh kasih dan ucapan syukur

Skripsi ini Kupersembahkan untuk:

Bapa di Surga juru selamatku, Bunda Maria

pelindung, pengharapan, dan penghiburanku

Bapak dan Ibuku yang tersayang:

Ignatius Sukardiyo dan Yustina Tri Suharni

Adik-adikku tersayang:

F.A.Oktora Dwi H dan Damianus Fendy S

Masku yang tercinta:

Yulius Sunarsanto

Teman-teman angkatan ‘02

Almamaterku Sanata Dharma

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, Oktober 2007 Penulis

Christina Natalia Ika Purbawati

tidak dapat membantu menyelesaikan permasalahan tersebut. Program linear hanya terbatas pada analisis tunggal. Maka untuk menyelesaikannya diperlukan alat analisis yang tepat, yaitu program tujuan ganda. Terdapat beberapa cara untuk menyelesaikan program tujuan ganda, misalkan menggunakan prinsip efisiensi dan deviasi. Ide dasar dalam menyelesaikan masalah program tujuan ganda adalah mengubah beberapa fungsi tujuan menjadi satu fungsi tujuan saja.

Apabila penyelesaian optimal sulit didapatkan, maka dalam menyelesaikannya dapat digunakan dengan cara mencari beberapa penyelesaian layak. Kemudian membandingkan dua dari beberapa penyelesaian layak tesebut sehingga diperoleh penyelesaian yang efisien. Penyelesaian layak disebut efisien jika penyelesaian tersebut tidak didominasi oleh penyelesaian layak yang lain. Salah satu ide untuk menyelesaikan masalah program tujuan ganda dengan menggunakan efisiensi adalah mengalikan setiap fungsi tujuan dengan faktor bobot sesuai dengan prioritasnya kemudian menambahkan fungsi-fungsi tersebut.

Deviasi adalah jarak batas yang dapat dicapai oleh fungsi tujuan sebagaimana yang dikehendaki oleh berbagai fungsi kendala. Ide dasar untuk menyelesaikan masalah program tujuan ganda dengan menggunakan deviasi adalah menambahkan hasil kali dari setiap deviasi pada fungsi tujuan dengan faktor bobot. Kemudian permasalahan diselesaikan dengan metode simpleks sama seperti pada program linear.

cannot help to solve those problems. Linear programming is only limited on the single analysis. Thus, to solve the problems, it is needed to employ the correct analysis means, that is, multiple objective programming. There are several ways to solve the multiple objective programming, for example, by employing efficiency and deviation principles. The basic idea in solving the problems of multiple objective programming is changing some purpose functions into one purpose function only.

If the optimal solution is difficult to obtain, it is required to find some suitable solutions to solve the problems. Then, the next step is comparing two from several suitable solutions in order to obtain the most efficient solution. Suitable solution can be considered efficient if that solution is not dominated by other suitable solutions. One idea in solving the problems of multiple objective programming efficiently is multiplying every purpose function with burden factor along with its priority, and then adding those functions.

Deviation is border distance which can be reached by purpose function as it is desired by other obstacle functions. The basic idea to solve the problems of multiple objective programming be employing deviation is adding the multiple results of each deviation on purpose function with burden factor. Then, the problems are solved with simplex method, the same with linear programming.

kasih-Nya dan melimpahkan karunia-Nya, memberikan kekuatan, menuntun dan memberkati penulis secara luar biasa sehingga penulisan skripsi ini dapat diselesaikan.

Skripsi ini disusun untuk memenuhi salah satu syarat memperoleh gelar Sarjana Sains di Program Studi Matematika Jurusan Matematika Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

Penulis dalam menyusun skripsi ini dari awal sampai akhir mendapat dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini penulis menyampaikan ucapan terima kasih yang sebesar-besarnya kepada:

1. Ir. Gregorius Heliarko, S.J., S.S., BST, M.Sc., M.A. selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta dan Bapak Ir. Ig. Aris Dwiatmoko, M.Sc selaku dosen pembimbing akademik.

2. Ibu Lusia Krismiyati Budiasih selaku Kaprodi Matematika dan dosen pembimbing yang dengan kesabarannya telah banyak membimbing dan memberikan petunjuk dalam penyusunan skripsi ini.

3. Bapak YG. Hartono, S.Si.,M.Sc dan Bapak St. Eko Parmadi, S.Si.,M.Kom sebagai dosen penguji atas diskusi dan masukan-masukannya untuk skripsi ini. 4. Bapak dan Ibu dosen serta staf karyawan terima kasih untuk bimbingan dan

bantuan serta sabar mendidik penulis sampai akhir semester.

6. Adik-adikku Tora dan Fendy, terima kasih untuk cinta, doa, dukungan, pengertian dan motivasinya.

7. Kangmas ku Yulius yang telah menemaniku dalam suka maupun duka. ”Terima kasih mas atas semuanya”, dan “I Love You”.

8. Keluarga besarku di Yogyakarta terima kasih untuk doa dan dukungannya, “Ulin, makasih atas dukungannya.”

9. Sahabat-sahabatku: Ria, Presti, Nita. Semua anak-anak MUDIKA Santo Agustinus Purbalingga. Thanks atas dukungannya ya...

10. Teman-teman seperjuanganku di Matematika 2002: Preezk, Archy, Vida, Lenta, Debby, Lia, Sari, Aan, Tato, Bani, Lili, Taim, Ijup, Markus, Felix, Retno, Galih, Aning, Desy, Rita, Wuri, Deon, Cheea, Nunung, Dani, Palma, dan Asih. Kakak-kakak dan adik-adik angkatan terima kasih untuk bantuan dan keramahannya.

11. Teman-teman kostku: Agnes, Yogi, Sinta, Alin, Moy, Cici, Diah (makasih atas pinjaman laptopnya ya...), Ata, De Raras (makasih atas bantuannya selama ini dan dukungannya), De Evrin (thanks buat tumpangannya), Nana, Cicil, Ani, Ana, Fery, Anas, Mina, Putri makasih buat kebersamaan dan keceriaan kita selama ini.

13. Semua pihak yang telah turut membantu hingga selesainya skripsi ini yang tidak dapat disebutkan satu persatu.

Semoga kasih Tuhan selalu menyertai semua pihak yang telah membantu dalam penyusunan skripsi ini. Penulis menyadari sepenuhnya bahwa penyusunan ini jauh dari sempurna, untuk itu saran dan kritik yang sifatnya membangun penulis menerima dengan senang hati demi perbaikan skripsi ini. Penulis berharap semoga skripsi ini dapat memberikan manfaat bagi setiap orang dan semua pihak.

Yogyakarta, Oktober 2007 Hormat Penulis

Christina Natalia Ika Purbawati

HALAMAN JUDUL... i

HALAMAN JUDUL (Inggris)... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN... iv

HALAMAN PERSEMBAHAN... v

PERNYATAAN KEASLIAN KARYA... vi

ABSTRAK ... vii

ABSTRACT... viii

KATA PENGANTAR ... ix

DAFTAR ISI... xii

BAB I PENDAHULUAN A. Latar Belakang Masalah... 1

B. Perumusan Masalah ... 2

C. Pembatasan Masalah ... 3

D. Tujuan Penulisan... 3

E. Metode Penulisan ... 3

F. Manfaat Penulisan... 3

G. Sistematika Penulisan ... 4

C. Program Linear dengan Metode Grafik ... 12

D. Program Linear dengan Metode Simpleks... 19

E. Dualitas Pada Program Linear... 32

BAB III PROGRAM TUJUAN GANDA A. Faktor Bobot Dalam Masalah Program tujuan Ganda ... 40

B. Penyelesaian Efisien ... 45

C. Efisiensi dan Faktor Bobot... 56

D. Deviasi Dalam Model Program Tujuan Ganda... 66

E. Program Tujuan Ganda Dengan Metode Grafik ... 69

F. Program Tujuan Ganda Dengan Metode Simpleks... 77

BAB IV PENUTUP A. Kesimpulan ... 94

B. Saran... 95

DAFTAR PUSTAKA ... 96

A. Latar Belakang Masalah

Dalam dunia nyata sering dijumpai masalah efisiensi atau alokasi dari sumber

yang terbatas yang akan dioptimalkan. Inilah yang disebut masalah optimasi.

Optimasi dapat didefinisikan sebagai suatu proses untuk memaksimumkan atau

meminimumkan fungsi yang disebut fungsi tujuan yang bergantung pada sejumlah

variabel keputusan berhingga yang saling bebas atau dapat juga berkaitan melalui

satu atau lebih kendala. Optimasi dapat diselesaikan dengan menggunakan

program linear.

Dunia nyata yang di hadapi saat ini adalah dunia yang penuh dengan berbagai

tujuan sebagai target dan sasaran. Dalam keadaan di mana seseorang pengambil

keputusan dihadapkan kepada suatu persoalan yang mengandung beberapa tujuan

di dalamnya, maka program linear tidak dapat membantunya untuk memberikan

pertimbangan yang rasional. Program linear hanya terbatas pada analisis tujuan

tunggal (unidimensional). Oleh karena itu, diperlukanlah alat analisis yang tepat,

yaitu program tujuan ganda. Program tujuan ganda dapat bergerak dalam

masalah-masalah yang tujuannya unidimensional (tujuan tunggal) maupun

multidimensional (tujuan ganda, dan lebih dari dua). Hal inilah yang melandasi

penulisan skripsi ini.

Program tujuan ganda, yang dalam bahasa asing dikenal sebagai multiple

objective programming atau goal programming merupakan modifikasi atau

variasi khusus dari program linear. Secara umum, dalam program tujuan ganda

yang memiliki beberapa tujuan akan dimaksimumkan satu fungsi tujuan baru.

Dalam menyelesaikan program tujuan ganda, tidak mudah untuk mendapatkan

penyelesaian yang serentak yang dapat memenuhi semua fungsi tujuan. Maka

untuk menyelesaikannya dapat digunakan beberapa cara, misalkan menggunakan

prinsip efisiensi dan deviasi. Program tujuan ganda berusaha untuk

meminimumkan deviasi di antara berbagai tujuan atau sasaran yang di tetapkan,

yaitu meminimumkan jarak batas yang dapat dicapai oleh fungsi tujuan

sebagaimana yang dikehendaki oleh berbagai kendala yang mengikat fungsi

tujuan tersebut sebagai syaratnya. Dengan analisis program tujuan ganda, akan di

coba supaya memuaskan atau memenuhi target (paling tidak mendekati target)

yang telah ditentukan.

B. Perumusan Masalah

Pokok permasalahan yang akan dibahas dalam skripsi adalah

a. Bagaimana mendapatkan penyelesaian yang efisien dalam program tujuan

ganda?

b. Bagaimana meminimumkan deviasi di antara beberapa fungsi tujuan yang

ditetapkan dalam program tujuan ganda?

c. Bagaimana aplikasi atau terapan program tujuan ganda dalam kehidupan

C. Pembatasan Masalah

Pembahasan masalah program tujuan ganda dalam skripsi ini hanya dibatasi

pada kendala yang berbentuk linear, dan dikhususkan untuk pola maksimum saja.

Konsep-konsep dalam aljabar linear juga tidak dijabarkan.

D. Tujuan Penulisan

Tujuan penulisan skripsi ini untuk memahami lebih dalam konsep-konsep

program linear yang mendasari program tujuan ganda, serta mengenal, mengerti,

dan memahami konsep-konsep yang ada dalam program tujuan ganda.

E. Metode Penulisan

Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dikerjakan

dengan cara mencari, mempelajari dan memahami materi-materi yang berkaitan

dengan program tujuan ganda dari referensi-referensi yang ada di buku, sehingga

tidak ditemukan hal baru.

F. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah dapat memberikan

kejelasan lebih lengkap mengenai program linear sebagai dasar dari program

tujuan ganda, serta bagi pembaca dapat memberikan wawasan mengenai program

G. Sistematika Penulisan

Bab pertama adalah pendahuluan, yang berisi tentang latar belakang masalah,

perumusan masalah, pembatasan masalah, tujuan penulisan, metode penulisan,

manfaat penulisan, dan sistematika penulisan.

Bab kedua adalah landasan teori, pada bab ini diuraikan tentang sejarah

program linear, perumusan program linear, penyelesaian masalah program linear

menggunakan metode grafik dan metode simpleks, serta masalah dualitas pada

program linear.

Bab ketiga adalah program tujuan ganda. Bab ini menguraikan mengenai

faktor bobot dalam masalah program tujuan ganda, bagaimana mendapatkan

penyelesaian yang efisien, serta masalah program tujuan ganda dengan

menggunakan deviasi.

Bab keempat adalah penutup, pada bab ini berisi kesimpulan dan saran

A. Sejarah Program Linear

Program linear yang dalam bahasa Inggris disebut linear programming, adalah

salah satu teknik analisis dari kelompok teknik riset operasi yang memakai model

matematika. Tujuannya adalah untuk mencari, memilih, dan menentukan alternatif

yang terbaik dari antara sekian alternatif layak yang tersedia.

Kelahiran teknik program linear sebenarnya belum lama. Dr. George Dantzig,

seorang ahli matematika bangsa Amerika Serikat dapat disebut sebagai bapak

lahirnya pemakaian teknik program linear tersebut, yaitu dengan

dikembangkannya metode simpleks pada tahun 1947. Sebelum lahirnya karya

Dantzig yang sistematis dan terkenal itu, terdapat pula beberapa ahli matematika

lainnya seperti Van Neuman dan Leontief yang melahirkan teknik-teknik

penyelesaian masalah dengan memakai pendekatan aljabar linear pada tahun

1930-an (B. D. Nasendi dan Affendi Anwar, 1985 ).

Penerapan program linear untuk pertama kalinya adalah di bidang

perencanaan militer, khususnya dalam Perang Dunia II oleh angkatan bersenjata

Amerika Serikat dan Inggris. Sejak itulah berbarengan dengan berkembangnya

waktu, pembangunan, dan teknologi, tenik-teknik analisis program linear dengan

cepat sekali menjalar dan diterapkan dalam berbagai bidang dan disiplin ilmu

dalam rangka memecahkan berbagai permasalahan yang dihadapi.

Sebagai contoh, di bidang kehutanan misalnya. Untuk pertama kalinya

program linear dipakai sebagai alat perencanaan di tahun 1955, yakni untuk

memecahkan masalah produksi dan distribusi kayu lapis, suplai bahan baku dari

hutan ke pabrik, kemudian dari pabrik ke pusat-pusat konsumen dan sebagainya.

B. Perumusan Masalah Program Linear

Program linear pada hakikatnya merupakan suatu teknik perencanaan yang

bersifat analitis yang analisis-analisisnya memakai model matematika dengan

tujuan menemukan beberapa kombinasi alternatif pemecahan masalah, kemudian

dipilih mana yang terbaik diantaranya dalam rangka menyusun strategi dan

langkah-langkah kebijakan lebih lanjut tentang alokasi sumber daya dan dana

yang terbatas guna mencapai tujuan atau sasaran yang diinginkan secara optimal.

Penekanannya di sini adalah pada alokasi optimal atau kombinasi optimum,

artinya suatu langkah kebijakan yang pertimbangannya telah dipertimbangkan

dari segala segi untung dan rugi secara baik, seimbang dan serasi. Artinya yang

berdaya guna (efisien) dan berhasil guna (efektif). Alokasi optimal tersebut tidak

lain adalah memaksimumkan atau meminimumkan fungsi tujuan yang memenuhi

persyaratan-persyaratan yang dikehendaki oleh kendala ke dalam bentuk

ketidaksamaan linear (Siswanto, 1993).

Model program linear mempunyai 3 unsur utama, yaitu :

1. Peubah keputusan

Peubah keputusan adalah peubah persoalan yang akan mempengaruhi nilai

peubah keputusan tersebut harus dilakukan terlebih dahulu sebelum

merumuskan fungsi tujuan dan kendala-kendalanya. Cara untuk menemukan

peubah-peubah ini adalah dengan mengajukan pertanyaan : “keputusan apa

yang harus dibuat agar nilai fungsi tujuan maksimum atau minimum”.

2. Fungsi tujuan

Dalam model program linear, tujuan yang hendak dicapai harus

diwujudkan ke dalam sebuah fungsi matematik linear. Selanjutnya, fungsi itu

dimaksimumkan atau diminimumkan terhadap kendala-kendala yang ada.

3. Kendala-kendala fungsional

Manajemen menghadapi pelbagai kendala dalam mewujudkan tujuannya.

Kendala-kendala tersebut harus dituangkan ke dalam fungsi matematik linear.

Secara umum, model dasar program linear dapat dirumuskan sebagai berikut,

maksimumkan (atau minimumkan)

n nx

c x

c x c

z= _{1 1} + _{2 2} +L+

dengan kendala :

+ + . . . +

11

a x₁ a₁₂ x₂ a_1n x_n ≤ atau ≥ b₁ + + . . . +

21

a x₁ a₂₂ x₂ a_2n x_n ≤ atau ≥ b₂

. . . . .

. . . . .

. . . . .

+ + . . . +

1

p

a x₁ ap₂ x2 apn xn ≤ atau ≥ b p

0 untuk j = 1, 2, 3, ..., n

j

Perumusan di atas dapat diringkas sebagai berikut :

maksimumkan (minimumkan)

dengan kendala

∑

= = n j j jx c z 1

∑

= n j ij a 1 j

x ≤ atau ≥ b_i i = 1, 2, 3, ..., p (2.2.1)

0 (2.2.2)

j

x ≥

dengan :

j

x = peubah pengambilan keputusan ke-j

j

c = koefisien peubah pengambilan keputusan ke-j

ij

a = koefisien peubah pengambilan keputusan ke-j dalam kendala ke-i

i

b = nilai sebelah kanan dari kendala ke-i

z = nilai suatu fungsi tujuan

n = banyaknya peubah pengambilan keputusan

p = banyaknya kendala

Kendala (2.2.1) disebut kendala utama, sedangkan kendala (2.2.2) disebut

kendala tak negatif.

Dalam perumusan program linear di atas, kendala memuat hubungan

(

atau

atau . Jika perumusan program linear berbentuk

)

, ≤

( )

≥ ,

( )

=

maksimumkan

∑

= = n j j jx c z 1

dengan kendala

∑

= n j ij a 1 j

x ≤ bi i = 1, 2, 3, ..., p

0

j

maka bentuk di atas disebut pola maksimum baku. Tetapi jika perumusan

program linear berbentuk

minimumkan

∑

=

= n

j j jx c z

1

dengan kendala

∑

i = 1, 2, 3, ..., p

=

n j

ij a

1

j

x ≥ b_i

0

j

x ≥

maka bentuk di atas disebut pola minimum baku.

Ada 2 metode untuk menyelesaikan permasalahan program linear, yaitu :

1. Metode grafik

2. Metode secara aljabar, dalam hal ini memakai algoritma simpleks.

Sebelum membahas kedua metode ini, akan diberikan beberapa definisi

sebagai berikut.

Definisi 2.2.1

Penyelesaian layak adalah pasangan

(

x₁,L,x_n

)

yang memenuhi semua kendala, baik kendala utama maupun kendala tak negatif.

Definisi 2.2.2

Daerah layak adalah himpunan semua penyelesaian layak yang memenuhi

Definisi 2.2.3

Penyelesaian optimal adalah penyelesaian layak yang membuat optimum

fungsi tujuan.

Definisi 2.2.4

Penyelesaian basis adalah penyelesaian yang memenuhi kendala utama.

Definisi 2.2.5

Penyelesaian layak basis adalah penyelesaian basis dan memenuhi kendala

tak negatif.

Definisi 2.2.6

Bentuk kanonik dari masalah program linear dapat didefinisikan sebagai

berikut :

(i) Jika permasalahan menginginkan untuk meminimumkan fungsi tujuan. Maka

perumusan menjadi

minimumkan

∑

=

= n

j j jx c z

1

dengan kendala

∑

i = 1, 2, 3, ..., p

=

n j

ij a

1

j

x ≥ bi

0

≥

j

x

Untuk mengubahnya menjadi bentuk kanonik, perlu ditambahkan peubah

adalah peubah yang digunakan pada ruas kiri supaya ruas yang semula longgar

menjadi ketat sehingga nilainya sama dengan ruas yang lainnya. Banyaknya

peubah surplus harus sama dengan banyaknya kendala pada model program

linear yang bersangkutan. Setiap peubah surplus dalam fungsi tujuan

koefisiennya adalah 0. Peubah semu digunakan supaya tablo awal memuat

penyelesaian basis yang layak. Bila ada peubah semu yang masuk, maka

disusun fungsi tujuan baru yaitu

i v i v i Mv f

f = + (M positif besar). Maka bentuk

kanonik untuk masalah meminimumkan adalah

minimumkan

∑

∑

∑

= = = + + = p i i p i i n j j

jx t Mv

c z 1 1 1 . 0

dengan kendala

∑

- + = i = 1, 2, 3, ..., p

= n j ij a 1 j

x ti vi bi

0

≥

i

t v_i ≥0 x_j ≥0 Dalam hal ini

= 0 jika = i = 1, 2, 3, ..., p

i t

∑

= n j ij a 1 j

x b_i

> 0 jika > i = 1, 2, 3, ..., p

i t

∑

= n j ij a 1 j

x bi

(ii) Jika permasalahan menginginkan untuk memaksimumkan fungsi tujuan. Maka

perumusan menjadi

maksimumkan

∑

= = n j j jx c z 1

dengan kendala

∑

= n j ij a 1 j

0

≥

j

x

Untuk mengubahnya menjadi bentuk kanonik, perlu ditambahkan peubah

pengetat yaitu, peubah slack . Banyaknya peubah slack harus sama dengan

banyaknya kendala pada model program linear yang bersangkutan. Setiap

peubah slack dalam fungsi tujuan koefisiennya adalah 0. Maka perumusan

menjadi

i

s

maksimumkan

∑

∑

= = + = p i i n j j

jx s

c z 1 1 . 0

dengan kendala

∑

+ = i = 1, 2, 3, ..., p

= n j ij a 1 j

x s_i b_i

0

≥

i

s x_j ≥0 Dalam hal ini

= 0 jika = i = 1, 2, 3, ..., p

i s

∑

= n j ij a 1 j

x b_i

> 0 jika < i = 1, 2, 3, ..., p

i s

∑

= n j ij a 1 j

x b_i

C. Program Linear Dengan Metode Grafik

Metode analisis grafik suatu persoalan program linear memfokuskan diri

hanya pada perpotongan garis-garis dengan memakai pendekatan dua dimensi.

Meskipun dalam praktek masalah program linear jarang yang hanya memuat dua

peubah, tetapi metode grafik mempermudah orang dalam memahami

lebih dari tiga dimensi, analisis dilakukan dengan cara aljabar yakni algoritma

simpleks.

Jika melakukan cara analisis grafik untuk suatu permasalahan program linear,

ada empat langkah yang harus ditempuh. Langkah-langkah tersebut adalah :

Langkah 1

Rumuskan permasalahan program linear ke dalam model matematika sesuai

dengan peraturan dan syarat-syarat yang diperlukan oleh suatu model program

linear, yaitu harus ada fungsi tujuan, kendala, dan syarat ikatan non-negatif.

Langkah 2

Gambarkan grafik dua dimensi yang menunjukkan dimensi dua peubah

pengambilan keputusan. Kemudian kendala-kendala yang ada di tempatkan pada

grafik dua dimensi tersebut, sesuai dengan persyaratan ketidaksamaannya.

Langkah 3

Gambarkan fungsi tujuan, sehingga diperoleh garis selidik, yakni garis lurus

dari fungsi tujuan yang menggambarkan pasangan-pasangan yang

memberikan nilai z yang sama. Kemudian pilihlah garis mana yang menyinggung

titik sudut optimal.

(

x1,L,xn

)

Langkah 4

Buat kesimpulannya dan hitung berapa jumlah yang optimal.

Untuk lebih memahaminya, akan diberikan sebuah contoh permasalahan

Contoh 2.3.1

Sebuah industri berkecimpung dalam proses produksi dua macam produk,

yaitu produk X dan Y. Produk-produk tersebut dapat dijual dengan harga dasar

sebesar Rp 3.000,00 per unit untuk produk X dan Rp 3.000,00 juga per unit untuk

produk Y. Kedua macam produk ini memerlukan bahan baku yang sama dalam

jumlah yang sama pula per unit. Di dalam proses produksi diperlukan tiga jenis

mesin yang lama waktu pemakaian mesin berbeda untuk tiap-tiap produk.

Produk X memerlukan waktu 2 jam untuk proses produksi pada mesin A, 2

jam pada mesin B, dan 4 jam pada mesin C. Sedangkan produk Y memerlukan

waktu 1 jam pada mesin A, 3 jam pada mesin B, dan 3 jam pada mesin C.

Lamanya waktu mesin-mesin tersebut untuk beroperasi sangat terbatas. Dari

tiga jenis mesin terdapat 3 unit mesin tipe A yang beroperasi selama 10 jam per

hari per mesin, kemudian terdapat 6 unit mesin tipe B yang beroperasi selama 10

jam per hari per mesin, dan terdapat pula 9 unit mesin tipe C yang beroperasi

selama 8 jam per hari per mesin.

Penyelesaian :

Untuk menyelesaikan permasalahan tersebut, akan digunakan 4 langkah yang

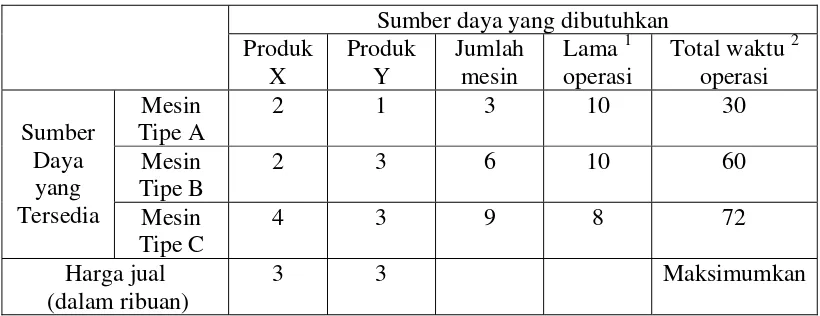
telah dipaparkan di muka. Apabila permasalahan tersebut disusun dalam bentuk

Sumber daya yang dibutuhkan Produk

X

Produk Y

Jumlah mesin

Lama 1 operasi

Total waktu 2 operasi Mesin

Tipe A

2 1 3 10 30

Mesin Tipe B

2 3 6 10 60 Sumber

Daya yang

Tersedia Mesin Tipe C

4 3 9 8 72

Harga jual (dalam ribuan)

3 3 Maksimumkan

Tabel 2.3.1 Tabel perumusan permasalahan untuk Contoh 2.3.1

1

Lama operasi dalam jam per hari per mesin

2

Total waktu operasi adalah jumlah mesin lama operasi

Langkah 1

Rumuskan permasalahan program linear tersebut ke dalam model matematika.

maksimumkan z = 3 x + 3 y (dalam ribuan)

dengan kendala 2 x + y ≤ 30

2 x + 3 y ≤ 60

4 x + 3 y ≤ 72

x 0 ; ≥ y 0 ≥

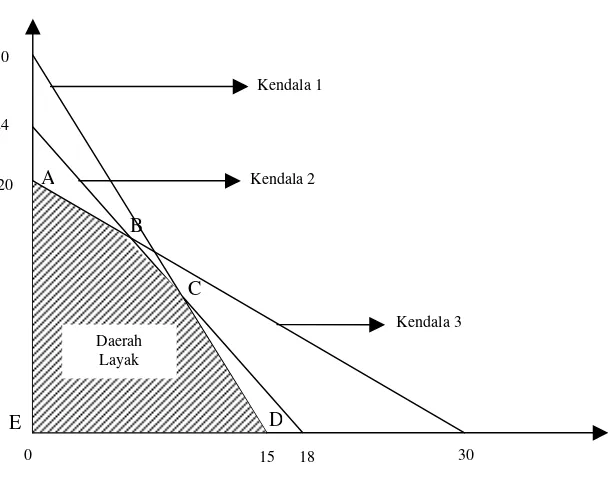
Langkah 2

Gambarlah sebuah grafik dua dimensi, dengan nilai produk X merupakan nilai

pada sumbu horisontal (absis), dan nilai produk Y pada sumbu vertikal (ordinat).

Lalu gambar pertidaksamaan kendala pada grafik dua dimensi tersebut. Sehingga

30

24

20 A

B

C

Kendala 1

Kendala 2

Kendala 3 Daerah

Layak

0

E D

30 18

15

Gambar 2.3.1 Daerah layak untuk Contoh 2.3.1

Dari perpotongan-perpotongan pertidaksamaan linear pada Gambar 2.3.1,

didapatkan daerah layak ABCDE yang merupakan perpaduan dari ketiga garis

tadi. Daerah layak ABCDE tersebut merupakan kombinasi dari berbagai titik

produk jenis X dan produk jenis Y yang memenuhi kendala yang diminta.

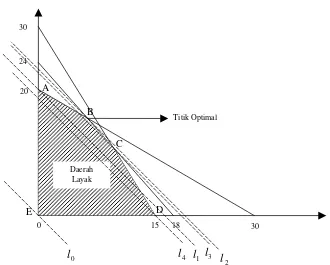
Langkah 3

Telitilah kelima titik ABCDE yang dapat memenuhi kriteria pengambilan

keputusan, yaitu yang menyebabkan pendapatan maksimum. Pendapatan akan

maksimum jika garis selidikmenyinggung titik atau puncak tertinggi dari daerah

layak tersebut atau dengan kata lain garis selidik harus digeser ke kanan.

Untuk memilih garis selidik yang menyinggung titik optimal dapat didukung

dengan menentukan kelima titik pada daerah layak. Yang perlu di analisis

1. Analisis titik B. Titik B merupakan perpotongan antara persamaan

2 x + 3 y = 60 dan

4 x + 3 y = 72

Jika kedua persamaan tersebut ditulis dalam matriks, maka menjadi

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 72 60 3 4 3 2 y x ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 96 36 6 1 72 60 2 4 3 3 6 1 y x Jadi, ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 16 6 y x

Dari hasil di atas dapat terlihat bahwa nilai x = 6 dan y = 16. Jadi, titik B

terletak pada (6,16).

2. Analisis titik C. Titik C merupakan perpotongan antara persamaan

2 x + y = 30 dan

4 x + 3 y = 72

Jika kedua persamaan tersebut ditulis dalam matriks, maka menjadi

Dari hasil di atas dapat terlihat bahwa nilai x = 9 dan y = 12. Jadi, titik B

terletak pada (9,12).

30

24

20 A

B

C

Daerah Layak

Titik Optimal

18 15

D E

0 30

3

l

l l l₁

2

l

4 0

Gambar 2.3.2. Garis selidik untuk Contoh 2.3.1

Dari Gambar 2.3.2 terlihat bahwa setelah garis selidik digeser ke kanan, pada

daerah layak didapat garis selidik yang menyinggung titik optimal yaitu garis l₂.

Langkah 4

Titik Produk X Produk Y

Nilai Pendapatan (dalam ribuan)

(z = 3 x + 3 y)

A 0 20 z = 3.0+3.20 = 60

B 6 16 z = 3.6+3.16 = 66

C 9 12 z = 3.9+3.12 = 63

D 15 0 z = 3.15+3.0 = 45

E 0 0 z = 3.0+3.0 = 0

Berdasarkan Gambar 2.3.2 dan Tabel 2.3.2, dapat disimpulkan bahwa titik B

merupakan titik optimal karena titik B menghasilkan nilai pendapatan tertinggi

sebesar Rp 66.000. Sedangkan kombinasi produksi yang efisien dan efektif adalah

6 unit produk X dan 16 unit produk Y.

D. Program Linear Dengan Metode Simpleks

Seperti diuraikan sebelumnya, permasalahan program linear tidak hanya dapat

diselesaikan dengan metode grafik. Tetapi dapat juga diselesaikan dengan metode

simpleks.

Perumusan program linear dapat ditulis dalam bentuk sebagai berikut :

minimumkan z = cTx (2.4.1)

dengan kendala Ax = b (2.4.2)

x ≥ 0

dengan b ≥ 0.

Misalkan xadalah penyelesaian layak basis, yang terdiri dari peubah basis

dan peubah nonbasis maka

B

x

N

x

(2.4.3)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =

B N

x x x

Misalkan cT adalah koefisien dari x pada fungsi tujuan yang terdiri dari koefisien

peubah basis dan koefisien peubah nonbasis . Maka fungsi tujuan dapat

ditulis sebagai berikut :

T B

c cTN

(2.4.4) B

x c x cT_{N N} T_B

z= +

[

N B

]

A= (2.4.5)

dengan B adalah matriks koefisien dari peubah pengetat untuk serta B

mempunyai invers dan N adalah matriks koefisien dari peubah pengambilan

keputusan untuk . Maka kendala

B

x

N

x Ax=b dapat dinyatakan sebagai berikut

(2.4.6)

[

]

x x b

x x

x _⎥= + =

⎦ ⎤ ⎢ ⎣ ⎡

= N B

B N B N B N A

Dari persamaan (2.4.6) didapat persamaan

= + B N B

Nx x b (2.4.7)

atau Bx_B =b−Nx_N (2.4.8)

maka peubah basis dapat ditulis sebagai berikut

(2.4.9)

N B B b B Nx

x = −1 − −1

Jika persamaan (2.4.9) disubstitusikan ke persamaan (2.4.4) maka akan

didapat

(

)

N

T N N T

B B B N

z=c −1b− −1 x +c x _(2.4.10)

atau N (2.4.11)

T N N T B T

BB B N

z=c −1b−c −1 x +c x

atau z=cT_BB−1b+

(

cT_N −cT_BB−1N

)

x_N (2.4.12) Misalkan = TBB−1 atau

T

c

y

(

)

B

T T T

BB B c

c

y= −1 = − , maka persamaan (2.4.12)

menjadi

(

)

N

T T N T

N

Peubah y disebut peubah pengali simpleks. Nilai-nilai untuk peubah basis dan

fungsi tujuan didapat dengan menentukan = 0, sehingga diperoleh

dan .

N

x

b

xB =bˆ=B−1 zˆ=cTB−1b

B

Misalkan cˆ_j adalah eleman peubah cˆT_N ≡

(

cT_N −cT_BB−1N

)

yang bersesuaian dengan x_j. Koefisien cˆ_j disebut nilai tereduksi untuk x_j.

Misalkan zˆ=cT_BB−1b dan cˆ_NT ≡

(

cT_N −cT_BB−1N

)

maka dari persamaan (2.4.12) dapat diperoleh

(2.4.14)

N T N

c z z= ˆ+ˆ x

Untuk menguji keoptimalannya, akan diselidiki apa yang terjadi pada fungsi

tujuan (2.4.14) jika setiap peubah nonbasis ditingkatkan dari nol.

(i) Jika cˆ_j> 0 maka fungsi tujuan akan meningkat, (ii) Jika cˆ_j= 0 maka fungsi tujuan tidak berubah, (iii) Jika < 0 maka fungsi tujuan akan menurun. cˆ_j

Jika basis yang sekarang belum optimal

(

xB <0

)

maka peubah xt (xt x )

dengan dapat dipilih menjadi basis baru.

∈ n

0 ˆ_t <

c

Jika peubah baru x_t telah dipilih, maka harus ditentukan seberapa besar x_t

dapat ditingkatkan sebelum kendala tak negatif dilanggar. Ini akan menentukan

peubah yang mana (jika ada) akan meninggalkan basis.

Untuk penyelesaian basis, = 0. Dengan demikian, kendala dapat

disederhanakan menjadi

N

x Ax=b

b x_B =

xt (2.4.15) t

B =bˆ−Aˆ

x

dengan bˆ=B−1b, Aˆt adalah peubah B At dengan adalah kolom ke-t dari A.

1

−

t

A

Untuk menentukan nilai x_t, persamaan (2.4.15) akan diuji menurut komponennya, yaitu

x_t (2.4.16)

( )

xB t =bˆi −aˆit

dengan aˆ_it komponen ke-i dari A_tdan bˆ_i adalah komponen ke-i dari . bˆ

(i) Jika aˆ_it > 0, maka

( )

x_{B i} akan berkurang akibat peubah x_t (yang masuk menjadi basis) bertambah besar, dan

( )

xB _i akan sama dengan nol jika

x_t it i a b ˆ ˆ = ,

(ii) Jika aˆ_it < 0, maka

( )

x_{B i} akan bertambah besar, (iii) Jika aˆ_it = 0, maka

( )

x_{B i} tidak berubah.

Dengan demikian peubah x_t dapat ditingkatkan sepanjang semua peubah tidak negatif, yaitu sampai mencapai nilai

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ > = ≤ ≤ 0 ˆ : ˆ ˆ

min

1 it it i m i t a a b

x (2.4.17)

Persamaan (2.4.17) merupakan uji rasio. Nilai minimum dari uji rasio

mengidentifikasi peubah nonbasis baru, sehingga dapat ditentukan penyelesaian

layak basis baru, dengan x_t adalah peubah basis barunya. Bentuk

dan

t t B B x Ax

Dapat digunakan untuk menentukan nilai baru dari fungsi tujuan dan peubah basis

di dalam basis yang baru. Peubah x_t merupakan pendekatan dari nilai x_t; peubah nonbasis yang lain masih bernilai nol.

Dalam permasalahan program linear yang berpola minimum, fungsi tujuan

akan makin diperkecil menuju ke nilai minimumnya. Uraian mengenai metode

simpleks di atas dapat disederhanakan dengan menggunakan tablo simpleks.

Secara garis besar, langkah-langkah menganalisis permasalahan program linear

yang berpola minimum dengan tablo simpleks adalah sebagai berikut:

1. Mengkonversi ke dalam bentuk kanonik.

2. Menyusun tablo.

Susun tablo awal dari persamaan yang sudah diubah dalam bentuk

kanonik. Tabel yang disebut dengan tablo simpleks digambarkan sebagai

berikut :

j

c c₁ c₂ . . . c_n

i

c xi\xj x1 x2 . . . xn bi Ri

1 c 2 c . . . m c 1 x 2 x . . . m x . . . 11

a a₁₂ a_1n

. . .

21

a a₂₂ a_2n

. . . . . . . . . . . . 1 m

a a_m2 a_mn

1 b 2 b . . . m b 1 R 2 R . . . m R j

z z₁ z₂ . . . zn z j

dengan :

j

x = peubah pengambilan keputusan ke-j

j

c = koefisien peubah pengambilan keputusan ke-j

ij

a = koefisien peubah pengambilan keputusan ke-j dalam kendala ke-i

i

b = nilai sebelah kanan dari kendala ke-i

i

x = peubah yang menjadi basis ke-i dalam tablo

i

c = koefisien peubah yang menjadi basis ke-i dalam tablo x_i

j

z =

∑

=

m i

i

c

1

ij

a (hasil kali dari c_i dengan kolom a_ij)

z =

∑

=

m i

i

c

1

i

b (hasil kali dari c_i dengan b_i)

j

z - c_j= selisih z_jdengan c_j

Tablo ini hanya berlaku pada iterasi awal saja. Pada iterasi-iterasi

berikutnya susunan tablo masih sama, hanya hasilnya saja yang berbeda

menurut operasi elementernya.

3. Menguji keoptimalannya.

Berdasarkan persamaan (2.4.14), tablo akan optimal jika memenuhi syarat :

j

z - c_j ≤ 0 untuk semua j

4. Memperbaiki tablo.

Memperbaiki tablo berarti mengganti satu peubah basis supaya

penyelesaian yang memenuhi kendala-kendala. Berdasarkan persamaan

(2.4.16), syarat untuk memilih peubah x_j supaya masuk menjadi basis adalah:

KUNCI I Pilih j dengan - > 0 yang terbesar, maka terpilih

untuk menjadi basis.

j

z c_j x_j

Selanjutnya, berdasarkan persamaan (2.4.17) dapat disusun Ri yaitu Ri=

ij i

a b

.

Dan pilihlah R_i dengan syarat :

KUNCI II Pilih i denganR_i yang terkecil, maka x_i terpilih untuk keluar dari basis.

Lalu baris-i disebut baris kunci dan unsur pada baris kunci yang juga pada

kolom kunci disebut unsur kunci.

Dalam permasalahan program linear dengan pola maksimum, beberapa

petunjuk akan berlawanan dengan petunjuk dalam pola minimum. Secara garis

besar, langkah-langkah menganalisis permasalahan program linear yang berpola

maksimum adalah sebagai berikut :

1. Mengkonversi ke dalam bentuk kanonik.

2. Menyusun tablo.

Susunan tablo awal sama dengan susunan tablo awal pada pola minimum.

3. Menguji keoptimalannya.

Tablo akan optimal jika memenuhi syarat :

- 0 untuk semua j

j

4. Memperbaiki tablo.

Memperbaiki tablo berarti mengganti satu peubah basis supaya

mendapatkan suatu penyelesaian baru yang layak, yaitu himpunan

penyelesaian yang memenuhi kendala-kendala. Syarat untuk memilih peubah

supaya masuk menjadi basis adalah :

j

x

KUNCI I Pilih j dengan - < 0 yang terkecil, maka terpilih

untuk menjadi basis.

j

z c_j x_j

Selanjutnya, tulis = R_i

ij i

a b

. Dan pilihlah R_i dengan syarat :

KUNCI II Pilih i denganRi yang terkecil, maka xi terpilih untuk keluar

dari basis.

Kunci II ini tidak berbeda dalam pola maksimum dan pola minimum, karena

tujuannya memang sama, yaitu supaya penyelesaian basis baru tetap juga

layak.

Lalu baris-i disebut baris kunci dan unsur pada baris kunci yang juga pada

kolom kunci disebut unsur kunci.

Agar lebih memahami langkah-langkah di atas, selesaikan permasalahan

program linear pada Contoh 2.3.1 dengan menggunakan metode simpleks.

Iterasi 1

Langkah 1

dengan kendala 2 x + y ≤ 30

2 x + 3 y ≤ 60

4 x + 3 y ≤ 72

x 0 ; ≥ y ≥ 0

Ubahlah pertidaksamaan di atas menjadi persamaan. Dengan menambahkan 3

peubah slack, soal akan menjadi bentuk kanonik yaitu sebagai berikut :

maksimumkan z = 3 x + 3 y + 0r + 0s + 0t

dengan kendala 2 x + y + 1r + 0s + 0t = 30

2 x + 3 y + 0r + 1s + 0t = 60

4 x + 3 y + 0r + 0s + 1t = 72

x 0 ; ≥ y ≥ 0 ; r≥ 0 ; s≥ 0 ; t≥ 0

r, s, t adalah peubah slack.

Langkah 2

Tablo awal dari masalah di atas adalah sebagai berikut

j

c 3 3 0 0 0

i

c xi\xj x y r s t b i R i

0

0

0

r

s

t

2 1 1 0 0

2 3 0 1 0

4 3 0 0 1

30

60

72

30

20

24

j

z 0 0 0 0 0 0

j

Langkah 3

Dari tablo awal di atas, masih ada - < 0. Jadi, tablo awal belum optimal

atau maksimum.

j

z c_j

Langkah 4

Dengan membuat nilai kedua peubah bebas x dan y adalah nol akan

diperoleh

(x, y, r, s, t) = (0, 0, 30, 60, 72) (2.4.1)

Persamaan fungsi tujuan z = 3 x + 3 y + 0r + 0s + 0t dapat ditulis

z - 3 x - 3 y - 0r - 0s - 0t = 0 (2.4.2)

Bila (2.4.1) dimasukkan dalam fungsi tujuan diperoleh nilai

z = 3.0 + 3.0 + 0.30 + 0.60 + 0.72 = 0

Dan nilai 0 inilah yang diperoleh z dalam tablo awal yang artinya pada iterasi

1 ini industri tersebut belum mulai berproduksi dan tablo awal harus diperbaiki.

Dalam tablo awal di atas x₁, x₂ = min

{

z_j −c_j

}

. Misal pilih yang masuk menjadi basis. Jadi kolom disebut kolom kunci. = min

{

. Maka

2

x

2

x R₂ Ri

}

x2

terpilih untuk keluar dari basis. Dan baris x₂ disebut baris kunci. Dengan demikian unsur kuncinya adalah 3.

Iterasi 2

Langkah 2

j

c 3 3 0 0 0

i

c xi\xj x y r s t b i R i

0

3

0

r

Y

T

1,33 0 1 -1,33 0

0,66 1 0 0.33 0

2 0 0 0 1

10

20

12

7,5

30

6

j

z 2 3 0 1 0 60

j

z - c_j -1 0 0 1 0 60

Tablo Kedua

Langkah 3

Dari tablo kedua di atas masih ada - < 0. Jadi tablo kedua belum

optimal.

j

z c_j

Langkah 4

1

x = min

{

zj −cj

}

, jadi kolom terpilih sebagai kolom kunci. Dan artinya

masuk ke dalam basis. = min

1

x

1

x R₃

{ }

R_i . Oleh karena itu baris x3 terpilih

menjadi baris kunci dan x3 terpilih untuk keluar dari basis. Setelah mendapatkan

kolom kunci dan baris kunci, ditemukanlah unsur kunci yaitu 2.

Iterasi 3

Langkah 2

j

c 3 3 0 0 0

i

c xi\xj x y r s t b i R i

0

3

3

r

y

x

0 0 1 -0,33 -0,66

0 1 0 0,33 0,33

1 0 0 0 0,5

2

16

6

j

z 3 3 0 1 0,5 66

j

z - c _j 0 0 0 1 0,5 66 Tablo Ketiga

Langkah 3

Dari tablo ketiga diatas, - sudah memenuhi syarat - 0 untuk

semua j. Jadi, tablo ketiga sudah optimal dan tablo tersebut dapat disebut sebagai

tablo optimal.

j

z c_j z_j c_j ≥

Nilai peubah basis r, y, x sudah dapat terbaca pada kolom yaitu 2, 16, 6,

sedangkan nilai s, t adalah nol karena mereka bukan peubah basis. Sehingga

penyelesaian optimal soal ini adalah

i

b

(x, y, r, s, t) = (6, 16, 2, 0, 0)

dengan nilai program z = 66.

Jadi, penyelesaian optimalnya adalah z = Rp 66.000 dengan kombinasi

Apabila perumusan di atas ditulis dalam program QM maka menjadi

Penyelesaian optimal dari permasalahan di atas adalah

( ) (

x,y = 6,16

)

dengan

nilai z_maks =66.

E. Dualitas Dalam Program Linear

Dalam pembicaraan mengenai program linear dan beberapa model yang

terkait, timbul hubungan dual antara dual soal program linear tertentu dan

masing-masing penyelesaian optimumnya akan berkaitan sehingga setiap persoalan

program linear selalu memiliki dua macam analisis, yaitu analisis primal dan

analisis dual yang biasanya disebut analisis primal-dual.

Untuk dapat menyusun suatu permasalahan program linear ke dalam dual,

maka selalu harus dirumuskan terlebih dahulu ke dalam bentuk kanonik. Kendala

utama suatu permasalahan program linear dapat memuat kendala dengan

hubungan

( )

≤ atau

( )

≥ atau

( )

= . Untuk keperluan dualitas maka kendala utama

suatu permasalahan perlu diubah sehingga semua hubungannya berbentuk

( )

≤

atau semua berbentuk

(

. Hal ini dapat dikerjakan bila tidak ada syarat bahwa

0.

)

≥

i

b ≥

Jika bentuk masalah primal

P. maksimumkan z =

∑

=

n j

j c

1

j

x

dengan kendala

∑

=

n j

ij a

1

j

x ≤ b_i i = 1, 2, 3, ..., p

0

≥

j

maka masalah tersebut dapat diubah ke dalam bentuk minimum, yaitu dengan

mengganti koefisien peubah pengambilan keputusan pada fungsi tujuan dengan

nilai sebelah kanan dari kendala ke-i. Selain itu, fungsi kendalanyapun berubah di

mana nilai sebelah kanan dari kendala ke-i menjadi koefisien peubah pengambilan

keputusan dalam fungsi tujuan dan peubah pengambilan keputusannya menjadi y

atau variabel yang lain. Untuk lebih jelasnya, model di atas dapat diubah menjadi

sebagai berikut :

D. minimumkan z =

∑

=

p i

i b

1

i

y

dengan kendala

∑

j = 1, 2, 3, ..., n

=

p i

ij a

1

i

y ≥ cj

0

≥

i

y

Bila kasus pemrograman linear yang asli kita sebut primal, maka kasus

pemrograman yang lain yang berkaitan dengannya kita sebut dual.

Untuk lebih memahami, akan diberikan suatu permasalahan program linear.

Contoh 2.5.1

Diketahui soal primal

minimumkan z=2x₁ +6x₂ +7x₃

dengan kendala x₁ +2x₂ +5x₃ ≥4 3 2 2x₁ −x₂ + x₃ ≥

1 5

3x₁ + x₂ +x₃ ≥

0 , , _{2 3}

1 x x ≥

Ubah dalam bentuk dual dan tentukan penyelesaian optimal soal primal.

Penyelesaian :

Soal dualnya menjadi

maksimumkan g =4u+3v+w

dengan kendala u+2v+3w≤2

6 5 2u−v+ w≤

7 2

5u+ v+w≤

0 , ,v w≥ u

Iterasi 1

Langkah 1

Ubah pertidaksamaan di atas menjadi persamaan. Dengan menambahkan 3

peubah slack, soal akan menjadi bentuk kanonik yaitu sebagai berikut :

maksimumkan g =4u+3v+w+0a+0b+0c

dengan kendala u+2v+3w+a=2

6 5

2u−v+ w+b=

7 2

5u+ v+w+c=

0 , , , ,

,v w a b c≥ u

a, b, c adalah peubah slack.

Langkah 2

j

c 4 3 1 0 0 0

i

c x_i\x_j u v w a b c b i R i

0

0

0

a

b

c

1 2 3 1 0 0

2 -1 5 0 1 0

5 2 1 0 0 1

2

6

7

2

3

5 7

j

z 0 0 0 0 0 0 0

j

z - c_j -4 -3 -1 0 0 0 Tablo Awal

Langkah 3

Dari tablo awal di atas, masih ada - < 0. Jadi, tablo awal belum optimal

atau maksimum.

j

z c_j

Langkah 4

Dalam tablo awal di atas x₁ = min

{

zj −cj

}

. Jadi masuk menjadi basis.

Kolom disebut kolom kunci. Dalam tablo awal, = min

{

. Maka

1

x

1

x R₃ Ri

}

x3

terpilih untuk keluar dari basis. Jadi, baris x₃ disebut baris kunci. Dengan demikian unsur kuncinya adalah 5.

Iterasi 2

Langkah 2

j

c 4 3 1 0 0 0

i

c xi\xj u v w a b c b i R i

0 0 4 a b u 0 5 8 5 14

1 0 -5 1

0 -5 9

5 23

0 1 -5 2 1 5 2 5 1

0 0 5 1 5 3 5 16 5 7 8 3 -9 16 2 7 j z 4 5 8 5 4

0 0 5 4

5 28

j

z - c_j

0 -5 7

-5 1

0 0 5 4

Tablo Kedua

Langkah 3

Dari tablo kedua di atas masih ada - < 0. Jadi tablo kedua belum

optimal.

j

z c_j

Langkah 4

2

x = min

{

zj −cj

}

, jadi kolom terpilih sebagai kolom kunci. Dan artinya

masuk ke dalam basis. = min

2

x

2

x R₁

{ }

R_i . Oleh karena itu baris x₁ terpilih

menjadi baris kunci dan x₁ terpilih untuk keluar dari basis. Setelah mendapatkan kolom kunci dan baris kunci, ditemukanlah unsur kunci yaitu

5 8

Iterasi 3

Langkah 2

Setelah itu dapat disusun tablo baru yaitu tablo ketiga.

j

c 4 3 1 0 0 0

i

c x_i\x_j u v w a b c b i R i

0 0 4 v b u

0 1 8 14

8 5

0 -8 1

0 0 4 31

8 9

1 -8 5

1 0 -2 1 -4 1 0 4 1 8 3 8 31 4 5 j z

4 3 8 26 8 7 0 8 5 8 49 j

z - cj _{0 0}

8 18 8 7 0 8 5 Tablo Ketiga Langkah 3

Dari tablo ketiga diatas, - sudah memenuhi syarat - 0 untuk

semua j. Jadi, tablo ketiga sudah optimal dan tablo tersebut dapat disebut sebagai

tablo optimal.

j

z cj zj cj ≥

Dari tablo optimal di atas penyelesaian optimal bagi soal dual sudah dapat

terbaca secara langsung pada kolom b i yaitu

(

)

⎟

⎠ ⎞ ⎜

⎝ ⎛ = ,0

8 3 , 4 5 ,

,v w

u dengan nilai

8 49

=

maks

g . Dari tablo optimal di atas juga dapat diperoleh penyelesaian soal

peubah slack berada. Sehingga penyelesaian optimal bagi soal primal adalah

(

)

⎟

⎠ ⎞ ⎜

⎝ ⎛ =

8 5 , 0 , 8 7 ,

, _{2 3}

1 x x

x dengan nilai

8 49

=

maks

z .

Berikut akan diberikan penyelesaian menggunakan QM. Permasalahan yang

pertama diketahui adalah masalah primal. Jadi, dicari penyelesaian permasalahan

Hasil penyelesaian dari permasalahan di atas, akan ditunjukkan dalam tabel

optimal sebagai berkut

Dari tablo optimal di atas dapat diketahui bahwa penyelesaian optimal untuk

masalah primal adalah

(

)

⎟

⎠ ⎞ ⎜

⎝ ⎛ =

8 5 , 0 , 8 7 ,

, _{2 3}

1 x x

x dengan nilai

8 49

=

maks

z . Dari tablo

optimal tersebut dapat diketahui penyelesaian optimal untuk masalah dual, yaitu

pada sisi paling kanan dan dibaca dari atas. Dan apabila ada penyelesaian yang

bernilai negatif, maka penyelesaian tersebut haruslah bernilai positif. Jadi,

penyelesaian optimal dari masalah dual adalah

(

)

⎟

⎠ ⎞ ⎜

⎝ ⎛ = ,0

8 3 , 4 5 ,

, _{2 3}

1 x x

x dengan nilai

8 49

=

maks

40

Pada bagian sebelumnya telah dibahas lebih jauh mengenai program linear.

Pada bab ini akan dibahas lebih jauh mengenai program tujuan ganda. Program

tujuan ganda memiliki beberapa fungsi tujuan. Maka tidak mudah untuk

mendapatkan penyelasaian serentak yang memenuhi semua fungsi tujuan. Untuk

menyelesaikannya terdapat beberapa cara, misalkan dengan menggunakan

efisiensi dan deviasi. Dalam program tujuan ganda semua fungsi tujuan harus

diubah dahulu supaya diperoleh satu fungsi tujuan saja. Salah satu ide untuk

menyelesaikan masalah program tujuan ganda menggunakan efisiensi adalah

mengalikan setiap fungsi tujuan dengan faktor bobot sesuai dengan prioritasnya

dan kemudian menambahkan fungsi-fungsi tujuan tersebut. Faktor bobot dipilih

untuk menggambarkan pentingnya tujuan sesuai dengan prioritasnya. Di dalam

kasus ini, fungsi tujuan dikhususkan untuk dimaksimumkan saja.

A. Faktor Bobot Dalam Masalah Program Tujuan Ganda

Secara umum, masalah program tujuan ganda yang memiliki m fungsi tujuan

linear adalah sebagai berikut

maksimumkan

∑

=

= n

j j kjx c z

1

k = 1, 2, 3, ..., m

dengan kendala

∑

=

n j

ij a

1

j

x ≤ bi i = 1, 2, 3, ..., p

0

≥

j

dengan :

j

x = peubah pengambilan keputusan ke-j

kj

c = koefisien peubah pengambilan keputusan ke-j dalam fungsi tujuan ke-k

ij

a = koefisien peubah pengambilan keputusan ke-j dalam kendala ke-i

n = banyaknya peubah pengambilan keputusan

m = banyaknya fungsi tujuan

p = banyaknya kendala

Untuk lebih memahami program tujuan ganda dengan faktor bobot, akan

diberikan contoh sebagai berikut

Contoh 3.1.1

Sebuah pabrik dapat menghasilkan 3 produk, yaitu A, B, dan C. Pabrik

tersebut memiliki persediaan 250 unit untuk input tipe I dan 210 unit untuk input

tipe II. Produk A membutuhkan 7 unit input tipe I dan 6 unit input tipe II, produk

B membutuhkan 5 unit input tipe I dan 9 unit input tipe II, dan produk C

membutuhkan 6 unit input tipe I dan 5 unit input tipe II.

Jika x₁, x₂, danx₃ masing-masing adalah variabel untuk satu produk A, B, dan C maka jumlah yang dihasilkan oleh pabrik tersebut jika ditulis dalam

pertidaksamaan adalah sebagai berikut :

2507x₁ +5x₂ +6x₃ ≤

2106x₁ +9x₂ +5x₃ ≤

0 , , _{2 3}

1 x x ≥

x

Misalkan harga jual dari produk A, B, dan C adalah 1; 0,8; dan 0,9 (dalam

ratusan ribu). Jika pabrik ingin memaksimumkan total pendapatannya, maka dapat

didefinisikan fungsi tujuan sebagai berikut

3 2

1

1 x 0,8x 0,9x

z = + + (3.1.2)

Selain itu, pabrik juga merasa bahwa total penjualan sangat penting. Maka

pabrik juga perlu memaksimumkan

3 2 1

2 x x x

z = + + (3.1.3)

Pabrik juga akan memaksimumkan ekspor. Jika 40% dari produk A, 60%

produk B, dan 20% produk C yang dihasilkan diekspor, maka pabrik akan

memaksimumkan

3 2

1

3 0,4x 0,6x 0,2x

z = + + (3.1.4)

Jika dipilih faktor bobot 10 untuk pendapatan, 1 untuk penjualan, dan 5 untuk

ekspor, maka fungsi tujuan pada persamaan (3.1.2), (3.1.3), dan (3.1.4)

masing-masing akan menjadi

= ∗

1

z 10 *

(

x₁+0,8x₂ +0,9x₃

)

= 10x₁ + 8x₂ + 9x₃ (3.1.5)

= ∗

2

z 1 *

(

x₁+x₂ +x₃

)

=x₁ +x₂ +x₃ (3.1.6)

= ∗

3

z 5 *

(

0,4x₁ +0,6x₂ +0,2x₃

)

=2x1 + 3x2 +1x3 (3.1.7)

Jika ketiga persamaan tersebut dijumlahkan maka diperoleh fungsi tujuan

Apabila permasalahan di atas dirumuskan dalam program linear, maka

menjadi

maksimumkan z = 13x₁+12x₂ +11x₃

dengan kendala 7x₁ +5x₂ +6x₃ ≤250

6x₁ +9x₂ +5x₃ ≤210

0 , , _{2 3}

1 x x ≥

x

Pada kendala di atas, banyaknya variabel lebih besar daripada banyaknya

pertidaksamaan kendala, maka ada satu variabel yang bebas. Misalkan x₂ =0. Jadi perumusan masalah program linear berubah menjadi

maksimumkan z = 13x₁ +11x₃

dengan kendala 7x₁ +6x₃ ≤250

6x₁ +5x₃ ≤210

0 , ₃

1 x ≥

x

Permasalahan di atas akan diselesaikan menggunakan metode simplek.

Jika perumusan permasalahan di atas diubah menjadi bentuk kanonik, maka

dengan menambahkan peubah slack perumusan menjadi

maksimumkan z = 13x₁ +11x₃ +0r+0s

dengan kendala 7x₁ +6x₃ +r =250 2106x₁ +5x₃ +s=

0 , , , ₃

1 x r s≥

x

Permasalahan di atas akan diselesaikan menggunakan program QM.

Perumusan permasalahan di atas dalam QM adalah sebagai berikut

Dari perumusan di atas, didapat tablo optimal sebagai berikut

Dari tablo optimal di atas diperoleh penyelesaian optimal, yaitu

Secara umum, jika wk adalah bobot untuk fungsi tujuan ke-k maka dapat

dirumuskan model sebagai berikut :

(

w wm

)

LP ₁,L, :

maksimumkan

∑∑

(

)

= =

= m

k n j

j kj kc x w z

1 1

dengan kendala

∑

=

≤

n j

i j ijx b a

1

i = 1, . . . , p

0

≥

j

x untuk semua j

dengan :

k

w = bobot untuk fungsi tujuan ke-k

j

x = peubah pengambilan keputusan ke-j

kj

c = koefisien peubah pengambilan keputusan ke-j dalam fungsi tujuan ke-k

ij

a = koefisien peubah pengambilan keputusan ke-j dalam kendala ke-i

i

b = nilai di sebelah kanan dari kendala ke-i

n = banyaknya peubah pengambilan keputusan

p = banyaknya kendala

B. Penyelesaian Efisien

Pada program tujuan ganda yang memiliki beberapa tujuan, tidak mudah

untuk mendapatkan penyelesaian yang dapat memaksimumkan semua fungsi

penyelesaian layak. Kemudian membandingkan dua dari beberapa penyelesaian

layak tersebut supaya mendapatkan penyelesaian yang efisien.

Definisi 3.2.1

Penyelesaian layak

(

x₁,L,x_n

)

mendominasi

(

y₁,L,y_n

)

, jika

∑

∑

= =

≥ n

j

j kj n

j

j

kjx c y c

1 1

untuk semua k (3.2.1)

dan

∑

∑

= =

> n

j

j kj n

j

j

kjx c y c

1 1

untuk paling sedikit satu k (3.2.2)

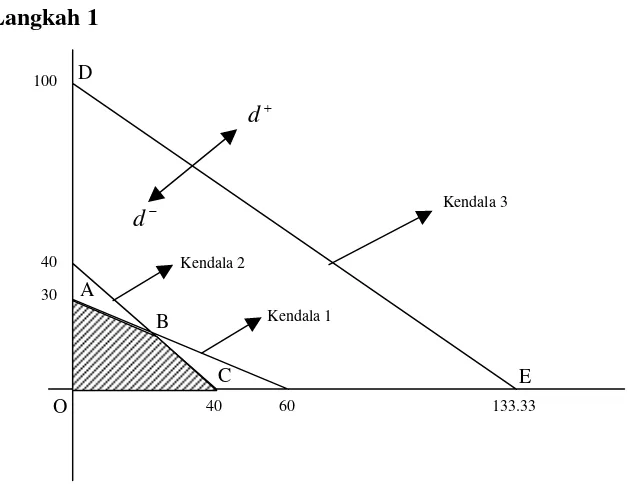
Contoh 3.2.1

maksimumkan z₁ = x₁ +x₂ +x₃

3 2 1

2 2x 3x x

z = + +

dengan kendala 7x₁ +5x₂ +6x₃ ≤250 210 5

9

6x₁ + x₂ + x₃ ≤

0 , , _{2 3}

1 x x ≥

x

Misal ambil beberapa titik, yaitu A

(

10,4,12

)

, B

(

17,9,5

)

, C

(

16,7,7

)

, D

(

10,10,10

)

,

dan E

(

13,10,8

)

. Titik-titik tersebut merupakan penyelesaian layak jika memenuhi

semua kendala. Akan diuji apakah titik-titik tersebut layak atau tidak.

1. Titik A

(

10,4,12

)

7.10 + 5.4 + 6.12 = 162 < 250