長大橋非定常空気力の数値予測に関する基礎的研究
A fundamental study on numerical prediction of
unsteady aerodynamic forces for long-span bridges
2003
年
3
月
目 次 第1章 序論 1 1.1 本研究の背景 1 1.2 従来の研究の概要 4 1.3 本研究の概要 5 第2章 計算手法 8 2. 1 非圧縮性粘性流れの基礎方程式 8 2.1.1一般座標 8 2.1.2質量保存の式(連続の式) 10 2.1.3運動量の保存式 12 2.1.4基礎方程式のまとめ 17 2.2 数値計算法 18 2.2.1 擬似圧縮性解法 18 2.2.2 風上差分法 21 2.2.3 陰的解法 26 2.2.4 境界条件 28 2.3 乱流モデル 31 2.3.1 平均流の方程式 31 2.3.2 レイノルズ応力の方程式 32 2.3.3 乱流のモデル化 35 2.3.4 乱流モデルの選択 38 2.3.5 k – ε モデル 40 2.3.6 k – ω モデル 44 2.3.7 k – ωSSTモデル 47 第3章 解析コードの検証 55 3.1 層流の計算 55 3.1.1 正方キャビティ内流れ 55 3.1.2 円柱まわりの流れ 58
3.1.2.1 衝撃的に始動した円柱まわりの流れ 58 3.1.2.2 渦放出を伴う円柱まわりの流れ 65 3.2 乱流の計算 68 3.2.1 平板上の高レイノルズ数流れ 68 3.2.2 翼型まわりの流れ 71 3.2.3 2次元非対称ディフューザ流れ 75 3.2.4 2次元バックステップ流れ 77 第4章 長大橋非定常空気力の数値予測 80 4.1 振動翼型まわりの流れの数値計算 81 4.1.1 一定の角速度で急激に回転する翼型まわりの流れ 81 4.1.2 大振幅で運動する翼型まわりの流れ 84 4.2 長大橋一箱桁断面に作用する非定常空気力の数値予測 93 4.2.1 非定常圧力 93 4.2.2 非定常空気力 97 4.3 矩形断面柱に作用する非定常空気力の数値予測 104 4.4 2箱桁断面に作用する非定常空気力の数値予測 114
4.4.1 重合格子法(Chimera Grid Scheme) 114
4.4.2 Chimera コードの検証 117
4.4.3 長大橋2箱桁断面 121
4.4.4 基本形状2箱桁断面 124
第5章 結論 141
第1章 序論 1.1 本研究の背景 タコマ橋の落橋事故(図-1.1)に端を発する長大橋の耐風設計では,耐フラッター性能の評 価がまず考慮されるべき項目となっている.設計の立場から真に知りたいのはもちろん自然風 下での実橋の耐風応答性能であるが,それを前以て直接的に知ることは出来ず,模型実験の結 果から推定せざるを得ない.長大橋の耐風性を検討・評価する方法としては,現在でも3次元 全橋弾性模型を用いた風洞実験によるのが最も信頼性が高いと考えられている.しかし,高価 であるため日常的に実施することは困難である.その代替として,従来から橋桁部分模型を用 いた風洞実験が行われてきた.現在では,立体骨組全橋FEMモデルを用いたフラッター解析 の手法が確立されている.ただし,構造諸元には実橋のものを用いても,外力項の非定常空気 力は橋桁部分模型を用いた風洞実験の結果を用いざるを得ない.この非定常空気力を求める部 分(風洞実験)が,長大橋のフラッター解析の中で最も時間・費用がかかる部分となっている. 図-1.1 タコマ橋の落橋 ( http://www.pubs.asce.org/ceonline/art/art02/1102feat3a.jpg ) 非定常空気力という言葉には一般的な響きがあるが,ここでは狭い意味に限定して用いられ ている.静止した物体であっても,それに作用する流体力はカルマン渦などの非定常な現象に より一般には時間とともに変動している.しかし,空気力学の分野では, 振動する物体に作 用する変動空気力(の物体の振動と同じ周波数成分)を特に,(狭義の)非定常空気力と呼ん
でいる.非定常空気力はフラッタ−のような空気力の連成によって生ずる自励振動の解析に用 いられる.非定常空気力の役割を見るために以下でフラッタ−解析について簡単に触れる. 橋桁部分模型のような2自由度モデル(図-1.2)を考えるとその運動方程式は次のようにな る.
L
y
k
y
c
y
m
&&
+
y&
+
y=
(1.1)M
k
c
I
θ
&&
+
θθ
&
+
θθ
=
(1.2) ここで,mは物体の質量,c
y,k
yはそれぞれ撓み(上下)振動における減衰定数とばね定数,I
は慣性モーメント, , はそれぞれ捩れ(回転)振動における減衰定数とばね定数であ る.上式中の外力 および θc
k
θL
M
が非定常空気力で,それぞれ揚力および空力モーメントを表す. y U∞ θ M L 図-1.2 2自由度モデル 非定常空気力は,微小振動を仮定した場合,次のような線形式で表される.
⋅
+
⋅
=
πρ
ω
LηC
Lθθ
B
y
C
B
L
3 2 (1.3)
⋅
+
⋅
=
πρ
ω
MηC
Mθθ
B
y
C
B
M
4 2 (1.4) ここで,B
は橋桁の幅を表す.C
などは非定常空気力係数とよばれ,物体の形状が決まれば, 無次元振動数とレイノルズ数の関数であるが,通常,レイノルズ数依存特性は無視される.ま た,上式では位相も考慮しているので非定常空気力係数も複素数で表される.式(1.3),(1.4) を式(1.1),(1.2)に代入し,調和振動を仮定して, η L t ie
y
y
=
0 ω t ie
ωθ
θ
=
0 とおけば,(
)
(
4)
0
2 3 2 3 2 2 2=
+
−
+
⋅
−
⋅
−
+
−
+
θ
πρ
ω
ω
πρ
ω
πρ
ω
πρ
ω
ω
θ θ θ η θ ηy
C
B
I
c
i
k
C
B
C
B
C
B
m
c
i
k
M M L L y y (1.5) となる.したがって,(
)
(
4)
0
2 3 2 3 2 2 2=
+
−
+
⋅
−
⋅
−
+
−
+
θ θ θ η θ ηπρ
ω
ω
πρ
ω
πρ
ω
πρ
ω
ω
M M L L y yC
B
I
c
i
k
C
B
C
B
C
B
m
c
i
k
(1.6) を解けばよい.具体的な解法は省略し,図-1.3 に解析結果の一例を示す.式(1.6)のω の実部 は振動数を表し,虚部は減衰を表すから図-1.3 にはその両方が描かれている.図中,点Aに おいて減衰が正から負へと変化しており,この無次元振動数でフラッターが始まることがわか る.振動数は対応する実数部として得られているので,フラッターが発生し始める風速(フラ ッタ−限界風速)も分かる.また,対応する固有ベクトルからは,撓み・捩れの振幅比と位相 差が得られる.以上のように,非定常空気力が分かれば,耐風設計上最も重要なフラッター限 界風速やその振動形態を知ることができる. 平板のような薄翼については,次節に述べるように非定常空気力の理論解が存在する.しか しながら,橋梁断面の場合,その形状の複雑さから理論解は存在せず,そのまわりの流れが剥 離流であることから,そもそもポテンシャル流れの適用も疑問視されるため,一般には,前述 のように部分模型を用いて風洞実験から非定常空気力を求めることが行われている. 0 2 4 6 8 10 0.05 0.1 0.15 0.2Frequency
fB/U
-0.4 0 0.4 0.05 0.1 0.15 0.2 Logarithmic Damping fB/U A 図-1.3 フラッタ−解析結果の例 耐風設計の第一義的な目標はフラッターを防止することであるといってもよい.その防止対 策としては,①構造減衰を増す,②剛性を増す,③空気力学的考察から桁形状を改良する,な どが考えられる.しかし,①は実際上,困難である.②も困難である上,今日の経済性への要 求とも相容れない.したがって,③が唯一実際上とりうる対策といえる. 一方,近年の急速な計算機性能の向上とともに流れの数値計算が航空などの分野を中心とし て大きな進歩をとげてきた.流れの数値計算は全物理量が全ての時間・空間で得られるので, 流れの様子を可視化することも実験に比べ非常に容易であるといった長所を持ち,流れの面から断面形状を改良し耐風安定性を向上させることに貢献する可能性をもつ,と考えられる.加 えて,将来,橋梁断面の非定常空気力が流れの数値計算により精度よく求まるようになれば, 橋梁のフラッター解析もその半実験的な性格を脱することができ工学的な意義は大きいと言 える. 1.2 従来の研究の概要 非定常空気力は翼のフラッターが問題となった航空分野で最初に精力的に研究が行われた. 解析的な研究のみを概観すると,まず,Prandtlに指導を受けたBirnbaum1)( 1924 )の先駆的
な研究に始まり,Wagner2) ( 1925 ), Glauert3) ( 1929 ), Kussner4) ( 1929 )らの研究を経て,
Theodorsen5) ( 1935 )の古典的な振動翼の理論に至る.Theodorsenは,鉛直方向と回転方向に 振動する2次元平板に対する非常に簡明な理論の構築に成功した.平板の運動を,その上下面 においた湧き出しと吸い込みの組み合わせで表し,平板の運動による後流の渦は主流と同じ速 度で平板延長線上に流れ去るとの仮定のもと,両者を重ね合わせて振動平板まわりのポテンシ ャル流れを表現した. 後流に置かれた渦による流れが平板に沿う流れとなるためには,同じ 強さで向きが反対の渦を平板内に置かなければならない(平板が等角写像される円柱に関する 鏡像)が,これら循環(渦)の強さは,平板後端で流速が無限大にならないというKuttaの条 件から決定される.こうして,鉛直方向および回転方向に振動する平板に作用する空気力が Bessel (あるいは Hankel )函数を用いて,無次元振動数(振動数に平板長をかけ流速で割 ったもの)の関数として解析的に表せることを示した.Theodorsen らの理論は,米国におけ る戦前・戦中の航空機を対象としたフラッター解析の発達に大きな役割を果たした. 橋梁の分野では,まず,Bleich6) ( 1949 )がTheodorsenの空気力を半実験的に拡張して吊橋 断面に作用する非定常空気力を求めた.しかし,金子 7)( 1962 )の数値的な検討によると, Bleichの手法は,平板とかなり異なる断面形状に拡張するさいに無理な点がでてくるようであ った.非流線形の形状を持ち,一般に流れがその表面上で剥離するような橋梁断面に作用する非 定常空気力を解析的に求めようとする試みは以後ほとんど見られず,気流中で模型を強制加振 し,直接空気力を取り出す実験的方法がとられてきた.今日の実験法の基礎となったのは, Ukeguchiら8)( 1966 )の方法である. 1980 年代に入ると,計算機および計算法の発達に伴い,CFD( Computational Fluid
Dynamics )を橋梁(に関連したBluff Bodyまわりの流れ)に適用しようという研究が盛ん
た断面に作用する時間平均的な抗力・揚力の推定に主な関心があったようである(あるいは, 最終的な目標はフラッターなどの空力弾性振動であっても,研究のステップとして,まず静止 した断面の解析を行っていたという方が実状に近いのかもしれない).90 年代にはいって, 野村9) ( 1992 ) は,ALE有限要素法を用いて低Re数流れにおける円柱の渦励振の解析を試み ている.以後,橋梁分野においても流体・構造連成解析の研究が増えていった. CFDと言うと,通常,暗黙のうちに,Navier-Stokes方程式系の数値解析を想定するので, そういった意味では,CFDの解析例とは言えないが,Larsenら10) ( 1997 ) は離散渦法を用い て橋梁断面に作用する非定常空気力の解析を試みている.離散渦法の解析結果の信頼性につい ては議論のあるところではあるが,一般には,実験的に求める以外に方法がないと考えられて いた橋梁断面の非定常空気力が計算により求められたことのインパクトは,特に耐風設計の実 務に関わっている人々にとって小さくはなかったようである. Navier-Stokes系の計算では,橋梁断面ではないが,加藤11)( 1997 )が標準k-ε乱流モデ ルの生成項を修正したKato-Launderモデルを用いて正方角柱のたわみ振動時の非定常空気力 を計算している.また,嶋田ら12)は( 1998 )は,粘性底層では1方程式モデル(長さスケー ルは代数的に与える)を,それより外側ではKato-Launderモデルを用いる2-Layerモデルに よって,B/D=2および4の角柱のたわみ振動時の非定常空気力を求めた.Navier-Stokes系の 基礎方程式を用いた橋梁断面の非定常空気力の計算としては,Jenssenら13)( 1999 )がLES
解析を用いてGreat Belt East橋の非定常空気力の計算結果を報告したのが最初であろう.し
かしながら,彼らの計算結果は実験結果との一致が必ずしも良好ではなかった.翌年( 2000 ), 著者14)は,k -ω SST 乱流モデルを用いて偏平箱桁断面の非定常空気力が精度よく予測できる ことを示した. 1.3 本研究の概要 本研究は,橋梁に作用する非定常空気力を予測する数値解法の開発を目的としている.橋梁 まわりの流れの特性から,数値計算でシミュレートされるべき現象としては,剥離,再付着な どが挙げられる.従って,基礎方程式はNavier-Stokes系の方程式でなければならない.本研 究では,まず,その第一段階として,Navier-Stokes系の計算の中でも計算負荷の小さい2次
元RANS(Reynolds-Averaged Navier-Stokes Simulation)を用いて橋梁断面に作用する非定常空
気力を予測することの可能性について検討した.RANSに用いられる乱流モデルは,代数モデ
程式モデルが精度と経済性のバランスが最もよいと考えられる.2方程式モデルの中で最も一
般的な標準 k - ε モデルでは壁面近傍の領域は解像せずに wall function を用いる.しかしなが
ら,剥離や再付着の生ずる橋梁断面まわりの流れ場に対しても wall function が有効かどうかは
明らかではない.
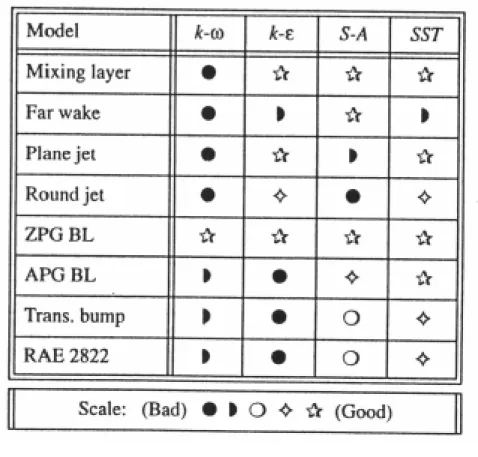
Bardinaら15)は,wall functionを用いずに壁近傍の領域も解く,所謂,低 Re 数型に属する4
つの乱流モデル(Launder-Sharma k - ε16),Wilcox k - ω17),Spalart-Allmaras18)およびMenter k -
ω SST19)を取り上げ,様々な流れ場に対するそれらモデルの性能評価を行い,相対評価では k -
ω SST (Shear Stress Transport) が最も優れた結果を与えたと報告している.本研究では,2次
元 RANS が橋梁断面の非定常空気力の予測に有効かどうかを調べる第一ステップとして,k - ω SSTモデルを用いたRANS計算コードを作成し,その適用性を検討した. 橋梁断面を対象とした強制振動法による非定常空気力の計測では,通常,比較的小振幅の範 囲の振動のもとで計測が行われる.しかしながら,非定常空気力の振幅依存性は無視し得ない テーマの一つであり,また,最近では橋梁断面を対象としたものではないものの大振幅時の非 定常空気力の報告20)もなされるようになっている.そこで,本研究では,大振幅非定常空気力 予測への本RANS計算コードの適用検討も合わせて行った. 以下,本論文の構成を述べる. まず,2章では計算手法について述べる.一般座標系で記述された2次元非圧縮性 Navier-Stokes 方程式を2.1節で導出した後,本研究で用いた Rogers ら21),22)の数値計算法に ついて2.2節で説明する.2.3節では乱流のモデル化と本研究で用いた k – ω SST乱流モデ ルについて説明する. 次に,3章では作成した計算コードの検証結果が示される.まず,比較的レイノルズ数の低 いケースに対して乱流モデルを用いずに計算を行い,流れ計算コード自体の検証を行った後, 続いて3.2節で,k – ω SST乱流モデルが適切にコード化され流れ解析コードに組み入れられ ていることを確認するために実施した検証解析の結果について述べる. 非定常空気力の数値予測については,第4章で述べる.まず,運動する物体まわりの流れ解 析機能の確認と将来の大振幅非定常空気力数値予測の予備的検討をかねて行った振動翼型の 解析が4.1節で述べられる.大振幅でピッチング運動するNACA0015およびNACA0012翼型 が対象である.4.2節では,最近の長大橋の基本形状である偏平六角形断面を対象として非定 常空気力の計算を行い,高レイノルズ数で行われた風洞実験の結果との比較からその適用性を 論ずる.4.3節では,より基本的な形状と考えられる幅(B)・高さ(D)比 B/D が5∼20 まで
の矩形柱の非定常空気力に対する本RANSコードの予測精度について検証する.4.4節では, 将来の超長大橋への適用が検討されている2箱桁断面に関する非定常空気力係数の予測精度
について論ずる.2箱桁断面の計算には,重合格子法(Chimera Grid Scheme23))を用いた.
まず,Chimera Grid Schemeについて説明し,続いてChimera Grid Schemeを用いた解析
コードの検証結果を示す.次に,2種類の形状の異なる2箱桁断面に対して本 RANS コード
を適用した結果が示される.一つは4.2節で対象とした偏平六角形断面の中央部を取り外した
断面であり,もう一つは,端部が半円形状をした2箱断面である.後者は,今回,本 RANS
コードの検証を目的として作成された断面であり,風洞実験も新たに行われた. 最後に第5章では,本研究のまとめが述べられ今後の課題が示される.
第2章 計算手法 2次元非圧縮性 Navier-Stokes 方程式を基礎方程式とし,数値計算手法は Rogers ら 21),22) の方法を用いた. 2.1 非圧縮性粘性流れの基礎方程式 ここでは,2次元非圧縮性流体の基礎方程式を一般座標24),25)を用いて表す. 2.1.1 一般座標 まず,デカルト座標
( , , )
t x y
と一般座標( , , )τ ξ η
との変換を以下のように表記する.t およびτ
は時間を表す.τ
ξ ξ
η η
=
=
=
t
t x y
t x y
( , , )
( , , )
⇔
(
(2.1.1)(
)
t
x
x
y
y
=
=
=
τ
τ ξ η
τ ξ η
, ,
, ,
)
両辺の全微分をとれば,それぞれ,
=
dy
dx
dt
d
d
d
y x t y x tη
η
η
ξ
ξ
ξ
η
ξ
τ
1
0
0
⇔
dt
dx
dy
x
x
x
y
y
y
d
d
d
=
1
0
0
τ ξ η τ ξ ητ
ξ
η
ここで,ξ
∂ξ
∂
xx
=
etc. としている.両者を組み合わせれば,
=
η
ξ
τ
η
η
η
ξ
ξ
ξ
η
ξ
τ
η ξ τ η ξ τd
d
d
y
y
y
x
x
x
d
d
d
y x t y x t0
0
1
0
0
1
よって,
=
1
0
0
0
1
0
0
0
1
0
0
1
0
0
1
η ξ τ η ξ τη
η
η
ξ
ξ
ξ
y
y
y
x
x
x
y x t y x t これより,0
0
=
+
+
=
+
+
τ τ τ τη
η
η
ξ
ξ
ξ
y
x
y
x
y x t y x t (2.1.2)
η η
ξ
ξ
ξ η (2.1.3) ξ η x y x y x x y y = 1 0 0 1 が得られる. 次に,各瞬間における共変基底{
e e
ξ,
η}
及び反変基底{
e eξ, η}
を求めておく.デカルト座標 の正規直交基底を{
i j,}
として,r
=
x
i
+
y
j
とすれば,まず, ξr
ξi
ξj
∂ξ
e
≡
∂
=
x
+
y
, ηr
ηi
ηj
∂η
e
≡
∂
=
x
+
y
. (2.1.4) まとめて,[
eξ eη]
[ ]
i j ξ η (2.1.5) ξ η = x x y y 反変基底は形式的にk
= ×
i
j
とすることにより,次のように定義される. e e k e e k ξ η ξ η ≡ × ,e k e e e k η ξ ξ η ≡ × (2.1.6) 定義より直ちに, eξ⋅ =eξ eη⋅eη =1,eξ⋅eη =eη⋅ =eξ 0. (2.1.7) また, eξ ηi ηj ξ η ξ η = y −x x x y y ,eη ξi ξj ξ η ξ η = −y +x x x y y であるから,まとめて,e
e
i
j
i
j
i
j
ξ η ξ η ξ η η η ξ ξ ξ η ξ ηξ
ξ
η η
=
−
−
=
=
− −x
x
y
y
y
x
y
x
x
x
y
y
x y x y 1 1 (2.1.8) 次に,ベクトルの成分の変換式を求める.任意のベクトルa
=
a
xi
+
a
yj
(a
x等は∂ ∂
a/ xの意 味ではない)が,共変基底{
を用いて,a e と表されたとすれば,その成分, とa
は,それぞれ両辺に}
e e
ξ,
η =aξ ξ +aηeηa
ξ ηe
ξ,e
ηを掛けることにより, a xax y y ξ = ⋅ ξ =ξ
+ξ
a e a a aη = ⋅a eη =η
xax+η
y y と求まる.まとめて書けば,a (2.1.9) a a a x y x y x y ξ η
ξ
ξ
η η
= 同様にして,a
=
a
ξe
ξ+
a
ηe
η(ここでも,a
ξ等は∂ ∂ξ
a/ の意味ではない)とすれば,[
a a]
[
a a]
x x (2.1.10) y y x y ξ η ξ η ξ η = となる.(
a aξ, η)
をベクトル の反変成分といい,a
( )
a a
ξ,
η を共変成分という. 2.1.2 質量保存の式(連続の式) 密度一定の流体の質量保存を上に述べた一般座標を用いて記述する.一般座標空間(
)
の 部分空間(
内で時間τ ξ η
, ,)
ξ η
,τ
に関し任意に固定された閉領域Ω( )
τ
=Ω0を考え,座標変換(
)
(
)
t
x
x
y
y
=
=
=
τ
τ ξ η
τ ξ η
, ,
, ,
によるΩ( )
τ
の像をV t
( )
とする. は一般に物理空間上に固定されてはいないが,閉領域を 構成するものとする.領域V
( )
Ωτ
=Ω0の境界をΣ( )
τ
=Σ0,領域V t
( )
の境界を と表すこと にする.このとき,( )
S t
ρ
を流体の密度,u
を流れの速度とすると,領域V
内の質量の保存は,次 式により表される. ( ) dV ( )(
u v) (
dS dt d t S t V − ⋅ − =∫
)
∫
ρ
ρ
(2.1.11) ここで,v
はS
上の点の移動速度を表す.d
S
=
n
dS
で, はn
S
上の外向き単位法線ベクトル である.上式の左辺は領域V
内の質量の変化率を,右辺は単位時間あたりに境界S
を通って領 域V に流れ込む流体の質量を表している.左辺を一般座標を用いて表記すれば, dV d d d d x x y y d d Jd d = ⋅k eξ ×eη = eξ eη k = ξ η = ξ ηξ
η
ξ η
ξ η
1ξ η
より, ( )∂τ
ρ
ξ
η
∂
η
ξ
ρ
τ
η
ξ
ρ
τ
τ d d J d d J d d d d J d d = =∫
∫
∫
Ω Ω Ω 1 1 1 0 0 ここで,J
x
x
y
y
x y x y=
=
−ξ
ξ
η η
ξ η ξ η 1 (2.1.12)とした.次に右辺を考える.まず,
Σ
は一般座標空間上で固定しているから,その像であるS
の移動速度v
は次のようになる. v=xτi+yτj (2.1.13)S
上の単位法線ベクトル を共変成分を用いて,n
n=nξeξ +nηeη (2.1.14) と表し(n
ξは∂ ∂ξ
n/ の意味ではない),流速ベクトル の反変成分をu
(
U V
,
)
で表せば,u
=
U
e
ξ+
V
e
η (2.1.15) 以上の準備をして,式(2.1.11)の右辺を書き直せば, ( )t(
Un Vn)
dS S( )t{
n(
x x y y) (
n x x y y}
dS Sη
η
ξ
ξ
ρ
ρ
ξ + η + ξ τ + τ + η τ + τ −∫
∫
)
式(2.1.2)を用いれば,これは, ( )(
U)
n dS S( )t(
V t)
n dS t t S η ξρ
η
ξ
ρ
+ − + −∫
∫
となる.発散定理を用いれば,(
)
ρ
(
η
)
ξ
η
∂η
∂
ξ
ρ
∂ξ
∂
d
d
V
J
U
J
t t
+
+
+
−
∫
Ω1
1
0 となるから,領域V
内の質量の保存は1
1
(
)
1
(
)
0
0=
+
+
+
+
∫
Ωη
ξ
η
ρ
∂η
∂
ξ
ρ
∂ξ
∂
ρ
∂τ
∂
d
d
V
J
U
J
J
t t と表せる.領域Ω
0は任意であるから,結局, 1 1(
)
1(
)
=0 + + + + t t V J U J J∂η
ρ
η
∂
ξ
ρ
∂ξ
∂
ρ
∂τ
∂
(2.1.16) 上式が一般の質量保存の式である. 式(2.1.16)で密度ρ
を一定とすれば,1
=
0
+
+
+
+
J
J
J
J
V
J
U
tη
t∂η
∂
ξ
∂ξ
∂
∂τ
∂
∂η
∂
∂ξ
∂
(2.1.17) が得られる.ここで,中括弧の中を考える.J
−1=
(
x y
ξ η−
x y
η ξ)
ξ
t=
−
x
τξ
x−
y
τξ
yη
t= −
x
τη
x−
y
τη
yであるから, + + J J J t t
η
∂η
∂
ξ
∂ξ
∂
∂τ
∂
1 =(
−)
− + − + ∂
∂τ
∂
∂ξ
ξ
ξ
∂
∂η
η
η
ξ η η ξ τ τ τ τ x y x y x J y J x J y J x y x y=
∂τ
∂
(
x y
ξ η−
x y
η ξ)
−
∂ξ
∂
(
x y
τ η−
y x
τ η)
−
∂η
∂
(
−
x y
τ ξ+
y x
τ ξ)
となって,恒等的に 1 =0 + + J J J t tη
∂η
∂
ξ
∂ξ
∂
∂τ
∂
(2.1.18) であることが分かる.よって,密度一定の流体の質量保存の式は最終的に,∂
∂ξ
∂
∂η
U
J
V
J
+
=
0
(2.1.19) となる.ここで,(
U V
,
)
は速度ベクトルu
=
u
i
+
v
j
の反変成分として定義したから,U
=
ξ
xu
+
ξ
yv
V
=
η
xu
+
η
yv
(2.1.20) である.また,ξ
x=
η
y=
1
,ξ
y=
η
x=
0
とすれば,質量保存の式は,∂
∂
∂
∂
u
x
v
y
+
=
0
(2.1.21) となってよく知られたデカルト座標による表現と一致する. 2.1.3 運動量の保存式 質量保存の式を導いたのと同様にして,領域V t
( )
内の流体について運動量の保存を考える.体 積力を無視すれば,運動量の保存は次のように表される. ( ) dV ( )(
) (
d)
( ) dS dt d t S t S t Vσ
ρ
ρ
∫
∫
r∫
u = u u−v ⋅ − S + (2.1.22) 左辺は領域V t
( )
内の流体の運動量の変化率を表し,右辺第1項は単位時間あたりに境界S
を通 って領域V に流れ込む流体の運動量を表している.右辺第2項は境界S
に作用する力を表し,r
σ
は応力ベクトルである.左辺を一般座標を用いて表せば,質量保存の時と同様にして, ( )∂τ
ρ
ξ
η
∂
η
ξ
ρ
τ
η
ξ
ρ
τ
τd
d
J
d
d
J
d
d
d
d
J
d
d
=
=
∫
∫
∫
Ω Ω Ωu
u
u
1
1
1
0 0右辺第1項も質量保存の時と同様にして, ( )
(
U)
n dS S( )t(
V t)
n dS t t S η ξρ
η
ξ
ρ
+ − + −∫
u∫
u となり,やはり発散定理から,(
)
ρ
(
η
)
ξ
η
∂η
∂
ξ
ρ
∂ξ
∂
d
d
V
J
U
J
t t
+
+
+
−
∫
Ωu
u
1
1
0 となる. 次に右辺第2項について考える.まず,デカルト座標の各軸に垂直な面に作用する 応力ベクトルをそれぞれ,σ
rx,σ
r
yとしたとき,微小領域の力の釣り合いからよく知られた次 の関係式が得られる.σ σ
r
=
r
xn
x+
σ
r
yn
y (2.1.23) ここで,σ
r
は単位ベクトルn
=
n
xi
+
n
yj
(n
x等は∂ ∂
n/ xの意味ではない)に垂直な面に作用 する応力ベクトルである.よって,第2項は, ( )t(
xnx yny)
dS Sσ
σ
r + r∫
となるが,さらに,S
の単位法線ベクトル の各デカルト成分を共変成分 を用いて書 き換えることにより,n
(
n n
ξ,
η)
( ){
(
n n)
(
n n)
}
dS S( )t{
(
x x y y) (
n x x y y)
n}
dS y y y x x x t S η ξ η ξ η ξξ
η
σ
ξ
η
σ
ξ
σ
ξ
σ
η
σ
η
σ
r + + r + =∫
r + r + r + r∫
となる.発散定理により,(
)
(
σ
η
σ
η
)
ξ
η
∂η
∂
ξ
σ
ξ
σ
∂ξ
∂
d
d
J
J
x x y y x x y y
+
+
+
∫
Ωr
r
r
r
1
1
0 よって,運動量保存の式は,(
) (
)
+ − + + ∫
Ω t J x x y y U J J∂ξ
ρ
ξ
σ
ξ
σ
ξ
∂
ρ
∂τ
∂
1 1 1 r r 0 u u + (
+)
−(
+)
=∂
∂η
ρ
η
σ η
σ η
ξ η
1 1 J uV t J x x y y d d 0 r r ここで,Ω
0は任意にとれるから,結局,(
) (
)
+
−
+
+
y y x x tJ
U
J
J
∂ξ
ρ
ξ
σ
ξ
σ
ξ
∂
ρ
∂τ
∂
1
1
1
r
r
u
u
+
(
+
)
−
(
+
)
=
∂
∂η
ρ
η
σ η σ η
1
1
J
u
V
tJ
x x y y0
r
r
上式を各成分に分ければ,
σ
r
x=
σ
xxi
+
σ
xyj
,σ
r
y=
σ
yxi
+
σ
yyj
として,(
) (
)
+
−
+
+
y yx x xx tJ
U
u
J
u
J
∂ξ
ρ
ξ
σ
ξ
σ
ξ
∂
ρ
∂τ
∂
1
1
1
+
(
+
)
−
(
+
)
=
∂
∂η
ρ
η
σ η σ η
1
1
0
J
u V
tJ
xx x yx y(
) (
)
+
−
+
+
y yy x xy tJ
U
v
J
v
J
∂ξ
ρ
ξ
σ
ξ
σ
ξ
∂
ρ
∂τ
∂
1
1
1
+
(
+
)
−
(
+
)
=
∂
∂η
ρ
η
σ η σ η
1
1
0
J
v V
tJ
xy x yy y ここで,応力σ
ijを次のように圧力p
と粘性応力τ
ijに分離する.σ
ij= −
p
δ τ
ij+
ij (2.1.24) すると,運動量の式は,(
)
(
)
+
+
+
+
+
+
u
uV
p
J
u
uU
p
J
u
J
x t∂η
η
xρ
η
tρ
∂
ρ
ξ
ρ
ξ
∂ξ
∂
ρ
∂τ
∂
1
1
1
=
(
+
)
(
)
+
+
∂
∂ξ
τ ξ τ ξ
∂
∂η
τ η τ η
1
1
J
xx x yx yJ
xx x yx y (2.1.25)(
)
(
)
+
+
+
+
+
+
v
vV
p
J
v
vU
p
J
v
J
y t∂η
η
yρ
η
tρ
∂
ρ
ξ
ρ
ξ
∂ξ
∂
ρ
∂τ
∂
1
1
1
=
(
+
)
(
)
+
+
∂
∂ξ
τ ξ τ ξ
∂
∂η
τ η τ η
1
1
J
xy x yy yJ
xy x yy y (2.1.26) となる. 次に上式の右辺の粘性項について考える. 非圧縮性流体で,粘性応力と歪み速度の関係式 が粘性係数をµ
として,τ
ijµ
∂
∂
∂
∂
i j j i u x u x = + (2.1.27) と表されるとする.すると,粘性項の例えば 方向成分は,i
u
x=
∂ ∂
u
/
x
, etc. として,∂
{
(
)
(
)
}
{
(
)
(
)
}
∂ξ
µ
ξ
ξ
∂
∂η
µ
η
η
J
u
x+
u
x x+
u
y+
v
x yJ
u
xu
x xu
yv
x y
+
+
+
+
となるが,これを更に次のように分けて考える.(
)
(
)
(
)
(
)
∂
∂ξ
µ
ξ
ξ
∂
∂η
µ
η
η
∂
∂ξ
µ
ξ
ξ
∂
∂η
µ
η
η
J
u
x x+
u
y yJ
u
x xu
y yJ
u
x xv
x yJ
u
x xv
x y
+
+
+
+
+
+
(2.1.28) もし,粘性係数
µ
が一定とすると,µ
を微分の外に出すこともできるから,上式の第3項と第 4項を合わせたものは,(
)
(
)
∂
∂ξ
µ
ξ
ξ
∂
∂η
µ
η
η
J
u
x x+
v
x yJ
u
x xv
x y
+
+
( )
( )
( )
( )
= ⋅ + + ⋅ + + ⋅ + + ⋅ + µ
ξ
ξ
ξ
ξ
η
η
η
η
ξ ξ ξ ξ η η η η x x x x y x y x x x x x y x y x J u J u J v J v J u J u J v J v( )
( )
{
}
{
( )
( )
}
= + + + + + + + µ
ξ
η
ξ
η
ξ
η
ξ
η
ξ η ξ η ξ η ξ η x x x y y x x x x x x y x J J u J J v J u u J v v 1 1( )
( )
( )
y( )
{
( ) ( )
}
=
+ −
+ −
+
+
+
µ
y
η ξy
ξ ηu
x
η ξx
ξ ηv
J
u
v
x x x x x y1
(
)
=
µ
+
J
u
xv
y x となるが,これは質量保存の式から である.よって,粘性係数0
µ
が一定の場合,粘性項は式 (2.1.28)の第1項と第2項のみとなる.このとき,共変微分の変換式u
x=
ξ
xu
ξ+
η
xv
η etc. を用いれば,粘性項の 方向成分は,i
∂ξ
∂
µ
{
(
ξ
ξ
) (
ξξ η ξ η
)
η}
∂η
∂
µ
{
(
ξ η ξ η
) (
ξη
η
)
η}
J
x yu
x x y yu
J
x x y yu
x yu
2+
2+
+
2 2
+
+
+
+
となる. 方向成分も同様であるから,結局,粘性係数j
µ
が一定のとき,運動量保存の式は,(
)
(
)
+
+
+
+
+
+
u
uV
p
J
u
uU
p
J
u
J
x t∂η
η
xρ
η
tρ
∂
ρ
ξ
ρ
ξ
∂ξ
∂
ρ
∂τ
∂
1
1
1
=
{
(
+
) (
+
+
)
}
{
(
) (
)
}
+
+
+
+
∂
∂ξ
µ
ξ
ξ
ξξ η ξ η
η∂η
∂
µ
ξ η ξ η
ξη
η
ηJ
x yu
x x y yu
J
x x y yu
x yu
2 2 2 2(
)
(
)
+
+
+
+
+
+
v
vV
p
J
v
vU
p
J
v
J
y t∂η
η
yρ
η
tρ
∂
ρ
ξ
ρ
ξ
∂ξ
∂
ρ
∂τ
∂
1
1
1
=
{
(
+
) (
+
+
)
}
{
(
) (
)
}
+
+
+
+
∂
∂ξ
µ
ξ
ξ
ξξ η
ξ η
η∂η
∂
µ
ξ η
ξ η
ξη
η
ηJ
x yv
x x y yv
J
x x y yv
x yv
2 2 2 2 となる.上式の両辺をρ
で割り,p
/
ρ
を改めて,p
と書くことにすれば,