BAB II TINJAUAN PUSTAKA

(1)

BAB II

TINJAUAN PUSTAKA

II.1. Konsep Dasar Metode Elemen Hingga

Struktur dalam istilah teknik sipil adalah rangkaian elemen-elemen yang sejenis maupun yang tidak sejenis. Elemen adalah susunan materi yang mempunyai bentuk relatif teratur. Elemen ini akan mempunyai sifat-sifat tertentu yang tergantung kepada bentuk fisik dan materi penyusunnya. Bentuk fisik dan materi penyusun elemen tersebut akan menggambarkan totalitas dari elemen tersebut. Totalitas sifat elemen inilah yang disebut dengan kekakuan elemen. Jika diperinci maka sebuah struktur mempunyai Modulus Elastis (E), Modulus Geser (G), Luas Penampang (A), Panjang (L) dan Inersia (I). Inilah satu hal yang perlu dipahami didalam pemahaman elemen hingga nantinya, bahwa kekakuan adalah fungsi dari E,G,A,L,I.

Kontinum dibagi-bagi menjadi beberapa bagian yang lebih kecil, maka elemen kecil ini disebut elemen hingga. Proses pembagian kontinum menjadi elemen hingga disebut proses “diskretisasi” (pembagian). Dinamakan elemen hingga karena ukuran elemen kecil ini berhingga (bukannya kecil tak berhingga) dan umumnya mempunyai bentuk geometri yang lebih sederhana dibanding dengan kontinumnya.

Dengan metode elemen hingga kita dapat mengubah suatu masalah dengan jumlah derajat kebebasan tertentu sehingga proses pemecahannya akan lebih sederhana. Misalnya suatu batang panjang yang bentuk fisiknya tidak lurus, dipotong-potong sependek mungkin sehingga terbentuk batang-batang pendek yang relatif lurus. Maka pada bentang yang panjang tadi disebut kontinum dan batang yang pendek disebut elemen hingga.

(2)

Suatu bidang yang luas dengan dimensi yang tidak teratur, dipotong-potong berbentuk segi tiga atau bentuk segi empat yang beraturan. Bidang yang dengan dimensi tidak beraturan tadi disebut kontinum, bidang segitiga atau segi empat beraturan disebut elemen hingga. Dan banyak lagi persoalan yang identik dengan hal diatas. Maka dari sini dapat dikatakan bahwa elemen hingga merupakan elemen diskrit dari suatu kontinum yang mana perilaku strukturnya masih dapat mewakili perilaku struktur kontinumnya secara keseluruhan.Pendekatan dengan elemen hingga merupakan suatu analisis pendekatan yang berdasarkan asumsi peralihan atau asumsi tegangan, bahkan dapat juga berdasarkan kombinasi dari kedua asumsi tadi dalam setiap elemennya.

Karena pendekatan berdasarkan fungsi peralihan merupakan teknik yang sering sekali dipakai, maka langkah-langkah berikut ini dapat digunakan sebagai pedoman bila menggunakan pendekatan berdasarkan asumsi tersebut :

1. Bagilah kontinum menjadi sejumlah elemen (Sub-region) yang berhingga dengan geometri yang sederhana (segitiga, segiempat. dan lain sebagainya).

2. Pada titik-titk pada elemen yang diperlakukan sebagai titik nodal, dimana syarat keseimbangan dan kompatibilitas dipenuhi.

3. Asumsikan fungsi peralihan pada setiap elemen sedemikian rupa sehingga peralihan pada setiap titik sembarangan dipengaruhi oleh nilai-nilai titik nodalnya.

4. Pada setiap elemen khusus yang dipilih tadi harus dipenuhi persyaratan hubungan regangan peralihan dan hubungan rengangan-tegangannya.

5. Tentukan kekakuan dan beban titik nodal ekivalen untuk setiap elemen dengan menggunakan prinsip usaha atau energi.

(3)

7. Selesaikan persamaan keseimbangan ini untuk mencari peralihan titik nodal. 8. Hitung tegangan pada titik tertentu pada elemen tadi.

9. Tentukan reaksi perletakan pada titik nodal yang tertahan bila diperlukan.

II.2 Tegangan Dan Regangan Dalam Kontinum Elastis

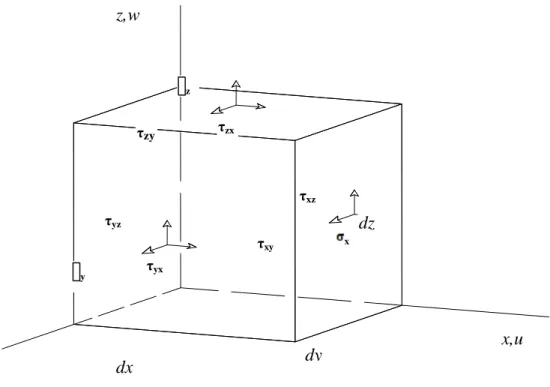
Dalam pembahasan ini diasumsikan bahwa kontinum yang dianalisis terdiri atas materal elastis dengan regangan kecil. Hubungan antara regangan dan tegangannya dapat digambarkan dalam suatu sistem koordinat ortogonal yang mengikuti kaidah tangan kanan misalnya dalam sebuah koordinat cartesius.

Gambar 2.1 memperlihatkan sebuah elemen yang amat kecil dalam sumbu koordinat Cartesius yang panjang sisi-sisinya dinyatakan dengan dx, dy, dan dz. Tegangan normal dan tegangan geser digambarkan dengan anak panah pada permuakaan elemen tadi. Tegangan normal diberi notasi x, y, dan z, sedangkan tegangan geser diberi notasi τxy, τyz, dan

(4)

Dari persamaan keseimbangan elemen tadi didapatkan hubungan sebagai berikut:

Gambar 2.1 Tegangan pada sebuah elemen yang sangat kecil (Sumber: Elemen Hingga Untuk Analisis Struktur, Paul R. Johnston dan William Weauver Jr)

τxy = τyx τyz = τzy τzx = τxz………. (a)

Tegangan – regangan yang dilukiskan dalam gambar akan menimbulkan regangan normal dan regangan geser. Regangan normal εx, εy, dan εz didefinisikan sebagai:

ε

x =

ε

y =

ε

z = ………. (b)

dimana u, v, dan w merupakan translasi dalam arah x, y, dan z. Regangan geser, γxy, γyz dan

lain-lain dinyatakan dalam rumus berikut ini:

γxy =

+

= γyx; γyz =

+

= γzy; γzx =

+

= γxz .….. (c)

(Sumber: Elemen Hingga Untuk Analisis Struktur, Paul R. Johnston dan William Weauver Jr) x τxy τxz τzy z τyx τyz y τzx z,w y,v x,u dz dx dy

(5)

Dari persamaan ini dapat dilihat bahwa hanya ada tiga regangan geser yang bebas. Untuk mempermudah, keenam tegangan bebas beserta keenam regangannya akan dituliskan dalam bentuk matriks kolom (atau vektor) seperti berikut:

σ = =

ε

= = ……… (d)

Hubungan tegangan – regangan untuk material isotropik diturunkan dari teori elastisitas seperti berikut ini:

ε

x = =

ε

x = = …….………. (e)

ε

x = =

(Sumber: Elemen Hingga Untuk Analisis Struktur, Paul R. Johnston dan William Weauver Jr) Dimana G =

Dalam persamaan ini E = modulus elastisitas (modulus Young), G = modulus geser, dan v = rasio Poisson. Dalam bentuk matriks, hubungan yang terdapat pada persamaan dapat dituliskan sebagai:

(6)

dimana

C = ……… (2.2 – 2)

Matriks C merupakan operator yang menghubungkan vektor regangan ε dengan vektor tegangan σ. Dan dengan meng-invers persamaan (2.2 – 1) didapatkan hubungan tegangan – regangan seperti berikut ini:

σ = E ε………..……… (2.2 – 3) dimana

E =C -1 = (2.2 – 4)

Matriks E adalah operator yang menghubungkan vektor tegangan σ dengan vektor regangan ε.

(7)

II.3 Finite Element Method

Dalam pembahasan ini, persamaan-persamaan metode elemen hingga akan diturunkan dengan menggunakan prinsip usaha virtual. Sebuah elemen hingga tiga dimensi yang terletak pada salib sumbu cartesius dengan koordinat x, y, dan z.

 Peralihan umum (general displacement) yang terjadi pada sembarang titik dalam elemen dinyatakan dengan vektor kolom u:

u = ………... (2.3 – 1)

dimana u, v, dan w berturut-turut merupakan translasi dalam arah x, y, dan z.

 Gaya tubuh (body forces) yang bekerja pada elemen, gaya-gaya ini akan dimasukkan ke dalam vektor b, seperti berikut:

b = ………... (2.3 – 2)

Notasi bx, by, dan bz mewakili komponen-komponen gaya (persatuan voume, luas atau

panjang) yang bekerja pada sembarang titik sesuai dengan arah x, y, dan z.

 Peralihan titik nodal (nodal displacement) q yang diperhitungkan hanyalah berupa translasi dalam arah x, y, dan z. Bila nen = jumlah titik nodal elemen, maka:

q = {q i} (i = 1,2,...,nen) ………... (2.3 – 3)

(8)

 Gaya titik nodal (nodal actions) p diambil dalam arah x, y, dan z:

p = {pi} (i = 1,2,...,nen) ………... (2.3 – 4)

dimana:

pi = ……… (b)

Hubungan antara peralihan umum dan peralihan titik nodal dinyatakan oleh fungsi bentuk peralihan (displacement shape function) sebagai berikut:

u = f q………. (2.3 – 5)

Dalam persamaan ini notasi f adalah matriks segiempat yang menunjukkan bahwa u sepenuhnya tergantung pada q.

Hubungan regangan-peralihan diperoleh dengan menurunkan matriks peralihan umum. Proses ini ditunjukkan dalam pembentukan matriks d yang disebut operator diferensial linier dan dapat dinyatakan dalam bentuk perkalian matriks:

ε = d u………. (2.3 – 6)

Dalam persamaan ini operator d menyatakan hubungan antara vektor regangan ε dengan vektor peralihan umum (vektor u). Dengan substitusi persamaan (2.3 – 5) ke dalam (2.3 – 6) diperoleh:

ε= B q………. (2.3 – 7)

dimana:

(9)

Matriks B menunjukkan regangan yang terjadi pada sembarang titik dalam elemen akibat satu satuan peralihan titik nodal.

Dari persamaan (2.2 – 3) telah diperoleh hubungan tegangan – regangan dalam bentuk matriks sebagai berikut:

σ = E ε……… (2.3 – 9)

dimana E adalah matriks yang menghubungkan tegangan σ dan regangan ε. Dengan mensubstitusikan persamaan (2.4 – 7) ke dalam (2.4 – 9) diperoleh:

σ = E B q……… (2.3 – 10)

dimana perkalian E B menunjukkan tegangan pada sembarang titik bila terjadi satu satuan peralihan titik nodal.

Prinsip usaha virtual: Bila ada suatu struktur dalam keadaan seimbang, dikerjakan

suatu peralihan virtual yang kecil dalam batas-batas deformasi yang masih dapat diterima, maka usaha virtual dari beban luar tadi sama dengan energi regangan virtual dari tegangan dalamnya. Bila prinsip di atas kita terapkan pada elemen hingga, akan diperoleh:

δUe = δWe………... (2.3 – 11)

dimana δU adalah energi regangan virtual dari tegangan dalam dan δW merupakan

usaha virtual beban luar yang bekerja pada elemen. Untuk memperoleh kedua nilai tersebut, diasumsikan adanya peralihan virtual kecil yang dinyatakan dalam vektor δq. Jadi,

(10)

Kemudian peralihan umum virtual akan menjadi:

δu = f δq……….. (d)

Dengan menggunakan hubungan regangan peralihan dalam persamaan (2.2 – 7), kita

dapatkan:

δε = B δq……….……. (e)

Energi regangan virtual dalam δU dapat dituliskan sebagai berikut:

δUe = ……….….. (f)

Usaha virtual luar dari gaya titik nodal dan gaya tubuh menjadi:

δWe = ………. (g)

Dengan substitusi persamaan (f) dan (g) ke dalam persamaan (2.3 – 11) akan dihasilkan:

= ………... (h)

Kemudian substitusi persamaan (2.3 – 9) untuk mengganti σ, dan dengan menggunakan transpose dari persamaan (d) dan (e) akan diperoleh:

= ………. (i)

Selanjutnya, substitusi persamaan (2.3 – 7) untuk nilai serta bagilah ruas kiri dan kanan dengan sehingga persamaan (i) akan menjadi:

(11)

Persamaan (j) dapat dituliskan kembali menjadi: K q = p + pb………..……… (2.3 – 12) dimana K = ………... (2.3 – 13) dan pb = ………... (2.3 – 14)

(Sumber: Elemen Hingga Untuk Analisis Struktur, Paul R. Johnston dan William Weauver Jr)

Matriks K dalam persamaan (2.3 – 13) adalah matriks kekakuan elemen, yaitu gaya yang terjadi pada titik nodal akibat adanya satu satuan peralihan titik nodal. Sedangkan vektor pb pada persamaan (2.3 – 14) menunjukkan gaya nodal ekuivalen akibat

bekerjanya gaya tubuh dalam vektor b.

Tegangan dan regangan yang diturunkan di atas hanya bergantung pada peralihan titik nodal. Bila terjadi regangan awal 0, maka regangan total dapat dituliskan sebagai berikut:

= 0 + C ………. (2.3 – 15)

dimana C adalah matriks hubungan regangan – tegangan. Dari persamaan (2.2 – 4) telah kita dapatkan:

C = -1………... (2.3 – 16)

Dengan menyelesaikan vektor tegangan pada persamaan (2.3 – 15) akan diperoleh:

(12)

Bila persamaan ini digunakan untuk mengganti dalam persamaan (h), maka akhirnya rumus tersebut akan menghasilkan:

K q = p + pb + p0……….. (2.3 – 18)

dimana

p0 = ………. (2.3 – 19)

Kita dapat menganggap vektor p0 merupakan beban titik nodal ekuivalen akibat regangan

awal, sama halnya dengan yang ditimbulkan oleh perubahan temperatur.

II.4 Fungsi Bentuk Dan Peralihan Umum Dalam Bentuk Operasi Matriks

Asumsikan bahwa fungsi peralihan dinyatakan sebagai perkalian antara matriks geometri q dengan vektor dari konstanta sembarang c sebagai berikut:

u = g c……… (2.4 – 1) Kemudian dicari operator g untuk setiap titik nodal sehingga:

q = h c……… (2.4 – 2)

Di mana, h = { gi }(i = 1,2,...,nen)………. (a)

dan g1 menunjukkan matriks g yang dihitung pada titik nodal ke i. Dengan mengasumsikan

bahwa matriks h adalah matriks bujur sangkar dan nonsingular, carilah konstanta c dalam persamaan (2.4 – 2):

c = h-1 q………... (2.4 – 3)

Substitusikan persamaan (2.4 – 3) ke dalam (2.4 – 1) untuk memperoleh: u = g h-1 q... (b)

(13)

f = g h-1………... (2.4 – 4)

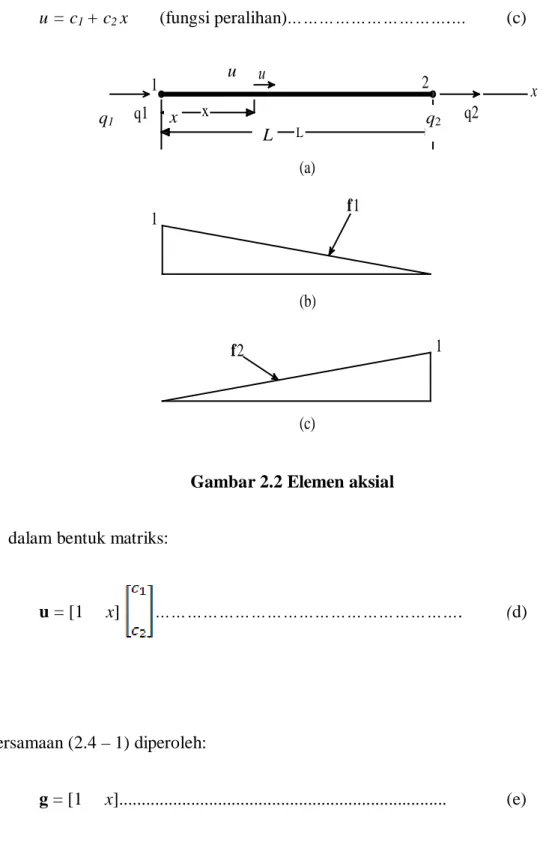
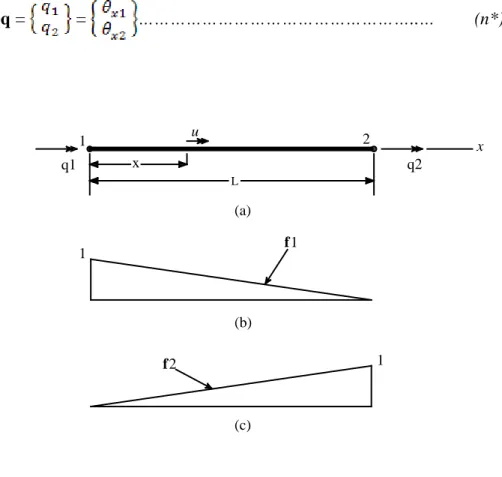
Sebagai contoh, untuk elemen aksial 1 dimensi asumsikan bahwa peralihan u di sembarang titik pada elemen merupakan fungsi linier dari x, seperti berikut ini:

u = c1 + c2 x (fungsi peralihan)……….… (c)

Gambar 2.2 Elemen aksial

dalam bentuk matriks:

u = [1 x] ………. (d)

dari persamaan (2.4 – 1) diperoleh:

g = [1 x]... (e) L x q2 q1 x 1 2 1 1 f1 f2 (a) (b) (c) q1 q2 u x L

(14)

fungsi peralihan ini dapat dinyatakan dalam fungsi bentuk peralihan dengan mencari kedua konstantanya, yaitu c1 dan c2.

Pada x = 0, didapat c1 = q1 ; untuk x = L akan diperoleh q2 = c1 + c2 L

Jadi c2 = (q2 – q1)/L. Bila konstanta ini disubstitusikan ke dalam persamaan (c) akan

diperoleh:

u = q1+ x………... (f)

Persamaan ini bukan lagi merupakan fungsi konstanta, melainkan fungsi dari peralihan titik nodal. Bila persamaan (f) digabungkan dengan (2.3 – 5) maka akan dapat dituliskan kembali menjadi:

u = = f q……….…. (g)

dimana fungsi bentuk yang didapat dalam bentuk matriks sebagai berikut:

f = [ f1 f2 ] =

Kedua fungsi bentuk peralihan ini diperlihatkan dalam Gambar 2.6 (b) dan (c).

Fungsi bentuk peralihan (shape function) bisa juga diperoleh dengan menghitung matriks g pada titik nodal 1 dan 2 [lihat persamaan (2.4 – 2)]:

= ………..……. (h)

sehingga diperoleh:

(15)

invers dari matriks h adalah:

h-1 = ……….…… (j)

kemudian dari persamaan (2.4 – 4) diperoleh:

f = g h-1 =

,

yang sama dengan persamaan (g).

Hubungan regangan peralihan untuk elemen aksial hanya terdiri dari satu turunan saja sesuai persamaan (b) dalam sub-bab 2.2:

ε =

ε

x = d u =

=

= B q

maka: B =

=

[-1 1]

Dengan cara yang sama, didapat hubungan tegangan – regangan [persamaan (2.3 – 9) dan (2.3 – 10)] sebagai berikut:

σ = σx = E ε = E εx = EB q

Jadi: E = E dan E B =

[-1 1]

……… (k)

Dengan mengasumsikan luas penampang A besarnya konstan, maka kekakuan elemen dapat dihitung dari persamaan (2.3. – 13) seperti berikut ini:

K = =

[-1 1]

K =

(16)

II.5 Grid Element

Grid adalah sebuah struktur yang terbentuk dari rangkaian balok-balok yang terhubung secara kaku pada nodal, dimana seluruh balok dan nodal tersebut berada pada bidang (X-Y) yang sama. Penggambaran ini identik dengan penggambaran portal bidang. Perbedaan antara struktur grid dan portal terletak pada arah beban yang bekerja pada struktur dan respons struktur terhadap beban tersebut. Pada portal bidang seluruh beban bekerja pada bidang portal dan seluruh peralihan juga terjadi pada bidang tersebut.

Balok-balok portal mengalami lentur dan deformasi aksial pada arah bidang. Pada struktur grid seluruh beban bekerja pada arah tegak lurus bidang, demikian juga dengan peralihan yang terjadi. Balok-balok grid mengalami lentur keluar bidang dan juga puntir.

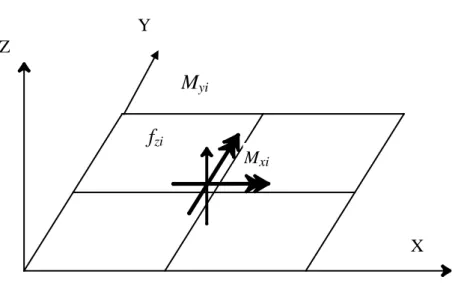
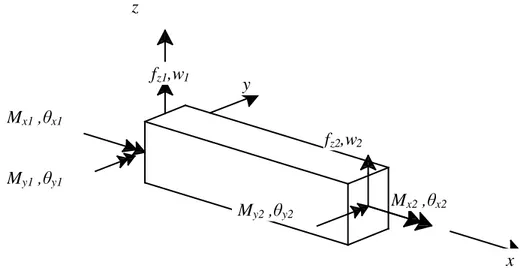
Sistem koordinat global yang akan kita pakai untuk menempatkan struktur grid adalah pada bidang X-Y. Beban vertikal akan bekerja pada arah Z dan momen nodal bekerja pada bidang grid seperti tampak pada Gambar 2.3. Gambar 2.4 memperlihatkan sistem koordinat lokal elemen yang digunakan.

Gambar 2.3 Arah Positif Gaya Nodal Struktur dalam Sistem Global (Sumber : Metode Elemen Hingga Untuk Skeletal, Prof. Dr. Ir. Irwan Katili)

f

zi Mxi

M

yi Y Z X

(17)

Pada elemen grid, terdapat efek lentur terhadap sumbu horizontal penampang seperti halnya balok, dan juga efek puntir terhadap sumbu batang, yang berarti dapat menahan momen torsi. Karenanya, pada setiap nodal terdapat: peralihan vertikal wi, rotasi terhadap sumbu horizontal penampang (arah y) akibat momen lentur, dan rotasi terhadap sumbu elemen akibat torsi. Tiap nodal mempunyai 3 derajat kebebasan (wi, θxi, θyi ).

Gambar 2.4 Sistem Koordinat Lokal Elemen (Sumber : Metode Elemen Hingga Untuk Skeletal, Prof. Dr. Ir. Irwan Katili)

II.5.1 Efek Lentur

Efek lentur akan terjadi terhadap sumbu y elemen, dan efek puntir terjadi terhadap sumbu x elemen. Peralihan nodal dan gaya batang dianggap positif bila bekerja pada arah koordinat positif. Kita gunakan aturan tangan kanan unuk arah efek lentur dan torsi. Gambar 2.5 menunjukkan arah positif untuk gaya dan peralihan elemen. θx1, θy1, θx2, dan θy2

adalah rotasi, sedangkan w1 dan w2 adalah translasi pada arah z.

z y

(18)

Gambar 2.5 Gaya dan Peralihan Elemen Positif (Sumber : Metode Elemen Hingga Untuk Skeletal, Prof. Dr. Ir. Irwan Katili)

Gambar 2.5 melukiskan elemen lentur (flexural element) lurus yang melendut pada bidang utama x-z. Dalam gambar ditentukan adanya sebuah peralihan umum w, yaitu translasi dalam arah z. Jadi:

u = w

Gaya tubuh yang ditinjau merupakan komponen tunggal bz (gaya per satuan panjang) yang bekerja dalam arah z.

Maka:

b = bz

Pada titik nodal 1 [lihat gambar 2.6 (a)]:

q1 : translasi dalam arah z dan rotasi kecil dalam arah y (mata panah tunggal)

q2 : rotasi kecil dalam arah y ( mata panah ganda)

Hal yang sama juga berlaku untuk titik nodal 2 peralihan yang diberi nomor 3 dan 4 berturut-turut merupakan translasi dan rotasi yang kecil. Maka, vektor peralihan titik nodal akan menjadi: z fz1,w1 y Mx1,θx1 x My2,θy2 My1,θy1 Mx2,θx2 fz2,w2

(19)

q = {q1, q2, q3, q4} = {w1, θy1, w2, θy2}……….... (a*)

dimana:

θy1 =

θy2 =

Turunan (putaran sudut) ini dapat dianggap sebagai suatu rotasi yang kecil walaupun sebenarnya mempengaruhi perubahan translasi pada titik nodal tersebut. Aksi titik nodal yang terjadi pada titik nodal 1 dan 2 adalah:

p = {p1, p2, p3, p4} = {py1, Mx1, py2, Mx2}

py1 dan py2 : gaya dalam arah y pada titik nodal 1 dan 2

Mz1 dan Mz2 : momen dalam arah y pada titik nodal 1 dan 2

Karena ada 4 peralihan titik nodal, fungsi peralihan lengkap untuk elemen lentur ini dapat diasumsikan sebagai berikut:

w = c1 + c2 x + c3 x2 + c4 x3……….……. (a)

(Sumber: Bahan kuliah Metode Elemen Hingga, Prof. Dr. Ing. Johannes Tarigan)

matriks translasi g menjadi:

(20)

Peralihan kedua (rotasi) pada setiap titik nodal memiliki hubungan diferensial dengan peralihan yang pertama (translasi). Matriks rotasi (turunan pertama g terhadap x)adalah: = [0 1 2x 3x2]……… (c)

Gambar 2.6 Elemen Lentur dan Fungsi Bentuk

(Sumber: Elemen Hingga Untuk Analisis Struktur, Paul R. Johnston dan William Weauver Jr) 1 1 1 1 (a) (b) (e) (c) (d) z y x w

(21)

Bentuk matriks h dari kedua nodal 1 (x = 0) dan nodal 2 (x = L):

h = = ………. (d)

invers dari matriks h adalah:

h-1 = ………..… (e)

Dari mengalikan kembali h-1 dengan g akan diperoleh matriks fungsi bentuk peralihan dalam matriks f sebagai berikut:

f = g h-1 =

[

f1 f2 f3 f4

]

f =

[

1 x x2 x3

]

f =

[

2x3 – 3x2 L + L3 x3L – 2x2 L2 + xL3 - 2x3 + 3x2 L

x3 L – x2 L2

]

……….. (f) dimana fungsi bentuk yang didapat adalah:

f1 =

(translasi pada titik 1 terhadap sumbu-z elemen: wz1)

f2 =

(rotasi pada titik 1 terhadap sumbu-y elemen: θy1)

f3 =

(translasi pada titik 2 terhadap sumbu-z elemen: wz2)

f4 =

(rotasi pada titik 2 terhadap sumbu-y elemen: θy2)

(22)

Keempat fungsi bentuk ini dilukiskan dalam Gambar 2.6 (b), (c), (d), dan (e) yaitu perubahan

w sepanjang elemen akibat dari satu satuan peralihan titik nodal dari keempat arah peralihan

q1, q2, q3, dan q4.

Hubungan regangan-peralihan dapat diturunkan untuk elemen lentur dengan mengasumsikan bahwa penampang yang rata akan tetap rata selama deformasi seperti yang ditunjukkan dalam Gambar 2.7. Translasi u dalam arah x pada setiap titik dalam penampang adalah:

u = - y ……….. (g)

dengan menggunakan hubungan ini, kita dapat memperoleh persamaan regangan lentur:

ε

x = = - y = - y

ø

………...……. (h)

dengan

ø

adalah kelengkungan.

ø

= ……….…… (i)

Dari persamaan (h) dapat kita lihat bahwa operator diferensial linier d yang menghubungkan

ε

xdengan w adalah:

(23)

Gambar 2.7 Deformasi Lentur

Kemudian persamaan (2.3 – 8) akan memberikan matriks regangan-peralihan B seperti di bawah ini:

B = d f =

[

12x - 6L 6xL - 4L2 -12x + 6L 6xL - 2L2

]

.. (k)

Hubungan antara tegangan lentur σx dan regangan lentur εx dinyatakan dengan:

σx =E εx……….. (l)

Maka:

E = E dan E B = E B……….... (m)

Kekakuan elemen dapat diperoleh dari persamaan (2.3 – 13) dan akan memberikan hasil seperti berikut ini:

K = z, w y, v x, u dw/dx dA σx y dx

(24)

K =

[

12x - 6L 6xL - 4L2 -12x + 6L 6xL - 2L2 ]dA dx

Melalui perkalian dan integrasi (dengan EI konstan) akan dihasilkan:

K =

...

dx

dimana: Ix = dA menyatakan besarnya momen inersia penampang terhadap garis netral.

(25)

K =

...

K =

L

(26)

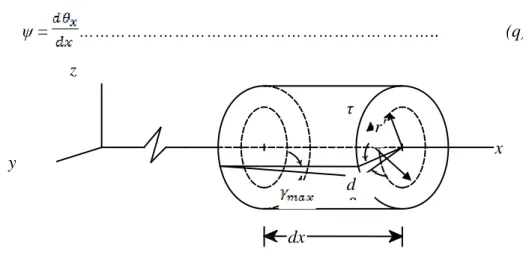
II.5.2 Efek Torsi

Gambar 2.8 melukiskan sebuah elemen torsi yang dapat berupa tongkat pada mesin atau batang pada struktur grid. Element ini juga memiliki peralihan umum tunggal θx, yaitu rotasi kecil dalam arah x. Jadi, u = [ θxi ]. Akibat adanya peralihan elastis ini (rotasi kecil tadi)

akan dihasilkan gaya tubuh b = Mx berupa momen (persatuan panjang) yang bekerja dalam

arah sumbu x positif.

Peralihan titik nodal terdiri dari rotasi aksial yang kecil pada titik nodal 1 dan 2. Maka:

q = = ………..… (n*) L x q2 q1 u x 1 2 1 1 f1 f2 (a) (b) (c)

Gambar 2.8 Elemen Torsi dan Fungsi Bentuk

Gaya titik nodal yang dihasilkan pada titik 1 dan 2 adalah:

(27)

Karena hanya ada dua peralihan titik nodal pada elemen torsi ini, maka dapat digunakan fungsi peralihan yang linier, yaitu:

θx = c1 + c2 x……… (n)

Fungsi bentuk peralihan pada elemen torsi ini sama seperti yang diperlihatkan dalam Gambar 2.9 (b) dan (c).

f = g h-1 =

[

f1 f2

]

= ………. (o)

Kemudian turunkan hubungan regangan-peralihan untuk elemen torsi dengan penampang lingkaran seperti yang terlihat dalam Gambar 2.9. Asumsikan jari-jari penampang tetap lurus selama terjadi deformasi torsi. Disini dapat disimpulkan bahwa regangan geser γ akan bervariasi linier terhadap panjang jari-jari r seperti berikut:

γ = r = rψ……….…… (p)

dimana ψ adalah putaran (twist), yaitu besarnya perubahan dari putaran sudut. Jadi:

ψ = ……….. (q)

Gambar 2.9 Deformasi Torsi

y z x dx d r τ

(28)

Dari persamaan dapat dibuktikan bahwa nilai maksimum regangan geser terjadi pada permukaan.

γmax = Rψ

dimana R adalah jari-jari penampang (lihat gambar). Selanjutnya, pada persamaan jelas terlihat bahwa operator diferensial linier d yang menghubungkan γ dengan θx adalah:

d = r ……….……….. (r)

maka, matriks regangan-peralihan B akan menjadi:

B = d f =

[-1 1]

………... (s)

yang mirip dengan matriks B pada elemen aksial, kecuali muncul nilai r.

Pada elemen torsi, hubungan antara tegangan geser τ dengan regangan gesernya γ dinyatakan dengan:

τ = G γ………. (t)

dimana simbol G menunjukka n modulus geser material.

Jadi: E = G dan E B = G B……… (u)

Kekakuan torsi sekarang bisa diperoleh dengan menurunkan (persamaan 2.4 – 13) sebagai berikut:

K =

(29)

K =

Dengan GJ konstan. Momen inersia polar J didefinisikan sebagai:

J = =

Untuk penampang bukan lingkaran/sembarang, momen inersia polar J diturunkan dari rumus:

+

= -2 G v’

,

dimana: ϕ = fungsi torsi

Dengan bantuan penyelesaian memakai teori Prand’l maka:

J =

(30)

Dengan notasi matriks, persamaan-persamaan dalam elemen yang mengalami lentur dan torsi pada grid element dapat ditulis sebagai persamaan keseimbangan elemen pada sistem koordinat lokal sebagai berikut:

Klokal =

Bila tidak ada beban nodal ekuivalen yang bekerja pada elemen grid, dan dengan mengembalikan kembali bentuk persamaan keseimbangan elemen pada persamaan (2.3 – 12), maka:

p = K q

=

(31)

II.5.3 Transformasi pada sistem koordinat

Seperti halnya elemen rangka dan portal, kita harus mentransformasikan matriks kekakuan elemen yang mengacu pada koordinat elemen ke dalam sistem koordinat global. Sumbu X dan Y (global) akan terletak pada bidang struktur dan karenanya berada pada bidang yang sama dengan sumbu x dan y (lokal) elemen. Sumbu z lokal dan global paralel satu sama lain.

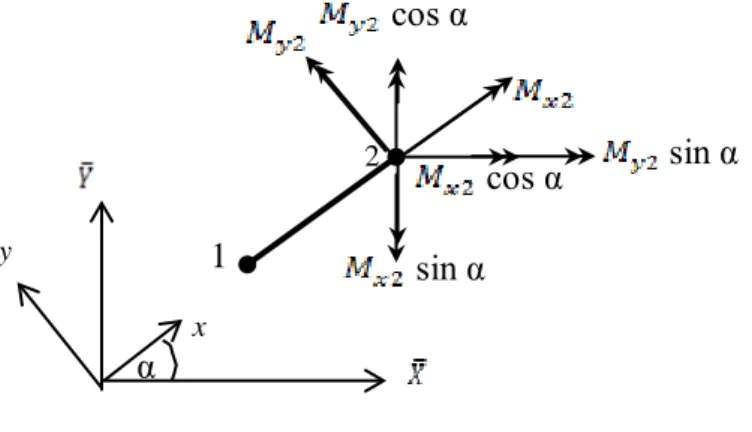
Pada Gambar 2.10, kita harus mentransformasi peralihan dengan memutar terhadap sumbu z. Bila α adalah sudut antara sumbu x elemen dan sumbu global,

Sumbu (global) berimpit dengan sumbu z (lokal), maka translasi tegak lurus bidang - maupun x-y adalah Wi = wi.

1

Gambar 2.10 Transformasi koordinat lokal ke koordinat global

Σ Mx = 0 = Mx2 Cos α + My2 Sin α + 0 Σ My = 0 = Sin α + My2 Cos α + 0 sin α x y α 2 cos α cos α sin α

(32)

Σ Fz = 0 = 0 + 0 + wz2

{ } = =

Analog:

{ } = =

Pada titik simpul 1 berlaku juga seperti simpul 2, maka untuk satu elemen berlaku :

{ } = [ ] { } { } = = ……… (a)

(Sumber: Bahan Kuliah Metode Elemen Hingga, Prof. Dr. Ing Johannes Tarigan)

Untuk displacement vektor berlaku juga :

= [ ] ……… (b)

Analog :

= [ ]

{ } = = -1 { }

= [ ]-1

dari persamaan (a) dan (b) :

[ ] { } = [ ] ……….. (c)

(33)

{ } = [ ] [ ] = …………..……. (d) dimana : = [ ] [ ] = [ ] [ ]………... (e)

Keterangan : [ ] = [ ] karena [ ] matriks Orthogonal.

Matriks transformasi:

[ ] =

Matriks kekakuan elemen dalam sistem koordinat lokal adalah:

= -1 -1 T -1 T T

(34)

Jika: Sin α = S

Cos α = C, maka:

=[ ] [ ]

=

Dengan menyelesaikan persamaan diatas, diperoleh matriks kekakuan elemen dalam sistem koordinat global:

=

(35)

II.5.4 Keseimbangan dan Menentuan dari Matriks Kekakuan.

Kondisi kompatibilitas mensyaratkan bahwa peralihan untuk semua titik pada suatu struktur yang terbebani harus kompatibel dengan seluruh peralihan pada struktur.Dengan demikian, pada saat struktur dibagi-bagi menjadi elemen-elemen, kondisi kompatibilitas memerlukan beberapa persyaratan sebagai berikut:

 Peralihan nodal yang merupakan pertemuan beberapa elemen haruslah kontinu dan pergerakannya selalu bersama.

 Peralihan nodal struktur harus konsisten dengan perilaku nodal yang telah ditetapkan.  Peralihan nodal pada tumpuan harus memenuhi kondisi batas dari peralihan yang

telah ditentukan sebelumnya.

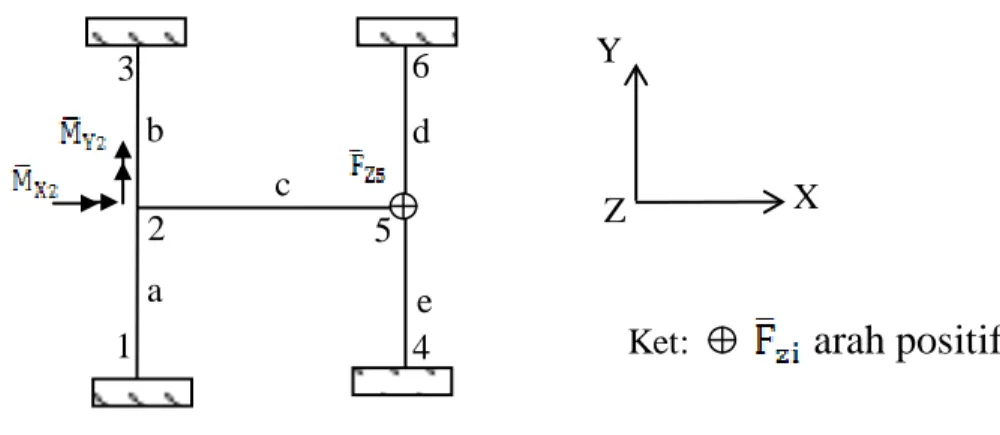
Sebagai contoh, diketahui konstruksi seperti Gambar 2.11. Tujuannya adalah untuk mencari matriks kekakuan dari konstruksi tersebut.

Ket:

arah positif

Gambar 2.11 Penomoran untuk nodal dan batang 1 2 5 4 a b d e c Z Y X 6 3

(36)

Elemen Simpul 1 (awal) Simpul 2 (akhir) a 1 2 b 2 3 c 2 5 d 4 5 e 5 6

, , , sesuai dengan persamaan di atas

dengan = = = =

dengan = 0

(37)

Untuk system Koordinat X – Y berlaku :

= = = ……..… (f)

Untuk menjamin kompatibilitas dari perubahan bentuk maka harus ditetapkan :

= + + = = = + + = =

Untuk keseragaman maka perlu dibuat definisi arah positif dari gaya-gaya dalam .

= ………..….. (h)

(Sumber: Bahan Kuliah Metode Elemen Hingga, Prof. Dr. Ing Johannes Tarigan) ……….…… (g)

(38)

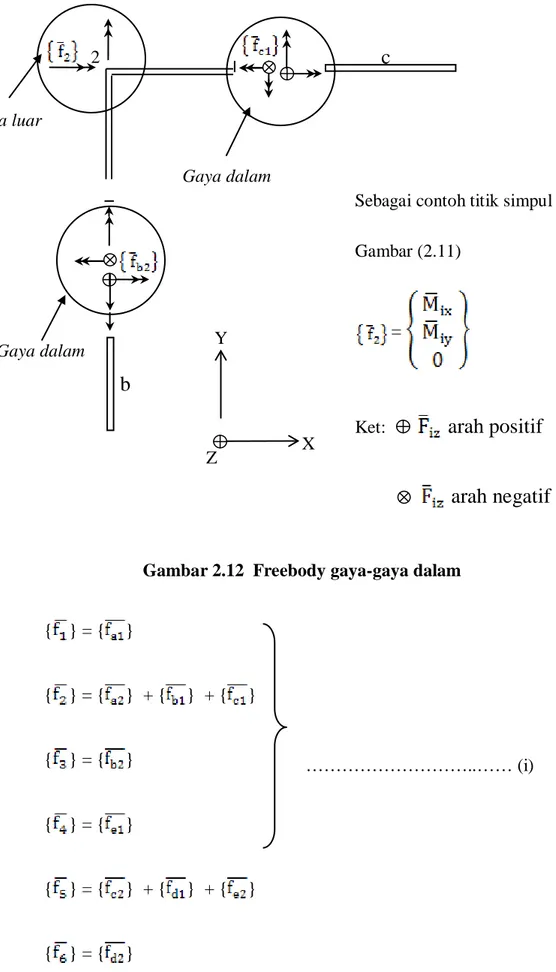
Sebagai contoh titik simpul 2 Gambar (2.11)

=

Ket:

arah positif

arah negatif

Gambar 2.12 Freebody gaya-gaya dalam

{ } = { } { } = { } + { } + { } { } = { } { } = { } { } = { } + { } + { } { } = { }

Gaya luar Gaya dalam Gaya dalam

c

b

………..…… (i) Y X Z 2

(39)

Dari persamaan f dan g didapat : { } = { } + { } { } = { } + { } + { } + { } + { } + { } { } = { } + { } { } = { } + { } { } = { } + { } + { } + { } + { } + { } { } = { } + { }

Persamaan (j) diatas jika disusun dalam bentuk matriks menjadi:

{ } = { }……….… (k)

dimana :

{ } = vektor dari gaya-gaya luar pada titik simpul

{ } = vektor dari perpindahan (displacement)

= matriks kekakuan simetris

(40)

=

……….…. (m)

II.5.5 Syarat keseimbangan

Pada persamaan (k) banyaknya persamaan sesuai dengan banyaknya yang tidak diketahui. Untuk contoh Gambar 2.11, maka perpindahan (displacement) adalah:

θx1 = θy1 = wz1 = θx3 = θy3 = wz3 = θx4 = θy4 = wz4 = θx6 = θy6 = wz6 = 0 …... (m)

{ } = ; { } = ; { } = ; { } =

{ } = ; { } =

{ } = ; { } = ; { } = ; { } =

dimana vektor gaya-gaya dalam yang timbul pada simpul 1, 3, 4, 6 akibat pembebanan pada struktur (simpul 2) belum diketahui. Dari persamaan (m) terdapat 18 bilangan anu tidak diketahui diantaranya 6 displacement (perpindahan) dan 12 gaya/momen, lihat pada Gambar 2.13.

(41)

Gambar 2.13 Reaksi Tumpuan dan Displacement pada Grid

Untuk Gambar 2.11, matriks keseluruhan 18 x 18 dapat dijadikan matriks 6 x 6. Dengan kondisi batas yang telah diketahui, maka baris ke 1 s/d 3, 7 s/d 9, 10 s/d 12, dan 16 s/d 18 dapat dicoreng.

Dengan THEORI – CHOLESKY,

{ } = { } ……….… (n)

Sehingga persamaan dapat diselesaikan.

2 5 θx2 θy2 wz2 θx5 θy5 wz5 3 1 4 6 X Y Z -1

(42)

II.6 Beban Nodal Ekuivalen

Analisa struktur dengan metode elemen hingga mengharuskan struktur hanya memikul beban yang bekerja di titik kumpul. Akan tetapi, beban sebenarnya pada struktur secara umum tidak memenuhi syarat tersebut. Sebaliknya, beban bisa bekerja si titk kumpul atau pada batang. Agar syarat di atas terpenuhi, beban pada batang harus diganti denagn beban ekivalen di titik kumpul. Beban titik kumpul yang ditentukan dari beban pada batng disebut beban titik kumpul ekivalen. Bila beban ini dijumlahkan dengan beban titk kumpul sebenarnya, maka beban total yang dihasilkan disebut beban titik kumpul gabungan. Selanjutnya dtruktur dapat dianalisa.

Agar memudahkan analisa, beban titik kumpul gabungan harus demikian besar hingga perpindahan struktur yang ditimbulkannya sama dengan perpindahan akibat beban sebenarnya. Hal ini tercapai bila beban ekivalen dihitung berdasarkan gaya jepit ujung memperlihatkan balok ABC yang bertumpu di titik A dan B serta, memikul sejumlah beban. Beberapa di antara beban ini adalah beban titik kumpul sebenarnya sedang beban lainnya bekerja pada. Untuk mengganti beban batang dengan beban titik kumpul ekivalen, titik kumpul struktur dikekang terhadap semua perpindahan. Untuk balok terjepit. Bila balok terjepit ini memikul beban batang, maka akan timbul gaya jepit ujung. Disini gaya ujung ditunjukkan sebagai aksi pengekang pada struktur terkekang. Jika aksi pengekang ini dibalikkan arahnya, aksi ini menjadi himpunan gaya dan kopel yang ekivalen dengan beban batang. Penjumlahan beban titik kumpul ekivalen ini dengan beban titik kumpul ekivalen ini dengan beban titik kumpul semula menghasilkan beban titik gabungan.

Umumnya beban titik kumpul gabungan untuk sembarang struktur dapat ditentukan dengan prosedur gambar. Langkah pertama ialah memisahkan beban titik kumpul sebenarnya dari beban batang. Perpindahan titik kumpul struktur kemudian dikekang dengan

(43)

memberikan pengekang titik kumpul yang sesuai. Selanjutnya, aksi pengekang akibat beban batang pada struktur terkekang dihitung.

Beban-beban yang bekerja di antara nodal elemen (merata, temperatur) yang bekerja pada elemen harus ditransformasikan menjadi beban nodal sehingga sesuai dengan tipe peralihan nodal yang didefinisikan.Dalam metode Beban Nodal Ekuivalen (BNE), kita tetapkan kerja luar atau kerja eksternal yang dihasilkan oleh beban nodal ekuivalen sama besarnya dengan kerja yang dihasilkan oleh beban yang bekerja di antara nodal elemen. Beban titik nodal ekuivalen yang disebabkan oleh beban merata bz per satuan panjang seperti tampak pada Gambar 2.16 (a) dapat dihitung dari persamaan (2.4 – 14) dengan f mengacu pada persamaan (f) pada sub-bab 2.6.1 seperti berikut ini:

pb = dx = dx = =

L x 1 2 L x 1 2

Gambar 2.16 Elemen Lentur Dengan Pembebanan Merata

z y bz bz z y bz x/L q1 q2 q3 q4 q1 q2 q3 q4 (a) (b) x x

(44)

Dengan cara yang sama, dapat diturunkan beban titik nodal ekuivalen untuk pembebanan segitiga (Gambar 2.16 (b)) seperti yang ditunjukkan oleh persamaan di bawah ini:

pb = dx = dx = =

Untuk pembebanan bz yang pada umumnya searah dengan gravitasiKarena sistem koordinat pembebanan yang digunakan pada grid bekerja pada bidang x-z (lokal), maka beban nodal ekuivalen menjadi berlawanan tanda dari persamaan di atas.

Selanjutnya untuk beban titik nodal ekuivalen yang disebabkan oleh berbagai kondisi pembebanan disusun menurut tabel 2.3.

(45)

Tabel 2.2 Beban Nodal Ekuivalen (BNE) untuk Grid z x L -bz L a = = = = -bz = = = L -bz = -bz -bz L a b a L = = = = = = = = = = = =

(46)

Keterangan: bz dan P adalah bilangan positif

(Sumber: Metode Elemen Hingga Untuk Skeletal, Prof. Dr. Ir. Irwan Katili)

z x L/2 -P L a = = = = -P = = = M = = = = = L/2 b L/2 L/2 -P L/3 = = = = M = = = = a b L/3 L/3 -P

(47)

Tabel 2.3 Gaya Internal Ekuivalen (GIE) untuk Grid z x L -bz L a = = = = -bz = = = L -bz = -bz -bz L a b a L = = = = = = = = = = = =

(48)

Keterangan: bz dan P adalah bilangan positif

(Sumber: Metode Elemen Hingga Untuk Skeletal, Prof. Dr. Ir. Irwan Katili)

z x L/2 -P L a = = = = -P = = = M = = = = = L/2 b L/2 L/2 -P L/3 = = = = M = = = = a b L/3 L/3 -P

(49)

Dengan notasi matriks, gaya-gaya dalam pada grid element dapat ditulis sebagai persamaan keseimbangan elemen pada sistem koordinat lokal sebagai berikut:

Ke =

= [ ]

(50)

II.6 Rasio Tegangan

Balok adalah komponen struktur yang fungsi utamanya memikul beban transversal, seperti beban tetap/gravitasi dan beban hidup. Balok terdiri dari kombinasi komponen tarik dan komponen tekan, sehingga konsep batang tarik dan batang tekan dapat digunakan pada perencanaan balok.Komponen tekan dari suatu balok disokong seluruhnya oleh komponen tarik yang stabil. Jadi, tekuk global dari komponen tekan tidak terjadi sebelum kapasitas momen batas penampang belum tercapai.

Balok yang hanya memikul momen lentur murni saja jarang dijumpai dalam peraktek, dan biasanya juga mengalami gaya aksial. Komponen struktur seperti ini dikenal sebagai balok-kolom yang akan dibahas lebih lanjut.

II.6.1 Penampang dengan lentur simetris

Suatu penampang yang mempunyai satu sumbu simetri dibebani momen lentur sembarang melalui titik pusat geser, maka momen lentur tersebut dapat diuraikan atas komponen arah sumbu kuat (M_xx) dan sumbu lemah (M_yy), dalam arah sumbu-sumbu utamanya (gambar 2.17)

Gbr.2.17 Balok dengan lentur murni xx

M

yy

M

(51)

Bila I_xx dan I_yy adalah momen inersia dalam arah sumbu kuat dan lemah penampang, maka tegangan normal dapat dihitung dari rumus yang telah dikenal sebagai:

y yy x xx x yy xx y xx S M S M f Iyy c M I c M f ± ± = ± ± = (2.6-1)

(Sumber: Bahan Kuliah Struktur Baja, Ir. Daniel, MT)

dimana S_x dan S_y adalah modulus penampang seperti diperlihatkan pada gambar (3.4)

Gbr. 2.18 Modulus elastis untuk bentuk yang simetris (Sumber: Bahan Kuliah Struktur Baja, Ir. Daniel, MT)

II.6.2 Perilaku kestabilan lateral balok

Pada balok yang komponen sayap tekannya mempunyai stabilitas dalam arah lateralnya, maka satu-satunya faktor mempengaruhi tercapainya kapasitas momen batasnya adalah tekuk lokal pada sayap tekan atau pada badan.Distribusi tegangan normal pada suatu profil WF akibat momen lentur yang berbeda intensitasnya. Pada beban kerja penampang masih elastis dan mencapai maksimum pada saat serat terluar mencapai tegangan leleh F . _y

x y y x x y y x y y x x y c x c c y y xx c I x S = x yy c I y S = Sx = I_cxx_y

(52)

Bila serat terluar telah mencapai F , maka momen nominal _y M atau momen leleh _n M_y

ditentukan sebagai

M_n =M_y =S_xF_y (2.6-2)

Bila seluruh serat telah mencapai strain sama atau lebih besar dari yield strain ε_y =F_y_/E_s, momen nominal yang disebut sebagai momen plastis M , dan dihitung sebagai: _p

M_p =F_yZ (2.6-3)

dimana Z adalah modulus plastis penampang. Sedangkan rasio M_p /M_y yang merupakan propertis dari penampang dan tidak tergantung kepada propertis dari material. Rasio ini dikenal sebagai faktor bentuk (shape factor) ξ. Jadi,

S Z S F Z F M M y y y p = = = ξ (2.6-4)

Untuk profil WF, faktor bentuk akibat lentur pada sumbu kuat berkisar 1,09 s/d 1,18

Elastis Keadaan Leleh Elastoplastis Plastis

Gbr. 3.5 Distribusi tegangan pada tahap pembebanan yang berbeda (Sumber: Bahan Kuliah Struktur Baja, Ir. Daniel, MT)

x x y f f < y M M < M =My y f f = f = fy p y M M M < < y f f = p M M =

(53)

II.6.3 Perencanaan lateral balok dengan sikongan dengan metode LRFD Persyaratan kekuatan balok yang memikul momen lentur adalah:

φ_bM_n≥M_u (2.6-5) dimana

φ_b = resistance factor for flexure = 0,9 =

n

M nominal moment strengths =

u

M factored service load moment

Besarnya rasio tegangan yang dihasilkan dengan perbandingan antara

momen dan normal ultimate sesuai dengan persamaan interaksi menurut

peraturan SNI-LRFD 2000 dan AISC-LRFD 1993 diberikan sebagai berikut :

0 , 1 9 8 = + n b u n u M M P P φ φ ; untuk n ≥0,2 u P P φ 0 , 1 2 + b n = u n u M M P P φ φ ; untuk n <0,2 u P P φ

(54)

II.7 Jembatan

Jembatan adalah suatu konstruksi yang gunanya untuk meneruskan jalan melalui suatu rintangan yang berada lebih rendah. Jembatan dapat dibagi dalam golongan seperti berikut:

 Jembatan-jembatan tetap

 Jembatan-jembatan dapat bergerak Golongan I dapat dibagi dalam:

• Jembatan kayu,melulu untuk lalu-lintas biasa pada bentang keci dan untuk jembatan pembantu

• Jembatan baja terdiri atas:

1. Jembatan yang sederhana dimana lantai kendaraan langsung berada di bawah kendaraan.Untuk gelagar-gelagar itu dipergunakan gelagar yang dikonstuir atau gelagar canai.

2. Jembatan gelagar kembar:melulu untuk lalu lintas kereta api

3. Jembatan pemikul lintang dan pemikul memanjang gelagar induknya adalah gelagar dinding penuh

4. Jembatan pelengkung 5. Jembatan gantung • Jembatan dari beton bertulang • Jembatan batu

(55)

Golongan II

• Jembatan yang dapat berputar di atas poros mendatar,yaitu: 1. Jembatan angkat

2. Jembatan Baskul 3. Jembatn lipat straus

• Jembatan yang dapat yang dapat berputar di atas poros mendatar juga termasuk poros yang dapat berpindah sejajar dan mendatar,seperti jembatan baskul beroda

• Jembatan yang dapat berputar atas suatu poros tegak atau jembatan putar • Jembatan angkat

Konstruksi jembatan terdiri dari dua komponen utama:

1. Bangunan bawah;meliputi pondasi,abutmen dan pancang

2. Bangunan atas meliputi;gelagar induk terbentang dari titik tumpu ke titik tumpu,konsturksi tumpuan di atas pangkal jembatan atau pancang,konstruksi dari lantai dan pertambatan lintang dan pertambatan memanjang

Melihat pelaksanaan bangunan atas kita ketahui:

 Jembatan balok adalah pada beban tegak lurus juga timbul reaksi tumpuan tegak lurus  Jembatan lengkung

(56)

II.7.1 Peraturan Muatan untuk Jembatan jalan

Dalam perencanaan suatu jembatan jalan raya,muatan-muatan dan gaya-gaya yang harus diperhatikan tegangan-tegangan yang terjadi pada setiap bagian jembatan tersebut adalah sebagai mana tersebut di bawah ini:

1.1.Muatan Primer

Mutan primer adalah muatan yang merupakan muatan utama dalam perhitungan untuk setiap perencanaan jembatan.Yang termasuk mutan primer adalah:

1.Muatan Mati 2.Muatan Hidup 3.Kejut

1.2.Muatan Sekunder

Muatan sekunder adalah muatan pada jembatan-jembatan yang merupakan muatan sementara,yang selalu bekerja untuk perhitungan tegangan pada setiap perencanaan jembatan.Pada umumnya muatan ini mengakibatkan tegangan-tegangan yang relatif kecil dari pada tegangan akibat muatan primer dan biasanya terutama tergantung dari bentang,sistem jembatan,bahan dan keadaan setempat.Yang termasuk muatan sekunder adalah:

1.Muatan angin

2.Gaya akibat perbedaan suhu 3.Gaya akibat rangkak dan sudut 4.Gaya rem dan traksi

(57)

1.3. Muatan Khusus

Muatan khusus adalah muatan yang merupakan pemuatan khusus untukm perhitungan teganganpada perencanaan jembatan.Muatan ini bersifat:

 Tak selalu bekerja pada jembatan

 Hanya berpengaruh pada sebagian konstruksi jembatan  Tergantung pada keadaan setempat

 Hanya bekerja pada sistem-sistem tertentu Yang muatan khusus adalah:

1. Gaya akibat gempa bumi 2. Gaya sentrifugal

3. Gaya akibat gesekan pada tumpuan-tumpuaan bergerak 4. Gaya tumbukan

5. Gaya dan muatan selama pelaksanaan

6. Gaya akibat aliran air dan benda-benda hanyutan 7. Gaya akibat tekanan tanah

Muatan-muatan dan gaya-gaya yang lain dari yang tersebut di atas perlu diperhatikan,apabila hal tersebut menyangkut kekhususan dari suatu jembatan,antara lain sehubungan dengan bentuk sistem dan keadaan setempat jembatan.

(58)

II.7 .2 Kombinasi Muatan untuk Jembatan jalan

Banguan jembatan beserta bagian-bagiaannya harus ditinjau terhadap kombinasi akibat beberapa muatan/gaya yang mungkin bekerja.Tegangan yang digunakan yang dinyatakan dalam persen terhadap tegangan yangdiijinkan untuk beberapa kombinasi muatan/gaya adalah sebagai berikut:

Kombinasi muatan/gaya Tegangan yang digunakan dalam persen terhadap tegangan yang diijinkan

I :M+H+K+Ta+AH 100 II :M+Ta+AH+F+A+SR+T 125 III :Kombinsi(I)+R+F+A+SR+T 140 IV :M+Ta+AH+Gb V :M+P 130 Dimana:  M= mutan mati  H= muatan hidup  Ta= tekanan tanah  A= muatan angin  R =gaya rem

 SR= susut dan rangkak  T= suhu

 F= tekanan geser dari tumpuan gerak  AH= aliran arus

 Gp= gempa bumi

(59)

II.8. Data Teknis yang digunakan

o Jembatan :jembatan baja,untuk jalan raya,golongan I o Gelagar :panjang(30 m);lebar (7,5 m)

o Pelat lantai ditentukan dan kekakuan lantai diabaikan o Profil yang digunakan sesuai keperluan

o Mutu baja yang digunakan ditentukan