Unit 1 KONSEP DASAR ARITMETIKA. Josef Tjahjo Baskoro Clara Ika Sari Budhayanti. Pendahuluan

KONSEP DASAR ARITMETIKA

Josef Tjahjo Baskoro

Clara Ika Sari Budhayanti

Pendahuluan

ateri yang akan Anda pelajari pertama kali pada mata kuliah pemecahan masalah matematika adalah konsep dasar aritmetika. Kompetensi dasar yang harus dikuasai setelah mempelajari unit ini adalah Anda mampu menggunakan konsep dasar aritmetika khususnya konsep dalam perpangkatan dan akar bilangan serta barisan dan deret dalam menyelesaikan masalah matematika atau masalah lainnya. Oleh karena itu dalam unit ini akan dipelajari konsep perpangkatan dan akar bilangan serta barisan dan deret aritmetika dan geometri. Unit ini terbagi menjadi dua subunit yaitu subunit pertama berisi perpangkatan dan akar bilangan sedangkan subunit kedua berisi barisan dan deret. Bahan ajar mengenai materi ini, selain disediakan dalam bentuk bahan ajar cetak juga disediakan dalam bentuk bahan ajar berbasis web.

Materi yang dibahas pada unit ini merupakan materi prasyarat yang harus dikuasai untuk mempelajari materi pemecahan masalah matematika. Oleh karena itu, pelajari unit ini sampai Anda menguasai dengan baik dan benar. Kerjakan semua latihan yang diberikan dan lihat kembali hasil pekerjaan Anda tersebut, kemudian bandingkan dengan pembahasan yang tersedia. Jika mengalami kesulitan, jangan segan untuk bertanya kepada rekan yang Anda anggap mampu atau dosen pengampu mata kuliah ini. Setelah Anda selesai mengkaji materi dan berlatih mengerjakan soal-soal, kerjakan tes formatif yang ada dalam setiap subunit untuk mengukur tingkat penguasaan Anda terhadap materi. Cobalah Anda kerjakan sendiri, kemudian bandingkan jawaban Anda tersebut dengan kunci jawaban tes formatif yang ada pada bagian akhir unit. Jika tingkat penguasaan Anda masih dibawah standar yang disyaratkan, pelajari kembali materi terutama di bagian yang Anda kurang mengerti. Selamat belajar dan tetap bersemangat, semoga Anda sukses.

M

Subunit 1

Perpangkatan dan Akar Bilangan

Perpangkatan

erpangkatan bilangan adalah perkalian berulang atau berganda suatu bilangan dengan faktor-faktor bilangan yang sama. Bentuk perpangkatan adalah sebagai berikut.

a × a × ... × a = an n faktor

Bentuk umumnya adalah

a

n, di mana

a

disebut bilangan pokok atau bilangan dasar, sedangkan

n

disebut pangkat atau eksponen.

Contoh :

• 23 (dibaca dua pangkat tiga) = 2 × 2 × 2 = 8 • 52 (dibaca lima pangkat dua) = 5 × 5 = 25

Perpangkatan bilangan sangat berguna untuk meringkas bentuk perkalian berulang dalam jumlah besar.

Selanjutnya kita akan mempelajari beberapa sifat yang berlaku dalam perpangkatan. Terdapat 6 sifat operasi perpangkatan yaitu:

1.

(

a×b

)

n =an×bn 2. am×an =am+n 3. _am _:an =_am−n 4.

(

)

n n n b a b a: = : 5.

( )

am n =am×n 6. n _n a a− = 1 dengan a≠0

Bukti kebenaran dari sifat-sifat di atas dapat Anda lakukan setelah Anda mempelajari unit 7 mengenai penalaran induktif dan deduktif. Sementara ini Anda dapat

menggunakan sifat-sifat tersebut untuk menyelesaikan soal-soal mengenai perpangkatan.

Pada perpangkatan, bilangan pokok dapat berupa bilangan bulat maupun pecahan, demikian juga untuk pangkat atau eksponen. Pangkat juga dapat berupa bilangan nol. Dalam perpangkatan, kedua komponen (bilangan pokok dan pangkat) sama pentingnya. Namun demikian, perubahan hasil perpangkatan terutama ditentukan oleh nilai pangkatnya. Oleh karena itu pembedaan nilai pangkat akan dibahas secara khusus.

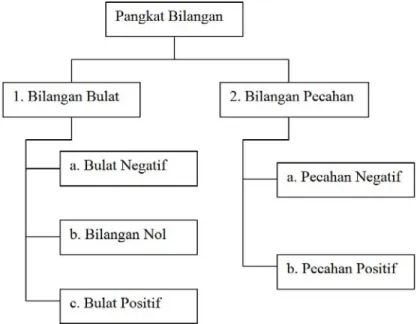
Pangkat dapat berupa bilangan nol, bilangan bulat (positif dan negatif), bilangan pecahan (rasional) dan bilangan irrasional. Bilangan irrasional tidak dibahas pada bahan ajar ini. Untuk lebih jelasnya dapat dilihat skema berikut ini.

Gambar 1.1 Skema Pangkat Bilangan

Bagaimana jika suatu bilangan dipangkatkan dengan nol? Sembarang bilangan bila dipangkatkan nol akan menghasilkan nilai 1, tidak perduli apakah bilangan pokoknya merupakan bilangan positif atau negatif.

Contoh : • 50 = 1 • 1 7 1 0 ₌ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

Seperti yang telah dikemukakan sebelumnya perpangkatan bilangan adalah bentuk perkalian berulang atau berganda. Berdasarkan Skema Pangkat Bilangan, pangkat

dapat berupa bilangan bulat positif atau negatif. Pangkat bilangan bulat positif merupakan bentuk perkalian berulang yang sebenarnya. Nilai pangkat/eksponen menunjukkan banyaknya perkalian berulang (faktor) nilai itu sendiri.

Sembarang bilangan bila dipangkatkan 1 akan menghasilkan bilangan itu sendiri. Contoh: • 21 = 2 • 8 1 8 1 1₌ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

Baik bilangan pokok yang merupakan bilangan bulat maupun pecahan, bila dipangkatkan dengan 1 maka hasil perpangkatannya bernilai tetap sama yaitu bilangan itu sendiri.

Sembarang bilangan bila dipangkatkan 2 akan menghasilkan perkalian berulang 2 kali bilangan itu sendiri. Contoh :

• 32 = 3 × 3 = 9 • 102 = 10 × 10 = 100 • 25 4 5 2 5 2 5 2 2_{= × =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ atau 25 4 5 5 2 2 5 2 5 2 2 2 2 = × × = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

Sembarang bilangan bila dipangkatkan 3 akan menghasilkan perkalian berulang 3 kali bilangan itu sendiri.

Contoh : • 43 = 4 x 4 x 4 = 64 • 103 = 10 x 10 x 10 = 1000 • 27 8 3 2 3 2 3 2 3 2 3 _{= × × =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ atau 27 8 3 3 3 2 2 2 3 2 3 2 3 3 3 = × × × × = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

Perbandingan pembilang dan penyebut dalam bilangan pokok pecahan bersifat tetap. Pangkat bilangan bulat negatif atau sering disebut pangkat tak sebenarnya, menunjukkan bahwa perkalian berulang pecahan/kebalikan bilangan itu sendiri. Bentuk umumnya sebagai berikut.

di mana n adalah bilangan bulat positif.

Sembarang bilangan bila dipangkatkan -1 akan menghasilkan kebalikan bilangan itu sendiri. Contoh : • 3−1= 1 =1 1 n n a a − ₌

• 8 8 1 1 8 1 1_{= =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − • 3 8 8 3 1₌ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

Terlihat bahwa bila bilangan pokoknya adalah bilangan bulat, maka pangkat -1 nya adalah pecahan / kebalikannya. Secara umum berlaku

a b b a b a _{= =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −1 1

Sembarang bilangan bila dipangkatkan -2 akan menghasilkan kuadrat kebalikan bilangan itu sendiri.

Contoh : • 4 1 2 1 2−2 = ₂ = • 9 9 1 1 3 1 1 3 1 2 2 = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − • 4 1 6 4 25 25 4 1 5 2 1 5 2 2 2 = = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

Bila bilangan pokok berbentuk pecahan dipangkatkan -2, maka hasilnya dapat berupa bilangan bulat ataupun bilangan pecahan.

Sembarang bilangan bila dipangkatkan -3 akan menghasilkan bilangan kubik dari kebalikan bilangan itu sendiri. Contoh :

• 27 1 3 1 3−3= ₃ = • 27 64 64 27 1 4 3 1 4 3 1 4 3 3 3 3 3 = = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

Akar Bilangan

Pada dasarnya pengertian akar bilangan dapat dijelaskan melalui perpangkatan. Akar bilangan merupakan perpangkatan dengan pangkat/eksponen bilangan pecahan. Pangkat bilangan pecahan disebut juga pangkat rasional. Secara umum definisi akar bilangan adalah sebagai berikut.

Definisi : n _{a (dibaca : akar n dari bilangan a) adalah bilangan yang apabila}

dipangkatkan dengan n hasilnya sama dengan a.

n _{a dapat juga ditulis a}n

1

Contoh : Akar bilangan 2 atau sama dengan pangkat pecahan 2 1

•

4 4 4 2 2 2 1 2 2 1 2 = = = × =

•

( )

( )

3 2 3 2 3 2 9 4 9 4 9 4 9 4 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 = = = = = = × ×

Akar bilangan 3 atau sama dengan pangkat pecahan 3 1

•

8 8 2 3 2 1 3 3 1 3 = = × =

•

( )

( )

3 2 3 2 3 2 27 8 27 8 27 8 3 1 3 3 1 3 3 1 3 3 1 3 3 1 3 1 3 3 3 = = = = = × ×

Latihan

Selanjutnya kerjakan latihan berikut untuk memantapkan pemahaman Anda terhadap materi.

1. Sederhanakanlah perpangkatan berikut ini. a.

( ) (

53 2: 55×54

)

b.

(

5−5×m×n6

) (

−2: 5−7×m8×n9

)

2. Nyatakan perpangkatan berikut dalam pangkat positif. a.

(

c−7×m5×n−9

) (

−2 c−10×m8×n−9

)

3. Hitunglah perpangkatan berikut ini. a. 2−3

b. 3 1

8

Bagaimana Saudara, apakah Anda mengalami kesulitan? Tentu saja tidak, namun demikian Anda dapat membandingkan jawaban yang Anda temukan dengan pembahasan berikut ini.

Pedoman Jawaban Latihan

1. Menyederhanakan perpangkatan.

a. Dengan menggunakan sifat 2 dan 5 diperoleh

( ) (

53 2: 55×54

)

=53.2:55+4

sehingga diperoleh

( ) (

53 2: 55×54

)

=56:59=56−9, kemudian menggunakan sifat 3. Jadi hasil penyederhanaan perpangkatan

( ) (

53 2: 55×54

)

adalah

3 5− .

b. Dengan menggunakan sifat 5 diperoleh

(

5 6

) (

2 7 8 9

) (

10 2 12

) (

7 8 9

)

5 : 5 5 : 5− ×m×n − − ×m ×n = ×m− ×n− − ×m ×n

Selanjutnya dengan menggunakan sifat 3 diperoleh perpangkatan yang lebih sederhana yaitu 510−(−7)×m−2−8×n−12−9 =517×m−10×n−21.

2. Menyatakan perpangkatan dalam pangkat positif.

a. Dengan menggunakan sifat-sifat perpangkatan,

(

_c−7×_m5×_n−9

) (

−2 _c−10×_m8×_n−9

)

_{akan dinyatakan dalam pangkat positif}

sebagai berikut.

(

14_× −10_× 18

)(

−10_× 8_× −9

)

n m c n m c menggunakan sifat 5 9 2 4 _{m n} c × − × menggunakan sifat 2 2 9 4 m n c × menggunakan sifat 6

b. Analog dengan pengerjaan a, perpangkatan

(

_{7 5 9}

) (

2 _{10 8 9}

)

2 : − − − − − _{× × × ×} n m c n m

c akan dinyatakan dalam pangkat

positif berikut ini.

(

14 10 18

) (

20 16 18

)

: − − − _{× × ×} ×m n c m n c menggunakan sifat 5 36 26 34 n m c × − × menggunakan sifat 3

26 36 34 m n c menggunakan sifat 6 3. Menghitung perpangkatan. a. 8 1 2 1 2−3 = ₃ = b. 83 3 8 2 1 = =

Materi mengenai perpangkatan dan akar bilangan telah selesai dibahas. Selanjutnya silahkan Anda kembali mengingat materi apa yang telah Anda pelajari pada subunit ini dengan membaca rangkuman. Kemudian silahkan Anda mengerjakan tes formatif 1, agar Anda dapat mengetahui tingkat pemahaman atau penguasaan materi ini.

Rangkuman

Perpangkatan bilangan adalah perkalian berulang atau berganda suatu bilangan dengan faktor-faktor bilangan yang sama

a × a × ... × a = an n faktor

di mana

a

disebut bilangan pokok atau bilangan dasar, sedangkan

n

disebut pangkat atau eksponen. Berikut beberapa sifat operasi perpangkatan yaitu:

1.

(

a×b

)

n =an×bn 2. _am×_an =_am+n 3. am :an =am−n 4.

(

a:b

)

n =an :bn 5.

( )

am n =am×n 6. n _n a a− = 1 dengan a≠0

Setiap bilangan yang dipangkatkan dengan bilangan nol, hasilnya merupakan bilangan 1, sedangkan setiap bilangan yang dipangkatkan dengan 1, hasilnya merupakan bilangan itu sendiri.

Akar suatu bilangan merupakan perpangkatan dengan pangkat bilangan pecahan. Bentuk umum akar bilangan adalah n _{a (dibaca : akar n dari bilangan a) yaitu}

bilangan yang apabila dipangkatkan dengan n hasilnya sama dengan a.

n _{a dapat juga ditulis a}n

Tes Formatif 1

Kerjakanlah tes formatif berikut untuk mengetahui tingkat penguasaan Anda terhadap materi perpangkatan dan akar bilangan dengan cara memberi tanda silang (X) pada pada salah satu jawaban yang Anda anggap benar.

1. Berikut ini yang merupakan definisi perpangkatan adalah ……. A. penambahan berulang bilangan yang sama

B. pengurangan berulang bilangan yang sama C. perkalian berulang bilangan yang sama D. pembagian berulang bilangan yang sama 2. Bentuk sederhana dari perpangkatan

(

₅

)

2 3 2 x y x − − adalah ……. A. xy6 C. x−5y−5 B. x5y−5 D. x−9y6 3. Bentuk perpangkatan ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − 3 3 2 3 ₁ 5 x

x jika dinyatakan dalam pangkat positif

adalah …… A. 1₄ x C. 9 3 5 x B. x 9 5 1 D. ₉ 18 5 x 4. Nilai dari

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ _× − − − 3 3 3 3 2 5 1 5 5 5 adalah ……. A. 5−7 C. 5 3 B. 0 _D. 12 5

5. Bilangan 32 merupakan penyederhanaan dari perpangkatan ……

A.

(

22×2−1

)

3 C. 20×24

B. 44×2−3 _D.

(

_{2 1}

)

2

2

4 × −

6. Arti dari n _{a adalah ……}

A. a−n

C. _an

B. _a n 1 − D. an 7. Nilai dari _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 2 8 27 9 16 adalah …… A. 1 C. 6 B. 2 D. 8

8. Bilangan 15 merupakan nilai dari …….

A. 5 _{75 C.}

( )( )

3 ₉ 2₁₀ B.

( )( )

3 ₅ 3 _{3 D.}

( )( )

3₁₂₅ 4 ₈₁ 9. Nilai dari 4 2 3 2 : 3 2 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ adalah …… A. 9 4 C. 85 20 B. 72 12 D. 729 64

10.Bilangan yang merupakan nilai dari _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 2 2 27 1 4 3 adalah …… A. 6 1 C. 18 1 B. 12 1 D. 24 1

Umpan Balik Dan Tindak Lanjut

Setelah mengerjakan tes formatif 1, bandingkan jawaban Anda dengan kunci jawaban yang terdapat pada akhir unit ini. Jika Anda dapat menjawab dengan benar minimal 80%, Anda dinyatakan berhasil dengan baik. Selamat, silahkan Anda mempelajari sub unit selanjutnya. Sebaliknya jika jawaban benar Anda kurang dari 80%, pelajari kembali uraian dalam sub unit ini, terutama bagian-bagian yang belum Anda kuasai dengan baik.

Subunit 2

Barisan dan Deret

arisan dan deret yang akan dibahas di sini khususnya barisan dan deret aritmetika serta geometri. Dalam subunit ini juga akan dibahas mengenai notasi sigma yang menjadi dasar untuk penulisan deret.

Barisan

Sebelum kita mempelajari barisan, coba Anda amati pola bilangan pada himpunan berikut ini.

1. Himpunan bilangan asli : {1, 2, 3, 4, 5, …} 2. Himpunan bilangan bulat : {…, -2, -1, 0, 1, 2, …} 3. Himpunan bilangan asli ganjil : {1, 3, 5, 7, 9, …} 4. Himpunan bilangan asli genap : {2, 4, 6, 8, 10, …}

Setiap anggota himpunan di atas dapat diurutkan sehingga mempunyai keteraturan atau pola. Penulisan beberapa anggota himpunan secara terurut seperti di atas akan dapat menyatakan anggota himpunan yang lain yang mempunyai pola sama.

Urutan bilangan yang mempunyai pola atau keteraturan tertentu disebut barisan. Pada contoh himpunan di atas, diperoleh barisan bilangan seperti berikut ini.

1. Barisan bilangan asli 1, 2, 3, 4, 5, … 2. Barisan bilangan bulat …, -2, -1, 0, 1, 2, … 3. Barisan bilangan (asli) ganjil 1, 3, 5, 7, 9, … 4. Barisan bilangan (asli) genap 2, 4, 6, 8, 10, …

Nama barisan dicirikan oleh bilangan-bilangan yang membentuk barisan tersebut. Adapula barisan yang diberi nama sesuai dengan penemunya.

Contoh : Barisan bilangan Fibonacci 1, 1, 2, 3, 5, 8, … yang ditemukan pada tahun 1200 oleh Leonardo Fibonacci.

Masing-masing bilangan pada suatu barisan disebut suku barisan dan dipisahkan dengan tanda koma. Suku pertama dilambangkan dengan u₁, suku kedua dilambangkan dengan u₂ dan seterusnya. Jadi secara umum suatu barisan yang terdiri dari n suku ditulis dalam bentuk sebagai berikut.

n

u u u

u₁, ₂, ₃,...,

Indeks pada barisan di atas menyatakan banyaknya suku dan disebut panjang barisan. Untuk n bilangan asli berhingga, barisan itu disebut barisan berhingga.

Pada contoh barisan bilangan yang telah disebutkan di atas, dua barisan bilangan pertama mempunyai pola yang sama yaitu suku barisan diperoleh dari suku sebelumnya ditambah 1. Perbedaan kedua barisan tersebut terletak pada suku awalnya saja. Suku barisan bilangan pada contoh keempat dan kelima diperoleh dengan menambah suku sebelumnya dengan bilangan 2. Perbedaan pada suku awal akan memberikan perbedaan pada suku-suku berikutnya.

Selanjutnya kita akan mempelajari barisan aritmetika dan geometri. Untuk memahami pengertian barisan aritmetika, coba Anda perhatikan contoh-contoh barisan berikut ini.

Contoh : 1. Barisan 2, 4, 6, 8, … 2. Barisan 4, 1, -2, -5, … 3. Barisan 3, 2 2 1 , 2, 1 2 1 , …

Pada setiap barisan di atas, apakah Anda bisa melihat bahwa selisih dua suku yang berurutan selalu tetap (konstan)? Barisan dengan ciri seperti itu disebut barisan aritmetika dan selisih dua suku yang berurutan disebut beda dan dilambangkan dengan b. Coba Anda tentukan beda masing-masing barisan pada contoh di atas kemudian cocokkan jawaban Anda dengan pembahasan berikut ini.

1. Beda barisan 2, 4, 6, 8, … dapat diketahui dengan cara mengurangkan suku barisan (kecuali suku awal) dengan suku sebelumnya. Jadi beda barisan tersebut adalah b=4−2=6−4=8−6=2.

2. Beda barisan 4, 1, -2, -5, … adalah b=1−4=(−2)−1=(−5)−(−2)=−3. 3. Beda barisan 3, 2 2 1 , 2, 1 2 1 , … adalah 2 1 2 2 1 1 2 1 2 2 3 2 1 2 − = − = − =− = b .

Jika kita ingin menentukan suku ke sekian dari suatu barisan aritmetika, berarti kita harus mempunyai rumus untuk suku ke-n dari barisan aritmaetika. Misalkan suku awal dan beda dari barisan aritmetika dilambangkan dengan a dan b. Untuk menentukan rumus suku ke-n suatu barisan aritmetika, perhatikan bagan berikut ini.

Jadi berdasarkan bagan di atas diperoleh rumus suku ke-n dari barisan aritmetika yaitu

(

n

)

b a u_n = + −1 .

Latihan 1

Setelah Anda mengetahui rumus umum suku ke-n dari barisan aritmetika, silahkan Anda berlatih mengerjakan contoh-contoh soal berikut ini.

1. Dari barisan aritmetika berikut ini, tentukan rumus suku ke-n dan suku ke 26. a. 1, 7, 13, 19, … b. 8, 1, -6, -13, … c. 10, 4 1 9 , 2 1 8 , 4 3 7 , …

2. Jika diketahui pada suatu barisan aritmetika, suku ke-10 adalah 41 dan suku ke-5 adalah 21. Tentukan suku ke-125.

Pedoman Jawaban Latihan

Bagaimana Saudara, apakah Anda mengalami kesulitan? Coba Anda cocokkan jawaban yang telah Anda kerjakan dengan pembahasan berikut ini.

1. a. Pada barisan 1, 7, 13, 19, …diketahui suku awal a=1 dan beda b=6 maka rumus suku ke-n dari barisan tersebut adalah u_n =1+

(

n−1

)

6 atau

5

6 −

= n

u_n . Dari rumus ini dapat ditentukan suku ke-26 yaitu

( )

26 5 156 5 155 6

26 = − = − =

u .

b. Pada barisan 8, 1, -6, -13, …, diketahui suku awal a =8 dan beda 7

8 1− =− =

b maka rumus ke-n dari barisan tersebut adalah

(

n

)

n

u_n =8+ −1(−7)=15−7 , sehingga dari sini dapat ditentukan suku ke-26 yaitu u₂₆=15−7(26)=15−182=−167. c. Pada barisan 10, 4 1 9 , 2 1 8 , 4 3

7 , …diketahui suku awalnya adalah a=10 dan beda 4 3 10 4 1 9 − =− =

b . Rumus ke-n dari barisan tersebut adalah

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − + = 4 3 1 10 n u_n atau u_n

(

43 3n

)

4 1 ₋

= . Dari sini kita akan tentukan

suku ke-26 yaitu

(

( )

)

(

)

4 3 8 4 35 35 4 1 26 3 43 4 1 26 = − = − =− =− u .

2. Diketahui suku ke-10 dari suatu barisan aritmetika adalah 41 dan suku ke-5 sama dengan adalah 21 maka u₁₀ =a+

(

10−1

)

b=a+9b=41 dan

(

5 1

)

4 21

5 =a+ − b=a+ b=

u . Dari sini diperoleh

41 9 = + b a 21 4 = + b a 20 5b= 4 = b sehingga a+4(4)=21 5 = a

Jadi rumus ke-n barisan tersebut adalah u_n =5+

(

n−1

)

4=4n+1 sehingga suku ke-125 adalah u₁₂₅ =4(125)+1=500+1=501.

Kita telah bersama-sama mempelajari barisan aritmetika. Sekarang kita akan mempelajari barisan lain yang juga sering kita temui dalam kehidupan sehari-hari yaitu barisan geometri. Sebelum kita mempelajari barisan geometri, kita simak dahulu cerita berikut ini.

Alkisah di suatu negeri, seorang raja akan memberikan apapun yang diminta sebagai hadiah kepada juara catur di negeri itu. Juara catur meminta hadiah beras yang jumlahnya adalah banyak beras di kotak terakhir pada papan catur dengan aturan banyak beras di setiap kotak papan catur adalah sebagai berikut. Banyaknya beras di kotak pertama 1 kg, di kotak kedua sebanyak 2 kg, di kotak ketiga sebanyak 4 kg, dan seterusnya. Sang raja langsung menyetujui permintaan tersebut. Dia berpikir bahwa permintaan itu sangat sederhana.

Bagaimana Saudara, apakah Anda setuju dengan pemikiran raja tersebut? Apakah permintaan juara catur tersebut sangat sederhana? Sebenarnya berapa kg beras yang diminta sebagai hadiah? Kita akan selidiki bersama kasus ini. Kita perhatikan barisan bilangan yang menyatakan banyak beras yang diminta oleh juara catur yaitu 1, 2, 4, 8, 16, dan seterusnya. Coba Anda perhatikan bahwa setiap dua suku yang berurutan mempunyai perbandingan yang tetap. Pada barisan itu perbandingan yang tetap

tersebut adalah 2 8 16 2 8 2 4 1 2 _{= = = =}

. Perbandingan yang tetap itu disebut rasio dan dilambangkan dengan r. Jadi rasio barisan 1, 2, 4, 8, 16, … adalah r=2. Barisan yang mempunyai perbandingan tetap antara suku-suku yang berurutan disebut barisan geometri. Jadi secara umum, barisan geometri berbentuk

n u u u u₁, ₂, ₃,..., dengan r u u n n = −1

Selanjutnya, apakah Anda bisa menentukan rumus suku ke-n dari barisan geometri tersebut? Kita akan selidiki bersama-sama.

r u u = 1 2 _{sehingga u u r} 1 2 = r u u = 2 3 _{sehingga u u r} 2 3 = , karena u2 =u1r maka 2 1 1 3 u .r.r u r u = = r u u = 3 4 _{sehingga u u r} 3 4 = , karena 2 1 3 u r u = maka u₄ =u₁.r2.r=u₁r3 dan seterusnya sampai dengan suku ke-n yaitu u_n =u₁rn−1

Jadi rumus suku ke-n dari suatu barisan geometri adalah u_n =u₁rn−1.

Kita kembali ke kasus sang raja dan juara catur. Berapa kg beras yang diminta juara catur? Banyak kotak pada papan catur adalah 64. Jadi kita akan menentukan suku ke-64 dari barisan 1, 2, 4, 8, 16, …sebagai berikut.

63 63 1 64 1 64 2 2 . 1 = = = − r u u

Ternyata banyak sekali beras yang diminta juara catur yaitu sebanyak _{2 kg.} 63

Latihan 2

Saudara, Anda telah belajar mengenai barisan geometri. Pemahaman Anda terhadap konsep ini akan lebih meningkat jika Anda berlatih menyelesaikan soal-soal berkaitan dengan barisan geometri. Berikut ini soal tentang barisan geometri, silahkan Anda menyelesaikan soal-soal tersebut.

1. Tentukan rasio, rumus ke-n dan suku ke-10 dari tiap barisan geometri berikut ini.

a. 2, 6, 18, 54, … b. 32, 16, 8, 4, … c. 4, -8, 16, -32, … d. 3 , 6, 12 3, 72, …

2. Suku pertama dari suatu barisan geometri sama dengan 4 dan suku ke-4 sama dengan 12. Tentukan rasio dan suku ke-8.

Pedoman Jawaban Latihan

Bagaimana Saudara, apakah Anda menemui kesulitan? Untuk melihat seberapa jauh pemahaman Anda mengenai barisan geometri, silahkan cocokkan penyelesaian yang Anda buat dengan pembahasan penyelesaian soal berikut ini.

1. a. Rasio pada barisan geometri pada 1a adalah 3 2 6 ₌ =

r . Suku pertama dari

barisan geometri itu adalah u₁=2 maka rumus suku ke-n u_n =2.3n−1. Dari rumus tersebut dapat ditentukan suku ke-10 sebagai berikut.

39366 19683 . 2 3 . 2 3 . 2 101 9 10 = = = = − u

Jadi suku ke-10 barisan geometri 2, 6, 18, 54, ... adalah 39366. b. Rasio barisan geometri pada 1b adalah

2 1 32 16 ₌ =

r . Suku pertama dari

barisan tersebut adalah u₁=32 maka rumus suku ke-n barisan tersebut

1 2 1 32 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = n n

u . Dari rumus tersebut ditentukan suku ke-10 sebagai

berikut. 16 1 512 1 32 2 1 32 2 1 32 9 1 10 10 ⎟= ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − u

Jadi suku ke-10 barisan geometri 32, 16, 8, 4, ... adalah 16

1 .

c. Rasio barisan geometri pada 1c adalah 2

4 8 ₌₋ − =

r . Suku pertama dari

barisan tersebut adalah u₁=4 maka rumus suku ke-n u_n =4

( )

−2 n−1. Dari rumus tersebut dapat ditentukan suku ke-10 dari barisan sebagai berikut.

( )

2 4

( )

2 4

(

512

)

2048

4 10 1 9

10 = − = − = − =−

−

u

Jadi suku ke10 dari barisan 4, 8, 16, 3, dan seterusnya sama dengan -2048.

d. Rasio barisan geometri pada 1d adalah 2 3

3 3 6 3 6 = = = r . Suku

pertama barisan adalah u₁= 3 maka rumus rumus suku ke-n

( )

1 3 2 3 − = n n

u . Dari rumus ini dapat ditentukan suku ke-10 dari barisan

sebagai berikut.

( )

2 3 3

( )

2 3

( )

2

( )

3 512

( )

3 512

( )

243 124416 3 10 1 9 9 10 5 10 = = = = = = − u

Jadi suku ke-10 dari barisan geometri 3 , 6, 12 3, 72, .... sama dengan 124416.

2. Diketahui u₁ =4 dan u₄ =12 maka

3 3 3 1 4 1 3 3 12 4 12 = = = = − r r r r u

Suku ke 8 dari deret adalah

( )

3 3 1 2 3 7 7 3 1 8 1 8 = =4× 3 =4×3 =4×3 ×3 =36 3 − r u u .

Bagaimana Saudara, apakah penyelesaian Anda benar semua? Sejauh mana pemahaman Anda mengenai barisan geometri? Jika menurut Anda, pemahaman mengenai konsep ini kurang, jangan segan untuk mepelajari kembali konsep ini sebelum kita mempelajari konsep berikutnya. Konsep yang akan kita pelajari selanjutnya adalah mengenai konsep notasi sigma yang menjadi landasan dalam penulisan deret bilangan. Jika Anda sudah siap, kita akan lanjutkan dengan mempelajari konsep notasi sigma berikut ini.

Notasi Sigma

Notasi sigma banyak digunakan dalam matematika khususnya bidang statistika. Penggunaan notasi sigma di dalam statistika antara lain digunakan dalam menentukan mean, simpangan baku, dan ragam. Sebelum membahas notasi sigma, perhatikan jumlah lima bilangan ganjil berikut ini.

1 + 3 + 5 + 7 + 9

Menurut Anda bagaimanakah pola lima bilangan tersebut? Pola barisan tersebut adalah sebagai berikut.

Suku ke-1 = 1= 2(1) – 1 Suku ke-2 = 3 = 2(2) – 1 Suku ke-3 = 5 = 2(3) – 1 Suku ke-4 = 7 = 2(4) – 1 Suku ke-5 = 9 = 2(5) – 1

Jadi secara umum pola barisan bilangan di atas adalah 2k – 1 dengan k = 1, 2, 3, 4, 5. Penjumlahan lima bilangan asli yang ganjil di atas dapat disingkat dengan menggunakan notasi sigma. Lambang notasi sigma adalah Σ yang merupakan huruf

kapital Yunani yang berarti penjumlahan. Notasi ini pertama kali diperkenalkan oleh Leonhard Euler pada tahun 1755. Jadi penulisan 1 + 3 + 5 + 7 + 9 dengan menggunakan notasi sigma adalah sebagai berikut.

∑

= − 5 1 ) 1 2 ( k k

Lambang k=1 disebut batas bawah dan k =5 disebut batas atas. Secara umum bentuk notasi sigma didefinisikan sebagai berikut.

n n k k a a a a a = + + + +

∑

= ... 3 2 1 1

Latihan 3

Selanjutnya silahkan Anda berlatih menyelesaikan soal-soal berikut ini.

1. Tuliskan tiap penjumlahan berikut ini dengan menggunakan notasi sigma. a. 3+5+7+9+11 b. 1+4+9+16+25+36 c. 11 6 9 5 7 4 5 3 3 2 1+ + + + +

2. Setiap notasi sigma berikut ini, tuliskan dalam suku-suku penjumlahan kemudian hitunglah jumlahnya.

a.

∑

(

)

= + 6 1 1 3 i i b.

∑

(

)

= − 5 1 4 1 k k c.

∑

= 4 1 2 i i

Pedoman Jawaban Latihan

Cocokkan penyelesaian Anda dengan pembahasan berikut ini.

1. a. Perhatikan pola bilangan pada penjumlahan 3+5+7+9+11. Suku ke-1 = 3 = 2(1) + 1

Suku ke-2 = 5 = 2(2) + 1 Suku ke-3 = 7 = 2(3) + 1 Suku ke-4 = 9 = 2(4) + 1 Suku ke-5 = 11 = 2(5) + 1

Secara umum pola bilangan pada penjumlahan tersebut adalah 2k+1 dengan k =1,2,3,4,5. Jadi notasi sigma untuk penjumlahan

11 9 7 5 3+ + + + adalah

∑

= + 5 1 1 2 k k .

b. Pola bilangan pada penjumlahan 1+4+9+16+25+36 adalah sebagai berikut. Suku ke-1 = 1 = 1 2 Suku ke-2 = 4 = ₂ 2 Suku ke-3 = 9 = 32 Suku ke-4 = 16 = 4 2 Suku ke-5 = 25 = 5 2 Suku ke-6 = 36 = 6 2

Jadi secara umum pola bilangan pada penjumlahan tersebut adalah 2

k dengan 6k=1,2,3,4,5, sehingga notasi sigma dari penjumlahan itu adalah

∑

= 6 1 2 k k .

c. Coba Anda perhatikan pola bilangan pada penjumlahan

11 6 9 5 7 4 5 3 3 2

1+ + + + + . Apakah Anda bisa melihat bahwa

bilangan-bilangan yang menjadi pembilang merupakan 6 bilangan-bilangan asli pertama dan bilangan yang menjadi penyebut merupakan 6 bilangan (asli) ganjil pertama. Pola bilangan ganjil secara umum adalah 2k−1 dengan

6 , 5 , 4 , 3 , 2 , 1 = k . Jadi penjumlahan 11 6 9 5 7 4 5 3 3 2 1+ + + + + dapat ditulis

dengan menggunakan notasi sigma yaitu

∑

= − 6 12 1 k k k .

2. Selanjutnya kita akan menentukan suku-suku penjumlahan dan kemudian menghitung hasil penjumlahannya.

a.

(

) (

) (

) (

) (

) (

) (

)

69 19 16 13 10 7 4 1 6 . 3 1 5 . 3 1 4 . 3 1 3 . 3 1 2 . 3 1 1 . 3 1 3 6 1 = + + + + + = + + + + + + + + + + + = +

∑

= i i

b.

(

) (

) (

) (

) (

) (

)

( ) ( ) ( ) (

) (

)

55 19 15 11 7 3 5 . 4 1 4 . 4 1 3 . 4 1 2 . 4 1 1 . 4 1 4 1 5 1 − = − + − + − + − + − = − + − + − + − + − = −

∑

= k k c. 30 16 8 4 2 2 2 2 2 2 1 2 3 4 4 1 = + + + = + + + =

∑

= i i

Pada notasi sigma, terdapat beberapa sifat yang sangat berguna dalam melakukan penghitungan atau manipulasi aljabar. Sifat-sifat tersebut sebagai berikut.

Sifat 1. nA A n i =

∑

=1

dengan A suatu konstanta

Contoh : 10 ) 2 ( 5 2 2 2 2 2 2 5 5 1 = = + + + + =

∑

= 14 24suku4 34 i Sifat 2.

∑

∑

= = = n i i n i i A u Au 1 1 Contoh :

(

)

∑

∑

= = = + + + = + + + = 4 1 4 3 2 1 4 3 2 1 4 1 2 2 2 2 2 2 2 i i i i u u u u u u u u u u Sifat 3.

(

)

_∑

_∑

∑

= = = ± = ± n i i n i i n i i i v u v u 1 1 1 Sifat 4.

∑

∑

∑

= + = = = + n i i n m i i m i i u u u 1 1 1

Sifat 5.

∑

∑

∑

+ = − − = + = = = 1 2 1 1 0 1 1 n i i n i i n i i u u u

Anda dipersilahkan mencari contoh penggunaan sifat 3, 4, dan 5.

Deret

Jika suku-suku dalam suatu barisan dijumlahkan maka penjumlahan berurut dari suku-suku barisan tersebut disebut deret. Apakah Anda telah mendengar mengenai cerita tentang matematikawan yang bernama Carl Friederich Gauss? Ketika Gauss masih di sekolah dasar, dia diminta oleh gurunya untuk menjumlahkan 100 bilangan asli pertama. Gauss menggunakan teknik menghitung sederhana tetapi keefektifan cara menghitung yang dilakukan Gauss tidak diragukan lagi. Ia memisalkan S adalah jumlah 100 bilangan asli yang pertama seperti berikut ini.

100 ... 3 2 1+ + + + = S 1 ... 98 99 100+ + + + = S 101 ... 101 101 101 2S = + + + + 10100 ) 101 ( 100 2S = = 5050 = S

Teknik menghitung Gauss ini, selanjutnya digunakan untuk mendapatkan rumus jumlah n suku pertama deret aritmetika berikut ini.

) ( 2 1 n n n a U S = + atau [2 ( 1) ] 2 1 b n a n S_n = + −

Salah satu sifat penting dari S_n adalah S_n−S_n−1 =u_n.

Latihan 4

Anda telah mendapatkan rumus jumlah n suku pertama deret aritmetika, maka sekarang selesaikan soal berikut.

1. Tentukan jumlah 10 suku pertama pada deret aritmetika ...

2 1 2 2 2 1 1 + + +

2. Jika pada suatu deret aritmetika, diketahui suku ke-5 sama dengan 40 dan suku ke-8 sama dengan 25, maka tentukan jumlah 12 suku pertama dari deret aritmetika tersebut.

Pedoman Jawaban Latihan

Cocokkan jawaban Anda dengan pembahasan berikut.

1. Dari deret aritmetika ...

2 1 2 2 2 1

1 + + + diketahui suku pertama

2 1 1 = a dan beda 2 1 =

b . Nilai suku pertama dan beda tersebut kita masukkan ke dalam

rumus jumlah n suku pertama dari barisan aritmetika, sehingga diperoleh:

(

)

2 75 2 15 5 2 9 3 5 2 1 9 2 3 2 5 2 1 1 10 2 1 1 . 2 ) 10 ( 2 1 ] ) 1 ( 2 [ 2 1 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{+ −} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − + = n a n b S_n

2. Diketahui 40u₅ = dan u₈ =25 sehingga dari sini diperoleh

40 4 40 5 = + = b a u 25 7 25 8 = + = b a u

Dari kedua persamaan di atas diperoleh

25 7 40 4 = + = + b a b a 5 15 3 − = = − b b

Jika diketahui b=−5 maka

60 40 20 40 ) 5 ( 4 = = − = − + a a a

(

)( )

[

]

[

]

30 55 60 6 5 1 12 60 12 . 2 1 = − = − − + = n S

Jadi jumlah 12 suku pertama dari barisan aritmetika yang dimaksud adalah 30.

Anda telah berlatih menyelesaikan soal berkaitan dengan deret aritmetika. Sekarang Anda akan mempelajari deret geometri. Secara umum, jumlah n suku pertama dari suatu deret geometri adalah

(

)

(

1

)

1 − − = r r a S n n dengan r>1 atau

(

)

(

r

)

r a S n n ₋ − = 1 1 dengan r<1. Seperti pada deret aritmetika, deret geometri berlaku juga S_n −S_n−1 =u_n.

Latihan 5

Selanjutnya selesaikan soal berikut.

1. Tentukan jumlah 6 suku pertama deret geometri 1+2+4+...

2. Jika jumlah deret geometri 2+22+23+...+2n =254 maka tentukan nilai n.

Pedoman Jawaban Latihan

Apakah Anda mengalami kesulitan menyelesaikannya? Anda dapat mencocokkan jawaban Anda dengan pembahasan berikut ini.

1. Deret geometri 1+2+4+... mempunyai rasio 2 1

1 2 _{= >} =

r maka untuk

menentukan jumlah 6 suku pertama deret tersebut menggunakan rumus

(

)

(

)

(

)

₆₃ 1 1 64 1 2 1 2 . 1 1 1 6 6 = − = − − = − − = S r r a S n n

Jadi jumlah 6 suku pertama deret 1+2+4+... adalah 63.

2. Deret geometri 2+22 +23 +...+2n =254 _{mempunyai a}=_{2 dan} 1

2 2 22 _{= >} =

r . Menentukan nilai n dari deret geometri tersebut sebagai

(

)

(

)

(

)

7 2 128 2 1 127 1 2 2 254 1 2 1 2 2 254 1 1 = = = + − = − − = − − = n r r a S n n n n n n

Jadi nilai n yang memenuhi deret geometri 2+22+23 +...+2n =254 adalah 7.

Rangkuman

Urutan bilangan yang mempunyai pola atau keteraturan tertentu disebut barisan. Masing-masing bilangan pada suatu barisan disebut suku barisan dan dipisahkan dengan tanda koma. Suku pertama dilambangkan dengan u₁, suku kedua dilambangkan dengan u₂ dan seterusnya. Jadi secara umum suatu barisan yang terdiri dari n suku ditulis dalam bentuk sebagai berikut.

n

u u u

u₁, ₂, ₃,...,

Indeks pada barisan di atas menyatakan banyaknya suku dan disebut panjang barisan. Untuk n bilangan asli berhingga, barisan itu disebut barisan berhingga. Barisan dengan selisih dua suku yang berurutan selalu tetap (konstan) disebut barisan aritmetika dan selisih dua suku yang berurutan disebut beda. Rumus suku ke-n dari barisan aritmetika yaitu

(

n

)

b a

u_n = + −1 .

Barisan yang mempunyai perbandingan tetap antara suku-suku yang berurutan disebut barisan geometri. Jadi secara umum, barisan geometri berbentuk

n u u u u₁, ₂, ₃,..., dengan r u u n n = −1

dimana r adalah konstanta

Rumus suku ke-n dari suatu barisan geometri adalah u_n =u₁rn−1.

Jika suku-suku dalam suatu barisan dijumlahkan maka penjumlahan berurut dari suku-suku barisan tersebut disebut deret. Dalam penulisan deret akan lebih mudah menggunakan notasi sigma. Secara umum bentuk notasi sigma didefinisikan sebagai berikut. n n k k a a a a a = + + + +

∑

= ... 3 2 1 1

Rumus jumlah n suku pertama deret aritmetika adalah:

) ( 2 1 n n n a U S = + atau [2 ( 1) ] 2 1 b n a n S_n = + −

Salah satu sifat penting dari S_n adalah S_n−S_n−1 =u_n.

Sedangkan jumlah n suku pertama dari suatu deret geometri adalah:

(

)

(

1

)

1 − − = r r a S n n dengan r>1 atau

(

)

(

r

)

r a S n n ₋ − = 1 1 dengan r<1.

Tes Formatif 2

Kerjakanlah tes formatif berikut untuk mengetahui tingkat penguasaan Anda terhadap materi barisan dan deret dengan cara memberi tanda silang (X) pada pada salah satu jawaban yang Anda anggap benar.

1. Suku ke-7 dari barisan ,_L

2 1 2 , 3 , 2 1 3 , 4 adalah ... A. 0 C. 1 B. 2 1 D. 2 1 1 2. Rumus suku ke-n barisan −1,4,9,14,_K adalah ...

A. n2 C. (n−1).5

B. 5n−6 D. −1+(n−1).4

3. Barisan 10, 3, -4, -11, ... merupakan ...

A. barisan aritmetika C. deret aritmetika

B. barisan geometri D. deret geometri

4. Rumus umum suku ke-n barisan geometri adalah ... A. u_n =a+

(

n−1

)

b C. r u u n n = −1 B. u_n =u₁rn−1 _{D. [2 ( 1) ]} 2 1 b n a n u_n = + − 5. Barisan ,_L 9 1 1 , 3 1 3 , 10 , 30 mempunyai ... A. beda 20 C. rasio 20 B. beda 3 1 D. rasio 3 1

6. Deret 2+5+10+17+26 jika dinyatakan dengan notasi sigma adalah ... A.

∑

_n2 +1 C.

∑

= + n k k 1 2 ₁ B.

∑

= + 5 1 2 1 k k D.

∑

2+5+10+17+26 7. ... 3 1 2_{+ =}

∑

= k k k A. 12 C. 20 B. 14 D. 28

8. Jumlah deret 2+5+8+11+_Ladalah... A. n2 C. 2 3_n2 −_n B. n2 +2n D. 2 3n2+n

9. Jumlah 6 suku pertama deret geometri dengan rumus suku

1 2 1 30 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = n n u adalah ... A. 12 165 C. 16 945 B. 12 660 D. 64 3780

10.Jika diketahui suku ketiga barisan aritmetika adalah 11 dan suku kesepuluh adalah 39 maka rumus suku ke-n barisan tersebut adalah ...

A. 3n+1 C. 3n+7

B. 4n−1 D. 4n+7

Umpan Balik Dan Tindak Lanjut

Setelah mengerjakan tes formatif 2, bandingkan jawaban Anda dengan kunci jawaban yang terdapat pada akhir unit ini. Jika Anda dapat menjawab dengan benar minimal 80%, Anda dinyatakan berhasil dengan baik. Selamat, silahkan Anda mempelajari materi pada unit selanjutnya. Sebaliknya jika jawaban benar Anda kurang dari 80%, pelajari kembali uraian dalam sub unit ini, terutama bagian-bagian yang belum Anda kuasai dengan baik.

Kunci Tes Formatif

Kunci Tes formatif 1

1. C. 2. D.

(

)

4 6 5 9 6 5 2 3 2 . . .y x x y x x y x − − − − − = = 3. C. ₉ 3 3 9 3 6 9 3 3 2 3 5 5 . 5 1 5 x x x x x x ⎟⎠= = = ⎞ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − − − − 4. C.

(

)

( )

3 0 3 1 3 3 3 3 2 5 5 5 5 1 5 5 . 5 _{= =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ − − − − 5. B. 44×2−3=

( )

22 4×2−3=28×2−3=25 =32 6. C. 7. B. 2 2 3 3 4 8 27 9 16 3 2 ⎟= ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 8. D.

( )( )

3125 4 81 =5.3=15 9. A. 9 4 3 2 3 2 . 3 2 3 2 : 3 2 3 2 : 3 2 4 2 2 4 2 1 4 4 2 ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 10.A.

( )

6 1 3 . 2 1 3 . 2 3 3 1 4 3 27 1 4 3 2 3 2 1 2 1 3 2 1 2 1 2 2 = = = ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

Kunci Tes Formatif 2

11.C. Barisan ,_L 2 1 2 , 3 , 2 1 3 ,

4 merupakan barisan aritmetika dengan suku awal a

= 4 dan beda b = 2 1

− , sehingga suku ke-7 adalah

(

)

4 3 1. 2 1 1 7 4 7 ⎟= − = ⎠ ⎞ ⎜ ⎝ ⎛− − + = u

12.B. Barisan −1,4,9,14,_K merupakan barisan aritmetika dengan a=−1 dan beda b=5. Suku ke-n barisan tersebut adalah:

6 5 5 5 1 5 ) 1 ( 1 ) 1 ( − = − + − = − + − = − + = n n n b n a u_n

13.A. Barisan tersebut mempunyai selisih dua suku yang berurutan selalu tetap (konstan), yaitu -7.

14.B.

15.D. Barisan tersebut merupakan barisan geometri dengan rasio 3 1 . 16.B. 17.C. (12 1) (22 2) (32 3) 2 6 12 20 3 1 2 + = + + + + + = + + =

∑

= k k k .

18.D. Deret tersebut merupakan deret aritmetika dengan suku awal a = 2 dan beda b = 3, sehingga jumlah suku ke-n adalah

2 3 ] 1 3 [ 2 1 ] 3 3 4 [ 2 1 ] 3 ). 1 ( 2 . 2 [ 2 1 ] ) 1 ( 2 [ 2 1 2 n n n n n n n n b n a n S_n + = + = − + = − + = − + = 19.C. 1 2 1 30 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = n n u diketahui u₁ =30 dan 0 2 1 _< =

r maka jumlah 6 suku

pertama dari deret tersebut adalah

16 945 64 63 60 2 1 64 1 1 30 2 1 1 2 1 1 30 6 6 ⎟= ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = S

20.B. Diketahui u₃ =a+2b=11 dan u₁₀ =a+9b=39. Dari kedua persamaan tersebut diperoleh suku pertama a =3 dan beda b=4 sehingga rumus

umum suku ke-n barisan aritmetika tersebut adalah

1 4 4 ) 1 ( 3+ − = − = n n u_n .

Daftar Pustaka

Wirodikromo, S. 1996. Matematika. Jakarta : Erlangga

________.2004. Aritmetika. [Online}. Tersedia di:

Glosarium

Akar bilangan : Kebalikan dari perpangkatan

Barisan aritmetika : Barisan dengan selisih dua suku yang berurutan selalu tetap (konstan)

Barisan geometri : Barisan yang mempunyai perbandingan tetap antara suku-suku yang berurutan

Bilangan pokok : Bilangan yang dipangkatkan dalam suatu perpangkatan

Deret : Penjumlahan berurut dari suku-suku barisan

Eksponen : Bilangan pangkat

Notasi sigma : Sebuah notasi yang menyatakan penjumlahan. Panjang barisan : Bilangan yang menyatakan banyak suku barisan Suku barisan : Bilangan yang terdapat dalam suatu barisan