BAB 2
LANDASAN TEORI
2.1 Definisi Kamus
Kamus menurut KBBI (Kamus Besar Bahasa Indonesia) merupakan buku acuan yang memuat kata dan ungkapan, biasanya disusun menurut abjad berikut keterangan dan makna, pemakaian atau terjemahan (Argakusumah, 2014). Selain itu, kamus merupakan buku yang memuat kumpulan istilah atau nama yang disusun menurut abjad beserta dengan penjelasan makna dan pemakaiannya.
2.2 Definisi Algoritma
Algoritma adalah urutan langkah-langkah logis penyelesaian masalah yang disusun secara sistematis (Rinal Munir, 1999). Kata logis merupakan kata kunci. Langkah-langkah tersebut harus logis, ini berarti nilai kebenarannya harus dapat ditentukan, benar atau salah. Langkah-langkah yang tidak benar dapat memberikan hasil yang salah.
Algoritma adalah jantung ilmu komputer atau informatika. Banyak cabang ilmu komputer yang diacu dalam terminologi algoritma. Dalam kehidupan sehari-hari banyak terdapat proses yang digambarkan dalam suatu algoritma. Cara membuat kue atau masakan, misalnya dinyatakan dengan suatu resep. Resep makanan adalah suatu algoritma.
2.2.1 Definisi Algoritma String Matching
String Matching adalah pencarian sebuah pattern pada sebuah teks (kurnaedi, 2012). Prinsip
kerja algoritma string matching adalah sebagai berikut :
1. Memindai teks dengan bantuan sebuah window yang ukurannya sama dengan panjang pattern.
2. Menempatkan window pada awal teks.
3. Membandingkan karakter pada window dengan karakter dari pattern. Setelah pencocokan (baik hasilnya cocok atau tidak cocok), dilakukan shif ke kanan pada window. Prosedur ini dilakukan berulang-ulang sampai window berada pada akhir
String Matching dibagi menjadi dua, yaitu exact string matching dan heuristic (statistical
matching). Exact matching digunakan untuk menemukan pattern yang berasal dari satu teks.
Contoh pencarian exact matching adalah pencarian kata “pelajar” dalam kalimat “ saya seorang pelajar” atau “saya seorang siswa”. Sistem akan memberikan hasil bahwa kata pelajar dan siswa bersinonim. Algoritma exact matching diklasifisikan menjadi tiga bagian menurut arah pencariannya, yaitu :
1. Arah pencarian dari kiri ke kanan.
Algoritma yang termasuk dalam kategori ini adalah Brute Force, Morris dan Pratt (yang kemudian dikembangkan oleh Knuth, Morris dan Pratt).
2. Arah pembacaan dari kanan ke kiri.
Algoritma yang termasuk dalam kategori ini adalah Boyer Moore yang kemudian dikembangkan menjadi algoritma Turbo Boyer Moore, Tuned Boyer Moore dan Zhu Takaoka.
3. Arah pencarian yang ditentukan oleh program.
Algoritma yang termasuk dalam kategori ini adalah algoritma Colussi dan Crochemore-Perrin.
Heuristic matching adalah teknik yang digunakan untuk menghubungkan dua data
terpisah ketika exact matching tidak mampu mengatasi karena pembatasan pada data yang tersedia. Heuristic matching dapat dilakukan dengan perhitungan distance antara pattern dengan teks. Exact dan heuristic matching memiliki kemiripan makna tetapi berbeda tulisan.
2.2.1.1 Algoritma Turbo Boyer Moore
Algoritma Turbo Boyer Moore adalah sebuah algoritma pencocokan pola tertentu terhadap suatu kalimat atau paragraf. Algoritma ini merupakan varian dari Algoritma Boyer Moore yang memungkinkan terjadinya ‘lompatan’ melewati segmen yang tidak memerlukan preprosessing tambahan dengan kecepatan yang baik. Algoritma Turbo Boyer Moore
Pertama : inisialisasi, karena algoritma ini menggunakan good suffix shif dan bad character shif dari Algoritma Boyer Moore maka untuk inisialisasi dijalankan prosedur preBmBc dan
preBmGs seperti Algoritma Boyer Moore.
Kedua : Melakukan proses pencocokan karakter pada pattern dengan karakter pada teks. Jika terjadi ketidakcocokan maka dilakukan pergeseran terbesar berdasarkan tabel BmBc, tabel BmGs dan turbo shif.
Adapun Prinsip Kerja dari Algoritma Turbo Boyer Moore adalah sebagai berikut : 1. Algoritma Boyer Moore mulai melakukan pencocokan pattern pada awal teks.
2. Dari kanan ke kiri, algoritma ini akan mencocokkan karakter per karakter pattern dengan karakter pada teks yang bersesuaian sampai salah satu kondisi berikut dipenuhi: a) Di pattern dan di teks yang dibandingkan tidak cocok (missmatch).
b) Semua karakter di pattern cocok. Algoritma akan memberitahukan penemuan di posisi ini.
c) Algoritma kemudian menggeser pattern dengan memaksimalkan nilai pergeseran good suffix dan pergeseran bad character, lalu mengulangi langkah b sampai
patern berada di ujung teks.
Untuk fase pencarian dalam algoritma Turbo Boyer Moore, proses yang dilakukan hampir sama dengan fase pencarian pada Algoritma Boyer Moore. Yang membedakan adalah adanya variabel yang berfungsi untuk menampung nilai pergeseran apabila pada putaran sebelumnya nilai yang diambil untuk pergeseran berasal dari tabel good suffix shift. Nilai ini nantinya akan digunakan sebagai nilai yang mungkin digunakan untuk pergeseran pattern. Fase inisialisasi pada algoritma ini sama dengan fase inisialisasi pada algoritma Boyer Moore, yaitu mempunyai kompleksitas waktu dan ruang sebesar O(n + σ) dengan σadalah besar ruang alfabet. Sedangkan pada fase pencocokan, algoritma ini mempunyai kompleksitas waktu sebesar O(m) dengan jumlah pencocokan karakter pada algoritma ini adalah 2m. Contoh :
Teks : Titik Berat Benda Pattern : Benda
Temu Pola 1
Tabel 2.2 Pergeseran karakter TBM 1
T I T I K B E R A T B E N D A 1
B E N D A
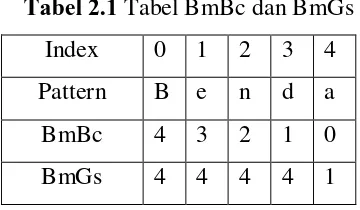
Terlihat perbedaan pada index K :
- Geser BmBc(K) – m + ( index bawah + 1) = 5 – 5 + 5 = 5 - BmGs[4] = 1
Sehingga geser pattern sebesar 5 (nilai maksimal dari kedua perhitungan)
Temu Pola 2
Tabel 2.3 Pergeseran karakter TBM 2
T I T I K B E R A T B E N D A 1 -
B E N D A
Terlihat perbedaan pada index R , maka :
- Geser BmBc(R) – m + ( index bawah + 1 ) = 5 – 5 + 4 = 4 - BmGs[3] = 4
Sehingga geser pattern sebesar 4 (nilai maksimal dari kedua perhitungan)
Temu Pola 3
Tabel 2.4 Pergeseran karakter TBM 3 T I T I K B E R A T B E N D A
1 B E N D A
Terlihat perbedaan pada index E , maka :
- Geser BmBc(E) – m + ( index bawah + 1 ) = 3– 5 + 5 = 3 - BmGs[4] = 1
Temu Pola 4
Tabel 2.5 Pergeseran karakter TBM 4 T I T I K B E R A T B E N D A
- - - - - B E N D A
Pada temu pola 4, tidak perlu dilakukan pergeseran lagi karena sudah sampai pada indeks terakhir.
2.2.1.2 Algoritma String Matching on Ordered Alphabets
Algoritma String Matching on Ordered Alphabets ialah algoritma yang mirip dengan algoritma pencarian satu-satu (brute force). Perbedaanya adalah pada saat dilakukan percobaan untuk menyamakan string dimana ‘jendela’ diposisikan oleh substring y[j..j+m-1], saat prefix u dari x telah ditemukan dan ketidaksamaan terjadi antara karakter a dalam x dengan b dalam kata y.
y x
Gambar 2.1 Percobaan pada algoritma string matching on ordered alphabets Algoritma ini akan menghitung periode ub seperti pada gambar diatas. Jika tidak berhasil dalam menemukan periode yang tepat, algoritma ini akan beralih untuk menghitung perkiraannya.
Algoritma String Matching on Ordered Alphabets melakukan 37 kali perbandingan karakter. Pada kasus terburuk, algoritma ini melakukan perbandingan karakter sebanyak 6n+5 perbandingan danmenghasilkan kompleksitas waktu pencariannya O(n).
Contoh :
Teks : Titik Berat benda Pattern : Benda
Perhitungan Pergeseran : Untuk proses pergeseran dihitung berdasarkan banyaknya string yang sama ditambah dengan string yang berbeda. Jika karakter string teks dan pattern tidak sama, lakukan pengecekan ke string berikutnya.
U B
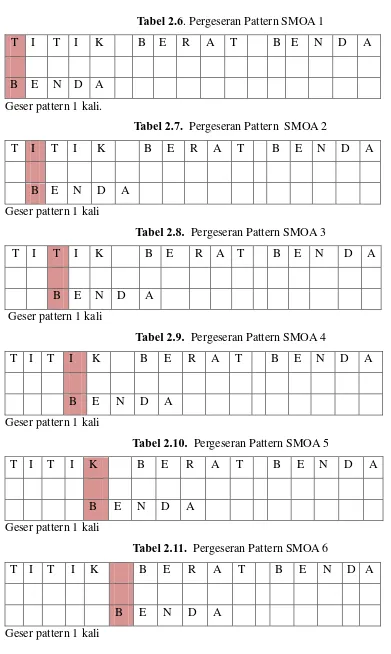
Tabel 2.6. Pergeseran Pattern SMOA 1
T I T I K B E R A T B E N D A
B E N D A Geser pattern 1 kali.
Tabel 2.7. Pergeseran Pattern SMOA 2
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 1 kali
Tabel 2.8. Pergeseran Pattern SMOA 3
T I T I K B E R A T B E N D A
B E N D A Geser pattern 1 kali
Tabel 2.9. Pergeseran Pattern SMOA 4
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 1 kali
Tabel 2.10. Pergeseran Pattern SMOA 5
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 1 kali
Tabel 2.11. Pergeseran Pattern SMOA 6
T I T I K B E R A T B E N D A
B E N D A
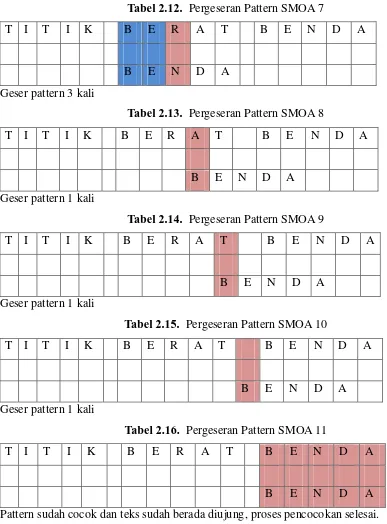
Tabel 2.12. Pergeseran Pattern SMOA 7
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 3 kali
Tabel 2.13. Pergeseran Pattern SMOA 8
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 1 kali
Tabel 2.14. Pergeseran Pattern SMOA 9
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 1 kali
Tabel 2.15. Pergeseran Pattern SMOA 10
T I T I K B E R A T B E N D A
B E N D A
Geser pattern 1 kali
Tabel 2.16. Pergeseran Pattern SMOA 11
T I T I K B E R A T B E N D A
B E N D A
Pattern sudah cocok dan teks sudah berada diujung, proses pencocokan selesai.
2.3 Definisi Android
Android dipuji sebagai “platform mobile pertama yang lengkap, terbuka dan bebas”. 1. Lengkap (Complete Platform) : para desainer dapat melakukan pendekatan yang
komprehensif ketika mereka sedang mengembangkan platform Android. Android merupakan sistem operasi yang aman dan banyak menyediakan tools dalam membangun software dan memungkinkan peluang pengembangan aplikasi.
2. Terbuka (Open Source Platform) : Platform Android disediakan melalui lisensi open source. Pengembang dapat dengan bebas untuk mengembangkan aplikasi. Android
sendiri menggunakan Linux Kernel 2.6.
3. Bebas (Free Platform) : Android adalah platform/aplikasi yang bebas untuk develope. Tidak ada lisensi atau biaya royalti untuk dikembangkan pada platform Android. Tidak ada biaya keanggotaan diperlukan. Tidak ada biaya pengujian. Tidak ada kontrak yang diperlukan. Aplikasi untuk Android dapat didistribusikan dan diperdagangkan dalam bentuk apapun.
2.4 Kompleksitas Algoritma
Algoritma ialah urutan-urutan langkah logis dalam menyelesaikan suatu masalah secara sistematis. Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang bagus adalah algoritma yang mangkus (efficient). Kemangkusan algoritma diukur dari waktu (time), eksekusi algoritma dan kebutuhan ruang (space) memori.
Algoritma yang mangkus ialah algoritma yang meminimumkan kebutuhan waktu dan ruang. Kebutuhan waktu dan ruang suatu algoritma bergantung pada ukuran masukan (n), yang menyatakan jumlah data yang diproses. Kemangkusan algoritma dapat digunakan untuk menilai algoritma yang bagus dari sejumlah algoritma penyelesaian masalah. Model abstrak pengukuran waktu/ruang harus independen dari pertimbangan mesin dan compiler apapun. Besaran yang dipakai untuk menerangkan model abstrak pengukuran waktu/ruang ini adalah kompleksitas algoritma.
Kompleksitas algoritma diukur berdasarkan kinerja dengan menghitung waktu eksekusi suatu algoritma. Waktu eksekusi algoritma dapat diklasifisikan menjadi tiga kelompok besar, yaitu best-case (kasus terbaik), average-case (kasus rerata) dan worst-case (kasus terjelek). Pada pemograman yang dimaksud dengan kasus terbaik, kasus rerata dan kasus terjelek dalam suatu algoritma adalah besar kecilnya atau hanya sedikitnya sumber-sumber yang digunakan oleh suatu algoritma. Makin sedikit makin baik, makin banyak makin jelek. Biasanya sumber-sumber yang paling dipertimbangkan tidak hanya waktu eksekusi tetapi bisa juga besar memori, catu-daya dan sumber-sumber lain (subandijo, 2011).
2.6 Notasi Big O
Notasi Big O adalah cara yang digunakan untuk menguraikan laju pertumbuhan suatu fungsi yang tidak lain adalah time complexity suatu algoritma (subandijo, 2011). Secara sederhana notasi Big O didefinisikan sebagai berikut:
Jika n adalah ukuran masukan dan f(n) serta g(n) adalah fungsi positif dari n maka f(n) adalah O(g(n)) jika dan hanya jika terdapat konstanta positif c dan integer positif n0 sedemikian rupa
sehingga f(n) ≤ c g(n) untuk semua n ≥ n0.
Secara tidak formal, suatu algoritma disebut menunjukkan laju pertumbuhannya merupakanorder suatu fungsi matematika jika untuk ukuran masukan n, fungsi f(n) dikalikan konstanta positifmerupakan batas atas atau limit dari waktu eksekusi algoritma tersebut. Dengan kata lain untuk ukuran masukan n yang lebih besar daripada n0 dan konstanta c,
waktu eksekusi algoritma tidak akanmelampaui c * f(n). Sebagai contoh, karena waktu eksekusi insertion sort tumbuh secara kuadratik dengan besarnya masukan n ketika ukuran masukan naik, insertion sort dikatakan mempunyai order O (n2).
n n2 n 10 T(n)
0 0 0 10 10
10 100 10 10 120
100 10000 100 10 10110
1000 1000000 1000 10 1001010
10000 100000000 10000 10 100010010
Meskipun notasi ini dikembangkan sebagai bagian dari matematika murni, notasi ini kerap dipakai pada analisis algoritma untuk menguraikan algoritma pemakaian sumber-sumber komputasi, kasus terburuk atau kasus rerata waktu eksekusi atau pemakaian memori suatu algoritma kerapdisajikan sebagai fungsi dari besaran masukan menggunakan notasi Big O. Hal ini memungkinkan perancang algoritma memprediksi perilaku algoritmanya dan menentukan algoritma mana yang akan digunakan tak tergantung pada arsitektur komputer dan clock rate. Karena notasi Big O mengabaikan nilai konstanta dan kelipatannya dan juga mengabaikan efisiensi untuk argumen-argumen dalam ukuran yang lebih kecil ordernya, maka notasi Big O tidak selalu mencerminkan algoritma yang paling cepat pada data tertentu, tetapi pendekatan ini tetap sangat efektif untuk membandingkan berbagai algoritma saat ukuran data masukan menuju tak terhingga.
Konsep O(n) dikenal sebagai salah satu metode asymptotic analysis untuk menyatakan batas atas asimptotik. Sebagai contoh, T(n) = 13n3+ 42n2+ 2n log n + 4n di mana T merupakanfungsi dari obyek masukan n, ditulis sebagai T(n). Jika n tumbuh menjadi lebih
besar maka nilai n3akan jauh lebih besar daripada n2, n log n dan n sehingga n3 mendominasi T(n). Waktu eksekusi T(n)secara garis besar mempunyai order n3 dan notasinya ditulis sebagai O(n3).
Dua metode lain yang dikenal adalah Ω (n) untuk menyatakan batas bawah asimtotik dan Ɵ(n) untuk menyatakan tight bound asymptotic. Secara formal T(n) didefinisikan sebagai berikut: T(n) = O(f(n)) jika terdapat konstanta c dan n0 sedemikian rupa sehingga T(n) < c *
f(n) untuk n >n0. Ini berarti bahwa untuk n >n0 maka c * f(n) merupakan batas atas dari T(n).
Sebagai contoh, jika T(n) = 1000n dan f(n) = n2, n0 = 1000 dan c = 1 maka T(n) ≤ 1 * f(n)
Notasi Big O adalah cara yang sangat menyenangkan untuk menyajikan skenario keadaanterjelek suatu algoritma, meskipun ia juga dapat digunakan untuk menyajikan kasus rerata. Sebagai contoh, skenario kasus terjelek quick sort adalah O(n2), tetapi rerata waktu eksekusinya adalah O(n log n).
2.5 Penelitian yang Relevan
Berikut ini beberapa penelitian yang terkait dengan Algoritma Turbo Boyer Moore dan String Matching on Ordered Alphabets :
1. Vina Sagita, Maria Irmina Prasetiyowati (2013) dalam jurnal yang berjudul studi perbandingan implementasi algoritma boyer moore, turbo boyer moore dan tuned
boyer moore dalam pencarian string. Menyatakan bahwa algoritma Turbo Boyer
Moore merupakan algoritma tercepat kedua dari ketiga varian algoritma tersebut.
2. Rizal (2015) dalam jurnal yang berjudul permainan tebak kata bahasa aceh menggunakan algoritma turbo boyer moore. Menyatakan bahwa pencocokan string
yang diterapkan pada aplikasi permainan tebak kata bahasa aceh berhasil diterapkan dan menghasilkan pencocokan yang sesuai dengan yang di harapkan. Algoritma Turbo Boyer Moore melakukan pencocokan dengan sangat cepat.
3. Priskila Ifke Goni (2013) dalam skripsi yang berjudul penerapan algoritma turbo boyer moore untuk pendeteksian kemiripan dokumen berbasis android. Menyatakan
bahwa dalam proses pendeteksian, Algoritma Turbo Boyer Moore dijadikan sebagai string (pattern) matching. Berdasarkan dokumen yang diuji kinerja dari algoritma
Turbo Boyer Moore bergantung pula pada hasil akhir dari tahap preprocessing yakni