MODEL SEIRS-LSEI PADA PENYAKIT CHIKUNGUNYA SUAEDAH

SUAEDAH

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2012

PERNYATAAN MENGENAI TESIS

DAN SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul model SEIRS-LSEI pada penyakit chikungunya adalah karya saya sendiri dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam daftar pustaka di bagian akhir tesis ini.

Bogor, Juli 2012 Suaedah NRP G551090201

Chikungunya is a disease caused by the chikungunya virus. It is spread to human through the bites of Aedes aegypti and Aedes albopictus mosquitoes. A SEIRS-LSEI model is proposed to formulate the dynamic of chikungunya disease from mosquito to human. SEIRS-LSEI model of chikungunya has four equilibrium points, i.e. two disease free and two endemic points. The stability of those points are determined according to the eigen values of Jacobi matrix. The existence of the disease are controlled by the basic reproduction number

In this thesis, the dynamical analysis of interaction between human and mosquito is given by some illustrative examples. We consider two policies in controlling mosquito population, i.e. spraying and using antimosquito lotion. Mosquito spraying will increase the parameter of mosquito mortality, while spraying antimosquito lotion will decrease the parameter of average daily biting. The dynamics of the disease is mainly determined by the intensity of interaction of human susceptible with infected mosquito. Simulation results confirm that, if the rate of mosquito mortality increases by spraying, then the population of infected human decreases, such that the population of suscepted human increases. The same situation happens when the average daily biting of infected mosquito decreases by lotion usage.

. If the number is less than one, then the disease can be removed from the population. On the other hand, if the number is greater than one, then the disease remains in the population.

Keywords: Chikungunya, SEIRS-LSEI Model, human-mosquito interaction,

RINGKASAN

SUAEDAH. Model SEIRS-LSEI pada Penyakit Chikungunya. Di bawah bimbingan TONI BAKHTIAR dan ALI KUSNANTO.

Chikungunya adalah penyakit yang disebabkan oleh virus chikungunya yang disebarkan ke manusia melalui gigitan nyamuk Aedes aegypti dan nyamuk Aedes albopictus (Pialoux et al., 2007). Model matematika penyebaran penyakit chikungunya yang diperkenalkan oleh Dumont et al., 2008, dengan mengklasifikasikan menjadi dua populasi yaitu populasi manusia berbentuk SEIR (Susceptible-Exposed-Infected-Resistant) dan populasi nyamuk berbentuk LSEI (Larvae-Susceptible-Exposed-Infected). Dalam tulisan ini dikembangkan model SEIR (Dumont et al., 2008) pada penyakit chikungunya dengan menambahkan asumsi bahwa individu yang mempunyai kekebalan tubuh setelah terserang penyakit menjadi rentan kembali walaupun peluangnya sangat kecil, sehingga model ini disebut model SEIRS (Susceptible-Exposed-Infected-Resistant- Susceptible).

Tujuan utama dalam penulisan ini adalah (1) Mengkonstruksi model penyebaran penyakit chikungunya model SEIRS-LSEI, (2) Melakukan analisis kestabilan model penyebaran penyakit chikungunya, (3) Melakukan simulasi numerik terhadap model SEIRS untuk melihat pengaruh perubahan nilai parameter, yakni laju kematian nyamuk dan rata-rata gigitan nyamuk terinfeksi terhadap dinamika populasi manusia rentan per hari.

Dari model SEIRS-LSEI pada penyakit chikungunya yang dilakukan secara simultan maka didapat 4 (empat) titik tetap yaitu: dua titik tetap tanpa penyakit dan dua titik tetap endemik di mana kestabilannya dipengaruhi oleh nilai eigen dan bilangan reproduksi dasar (R0). Jika R0 ˂ 1, maka penyakit chikungunya

akan menghilang dari populasi dan jika R0

Simulasi yang dilakukan yaitu melalui penyemprotan dan penggunaan obat anti nyamuk, dengan mengubah-ubah laju kematian nyamuk (µ

≥ 1, maka penyakit chikungunya akan menetap di dalam populasi.

m

Dinamika populasi ketika bilangan reproduksi dasar kurang dari satu lebih cepat menuju kestabilan dibandingkan ketika bilangan reproduksi dasar lebih besar dari satu. Semakin kecil bilangan reproduksi dasar maka populasi semakin cepat menuju kestabilan.

) dan rata-rata gigitan nyamuk (B). Dari hasil kajian analitik dan simulasi numerik dapat disimpulkan, bahwa titik tetap tanpa penyakit berada dalam kestabilan ketika bilangan reproduksi dasar kurang dari satu dan titik tetap endemik berada dalam kestabilan ketika bilangan reproduksi dasar lebih dari satu.

manusia rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin sedikit. Jika rata-rata gigitan nyamuk terinfeksi naik, maka jumlah subpopulasi manusia rentan semakin berkurang sedangkan subpopulasi lainnya semakin bertambah. Artinya, semakin besar rata-rata gigitan nyamuk terinfeksi maka jumlah manusia rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin banyak.

Pada populasi nyamuk, jika laju kematian nyamuk naik, maka jumlah subpopulasi nyamuk rentan semakin bertambah sedangkan subpopulasi lainnya semakin berkurang. Artinya, semakin besar laju kematian nyamuk maka jumlah nyamuk rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin sedikit. Jika rata-rata gigitan nyamuk terinfeksi naik, maka jumlah subpopulasi nyamuk rentan semakin berkurang sedangkan subpopulasi lainnya semakin bertambah. Artinya, semakin besar rata-rata gigitan nyamuk terinfeksi maka jumlah nyamuk rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin banyak.

Kata kunci: Chikungunya, model SEIRS-LSEI, bilangan reproduksi, interaksi populasi manusia dengan populasi nyamuk.

Hak cipta milik Institut Pertanian Bogor, tahun 2012 Hak cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin Institut Pertanian Bogor.

SUAEDAH

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2012

Program Studi : Matematika Terapan

Disetujui Komisi Pembimbing

Dr. Toni Bakhtiar, M.Sc. Drs. Ali Kusnanto, M.Si.

Ketua Anggota

Diketahui

Ketua Program Stuti Dekan Sekolah Pascasarjana

Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Dr. Ir. Dahrul Syah, M.Sc.Agr.

PRAKATA

Puji syukur kehadirat Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini dapat dilaksanakan dan diselesaikan dengan baik.

Penelitian ini diberi judul Model SEIRS-LSEI pada Penyakit Chikungunya. Karya ilmiah ini tidak akan mungkin terselesaikan tanpa adanya dorongan, bantuan dan kritikan membangun dari berbagai pihak. Terimakasih penulis ucapkan kepada Dr. Toni Bakhtiar, M.Sc. dan Drs. Ali Kusnanto, M.Si. selaku pembimbing serta Dr. Ir. Hadi Sumarno, M.S. selaku penguji yang banyak memberikan saran.

Demikian pula, penulis mengucapkan terimakasih kepada Kementerian Agama Republik Indonesia yang telah memberikan beasiswa. Ungkapan terima kasih juga disampaikan kepada ibu, bapak, suami dan anakku, serta rekan-rekan seperjuangan di S2 angkatan 2009, Keluarga besar MTsN Kandanghaur, Indramayu serta berbagai pihak yang tak dapat penulis sebutkan satu per satu, penulis mengucapkan banyak terima kasih, dan semoga Allah SWT melimpahkan keberkahan serta kemanfaatan atas keberhasilan ini. Amien.

Penulis menyadari bahwa karya ilmiah ini masih jauh dari sempurna, walaupun demikian penulis tetap berharap semoga karya ilmiah ini dapat memberikan kontribusi pada bidang matematika dan bidang-bidang lainnya.

Bogor, Juli 2012 Suaedah

Penulis dilahirkan di Indramayu pada tanggal 07 Maret 1972 dari Bapak Sokhibi dan Ibu Daerih. Penulis merupakan anak keenam dari sembilan bersaudara.

Tahun 1991 penulis lulus dari SMAN Kandanghaur Indramayu. Pada Tahun 1997 penulis melanjutkan kuliah di Sekolah Tinggi Agama Islam Negeri Cirebon, mengambil program studi Matematika dan lulus pada tahun 2003. Tahun 2005 mendapat SK CPNS sebagai guru di Madrasah Tsanawiyah Negeri (MTsN) Kandanghaur, Indramayu.

Pada tahun 2009 penulis lulus seleksi masuk Program Magister pada Program Studi Matematika Terapan di Institut Pertanian Bogor melalui jalur Beasiswa Utusan Daerah Kementerian Agama Republik Indonesia.

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... xi

DAFTAR TABEL ... xii

DAFTAR LAMPIRAN ... xiii

I PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan ... 2

II LANDASAN TEORI ... 3

2.1 Sistem Persamaan Diferensial (SPD) ... 3

2.1.1 Sistem Persamaan Diferensial Linear (SPDL) ... 3

2.1.2 Sistem Persamaan Diferensial Taklinear (SPDTL) ... 3

2.1.3 Sistem Persamaan Diferensial Mandiri ... 3

2.2 Titik Tetap ... 4

2.2.1 Titik Tetap Stabil ... 4

2.2.2 Titik Tetap Takstabil ... 4

2.2.3.Pelinearan ... 4

2.3 Nilai Eigen dan Vektor Eigen ... 5

2.4 Analisis Kestabilan Titik Tetap………... 6

2.5 Bilangan Reproduksi Dasar ... 6

III MODEL PENYEBARAN PENYAKIT CHIKUNGUNYA ... 7

3.1 Model SEIRS……….. 7

3.2 Kerangka Analisis ... 12

IV HASIL DAN PEMBAHASAN……….………. 13

4.1 Penentuan Titik Tetap ... 13

4.2 Analisis Kestabilan Titik Tetap ... 15

4.2.1 Kestabilan Titik Tetap T1 4.2.2 Kestabilan Titik Tetap T ... 16

2 ... 17

V SIMULASI ... 21

5.1 Parameter Yang Ditetapkan ... 21

5.2 Simulasi Analisis Kestabilan ... 22

5.2.1 Populasi untuk kondisi R0 ˂ 1……….... 22

5.2.2.1 Populasi manusia……… 28

5.2.2.2 Populasi nyamuk……… 30

VI SIMPULAN DAN SARAN……… 34

DAFTAR GAMBAR

1 Model kompartemen penyakit chikungunya……… 8 2 Bagan kerangka analisis………... 12 3 Dinamika populasi manusia rentan terhadap waktu t untuk kondisi

R0

4 Dinamika populasi manusia terekspos terhadap waktu t untuk kondisi ˂ 1………. 22

R0

5 Dinamika populasi manusia terinfeksi terhadap waktu t untuk kondisi ˂ 1………... 23

R0

6 Dinamika populasi manusia sembuh terhadap waktu t untuk kondisi

˂ 1………... 24

R0

7 Dinamika populasi nyamuk berupa larva terhadap waktu t untuk kondisi ˂ 1………... 24

R0

8 Dinamika populasi nyamuk rentan terhadap waktu t untuk kondisi

˂ 1………... 25

R0

9 Dinamika populasi nyamuk terekspos terhadap waktu t untuk kondisi

˂ 1………... 26

R0

10 Dinamika populasi manusia terinfeksi terhadap waktu t untuk kondisi ˂ 1...……… 26

R0

11 Dinamika populasi manusia rentan terhadap waktu t untuk kondisi

˂ 1……… 27

R0

12 Dinamika populasi manusia terekspos terhadap waktu t untuk kondisi ˃ 1.………. 28 R0

13 Dinamika populasi manusia terinfeksi terhadap waktu t untuk kondisi ˃ 1.……….. 29

R0

14 Dinamika populasi manusia sembuh terhadap waktu t untuk kondisi

˃ 1..………. 29

R0

15 Dinamika populasi nyamuk berupa larva terhadap waktu t untuk kondisi ˃ 1..………. 30

R0

16 Dinamika populasi nyamuk rentan terhadap waktu t untuk kondisi

˃ 1...………. 30

R0

17 Dinamika populasi manusia terekspos terhadap waktu t untuk kondisi ˃ 1..………. 31

R0 ˃ 1..……….

32

DAFTAR TABEL

1 Kondisi kestabilan titik tetap………... 20 2 Parameter model..……… 21

DAFTAR LAMPIRAN

1 Menentukan titik tetap……… 37 2 Penentuan bilangan reproduksi dasar………... 38

3 Bukti Teorema 1………. 39 4 Membuat program simulasi untuk kondisi R0

5 Membuat program simulasi untuk kondisi R

˂ 1………. 48

0 ˃ 1....……….

1

I PENDAHULUAN 1.1 Latar Belakang

Chikungunya adalah penyakit yang disebabkan oleh virus chikungunya yang disebarkan ke manusia melalui gigitan nyamuk Aedes aegypti dan nyamuk Aedes albopictus (Pialouk et al., 2007). Nyamuk yang menggigit manusia penderita chikungunya akan terinfeksi oleh virus chikungunya dan setelah sekitar seminggu, nyamuk tersebut dapat menularkan virus pada manusia lain yang sehat. Kondisi iklim dari satu tempat ke tempat lain bisa berubah cepat. Ini merupakan fakta penting karena hidup nyamuk ini sangat terkait dengan suhu dan kelembaban (Dumont et al., 2008). Pada musim hujan, tempat perkembangbiakan Aedes aegypti yang pada musim kemarau tidak terisi, mulai terisi oleh air. Selain itu pada musim hujan semakin banyak tempat-tempat penampungan air alamiah yang terisi air hujan yang dapat digunakan sebagai tempat perkembangan nyamuk ini. Karena itu, pada musim penghujan populasi nyamuk Aedes aegypti meningkat, sehingga bertambahnya populasi nyamuk menyebabkan faktor peningkatan penyakit chikungunya jika dalam daerah tersebut ada penderitanya.

Gejala chikungunya muncul antara 2 sampai 4 hari setelah gigitan dan ditandai oleh demam tinggi, sakit kepala, dan arthritis pada beberapa sendi (seperti pergelangan kaki dan pergelangan tangan). Manifestasi penyakit berlangsung tiga sampai sepuluh hari. Virus ini bersifat self limiting disease, yaitu hilang dengan sendirinya. Namun, rasa nyeri masih tertinggal dalam hitungan minggu sampai bulan. Tidak ada vaksin maupun obat, penderita biasanya cukup minum obat penurun panas dan penghilang rasa sakit. Yang penting penderita cukup istirahat, minum, dan makan makanan bergizi (Pialouk et al., 2007). Satu-satunya cara mencegah penularan penyakit ini adalah dengan memutus rantai penularan dengan cara memberantas nyamuk tersebut, sebagaimana sering disarankan dalam pemberantasan penyakit demam berdarah dengue, yaitu dengan cara menguras tempat penampungan air bersih, bak mandi, vas bunga, dan sebagainya (Chandra, 2006).

Dalam penelitian ini akan dibahas sebuah model matematika penyebaran penyakit chikungunya yang diperkenalkan oleh Dumont et al., 2008. Model ini

merupakan modifikasi dari Model SEIR. Modifikasi dilakukan dengan menambahkan asumsi bahwa individu yang memunyai kekebalan tubuh setelah terserang penyakit dapat menjadi rentan kembali walaupun peluangnya sangat kecil (Labadie et al., 2010), sehingga model ini disebut model SEIRS (Susceptible-Exposed-Infected-Resistant-Susceptible). Selanjutnya, dilakukan analisis kestabilan dan simulasi numerik pada model-model tersebut. Perhitungan dalam analisis kestabilan dan simulasi numerik dilakukan dengan pemrograman berbasis fungsional

1.2 Tujuan Penelitian

.

Penelitian ini bertujuan untuk:

1. Mengkonstruksi model penyebaran penyakit chikungunya pada model SEIRS-LSEI,

2. Melakukan analisis kestabilan model penyebaran penyakit

Chikungunya,

3. Melakukan simulasi numerik untuk melihat seberapa besar pengaruh parameter tertentu yaitu laju kematian nyamuk , dan rata-rata gigitan nyamuk terinfeksi pada manusia rentan per hari.

3

II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial

Definisi 1 (Sistem Persamaan Diferensial)

Sistem persamaan diferensial (SPD) adalah suatu persamaan yang dinyatakan sebagai:

(1) dengan

, dan

Jika taklinear terhadap sistem (1) disebut SPD taklinear dan jika linear maka SPD (1) disebut linear.

(Braun, 1983)

Definisi 2 (Sistem Persamaan Diferensial Linear Orde Satu)

SPD linear dapat dinyatakan sebagai:

(2)

dengan adalah matriks koefisien konstan berukuran dan adalah vektor konstan. Sistem tersebut dinamakan SPD linear orde satu dengan kondisi awal . Jika , maka sistem dikatakan homogen dan jika , maka sistem

Definisi 3 (Sistem Persamaan Diferensial Mandiri)

Misalkan suatu sistem persamaan diferensial dinyatakan sebagai berikut: (3) dengan merupakan fungsi kontinu bernilai real dari dan memunyai turunan parsial kontinu. Sistem (3) disebut sistem persamaan diferensial mandiri (autonomous) karena tidak memuat t secara eksplisit didalamnya.

(Tu, 1994)

2.2 Titik Tetap Definisi 4 (Titik Tetap)

Misalkan diberikan sistem persamaan diferensial mandiri (3). Titik disebut titik tetap atau titik kritis atau titik kesetimbangan jika .

(Tu, 1994)

Definisi 5 (Titik Tetap Stabil)

Misalkan adalah titik tetap sebuah SPD dan x(t) adalah solusi yang memenuhi kondisi awal x(0) = dengan . Titik dikatakan titik tetap stabil jika untuk sembarang terdapat r sedemikian sehingga jika posisi awal memenuhi maka solusi x(t) memenuhi , untuk t .

(Verhulst, 1990)

Definisi 6 (Titik Tetap Takstabil)

Misalkan dan x(t) adalah sebuah solusi SPD

dengan nilai awal x(0) = dengan Titik dikatakan titik tetap takstabil jika terdapat > 0 dan untuk sebarang r > 0 terdapat nilai awal yang memenuhi sehingga solusi x(t) memenuhi , untuk t > 0.

5

Untuk menganalisis kestabilan titik tetap dari suatu SPD taklinear dapat dilakukan dengan pelinearan pada sistem persamaan diferensialnya.

2.3 Pelinearan

Analisis kestabilan sistem persamaan diferensial taklinear dapat dilakukan melalui analisis sistem linear padanannya. Misalkan diberikan sistem persamaan diferensial taklinear sebagai berikut:

. (4) Dengan menggunakan ekspansi Taylor di sekitar titik tetap , maka sistem

persamaan (4) dapat ditulis:

(5) dengan adalah matriks Jacobi, yaitu

A , (6)

dan adalah suku berorde tinggi yang bersifat . Selanjutnya, pada persamaan (5) disebut pelinearan dari sistem persamaan diferensial taklinear pada persamaan (4) dan ditulis dalam bentuk (Tu, 1994).

2.4 Nilai Eigen dan Vektor Eigen

Diberikan matriks koefisien konstan berukuran n × n, dan SPD homogen berikut:

, (7)

Suatu vektor taknol x dalam ruang disebut vektor eigen dari jika untuk suatu

skalar λ berlaku:

Nilai skalar λ dinamakan nilai eigen dari . Untuk mencari nilai λ dari matriks , maka persamaan (8) dapat ditulis kembali sebagai berikut:

(9) dengan I matriks identitas. Persamaan (9) memunyai solusi taknol jika dan hanya

jika

Persamaan (10) disebut persamaan karakteristik dari matriks .

(Anton, 1997) Analisis Kestabilan Titik Tetap

Kestabilan titik tetap dari sistem ditentukan berdasarkan tanda nilai eigen matriks A sebagai berikut:

1. Sistem adalah stabil jika dan hanya jika setiap nilai eigen adalah bernilai negatif.

2. Sistem adalah takstabil jika dan hanya jika minimal satu nilai eigen dari bernilai taknegatif.

(Borrelli dan Coleman 1998)

2.5 Bilangan Reproduksi Dasar

Bilangan reproduksi dasar, dinotasikan dengan R

Kondisi yang akan timbul adalah:

0 ialah nilai harapan

terjadinya infeksi per satuan waktu. Infeksi ini terjadi pada suatu populasi yang seluruhnya rentan yang dihasilkan oleh satu jenis individu yang sudah terinfeksi.

1 Jika R0 1, penyakit chikungunya akan hilang dari populasi.

2 Jika R0 1, penyakit chikungunya akan menetap di dalam populasi.

R0 dalam penelitian ini ditentukan dengan menggunakan metode yang

dikenalkan oleh Watmough (2008) dan van den Driessche dan Watmough (2005) yaitu mengkonstruksi suatu matriks yang berasal dari subpopulasi-subpopulasi

7

yang menyebabkan infeksi saja. Matriks tersebut dinamakan dengan the next generation matrix. Nilai eigen taknegatif dengan modulus terbesar matriks ini yang nantinya digunakan sebagai nilai R0.

III MODEL PENYEBARAN PENYAKIT CHIKUNGUNYA 3.1 Model SEIRS-LSEI

Model SEIR (Susceptible-Eexposed-Infected-Resistant) pada penyakit chikungunya dikenalkan oleh Dumont et al., (2008) dengan mengklasifikasikan total populasi manusia sebagai host ke dalam empat kelas, yaitu manusia yang rentan (susceptible) , manusia yang terekspos (exposed) , manusia yang terinfeksi (infected) , dan manusia yang sembuh (resistant) . Manusia yang rentan adalah manusia yang tidak terkena infeksi dan bukan imun. Manusia yang terekspos adalah manusia yang telah diinfeksi oleh virus ketika masa inkubasi intrinsik dalam tubuh manusia sedang berlangsung. Manusia yang terinfeksi adalah manusia yang tertular virus chikungunya dan dapat menularkan virus tersebut kepada individu lain dengan perantara nyamuk. Manusia sembuh adalah manusia yang telah sembuh dari penyakit chikungunya. Dapat juga ditulis:

Sedangkan total populasi nyamuk sebagai vektor dibagi menjadi empat kelas, yaitu larva (larvae) , nyamuk yang rentan (susceptible) , nyamuk yang terekspos (exposed) , dan nyamuk yang terinfeksi (infected) . Larva adalah jentik-jentik nyamuk atau anak nyamuk yang baru lahir. Nyamuk yang rentan adalah nyamuk yang belum tertular virus. Nyamuk yang terekspos adalah nyamuk yang diinfeksi oleh virus ketika masa inkubasi ekstrinsik dalam tubuh nyamuk sedang berlangsung. Sedangkan nyamuk yang terinfeksi adalah nyamuk yang tertular virus dan dapat menularkan virus tersebut kepada individu lain. Dapat juga ditulis:

9 µ0Nh µh B mh _Lη µ L µh vh C hm µm µh ηh ηm µm µh µm

Gambar 1 Model kompartemen penyakit chikungunya. Manusia Nyamuk

Model SEIR ini selanjutnya dimodifikasi dengan menambahkan asumsi bahwa individu yang mempunyai kekebalan tubuh setelah terserang penyakit menjadi rentan kembali walaupun peluangnya sangat kecil (Labadie et al., 2010), sehingga model ini disebut model SEIRS (Susceptible-Exposed-Infected-Resistant-Susceptible).

Secara skematis, pola penyebaran penyakit chikungunya dapat digambarkan dalam bentuk bagan seperti yang diperlihatkan pada Gambar 1.

Model SEIRS pada Gambar 1 menjelaskan laju perpindahan individu antara kelas S, E, I, R dan S. Diasumsikan bahwa laju kelahiran (µ0) dan laju kematian

(µh) di setiap kelas adalah sama, yaitu µ0 = µh. Model penyebaran virus

chikungunya sebelumnya menggunakan asumsi semua telur nyamuk sehat. Individu lahir di kelas rentan (Sh) dengan laju kelahiran sebesar µ0. Manusia yang berada di

kelas rentan akan mati dengan laju kematian sebesar µh, atau masuk ke kelas

terekspos (Eh) karena terjangkit penyakit dengan laju penularan sebesar βmh Jadi

βmh merupakan tingkat interaksi antara nyamuk yang terinfeksi dengan manusia

yang rentan sehingga menjadi manusia yang terekspos artinya tidak ada kontak µb µb µb Susceptible Sh Exposed Eh Infected Ih Resistant Rh Larvae Lm Susceptible Sm Exposed Em Infected Im

langsung dari kelas rentan (Sh) ke kelas terekspos (Eh). Selanjutnya manusia yang

berada di kelas terekspos akan mati dengan laju kematian sebesar µh, atau masuk ke

kelas terinfeksi (Ih) dengan laju perubahan sebesar νh. Selanjutnya manusia yang

berada di kelas terinfeksi akan mati dengan laju kematian sebesar µh, atau sembuh

dengan laju penyembuhan sebesar ηh sehingga dimasukkan ke kelas sembuh (Rh).

Kemudian manusia di kelas sembuh akan mati dengan laju kematian sebesar µh

Dari penjelasan di atas dapat dituliskan dalam bentuk persamaan-persamaan berikut:

, atau menjadi rentan kembali karena sistem kekebalan tubuh dapat hilang sehingga kembali masuk ke kelas rentan dengan laju hilangnya kekebalan sebesar θ.

Persamaan untuk populasi manusia

(1)

(2)

(3)

(4)

dengan

adalah total populasi manusia,

B adalah rata-rata gigitan nyamuk terinfeksi pada manusia terekspos (per hari),

adalah peluang transmisi dari nyamuk yang terinfeksi ke manusia (per gigitan),

adalah laju kematian manusia secara alami (per hari), adalah rata-rata rentang hidup manusia,

adalah rata-rata periode viremic di mana seekor nyamuk rentan saat menggigit manusia yang sedang mengalami viremia maka nyamuk rentan

11

tersebut akan tertular (per hari),

adalah periode inkubasi intrinsik (proses masuknya virus dalam tubuh manusia) per hari,

adalah laju hilangnya kekebalan tubuh,

adalah merupakan laju terjadinya interaksi antara nyamuk yang terinfeksi dengan manusia rentan,

adalah laju kelahiran manusia secara alami (per hari), dengan µ0 = µh

Model LSEI pada Gambar 1 menjelaskan laju perpindahan nyamuk antara kelas L, S, E, dan I. Nyamuk berupa larva ( mati dengan laju kematian sebesar atau tumbuh menjadi nyamuk dewasa dengan laju sebesar Nyamuk dewasa di kelas SEI di asumsikan dapat menghasilkan larva dengan laju atau mati dengan laju , atau terjangkit penyakit dengan laju penularan sebesar Jadi merupakan tingkat interaksi antara manusia yang terinfeksi dengan nyamuk yang rentan, artinya nyamuk yang rentan menjadi terekspos karena pengaruh gigitan dari manusia yang terinfeksi dalam arti tidak ada kontak langsung antara kelas nyamuk yang rentan ( ) dan kelas terekspos ( ). Nyamuk yang baru lahir digolongkan ke kelas terekspos ( ) dengan laju kelahiran sebesar , selanjutnya laju perubahan dari nyamuk yang terekspos menjadi terinfeksi sebesar . Nyamuk di kelas terinfeksi ( ) akan mati dengan laju kematian sebesar . Keadaan populasi nyamuk mengalami perubahan karena asumsi sebagian telur nyamuk terinfeksi. Jumlah nyamuk yang rentan ( ) akan meningkat karena bertambahnya kelahiran nyamuk sehat dan akan berkurang karena gigitan nyamuk kepada populasi manusia terinfeksi serta karena kematian alami. Populasi nyamuk yang terkena infeksi ( ) akan meningkat karena kelahiran nyamuk terinfeksi, gigitan nyamuk kepada populasi manusia terinfeksi dan berkurang karena kematian alami. Perubahan musim membuat perubahan suhu, sehingga pola musiman mempengaruhi di dalam penyebaran penyakit chikungunya. Variasi di dalam masa inkubasi ekstrinsik disebabkan oleh perubaha-perubahan suhu, semakin rendah suhu masa inkubasi semakin lama.

.

Garis yang menghubungkan model SEIRS dan LSEI pada gambar menjelaskan bahwa hubungan efektif (langsung atau tidak langsung) antara nyamuk

yang terinfeksi dengan manusia yang terekspos adalah awal penyebaran penyakit chikungunya dari dunia nyamuk ke dunia manusia.

Dari penjelasan di atas dapat dituliskan dalam bentuk persamaan-persamaan berikut:

Persamaan untuk populasi nyamuk

dengan kondisi dan + =

di mana Nm

C adalah rata-rata gigitan individu nyamuk pada manusia (per hari), adalah total populasi nyamuk (ekor),

adalah peluang transmisi dari manusia yang terinfeksi ke nyamuk (per gigitan),

adalah laju kelahiran nyamuk secara alami (per hari), adalah laju kematian tahap larva (per hari),

adalah rata-rata rentang hidup nyamuk dewasa, adalah laju kematian alami larva (per hari),

adalah tingkat transisi (pematangan) dari larva menjadi dewasa (per hari), adalah masa inkubasi ekstrinsik (proses masuknya virus ketubuh nyamuk) per hari,

adalah kapasitas maksimal larva yang hidup,

C adalah merupakan laju terjadinya interaksi antara manusia yang terinfeksi dengan nyamuk yang rentan.

13

Jika faktor lingkungan (musim) dipertimbangkan maka dapat dilakukan penyesuaian terhadap total populasi nyamuk dan laju kelahiran nyamuk. Misalnya dengan menjadikan kedua parameter tersebut sebagai fungsi dari waktu, yaitu

dan Nilai parameter-parameter yang lain pun dapat disesuaikan dengan lokasi di mana model akan diterapkan.

Model ini menggunakan beberapa asumsi sebagai berikut: 1 Total populasi adalah konstan,

2 manusia dan nyamuk diasumsikan lahir rentan, 3 nyamuk tidak pernah sembuh setelah terinfeksi virus, 4 larva diasumsikan sehat.

Selanjutnya dilakukan analisis kestabilan model penularan penyakit chikungunya yang menghasilkan beberapa titik tetap. Analisis titik tetap tersebut nantinya akan dihasilkan syarat kestabilan untuk masing-masing titik tetap.

3.2 Kerangka Analisis

Adapun kerangka analisis yang akan dikaji dan diterapkan pada model adalah sebagai berikut:

1 Menentukan titik tetap dari persamaan (1)–(8),

2 melakukan pelinearan di sekitar titik tetap terhadap model taklinear (1)-(8), 3 menentukan nilai eigen,

4 menentukan bilangan reproduksi dasar (R0

5 menganalisis kestabilan dengan simulasi. ),

Secara skematis, kerangka analisis dapat digambarkan dalam bentuk bagan seperti yang diperlihatkan pada Gambar 2.

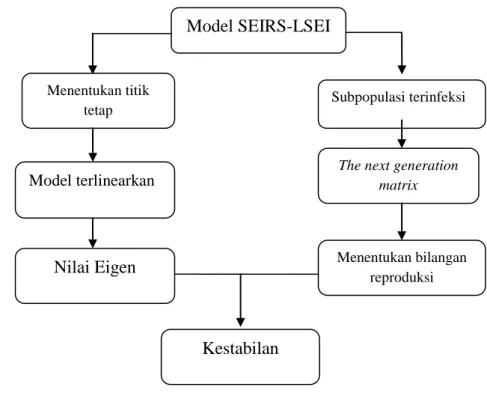
Gambar 2 Bagan kerangka analisis. Model SEIRS-LSEI

Menentukan titik tetap

Subpopulasi terinfeksi

The next generation matrix Menentukan bilangan reproduksi Model terlinearkan Nilai Eigen Kestabilan

15

IV HASIL DAN PEMBAHASAN

4.1 Penentuan Titik Tetap

Dalam menentukan suatu solusi yang tidak berubah menurut waktu sering digunakan analisis titik tetap pada sistem persamaan diferensial. Untuk sistem persamaan (1)–(8), titik tetap diperoleh pada saat , , ,

, , , , dan sehingga sistem persamaan

tersebut dapat ditulis sebagai berikut:

= 0 . (4.1) Sistem persamaan (4.1) di atas memiliki empat titik tetap, yaitu:

1 Titik tetap T1 2 Titik tetap T ( , 0, 0, 0, 0, 0, 0, 0), 2 3 Titik tetap T ( , 0, 0, 0, , 3 , ( , , , , , , , ) dengan,

4 Titik tetap T4 ( , , , , , , , ) dengan,

17

Penentuan titik tetap ini dapat dilihat pada Lampiran 1.

4.2. Analisis Kestabilan Titik Tetap

Misalkan dari model (4.1) didefinisikan fungsi-fungsi sebagai berikut: 𝑓𝑓5[𝑆𝑆ℎ,

𝐸𝐸

ℎ, 𝐼𝐼ℎ, 𝑅𝑅ℎ, 𝐿𝐿𝑚𝑚, 𝑆𝑆𝑚𝑚, 𝐸𝐸𝑚𝑚, 𝐼𝐼𝑚𝑚] = 𝜇𝜇𝑏𝑏�1 −𝑙𝑙_𝐾𝐾𝑚𝑚� (𝑆𝑆𝑚𝑚 + 𝐸𝐸𝑚𝑚 + 𝐼𝐼𝑚𝑚) − 𝜂𝜂𝐿𝐿𝐿𝐿𝑚𝑚 − 𝜇𝜇𝐿𝐿𝐿𝐿𝑚𝑚

(4.3)

Dengan menggunakan (6) terhadap (4.3) diperoleh matriks Jacobi sebagai berikut:

(4.4) Penentuan matriks Jacobi ini dapat dilihat pada Lampiran 2.

4.2.1 Kestabilan titik tetap T1

Untuk menentukan kestabilan titik tetap T

1 ( , 0, 0, 0, 0, 0, 0, 0) yaitu

dengan melakukan pelinearan pada (4.1) di atas. Titik T1

(4.5) ( , 0, 0, 0, 0, 0, 0) disubstitusi ke matriks Jacobi (4.4), sehingga diperoleh:

Dengan menyelesaikan persamaan karakteristik diperoleh nilai-nilai eigen berikut:

19

– .

Karena semua parameter yang terlibat bernilai positif, maka , , , , , dan . Untuk akan bernilai negatif

jika . Untuk akan

bernilai negatif jika maka

jadi titik tetap T1 stabil. Tetapi untuk akan

bernilai positif jika , maka

jadi titik tetap T1 sadel. Jadi T1 dapat dikatakan

stabil dan juga T1 dapat dikatan sadel.

4.2.2 Kestabilan titik tetap T

Kestabilan titik tetap tanpa penyakit ini diberikan oleh teorema berikut. 2

Teorema 1. Jika , maka (Nh, 0, 0, 0, Lm0, Sm0, 0, 0) adalah

titik tetap bebas penyakit sistem (1) (2), yang stabil asimtotik lokal jika R0 < 1 dan tidak stabil asimtotik lokal jika R0

Bukti :

> 1.

Dari persamaan (4.1) titik tetap diperoleh pada pada saat , ,

, , , , , dan dengan:

,

,

Dengan pemrograman berbasis fungsional diperoleh titik tetap = ( , 0,

0, 0, , . Menyimpulkan bahwa

atau , Kemudian dan ini

bahwa dan Karena , maka

akibatnya adalah equilibrium bebas penyakit. (lihat lampiran 3)

Dengan mengambil sistem persamaan (4.1) dan menyusunnya kembali dalam urutan subpopuasi-subpopulasi yang menyebabkan infeksi saja, yaitu ,

, , dan

diperoleh sistem persamaan sebagai berikut :

21

Dari sistem di atas, diperoleh matriks-matriks

Φ = , ς =

sehingga,

F = , V = .

Selanjutnya, dihitung matriks K = FV-1 sebagai berikut:

K =

.

Berdasarkan Van den Driessche dan Watmough 2005, bilangan reproduksi dasar R0

) = R

merupakan nilai eigen dengan modulus terbesar matriks K, ditulis:

0

Selanjutnya diperoleh : 0

R0

Terlihat bahwa R

= .

0 dipengaruhi oleh banyak parameter. Sebagai contoh jika

rata-rata gigitan nyamuk (B) diperbesar, maka R0 akan membesar. Artinya,

peluang penyakit akan menetap di dalam populasi juga semakin besar. Untuk meperkecil R0

Berikut adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh. , maka laju kematian nyamuk diperbesar. Akibatnya, penyakit akan menghilang dari populasi.

Tabel 1 Kondisi kestabilan titik tetap

Kondisi T1 T2

dan Sadel Stabil

dan Sadel Tidak Stabil

Dari Tabel 1 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh saling bertentangan. Ketika titik tetap pertama stabil, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama sadel, titik tetap dua stabil.

Titik tetap T3 dan titik tetap T4 akan di cari dengan melakukan simulasi.

Hal ini dilakukan karena kedua titik tetap tersebut sulit ditentukan secara analitik.

23

5.1 Parameter yang Ditetapkan

Misalkan dalam suatu pengamatan diperoleh parameter-parameter seperti dalam Tabel 2.

Tabel 2 Parameter model Var/pa

r

Keterangan Simulasi

B Rata-rata gigitan nyamuk terinfeksi pada manusia terekspos (per hari)

0,05 0.05

C Tingkat interaksi manusia yang terinfeksi dengan nyamuk yang rentan (per hari)

1 1

Peluang transmisi dari nyamuk yang terinfeksi ke manusia (per gigitan)

0.5 0.5

Peluang transmisi dari manusia yang terinfeksi ke nyamuk (per gigitan)

0.37 0.37

K Kapasitas maksimal larva yang hidup

3 Laju kematian manusia (per hari)

Rata-rata periode viremik (per hari) 1/30 1/30 Laju kelahiran nyamuk (per hari) 1/6 20

Laju kematian nyamuk (per hari) 2/7 1/7 Masa inkubasi ekstrinsik (proses

masuknya virus ke tubuh nyamuk)

1/3 1/3

Tingkat transmisi (pematangan) dari larva menjadi dewasa

0.1 0.1

Periode inkubasi intrinsik (proses

masuknya virus dalam tubuh manusia)

1/30 20

θ Laju konstan hilangnya kekebalan tubuh

0.001 0.001 Laju kematian larva (per hari)

Laju kelahiran manusia secara alami (per hari).

1/3 1/3

5.2.1 Populasi untuk Kondisi 5.2.1.1 Populasi Manusia

Kondisi adalah kondisi di mana populasi akan stabil menuju musnahnya virus dari populasi.

Berdasarkan nilai-nilai parameter yang ada pada Tabel 2 dan dengan mengambil nilai dan B yang sudah ditetapkan, diperoleh gambar dinamika populasi di bawah ini untuk nilai dan B dengan nilai .

Nilai awal total populasi manusia yang seluruhnya rentan adalah 1000. Nilai awal total populasi nyamuk yang berupa larva adalah 3000 dengan jumlah nyamuk yang terinfeksi 20%.

Gambar 3 Dinamika populasi manusia rentan terhadap waktu untuk kondisi .

Gambar 3 menunjukkan bahwa jika laju kematian nyamuk bertambah besar dua kali lipat dari laju kematian nyamuk semula, maka jumlah subpopulasi manusia rentan semakin bertambah. Peningkatan laju kematian nyamuk menyebabkan penurunan pada jumlah nyamuk termasuk nyamuk terinfeksi. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekspos semakin berkurang.

Sebaliknya, jika laju kematian nyamuk turun dan nilai parameter lainnya tetap, maka jumlah subpopulasi manusia rentan semakin berkurang sedangkan jumlah sub populasi lainnya semakin bertambah. Penurunan laju kematian nyamuk menyebabkan peningkatan pada jumlah nyamuk termasuk nyamuk

0 50 100 150 200 250 300 350t 92 94 96 98 100 sh m2



7 m1



7

25

terinfeksi. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekspos semakin bertambah. Gambar 3 menunjukkan bahwa pada subpopulasi manusia rentan ( ), di awal simulasi mengalami penurunan kemudian meningkat hingga stabil ke .

Gambar 4 Dinamika populasi manusia terekspos terhadap waktu untuk kondisi .

Gambar 4 menunjukkan bahwa jika laju kematian nyamuk bertambah besar dua kali lipat dari laju kematian nyamuk semula, maka jumlah subpopulasi manusia terekspos mengalami penurunan karena virus tidak dapat bertahan dalam populasi. Peningkatan laju kematian nyamuk menyebabkan penurunan pada jumlah nyamuk termasuk nyamuk terinfeksi. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekpos semakin berkurang.

Sebaliknya, jika laju kematian nyamuk turun dan nilai parameter lainnya tetap, maka jumlah subpopulasi manusia terekspos semakin bertambah. Penurunan laju kematian nyamuk menyebabkan peningkatan pada jumlah nyamuk termasuk nyamuk terinfeksi. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekspos semakin berkurang. Pada subpopulasi manusia terekspos ( ), awalnya mengalami peningkatan kemudian menurun hingga stabil ke

50 100 150 200 250 300 350t 0.2 0.4 0.6 0.8 1.0 1.2 eh m 2



7 m 1



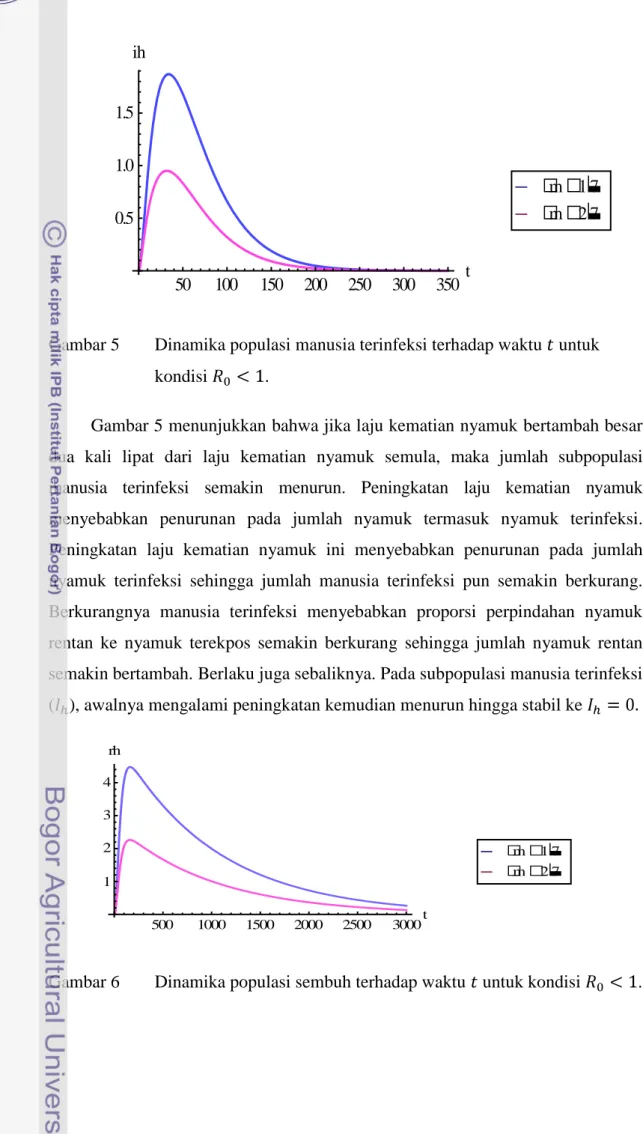
7

Gambar 5 Dinamika populasi manusia terinfeksi terhadap waktu untuk kondisi .

Gambar 5 menunjukkan bahwa jika laju kematian nyamuk bertambah besar dua kali lipat dari laju kematian nyamuk semula, maka jumlah subpopulasi manusia terinfeksi semakin menurun. Peningkatan laju kematian nyamuk menyebabkan penurunan pada jumlah nyamuk termasuk nyamuk terinfeksi. Peningkatan laju kematian nyamuk ini menyebabkan penurunan pada jumlah nyamuk terinfeksi sehingga jumlah manusia terinfeksi pun semakin berkurang. Berkurangnya manusia terinfeksi menyebabkan proporsi perpindahan nyamuk rentan ke nyamuk terekpos semakin berkurang sehingga jumlah nyamuk rentan semakin bertambah.Berlaku juga sebaliknya. Pada subpopulasi manusia terinfeksi ( ), awalnya mengalami peningkatan kemudian menurun hingga stabil ke

Gambar 6 Dinamika populasi sembuh terhadap waktu untuk kondisi . 50 100 150 200 250 300 350 t 0.5 1.0 1.5 ih m2



7 m1



7 500 1000 1500 2000 2500 3000t 1 2 3 4 rh m2



7 m1



7

27

Gambar 6 menunjukkan bahwa jika laju kematian nyamuk bertambah besar dua kali lipat dari laju kematian nyamuk semula, maka jumlah subpopulasi manusia sembuh semakin menurun. Peningkatan laju kematian nyamuk menyebabkan penurunan pada jumlah nyamuk termasuk nyamuk terinfeksi. Pada subpopulasi manusia sembuh ( ), di awal simulasi mengalami peningkatan kemudian menurun hingga stabil ke kemungkinan terkena kembali.

5.2.1.1 Populasi Nyamuk

Berdasarkan nilai-nilai parameter yang ada pada Tabel 2 dan dengan mengambil nilai dan B yang sudah ditetapkan, diperoleh gambar dinamika populasi nyamuk di bawah ini.

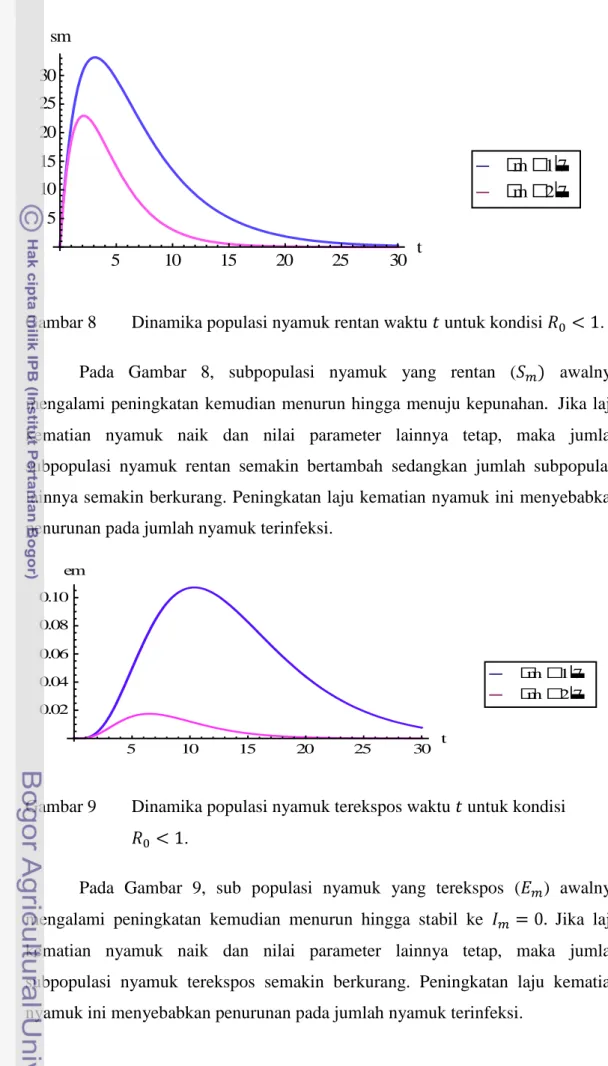
Gambar 7 Dinamika populasi nyamuk berupa larva waktu untuk kondisi .

Pada Gambar 7, jumlah subpopulasi nyamuk yang berupa larva ( ), awal simulasi mengalami penurunan hingga menuju kepunahan.

5 10 15 20 25 30 t 20 40 60 80 100 lm m 2



7 m 1



7

Gambar 8 Dinamika populasi nyamuk rentan waktu untuk kondisi . Pada Gambar 8, subpopulasi nyamuk yang rentan ( awalnya mengalami peningkatan kemudian menurun hingga menuju kepunahan Jika laju kematian nyamuk naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk rentan semakin bertambah sedangkan jumlah subpopulasi lainnya semakin berkurang. Peningkatan laju kematian nyamuk ini menyebabkan penurunan pada jumlah nyamuk terinfeksi.

Gambar 9 Dinamika populasi nyamuk terekspos waktu untuk kondisi .

Pada Gambar 9, sub populasi nyamuk yang terekspos ( ) awalnya mengalami peningkatan kemudian menurun hingga stabil ke Jika laju kematian nyamuk naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk terekspos semakin berkurang. Peningkatan laju kematian nyamuk ini menyebabkan penurunan pada jumlah nyamuk terinfeksi.

5 10 15 20 25 30 t 5 10 15 20 25 30 sm m 2



7 m 1



7 5 10 15 20 25 30 t 0.02 0.04 0.06 0.08 0.10 em m2



7 m1



7

29

Gambar 10 Dinamika populasi nyamuk terinfeksi waktu untuk kondisi .

Pada Gambar 10, subpopulasi nyamuk yang terinfeksi ( ), dari awal simulasi mengalami penurunan hingga stabil ke . Jika laju kematian nyamuk naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk terinfeksi semakin berkurang. Peningkatan laju kematian nyamuk ini menyebabkan penurunan pada jumlah nyamuk terinfeksi sehingga jumlah manusia terinfeksi pun semakin berkurang.

Dengan demikian, dapat dikatakan bahwa jumlah tiap subpopulasi stabil ke titik tetap tanpa penyakit

Ini menunjuk-kan bahwa sub-sub populasi manusia terekpos dan terinfeksi serta nyamuk terekpos dan terinfeksi menuju nol.

Dari gambar 3-6 dapat disimpulkan bahwa jika laju kematian nyamuk bertambah besar dua kali lipat dari laju kematian nyamuk semula, maka jumlah sub populasi manusia rentan semakin bertambah sedangkan jumlah subpopulasi lainnya semakin berkurang. Peningkatan laju kematian nyamuk menyebabkan penurunan pada jumlah nyamuk termasuk nyamuk terinfeksi. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekpos semakin berkurang.

Pada populasi nyamuk sebagaimana ditunjukkan oleh Gambar 7-10 jika laju kematian nyamuk naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk rentan semakin bertambah sedangkan jumlah subpopulasi lainnya semakin berkurang. Peningkatan laju kematian nyamuk ini menyebabkan

5 10 15 20 25 30 t 5 10 15 im m 2



7 m 1



7

penurunan pada jumlah nyamuk terinfeksi sehingga jumlah manusia terinfeksi pun semakin berkurang.

5.2.2 Populasi untuk Kondisi 5.2.2.1 Populasi Manusia

Kondisi akan dianalisis untuk satu kondisi yaitu . Berdasarkan nilai-nilai parameter yang ada pada Tabel 2 dan dengan mengambil nilai-nilai parameter dan B pada interval yang sudah ditetapkan, diperoleh gambar dinamika populasi di bawah ini untuk nilai dan B .

Nilai awal total populasi manusia yang seluruhnya rentan adalah 1000. Nilai awal total populasi nyamuk yang berupa larva adalah 3000 dengan jumlah nyamuk yang terinfeksi 20%.

Gambar 11 Dinamika populasi manusia rentan terhadap waktu untuk kondisi .

Gambar 11 menunjukkan bahwa jumlah subpopulasi manusia rentan ( ) setelah tertular virus, dari awal simulasi mengalami penurunan hingga stabil ke . Jika rata-rata gigitan nyamuk bertambah besar dari rata-rata gigitan nyamuk semula, maka jumlah subpopulasi manusia rentan semakin berkurang sedangkan jumlah sub populasi lainnya semakin bertambah. Peningkatan rata-rata gigitan nyamuk terinfeksi dapat meningkatkan nilai peluang kontak antara nyamuk terinfeksi dengan manusia rentan. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekspos semakin bertambah.

20 40 60 80 100t 20 40 60 80 100 sh B0.5 B0.05

31

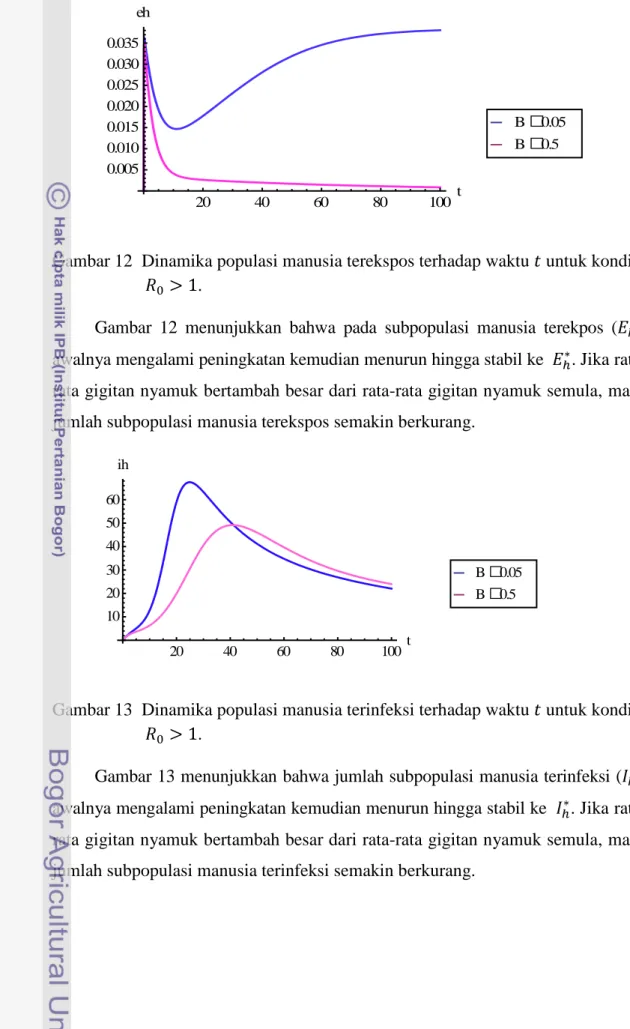
Gambar 12 Dinamika populasi manusia terekspos terhadap waktu untuk kondisi .

Gambar 12 menunjukkan bahwa pada subpopulasi manusia terekpos ( ), awalnya mengalami peningkatan kemudian menurun hingga stabil ke . Jika rata-rata gigitan nyamuk bertambah besar dari rata-rata-rata-rata gigitan nyamuk semula,maka jumlah subpopulasi manusia terekspos semakin berkurang.

Gambar 13 Dinamika populasi manusia terinfeksi terhadap waktu untuk kondisi .

Gambar 13 menunjukkan bahwa jumlah subpopulasi manusia terinfeksi ( ), awalnya mengalami peningkatan kemudian menurun hingga stabil ke . Jika rata-rata gigitan nyamuk bertambah besar dari rata-rata-rata-rata gigitan nyamuk semula,maka jumlah subpopulasi manusia terinfeksi semakin berkurang.

20 40 60 80 100t 0.005 0.010 0.015 0.020 0.025 0.030 0.035 eh B0.5 B0.05 20 40 60 80 100 t 10 20 30 40 50 60 ih B0.5 B0.05

Gambar 14 Dinamika populasi manusia sembuh terhadap waktu untuk kondisi .

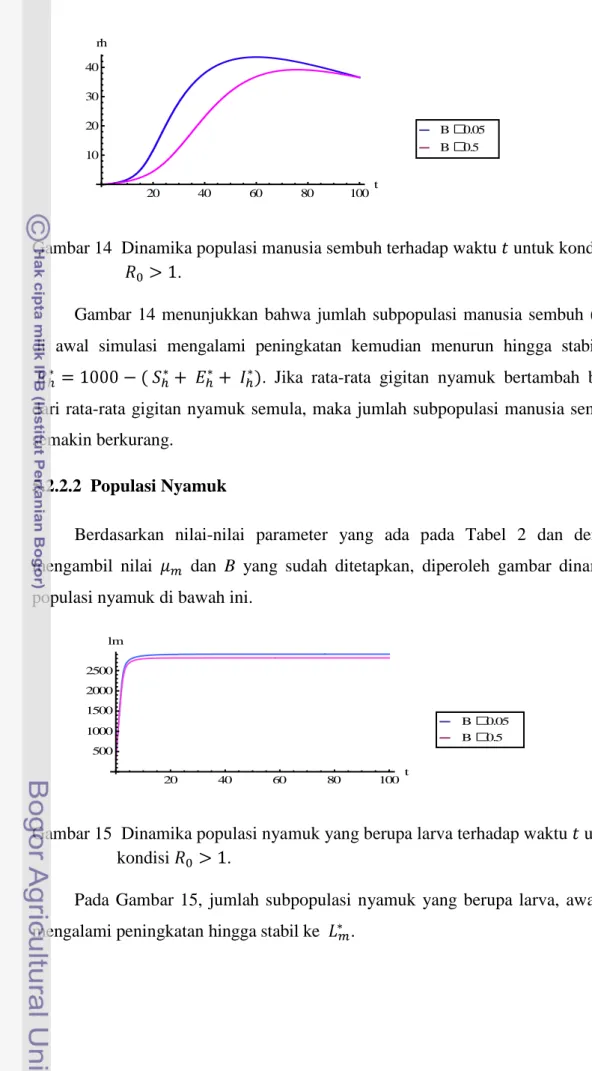
Gambar 14 menunjukkan bahwa jumlah subpopulasi manusia sembuh ( ), di awal simulasi mengalami peningkatan kemudian menurun hingga stabil ke

. Jika rata-rata gigitan nyamuk bertambah besar dari rata-rata gigitan nyamuk semula, maka jumlah subpopulasi manusia sembuh semakin berkurang.

5.2.2.2 Populasi Nyamuk

Berdasarkan nilai-nilai parameter yang ada pada Tabel 2 dan dengan mengambil nilai dan B yang sudah ditetapkan, diperoleh gambar dinamika populasi nyamuk di bawah ini.

Gambar 15 Dinamika populasi nyamuk yang berupa larva terhadap waktu untuk kondisi .

Pada Gambar 15, jumlah subpopulasi nyamuk yang berupa larva, awalnya mengalami peningkatan hingga stabil ke .

20 40 60 80 100t 10 20 30 40 rh B0.5 B0.05 20 40 60 80 100t 500 1000 1500 2000 2500 lm B0.5 B0.05

33

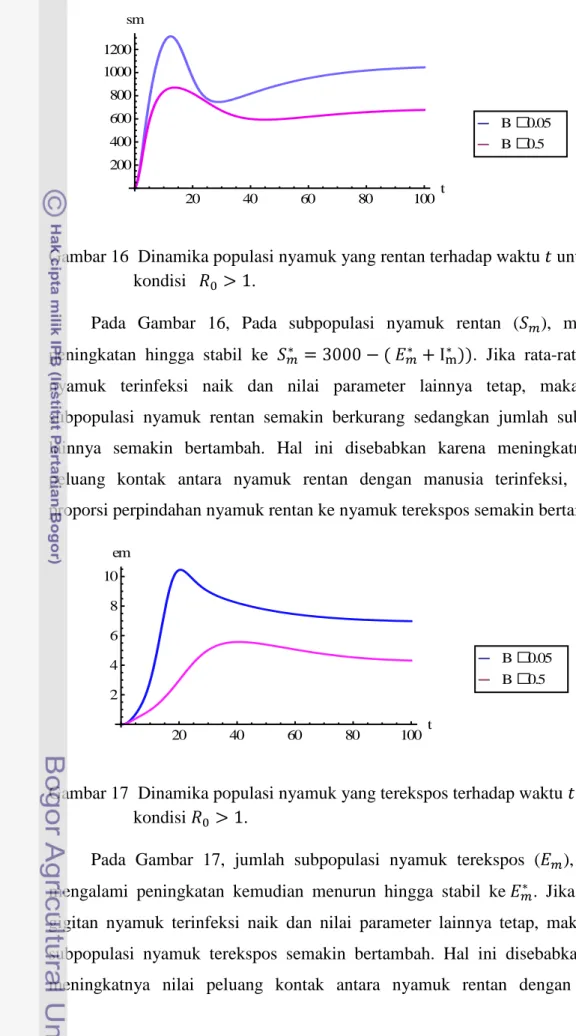
Gambar 16 Dinamika populasi nyamuk yang rentan terhadap waktu untuk kondisi .

Pada Gambar 16, Pada subpopulasi nyamuk rentan ( ), mengalami peningkatan hingga stabil ke . Jika rata-rata gigitan nyamuk terinfeksi naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk rentan semakin berkurang sedangkan jumlah subpopulasi lainnya semakin bertambah. Hal ini disebabkan karena meningkatnya nilai peluang kontak antara nyamuk rentan dengan manusia terinfeksi, sehingga proporsi perpindahan nyamuk rentan ke nyamuk terekspos semakin bertambah.

Gambar 17 Dinamika populasi nyamuk yang terekspos terhadap waktu untuk kondisi .

Pada Gambar 17, jumlah subpopulasi nyamuk terekspos ( ), awalnya mengalami peningkatan kemudian menurun hingga stabil ke . Jika rata-rata gigitan nyamuk terinfeksi naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk terekspos semakin bertambah. Hal ini disebabkan karena meningkatnya nilai peluang kontak antara nyamuk rentan dengan manusia

20 40 60 80 100 t 200 400 600 800 1000 1200 sm B0.5 B0.05 20 40 60 80 100 t 2 4 6 8 10 em B0.5 B0.05

terinfeksi, sehingga proporsi perpindahan nyamuk rentan ke nyamuk terekspos semakin bertambah.

Gambar 18 Dinamika populasi nyamuk yang terinfeksi terhadap waktu untuk kondisi .

Pada Gambar 18, Jumlah subpopulasi nyamuk terinfeksi ( ), dari awal simulasi mengalami penurunan hingga stabil ke .

Jadi, dapat dikatakan bahwa jumlah tiap subpopulasi stabil ke titik tetap endemik , , , , , , , .

Dari Gambar 11-14 di atas dapat disimpulkan bahwa jika rata-rata gigitan nyamuk bertambah besar dari rata-rata gigitan nyamuk semula, maka jumlah sub populasi manusia rentan semakin berkurang sedangkan jumlah subpopulasi lainnya semakin bertambah. Peningkatan rata-rata gigitan nyamuk terinfeksi dapat meningkatkan nilai peluang kontak antara nyamuk terinfeksi dengan manusia rentan. Akibatnya, proporsi perpindahan manusia rentan ke manusia terekspos semakin bertambah.

Ini menunjukkan bahwa sub-sub populasi manusia terekspos dan terinfeksi serta nyamuk terekspos dan terinfeksi menuju ke nilai yang tidak nol.

Sedangkan pada populasi nyamuk, jika rata-rata gigitan nyamuk terinfeksi naik dan nilai parameter lainnya tetap, maka jumlah subpopulasi nyamuk rentan semakin berkurang sedangkan jumlah subpopulasi lainnya semakin bertambah. Hal ini disebabkan karena meningkatnya nilai peluang kontak antara nyamuk

20 40 60 80 100 t 200 400 600 800 1000 1200 im B0.5 B0.05

35

rentan dengan manusia terinfeksi, sehingga proporsi perpindahan nyamuk rentan ke nyamuk terekspos semakin bertambah.

VI KESIMPULAN DAN SARAN

6.1 Kesimpulan

Dalam tulisan ini telah diberikan model SEIRS-LSEI pada penyakit chikungunya. Dari model tersebut dihasilkan empat titik tetap, yaitu dua titik tetap tanpa penyakit dan dua titik tetap endemik. Secara umum model yang dihasilkan dapat menunjukkan adanya endemi di suatu daerah untuk nilai parameter tertentu.

Secara simulasi numerik dari grafik bidang solusi dapat dilihat, bahwa: a. Jika laju kematian nyamuk naik, maka jumlah subpopulasi manusia rentan

semakin bertambah sedangkan subpopulasi lainnya semakin berkurang. Artinya, semakin besar laju kematian nyamuk maka jumlah manusia rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin sedikit.

b. Jika rata-rata gigitan nyamuk terinfeksi naik, maka jumlah subpopulasi manusia rentan semakin berkurang sedangkan subpopulasi lainnya semakin bertambah. Artinya, semakin besar rata-rata gigitan nyamuk terinfeksi maka jumlah manusia rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin banyak.

c. Jika laju kematian nyamuk naik, maka jumlah subpopulasi nyamuk rentan semakin bertambah sedangkan subpopulasi lainnya semakin berkurang. Artinya, semakin besar laju kematian nyamuk maka jumlah nyamuk rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin sedikit.

d. Jika rata-rata gigitan nyamuk terinfeksi naik, maka jumlah subpopulasi nyamuk rentan semakin berkurang sedangkan subpopulasi lainnya semakin bertambah. Artinya, semakin besar rata-rata gigitan nyamuk terinfeksi maka jumlah nyamuk rentan yang menjadi terekspos dan selanjutnya terinfeksi semakin banyak.

37

6.2 Saran

Dalam upaya penanggulangan wabah penyakit chikungunya, disarankan untuk meningkatkan laju kematian nyamuk ( ) dan menurunkan rata-rata gigitan nyamuk terinfeksi (B). Peningkatan laju kematian nyamuk dapat dilakukan antara lain dengan cara pemberantasan sarang nyamuk melalui penyemprotan dan pemakaian obat anti nyamuk. Untuk menurunkan rata-rata gigitan nyamuk terinfeksi dapat dilakukan dengan menggunakan lotion dan memasang kelambu (jaring nyamuk) di dalam rumah.

38

DAFTAR PUSTAKA

Anderson, May R. M. (1991), Infectiaus Diseases of Humans: Dynamics and Control, Oxford University Press, Oxpord.

Anton Howard. 1997. Aljabar Linear Elementer. Jakarta: Penerbit Erlangga. Braun, M. 1983. Differential Equations and Their Applications. New York :

Springer-Verlag

Borelli RL, Coleman CS. 1998. Differential Equations. USA: John Wiley and Sons, INC.

Chandra B. 2006. Pengantar Kesehatan Lingkungan. Jakarta: Penerbit Buku Kedokteran EGC

Dumont Y, Chiroleu F, Domerg C (2008). On a temporal model for the Chikungunya disease: Modelling, theory and numerics. Mathematical Biosciences, 213:80-91.

Edelstein-Keshe L. 1988. Mathematical Models in Biology. New York : Random House.

Labadie et al (2010). Chikungunya disease in nonhuman primates involves long-term viral persistence in macrophages. The Journal of Clinikal Investigation, 120(3):894-906

Pialoux G, Gauzere B. A, Jaureguiberry S, Strobel M (2007). Chikungunya, an epidemic arbovirosis. Lancet Infect. Dis. 7:319.

Szidarovszky F. dan AT.Bahill. 1998. Linear System Theory. CRC Press. Florida. Tu PNV. 1994. Dinamical System, An Introduction with Applications in

Economics and Biology. New York : Springer-Verlag.

van den Driessche, P., Watmough, J., 2005. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences. 180 (2002) 29.

van den Driessche, P., Watmough, J., 2008. Chapter 5: Further Notes on the Basic Reproduction Number. In: Brauer, F., van den Driessche, P., Wu, J. (Eds.),

Mathematical Epidemiology, Vol. 1945. Lecture Notes in Mathematics, Springer, pp. 159–178.

Verhulst F. 1990. Nonlinear Differential Equation and Dynamical System. Springer-Verlag. Heidelberg, Germany.

40

Lampiran 1. Penentuan Titik Tetap

Clear[f1,f2,f3,f4,f5,f6,f7,sh,eh,ih,rh,lm,sm,em,im,µh,b,βmh,θ,νh,ηh,µb,k,ηl,µl,c, βhm,µm,ηm,sol]

f1[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=µh nh-b βmh im/nh sh-µh sh+θ rh; f2[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=b βmh im/nh sh-νh eh-µh eh; f3[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=νh eh-ηh ih-µh ih;

f4[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=ηh ih-µh rh-(θ+µh)rh;

f5[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=µb (1-lm/k)(sm+em+im)-ηl lm-µl lm; f6[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=-c βhm ih/nh sm-µm sm+ηl lm; f7[sh_,eh_,ih_,rh_,lm_,sm_,em_,im_]:=c βhm ih/nh sm-µm em-ηm em;

Lampiran 2. Penentuan Bilangan Reproduksi Dasar (R0)

Dengan mengambil sistem persamaan (4.1) dan menyusunnya kembali dalam urutan sub-sub populasi yang menyebabkan infeksi saja, yaitu , , , dan diperoleh sistem persamaan sebagai berikut:

Dari sistem di atas, diperoleh matriks-matriks

Φ = dan ς =

Sehingga,

F = dan V =

42

sehingga bilangan reproduksi dasar adalah

=

Populasi manusia (1) (2) ( ( )

44

(1) (3)

(2) = (6)

Populasi Nyamuk

46

atau

jika Dan

48

Lanjutan teorema I

Bilangan Reproduksi

Dengan mengambil sistem persamaan (4.1) dan menyusunnya kembali dalam urutan sub-sub populasi yang menyebabkan infeksi saja, yaitu , , , dan diperoleh sistem persamaan sebagai berikut:

Dari sistem di atas, diperoleh matriks-matriks

sehingga,

50

Selanjutnya, dihitung matriks K = FV-1 sebagai berikut: K = FV-1

52

Clear[sol1,sh,eh,ih,rh,lm,sm,em,im,µh,b,βmh,θ,νh,ηh,µb,k,ηl,µl,c,βhm,µm,ηm, sol];Needs["PlotLegends`"];

(* Masukkan nilai parameter *) µb:=1/6; c:=1; βmh:=0.5; βhm := 0.37; µh:=1/(78*T); ηh:=1/30; µm1:=2/7; b:=0.05; µl:=1/3; ηl:=0.1; νm:=1/3; νh:=1/30; k:=3*1000; θ:=0.001; ηm:=1/9; t0:=0; T:=30; nh[t_]:=sh[t]+eh[t]+ih[t]+rh[t] sol1[µm_]:=NDSolve[{ sh'[t] µh nh[t]-b βmh im[t]/nh[t] sh[t]-µh sh[t]+θ rh[t], eh'[t] b βmh im[t]/nh[t] sh[t]-νh eh[t]-µh eh[t],

rh'[t] ηh ih[t]-µh rh[t]-(θ+µh)rh[t],

lm'[t] µb (1-lm[t]/k) (sm[t]+em[t]+im[t])-ηl lm[t]-µl lm[t], sm'[t] -c βhm ih[t]/nh[t] sm[t]-µm sm[t]+ηl lm[t],

em'[t] c βhm ih[t]/nh[t] sm[t]-µm em[t]-ηm em[t],

im'[t] ηm em[t]-µm im[t],

sh[t0]==100,eh[t0]==0,ih[t0] 0,rh[t0] 0, lm[t0] 3*100,

sm[t0] 0,em[t0] 0,im[t0] 60},{sh[t],eh[t],ih[t],rh[t],lm[t],sm[t],em[t],im[t]},{t,t0,T}]

fsh[i_]:=sol1[i][[1,1,2]]; Plot[Evaluate[Table[fsh[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","sh"},AxesOrigin→{0,0}] feh[i_]:=sol1[i][[1,2,2]]; Plot[Evaluate[Table[feh[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","eh"},AxesOrigin→{0,0}] fih[i_]:=sol1[i][[1,3,2]]; Plot[Evaluate[Table[fih[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","ih"},AxesOrigin→{0,0}] frh[i_]:=sol1[i][[1,4,2]]; Plot[Evaluate[Table[frh[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","rh"},AxesOrigin→{0,0}] flm[i_]:=sol1[i][[1,5,2]]; Plot[Evaluate[Table[flm[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","lm"},AxesOrigin→{0,0}]

54 fsm[i_]:=sol1[i][[1,6,2]]; Plot[Evaluate[Table[fsm[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","sm"},AxesOrigin→{0,0}] fem[i_]:=sol1[i][[1,7,2]]; Plot[Evaluate[Table[fem[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","em"},AxesOrigin→{0,0}] fim[i_]:=sol1[i][[1,8,2]]; Plot[Evaluate[Table[fim[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"µm = 1/7","µm = 2/7"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","im"},AxesOrigin→{0,0}]

Clear[sol1,sh,eh,ih,rh,lm,sm,em,im,µh,b,βmh,θ,νh,ηh,µb,k,ηl,µl,c,βhm,µm,ηm,s ol];Needs["PlotLegends`"];

(* Masukkan nilai parameter *) µb:=20; c:=1; βmh:=0.5; βhm := 0.37; µh:=1/78; ηh:=1/30; µm1:=1/7; b:=0.05; µl:=1/3; ηl:=0.1; νm:=1/3; νh:=20; k:=3*1000; θ:=0.001; ηm:=20; t0:=0; T:=100; nh[t_]:=sh[t]+eh[t]+ih[t]+rh[t] sol1[µm_]:=NDSolve[{ sh'[t] µh nh[t]-b βmh im[t]/nh[t] sh[t]-µh sh[t]+θ rh[t],

eh'[t] b βmh im[t]/nh[t] sh[t]-νh eh[t]-µh eh[t], ih'[t] νh eh[t]-ηh ih[t]-µh ih[t],

rh'[t] ηh ih[t]-µh rh[t]-(θ+µh)rh[t],

lm'[t] µb (1-lm[t]/k) (sm[t]+em[t]+im[t])-ηl lm[t]-µl lm[t], sm'[t] -c βhm ih[t]/nh[t] sm[t]-µm sm[t]+ηl lm[t],

em'[t] c βhm ih[t]/nh[t] sm[t]-µm em[t]-ηm em[t],

im'[t] ηm em[t]-µm im[t],

sh[t0]==100,eh[t0]==0,ih[t0] 0,rh[t0] 0, lm[t0] 3*100,

sm[t0] 0,em[t0] 0,im[t0] 60},{sh[t],eh[t],ih[t],rh[t],lm[t],sm[t],em[t],im[t]},{t,t0,T}]

fsh[i_]:=sol1[i][[1,1,2]]; Plot[Evaluate[Table[fsh[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","sh"},AxesOrigin→{0,0}] feh[i_]:=sol1[i][[1,2,2]]; Plot[Evaluate[Table[feh[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","eh"},AxesOrigin→{0,0}] fih[i_]:=sol1[i][[1,3,2]]; Plot[Evaluate[Table[fih[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","ih"},AxesOrigin→{0,0}] frh[i_]:=sol1[i][[1,4,2]]; Plot[Evaluate[Table[frh[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","rh"},AxesOrigin→{0,0}] flm[i_]:=sol1[i][[1,5,2]];

Plot[Evaluate[Table[flm[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","lm"},AxesOrigin→{0,0}] fsm[i_]:=sol1[i][[1,6,2]]; Plot[Evaluate[Table[fsm[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","sm"},AxesOrigin→{0,0}] fem[i_]:=sol1[i][[1,7,2]]; Plot[Evaluate[Table[fem[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,0.3},LegendTextSpace→3,LegendSize→0.5, ShadowBackground→White,AxesLabel→{"t","em"},AxesOrigin→{0,0}] fim[i_]:=sol1[i][[1,8,2]]; Plot[Evaluate[Table[fim[i],{i,µm1,2*µm1,µm1}]],{t,0,T},PlotLegend→{"B = 0.05","B = 0.5"},LegendPosition→{1,-0.3},LegendTextSpace→3,LegendSize→0.5,ShadowBackground→White,AxesLabel→{ "t","im"},AxesOrigin→{0,0}]