KECERDASAN BUATAN
“SISTEM INFERENSI FUZZY (METODE TSUKAMOTO) UNTUK
PENENTUAN KEBUTUHAN KALORI HARIAN”
OLEH
AMARILIS ARI SADELA (E1E1 10 086)
SITI MUTHMAINNAH (E1E1 10 082)
SAMSUL (E1E1 10 091)
NUR IMRAN RUSLAN (E1E1 10 097)
EDWIN SAPUTRA (E1E1 10 085)
JURUSAN TEKNIK INFORMATIKA
FAKULTAS TEKNIK
UNIVERSITAS HALU OLEO
KENDARI
BAB I PENDAHULUAN
1.1 Latar Belakang
Kecerdasan buatan (Artificial Intelligence) merupakan suatu inovasi baru dalam ilmu pengetahuan. Adanya kecerdasan buatan dimulai sejak munculnya komputer modern pada tahun 1940 dan tahun 1950. Ini merupakan kemampuan mesin-mesin elektronika baru untuk menyimpan sejumlah besar info dan memprosesnya dengan kecepatan yang sangat tinggi menandingi kemampuan manusia. Mulai dari sinilah telah banyak realisasi yang terjadi. Hal ini terbukti dengan adanya sistem komputer yang menyusut dalam ukuran. Selain itu pertambahan memori dalam kapasitas penyimpanan secara langsung yang mana semua itu sama dengan kapasitas penyimpanan pada otak manusia. Beberapa macam bidang yang menggunakan kecerdasan buatan antara lain sistem pakar, permainan komputer (games), jaringan syaraf tiruan, robotika dan logika fuzzy.
Logika Fuzzy merupakan suatu logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar atau salah. Dalam logika klasik dinyatakan bahwa segala hal dapat diekspresikan dalam istilah binary (0 atau 1, hitam atau putih, ya atau tidak), sedangkan logika fuzzy memungkinkan nilai keanggotaan antara 0 dan 1, tingkat keabuan dan juga hitam dan putih, dan dalam bentuk linguistik, konsep tidak pasti seperti "sedikit", "lumayan" dan "sangat". Logika ini berhubungan dengan himpunan fuzzy dan teori kemungkinan. Logika fuzzy ini diperkenalkan oleh Dr. Lotfi Zadeh dari Universitas California, Berkeley pada 1965. Logika fuzzy dapat digunakan dalam bidang teori kontrol, teori keputusan, dan beberapa bagian dalam managemen sains. Selain itu, kelebihan dari logika fuzzy adalah kemampuan dalam proses penalaran secara bahasa (linguistic reasoning), sehingga dalam perancangannya tidak memerlukan persamaan matematik dari objek yang dikendalikan. Adapun salah satu contoh aplikasi
logika fuzzy dalam dalam bidang kesehatan adalah Aplikasi Fuzzy Inference System (FIS) Tsukamoto untuk menentukan kebutuhan kalori harian.
Pada Metode Tsukamoto, setiap konsekuen pada aturan yang berbentuk IF-Then harus direpresentasikan dengan suatu himpunan fuzzy dengan fungsi keanggotaan yang monoton. Sebagai hasilnya, output hasil inferensi dari tiap-tiap aturan diberikan secara tegas (crisp) berdasarkan α- predikat (fire strength). Hasil akhirnya diperoleh dengan menggunakan rata-rata terbobot.
Metode ini nantinya akan digunakan untuk membangun sebuah sistem inferenzy fuzzy yang bertujuan untuk melakukan perhitungan terhadap kebutuhan energi harian bagi seorang pasien.
1.2 Rumusan Masalah
Berdasarkan latar belakang yang telah di paparkan sebelumnya, permasalahan yang akan di bahas yaitu bagaimana menentukan kebutuhan kalori harian dengan menggunakan sistem inferensi fuzzy (Metode Tsukamoto).
1.3Tujuan
Tujuan dari penulisan makalah ini adalah menerapkan metode FIS
Tsukamoto dalam menentukan kebutuhan kalori harian.
1.4 Manfaat
Makalah ini diharapkan dapat bermanfaat sebagai bahan studi penerapkan metode FIS Tsukamoto dalam menentukan kebutuhan kalori harian.
BAB II LANDASAN TEORI
2.1 Dari Himpunan Klasik ke Himpunan Samar (fuzzy)
Misalkan U sebagai semesta pembicaraan (himpunan semesta) yang berisi semua anggota yang mungkin dalam setiap pembicaraan atau aplikasi. Misalkan himpunan tegas A dalam semesta pembicaraan U. Dalam matematika ada tiga metode atau bentuk untuk menyatakan himpunan, yaitu metode pencacahan, metode pencirian dan metode keanggotaan. Metode pencacahan digunakan apabila suatu himpunan didefinisikan dengan mancacah atau mendaftar anggotaanggotanya. Sedangkan metode pencirian, digunakan apabila suatu himpunan didefinisikan dengan menyatakan sifat anggota-anggotanya. (Setiadji, 2009: 8).
Dalam kenyataannya, cara pencirian lebih umum digunakan, kemudian setiap
himpunan A ditampilkan dengan cara pencirian sebagai berikut:
A={x∈U| x memenuhi suatu kondisi} (2.1)
Metode ketiga adalah metode keanggotaan yang mempergunakan fungsi keanggotaan nol-satu untuk setiap himpunan A yang dinyatakan sebagai μA(x).
(2.2)
Menurut Nguyen dkk (2003: 86) fungsi pada persamaan (2.2) disebut fungsi karakteristik atau fungsi indikator. Suatu himpunan fuzzy A di dalam semesta pembicaraan U didefinisikan sebagai himpunan yang bercirikan suatu fungsi keanggotaan μA, yang mengawankan setiap x∈U dengan bilangan real di
dalam interval [0,1], dengan nilai μA(x) menyatakan derajat keanggotaan x di dalam A. Dengan kata lain jika A adalah himpunan tegas, maka nilai keanggotaannya hanya terdiri dari dua nilai yaitu 0 dan 1. Sedangkan nilai keanggotaan di himpunan fuzzy adalah interval tertutup [0,1].
2.2 Atribut
Himpunan fuzzy memiliki 2 atribut (Sri Kusumadewi dan Hari Purnomo, 2004: 6), yaitu:
2.2.1 Linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami, seperti: Muda, Parobaya, Tua.
2.2.2 Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu variabel seperti: 40, 25, 50, dsb.
2.3 Istilah-istilah dalam logika fuzzy
Ada beberapa istilah yang perlu diketahui dalam memahami sistem fuzzy, yaitu: 2.3.1 Variabel fuzzy
Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem fuzzy (Sri Kusumadewi dan Hari Purnomo, 2004: 6). Contoh: Umur, Temperatur, Permintaan, Persediaan, Produksi, dan sebagainya.
2.3.2 Himpunan fuzzy
Misalkan X semesta pembicaraan, terdapat A di dalam X sedemikian sehingga:
A={ x,μA[x] | x ∈ X , μA : x→[0,1] } (2.3)
Suatu himpunan fuzzy A di dalam semesta pembicaraan X didefinisikan sebagai himpunan yang bercirikan suatu fungsi keanggotaan μA, yang mengawankan setiap x∈X dengan bilangan real di dalam interval [0,1], dengan nilai μA(x) menyatakan derajat keanggotaan x di dalam A (Athia Saelan, 2009: 2).
Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy. Misalkan X=Umur adalah variabel
fuzzy. Maka dapat didefinisikan himpunan “Muda”, “Parobaya”, dan “Tua” (Jang dkk ,1997:17).
2.3.3 Semesta Pembicaraan
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi batas atasnya. Contoh: semesta pembicaraan untuk variabel umur: *0,+∞). (Sri Kusumadewi dan Hari Purnomo,2004:7). Sehingga semesta pembicaraan dari variable umur adalah 0 ≤ umur < +∞. Dalam hal ini, nilai yang diperbolehkan untuk dioperasikan dalam variable umur adalah lebih besar dari atau sama dengan 0, atau kurang dari positif tak hingga.
2.3.4 Domain
Domain himpunan fuzzy adalah keseluruhan nilai yang diijinkan dalam semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy.
Seperti halnya semesta pembicaraan, domain merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai domain dapat berupa bilangan positif maupun negatif. Contoh domain himpunan
fuzzy:
Muda =[0,45] (Sri Kusumadewi dan Hari Purnomo, 2004: 8). 2.3.5 Fungsi Keanggotaan
Jika X adalah himpunan objek-objek yang secara umum dinotasikan dengan x, maka himpunan fuzzy A di dalam X didefinisikan sebagai himpunan pasangan berurutan (Jang dkk ,1997:14):
μA(x) disebut derajat keanggotaan dari x dalam A, yang mengindikasikan derajat x berada di dalam A (Lin dan Lee,1996: 10). Dalam himpunan fuzzy terdapat beberapa representasi dari fungsi keanggotaan, salah satunya yaitu representasi linear. Pada representasi linear, pemetaan input ke derajat keanggotaannya digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas. Ada 2 keadaan himpunan fuzzy yang linear, yaitu representasi linear naik dan representasi linear turun.
2.3.6 Representasi linear NAIK
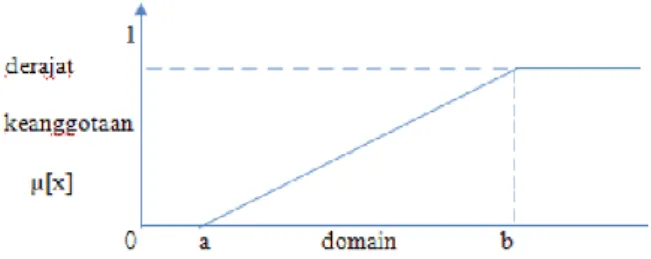
Pada representasi linear NAIK, kenaikan nilai derajat keanggotaan himpunan fuzzy (μ*x+) dimulai pada nilai domain yang memiliki derajat keanggotaan nol [0] bergerak ke kanan menuju ke nilai domain yang memiliki derajat keanggotaan lebih tinggi. Fungsi keanggotaan representasi linear naik dapat dicari dengan cara sebagai berikut:
Himpunan fuzzy pada representasi linear NAIK memiliki domain (-∞,∞) terbagi menjadi tiga selang, yaitu: *0,a+ , *a, b+, dan *b,∞).
a) Selang [0,a]
Fungsi keanggotaan himpunan fuzzy pada representasi linear NAIK pada selang [0,a] memiliki nilai keanggotaan=0
b) Selang [a, b]
Pada selang [a,b], fungsi keanggotaan himpunan fuzzy pada representasi linear NAIK direpresentasikan dengan garis lurus yang melalui dua titik, yaitu dengan koordinat (a,0) dan (b,1). Misalkan fungsi keanggotaan fuzzy NAIK dari x disimbolkan dengan μ*x+, maka persamaan garis lurus tersebut adalah:
c) Selang [b,∞)
Fungsi keanggotaan himpunan fuzzy pada representasi linear NAIK pada selang *xmax, ∞) memiliki nilai keanggotaan=0. Dari uraian di atas, fungsi keanggotaan himpunan fuzzy pada representasi linear NAIK, dengan domain (-∞,∞) adalah:
(2.6)
Himpunan fuzzy pada representasi linear NAIK direpresentasikan pada Gambar 2.1.
Gambar 2.1 Grafik representasi linear naik (Sri Kusumadewi dan Hari Purnomo, 2004:9)
2.3.7 Representasi linear TURUN
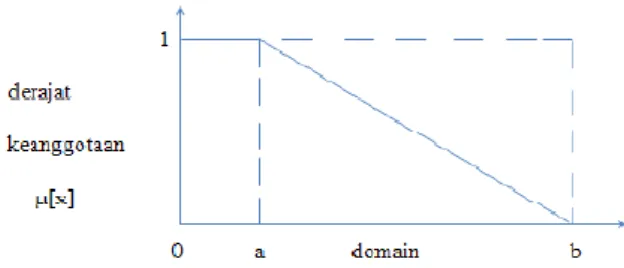
Sedangkan pada representasi linear TURUN, garis lurus dimulai dari nilai domain dengan derajat keanggotaan himpunan fuzzy (μ*x+) tertinggi pada sisi kiri, kemudian bergerak menurun ke nilai domain yang memiliki derajat keanggotaan himpunan fuzzy lebih rendah. Fungsi keanggotaan representasi linear TURUN dapat dicari dengan cara sebagai berikut:
Himpunan fuzzy pada representasi linear TURUN memiliki domain (-∞,∞) terbagi menjadi tiga selang, yaitu: *0,a+ , *a, b+, dan *b,∞).
a) Selang [0,a]
Fungsi keanggotaan himpunan fuzzy pada representasi linear TURUN pada selang [0,a] memiliki nilai keanggotaan=0
b) Selang [a, b]
Pada selang [a,b], fungsi keanggotaan himpunan fuzzy pada representasi linear TURUN direpresentasikan dengan garis lurus yang melalui dua titik, yaitu dengan koordinat (a,1) dan (b,0). Misalkan fungsi keanggotaan fuzzy TURUN dari x disimbolkan dengan μ*x+, maka persamaan garis lurus tersebut adalah:
Karena pada selang [a,b], gradien garis lurus=-1, maka persamaan garis lurus tersebut menjadi:
c) Selang [b,∞)
Fungsi keanggotaan himpunan fuzzy pada representasi linear TURUN pada selang [b, ∞] memiliki nilai keanggotaan=0 Dari uraian di atas, fungsi keanggotaan himpunan fuzzy pada representasi linear TURUN, dengan domain (-∞,∞) adalah:
(2.7)
Himpunan fuzzy pada representasi linear turun direpresentasikan pada Gambar 2.2.
Gambar 2.2 Grafik representasi linear turun (Sri Kusumadewi dan Hari Purnomo, 2004: 10)
2.4 Teori Operasi Himpunan
Menurut Lin dan Lee (1996: 27) Ada dua operasi pokok dalam himpunan
fuzzy, yaitu:
2.4.1 Konjungsi fuzzy
Konjungsi fuzzy dari A dan B dilambangkan dengan A∧B dan didefinisikan oleh:
μ A∧B=μ A(x) ∩ μB(y)= min(μA(x), μB(y)) (2.7) 2.4.2 Disjungsi fuzzy
Disjungsi fuzzy dari A dan B dilambangkan dengan A∨B dan didefinisikan oleh:
μ A∨B=μ A(x) ∪ μB(y)= max(μA(x), μB(y)) (2.8)
2.5 Metode Fuzzy Inference System (FIS) Tsukamoto
Inferensi adalah proses penggabungan banyak aturan berdasarkan data yang tersedia. Komponen yang melakukan inferensi dalam sistem pakar disebut mesin inferensi. Dua pendekatan untuk menarik kesimpulan pada IF-THEN rule
(aturan jika-maka) adalah forward chaining dan backward chaining (Turban dkk, 2005:726).
2.5.1 Forward chaining
Forward chaining mencari bagian JIKA terlebih dahulu. Setelah semua kondisi dipenuhi, aturan dipilih untuk mendapatkan kesimpulan. Jika kesimpulan yang diambil dari keadaan pertama, bukan dari keadaan yang terakhir, maka ia akan
digunakan sebagai fakta untuk disesuaikan dengan kondisi JIKA aturan yang lain untuk mendapatkan kesimpulan yang lebih baik. Proses ini berlanjut hingga dicapai kesimpulan akhir .
2.5.2 Backward chaining
Backward chaining adalah kebalikan dari forward chaining. Pendekatan ini dimulai dari kesimpulan dan hipotesis bahwa kesimpulan adalah benar. Mesin inferensi kemudian mengidentifikasi kondisi JIKA yang diperlukan untuk membuat kesimpulan benar dan mencari fakta untuk menguji apakah kondisi JIKA adalah benar. Jika semua kondisi JIKA adalah benar, maka aturan dipilih dan kesimpulan dicapai. Jika beberapa kondisi salah, maka aturan dibuang dan aturan berikutnya digunakan sebagai hipotesis kedua. Jika tidak ada fakta yang membuktikan bahwa semua kondisi JIKA adalah benar atau salah, maka mesin inferensi terus mencari aturan yang kesimpulannya sesuai dengan kondisi JIKA yang tidak diputuskan untuk bergerak satu langkah ke depan memeriksa kondisi tersebut. Proses ini berlanjut hingga suatu set aturan didapat untuk mencapai kesimpulan atau untuk membuktikan tidak dapat mencapai kesimpulan.
Menurut Sri Kusumadewi dan Sri Hartati (2006:34) sistem inferensi fuzzy
merupakan suatu kerangka komputasi yang didasarkan pada teori himpunan
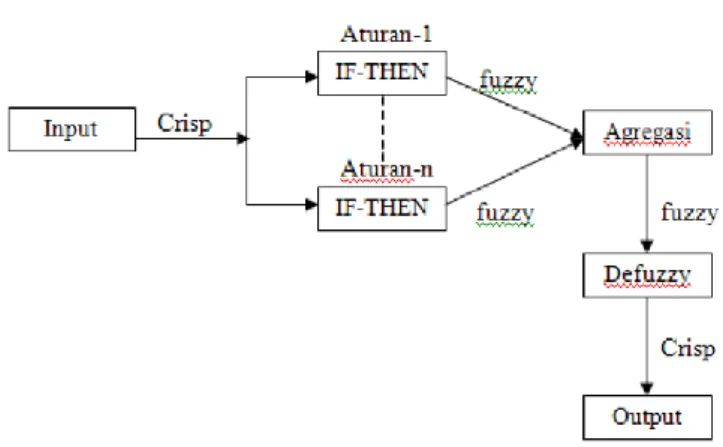
fuzzy, aturan fuzzy yang berbentuk IF-THEN, dan penalaran fuzzy. Secara garis besar, diagram blok proses inferensi fuzzy terlihat pada Gambar 2.3.
Gambar 2.3 Diagram Blok Sistem Inferensi Fuzzy (Sri Kusumadewi dan Sri Hartati, 2006: 34)
Sistem inferensi fuzzy menerima input crisp. Input ini kemudian dikirim ke basis pengetahuan yang berisi n aturan fuzzy dalam bentuk IF-THEN. Fire strength (nilai keanggotaan anteseden atau α) akan dicari pada setiap aturan. Apabila aturan lebih dari satu, maka akan dilakukan agregasi semua aturan. Selanjutnya pada hasil agregasi akan dilakukan defuzzy untuk mendapatkan nilai
crisp sebagai output sistem. Salah satu metode FIS yang dapat digunakan untuk pengambilan keputusan adalah metode Tsukamoto. Berikut ini adalah penjelasan mengenai metode FIS Tsukamoto. Pada metode Tsukamoto, implikasi setiap aturan berbentuk implikasi “Sebab-Akibat”/Implikasi “Input-Output” dimana antara anteseden dan konsekuen harus ada hubungannya. Setiap aturan direpresentasikan menggunakan himpunan-himpunan fuzzy, dengan fungsi keanggotaan yang monoton. Kemudian untuk menentukan hasil tegas (Crisp Solution) digunakan rumus penegasan (defuzifikasi) yang disebut “Metode rata-rata terpusat” atau “Metode defuzifikasi rata-rata terpusat (Center Average Deffuzzyfier) (Setiadji, 2009: 200).
BAB III PEMBAHASAN 3.1 Algoritma Aplikasi Perhitungan Kalori Harian :
1. Start
2. Masukkan aturan fuzzy berdasarkan kebutuhan
3. Masukkan batas bawah & batas atas masing-masing himpunan (Muda, Tua, Ringan, Berat, Tnggi, Rendah)
4. Masukkan Input :
• Usia (Input x)
• Berat badan (input y)
5. Hitung derajat keanggotaan masing-masing himpunan 6. Hitung z1-z4
7. Hitung rata-rata terbobot (z)
3.2 Variabel dan himpunan fuzzy
Sistem telah dibangun menggunakan VB6, dengan variabel-variabel input fuzzy yaitu: umur, dan berat badan. Tabel dibawah menunjukkan himpunan fuzzy untuk setiap variabel fuzzy beserta himpunannya.
Fungsi Variabel Himpunan Rentang
INPUT
Usia Muda [20-60]
Tua
Berat Badan Berat [40-80]
OUTPUT Kalori Tinggi [2500-6000] Rendah
Studi Permasalahan:
Seorang laki-laki berusia 30 tahun dengan berat badan 50 kg, ingin menentukan berapa banyak kebutuhan kalori hariannya digunakan pendekatan fuzzy.
Solusi:
Untuk menyelesaian permasalahan tersebut digunakan 4 aturan sbb:
[R1] IF Usia MUDA And Berat Badan RINGAN THEN Kalori RENDAH;
[R2] IF Usia MUDA And Berat Badan BERAT THEN Kalori RENDAH;
[R3] IF Usia TUA And Berat Badan RINGAN Kalori TINGGI; [R4] IF Usia TUA And Berat Badan BERAT THEN Kalori
TINGGI;
3.2.1 Memodelkan variabel fuzzy (Fuzzifikasi)
Ada 3 variabel fuzzy yang akan dimodelkan, yaitu: Usia, Berat badan, dan Kalori. 1. Usia; terdiri dari 2 himpunan fuzzy, yaitu Tua dan Muda. Fungsi
keanggotaan Permintaan direpresentasikan pada Gambar.
MUDA TUA 1 0 20 60 0,75 0,25 30
Fungsi Keanggotaan Himpunan Muda, dan Tua dari variabel Usia:
µUsiaMuda[x] = ,
µUsiaTua[x] = ,
Nilai keanggotaan himpunan Muda dan Tua dari variabel Usia bisa dicari dengan: µUsiaMuda[30] = (60-30)/40
= 0,75 µUsiaTua[30] = (30-20)/40
= 0,25
2. Berat Badan; terdiri dari 2 himpunan fuzzy, yaitu Berat dan Ringan. Fungsi keanggotaan Berat Badan direpresentasikan pada Gambar.
1, 60 − 𝑥 40 0, X ≤ 20 20 ≤ x ≤ 60 x ≥ 60 0, 𝑥 − 20 40 1, X ≤ 20 20 ≤ x ≤ 60 x ≥ 60 1 0 40 80 RINGAN BERAT 50 0,75 0,25
Fungsi Keanggotaan Himpunan Ringan dan Berat dari variabel Berat Badan:
µbbRingan[y] = ,
µbbBerat[y] =
Nilai keanggotaan himpunan Ringan dan Berat dari variabel Berat Badan bisa dicari dengan:
µbbRingan[50] = (80-50)/40
= 0,75 µbbBerat[50] = (50-40)/40
= 0,25
1. Kalori; terdiri dari 2 himpunan fuzzy, yaitu Rendah dan Tinggi. Fungsi keanggotaan Tips direpresentasikan pada Gambar.
1, 80 − 𝑦 40 0, y ≤ 40 40 ≤ y ≤ 80 y ≥ 80 0, 𝑦 − 40 40 1, y ≤ 40 40 ≤ y ≤ 80 y ≥ 80 1 0 2500 6000 RENDAH TINGGI
Fungsi Keanggotaan Himpunan Rendah dan Tinggi dari variabel Kalori:
µkaloriRendah[z] =
µkaloriTinggi[z] =
3.2.2 Cari nilai z untuk setiap aturan dengan menggunakan fungsi MIN pada aplikasi fungsi implikasinya :
[R1] IF Usia MUDA And Berat Badan RINGAN THEN Kalori RENDAH;
Nilai keanggotaan anteseden untuk aturan fuzzy [R1] yang dinotasikan dengan α1 diperoleh dengan rumus sebagai berikut:
α1 = μ usiaMUDA ᴖ bbRINGAN
= min(μ usiaMUDA [30+, μ bbRINGAN [50]) = min (0,75 : 0,75)
= 0,75
Menurut fungsi keanggotaan himpunan Kalori RENDAH dalam aturan fuzzy [R1], maka nilai z1 adalah:
(6000 – z) / (6000 – 2500) = 0,75 6000 – z = 2625 z = 3375 1, 6000 − 𝑧 3500 , 0, z ≤ 2500 2500 ≤ z ≤ 6000 z ≥ 6000 0, 𝑧 − 2500 3500 , 1, z ≤ 2500 2500 ≤ z ≤ 6000 z ≥ 6000
[R2] IF Usia MUDA And Berat Badan BERAT THEN Kalori RENDAH;
Nilai keanggotaan anteseden untuk aturan fuzzy [R2] yang dinotasikan dengan α2 diperoleh dengan rumus sebagai berikut:
α2 = μ usiaMUDA ᴖ bbBERAT
= min(μ usiaMUDA [30+, μ bbBERAT [50]) = min (0,75 : 0,25)
= 0,25
Menurut fungsi keanggotaan himpunan Kalori RENDAH dalam aturan fuzzy [R2], maka nilai z2 adalah:
(6000 – z) / (6000 – 2500) = 0,25
6000 – z = 875
z = 5125
[R3] IF Usia TUA And Berat Badan RINGAN Kalori TINGGI;
Nilai keanggotaan anteseden untuk aturan fuzzy [R3] yang dinotasikan dengan α3 diperoleh dengan rumus sebagai berikut:
α3 = μ usiaTUA ᴖ bbRINGAN
= min(μ usiaTUA [30+, μ bbRINGAN [50]) = min (0,25 : 0,75)
= 0,25
Menurut fungsi keanggotaan himpunan Tips Banyak dalam aturan fuzzy [R3], maka nilai z3 adalah:
(z – 2.500) / (6000 – 2500) = 0,25 z – 2.500 = 875
[R4] IF Usia TUA And Berat Badan BERAT THEN Kalori TINGGI;
Nilai keanggotaan anteseden untuk aturan fuzzy [R4] yang dinotasikan dengan α4 diperoleh dengan rumus sebagai berikut:
α4 = μ usiaTUA ᴖ bbBERAT
= min(μ usiaTUA [30+, μ bbBERAT [50]) = min (0,25, 0,25)
= 0,25
Menurut fungsi keanggotaan himpunan Tips Banyak dalam aturan fuzzy [R4], maka nilai z4 adalah:
(z – 2.500) / (6000 – 2500) = 0,25 z – 2.500 = 875
z = 3375
3.2.3 Menentukan Output Crisp (Deffuzzyfikasi)
Pada metode Tsukamoto, untuk menentukan output crisp digunakan defuzifikasi rata-rata terpusat, yaitu:
z = α1 ∗ z1+ α2 ∗ z2+α3 ∗ z3 +α4 ∗ z4 α1+ α2+ α3 + α4 z = (0,75 * 3375) + (0,25 * 5125) + (0,25 * 3375) + (0,25 * 3375) 1,5 z = 2531, 25 + 1281,25 + 843, 75 + 843, 75 1,5 z = 5500 1,5 = 3666,6
BAB IV PENUTUP
4.1Kesimpulan
Kesimpulan yang dapat diambil adalah sebagai berikut:
Dengan mengacu kepada solusi yang diberikan oleh metode Fuzzy Tsukamoto dalam membantu membuat keputusan. Salah satunya pengambilan keputusan dalam memberikan jumlah kalori yang dibutuhkan manusia sehari yang diperoleh berdasarkan variabel usia dan berat badan orang tersebut. Menentukan perkiraan besaran kalori yang diberikan kepada pengguna aplikasi bisa dilakukan secara mudah dan tepat dengan menggunakan Metode Fuzzy Tsukamoto.
4.2 Saran
Untuk pembuatan aplikasi selanjutnya yang menggunakan metode Fuzzy Tsukamoto agar mendapatkan output kalori lebih tepat dan akurat sebaiknya menambahkan variabel input fuzzy yang lain seperti tinggi badan, suhu tubuh, aktivitas, dan lain-lain.
DAFTAR PUSTAKA
Kusumadewi, S. 2003. Artificial Intelligence (Teknik dan Aplikasinya). Yogyakarta : Graha Ilmu.
Abdurrahman, Ginanjar.2011. Penerapan Metode Tsukamoto (Logika Fuzzy) Dalam Sistem Pendukung Keputusan Untuk Menentukan Jumlah Produksi Barang Berdasarkan Data Persediaan Dan Jumlah Permintaan.Yogyakarta. http://mfaridblog.blogspot.com/2012/04/makalah-ai.html
http://dinyistyanto.blogspot.com/2013/02/makalah-ai.html
http://www.yulyantari.com/tutorial/media.php?mod=detailsub&sub=18&bab=4 &mat=14