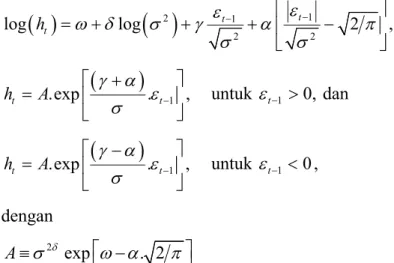PEMODELAN FLUKTUASI HARGA SAHAM BERPOLA EGARCH

PEMODELAN FLUKTUASI HARGA SAHAM

BERPOLA EGARCH

Oleh

MUSLIKAN

M0198012

SKRIPSI

ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET

SURAKARTA 2006

SKRIPSI

PEMODELAN FLUKTUASI HARGA SAHAM

BERPOLA EGARCH

yang disiapkan dan disusun oleh MUSLIKAN

M0198012 Dibimbing oleh

Pembimbing I Pembimbing II

Drs. Irwan Susanto, DEA Dra. Purnami Widyaningsih

NIP. 132134694 NIP. 131695204

telah dipertahankan di depan Dewan Penguji pada hari Senin, tanggal April 2006 dan dinyatakan telah memenuhi syarat

Anggota Tim Penguji Tanda Tangan

1. Dra. Sri Subanti, M.Si 1. .……… NIP. 131568293 2. Drs. Sugiyanto, M.Si 2. .……… NIP. 132000804 3. Drs. Wiranto, M.Kom 3. .……… NIP. 132044769 Disahkan oleh

Fakultas Matematika dan Ilmu Pengetahuan Alam

MOTO

َﻣ ﱠنِإ

ـ

ﻌْﻟا َﻊ

ُـ

ﺴ

ْـ

ﯾ ِﺮ

ُـ

ْﺴ

ـ

اًﺮ

*

َﻓـ

ﻓ اَذِﺈ

َـ

ْﻏَﺮ

ـ

ﻓ َﺖ

َـ

ﻧﺎ

ْـ

َﺼ

ـ

ْﺐ

*

Sesungguhnya sesudah kesulitan itu ada kemudahan. Maka apabila kamu telah selesai dari suatu urusan, kerjakanlah dengan sungguh-sungguh urusan yang lain.

(QS. Alam Nasyrah : 6-7)

َﻻ

ُﯾ

َﻜ

ـﱢﻠ

ـ

ُﻒ

َﻧ ﷲا

ـْﻔ

ـ

ًﺴ

ـ

إﺎ

ﱠﻻ

ُو

ْﺳ

ـ

َﻌ

ـ

َﮭ

ـﺎ

*

Allah tidak membebani seseorang melainkan sesuai dengan kesanggupannya (QS. Al Baqarah : 286)

PERSEMBAHAN

Skripsi ini kupersembahkan untuk Ayah dan Ibu tercinta, yang telah membesarkan, memelihara dan memberikan segala fasilitas kepada penulis

KATA PENGANTAR

Bismillaahi walhamdulillah, puji syukur penulis panjatkan ke hadirat Alloh SWT atas segala nikmat-Nya, sehingga penulis dapat menyelesaikan penulisan skripsi ini.

Penulis mengucapkan terima kasih kepada semua pihak yang telah membantu penulis dalam menyelesaikan penulisan skripsi ini, terutama penulis tujukan kepada

1. Bapak Irwan Susanto, DEA, Pembimbing I, yang telah memberikan banyak nasehat dan masukan kepada penulis,

2. Ibu Dra. Purnami Widyaningsih, Pembimbing II sekaligus Pembimbing Akademik yang dengan teliti dan sabar dalam memberikan nasehat, arahan dan koreksi terhadap penulis untuk mencapai hasil yang maksimal,

3. Ibu, Bapak, kakak dan adikku tercinta yang selalu memberi dukungan, dorongan dan do’a dalam menyelesaikan skripsi ini,

4. Teman-teman satu angkatan, Lanjar, Jaka, Ari W, Edy, Suwardi, Iwan dan masih banyak lagi yang lainnya atas bantuan fasilitas dan fikiran,

5. Dik Tukah tersayang, atas do’a dan dorongannya dalam mengembalikan semangat penulis untuk menyelesaikan skripsi ini.

Semoga skripsi ini dapat bermanfaat bagi penulis dan semua pihak yang membutuhkan.

Surakarta, April 2006

Penulis

ABSTRAK

Muslikan, 2006, PEMODELAN FLUKTUASI HARGA SAHAM BERPOLA

EGARCH. Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sebelas Maret Surakarta.

Volatilitas digunakan sebagai ukuran untuk melihat seberapa besar perubahan yang terjadi pada indikator-indikator ekonomi, salah satunya adalah perubahan harga saham. Pemodelan volatilitas harga saham bertujuan untuk mengetahui perubahan variansi dari sesatan model runtun waktu harga saham. Model EGARCH sebagai salah satu bentuk pemodelan volatilitas mampu mendeteksi ketaksimetrisan volatilitas akibat adanya isu-isu yang berbeda.

Tujuan dari penulisan skripsi ini adalah untuk mencari model volatilitas harga saham melalui pendekatan teoritis, dalam hal ini model EGARCH yang sesuai, dan mencari estimasi parameter model menggunakan metode maksimum likelihood. Metode yang digunakan adalah studi literatur. Adapun langkah-langkah yang digunakan dalam mencari estimasi parameter model EGARCH adalah dengan terlebih dahulu mengidentifikasi fungsi distribusi dari sesatan model runtun waktu, kemudian menentukan fungsi likelihoodnya. Selanjutnya dengan menggunakan algoritma skoring, parameter-parameter model EGARCH diestimasi.

Dari hasil pembahasan dapat disimpulkan bahwa estimasi parameter model

mempunyai bentuk turunan fungsi logaritma yang rekursif, yaitu loght

   sebagai fungsi dari loght i     .

ABSTRACT

Muslikan, 2006 MODELING ON RETURN VOLATILITY BY EGARCH

MODEL. Faculty of Mathematics and Natural Sciences, Sebelas Maret University, Surakarta.

Volatility is used to measure how big change that happen at economic indicators, one of them is volatility estimates of return. Modeling on return volatility aim to know the fluctuation of variance from residual time series model. An EGARCH model as one form of volatility models can detect the leverage or asymmetric effect at volatility model that caused by different news.

The purposes of this final project are to look for the volatility model of return through the theoretical approach i.e. the EGARCH model that appropriate, and to determine the parameter estimation model using the maximum likelihood method. The method is used in this final project is literature study. The steps are used to find the parameters estimation of the EGARCH model are identify the distribution function from the residual time series model first, and then determine the likelihood function. Finally, using scoring algorithm, the parameters of the EGARCH model are estimated.

From the investigation, it can be concluded that the parameters have the

recursive form of differential logarithm function, that is loght

   as function from logh_{t i}     .

DAFTAR ISI hal HALAMAN JUDUL………...…. i HALAMAN PENGESAHAN………..…………....……… ii MOTO………..………. iii PERSEMBAHAN………. iv KATA PENGANTAR………..………....… v ABSTRAK……… vi ABSTRACT……….. vii

DAFTAR ISI………. viii

BAB I PENDAHULUAN………. 1

1.1 Latar Belakang Masalah ……….……… 1

1.2 Rumusan Masalah ……….………. 2

1.3 Batasan Masalah ……….…..……….. 3

1.4 Tujuan ……….……… 3

1.5 Manfaat Penulisan. ……….……… 3

BAB II LANDASAN TEORI……….………. 4

2.1 Tinjauan Pustaka………. 4

2.1.1 Ruang Sampel……….……….. 4

2.1.2 Variabel Random……….………. 4

2.1.3 Fungsi Gamma……….………. 6

2.1.4 Proses Autoregresif ……….………. 6

2.1.5 Proses Moving Average ….……….………. 8

2.1.6 Proses ARMA ……….………. 8

2.1.7 Proses ARIMA ………..……….. 9

2.1.8 Kestasioneran ….……….………. 10

2.1.9 Model ARCH………... 11

2.1.10 Uji Eksistensi ARCH …..……….…….………... 12

2.1.11 Maksimum Likelihood ...……….………. 12

2.1.14 Penduga Efisien ……… 15

2.1.15 Eksponensial GARCH……….….……… 16

2.2. Kerangka Pemikiran……….……….. 17

BAB III METODE PENULISAN……… 19

BAB IV PEMBAHASAN……… 20 4.1 Identifikasi Model ……….. 20 4.2 Pendugaan Parameter ………. 25 4.3 Vektor Skor ……… 26 4.4 EGARCH (1,1) ……….. 28 4.5 Matriks Informasi ……….……….. 29 4.6 Algoritma Skoring ……….. 33

4.7 Langkah-langkah Pendugaan Parameter ……….….….…………. 36

BAB V PENUTUP ……….………. 37

5.1 Kesimpulan ………. 37

5.2 Saran ………... 37

BAB I PENDAHULUAN 1.1 Latar Belakang

Banyak fenomena di dalam bidang ekonomi dapat dimodelkan sebagai persamaan/pertidaksamaan matematika (ekonometri). Sebagai salah satu bidang disiplin ilmu, ekonometri telah mengalami banyak perkembangan. Laju inflasi, fluktuasi harga saham, fluktuasi nilai tukar mata uang dan masalah finansial lainnya adalah contoh dari beberapa fenomena yang telah banyak dikaji dan dikembangkan modelnya.

Dalam bidang ekonomi keuangan, volatilitas digunakan sebagai ukuran untuk melihat seberapa besar perubahan yang terjadi pada indikator-indikator ekonomi. Perubahan harga saham yang sering terjadi bahkan hampir setiap hari akan mempunyai volatilitas yang tinggi. Perubahan harga saham dapat dipengaruhi oleh informasi atau isu tentang perubahan ekonomi makro yang terjadi di masyarakat. Isu positif (good shock), misalnya kenaikan nilai tukar rupiah terhadap dolar, dapat meningkatkan kepercayaan terhadap kinerja perusahaan sehingga dapat menaikkan harga saham, sebaliknya isu yang negatif (bad shock), misalnya demo buruh, dapat menurunkan harga saham. Jika digambarkan dengan kurva, terlihat tidak simetris karena isu yang positif biasanya mempunyai pengaruh yang lebih kecil terhadap besarnya volatilitas jika dibandingkan dengan isu yang negatif (Nelson, 1991).

Model konvensional tentang volatilitas mengasumsikan bahwa volatilitas mempunyai variansi konstan dalam satu periode. Engle (1982) memperkenalkan suatu model tentang volatilitas yang mempunyai variansi berubah-ubah sepanjang waktu (heteroskedastic), dalam memodelkan laju inflasi di negara Inggris pada tahun 1970an, yaitu model runtun waktu bertipe Autoregressive conditional heteroskedasticity (ARCH). Hingga saat ini telah banyak tulisan tentang aplikasi model ARCH dalam beberapa masalah yang berkaitan dengan ekonomi keuangan. Salah satu diantaranya yang menarik dibahas dalam tulisan berikut adalah

bagaimana mencari model fluktuasi harga saham dengan pola ARCH yang mengandung fungsi eksponensial.

Generalize Autoregressive Conditional Heteroskedasticity (GARCH) adalah bentuk umum dari ARCH. Dalam beberapa persoalan keuangan, keluarga model GARCH telah sukses dan banyak digunakan, tetapi ada salah satu karakteristik data yang tidak terbaca dengan baik oleh model GARCH, yaitu ketaksimetrisan data disebabkan adanya guncangan (shock) dari luar yang mempengaruhi besar kecilnya volatilitas. Menurut Black di dalam Engle (1982), berpendapat bahwa terdapat korelasi yang negatif antara fluktuasi keuntungan modal (asset return volatility) saat ini dengan volatilitas returnyang akan datang. Isu positif mempunyai pengaruh lebih kecil terhadap volatilitas dibandingkan informasi buruk. Salah satu model ARCH yang mampu mendeteksi ketaksimetrisan data adalah model Exponential ARCH (EARCH). Sebagaimana model GARCH, model EGARCH (Exponential GARCH) adalah bentuk umum dari EARCH. Ada dua perbedaan yang mendasar antara model GARCH dan EGARCH yaitu secara grafik, kurva EGARCH sebagai fungsi dari return

mempuyai bentuk yang tidak simetris pada kedua sisinya (sisi negatif return dan sisi positif return) dan secara analitik, stasionaritas dan ergodisitas EGARCH lebih mudah diperiksa (Nelson, 1991).

Model EGARCH dengan orde q, p atau dapat ditulis EGARCH(q,p) adalah model volatilitas berpola ARCH yang nilainya tergantung dari q nilai-nilai terakhir dari volatilitas sebelumnya dan p nilai-nilai terakhir dari sesatan sebelumnya. Dalam skripsi ini dibahas pemodelan volatilitas terhadap fluktuasi harga saham berpola EGARCH dan metode algoritma skoring dalam mencari estimasi parameter model EGARCH, dengan asumsi bahwa perdagangan berlangsung secara kontinu atau banyaknya hari libur dalam perdagangan diabaikan.

1.2 Rumusan Masalah

Berdasarkan latar belakang masalah di atas, masalah yang dibahas dalam penulisan ini adalah

1. bagaimana cara mengidentifikasi model fluktuasi harga saham dengan volatilitas berpola EGARCH,

2. bagaimana mengestimasi parameter-parameter model EGARCH.

1.3 Batasan Masalah

1. Fluktuasi harga saham mempunyai model runtun waktu ARIMA(1,0,0) dengan sesatan mengandung gejala heterokedastisitas.

2. Perdagangan saham diasumsikan kontinu, atau dengan kata lain hari libur dalam perdagangan (non trading days) diabaikan.

1.4 Tujuan

Berdasarkan pada permasalahan yang ada, maka tujuan yang ingin dicapai dalam penulisan tugas akhir ini adalah

1. dapat mengidentifikasi model runtun waktu ARIMA(1,0,0) dengan sesatan berpola EGARCH.

2. mendapatkan estimasi parameter-parameter model EGARCH.

1.5 Manfaat Penulisan

Secara teoritis manfaat yang diharapkan dari penulisan ini adalah menambah wacana tentang pemodelan matematika dalam bidang keuangan khususnya tentang peramalan dengan sesatan mempunyai variansi heteroskedastik.

BAB II

LANDASAN TEORI .

2.1 Tinjauan Pustaka

Pada sub bab ini dikemukakan beberapa teori yang mendasari pembahasan pemodelan volatilitas harga saham dengan variansi heteroskedastik bertipe EGARCH. Beberapa konsep dasar statistik diantaranya tentang ruang sampel, variabel random, fungsi kepadatan peluang dan sebagainya, diberikan juga penurunan model ARIMA, model ARCH dan EARCH.

2.1.1 Ruang Sampel

Menurut Bain dan Engelhardt (1991), jika dilakukan suatu pengamatan terhadap data, maka himpunan dari semua hasil yang mungkin dari suatu pengamatan dinamakan ruang sampel dan dinotasikan dengan S.

2.1.2 Variabel Random

Variabel X dikatakan variabel random jika suatu fungsi yang terdefinisi dalam ruang sampel S, mempunyai hubungan dengan bilangan real sehingga

( )

X e x untuk setiap e dalam S. Jika himpunan dari semua nilai yang mungkin dalam variabel random X merupakan himpunan terhitung x₁,x₂,...,x_n maka X

disebut variabel random diskrit, tetapi jika semua nilai yang mungkin dalam variabel random X adalah himpunan tak terhitung, misalkan x

 

a,b dengan x, a

dan b real, maka X disebut variabel random kontinu. Bain dan Engelhardt (1991), menyajikan fungsi densitas probabilitas (fdp) dari X sebagai

 





, 1, ,...,2 n

f x P X x x x x x untuk X diskrit dan x

 

a,b untuk X

kontinu, dan mempunyai sifat 1. f

 

x 0 x

2.



 

1

x

x

3.



 

1

x

x

f untuk Xvariabel random kontinu,

sedangkan fungsi distribusi kumulatif (fdk) dari variabel random X disajikan sebagai F x

 

P X



x



, untuk X variabel random kontinu maka

 

 

F x f t dt

 



_

.

Definisi 2.1.1 (Bain dan Engelhart, 1991) Jika X variabel random kontinu dengan fdp f

 

x , maka harga harapan dari X dinotasikan E

 

x , didefinisikan

 



_

 

   xf x dx x E (2.1)

untuk nilai integral yang konvergen mutlak, jika tidak maka dikatakan harga harapan X tidak ada.

Teorema 2.1.1 (Bain dan Engelhart, 1991) Jika X dan Y variabel random kontinu, g

 

x dan h

 

y keduanya adalah fungsi, maka

   



g x h y



E



g

 

x



E

 

h

 

y

E  (2.2)

Persamaan (2.2) dapat diperluas lebih dari dua fungsi variabel random, yaitu jika X₁,...,X_k suatu barisan variabel random, u₁

 

x₁ ,...,u_k

 

x_k adalah barisan fungsi, maka E



u₁

 

x₁ ,...,u_k

 

x_k



 E



u₁

 

x₁



...E



u_k

 

x_k



(2.3)

Beberapa fdp kontinu yang sangat mendukung dalam pembahasan skripsi ini diantaranya adalah distribusi normal dan normal standar dan distribusi eksponensial. Bain dan Engelhardt (1991), mendefinisikan suatu variabel random

X berdistribusi normal dengan mean  dan variansi _2_{, dinotasikan}



,



~ N X jika X mempunyai fdp





₁   2 2 1 ; , 2 x f x   e      _ _ 

dengan    x ,  dan  adalah parameter yang masing-masing mempunyai nilai     dan 0 . Selanjutnya jika suatu variabel random Z berdistribusi normal dengan mean =0 dan  =1, maka Z dikatakan

mempunyai distribusi normal standar, biasanya dinotasikan Z : N

 

0,1 , dengan fdp

 

1 2₂ 2 z z e     ,  z (2.4)

Menurut Bain dan Engelhardt (1991), suatu variabel random kontinu X

berdistribusi eksponensial dengan parameter  0, jika X mempunyai fdp

 

, 1 x

f x_ e 





 untuk x0, dan sama dengan nol untuk x yang lain.

Definisi 2.1.2 (Bain dan Engelhardt, 1991) misalkan suatu barisan variabel random Y Y₁, ,...,₂ Y , masing-masing mempunyai fdk _n G y G y₁

 

, ₂

 

,...,G y dan _n

 

untuk suatu fdk dari Y G y , berlaku ,

 

lim _n

 

 

nG y G y untuk setiap y dengan

 

G y kontinu, maka dikatakan barisan Y Y₁, ,...,₂ Y konvergen dalam distribusi ke _n Y, dinotasikan d

n

Y Y.

2.1.3 Fungsi Gamma

Fungsi gamma, dinotasikan 

 

v , sebagaimana ditulis oleh Bain dan Engelhardt (1991), didefinisikan sebagai

 

_

_

   0 1_{e dx} x v v x _{, v0 (2.5)}

Teorema 2.1.2 (Bain dan Engelhardt, 1991) Fungsi gamma sebagaimana didefinisikan persamaan (2.5) memenuhi sifat

1. 

  

v    v 1

 

v 1



untuk v1 2. 

  

n  n1 !



untuk n1, 2,... dan 3. 1 2    _{ }   2.1.4 Proses Autoregresif

paling penting dalam runtun waktu adalah model stasioner, yang mengasumsikan proses tetap bergerak dalam suatu tingkat mean yang konstan.

Menurut Cryer (1986), proses autoregresif adalah proses regresi terhadap dirinya sendiri. Secara khusus proses autoregresif berorde-p untuk variabel random Y_t dapat ditulis dengan AR (p) yang memenuhi persamaan

t p t p t t t c Y Y Y Y  _{1 1}_{2 1}... _ 

Nilai yang disajikan deret Y_t adalah suatu kombinasi linier dari p nilai-nilai terakhir ditambah nilai sesatan _t.

Proses AR(1), dengan asumsi deretnya stasioner dapat ditulis sebagai





 

1 1 1 t t t t t t t Y Y L Y L Y            

dengan L adalah fungsi lag, didefinisikan sebagai i ₁ t t

L Y Y_ dan

 



1 1 ... P



P L L PL

     . Proses AR(1) stasioner, jika akar persamaan karakteristiknya yaitu ₁

  

L  1 ₁L



0 berada di luar lingkaran satuan atau

1

  . Sedangkan _t adalah white noise dengan E

 

 0 dan





2 0 . t untuk t E yang lain      _{ }  

Proses AR(2), dengan asumsi deretnya stasioner dapat ditulis sebagai





 

1 1 2 2 2 1 2 2 1 . t t t t t t t t Y Y Y L L Y L Y                 

Proses AR(2) stasioner jika akar persamaan karakteristiknya yaitu

2 1 1 2 1,2 2 4 2 L       

 berada di luar lingkaran satuan atau

2 1 2 1 1      

2.1.5 Proses Moving Average

Menurut Cryer (1986), proses moving average orde q, ditulis MA(q), dapat dinyatakan sebagai

 

1 1 2 2 ... , t t t t q t q t q t Y Y L                  

dengan persamaan karakteristiknya _q

 

L 0

Jika dipenuhi syarat invertibel maka proses MA(q) merupaka prosesyang stasioner. Syarat proses MA(q) ivertibel adalah akar dari _q

 

L 0 terletak di luar lingkaran satuan.

Proses MA(1) dapat dituliskan sebagai



1



1 . t t t t t Y Y L         

Proses MA(1) invertibel jika akar persamaan karakteristik ₁

  

L  1 L



0 terletak di luar lingkaran satuan atau  1. Sedangkan proses MA(2) dapat dituliskan sebagai



1 1 22



2 1 2 1 . t t t t t t Y Y L L                

Proses MA(2) dikatakan invertibel jika akar persamaan karakteristiknya yaitu

2 1 1 2 1,2 2 4 2 L       

 berada di luar lingkaran satuan atau

2 1 2 2 1 1 1 1.           2.1.6 Proses ARMA

Suatu proses ARMA (p,q) adalah gabungan dari proses autoregresif dan

moving average. Menurut Cryer (1986), proses tersebut dapat dinyatakan

1 1 2 2 ... 1 1 2 2 ...

t t t p t p t t t q t q







2



1 2 1 2 1 ... p 1 ... q p t q t L L L Y c L L L                  (2.6)

jika akar dari 2 1 2

1 ... p 0

p

z z z

  

     berada di luar lingkaran satuan, maka kedua ruas pada persamaan (2.6) dapat dibagi dengan



1 _{1 2} ... p



p L L L        , diperoleh

 

t t Y    L  dengan

 



_

1 2 2

_



2 1 2 1 ... 1 ... q q p p L L L L L L L                 , (2.7) 0 j j     



dan  c/ 1



    _{1 2} ... _p



.

Dari persamaan (2.7) terlihat bahwa stasioneritas proses ARMA tergantung hanya kepada parameter-parameter autoregresif



 ₁, ,...,₂ _p



dan tidak tergantung pada parameter-parameter moving average



 ₁, ,...,₂ _q



.

2.1.7 Proses ARIMA

Menurut Bowerman dan O’connell (1986), untuk menentukan model

Autoregressive Integrated Moving Average (ARIMA), pertama-tama digunakan pembedaan secara umum



₁ l



D



₁



d *

t t

Z  L L Y ,

guna mentransformasi data runtun waktu yang asli Y Y₁, ,...,₂ Y_n yang mempunyai variansi musiman ke dalam data runtun waktu yang stasioner Z Z_b, _b1,...,Z_{n b} , dengan cara memperhatikan perilaku fungsi autokorelasi dan autokorelasi parsial. Model ARIMA_{( , , )( , , )p d q P D Q} l _adalah

 

 

l

 

 

l p L P L Zt c q L Q L t

     

dengan

q adalah orde moving average tak musiman,

Q adalah orde moving average musiman,

l adalah panjang musiman,

 

p L

 adalah operator autoregresif tak musiman berorde p,

 

P L

 adalah operator autoregresif musiman berorde P,

 

q L

 adalah operator moving average tak musiman berorde q,

 

l

Q L

 adalah operator moving average musiman brorde Q,

c adalah konstanta dan

t

 adalah sesatan variabel random.

2.1.8 Kestasioneran

Menurut Makridakis, dkk (1999), model ARIMA hanya dapat diterapkan pada deret data yang stasioner. Kestasioneran data ada dua, yaitu stasioner terhadap mean dan stasioner terhadap variansi. Deret data dikatakan stasioner jika dibangkitkan oleh proses yang didasarkan pada mean yang konstan dan variansi yang konstan di sekitar meannya. Kemudian menurut Bowerman dan O’connell (1987) runtun waktu dikatakan stasioner jika sifat statistiknya (sebagai contoh mean dan variansi) dari runtun waktu tersebut betul-betul konstan terhadapa waktu. Dalam kenyatannya sangat jarang ditemukan data yang stasioner, khusunya di bidang ekonomi.

Jika data tidak stasioner terhadap mean maka dilakukan pembedaan pada data, dan jika tidak stasioner terhadap variansi maka dilakukan transformasi. Salah satu transformasi yang dapat digunakan adalah transformasi Box-Cox.

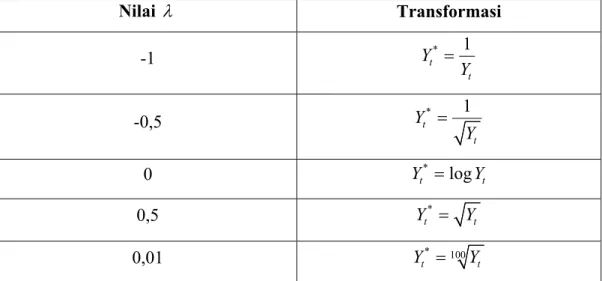
Definisi 2.1.3 (Cryer, 1986) Untuk suatu nilai parameter , didefinisikan transformasi Box-Cox sebagai berikut

 

 

1 , 0, log , 0. k t t t Y g Y Y      _     _ 

Untuk memperoleh transformasi yang sesuai sehingga diperoleh data yang stasioner terhadap variansi, perlu dikenakan beberapa nilai  pada data yang tidak stasioner. Kemudian diperiksa masing-masing hasil transformasi tersebut. Dari beberapa nilai  yang diberikan, dilakukan transformasi yang sesuai sebagai berikut Nilai  Transformasi -1 t* 1 t Y Y  -0,5 t* 1 t Y Y  0 Y_t* logY_t 0,5 * t t Y  Y 0,01 * ₁₀₀ t t Y  Y

Tabel 2.1 Transformasi Box-Cox

2.1.9 Model ARCH

Salah satu pendekatan model ekonometrik adalah dengan cara menjabarkan kuadrat sesatan yang diperoleh dari model autoregresif sehingga menjadi suatu autoregresif baru. Engle menyatakan bahwa suatu proses _t yang memenuhi

 

2 2 2 1 1 2 2 ... ~ 0,1 1,..., t t t t t t q t q t v h h v N iid t T                  (2.8)

disebut ARCH orde q atau _t ~ ARCH

 

q . Proses tersebut dapat disajikan menjadi _t_t1,...,_tq ~ N



0,h_t



, yang menunjukkan bahwa distribusi bersyarat dari _t mempunyai variansi h_t yang tergantung secara linier terhadap q nilai-nilai terakhir dari proses atau mempunyai variansi tidak konstan (heteroskedastic).

2.1.10 Uji Eksistensi ARCH

Uji eksistensi ARCH digunakan untuk menguji ada tidaknya efek heteroskedastisitas dalam data. Engle (1982), menyusun uji efek ARCH berdasarkan prinsip pengali Lagrange. Misalkan Y_t adalah himpunan pengamatan selama waktu t, dengan t1,...,T yang dipengaruhi faktor eksogen x_t, memenuhi model regresi linier Y_t x_t' _t dengan 'x_t adalah vektor



1k



untuk faktor eksogen yang dapat dinyatakan sebagai





'

1, 2,..., t t t tk

x  x x x .

Sedangkan  adalah vektor parameter berdimensi



k1



atau koefisien dari variabel eksogen yang dapat dinyatakan sebagai





1 1, 2,..., '

k k

 _     .

Selanjutnya dengan menggunakan metode kuadrat terkecil diperoleh sesatan ˆ_t kemudian disusun persamaan regresi _ˆ2

t  terhadap 2 2 2 1 2 1 ˆ_t ,ˆ_t ,...,ˆ  _{ }  2 2 2 1 1 ˆ_t ˆ_t ... _q ˆ_{t q} w_t     _   _  (2.9)

kemudian dibuat statistik uji

2



_LM TR dengan 2



R merupakan koefisien korelasi kuadrat berkaitan dengan model regresi pada persamaan (2.9) dan d

 

q

LM 2

  . Hipotesis nol, H0, menyatakan tidak

ada efek ARCH dalam data. Daerah kritis, menolak H0, jika _LM 

 

q .

2.1.11 Maksimum Likelihood

Pada variabel random kontinu, fungsi likelihood didefinisikan sebagai kepadatan bersama dari pengamatan



y₁,y₂,...,y_T



. Menurut Greene (1993), fungsi likelihood yang didefinisikan sebagai fungsi dari vektor parameter  dapat dinyatakan sebagai



1

, ,...,

2

;





;



 

T

T t

Penyelesaiannya dapat disederhanakan dengan log dari fungsi likelihood. Harga dari vektor parameter yang memaksimumkan fungsi ini disebut penduga maksimum likelihood, biasanya dinyatakan sebagai ˆ . Harga ˆ yang memaksimumkan fungsi likelihood, juga memaksimumkan log likelihoodnya. Jika logL

 

 didifferensialkan terhadap , kemudian disamadengankan nol, diperoleh akar, ˆ , sebagai penduga parameter . Secara analitik sulit ditemukan penduga maksimum likelihood dari parameter , sehingga diperlukan metode penyelesaian numerik, dalam hal ini digunakan metode optimasi. Ide dasar dari metode optimasi ini adalah mencari penduga parameter optimal, ˆ , yang memaksimumkan dengan proses yang berlangsung secara iteratif. Salah satu metode optimasi tersebut adalah metode skoring seperti dalam Hamilton (1994),

 1   log  

 

ˆ k ˆk ˆ k l k       _{   }   _ (2.10)

dengan k menyatakan iterasi, ˆ merupakan penduga vektor parameter, sedangkan

 k



ˆ penduga matriks informasi untuk vektor parameter  yang dievaluasi pada iterasi ke-k dan  

 

   _loglk

adalah turunan pertama dari fungsi log likelihood yang dievaluasi pada iterasi ke-k, sedangkan  

 

   _loglk

disebut vektor skor untuk parameter .

Matriks informasi, _, merupakan negatif dari harga harapan pada fungsi Hessian. Hamilton (1994), mendefinisikan fungsi Hessian, dinotasikan H_{n n }, sebagai turunan kedua dari l₁

 

 terhadap , ditulis

 

 

2 ' ' t  t         _        _  _ l l

Misalkan _t adalah suatu vektor random p1, dari ruang sampel S, yang mempunyai elemen '





1,..., t t t p

  _ _ , dan untuk sebarang _t, didefinisikan * t

elemen ke-m untuk 1 m p, yaitu *'





1,..., ,..., t t t m t p

     , definisi-definisi

berikut menjelaskan sifat simateris dan regular dari model ARCH.

Definisi 2.1.4 (Engle, 1982) Proses ARCH, sebagaimana didefinisikan persamaan (2.4), dikatakan simetris jika

a.

 

 

* t t

h  h  , untuk sebarang m dan _tS b.

 

_/

 

* _/

t i t i

h   h  

     untuk sebarang m, i dan _tS c.

 

_/

 

* _/

t t m t t m

h  _ h  _

     untuk sebarang m dan _tS . Definisi 2.1.5 (Engle, 1982) Proses ARCH, sebagaimana didefinisikan persamaan (2.4), dikatakan regular jika

a. minh

 

_t  untuk suatu  0dan _tS,

b. E



h

 

_t /_i h

 

_t /_{t m} _{t m 1}



ada untuk setiap i, m dan t

Teorema 2.1.3 ( Engle, 1982 ) Jika model ARCH memenuhi sifat simetris dan regular, maka  ˆ_ 0

2.1.12 Model GARCH

Model ARCH digeneralisasikan oleh Bollerslev (1986) dengan model GARCH, yaitu untuk q pada model ARCH (q), persamaan (2.8) dapat ditulis kembali menjadi

 

2 t t L h   (2.11) dengan

 

1 i i i L L     



L adalah fungsi lag, didefinisikan 2 2 i t t i

L  _ .

Secara numerik, menurut Hamilton (1994), 

 

L dapat dinyatakan sebagai pembagian dari dua polinomial dengan orde berhingga

 

 

_{ }

_p p q q L L L L L L L L L                    ... 1 ... 1 2 2 1 1 2 2 1 1 (2.12)

dengan syarat bahwa akar-akar dari 1

 

z 0 berada di luar lingkaran satuan. Jika persamaan (2.12) disubstitusikan ke dalam persamaan (2.11) diperoleh

 

 

2 1 t t L L h       

 







 



 

2 0 1 1 2 2 2 2 2 1 1 2 2 1 1 1 ... ... t t t t t p t p t t q t q L h L h h h h                                    





        p i q i i t i i t i t h h 1 1 2 0     (2.13)

dengan ₀ 



1₁₂ ..._r



. Persamaan (2.13) merupakan bentuk GARCH (p,q)

2.1.13 Penduga Tak Bias

Suatu penduga T, terhadap fungsi parameter  

 

dikatakan efektif atau tak bias jika harga harapan dari T sama dengan  

 

.

Definisi 2.1.6(Bain dan Engelhart, 1991) Suatu statistik T dikatakan penduga tak bias dari 

 

 jika memenuhi

   

T  

E

untuk setiap , jika tidak berlaku, maka T dikatakan estimator bias.

2.1.14 Penduga Efisien

Efisiensi dari suatu penduga dapat dilihat dari variansi penduga tersebut. Suatu penduga dikatakan efisien jika variansinya kecil, oleh karena itu suatu penduga dikatakan efisien, relatif terhadap penduga lain jika variansinya lebih kecil dari variansi penduga yang lain.

Definisi 2.1.7 (Bain dan Engelhardt, 1991) Misalkan T dan _{T keduanya penduga} *





 

_{ }

T T T T re var var ,   _{ .}

Lebih lanjut suatu penduga tak bias T terhadap 

 

 dikatakan efisien jika memenuhi _re



_T,_T



1 _{untuk setiap penduga tak bias T terhadap }

 

_{ .}

2.1.15 Exponential GARCH

Jika h_t adalah variansi bersyarat dari _t diberikan informasi pada waktu ke-t, maka h_t haruslah nonnegatif. Model GARCH menjamin hal ini dengan membuat h_t sebagai kombinasi linier dari variabel random positif. Cara lain untuk menjamin kenonnegatifan h_t adalah dengan membuat log

 

h_t sebagai fungsi linier dari waktu (t) dan lag dari v_t, yaitu

 





1 1 ln , 1 t t t t t k t k k v h h g v     _     



 (2.14)

dengan

 

_{t t,} dan

 

_{k k1,}, bernilai real, stokastik dan merupakan barisan skalar. Di dalam mendeteksi ketaksimetrisan volatilitas

 

h_t terhadap return

saham

 

_t , nilai g

 

v_t haruslah sebagai fungsi dari v_t pada kedua sisi tanda (-v_t

dan +v_t). Salah satu caranya adalah dengan cara membuat g

 

v_t sebagai kombinasi linier dari v_t dan |v_t|, yaitu

 

vt zt



vt Evt



g   

 



g vt



t, mempunyai mean 0, merupakan barisan variabel randon yang

independen dan berdistribusi identik (i.i.d). Sepanjang interval 0v_t , kurva

 

vt

g linier dengan gradient   , dan sepanjang interval v_t 0, kurva

 

vt

g linier dengan gradient   . Inilah yang menyebabkan variansi bersyarat

 

ht tidak simetris dalam merespon naik turunnya return saham.

Persamaan (2.14) juga dapat dinyatakan sebagai pembagian dua deret yang berhingga, yaitu







1



 

1 1 1 ... log( ) 1 ... t t t q q t t _p t p v h L L h g v L L     _            (2.15)

dengan syarat,



1



_i1,piyi



dan







_{i q}



i iy

, 1

1



tidak mempunyai akar sama dan akar dari



1





_i1,q



i

y

i



berada di luar lingkaran satuan.

Model EGARCH dapat diestimasi oleh maksimum likelihood dengan menentukan terlebih dahulu fungsi densitas untuk v_t. Nelson (1991), menyajikan suatu fungsi Generalized Error Distribution (GED), yaitu suatu fungsi pembangkit untuk variabel yang mempunyai bentuk eksponensial, sebagai fungsi densitas untuk v_t

 

 

1 2 1 exp , , 0 1 .2 v t t v t v v v f v v v v                              _{ } . 2.2 Kerangka Pemikiran

Model runtun waktu AR(1) pada fluktuasi harga saham dengan sesatan berpola heteroskedastik mempunyai fungsi variansi berupa var

 

_t h_t. Fungsi

t

h merupakan fungsi terhadap waktu. Gejala heteroskedastik dari data dapat berbentuk ARCH, GARCH, EGARCH atau yang lain. Dengan menggunakan test pengali Lagrange, dapat ditentukan apakah model yang disajikan memenuhi atau tidak.

Model EGARCH adalah salah suatu model EGARCH yang mampu membaca ketaksimetrisan volatilitas, h_t, akibat guncangan, shock, terhadap volatilitas, karena sesuai dengan realitas bahwasannya isu negatif, misalkan isu demo buruh, mempunyai efek lebih besar terhadap fluktuasi harga ketimbang isu positif, misalnya kebijakan pemerintah menunda kenaikan harga bahan bakar

Setelah model yang disajikan memenuhi, selanjutnya adalah melakukan pendugaan parameter-parameter model secara iteratif dengan menggunakan algoritma skoring.

BAB III

METODE PENULISAN

Dalam penulisan skripsi ini, metode yang digunakan adalah metode literatur yang berarti bahwa keseluruhan bahan untuk penulisan skripsi ini diambil dan bersumberkan pada buku-buku referensi dan teori-teori yang mendukung tujuan penulisan skripsi ini, meliputi

1. kajian terhadap model regresi dengan sesatan berpola EGARCH,

2. kajian terhadap pendugaan maksimum likelihood terhadap parameter  untuk model EGARCH(1,1) sebagai salah satu model EGARCH yang mempunyai bentuk cukup sederhana dan mudah untuk dilakukan pendugaan parameter, yang mencakup tahapan-tahapan menduga parameter dengan metode maksimum likelihood, kemudian mencari harga ˆ dengan menggunakan algoritma skoring.

BAB IV PEMBAHASAN

Misalkan dipunyai data runtun waktu harga saham dalam kurun waktu tertentu memenuhi bentuk model runtun waktu AR(1) dengan volatilitas mempunyai gejala heteroskedastik. Kemudian dilakukan pengujian model EGARCH sebagai salah satu model volatilitas harga saham yang dapat mendeteksi ketaksimetrisan volatilitas akibat adanya isu yang terjadi. Dalam bab ini dibahas mengenai metode pendugaan parameter model EGARCH menggunakan algorima skoring.

4.1 Identifikasi Model

Menurut Nelson (1991), pemodelan volatilitas dengan memanfaatkan model bertipe EGARCH dilakukan dengan mengasumsikan bahwa log dari perbandingan harga saham saat ini dengan harga saham sebelumnya (return), R_t, dapat direpresentasikan mengikuti proses autoregresif AR(1)

t t t a bR

R   _1  (4.1)

Dengan sesatan random _t, yang diperoleh pada pengamatan t1,...,T

berdistribusi identik dan independen (i.id) dengan mean = 0 dan variansi, h_t, berubah-ubah sebagai fungsi dari waktu (t) memenuhi persamaan (2.15), yaitu







1



 

1 1 1 ... log( ) 1 ... t t t p p t t _q t q v h L L h g v L L                 (4.2) dengan syarat 1 1 q i i i y        



 dan 1 1 p i i i y       





 tidak mempunyai akar yang sama,

 

t 1 t 1 t 1 t 1

g v_  v_ E v_ v_ , (4.3)

dan _t   log 1



N_t



, dengan N_t menyatakan banyaknya hari libur dalam perdagangan (non trading days). Misalkan diasumsikan bahwa perdagangan

berlangsung kontinu, dalam hal ini N_t 0, maka _t  dan persamaan (4.2) menjadi :







1



 

1 1 1 ... log( ) 1 ... p p t _q t q L L h g v L L               (4.4)

Sebagaimana penurunan model GARCH(p,q) dari model ARCH(p), untuk

p , maka persamaan (4.4) dapat ditulis menjadi :

 

 

 

 

 

1 1 1 1 2 2 1 1 2 2 log log

log log ... log

... q p t i t i j t j i j t t q t q t t p t p h h g v h h h g v g v g v                                





(4.5) dengan      ₁  ...  _p .

Jika persamaan (4.3) disubstitusikan ke dalam persamaan (4.5), maka diperoleh

 

 













1 1 1 1 2 2 1 1 1 1 2 2 2 2 log log

log log ... log

... q p t i t i j t j i j t t q t q t t t t t t p t p t p t p h h g v h h h v E v v v E v v v E v v                                            





(4.6)

selanjutnya model di atas dinamakan model EGARCH(q,p).

Parameter-parameter model EGARCH pada persamaan (4.6) diestimasi dengan menggunakan maksimum likelihood dengan terlebih dahulu menentukan fungsi densitas dari v_t. Nelson (1991), memperkenalkan suatu fungsi densitas untuk v_t, berupa fungsi pembangkit untuk variabel random yang mempunyai fungsi distribusi berbentuk eksponensial, yang dikenal sebagai generalized error

distribution (GED), yaitu

 

 

1 2 1 exp , , 0 , 1 .2 v t t v t v v v f v v v v                              _{ }

dengan 

 

g adalah fungsi gamma,  adalah suatu konstanta yang mempunyai nilai 1 2 2 1 2 3 v v v  _       _{ }   _{ }  _{ }   _{ }   _{ }       

dan v adalah suatu parameter positif yang menunjukkan ‘ketebalan ekor’ dari

 

vt

f yaitu jika v2, maka v_t mempunyai distribusi normal standar; untuk v<2, maka distribusi dari v_t mempunyai ekor lebih tebal daripada distribusi normal (contoh ketika v1, maka v_t berdistribusi double exponential) dan untuk v2, distribusi v_t mempunyai ekor lebih tipis dari pada normal.

Harga harapan untuk nilai mutlak v_t menurut persamaan (2.1) adalah

 

 

 

 



 

 

 



1 2 1 1 2 1 0 1 2 1 0 exp .2 1 exp 2 .2 1 2 exp .2 1 t t t t v t t v t v v t t v t v v t t t v v E v v f v dv v v v dv v v v v dv v v v v dv v                _{ }                  _      _         _ _ 









 

 

1



2 1 0 2 exp .2 1 v t _v t t t v v E v v v dv v               _ _ 



(4.7)

untuk menyelesaikan persamaan (4.7), bentuk integrannya ditransformasi terlebih

dahulu supaya memenuhi bentuk fungsi gamma. Misalkan v x

v t _{ }       2 1 maka

1 1 2v v t v  x  dan 1 ₁ 1 ₁ 2v v t dv x dx v  

 . Jika disubstitusikan ke persamaan (4.7) menjadi  

 

  1 1 1 1 ₁ 1 ₀ 1 1 1 1 2 ₁ 1 ₀ 1 2 ₁ 0 1 1 2 2 exp 2 1 .2 2 2 2 exp[ ] 1 .2 2 exp[ ] 1 2 2 1 v v v v t v v v v v v v v v v v v E v x x x dx v v v x x x dx v x x dx v v v         _       _       _      _{ }      _{ }      _{ }    _{ }      _{ }







jika v_t berdistribusi normal standar, dalam hal ini v2, maka 1 dan 2 /

t

E v   , sehingga persamaan (4.6) menjadi

 



 







1 1 2 2 1 1

2 2 1 1 2 2

log log log ... log

... 2 2 ... 2 t t t q t q t t p t p t t p t p h h h h v v v v v v                                       dengan _i  _i

Model EGARCH dapat ditentukan dengan asumsi bahwa mean dari y_t

diberikan x_t yang merupakan kombinasi linier dari lag variabel endogenous dan eksogenous termasuk himpunan pengamatan hingga t1, _t₁, dengan  adalah





 



 







1 1 1 2 2 1 1 2 2 1 1 2 2 ,

log log log ... log

... 2 2 ... 2 t t t t t t t q t q t t p t p t t p t p t t t y N x h h h h h v v v v v v y x                                              : (4.8)

denga _t menyatakan vektor pengamatan yang diperoleh sampai waktu t



_{' ' ' ' '}



' 1 1 0 1 1 1 0 1 , ,..., , ,..., , , ,..., , ,..., t y yt t y y y m x xt t x x x m   _{     } , dan t t t v h   .

Karena _t dapat dinyatakan sebagai

' t yt xt     dan t t t v h   maka



t t, t 1



t Var y x  _ h dengan

 

1 1 1 2 2 1 1 1 2 2 1 2 1 2 2 2

log log log ... log

... 2 2 ... 2 t t t t q t q t t p t t p t t p t t p t p t t p h h h h h h h h h h                                                 _  _          _ _{ }  _              ' 1 1 1 1 2 2 1 1 ' ' ' 1 1 2 2 2 1 2 2 1 ' ' 2 2 2 2 2

log log ... log

... 2 2 ... 2 t t t t q t q t t t t p t p t t p t t t t t t p t p p t t y x h h h h y x y x y x h h h y x y x h h                                                      _{  }  _ _              _ _{ }  _              =_z_t



,h_t



_'

dengan 1 1 1 , ,..., , ,..., , ,...,_{q p p}  _{ }       _ dan





 

 

1 ' 1 1 ' ' 1 1 1 ' 1 log log , 2 2 t t q t t t t t t p t p t t t t t p t p t p h h y x h z h y x h y x h y x h   _                                               _{  }      _   _         _   _        M M M 4.2 Pendugaan Parameter

Fungsi kepadatan bersyarat bersama adalah perkalian dari semua kepadatan bersyarat, ditulis









1 1,2 2,..., 1 1 2 2 1 , ,..., ; ; T T T T T t t Y X Y X Y X t f y x y x y x  f y x  





. Oleh karena itu, fungsi log pada m pengamatan pertama merupakan penjumlahan dari log likelihood. Nelson (1991), menyusun persamaan log likelihood untuk model EGARCH sebagai

 













 

 





 

   





 

1 1 1 1 ' 1 1 1 log ,

log / 1 log 2 log 1/

1/ 2 log 1/ 2 T T t t t t T t T T _v t t t t t t T t L f y x v v v h y x h                     _ _    











l (4.9) dengan l

 

 log f y x



t t,t1



untuk v2, maka 1 dan persamaan (4.9) menjadi

 







 



 

   





2 ' 1 1 / 2 log 2 1/ 2 T log 1/ 2 T t t T t t t t y x L T h h         







dengan  



 ,



Untuk mendapatkan nilai ˆ yang maksimum, yaitu dengan cara menurunkan log likelihood, kemudian disamadengankan nol. Namun pada kenyataannya, secara analitik, sulit ditemukan penduga maksimum likelihood dari parameter , sehingga diperlukan metode penyelesaian numerik. Dalam hal ini digunakan metode optimasi, yaitu menggunakan algoritma skoring seperti dalam Hamilton (1994), yaitu  1   log  

 

ˆk ˆk ˆ k lk       _{   }   _

dengan ˆ_ dinamakan matriks informasi dan logl

 







 disebut sebagai vektor

skor.

4.3 Vektor Skor

Salah satu perangkat untuk menyusun algoritma skoring adalah vektor skor. Menurut Hamilton (1994), turunan dari fungsi log likelihood bersyarat dari t

fungsi log likelihood pada persamaan (4.9) mempunyai vektor skor

 









     

 





1 2 ' log , 1/ 2 log 2 1/ 2 log 1/ 2 t t t t t t t t S f y x y x h h            _      _   _   



 





 



2 2 ' ' 2 2 2 ' ' 1 log 1 1 2 2 1 log 1 1 log 2 2 t t t t t t t t t t t t t t t t y x y x h h h h y x y x h h h h            _{  }         _  _  _   _    _{  }         _  _  _   _   sedangkan



_'



2



_'



2 ' ' t t t t y x y x                









2 ' 2 ' ' ' 2 t t t t t t y x y x x      _{ }                _           0  dan 1 1 1 1 1 1 1 1 1 1 log ... log ... 2 ... 2 log log 2 t p t t q t q p t t p t p t p t t p t q p t j t j i t i j j i j t j t j h h h h h h h h h h                                         _{      }      _{ }         _{   }         _{   }   _         _ _        _  _  _{ }    





'           









 





3 1 1 max , 3 1 1 1 2 log 1 ' 2 ' log 1 , ' 2 ' t j t j q p t j t j t j t i i j j i j t j q p q p t j t j t i t t i i j j i i j x h h h h h h z h h                               _  _    _{  } _{ }               _{ }   _{  }         











0









 





1 1 max , 1 1 1 2 log log 1 ' 2 ' log log 1 , ' 2 ' t j t j q p t j t j t j t i i j j i j _{t j} q p q p t j t j t i t t i i j j i i j x h h h h h h z h h                               _  _    _{  } _{ }               _{ }   _{  }         











0 , untuk _{t j} 0 dan









 





1 1 max , 1 1 1 2 log log 1 ' 2 ' log log 1 , ' 2 ' t j t j q p t j t j t j t i i j j i j _{t j} q p q p t j t j t i t t i i j j i i j x h h h h h h z h h                      _         _  _    _{  } _{ }               _{ }   _{  }         











0 , untuk _{t j} 0 4.4 EGARCH (1,1)

Salah satu model EGARCH yang menarik untuk dikaji, karena menggambarkan pengaruh suatu berita/isu terhadap volatilitas, adalah model EGARCH(1,1), yaitu

 

 

1 1 1 1 1 log log t t 2 t t t t h h h h                          (4.10) dengan 0, 0  1,h_t 0, 0  1,  1 dan  0

parameter  menggambarkan besarnya ketaksimetrisan (leverage effect). Terutama, jika ingin mencari pengaruh isu terbaru/terkini terhadap volatilitas,

yaitu jika lag dari variansi bersyarat, h_t1, dievaluasi pada level tak bersyarat, _2_, maka

 

 

2 1 1 2 2 log log t t 2 , t h                   _  _  





1 .exp . , t t h A          _{ }   untuk t1 0, dan





1 .exp . , t t h A          _{ }   untuk t1 0, dengan 2 _{exp . 2} A  _  _

jika digambarkan secara grafik fungsi h_t terhadap _t1, dengan mengambil contoh untuk nilai parameter-parameter   , , dan  masing-masing adalah 0.05, 0.1, -0.1 dan 0.24, maka terlihat ketaksimetrisan grafik fungi h_t terhadap _t1 positif dan _t1 negatif - 2 -1 1 2 ¶t-1 1 2 3 4 ht

Gambar 4.1 Pengaruh isu terhadap volatilitas.

4.5 Matriks Informasi

Penyajian dari matriks informasi, ˆ_, menurut persamaan (2.10) adalah

 

2 1 ˆ ' T t E T            _{  }  



l 1 t _