A
Multi-Agent-Based Power System
Hybrid Dynamic
State Estimator
Ankush Sharma, Suresh Chandra Srivastava, and Saikat Chakrabarti, Indian Institute of Technology Kanpur
For fast estimation
of power system
state, a
multi-agent-based power system
hybrid dynamic state
estimator uses field
measurements from
remote terminal
units and phasor
measurement units.
supervisory control and data acquisition (SCADA) system. With the advent of phasor measurement units (PMUs), the measure-ment data reporting rate has increased up to 50 frames per second for 50-Hz systems and up to 60 frames per second for 60-Hz systems. But SSE execution takes approxi-mately 30 to 60 seconds for a large sys-tem, indicating the updated measurements received from RTUs and PMUs aren’t be-ing utilized, which means that SSE results lag behind actual system states. The devel-opment of dynamic state estimation (DSE) tools could solve state estimation problems, enabling available measurements to be uti-lized when estimating system states.
Despite the introduction of agent-based software engineering,2,3 few efforts have been
made to apply a multi-agent-based approach to solving the power system SSE problem.4,5
To our knowledge, nothing in the literature describes solving the power system dynamic state estimation (PSDSE) problem using multi-agent-based software engineering.
However, quite a few efforts have fo-cused on solving this problem by using Kalman filters. One approach6 used the
extended Kalman filter (EKF) to estimate power system states. The EKF uses first- order approximation of the Taylor series to solve the measurement function, causing its state estimation results to deviate from actual values, thereby rendering the EKF not quite suitable for dynamic state estima-tion of nonlinear systems such as the power system. Other researchers7–9 used the
un-scented Kalman filter (UKF) to estimate the power system state, but because the UKF’s performance deteriorates with the increase in the number of state variables,10 it also
isn’t suitable for estimating the state in large power systems. Recently, the cubature Kalman filter (CKF)10–12 has demonstrated
potential benefits, such as accuracy and sta-bility for the large state vector, over other Kalman filtering techniques.
The CKF approach was originally de-veloped to track aircraft trajectories.10
C
onventional power system state estimation (PSSE) is performed with the
help of static state estimation (SSE) tools such as the weighted least squares
(WLS) approach.
1These tools use the measurements received from
remote
terminal units (RTUs)—typically, at an interval of 1 to 5 seconds—through a
quire Taylor series approximation of the nonlinear function and the Jacobian during its execution, and unlike with the UKF, its performance doesn’t deteriorate with the increase in the size of the state variable vec-tor.10 We developed a software-based
multi-agent model to scan and pro-cess the PMU and the conventional RTU measurements separately; this model then combines the CKF results in every Kalman filter cycle to esti-mate system states. To speed up the CKF processing, we used a factor-ization approach that factorizes the large measurement vector into sub-vectors. The CKF is processed in par-allel using the subvectors to estimate the complete power system’s various states.
Power System Dynamic Model
We can represent a nonlinear dynam-ical power system for state estimation in a discrete form with the help of the following equations:
xk+1=f(xk) +wk (1) zk+1=h(xk+1) +vk+1 (2)
wk=N(0, Qk) (3)
vk+1=N(0, Rk+1), (4)
where, xk is the state vector at the kth instant; zk is the measurement vector at the kth instant; wk is Gaussian pro-cess noise with zero mean; Qk is the process noise error covariance; and
vkis the Gaussian measurement noise with zero mean. In addition, Rk is the measurement noise error covariance, and f(•): ℜn→ℜn and h(•): ℜn→ℜm are the nonlinear functions for a state space of size n and the measurement space of size m, respectively. For the
subvectors of voltage magnitude mea-surements (Vmk), voltage angle mea-surements (pmk), real power injection measurements (Prmk), reactive power injection measurements (Qrmk), real power flow measurements (PFmk), and reactive power flow measurements (QFmk), received from the RTUs and PMUs at the instant k, which are given by
xk= [Vk | pk]T (5)
zk= [Vmk | pmk | Prmk | Qrmk | PFmk | QFmk]T, (6)
where subscript m indicates the size of the corresponding measurement samples at the kth instant.
We use the state forecasting tool13 in
our proposed approach to model the state transition function. This function accommodates variations in state due to changes in system parameters, such as load variations from one time step to another time step. Our proposed approach uses Holt’s two- parameter linear exponential smoothing tech-nique13 to forecast states. Using this
technique, we can define the state transition function f(•) as
f(xk−1) =ak−1+bk−1 (7)
ak1=ααk 1xk 1+(1−ααk 1)xk 1
− − − − −
− (8)
bk−1=ak−1 (ak−1−ak−2) + (1 −ak−1)bk−2, (9)
where ak−1 and ak−1 are the
param-eters at instant k − 1, containing values between 0 and 1; xk−−1 is the
predicted state vector at the instant
k − 1; ak−1 and bk−1 are the vectors
de-fined by Equations 8 and 9 at instant
k − 1. To define the measurement function h(•) for the power system, we use standard bus power injection equations (real and reactive), and the
Under the Bayesian estimation ap-proach, using the known posterior probability density value at the k− 1th instant, the prior probability density at the next instant k− can be calcu-lated using the Chapman-Kolmogorov equation, given by10
p
p p d
x z
x x x z x
( | )
( | ) ( | )
k k
k k k k k
1: 1
1 1 1: 1 1
∫
=
−
− − − −
ℜ
(10)
p(xk−1 1:|z k−1)=N( ˆxk−1|k−1,Px,k−1|k−1), (11)
where N( ˆxk−1|k−1,Px,k−1|k−1) is the stan-dard normal distribution for the Gaussian density, with xˆk−1|k−1 as the estimated value (mean) and Px,k−1|k−1
as the covariance at k − 1th instant. We can calculate the value of the probability density p(xk | xk−1) by
us-ing Equation 1. The minus (−) and plus (+) signs in the superscript indi-cate the prior and posterior values, re-spectively. The CKF is implemented in two steps, as follows.10
Time Update
In the first step, we calculate the esti-mated value of the mean xˆk k| 1
− and the error covariance Px,k|k−1 of the states
by using Equations 1 and 10, which are given by
)p d
xˆk k| −1=
∫
f x( k−1 (xk−1 1:|z k−1) xk−1 ℜ(12)
∫
=
−
+−
− ℜ
− − − −
− − −
)
f x( )p dP
f x x z x
x x
( ( | )
ˆ ˆ ,
x
Q k k
k k k k k
k k k k k
, | 1
1 T 1 1 1: 1 1
| 1 T| 1 1
(13)
where p(xk−1 | z1:k−1) is the posterior
M U L T I - A G E N T S
Measurement Update
In the second step, we calculate the predicted measurement zˆk k|−1, its asso-ciated innovation covariance Pzz,k|k−1,
and the cross covariance Pxz,k|k−1 by
using the following equations:
)
p dWhen the new measurements are re-ceived, the estimated mean of the state and its associated error covariance are updated at the k+th instant by us-ing the standard Kalman filterus-ing ap-proach, given by
xˆk k|
=
xˆk k|−1+
Kk(zk−
zˆk k| −1) (17) Pk k| =Pk k| −1−K Pk zz, |k k−1KTk (18) Kk=Pxz,k k| 1Pzz1,k k| 1−
− −. (19)
To estimate the system states, the solution of the integral terms in Equa-tions 10 through 16 is approximated
by using the third-degree spherical-radical cubature rule,15 given as
N
where S is the error covariance ma-trix, m is the mean value, e is the unity matrix, and w is the weight. The {x, w} set forms the cubature points. The details for the CKF ap-pear elsewhere.10
Power System Hybrid Dynamic State Estimation
In the power system, RTU data is typically reported every 1 to 5 sec-onds, whereas PMU data is reported every 20 to 200 milliseconds for 50-Hz systems and 17 to 167 milli-seconds for the 60-Hz system. The role of the multi-agents in our pro-posed approach is to process these measurements separately in a col-laborative manner for PSHDSE and then integrate PSHDSE results to fi-nally estimate the overall power sys-tem’s states.
Multi-Agent System
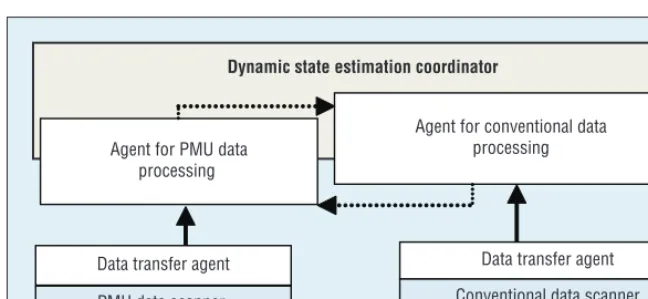
The multi-agent system comprises mul-tiple interacting autonomous agents that help manage the complex system by distributing the system execution tasks among themselves and sharing information interactively. The agents in the proposed system are intelligent software modules designed to scan and process RTU and PMU measurements in parallel, and then exchange the re-sults and status in a time-bound man-ner to coordinate final state estimates (see Figure 1).
The PMU (RTU) data scanner agent periodically checks the arrival of new data from the field PMUs (RTUs). The data transfer agent (DTA) does a sanity check on newly arrived data and acts as a first-level filter to identify and remove outli-ers from the measurement set. The other two agents—the PMU data processing agent (PDPA) and the conventional data processing agent (CDPA)—form part of the dynamic state estimation coordinator (DSEC) and play an important role in execut-ing our PSHDSE approach.
Specifically, the PDPA receives PMU data from the DTA at regu-lar intervals and runs the CKF. The CKF uses the latest available state es-timates and the latest available PMU measurements to execute its measure-ment update step. In our proposed approach, only the voltage magnitude and the angle measurements from the PMUs are considered for dynamic state estimation. This keeps the mea-surement equation for the CKF linear in nature, as given by
V e 0
0 is the zero subvector. It’s assumed that the measurements provided by various measurement devices are
Figure 1. Proposed multi-agent model for the power system hybrid dynamic state estimation (PSHDSE) formulation. The agents are intelligent software modules designed to scan and process remote terminal units (RTU) and phasor measurement units (PMU) in parallel, and then exchange the results and status in a time-bound manner to coordinate final state estimates.
Dynamic state estimation coordinator
Agent for PMU data processing
Agent for conventional data processing
PMU data scanner Data transfer agent
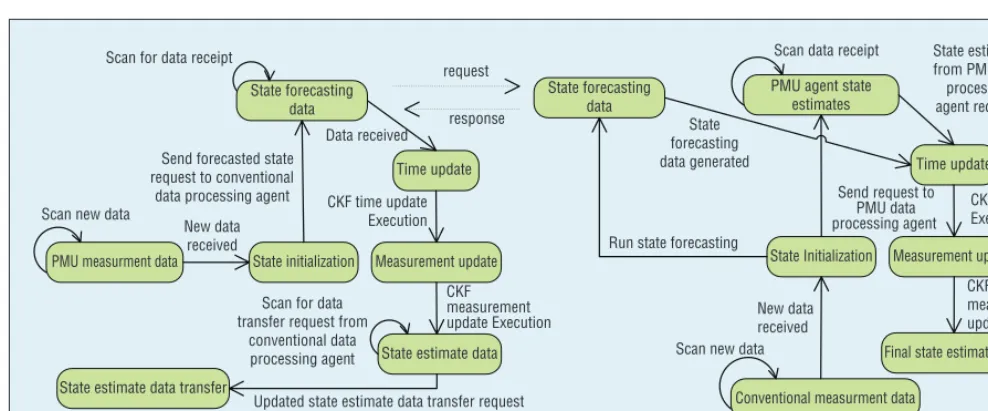
uncorrelated. Hence, Equation 22 can be divided into two independent equations for parallel and fast pro-cessing. Figure 2a shows the PDPA’s state transition diagram.
The CDPA execution process is divided into two parts. In the first, on arrival of the new RTU measure-ments, the CKF is executed to esti-mate overall system states, utilizing the latest RTU measurements and PDPA state estimates. In the second part, the CDPA forecasts the states by utilizing the previous state esti-mation results. The second part of the execution process repeats for two consecutive RTU measurement re-freshes—ultimately, the step is exe-cuted after receiving the request from the PDPA to provide the state fore-casting data. Figure 2b shows the CDPA’s state transition diagram.
Kalman Filtering Approach for PSHDSE
The existing CKF process10 is modified
in our work specifically for PSHDSE execution. In our proposed approach, to estimate the 2m − 1 states of an
m-bus power system using the CKF, 4m −2cubature points are required to
be evaluated per system state per iter-ation. For a bigger power system, due to the large size of the cubature point matrix (2m − 1 × 4m − 2), running the CKF without using a factoriza-tion approach is a time-consuming job. Hence, the state and measurement vec-tors are partitioned into subvecvec-tors, as in Equations 5 and 6, and the CKF is executed for the subvectors in parallel to save time. The CKF-based PSHDSE execution process assumes a flat start with initial voltage magnitudes and angles at all the power system’s buses assumed to be at 1 per unit (p.u.) and zero radians, respectively.
CDPA Time Update
The CDPA execution steps are as follows:
• Calculate the cubature points xi for the state vectors,
• Evaluate the cubature points at the instant k−, given as cubature point input. The field measurements and, hence their cu-bature points, are assumed to be uncorrelated. Therefore, utilizing the Cholesky factorization tech-nique, the square root of Pk−1|k−1 can
be divided into four independent submatrices, as shown in Equation 26. These submatrices are utilized by dividing the state equation into two independent equations contain-ing voltage magnitude (V) and the voltage angle (q) subvectors sepa-rately for fast processing, as shown in Equations 27 and 28:
x
Figure 2. State transition diagram: (a) the PMU data processing agent (PDPA) and (b) the conventional data processing agent (CDPA). CKF stands for cubature Kalman filter. The PDPA and the CDPA agents process the respective PMU and RTU measurements separately in various stages and regularly exchange the state forecasting data in a time-bound manner to coordinate the final state estimates.
Conventional measurment data State Initialization
Time update
Measurement update
Final state estimate data Scan new data
New data received Run state forecasting
data generated
CKF time update Execution
CKF measurement update execution Send request to
PMU data processing agent PMU measurment data State initialization
Time update
Measurement update
State estimate data Scan new data
New data received Send forecasted state request to conventional
data processing agent CKF time update Execution
Scan for data transfer request from
conventional data processing agent State estimate data transfer
CKF measurement update Execution
Updated state estimate data transfer request
M U L T I - A G E N T S
• Propagate the cubature points through the state function f(•), de-fined in Equations 7 through 9, against each state subvector j (V, q) state subvector are given by
)
• Calculate the estimated value of the state vector, given as
n
• Calculate the predicted state error covariance, given as
∑
On getting the state forecasting re-quest from the PDPA, the state vector and the state error covariance esti-mated in this step are sent to the PD-PA’s measurement update step.
PDPA Measurement Update The PDPA execution steps are as follows:
• Evaluate the cubature points utiliz-ing the updated state estimates, the state error covariance values pro-vided by the time update step, and the cubature points calculated in Equation 23 as
x P xˆ
ture point vector for the ith cuba-ture point input, and the superscript
P indicates the evaluated cubature point vector under the PDPA mea-surement update step. The cubature points in Equation 33 are evalu-ated by dividing the equation into subvectors, in the same manner as Equations 25 through 28.
• Propagate the cubature points through the measurement function against each measurement subvec-tor l (Vm, pm) at instant k−,
cubature point subvector for the ith cubature point input, and the lth measurement subvector hlP is the PDPA measurement function, as defined in Equation 22.
• Calculate the estimated value of the measurement vector at the k−th
• Calculate the estimated value of the innovation covariance,
• Calculate the estimated value of the cross covariance,
On arrival of fresh PMU measure-ments, the estimated state value and its associated error covariance are updated using Equations 17 through 19 at the k+th instant. These updated values are then sent to the PDPA time update step for further processing.
PDPA Time Update
The PDPA time update step is exe-cuted by using Equations 23 through 32 and the results of the PDPA mea-surement update step. The time and measurement update steps are ex-ecuted sequentially for every PMU measurement set received between two consecutive RTU measurements. The execution of the proposed PDPA time and measurement update steps is fast enough so that one cycle of the pro-cess completes before the arrival of the next PMU measurement set. On the arrival of the next RTU measurement or upon receiving a request from the CDPA, the updated state and the state error covariance values are sent to the CDPA measurement update step.
CDPA Measurement Update The CDPA execution steps are as follows:
• Evaluate the cubature points using the same process as followed in the PDPA measurement update step.
• Propagate the cubature points through the measurement function against each measurement subvector
l, as defined in Equation 6, at instant
k−. The propagated cubature points are given by
)
CDPA measurement subvector, and
hCl is the CDPA measurement func-tion14 against the lth measurement
subvector. The superscript C indi-cates the values corresponding to the CDPA measurement update step. The propagated cubature point sub-vector against the respective mea-surement subvector can be processed individually because all the measure-ments and their cubature points are assumed to be uncorrelated.
• Calculate the estimated value of the measurement vector,
• Calculate the estimated value of the innovation covariance,
• Calculate the estimated value of the cross covariance,
On arrival of the fresh RTU mea-surement set, the estimated state and its associated error covariance are updated again using Equations 17 through 19 at the k+th instant. After this step, one cycle of the PSHDSE
execution completes, utilizing the available PMU and RTU measure-ments. Executing the proposed PSHDSE is fast enough that the whole process completes before the arrival of the next RTU measurement set.
To compare EKF- and UKF-based methods with the CKF, we used a similar procedure, except the time and measurement update equations were utilized corresponding to the implemented KF. Details about the EKF6 and UKF7,8 time and
measure-ment update equations are well estab-lished in the literature.
Simulation Results
The methodology proposed in this work has been demonstrated on the 30-bus IEEE system16 and the
246-bus Indian Northern Regional Power Grid (NRPG; http://docslide.us/doc-uments/nrpg-datapdf.html). We de-veloped a Matlab-, Simulink-, and SimEvents-based application (www. mathworks. in/products/simevents), including software agents, to test and verify our proposed CKF-based PSHDSE approach. For compari-son, we also executed the EKF- and UKF-based PSHDSE approaches on the 30-bus IEEE and 246-bus NRPG systems. The actual values of the sys-tem states at various time instants are obtained by running the load flow repeatedly for the various operating conditions by varying the loads
ran-domly between ±5 percent and ±30 percent. Using different standard deviation quantities for the various types of measurements, the Gaussian noise is added into the actual values of the load-flow results to generate the RTU and PMU measurement sets.
Because we tested the PSHDSE methodology using simulated measure-ment data, data scanner modules aren’t implemented in the present approach. For the PSHDSE execution, we as-sume that RTU measurements refresh every one second and PMU measure-ments refresh every 40 milliseconds. The simulations are carried out on an Intel Core-i7 3.4-GHz processor-based computer with 4 Gbytes RAM.
30-Bus IEEE System
The PSHDSE was implemented on the 30-bus IEEE system using the RTU measurement sets for 100 sim-ulation time-steps under various loading conditions. Between the two consecutive RTU measurement simu-lation steps, 25 simusimu-lation time-steps for the PMU measurements were also processed.
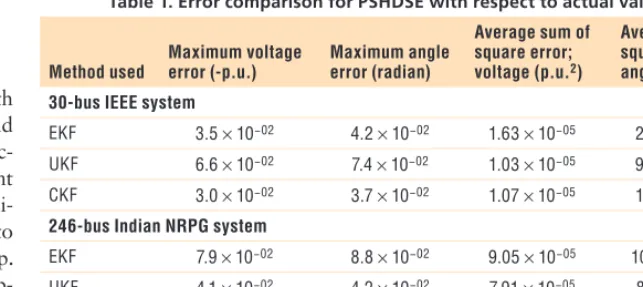
For the 30-bus IEEE system, the PMUs are considered at buses 6, 9, and 12. The values of a and b, used in the load-forecasting process, are estimated as 0.778 and 0.52, respec-tively, using 200 Monte Carlo (MC) simulations. Table 1 compares the es-timation errors of the CKF-, UKF-,
30-bus IEEE system
EKF 3.5 × 10−02 4.2 × 10−02 1.63 × 10−05 2.41 × 10−05
UKF 6.6 × 10−02 7.4 × 10−02 1.03 × 10−05 9.40 × 10−05
CKF 3.0 × 10−02 3.7 × 10−02 1.07 × 10−05 1.09 × 10−05
246-bus Indian NRPG system
EKF 7.9 × 10−02 8.8 × 10−02 9.05 × 10−05 10.24 × 10−05
UKF 4.1 × 10−02 4.2 × 10−02 7.91 × 10−05 8.14 × 10−05
CKF 2.3 × 10−02 2.8 × 10−02 7.20 × 10−05 6.08 × 10−05
M U L T I - A G E N T S
and EKF-based state estimation re-sults, as compared to the actual val-ues of the states for the 30-bus IEEE system. From Table 1, we can see that PSHDSE using the CKF is more accu-rate compared to that with the EKF and the UKF.
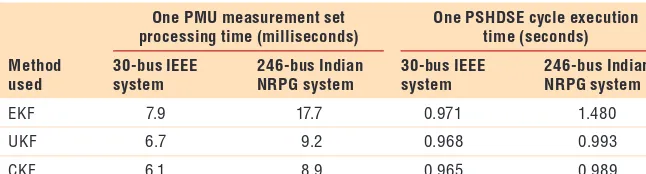
Table 2 compares the execution time in processing one PMU measure-ment set and one cycle of PSHDSE execution using the CKF, UKF, and EKF approaches for the 30-bus IEEE system. From the table, we can con-clude that the three KF approaches will finish processing one PMU mea-surement set well before the arrival of the next set. Furthermore, the execu-tion of one PSHDSE cycle completes before the arrival of the next RTU measurement set. Out of the three KF approaches, the CKF is the fastest: its cubature points and weights are
independent of the nonlinear mea-surement function, hence they can be calculated and stored offline.
246-Bus Indian NRPG System Similar to the 30-bus IEEE system, the 246-bus Indian NRPG system also processed two consecutive RTU measurement simulation time steps and 25 PMU measurement simula-tion time steps. For the 246-bus In-dian NRPG system, the PMUs are considered at 30 buses.
Similar to the previous case, the values of a and b, used for state fore-casting, are estimated as 0.83 and 0.64, respectively, via 200 MC sim-ulations. Table 1 compares the EKF, UKF, and CKF PSHDSE results with actual values; similar to the 30-bus IEEE system, PSHDSE using the CKF is the most accurate.
Table 2 compares the execution time for processing one PMU mea-surement set and one cycle of the PSHDSE execution using the CKF, UKF, and EKF approaches for the 246-bus NRPG system. In comparing the execution of one cycle, we can see that the EKF-based PSHDSE doesn’t complete its execution before the ar-rival of the next RTU measurement set—this is because the EKF needs an extra step to compute the derivatives of the measurement functions while processing the KF. The UKF and CKF approaches execute one PSHDSE cy-cle within a second. Because it’s the fastest of the three KF approaches, the CKF is a better choice for multi-agent-based PSHDSE.
T
he proposed method is generic and can be applied to larger power system networks. Hence, it could be adopted in various control centers to gain the faster situational awareness required in smart grid im-plementations. The proposed method can also be extended to estimate the dynamic states of the power system network under certain disturbances, such as power swing and voltage col-lapse.Acknowledgments
The Department of Science and Technology, New Delhi, India, provided partial financial support under project DST/EE/20100258.
References
1. F.C. Schweppe and J. Wildes, “Power System Static State Estimation, Part I: Exact Model,” IEEE Trans. Power Ap-paratus and System, vol. PAS-89, no. 1, 1970, pp. 120–125.
2. M. Wooldridge, “Agent-Based Software Engineering,” IEE Proc. Software Eng., vol. 144, no. 1, 1997, pp. 26–37. 3. N.R. Jennings, “On Agent-Based
Software Engineering,” Artificial
Table 2. Execution time comparison for PSHDSE with respect to actual values.
Method used
One PMU measurement set processing time (milliseconds)
One PSHDSE cycle execution time (seconds) 30-bus IEEE
system
246-bus Indian NRPG system
30-bus IEEE system
246-bus Indian NRPG system
EKF 7.9 17.7 0.971 1.480
UKF 6.7 9.2 0.968 0.993
CKF 6.1 8.9 0.965 0.989
T H E A U T H O R S
Ankush Sharma is currently working in the Power System Centre of Excellence (CoE) di-vision of Tata Consultancy Services (TCS), Pune, India. His research interests are state estimation, power system deregulation, smart grid technology, and IT applications in power system. Sharma has a PhD in electrical engineering from the Indian Institute of Technology Kanpur, India. Contact him at [email protected].
Suresh Chandra Srivastava is a professor in the Department of Electrical Engineering at the Indian Institute of Technology Kanpur. His research interests include energy manage-ment systems, synchrophasor applications, power system security, stability, and techni-cal issues in electricity markets. Srivastava has a PhD in electritechni-cal engineering from the Indian Institute of Technology Delhi, India. He’s a fellow of Indian National Academy of Engineering (INAE) India, Institution of Engineers (IE) India, and the Institution of Elec-tronics and Telecommunication Engineers (IETE) India and a senior member of IEEE. Contact him at [email protected].
tion for Electrical Distribution Net-works,” IEEE Trans. Power Systems, vol. 20, no. 2, 2005, pp. 652–658. 5. P.H. Nguyen and W.L. Kling,
“Distrib-uted State Estimation for Multi-Agent Based Active Distribution Networks,”
IEEE Power and Energy Soc. General Meeting, 2010, pp. 1–7.
6. J.K. Mandal, A.K. Sinha, and L. Roy, “Incorporating Nonlinearities of Measurement Function in Power System Dynamic State Estimation,” IEE Gen-eration, Transmission & Distribution, vol. 142, no. 3, 1995, pp. 289–296. 7. G. Valverde and V. Terzija, “Unscented
Kalman Filter for Power System Dy-namic State Estimation,” IET Genera-tion, Transmission & Distribution, vol. 5, no. 1, 2011, pp. 29–37.
form,” IEEE Trans. Power Systems, vol. 27, no. 2, 2012, pp. 942–950. 9. G. Valverde et al., “A Constrained
For-mulation for Hybrid State Estimation,”
IEEE Trans. Power Systems, vol. 26, no. 3, 2011, pp. 1102–1109.
10. I. Arasaratnam and S. Haykin, “Cu-bature Kalman Filters,” IEEE Trans. Automatic Control, vol. 54, no. 6, 2009, pp. 1254–1269.
11. B. Jia, M. Xin, and Y. Cheng, “High-De-gree Cubature Kalman Filter,” Automat-ica, vol. 49, no. 2, 2013, pp. 510–518. 12. I. Arasaratnam, S. Haykin, and T.R. Hurd, “Cubature Kalman Filtering for Continuous-Discrete Systems: Theory and Simulations,” IEEE Trans. Signal Processing, vol. 58, no. 10, 2010, pp. 4977–4993.
DistributionC, vol. 130, no. 5, 1983, pp. 237–244.
14. A. Abur and A.G. Exposito, Power System State Estimation: Theory and Implementation, Mercel Dekker, 2004, ch. 2, pp. 9–36.
15. A.H. Stroud, Approximate Calculation of Multiple Integrals, Prentice Hall, 1971.
16. S. Chakrabarti, and E. Kyriakides, “Op-timal Placement of Phasor Measurement Units for Power System Observability,”
IEEE Trans. Power Systems, vol. 23, no. 3, 2008, pp. 1433–1440.
Selected CS articles and columns are also available for free at http://ComputingNow.computer.org.
PURPOSE: The IEEE Computer Society is the world’s largest association of computing professionals and is the leading provider of technical information in the field.
MEMBERSHIP: Members receive the monthly magazine Computer, discounts, and opportunities to serve (all activities are led by volunteer members). Membership is open to all IEEE members, affiliate society members, and others interested in the computer field.
COMPUTER SOCIETY WEBSITE: www.computer.org
Next Board Meeting: 1–5 June 2015, Atlanta, GA, USA
EXECUTIVE COMMITTEE
President: Thomas M. Conte
President-Elect: Roger U. Fujii; Past President: Dejan S. Milojicic; Secretary: Cecilia Metra;
Treasurer, 2nd VP: David S. Ebert; 1st VP, Member & Geographic Activities: Elizabeth L. Burd; VP, Publications: Jean-Luc Gaudiot; VP, Professional & Educational Activities:
Charlene (Chuck) Walrad; VP, Standards Activities: Don Wright; VP, Technical & Conference Activities: Phillip A. Laplante; 2015–2016 IEEE Director & Delegate Division VIII: John W. Walz; 2014–2015 IEEE Director & Delegate Division V: Susan K. (Kathy) Land; 2015 IEEE Director-Elect & Delegate Division V: Harold Javid
BOARD OF GOVERNORS
Term Expiring 2015: Ann DeMarle, Cecilia Metra, Nita Patel, Diomidis Spinellis, Phillip A. Laplante, Jean-Luc Gaudiot, Stefano Zanero
Term Expriring 2016: David A. Bader, Pierre Bourque, Dennis J. Frailey, Jill I. Gostin, Atsuhiro Goto, Rob Reilly, Christina M. Schober
Term Expiring 2017: David Lomet, Ming C. Lin, Gregory T. Byrd, Alfredo Benso, Forrest Shull, Fabrizio Lombardi, Hausi A. Muller
EXECUTIVE STAFF
Executive Director: Angela R. Burgess; Director, Governance & Associate Executive Director: Anne Marie Kelly; Director, Finance & Accounting: John G. Miller; Director, Information Technology Services: Ray Kahn; Director, Membership: Eric Berkowitz;
Director, Products & Services: Evan M. Butterfield; Director, Sales & Marketing: Chris Jensen
COMPUTER SOCIETY OFFICES
Washington, D.C.: 2001 L St., Ste. 700, Washington, D.C. 20036-4928
Phone: +1 202 371 0101 • Fax: +1 202 728 9614 • Email: [email protected] Los Alamitos: 10662 Los Vaqueros Circle, Los Alamitos, CA 90720
Phone: +1 714 821 8380 • Email: [email protected]
MEMBERSHIP & PUBLICATION ORDERS
Phone: +1 800 272 6657 • Fax: +1 714 821 4641 • Email: [email protected] Asia/Pacific: Watanabe Building, 1-4-2 Minami-Aoyama, Minato-ku, Tokyo 107-0062,
Japan • Phone: +81 3 3408 3118 • Fax: +81 3 3408 3553 • Email: [email protected]
IEEE BOARD OF DIRECTORS
President & CEO: Howard E. Michel; President-Elect: Barry L. Shoop; Past President: J. Roberto de Marca; Director & Secretary: Parviz Famouri; Director & Treasurer:
Jerry Hudgins; Director & President, IEEE-USA: James A. Jefferies; Director & President, Standards Association: Bruce P. Kraemer; Director & VP, Educational Activities: Saurabh Sinha; Director & VP, Membership and Geographic Activities: Wai-Choong Wong;
Director & VP, Publication Services and Products: Sheila Hemami; Director & VP, Technical Activities: Vincenzo Piuri; Director & Delegate Division V: Susan K. (Kathy) Land; Director & Delegate Division VIII: John W. Walz