Pertemuan 1 Sistem Bilangan Real dan Fungsi 1.1 Pendahuluan - 1 Sistem Bilangan Real dan Fungsi

(1)

Pertemuan 1

Sistem Bilangan Real dan Fungsi

1.1Pendahuluan

Pada pertemuan pertama ini, kita akan membahas konsep-konsep dasar yang perlu

diketahui untuk mempelajari Kalkulus. Beberapa materi yang dibahas, antara lain: sistem

bilangan real, fungsi, dan trigonometri.

1.2Sistem Bilangan Real

Pada subbab ini, kita akan membahas tentang bilangan real, interval, dan nilai

absolut.

1.2.1 Bilangan real

Banyak contoh kasus dalam Kalkulus didasarkan ada sistem bilangan real. Bilangan

real adalah bilangan yang dapat dinyatakan sebagai desimal, seperti:

⁄ ⁄ √

Tanda memperlihatkan bahwa barisan digit desimal terus berlanjut, seterusnya.

Sistem bilangan real adalah sistem bilangan yang terdiri atas bilangan-bilangan real,

dan dinotasikan sebagai . Sifat-sifat sistem bilangan real dapat dibedakan dalam tiga

kategori, yakni sifat aljabar, sifat urutan, dan completeness.

Sifat aljabar menyatakan bahwa sistem bilangan real dapat ditambah, dikurang,

dikali, dan dibagi (kecuali oleh 0) untuk menghasilkan lebih banyak bilangan real.

Sifat urutan dari bilangan real memungkinkan kita untuk membandingkan nilai dari

dua bilangan real. Berikut beberapa contoh aturan yang dapat diturunkan berdasarkan sifat

(2)

Secara geometri, kita juga dapat membayangkan bilangan-bilangan real dengan

menaruhnya dalam satu garis lurus. Sifat completeness menyatakan bahwa terdapat cukup

bilangan real untuk mengisi seluruh garis bilangan real, tanpa lubang atau jarak sama sekali.

Banyak teorema Kalkulus yang gagal jika sistem bilangan real-nya tidak complete.

Terdapat beberapa himpunan bagian bilangan real, seperti bilangan asli, bilangan

bulat, dan bilangan rasional/ pecahan. Bilangan rasional lebih tepatnya adalah bilangan real

dimana bentuk desimalnya, berhenti ( ) atau berulang (

̅̅̅̅). Bilangan real yang tidak berbentuk rasional disebut bilangan irasional. Contohnya

seperti: √ .

Suatu himpunan adalah kumpulan obyek-obyek yang disebut sebagai elemen dari

himpunan tersebut. Jika merupakan suatu himpunan, notasi menyatakan bahwa

merupakan anggota himpunan , dan menyatakan bukan anggota himpunan .

Jika dan adalah himpunan, maka menyatakan gabungan kedua himpunan tersebut

dan menyatakan irisan kedua himpunan tersebut. Himpunan kosong adalah

himpunan yang tidak memiliki anggota sama sekali, dan dinotasikan sebagai .

1.2.2 Interval

Himpunan bagian dari garis bilangan disebut suatu interval jika terdiri atas minimal

dua bilangan dan mengandung seluruh bilangan real diantara dua elemennya. Sebagai

contoh, himpunan bilangan real sehingga merupakan suatu interval, demikian

pula himpunan seluruh sedemikian sehingga . Namun himpunan seluruh

bilangan real tak nol bukan merupakan suatu interval karena 0 tidak ada, sehingga

(3)

Gambar 1.1 Jenis-jenis interval

(Thomas’s Calculus, 11th

ed, p.4)

Contoh 1.1 Ketidaksamaan

Selesaikan ketidaksamaan berikut dan tentukan himpunan solusinya.

a.

b.

Jawaban

a.

kurangkan kedua sisi dengan 3

kurangkan kedua sisi dengan

bagi kedua sisi dengan

Himpunan solusinya adalah interval terbuka ( ).

b.

kali kedua sisi dengan 2

tambahkan kedua sisi dengan

kurangkan kedua sisi dengan

bagi kedua sisi dengan 5

(4)

1.2.3 Nilai absolut

Nilai absolut dari suatu bilangan , dinotasikan dengan | | dan didefinisikan sebagai

| | {

Selesaikan persamaan dan ketidaksamaan yang melibatkan nilai absolut berikut.

(5)

Solusi dari | | adalah dan .

b. | | berdasar sifat 6

kurangkan dengan

kali dengan

kali silang

Solusi dari | | adalah interval terbuka ( ).

1.3Garis, Lingkaran, dan Parabola

Pada subbab ini akan dibahas tentang koordinat, garis, jarak, lingkaran, dan parabola

dalam suatu bidang.

1.3.1 Koordinat Kartesius

Gambar 1.2 Koordinat Kartesius

(Thomas’s Calculus, 11th ed)

Sistem koordinat Kartesius didasarkan pada nama matematikawan abad 16 yakni

Rene Descartes. Sistem koordinat ini terdiri atas dua garis yang saling tegak lurus yang

disebut sumbu koordinat. Titik merupakan pasangan koordinat dan terletak di pasangan

berurutan ( ). Bilangan pertama adalah koordinat- (atau absis) dari , sementara

(6)

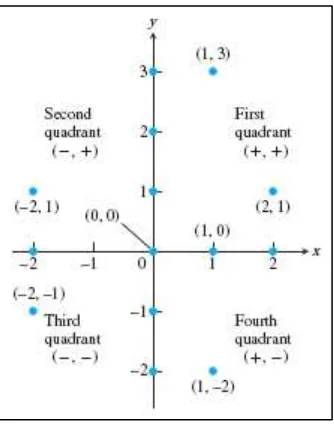
Sumbu koordinat Kartesius membagi bidang menjadi empat daerah atau kuadran,

yang dinomori berlawanan arah jarum jam.

Gambar 1.3 Kuadran dalam koordinat Kartesius

(Thomas’s Calculus, 11th ed)

1.3.2 Increment dan garis lurus

Saat suatu partikel bergerak dari satu titik ke titik lainnya dalam bidang, terjadi

perubahan nilai koordinatnya yang disebut increment. Jika berubah dari ke , increment dari adalah

.

Contoh 1.3 Increment

Tentukan increment dalam koordinat dan dari titik ( ) ke titik ( )!

Jawaban

, ( ) .

Diberikan dua titik ( ) dan ( ) dalam bidang koordinat. Sembarang

garis tidak vertikal dalam bidang memiliki sifat perbandingan berikut:

(7)

disebut sebagai kemiringan (slope) dari garis tidak vertikal . Sebuah garis dengan

slope positif naik ke kanan, garis dengan slope negatif turun ke kanan. Semakin besar nilai absolut dari slope, makin terjal kenaikan atau penurunannya. Slope untuk garis vertikal tidak

terdefinisikan, karena untuk garis vertikal adalah 0.

Kita dapat menentukan persamaan garis lurus yang melalui titik ( ) dan

(8)

Contoh 1.5 Menemukan slope dan -intercept

Garis yang saling paralel memiliki sudut kemiringan yang sama, sehingga memiliki

(9)

Jawaban

eksterior lingkaran terdiri atas titik-titik ( ) yang memenuhi

( ) ( )

terdiri atas seluruh kemungkinan nilai masukan disebut domain fungsi. Himpunan seluruh nilai dari ( ) dimana disebut range dari fungsi. Range fungsi bisa saja tidak mencakup seluruh elemen dalam himpunan . Dalam Kalkulus, persamaan fungsi kerap

(10)

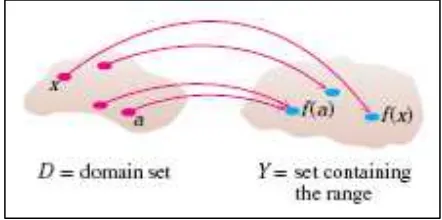
Sebuah fungsi juga dapat digambarkan sebagai suatu diagram panah. Setiap anak

panah menghubungkan suatu elemen dari domain ke elemen tunggal di himpunan .

Gambar 1.4 Sebuah fungsi dari himpunan ke himpunan

ed, p.20)

Cara lain untuk menggambarkan fungsi adalah melalui grafiknya. Jika adalah suatu

fungsi dengan domain , grafiknya terdiri atas titik-titik dalam bidang Kartesius yang koordinatnya merupakan pasangan input-output dari . Dalam notasi himpunan, grafiknya adalah

{( ( ))| }

Contoh 1.8 Grafik fungsi

Grafik dari suatu populasi lalat buah diperlihatkan dalam gambar berikut.

a. Temukan populasinya setelah 20 dan 30 hari.

b. Berapakah perkiraan range fungsi populasi tersebut terhadap interval waktu

?

Gambar 1.5 Grafik fungsi populasi lalat buah terhadap waktu

(11)

Jawaban

a. Dari gambar 1.5 di atas, dapat dilihat bahwa nilai populasi pada 20 hari adalah

( ) . Demikian pula, ( ) kira-kira sekitar 260.

b. Range dari fungsi populasi terhadap kira-kira adalah [ ]. Dapat dilihat pula bahwa populasinya makin mendekati nilai saat waktunya

bertambah besar.

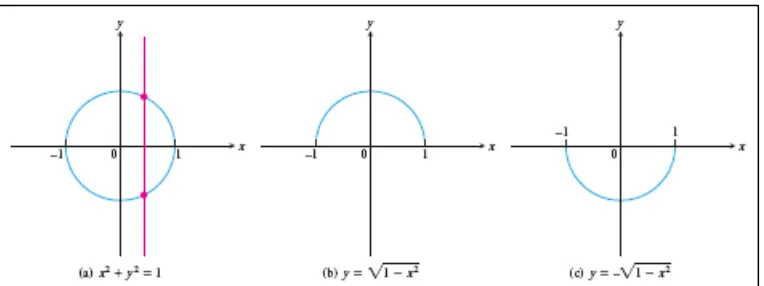
Tidak semua kurva grafik merupakan sebuah fungsi. Sebuah fungsi hanya dapat

memiliki satu nilai ( ) untuk setiap dalam domainnya, sehingga tidak ada garis vertikal

yang dapat menyinggung grafik sebuah fungsi lebih dari satu kali.

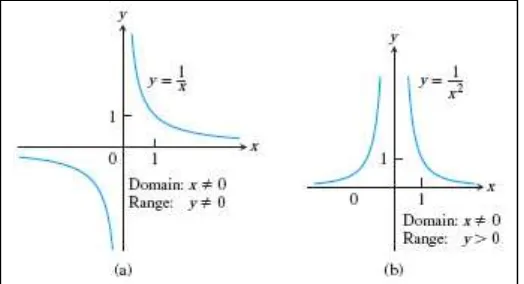
Gambar 1.6 Grafik lingkaran (a) bukan fungsi, grafik (b) dan (c) merupakan fungsi

ed, p.24)

Terkadang suatu fungsi dideskripsikan dengan menggunakan beberapa rumus

berbeda pada bagian berbeda domainnya. Misalnya fungsi nilai absolut,

| | {

Fungsi seperti demikian disebut sebagai fungsi piecewise.

1.5Identifikasi Fungsi

Terdapat beberapa jenis fungsi yang kerap dijumpai dalam Kalkulus, seperti fungsi

linear, fungsi pangkat, polinomial, fungsi rasional, fungsi aljabar, fungsi trigonometri, fungsi

eksponensial, fungsi logaritma, fungsi transcendental.

(12)

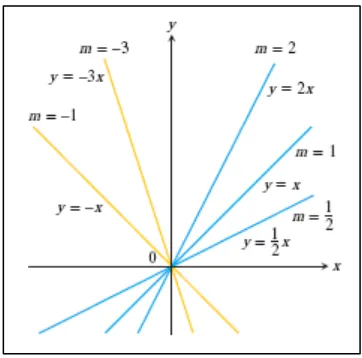
Suatu fungsi dengan bentuk ( ) , untuk konstanta dan , disebut sebagai

fungsi linear.

Gambar 1.7 Kumpulan garis memiliki slope dan seluruh garis melalui titik pusat

(Thomas’s Calculus, 11th ed, p.28)

Fungsi pangkat (power)

Sebuah fungsi ( ) , dimana suatu konstanta, disebut sebagai fungsi pangkat.

Terdapat beberapa kasus yang perlu diperhatikan.

a. , bilangan bulat positif

Gambar 1.8 Grafik dari ( ) , untuk

ed, p.29)

(13)

Gambar 1.9 Grafik dari ( ) , untuk (a) , dan (b)

ed, p.29)

c. a

Gambar 1.10 Grafik dari ( ) , untuk a

ed, p.30)

Polinomial

Sebuah fungsi disebut sebagai polinomial jika

(14)

dimana adalah bilangan bulat nonnegative dan bilangan merupakan konstanta real (disebut koefisien polinomial). Semua polinomial memiliki domain ( ). Jika koefisien pertama dan , maka disebut sebagai derajat polinomial.

Gambar 1.11 Contoh grafik polinomial

(Thomas’s Calculus, 11th ed, p.30)

Fungsi rasional

Fungsi rasional merupakan pecahan atau rasio dari dua polinomial

( ) ( )_{( )}

(15)

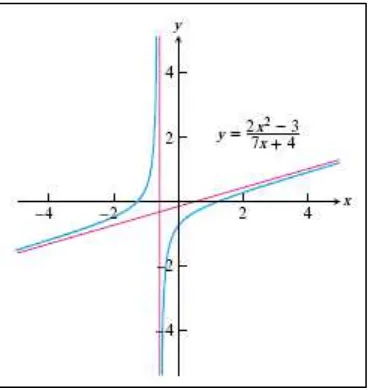
Gambar 1.12 Contoh grafik fungsi rasional

ed, p.31)

Fungsi aljabar

Fungsi aljabar merupakan sebuah fungsi yang dibangun dari polinomial-polinomial dengan

menggunakan operasi aljabar (tambah, kurang, kali, bagi, dan akar). Fungsi rasional

merupakan contoh khusus dari fungsi aljabar.

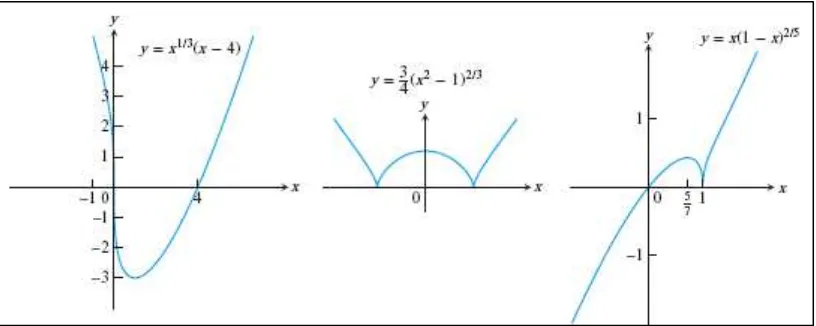
Gambar 1.13 Contoh grafik fungsi aljabar

ed, p.32)

Fungsi trigonometri

Fungsi trigonometri akan dibahas lebih lanjut di akhir bab ini.

Fungsi eksponensial

Fungsi dengan bentuk ( ) , dimana dan disebut sebagai fungsi

(16)

Gambar 1.14 Contoh grafik fungsi eksponensial

ed, p.32)

Fungsi logaritma

Fungsi dengan bentuk ( ) , dimana dan merupakan konstanta positif,

disebut sebagai fungsi logaritma. Fungsi ini merupakan invers dari fungsi eksponensial,

dimana domain fungsi adalah ( ) dan range adalah ( ).

Gambar 1.15 Contoh grafik fungsi logaritma

ed, p.33)

Fungsi transcendental

Fungsi ini merupakan fungsi yang tidak termasuk fungsi aljabar, seperti trigonometri, invers

trigonometri, eksponensial, logaritma, dan fungsi-fungsi lainnya.

1.6Operasi Fungsi

Seperti halnya bilangan, fungsi juga memiliki operasi-operasi, seperti penjumlahan,

(17)

fungsi baru. Jika dan merupakan fungsi, maka untuk setiap yang berada dalam domain

dan (yakni, ( ) ( )), maka

( )( ) ( ) ( )

Untuk sembarang nilai di ( ) ( ) dimana ( ) , dapat didefinisikan fungsi

(₎( ) ( )_{( )}

Fungsi juga dapat dikalikan dengan konstanta. Jika suatu bilangan real, maka fungsi

didefinisikan untuk seluruh dalam domain fungsi dengan

( )( ) ( )

Contoh 1.9 Operasi fungsi

Fungsi yang didefinisikan oleh rumus

( ) √ dan ( ) √

memiliki domain ( ) [ ) dan ( ) ( ]. Titik-titik yang berada dalam domain ini adalah titik-titik

[ ) ( ] [ ]

Operasi fungsi yang dapat berlaku untuk kedua fungsi di atas:

( )( ) √ √ domain [ ]

( )( ) ( ) ( ) √ ( ) domain [ ]

(18)

( ) ( )_{( )} √ _√ √ domain ( ].

Pada subbab ini akan dibahas dasar-dasar fungsi trigonometri. Fungsi trigonometri

penting karena sifatnya yang berulang dan dapat memodelkan banyak proses alami yang

berulang.

1.7.1 Ukuran radian

Ukuran radian dari sudut di titik pusat sebuah lingkaran sama dengan panjang

busur yang dipotong oleh dari lingkaran tersebut. Gambar berikut memperlihatkan

bahwa merupakan panjang busur yang dipotong dari sebuah lingkaran dengan

(19)

Gambar 1.16 Ukuran radian dari sudut adalah panjang dari busur pada lingkaran

dengan pusat di

ed, p.48)

Rumus konversi dari derajat ke radian:

1.7.2 Trigonometri

Gambar 1.17 Rasio trigonometri

ed, p.50)

Enam fungsi trigonometri dasar, antara lain sebagai berikut.

(20)

Gambar berikut memperlihatkan beberapa nilai fungsi trigonometri.

Gambar 1.18 Nilai untuk nilai tertentu

ed, p.51)

Gambar 1.19 Aturan CAST

ed, p.51)

1.7.3 Fungsi periodik, identitas, dan hukum Cosinus

Sebuah fungsi dikatakan periodik jika terdapat bilangan positif sedemikian

sehingga ( ) ( ) untuk setiap nilai dari . Nilai terkecil dari adalah periode dari

.

Gambar 1.20 Segitiga siku-siku

(21)

Koordinat suatu titik ( ) dalam sebuah bidang dapat dinyatakan sebagai jarak

dari titik pusat dan sudut yang dibentuk ruas garis dengan sumbu- positif. Karena

dan , maka

Bila , dengan menerapkan teorema Pythagoras diperoleh persamaan

Dengan membagi persamaan di atas, baik terhadap maupun ,

diperoleh

Rumus berikut juga berlaku untuk seluruh besar sudut dan .

( )

Gambar 1.21 Kuadrat dari jarak antara dan menghasilkan hukum cosinus

ed, p.54)

Jika dan adalah sisi-sisi segitiga dan adalah sudut lawan dari , maka

Persamaan di atas dikenal sebagai hukum Cosinus. Hukum ini memperumum teorema