SKRIPSI
SAFRINA
111402027
PROGRAM STUDI S1 TEKNOLOGI INFORMASI
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat memperoleh ijazah
Sarjana Teknologi Informasi
SAFRINA
111402027
PROGRAM STUDI S1 TEKNOLOGI INFORMASI
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : OPTIMALISASI PENYUSUNAN BARANG PADA
MOBIL BOX MENGGUNAKAN ALGORITMA FIREFLY
Kategori : SKRIPSI
Nama : SAFRINA
Nomor Induk Mahasiswa : 111402027
Program Studi : S1 TEKNOLOGI INFORMASI
Departemen : TEKNOLOGI INFORMASI
Fakultas : ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Sarah Purnamawati, S.T., M.Sc. Dr. Erna Budhiarti Nababan, M.IT NIP. 19830226 201012 2 003
Diketahui/disetujui oleh
Program Studi S1 Teknologi Informasi Ketua,
PERNYATAAN
OPTIMALISASI PENYUSUNAN BARANG PADA MOBIL BOX MENGGUNAKAN ALGORITMA FIREFLY
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing telah disebutkan sumbernya.
Medan, 22 Oktober 2015
PENGHARGAAN
Puji dan syukur penulis sampaikan kepada Allah SWT yang telah memberikan rahmat serta hidayah-Nya sehingga penulis dapat menyelesaikan skripsi ini sebagai syarat untuk memperoleh gelar Sarjana Teknologi Informasi.
Pertama, penulis ingin mengucapkan terima kasih kepada keluarga penulis, Ayahanda Drs. Safrizal, M.Hum., Ibunda Rama Diana, S.S., dan Adik penulis M. Safri
Ramadi Zalma, beserta seluruh keluarga besar yang selalu memberikan dukungan, motivasi, serta doa kepada penulis sehingga dapat menyelesaikan skripsi ini.
Penulis juga mengucapkan terima kasih kepada Ibu Dr. Erna Budhiarti Nababan, M.IT selaku Dosen Pembimbing I dan Ibu Sarah Purnamawati, S.T., M.Sc, selaku Dosen Pembimbing II yang telah meluangkan waktunya untuk membimbing penulis dalam penelitian serta penulisan skripsi ini. Terima kasih juga penulis ucapkan kepada Bapak Dr. Sawaluddin, M.IT selaku Dosen Pembanding I dan Bapak Seniman, S.Kom, M.Kom selaku Dosen Pembanding II yang telah memberikan saran dan kritik yang bermanfaat dalam penyempurnaan skripsi ini. Terima kasih penulis ucapkan kepada Ketua dan Sekretaris Program Studi S1 Teknologi Informasi, Dekan dan Wakil Dekan Fakultas Ilmu Komputer dan Teknologi Informasi, dan seluruh dosen serta staff pegawai di lingkungan Program Studi S1 Teknologi Informasi, yang telah membantu dan membimbing penulis selama masa perkuliahan.
Terima kasih penulis ucapkan kepada teman-teman penulis yang selalu memberikan dukungan dan semangat, Dina Fadhillah, Nurul Fatihah, Roya, Abidah, Shabrina, Icha, Farus, Indera, Nugha, Ismed, Bang Fay, Udin, Erick, Hans, Dhany,
Imam, Ryan, Roy, Ade, serta seluruh teman-teman angkatan 2011 dan teman-teman mahasiswa Teknologi Informasi lainnya. Semoga Allah SWT membalas segala kebaikan kalian.
ABSTRAK
Setiap perusahaan yang menjadikan proses pengiriman barang sebagai salah satu kegiatan usahanya dituntut untuk meningkatkan efisiensi dari segi transportasi. Salah satu cara yang dapat digunakan untuk meningkatkan efisiensi tersebut adalah dengan mengoptimalkan penggunaan ruang mobil box pengangkut barang dalam proses penyusunan barang. Proses penentuan susunan barang yang masih dilakukan secara manual membutuhkan waktu yang lama dan tidak optimal karena masih banyak terdapat sisa ruang kosong yang dapat diisi barang lain, sehingga dibutuhkan suatu metode yang dapat mengoptimalkan penyusunan barang pada mobil box tersebut. Metode yang diajukan pada penelitian ini adalah algoritma firefly untuk optimalisasi
penyusunan barang dalam bentuk tiga dimensi. Sebelum tahap optimalisasi dilakukan, susunan awal penyusunan ditentukan terlebih dahulu melalui pembangkitan bilangan acak. Hasil pengujian menunjukkan bahwa metode yang diajukan mampu mengoptimalkan penyusunan barang sesuai dengan fungsi objektif permasalahan yaitu memaksimalkan total volume barang yang dapat disusun pada mobil box, serta tidak melanggar batasan orientasi barang, kapasitas ruang mobil box, dan beban maksimal mobil box.
OPTIMIZATION OF THE GOODS ARRANGEMENT ON THE TRUCK
USING FIREFLY ALGORITHM
ABSTRACT
Each enterprise that has the delivery of goods as one of its business activities has to improve efficiency in transportation, by optimizing the utilization of truck space in the
process of goods arrangement. The process of determining the goods arrangement which is done manually is not time- and cost-efficient due to unutilized space that can be filled with other goods. Therefore, a method is needed for such optimization process. The method proposed in this research is firefly algorithm to optimize the packing in the form of three-dimensional packing problem. The initial arrangement will be determined by generating random numbers before the optimization phase. The result shows that the proposed method is able to optimize the packing process and meets the objective function of the problem which is to maximize the total volume of the goods that can be packed on the truck without violating the goods orientation, space of truck capacity, and truck weight limit constraints.
DAFTAR ISI
2.2.2 Three Dimensional Bin Packing Problem (3DBPP) 7
2.3 Permasalahan Optimalisasi Penyusunan Barang pada Mobil
Box 7
2.3.1 Gambaran umum objek 7
2.3.2 Fungsi objektif 10
2.3.3 Batasan (constraints) 12
2.4.1 Light Intensity (I) 16
3.3 Optimalisasi Penyusunan Barang pada Mobil Box 27
3.3.1 Inisialisasi 27
3.3.2 Penyusunan barang 29
3.3.3 Optimalisasi penyusunan barang menggunakan
algoritma firefly 34
3.4 Perancangan Sistem 45
3.4.1 Use case diagram 45
3.4.2 Proses user 47
3.4.3 Perancangan database 48
3.4.4 Rancangan tampilan antarmuka 50
BAB 4 IMPLEMENTASI DAN PENGUJIAN 55
4.1 Implementasi Sistem 55
4.1.1 Spesifikasi perangkat keras dan perangkat lunak
yang digunakan 55
4.1.2 Implementasi perancangan antarmuka 55
4.2 Pengujian Kinerja Sistem 64
BAB 5 KESIMPULAN DAN SARAN 75
5.1 Kesimpulan 75
5.2 Saran 75
DAFTAR TABEL
Hal.
Tabel 2.1. Penelitian terdahulu 21
Tabel 3.1. Parameter mobil box 26
Tabel 3.2. Parameter barang 26
Tabel 3.3. Urutan masuk barang awal 28
Tabel 3.4. Nilai posisi awal firefly f1 dan f2 38 Tabel 3.5. Nilai intensitas cahaya awal firefly f1 dan f2 38
Tabel 3.6. Perhitungan jarak dua firefly 39
Tabel 3.7. Posisi baru firefly f1 40
Tabel 3.8. Urutan masuk barang baru firefly f1 dan f2 41 Tabel 3.9. Perubahan nilai intensitas cahaya firefly setelah mengalami
Pergerakan 42
Tabel 3.10. Posisi akhir barang (solusi terbaik = firefly f1) 44 Tabel 3.11. Deskripsi use case sistem penyusunan barang 46
Tabel 4.1. Data mobil pengujian 65
Tabel 4.2. Data barang pengujian 65
Tabel 4.3. Hasil akhir penyusunan barang 68
Tabel 4.4. Parameter algoritma firefly 70
DAFTAR GAMBAR
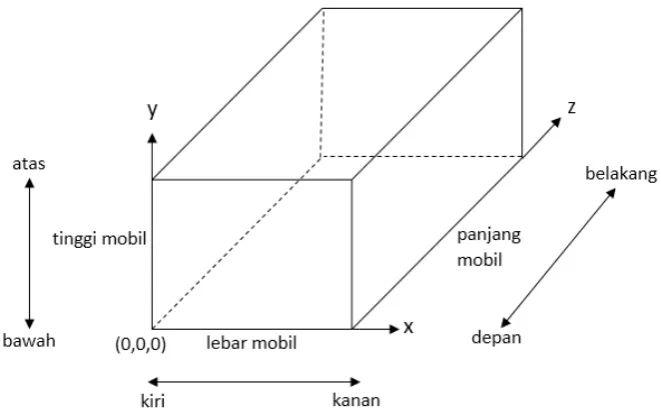
Hal. Gambar 2.1. Gambaran mobil box dalam koordinat tiga dimensi
(Susanto, 2009) 8
Gambar 2.2. Objek barang 8
Gambar 2.3. Variasi perotasian barang (Susanto, 2009) 9
Gambar 2.4. Penempatan barang pada mobil box 10
Gambar 2.5. Susunan I dan susunan II (Oktorini, 2008) 11
Gambar 2.6. Algoritma firefly (Yang, 2009) 15
Gambar 3.1. Arsitektur umum 25
Gambar 3.2. Penentuan penyusunan barang 30
Gambar 3.3. Variasi orientasi susunan barang 32
Gambar 3.4. Tahapan penerapan algoritma firefly 35 Gambar 3.5. Langkah-langkah algoritma firefly pada optimalisasi
penyusunan barang 36
Gambar 3.6. Sistem penyusunan barang 45
Gambar 3.7. User 47
Gambar 3.8. Database relationship 49
Gambar 3.9. Rancangan halaman login 50
Gambar 3.10. Rancangan halaman utama 51
Gambar 3.11. Rancangan halaman master 52
Gambar 3.12. Rancangan halaman optimalisasi 53
Gambar 4.1. Halaman login 56
Gambar 4.2. Halaman utama 56
Gambar 4.3. Halaman master 57
Gambar 4.4. Halaman optimalisasi 58
Gambar 4.5. Data pengiriman 59
Gambar 4.6. Kode pengiriman 59
Gambar 4.8. Posisi barang 61
Gambar 4.9. Sisa barang 61
Gambar 4.10. Halaman detail optimalisasi 62
Gambar 4.11. Halaman visualisasi susunan akhir barang 63 Gambar 4.12. Halaman visualisasi susunan beberapa barang 63
Gambar 4.13. Halaman laporan 64
Gambar 4.14. Hasil penyusunan tahapan inisialisasi 66 Gambar 4.15. Visualisasi susunan barang setelah tahapan inisialisasi 66 Gambar 4.16. Hasil penyusunan tahapan optimalisasi 67 Gambar 4.17. Visualisasi susunan barang setelah tahapan optimalisasi 70
Gambar 4.16. Peningkatan nilai fitness 72
ABSTRAK
Setiap perusahaan yang menjadikan proses pengiriman barang sebagai salah satu kegiatan usahanya dituntut untuk meningkatkan efisiensi dari segi transportasi. Salah satu cara yang dapat digunakan untuk meningkatkan efisiensi tersebut adalah dengan mengoptimalkan penggunaan ruang mobil box pengangkut barang dalam proses penyusunan barang. Proses penentuan susunan barang yang masih dilakukan secara manual membutuhkan waktu yang lama dan tidak optimal karena masih banyak terdapat sisa ruang kosong yang dapat diisi barang lain, sehingga dibutuhkan suatu metode yang dapat mengoptimalkan penyusunan barang pada mobil box tersebut. Metode yang diajukan pada penelitian ini adalah algoritma firefly untuk optimalisasi
penyusunan barang dalam bentuk tiga dimensi. Sebelum tahap optimalisasi dilakukan, susunan awal penyusunan ditentukan terlebih dahulu melalui pembangkitan bilangan acak. Hasil pengujian menunjukkan bahwa metode yang diajukan mampu mengoptimalkan penyusunan barang sesuai dengan fungsi objektif permasalahan yaitu memaksimalkan total volume barang yang dapat disusun pada mobil box, serta tidak melanggar batasan orientasi barang, kapasitas ruang mobil box, dan beban maksimal mobil box.
OPTIMIZATION OF THE GOODS ARRANGEMENT ON THE TRUCK
USING FIREFLY ALGORITHM
ABSTRACT
Each enterprise that has the delivery of goods as one of its business activities has to improve efficiency in transportation, by optimizing the utilization of truck space in the
process of goods arrangement. The process of determining the goods arrangement which is done manually is not time- and cost-efficient due to unutilized space that can be filled with other goods. Therefore, a method is needed for such optimization process. The method proposed in this research is firefly algorithm to optimize the packing in the form of three-dimensional packing problem. The initial arrangement will be determined by generating random numbers before the optimization phase. The result shows that the proposed method is able to optimize the packing process and meets the objective function of the problem which is to maximize the total volume of the goods that can be packed on the truck without violating the goods orientation, space of truck capacity, and truck weight limit constraints.
1.1. Latar Belakang
Dengan semakin berkembangnya dunia bisnis dan usaha, suatu perusahaan dituntut untuk meningkatkan efisiensi dalam segala bidang dengan menerapkan prinsip ekonomi yaitu dengan modal yang sekecil-kecilnya menghasilkan keuntungan yang sebesar-besarnya. Pada perusahaan yang menjadikan proses pengiriman barang sebagai salah satu kegiatan usahanya, efisiensi yang dituntut adalah bagaimana meminimalisir biaya pengeluaran untuk transportasi. Menurut Oktorini (2008), salah satu faktor yang menyebabkan besarnya biaya yang harus dikeluarkan perusahaan dalam dunia usaha adalah pengiriman barang dari satu tempat menuju tempat lain menggunakan jasa transportasi.
Hal yang harus dipikirkan dengan matang pada saat proses pengiriman barang adalah bagaimana menempatkan sejumlah barang secara optimal ke dalam mobil pengangkut barang. Masalah yang sering terjadi pada saat menyusun barang-barang yang akan dikirim adalah tidak optimalnya pemanfaatan ruang kosong yang ada di dalam mobil box pengantar barang. Banyaknya ruang kosong yang tersisa yang sebenarnya masih bisa digunakan untuk memuat lebih banyak barang lagi menyebabkan perusahaan harus mengeluarkan biaya lebih karena dibutuhkannya mobil lain untuk mengangkut sisa barang yang ada.
Masalah penyusunan barang tersebut termasuk ke dalam permasalahan Bin Packing Problem (BPP). Bin Packing bekerja dengan cara menempatkan sejumlah
Penelitian mengenai optimalisasi penyusunan barang sudah beberapa kali dilakukan. Optimalisasi penyusunan barang yang dilakukan diterapkan pada ruang atau bin yang berbeda-beda, seperti pada permasalahan penyusunan pallet dalam
ruang tiga dimensi yang dilakukan oleh Baltacioglu (2001) dengan menerapkan algoritma heuristik wall building dan layer in layer packing. Penyusunan barang dalam ruang tiga dimensi juga pernah dilakukan menggunakan algoritma Genetika (Oktorini, 2008). Penelitian selanjutnya menggunakan algoritma Greedy untuk mensimulasikan penyusunan barang dalam kontainer (Susanto, 2009). Metode yang digunakan pada penelitian ini diimplementasikan untuk mencari solusi pada permasalahan Three Dimensional Container Loading Problem dengan menggunakan parameter volume dan berat barang. Dan penelitian terbaru yaitu visualisasi penyusunan barang pada gudang menggunakan algoritma Steepest Ascent Hill Climbing untuk menentukan urutan barang yang disusun dari berat paling besar ke
berat paling kecil (Harefa, 2014).
Pada penelitian ini, penulis mengajukan algoritma Firefly untuk menyelesaikan masalah penyusunan barang. Algoritma Firefly pertama kali dikembangkan oleh Xin-She Yang pada akhir tahun 2007 di Cambridge University, yang didadasarkan pada tingkah laku berkedipnya kunang-kunang yang menghasilkan cahaya. Penelitian yang dilakukan Yang (2009) menunjukkan bahwa algoritma Firefly jauh lebih efisien dalam menemukan nilai optimum global dengan nilai evaluasi lebih tinggi dibandingkan
algoritma Particle Swarm Optimization dan Genetika. Algoritma firefly telah digunakan untuk menyelesaikan beberapa jenis permasalahan optimalisasi seperti optimalisasi kombinatorial, optimalisasi kontiniu, optimalisasi dengan batasan, dan optimalisasi multi-objektif (Fister et al., 2013). Algoritma Firefly juga telah digunakan
untuk menyelesaikan 2 Dimensional Bin Packing Problem (Chandra & Singh, 2014). Berdasarkan latar belakang di atas, maka penulis mengajukan penelitian
dengan judul “OPTIMALISASI PENYUSUNAN BARANG PADA MOBIL BOX
1.2. Rumusan Masalah
Permasalahan yang sering terjadi pada saat proses pengiriman barang adalah tidak optimalnya penyusunan tata letak barang yang akan dikirim pada mobil box pengantar
barang, sehingga masih banyaknya ruang kosong tersisa yang sebenarnya masih bisa digunakan untuk memuat lebih banyak barang lagi. Hal ini menyebabkan perusahaan harus mengeluarkan biaya lebih karena dibutuhkannya mobil lain untuk mengangkut sisa barang yang ada. Oleh karena itu, dibutuhkan pendekatan untuk menyelesaikan permasalahan ini yaitu bagaimana mengoptimalkan penyusunan barang pada mobil box sehingga penggunaan ruang pada mobil box dapat dioptimalkan.
1.3. Batasan Masalah
Permasalahan yang dibahas pada penelitian ini akan dibatasi ruang lingkup
pembahasannya, yaitu :
1. Barang-barang yang akan disusun berupa barang-barang yang sudah dikemas dalam bentuk balok dan kubus.
2. Tidak memperhatikan rute atau tujuan pengiriman barang (semua barang diturunkan di tempat yang sama).
3. Berat suatu barang yang berada di atas barang lain tidak mempengaruhi barang yang berada di bawahnya.
4. Hal-hal yang diperhatikan pada saat penyusunan barang adalah kapasitas ruang mobil box, beban maksimum yang dapat ditampung mobil, serta perotasian barang.
1.4. Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah untuk mengoptimalkan penyusunan barang pada mobil box menggunakan algoritma Firefly sehingga penggunaan ruang pada mobil box dapat dioptimalkan.
1.5. Manfaat Penelitian
Manfaat dari penelitian ini yaitu :
3. Memberi masukan bagi penelitian lain di bidang optimalisasi, khususnya konsep penyusunan barang dan algoritma Firefly.
1.6. Metodologi
Terdapat beberapa tahapan pada penelitian ini adalah sebagai berikut: 1. Studi Literatur
Studi literatur dilakukan dalam rangka mengumpulkan dan mempelajari informasi-informasi dari buku, paper, jurnal, atau sumber referensi lain mengenai optimalisasi, penyusunan barang, Bin Packing Problem dan Algoritma Firefly. 2. Analisis Permasalahan
Pada tahap ini dilakukan analisis terhadap bahan referensi yang telah dikumpulkan sebelumnya untuk mendapatkan pemahaman mengenai metode yang akan digunakan, yaitu algoritma Firefly untuk diimplementasikan dalam permasalahan optimalisasi penyusunan barang pada mobil box.
3. Perancangan
Pada tahap ini dilakukan perancangan perangkat lunak yang dibangun, seperti perancangan arsitektur dan antarmuka sistem. Proses perancangan dilakukan
berdasarkan hasil analisis terhadap studi literatur yang sudah dikumpulkan. 4. Implementasi
Pada tahap ini dilakukan implementasi analisis yang telah dilakukan ke dalam pembangunan program sesuai dengan alur yang ditentukan.
5. Pengujian
Pada tahap ini dilakukan pengujian terhadap aplikasi yang telah dibuat untuk menguji kemampuan algoritma Firefly dalam mengoptimalkan penyusunan barang, serta memastikan aplikasi telah berjalan sesuai dengan yang diharapkan.
6. Penyusunan Laporan
1.7. Sistematika Penulisan
Sistematika penulisan dari skripsi ini terdiri dari lima bagian utama sebagai berikut:
Bab 1: Pendahuluan
Bab ini berisi latar belakang, rumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian, metodologi penelitian, dan sistematika penulisan.
Bab 2: Landasan Teori
Bab ini berisi teori-teori yang digunakan untuk memahami permasalahan yang dibahas pada penelitian ini. Pada bab ini dijelaskan tentang optimalisasi, Bin Packing Problem, dan algoritma Firefly.
Bab 3: Analisis dan Perancangan Sistem
Bab ini berisi analisis dari metode yang digunakan yaitu algoritma Firefly dan penerapannya untuk optimalisasi penyusunan barang pada mobil box, serta perancangan sistem yang dibuat seperti pemodelan dengan flowchart dan usecase diagram.
Bab 4: Implementasi dan Pengujian Sistem
Bab ini berisi pembahasan tentang implementasi dari analisis dan perancangan sistem yang disusun pada Bab 3 dan hasil pengujian terhadap sistem yang dibangun.
Bab 5: Kesimpulan dan Saran
BAB 2
LANDASAN TEORI
2.1. Optimalisasi
Optimalisasi merupakan suatu proses untuk mengoptimalkan suatu solusi agar ditemukannya solusi terbaik dari sekumpulan alternatif solusi yang ada dengan menggunakan formulasi matematika. Optimalisasi dilakukan dengan memaksimalkan atau meminimalkan suatu fungsi objektif dengan tidak melanggar batasan yang ada (Sianturi, 2012). Dengan adanya optimalisasi, suatu sistem dapat meningkatkan efektifitasnya seperti meminimalisir biaya, meningkatkan keuntungan, meminimalisir waktu proses, dan sebagainya.
2.2. Bin Packing Problem
Bin Packing Problem adalah sebuah permasalahan optimalisasi kombinatorial yang termasuk dalam jenis Non-deterministic Polynomial-time (NP) hard yang pertama kali diperkenalkan oleh Garey dan Johnson pada tahun 1979. Bin Packing memiliki peran penting dalam menyelesaikan beberapa persoalan di dunia nyata seperti perencanaan transportasi, pemuatan kontainer, alokasi sumber daya, penjadwalan, serta kargo
pesawat dan kapal (Yesodha & Amudha, 2013). Pada permasalahan bin packing, diberikan sebuah bin dengan kapasitas tertentu V yang digunakan sebagai tempat dari seluruh objek n yang memiliki ukuran berbeda-beda, dan tujuannya adalah untuk meminimalkan bin yang digunakan agar seluruh objek n dapat ditempatkan ke dalam bin tersebut (Swain et al., 2014).
2.2.1. Two dimensional bin packing problem (2DBPP)
kepada dua variabel tersebut. 2DBPP biasanya digunakan untuk menyusun barang pada lantai ruang dan tidak adanya penumpukan barang. 2DBPP bisa juga digunakan
untuk menyusun barang dengan adanya penumpukan, tetapi semua barang tersebut harus memiliki variabel tinggi yang sama, sehingga variabel tinggi tersebut tidak akan mempengaruhi penyusunan barang yang memiliki variabel panjang dan lebar yang berbeda.
2.2.2. Three dimensional bin packing problem (3DBPP)
Pada 3DBPP, satu atau lebih bin yang tersedia dipilih untuk memuat barang-barang secara tiga dimensi sehingga ruang pada bin dapat dimaksimalkan (Li et al., 2014). Berbeda dengan 2DBPP yang hanya menggunakan dua variabel, 3DBPP menggunakan tiga variabel yaitu panjang, lebar, dan tinggi barang dalam melakukan penyusunan barang. Hal ini menyebabkan tingkat kesulitan 3DBPP lebih tinggi dari 2DBPP. Setiap item atau objek pada 3DBPP harus disusun sedemikian rupa agar item tersebut dapat dimuat ke dalam bin yang juga memiliki batasan panjang, lebar, dan tinggi. Jika pada 2DBPP penyusunan barang lebih ditekankan kepada penyusunan bidang segi empat pada dasar ruang (rectangle-to-floorplan packing), 3DBPP lebih ditekankan kepada penyusunan bangun segi empat pada ruang (box-to-room packing) (Sweep, 2003). 3DBPP juga termasuk ke dalam permasalahan pemuatan kontainer (Container Loading Problem).
Pada 3DBPP penyusunan barang dapat dibedakan menjadi single bin atau
multiple bins. Pada single bin, penyusunan barang yang dilakukan hanya
menggunakan sebuah bin, sehingga tujuan penyusunan hanya untuk meminimalkan
sisa ruang kosong pada bin tersebut. Sementara pada multiple bins, penyusunan barang yang dilakukan menggunakan lebih dari satu bin, sehingga tujuan penyusunannya adalah untuk meminimalkan jumlah bin yang digunakan.
2.3. Permasalahan Optimalisasi Penyusunan Barang pada Mobil Box
2.3.1. Gambaran umum objek
mobil. Mobil yang digunakan hanya satu buah (single bin). Gambaran umum objek mobil box dapat dilihat pada Gambar 2.1.
Gambar 2.1. Gambaran Mobil Box dalam Koordinat Tiga Dimensi
(Susanto, 2009)
Pada Gambar 2.1. dapat dilihat bahwa koordinat awal penyusunan (titik 0,0,0) berada di depan, kiri, dan bawah mobil. Sumbu x mewakili lebar mobil, sumbu y mewakili tinggi mobil, dan sumbu z mewakili panjang mobil.
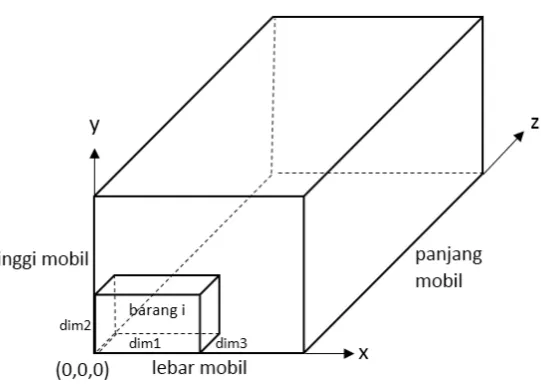
Barang yang akan disusun merupakan barang tiga dimensi berbentuk segi empat yang memiliki panjang, lebar, dan tinggi. Setiap barang juga memiliki berat sebagai batasan agar mobil box tersebut tidak membawa beban yang melebihi kapasistasnya. Gambaran umum objek barang dapat dilihat pada Gambar 2.2.
Pada Gambar 2.2. dapat dilihat bahwa barang i memiliki dimensi 1 yang sejajar dengan sumbu x, dimensi 2 yang sejajar dengan sumbu y, dan dimensi 3 yang
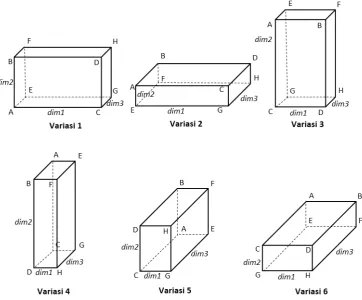
sejajar dengan sumbu z. Dimensi masing-masing barang ini ditentukan oleh perotasian barang. Apabila suatu barang i tidak dapat dirotasi maka barang tersebut hanya akan memiliki satu variasi nilai dimensi yaitu dimensi 1 sebagai panjang barang, dimensi 2 sebagai tinggi barang, dan dimensi 3 sebagai lebar barang. Namun, apabila suatu barang i dapat dirotasi maka barang tersebut akan memiliki enam variasi nilai dimensi. Pertukaran nilai dimensi untuk suatu barang yang dapat dirotasi dapat dilihat pada Gambar 2.3.
Gambar 2.3. Variasi Perotasian Barang (Susanto, 2009)
Pada Gambar 2.3. dapat dilihat bahwa pada enam variasi perotasian tersebut, nilai dimensi masing-masing posisi diubah sesuai dengan arah perputarannya. Seperti contoh pada Variasi 1, nilai dimensi 1 sama dengan AC yang merupakan panjang barang. Sedangkan pada Variasi 3 nilai dimensi 1 sama dengan CD yang merupakan
Gambar 2.4. Penempatan Barang pada Mobil Box
Pada Gambar 2.4. dapat dilihat bahwa penempatan suatu barang i di dalam mobil box didasarkan pada dimensi barang tersebut. Dimensi 1 barang akan menempati posisi lebar mobil, dimensi 2 barang akan menempati posisi tinggi mobil, serta dimensi 3 barang akan menempati posisi panjang mobil.
2.3.2. Fungsi objektif
Dalam melakukan penyusunan barang dengan berbagai ukuran pada mobil box, perlu dilakukannya optimalisasi agar penyusunan yang dilakukan optimal. Di dalam permasalahan optimalisasi ada beberapa hal yang harus ditentukan, yaitu fungsi objektif (objective function) dan batasan (constraint). Fungsi objektif merupakan suatu fungsi matematika yang merupakan tujuan utama pada permasalahan optimalisasi yang harus diminimalkan atau dimaksimalkan. Sebuah solusi yang dapat meminimalkan atau memaksimalkan (sesuai tujuan utama permasalahan) fungsi objektif adalah solusi optimal (Kumar, 2014). Fungsi objektif pada permasalahan
optimalisasi penyusunan barang adalah untuk memaksimalkan penggunaan ruang yang tersedia yaitu total volume barang yang dapat disusun pada suatu mobil box. Fungsi objektif tersebut dapat dilihat pada persamaan 2.1.
Dimana : = Fungsi Objektif
= Indeks Barang
= Jumlah Barang
= Masing-masing panjang, lebar, dan tinggi barang i
= Variabel biner yang mengidentifikasi dapat atau tidaknya barang
disusun pada mobil box. Bernilai 1 jika barang berada di mobil, 0 jika tidak.
Fungsi objektif berdasarkan persamaan 2.1. di atas digunakan sebagai nilai fitness yang dihasilkan masing-masing kandidat solusi. Namun, jika pada suatu kasus
terdapat beberapa solusi yang memiliki nilai fitness yang sama, maka akan dilakukan
pencarian nilai fitness kedua untuk menghitung total volume barang yang disusun pada ketinggian 0 – ½ tinggi mobil box. Kandidat solusi yang memiliki nilai fitness yang sama tersebut akan dibandingkan. Kandidat solusi yang menghasilkan total
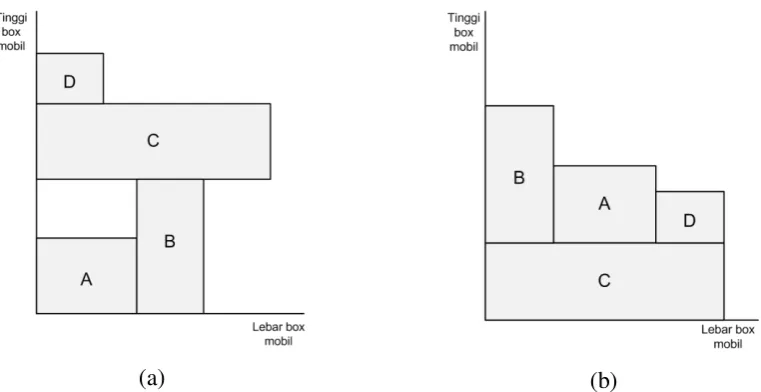
volume barang pada ketinggian 0 – ½ tinggi mobil box lebih besar akan diambil sebagai kandidat solusi dengan solusi terbaik. Keputusan tersebut diambil karena mempertimbangkan kepadatan benda yang berada di bawah. Semakin padat barang-barang yang berada di bawah, maka semakin bagus pola susunannya (Oktorini, 2008). Contoh dua solusi yang memiliki nilai fitness sama besar dapat dilihat pada Gambar 2.5.
(a) (b)
Pada Gambar 2.5. dapat dilihat bahwa susunan I dan susunan II memiliki nilai fitness yang sama besar jika menggunakan perhitungan fitness dengan menghitung total volume barang yang dapat disusun. Namun, jika dilihat dari pola susunan
penumpukan, maka susunan II lebih baik untuk diterapkan karena terdapat lebih sedikit ruang kosong di antara tumpukan benda yang berada di bawah.
2.3.3. Batasan (constraints)
Selain menentukan fungsi objektif, pada permasalahan optimalisasi juga harus ditentukan batasan permasalahan (constraint). Batasan atau constraint merupakan suatu kondisi yang harus dipenuhi pada permasalahan optimalisasi. Solusi yang dihasilkan dari fungsi objektif tidak boleh melanggar batasan-batasan tersebut. Constraint dalam permasalahan penyusunan barang dapat dibagi menjadi dua jenis, yaitu hard constraint dan soft constraint. Hard constraint digunakan untuk mendefinisikan batasan yang digunakan pada proses optimalisasi, sedangkan soft
constraint digunakan untuk membentuk fungsi objektif suatu permasalahan
optimalisasi (Hicks et al., 2006).
Hard Constraint
Hard constraint merupakan batasan yang harus selalu dipenuhi. Pola penyusunan yang melanggar hard constraint disebut solusi yang tidak layak (Bortfeldt & Wascher,
2012). Batasan-batasan dalam penyusunan barang tiga dimensi yang dikategorikan sebagai hard constraint adalah sebagai berikut :
1. Orientasi Barang
Barang yang disusun harus berbentuk kubus atau balok yang memiliki tiga
dimensi yaitu panjang, lebar, dan tinggi. Khusus barang berbentuk balok yang memiliki nilai berbeda untuk setiap dimensinya, terdapat barang yang bisa dan tidak bisa dirotasi penempatannya di dalam mobil box. Barang-barang yang dapat dirotasi akan mengalami pertukaran dimensi sebanyak enam variasi orientasi. Sedangkan barang yang tidak dapat dirotasi tidak boleh mengalami pertukaran dimensi, sehingga hanya memiliki satu variasi orientasi.
2. Beban Maksimum Mobil
boleh memiliki total berat yang melebihi beban maksimum yang dapat ditampung mobil. Model matematika dapat dilihat pada persamaan 2.2.
(2.2)
Dimana : = Indeks Barang
= Jumlah Barang
= Berat barang i
= Beban maksimum mobil box
= Variabel biner yang mengidentifikasi dapat atau tidaknya
barang i disusun pada mobil box. Bernilai 1 jika barang berada di mobil, 0 jika tidak.
3. Kapasitas Ruang Mobil Box
Penyusunan barang-barang pada penelitian ini hanya menggunakan satu buah mobil box (single bin). Batasan kapasitas ruang mobil box digunakan agar barang-barang yang disusun pada mobil box memiliki ukuran yang lebih kecil atau sama dengan ukuran mobil box. Volume dari barang-barang yang disusun tidak boleh melebihi volume box mobil. Model matematika dapat dilihat pada persamaan 2.3.
(2.3)
Masing-masing dimensi panjang, lebar, dan tinggi barang juga tidak boleh melebihi lebar, panjang, dan tinggi mobil. Model matematika dapat dilihat
pada persamaan 2.4.
Dimana : = Indeks Barang
= Jumlah Barang
= Masing-masing panjang, lebar, dan tinggi barang i
= Masing-masing panjang, lebar, dan tinggi mobil box
= Variabel biner yang mengidentifikasi dapat atau
tidaknya barang i disusun pada mobil box. Bernilai 1 jika barang berada di mobil, 0 jika tidak.
Soft Constraint
Soft constraint merupakan batasan yang tidak harus selalu dipenuhi untuk kondisi
tertentu. Pola penyusunan yang melanggar soft constraint masih dapat disebut solusi layak, tetapi sedapat mungkin untuk dipenuhi dan tidak melanggar batas tertentu (Bortfeldt & Wascher, 2012). Salah satu batasan dalam penyusunan barang tiga dimensi yang dikategorikan sebagai soft constraint adalah stabilitas beban (load stability). Stabilitas beban digunakan sebagai pendukung fungsi objektif dalam
menemukan solusi penyusunan yang lebih baik. Batasan ini digunakan untuk mengurangi ruang-ruang kosong yang berada pada susunan bawah mobil sehingga barang-barang yang berada di atasnya bisa lebih didukung oleh barang-barang yang berada di bawahnya. Batasan ini juga digunakan untuk mengurangi kemungkinan ambruknya barang yang berada di atas karena banyaknya ruang kosong yang berada pada susunan di bawahnya. Solusi yang digunakan untuk menjaga stabilitas beban mobil box adalah dengan memilih susunan yang memiliki ruang kosong paling sedikit pada ketinggian 0 – ½ tinggi mobil box.
2.4. Algoritma Firefly
1. Semua kunang-kunang merupakan unisex yang menyebabkan kunang-kunang dapat tertarik dengan kunang-kunang-kunang-kunang lain tanpa mempedulikan gender atau jenis kelaminnya.
2. Ketertarikan kunang-kunang berbanding lurus dengan intensitas cahayanya dan akan berkurang jika jarak di antara mereka meningkat. Untuk setiap dua kunang-kunang berkedip, kunang-kunang dengan cahaya yang lebih sedikit akan mendekati kunang-kunang dengan cahaya yang lebih terang. Jika di antara mereka tidak ada salah satu yang cahayanya lebih terang, maka ia akan bergerak secara acak.
3. Terangnya cahaya dari seekor kunang-kunang ditentukan oleh fungsi objektif (objective function).
Berdasarkan tiga aturan dasar diatas, langkah-langkah algoritma firefly dapat diringkas menjadi pseudo code yang dapat dilihat pada Gambar 2.6.
Gambar 2.6. Algoritma Firefly (Yang, 2009)
2.4.1. Light intensity (I)
Setiap firefly pada suatu populasi memiliki light intensity atau intensitas cahaya. Intensitas cahaya tersebut digunakan sebagai penentu apakah firefly akan melakukan
pergerakan atau tidak. Firefly yang memiliki intensitas cahaya lebih besar akan didekati oleh firefly lain yang memiliki intensitas lebih kecil. Pada permasalahan optimalisasi penyusunan untuk memaksimalkan fungsi objektif, nilai dari intensitas cahaya firefly akan sebanding dengan fungsi objektif dan dapat dihitung menggunakan
persamaan 2.5.
(2.5)
Dimana : = Intensitas cahaya firefly i (i = 1, 2, ... , n)
= Fungsi objektif
2.4.2. Distance (r)
Jarak antara dua buah firefly i dan j ditentukan menggunakan tabel Cartessian dan dapat dihitung menggunakan persamaan 2.6.
(2.6)
Dimana : = Jarak antara firefly i dan firefly j
= Dimensi setiap firefly
= Banyaknya dimensi k
= Posisi firefly i pada dimensi k
= Posisi firefly j pada dimensi k
2.4.3. Movement
Pergerakan firefly terjadi apabila ada suatu firefly yang memiliki nilai intensitas cahaya lebih kecil daripada firefly didekatnya. Firefly dengan intensitas cahaya lebih
pergerakan suatu firefly i mendekati firefly j untuk mendapatkan posisi baru firefly i dapat dihitung menggunakan persamaan 2.7.
Dimana : = Posisi firefly i yang baru
= Posisi firefly i sekarang
= Koefisien ketertarikan pada posisi 0
= Koefisien penyerapan cahaya (0.01 < < 100)
= Jarak antara firefly i dan firefly j
= Posisi firefly j
= Koefisien bilangan acak (0 < < 1)
= Bilangan acak (0 < < 1)
2.5. Library StdDraw3D
Standard Draw 3D (StdDraw3D) merupakan salah satu library Java yang digunakan untuk membuat grafik tiga dimensi. StdDraw3D bertujuan untuk memudahkan pengguna dalam membuat model, simulasi, dan game dengan visualisasi tiga dimensi di dalam bahasa pemrograman Java karena script pada library ini dibuat lebih sederhana (Martirosyan, 2011). StdDraw3D digunakan untuk membuat visualisasi susunan barang secara tiga dimensi.
2.6. Penelitian Terdahulu
Penelitian mengenai optimalisasi penyusunan barang sudah beberapa kali dilakukan. Optimalisasi penyusunan barang tersebut dilakukan pada ruangan atau bin yang berbeda-beda.
Permasalahan penyusunan pallet pada kontainer pernah diselesaikan oleh
menyusun barang pada layer yang sesuai, sementara layer in layer packing digunakan untuk menyusun barang pada sisa layer yang masih terdapat ruang kosong. Dimensi semua barang harus dianalisa terlebih dahulu sebelum penyusunan barang dimulai.
Hal ini dilakukan untuk menemukan beberapa nilai ketebalan layer (layerthickness) yang paling sesuai untuk keseluruhan barang agar ruang kosong pada kontainer dapat dikurangi. Penyusunan barang dilakukan sebanyak iterasi yang ada. Banyaknya jumlah iterasi ditentukan oleh orientasi pallet dan nilai layerthickness. Jumlah orientasi pallet bergantung pada dimensi pallet. Jika pallet memiliki 3 dimensi yang sama, maka pallet hanya memiliki 1 orientasi saja. Sedangkan jika pallet memiliki 3 dimensi dengan ukuran yang berbeda-beda, maka akan ada 6 orientasi pallet. Setiap iterasi dimulai dengan menyusun barang pada layer awal, yaitu layer dengan nilai layerthicknes pertama yang diambil dari kumpulan layerthickness yang sudah ditentukan sebelumnya. Jika ada 7 nilai layerthickness yang berbeda dan pallet memiliki 3 dimensi yang berbeda, maka jumlah iterasi adalah 6*7, yaitu 42 iterasi. Parameter yang digunakan adalah ukuran barang (panjang, lebar, dan tinggi). Semua barang dapat dirotasi sebanyak enam orientasi. Constraints yang digunakan hanyalah kapasitas ruang kontainer, yaitu dimensi barang tidak melebihi dimensi kontainer. Pada penelitian ini, penyusunan yang tidak stabil diperbolehkan. Hal ini menyebabkan ada beberapa barang yang tidak memiliki dasar, sehingga barang akan menggantung (Baltacioglu, 2001).
Pada tahun 2008, Oktorini melakukan penelitian untuk optimalisasi penyusunan barang dalam ruang tiga dimensi. Pada penelitiannya, ia menggunakan algoritma Genetika untuk menyusun barang pada ruang tiga dimensi seperti kontainer. Implementasi algoritma genetika dalam proses penyusunan barang yaitu dengan
meletakkan barang-barang yang diwakili oleh kode dan posisinya pada gen-gen dalam suatu kromosom lalu memperhatikan bisa atau tidaknya suatu barang menempati posisi tersebut tanpa mengubah posisi barang. Proses penempatan gen berlangsung setiap muncul generasi baru sampai iterasi maksimum tercapai. Pada tahapan reproduksi awal (generasi pertama), proses penempatan gen dilakukan dengan cara randomize. Mulai generasi 2 sampai terakhir, proses penempatan gen dilakukan sesuai
Hal-hal yang diperhatikan pada penyusunan barang di penelitian ini adalah beban maksimum yang dapat ditampung ruang, beban maksimum yang dapat ditampung barang, perotasian barang, dan letak titik berat suatu posisi barang terhadap barang
dibawahnya agar tumpukan tidak roboh dan menyebabkan kehancuran pada barang. Nilai fitness yang digunakan didasarkan pada jumlah satuan ruang yang terisi oleh barang, jumlah barang yang seimbang posisinya, dan jumlah barang yang utuh (Oktorini, 2008).
Penelitian selanjutnya yang dilakukan oleh Susanto (2009) menerapkan algoritma Greedy untuk melakukan penyusunan barang dalam kontainer. Ia juga menerapkan metode wall building approach untuk mengisi kontainer sesuai dengan layer yang sejajar kedalaman kontainer. Metode ini menerapkan aturan pengurutan untuk memilih nilai layer. Kotak dengan dimensi terbesar akan dipilih untuk dimuat pertama dan dimensinya akan dijadikan nilai layer dikarenakan kotak dengan dimensi terbesar akan sulit untuk dimuat jika diletakkan di urutan terakhir. Setelah nilai layer ditentukan, maka metode greedy diterapkan untuk melakukan penyusunan barang secara horizontal di setiap potongan layer. Pada setiap layer, barang yang tersisa akan dimasukkan secara berurutan sesuai urutan panjang barang yang terbesar terlebih dahulu. Parameter yang digunakan pada penelitian ini adalah volume dan berat barang, sedangkan constraint yang harus dipenuhi adalah kapasitas ruang pada kontainer dan beban maksimal yang dapat ditampung kontainer (Susanto, 2009).
Penelitian terbaru yang dilakukan oleh Harefa (2014) mengenai penyusunan barang menerapkan algoritma Steepest Ascent Hill Climbing untuk memvisualisasikan penyusunan barang pada sebuah gudang. Metode tersebut diterapkan untuk mengurutkan barang berdasarkan beratnya, sehingga urutan barang dimulai dari
Algoritma Firefly sudah diterapkan pada permasalahan Bin Packing oleh Kwesnady pada tahun 2013. Metode tersebut diterapkan dalam penyelesaian Two Dimensional Bin Packing Problem dengan fungsi objektif adalah meminimalkan
jumlah mobil yang diperlukan dalam pengiriman barang. Penyusunan barang hanya bersifat satu layer dan tidak adanya penumpukan barang, sehingga dari segi biaya tidak dapat dihitung nilainya secara aktual. Penempatan barang ke dalam mobil box juga tidak menggunakan rotasi, sehingga barang tidak dapat berubah posisi dari horizontal menjadi vertikal, dan sebaliknya. Hasil penyusunan yang diperoleh dari penggunaan algoritma firefly dapat berbeda-beda setiap kali dijalankan. Hal ini disebabkan oleh bilangan acak yang dihasilkan pada tahap inisialisasi awal. Parameter yang digunakan hanya dimensi panjang dan lebar barang (Kwesnady, 2013).
Algoritma firefly juga sudah digunakan untuk menyelesaikan masalah optimalisasi kombinatorial lain, seperti Travelling Salesman Problem (TSP) oleh Kumbharana dan Pandey pada tahun 2013. Fungsi tujuan dari permasalahan ini adalah meminimalkan jarak yang harus ditempuh untuk mengunjungi semua kota yang ada. Pada penelitian ini algoritma firefly diubah menjadi diskrit untuk menyelesaikan permasalahan permutasi. Tahapan inisialisasi awal dilakukan dengan menghasilkan urutan permutasi secara acak yang merupakan urutan kota yang akan dikunjungi. Kriteria berhenti yang digunakan pada penelitian ini adalah stagnasi, yaitu keadaan dimana hasil yang didapatkan stabil atau tidak ada lagi terjadi peningkatan. Ia juga
membandingkan kinerja algoritma firefly dengan beberapa algoritma metaheuristik lain seperti Ant Colony Optimization (ACO), Genetic Algorithm (GA), dan Simulated Annealing (SA). Hasil yang didapatkan oleh algoritma firefly dari implementasi menggunakan 6 jenis data rute kota lebih baik, yaitu menghasilkan total jarak tempuh
Tabel 2.1. Penelitian Terdahulu (lanjutan)
Perbedaan penelitian yang dilakukan dengan penelitian terdahulu adalah penggunaan algoritma firefly dalam menyelesaikan permasalahan bin packing dengan penambahan unsur tinggi (three dimensional packing problem). Penyusunan barang dilakukan pada mobil box dan bersifat tiga dimensi sehingga dapat memungkinkan
terjadinya penumpukan barang. Parameter yang digunakan adalah volume barang, volume mobil box, berat barang, beban maksimum mobil, dan perotasian barang. Fungsi objektif yang digunakan pada penelitian ini adalah memaksimalkan total volume barang yang dapat disusun pada mobil box. Adapun constraints yang digunakan pada penelitian ini adalah sebagai berikut :
1. Masing-masing barang memiliki posisi yang unik sehingga tidak akan terjadi barang yang saling tumpang tindih (overlapping).
2. Barang-barang yang tidak berada di dasar mobil box harus didukung oleh barang yang berada dibawahnya, sehingga tidak akan terjadi barang yang menggantung atau melayang (overhang).
4. Total berat barang yang disusun pada mobil box tidak boleh melebihi beban maksimum yang dapat ditampung mobil box.
5. Barang-barang yang memiliki sifat tidak dapat dirotasi tidak boleh mengalami
pertukaran dimensi pada saat penyusunan barang pada mobil box, sementara barang-barang yang memiliki sifat dapat dirotasi boleh mengalami pertukaran dimensi sebanyak enam variasi orientasi.
6. Untuk solusi yang menghasilkan nilai fitness yang sama, maka akan dilakukan pencarian nilai fitness kedua yaitu mencari susunan dengan ruang kosong paling sedikit di ketinggian 0 - 1/2 tinggi mobil box. Hal ini dilakukan untuk
BAB 3
ANALISIS DAN PERANCANGAN
Pada bab ini akan dibahas mengenai analisis dan perancangan sistem. Pada tahap analisis akan dilakukan analisis terhadap data yang digunakan menggunakan algoritma firefly untuk menemukan solusi penyusunan barang yang optimal. Pada tahap perancangan akan dibahas mengenai perancangan use case diagram, flowchart user, database, serta tampilan antarmuka sistem.
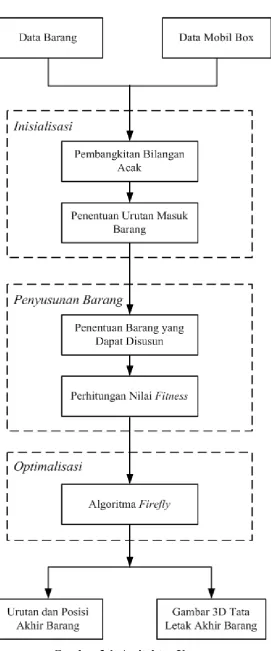
3.1. Arsitektur Umum
Metode yang diajukan untuk mengoptimalkan penyusunan barang pada penelitian ini terdiri dari beberapa tahapan yaitu input, proses, dan output. Input dari penelitian ini berupa data barang dan data mobil box. Data-data tersebut kemudian akan diproses melalui tiga tahapan yaitu, inisialisasi, penyusunan barang, dan optimalisasi. Pada tahapan inisialisasi, proses yang dilakukan adalah pembangkitan bilangan acak untuk menentukan urutan awal masuk barang sebanyak kandidat solusi yang diinginkan. Tahap selanjutnya adalah penyusunan barang. Pada tahap ini, barang-barang akan disusun berdasarkan urutan masuk barang yang dimiliki masing-masing kandidat solusi yang telah dihasilkan pada tahapan inisialisasi, kemudian dihitung nilai fitness barang-barang yang dapat disusun. Tahapan terakhir adalah optimalisasi penyusunan barang menggunakan algoritma firefly. Tahapan optimalisasi tersebut digunakan untuk
mengoptimalkan susunan barang yang sudah dihasilkan pada tahapan sebelumnya sehingga menghasilkan urutan penyusunan barang yang lebih baik. Output yang didapat dari proses ini berupa urutan masuk barang dan posisi barang yang sudah disusun, serta gambar tiga dimensi tata letak akhir barang. Detail setiap tahapan yang
3.2. Data yang digunakan
Data yang digunakan dalam penelitian ini ada dua jenis data, yaitu data mobil box dan data barang. Data mobil box dibutuhkan untuk mengetahui kapasitas ruang untuk penyusunan barang. Pada penelitian ini, mobil yang digunakan hanya satu buah (single bin). Parameter-parameter mobil box yang digunakan adalah panjang mobil, lebar mobil, tinggi mobil, dan beban maksimal yang dapat ditampung mobil. Contoh data mobil box beserta nilai dari parameter yang dibutuhkan dalam penelitian ini dapat dilihat pada Tabel 3.1.
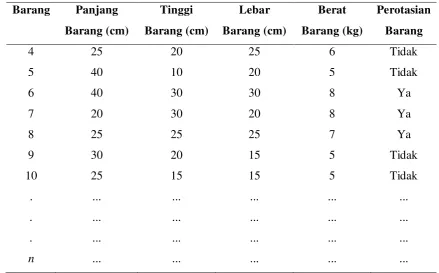
Data barang dibutuhkan untuk mengetahui berapa banyak barang yang akan disusun pada mobil box serta ukuran masing-masing barang. Barang yang akan disusun pada penelitian ini harus berbentuk balok dan kubus. Parameter-parameter barang yang digunakan adalah panjang barang, lebar barang, tinggi barang, berat barang, serta perotasian barang. Parameter dimensi barang seperti panjang, lebar, serta tinggi barang dibutuhkan untuk menentukan posisi barang pada mobil box. Parameter berat barang dibutuhkan untuk membatasi total berat barang yang disusun agar tidak melebihi beban maksimal yang dapat ditampung mobil box. Parameter perotasian barang dibutuhkan untuk mengetahui apakah barang tersebut bisa dirotasi dalam penyusunannya atau tidak. Contoh data barang beserta nilai dari parameternya yang dibutuhkan dalam penelitian ini dapat dilihat pada Tabel 3.2.
Tabel 3.2. Parameter Barang (lanjutan)
Pada Tabel 3.2. dapat dilihat parameter-parameter barang yang digunakan dalam penyusunan pada mobil box, seperti panjang, lebar, tinggi dan berat barang. Sedangkan perotasian barang merupakan constraint atau batasan, sehingga barang
yang memiliki nilai perotasian barang sama dengan ‘tidak’ adalah barang yang tidak
dapat dirotasi penyusunannya. Sedangkan barang yang memiliki nilai perotasian barang sama dengan ‘ya’ dapat dirotasi penyusunannya sebanyak enam variasi perputaran.
3.3. Optimalisasi Penyusunan Barang Pada Mobil Box
3.3.1. Inisialisasi
Pembangkitan Bilangan Acak
Pada penelitian ini, inisialisasi solusi awal penyusunan barang menggunakan pembangkitan bilangan acak. Sebelum urutan awal masuk barang ditentukan, terlebih dahulu harus dilakukan pembangkitan bilangan acak sebanyak jumlah barang dan kandidat solusi yang diinginkan. Sebagai contoh, jika kandidat solusi yang diinginkan berjumlah dua dan barang yang akan disusun berjumlah sepuluh, maka akan ada dua puluh bilangan acak yang dibangkitkan.
Penentuan Urutan Masuk Barang
Setelah bilangan acak dibangkitkan untuk masing-masing kandidat solusi, maka proses selanjutnya adalah penentuan urutan masuk barang. Penentuan urutan masuk barang dilakukan dengan cara mengurutkan nilai bilangan acak yang dimiliki masing-masing kandidat solusi dari terkecil hingga terbesar. Contoh urutan masuk barang yang didapatkan dari hasil pengurutan bilangan acak masing-masing kandidat solusi
dapat dilihat pada Tabel 3.3. kandidat solusi 1, bilangan acak terkecil berada pada barang 4 sehingga urutan barang 4 adalah 1 yang merupakan awal dari urutan, dan dilanjutkan ke urutan berikutnya sebanyak jumlah barang sehingga akan terbentuk satu kandidat solusi yang mewakilkan urutan masuk barang. Pada penerapannya dalam penyusunan barang, urutan ini merupakan urutan penyusunan barang, yaitu dimulai dari barang yang mendapatkan urutan 1 yaitu barang ke-4, ke-10, dan seterusnya hingga barang terakhir
3.3.2. Penyusunan barang
Setelah urutan masuk barang awal ditentukan, maka barang-barang akan disusun
berdasarkan urutan tersebut. Penyusunan barang pertama dimulai dari baris pertama ruang kiri, depan, dan bawah mobil box. Barang selanjutnya disusun di sebelah kanan barang pertama sepanjang lebar mobil box. Jika barang selanjutnya tidak dapat disusun di sebelah kanan, maka penyusunan dilanjutkan ke atas barang sebelumnya dan seterusnya sampai barang tidak dapat dimuat lagi ke atas. Kemudian penyusunan dilanjutkan ke baris kedua yaitu dimulai dari sebelah kiri tepat di belakang barang pertama diletak. Lalu penyusunan dilanjutkan seperti pada baris pertama yaitu ke sebelah kanan lalu ke atasnya. Jika ruang sudah tidak dapat terisi lagi, maka penyusunan untuk mobil tersebut akan berakhir. Pada tahap penyusunan barang ada langkah-langkah yang harus dilakukan yaitu penentuan barang yang dapat disusun dan perhitungan nilai fitness.
Penentuan Barang yang Dapat Disusun
Sebelum total volume barang yang berhasil disusun dihitung, terlebih dahulu harus ditentukan barang-barang mana saja yang dapat disusun pada mobil box. Penentuan barang ini sangat ditentukan oleh urutan masuk barang yang dimiliki masing-masing kandidat solusi. Pada setiap barang yang akan disusun berdasarkan urutannya, barang
tersebut akan diperiksa untuk menentukan posisi barang pada mobil box. Bisa atau tidaknya barang tersebut disusun ditentukan oleh nilai parameter yang dimiliki masing-masing barang. Ada batasan-batasan yang tidak boleh dilanggar oleh nilai parameter suatu barang agar barang tersebut dapat disusun pada mobil box seperti
Gambar 3.2. Penentuan Penyusunan Barang
Proses penentuan barang yang dapat disusun pada mobil box sesuai dengan langkah-langkah pada Gambar 3.2. menggunakan parameter mobil pada Tabel 3.1. dan parameter barang pada Tabel 3.2. berdasarkan urutan masuk barang yang terdapat pada Tabel 3.4. untuk kandidat solusi 1 dapat diilustrasikan sebagai berikut.
1. Simpan parameter mobil box yang digunakan, (P = 100, L = 60, T = 50, W = 100).
2. Barang diurutkan berdasarkan urutan masuk barang yang dimiliki kandidat solusi 1, yaitu 4-10-1-5-3-2-8-6-9-7.
Simpan data barang i, i=(1,2,...,n)
Simpan parameter mobil (panjang, lebar, tinggi, beban maksimum)
While (i <= n)
Simpan parameter barang i (panjang, lebar, tinggi, berat, perotasian)
If berat barang i + total berat barang tersusun <= beban maksimum mobil
If barang i dapat dirotasi
Analisa setiap parameter barang i sebanyak enam variasi orientasi barang Simpan nilai dimensi 1, dimensi 2, dan dimensi 3 barang sesuai variasi orientasi yang paling sesuai mengisi celah
Else
Tetapkan panjang barang sebagai dimensi 1, tinggi barang sebagai dimensi 2, dan lebar barang sebagai dimensi 3
If dimensi 1 barang i <= lebar mobil dan dimensi 2 barang i <= tinggi mobil dan dimensi 3 barang i <= panjang mobil
If (dimensi 1 barang i <= sisa lebar mobil) Susun barang i ke samping
Else if (dimensi 2 barang i <= sisa tinggi mobil) Susun barang i ke atas
Else if (dimensi 3 barang i <= sisa panjang mobil) Susun barang i ke belakang
Else
Barang i tidak dapat disusun Simpan koordinat posisi barang i
Update sisa lebar, panjang, dan tinggi mobil Update total berat barang tersusun
Else
Barang i tidak dapat disusun Ambil barang selanjutnya (i = i+1)
End While
3. Simpan parameter barang urutan pertama, yaitu barang 4 (p = 25, l = 25, t = 20, w = 6, rotasi = tidak).
4. Periksa berat barang (w = 6) apakah tidak melebihi batas beban maksimal mobil (W=100). Jika melebihi, barang tidak dapat disusun.
5. Periksa perotasian barang. Untuk barang yang dapat dirotasi, analisa setiap parameter barang dengan menukar nilai masing-masing dimensi barang sebanyak enam variasi orientasi untuk mencari orientasi mana yang paling sesuai mengisi celah pada mobil box. Simpan nilai dimensi 1, dimensi 2, dan dimensi 3 barang. Untuk barang yang tidak dapat dirotasi, tetapkan panjang barang sebagai dimensi 1, tinggi barang sebagai dimensi 2, dan lebar barang sebagai dimensi 3.
6. Periksa dimensi 1, dimensi 2, dan dimensi 3 barang (p = 25, t = 20, l = 25) apakah tidak melebihi lebar, tinggi, dan panjang mobil (L = 60, T = 50, P =
100). Jika melebihi, barang tidak dapat disusun.
7. Periksa masing-masing dimensi 1, dimensi 2, dan dimensi 3 barang dan bandingkan dengan masing-masing sisa lebar, tinggi, dan panjang mobil. Jika dimensi 1 barang (p = 25) lebih kecil dari sisa lebar mobil (L = 60), maka
barang disusun ke samping. Jika dimensi 2 barang (t = 20) lebih kecil dari sisa tinggi mobil (T = 50), maka barang disusun ke atas. Jika dimensi 3 barang (l = 25) lebih kecil dari sisa panjang mobil (P = 100), maka barang disusun ke belakang. Jika kondisi tidak terpenuhi, maka barang tidak dapat disusun. 8. Simpan koordinat dan posisi barang (cox= 0, coy= 0, coz= 0, px = 25 , py=
20, dan pz= 25).
9. Ubah sisa panjang, lebar, tinggi, dan beban maksimal mobil (P = 100-25 = 75, L = 60-25 = 35, T = 50-20 = 30, W = 100-6 = 94).
10.Ulangi langkah 3 hingga 9 untuk semua barang berdasarkan urutan masuk barang.
11.Ulangi langkah 2 hingga 10 untuk semua kandidat solusi.
dimensi barang tersebut. Sebagai contoh, kandidat solusi 2 memiliki urutan penyusunan yaitu 4-9-1-10-2-7-3-6-5-8. Barang 1 yang berada pada urutan ke-3
memiliki parameter panjang, tinggi, dan lebar berturut-turut adalah 40, 30, dan 30 serta memiliki sifat dapat dirotasi sehingga memiliki enam variasi orientasi seperti yang ditunjukkan oleh Gambar 2.3. Perbedaan susunan barang pada urutan ke-3 untuk enam variasi orientasi yang dimiliki barang 1 dapat dilihat pada Gambar 3.3.
(a) (b) (c)
(d) (e) (f)
Gambar 3.3. Variasi Orientasi Susunan Barang (a) Variasi 1; (b) Variasi 2;
(c) Variasi 3; (d) Variasi 4; (e) Variasi 5; (f) Variasi 6
Pada Gambar 3.3. dapat dilihat enam variasi susunan barang pada urutan ke-3. Pada variasi 1 dan 2, dimensi panjang barang ditetapkan sebagai dimensi 1 sehingga menempati lebar mobil. Pada variasi 3 dan 4, dimensi panjang barang ditetapkan sebagai dimensi 2 sehingga menempati tinggi mobil. Pada variasi 5 dan 6, dimensi panjang barang ditetapkan sebagai dimensi 3 sehingga menempati panjang mobil. Variasi 3 dan 4 tidak akan dipilih sebagai orientasi untuk barang 1 dikarenakan batasan kapasitas ruang mobil box dilanggar, yaitu tinggi penyusunan barang melebihi tinggi mobil box. Adapun orientasi barang 1 yang akan dipilih di antara variasi 1, 2, 5, dan 6 adalah variasi 1 atau 2. Hal ini dikarenakan nilai dimensi yang menempati panjang mobil pada variasi 1 dan 2, yaitu 30 cm, lebih mendekati nilai dimensi yang menempati panjang mobil untuk barang di urutan sebelumnya (barang 4), yaitu 25 cm,
Sedangkan pada variasi 5 dan 6, selisih nilai dimensi yang menempati panjang mobil sama dengan 15 cm, dikarenakan nilai dimensi yang menempati panjang mobil pada
variasi tersebut adalah 40 cm. Pemilihan orientasi barang yang paling sesuai dengan membandingkan selisih nilai dimensi yang menempati panjang mobil ini dilakukan agar celah yang tidak dapat terisi barang dapat diminimalkan.
Perhitungan Nilai Fitness
Pada setiap langkah penyusunan barang, masing-masing kandidat solusi akan dievaluasi dengan cara menghitung nilai fitness berdasarkan fungsi objektif yang diberikan, yaitu untuk memaksimalkan total volume barang yang dapat disusun pada mobil box. Nilai fitness dari masing-masing kandidat solusi didapatkan dengan cara menghitung total volume barang yang berhasil disusun pada mobil box. Perhitungan nilai fitness masing-
masing solusi ditentukan berdasarkan barang-barang apa saja yang dapat disusun
sesuai urutan masuk barang. Urutan masuk tersebut dievaluasi apakah menghasilkan susunan yang optimal dengan cara menghitung total volume barang yang berhasil disusun.
Pada Tabel 3.4, dapat dilihat bahwa kandidat solusi 1 memiliki urutan
f(x) 1 = (40*30*30*1) + (35*25*30*1) + (30*30*30*1) + (25*25*20*1) +
(40*20*10*1) + (40*30*30*0) + (20*20*30*0) + (25*25*25*1) + (30*15*20*0) + (25*15*15*1)
= (36000) + (26250) + (27000) + (12500) + (8000) + (0) + (0) + (15625) + (0) + (5625)
= 131000
Sedangkan total volume yang didapat jika urutan masuk barang yang dihasilkan oleh kandidat solusi 2 diterapkan adalah sebagai berikut.
f(x) 2 = (40*30*30*1) + (35*25*30*1) + (30*30*30*1) + (25*25*20*1) +
(40*20*10*1) + (40*30*30*1) + (20*20*30*1) + (25*25*25*0) + (30*15*20*1) + (25*15*15*1)
= (36000) + (26250) + (27000) + (12500) + (8000) + (36000) + (12000) + (0) + (9000) + (5625)
= 172375
Dari dua perhitungan total volume di atas dapat dilihat bahwa nilai fitness yang dihasilkan oleh kandidat solusi 1 adalah 131000 sedangkan nilai fitness yang dihasilkan oleh kandidat solusi 2 adalah 172375.
3.3.3. Optimalisasi Penyusunan Barang Menggunakan Algoritma Firefly
Pada tahapan optimalisasi penyusunan barang, penerapan algoritma firefly digunakan untuk mengoptimalkan susunan barang yang telah dihasilkan pada tahapan sebelumnya sehingga didapatkan solusi penyusunan yang lebih baik dibandingkan susunan yang dihasilkan sebelumnya sesuai dengan batasan-batasan yang ada. Tahapan penerapan algoritma firefly dalam optimalisasi penyusunan barang dapat
Gambar 3.4. Tahapan Penerapan Algoritma Firefly
Gambar 3.5. Langkah-langkah Algoritma Firefly pada Optimalisasi
Penyusunan Barang
Adapun penjelasan dari Gambar 3.5. adalah sebagai berikut :
Tahapan awal pada algoritma firefly adalah tahapan inisialisasi untuk
pembentukan populasi awal algoritma firefly. Pada tahapan ini parameter-parameter algoritma firefly ditentukan. Nilai posisi awal dari masing-masing
firefly juga akan ditentukan sesuai dengan bilangan acak yang dihasilkan pada
tahapan sebelumnya sebanyak jumlah barang yang akan disusun dan kandidat solusi yang diinginkan.
Kemudian nilai intensitas cahaya masing-masing firefly akan ditentukan sesuai
dengan nilai fitness yang dihasilkan pada tahapan sebelumnya. Lalu, lakukan pencarian nilai fitness kedua yaitu pencarian total volume barang untuk ketinggian 0-1/2 tinggi mobil.
Inisialisasi jumlah populasi firefly (n), jumlah generasi atau iterasi (t), jumlah barang (d)
Inisialisasi parameter algoritma firefly (α,o,)
Tentukan posisi awal masing-masing firefly xi (i=1,2,..,n)
Tetapkan nilai fitness awal firefly f(x) sebagai intensitas cahaya firefly x (Ix)
Hitung nilai fitness 2 firefly (f(x)2) While kriteria berhenti belum terpenuhi
For i = 1 sampai i = n
For j = i+1 sampai j = n
If (Ii) < (Ij) atau (Ii) = (Ij) dan f(i)2 < f(j)2
Lakukan pergerakan firefly i mendekati firefly j
End if
Evaluasi solusi dengan melakukan penyusunan barang berdasarkan posisi baru firefly
Hitung nilai fitness firefly baru
Tetapkan nilai fitness firefly baru sebagai nilai intensitas cahaya baru masing-masing firefly
Hitung nilai fitness 2 firefly
End for j
End for i
Urutkan firefly dari tertinggi hingga terendah berdasarkan nilai I Tetapkan firefly dengan nilai I tertinggi sebagai firefly terbaik (nbest)
End While
Pada tahapan pergerakan firefly, masing-masing firefly dibandingkan
berdasarkan nilai intensitas cahayanya. Firefly yang memiliki intensitas cahaya lebih kecil akan bergerak mendekati firefly yang memiliki intensitas cahaya lebih besar. Apabila terdapat firefly yang memiliki nilai intensitas cahaya sama, maka bandingkan nilai fitness 2 masing-masing firefly. Firefly yang memiliki nilai fitness 2 lebih kecil akan bergerak mendekati firefly yang memiliki nilai fitness 2 lebih besar. Dari proses pergerakan firefly tersebut akan didapatkan posisi baru bagi masing-masing firefly.
Solusi penyusunan akan dievaluasi sesuai dengan urutan masuk barang yang dihasilkan oleh posisi baru firefly dengan cara menyusun barang-barang
menggunakan urutan tersebut. Posisi baru masing-masing firefly ini akan menghasilkan solusi penyusunan yang baru juga sehingga nilai intensitas cahaya dan nilai fitness 2 masing-masing firefly akan berubah dikarenakan berubahnya urutan masuk barang masing-masing firefly.
Firefly lalu diurutkan berdasarkan intensitas cahayanya. Firefly yang memiliki
intensitas cahaya terbesar akan ditandai sebagai firefly terbaik pada iterasi ini dan akan dipertahankan untuk iterasi berikutnya.
Tahapan pergerakan firefly hingga pengurutan firefly akan terus diulang
sampai kriteria berhenti terpenuhi.
Firefly terbaik dari seluruh iterasi akan diambil sebagai solusi penyusunan
terbaik.
Inisialisasi Populasi Firefly
Tahapan inisialisasi populasi firefly dilakukan untuk membangkitkan populasi firefly. Tahapan inisialisasi dimulai dengan menentukan nilai dari parameter-parameter algoritma firefly seperti jumlah populasi firefly (n), jumlah generasi atau iterasi (t),
konstanta alpha (α), konstanta ketertarikan (o), dan konstanta gamma (). Setelah itu
dilanjutkan dengan menentukan banyaknya dimensi firefly yang akan digunakan sebagai posisi awal dari masing-masing firefly (xij). Terdapat dua dimensi yaitu
dimensi i dan dimensi j. Banyaknya dimensi i ditentukan oleh banyaknya populasi firefly yang merupakan jumlah kandidat solusi yang diinginkan sedangkan banyaknya
Setelah banyaknya dimensi ditentukan, pembangkitan bilangan acak dilakukan untuk menentukan nilai posisi awal masing-masing firefly, kemudian diisikan ke
dalam matriks solusi (i x j) dimana dimensi i akan mewakilkan kandidat solusi dan
dimensi j akan mewakilkan barang yang akan disusun. Setiap satu firefly i akan memiliki nilai posisi sebanyak j. Sebagai contoh, jika ada dua firefly dengan jumlah barang sebanyak sepuluh, maka akan ada dua puluh nilai posisi yang harus diisikan ke dalam matriks solusi. Adapun nilai posisi awal masing-masing firefly i (x) untuk setiap barang j dapat dilihat pada Tabel 3.4.
Tabel 3.4. Nilai Posisi Awal Firefly f1 dan f2
Pada penelitian ini, nilai intensitas cahaya masing-masing firefly ditentukan oleh fungsi objektif sesuai dengan Persamaan 2.5. yang dalam hal ini merupakan nilai
fitness. Nilai intensitas cahaya awal firefly ditentukan berdasarkan nilai fitness yang dihasilkan oleh masing-masing kandidat solusi pada tahapan perhitungan fitness sebelumnya. Nilai fitness yang dihasilkan masing-masing kandidat solusi akan dijadikan nilai intensitas cahaya awal masing-masing firefly. Nilai intensitas cahaya awal untuk masing-masing firefly f1 dan f2 sesuai dengan perhitungan fitness pada tahapan sebelumnya dapat dilihat pada Tabel 3.5.
Tabel 3.5. Nilai Intensitas Cahaya Awal Firefly f1dan f2
Firefly Intensitas Cahaya (I) Urutan Masuk Barang
f1 131000 4-10-1-5-3-2-8-6-9-7
f2 172375 4-9-1-10-2-7-3-6-5-8
yang memiliki nilai intensitas cahaya sesuai dengan nilai total volume barang yang dapat disusun oleh kandidat solusi 2.
Pergerakan Firefly
Pada tahapan ini, solusi yang dihasilkan oleh masing-masing firefly pada tahap sebelumnya akan dioptimalkan dengan cara mencari solusi lain sehingga diharapkan dapat menghasilkan solusi yang optimal. Pergerakan firefly terjadi apabila ada satu firefly yang intensitas cahayanya lebih besar daripada intensitas cahaya firefly yang berada di sekitarnya.
Pada penentuan nilai intensitas cahaya firefly sebelumnya diketahui bahwa firefly f1 memiliki intensitas cahaya sebesar 131000 sedangkan firefly f2 memiliki intensitas cahaya sebesar 172375. Dikarenakan intensitas cahaya firefly f2 lebih besar daripada intensitas cahaya firefly f1, maka firefly f1 akan bergerak mendekati firefly f2. Perhitungan dari pergerakan firefly dilakukan sebanyak barang yang ada sehingga akan menghasilkan posisi baru bagi firefly f1. Sebelum posisi baru dari masing-masing firefly untuk setiap dimensi j dihitung, jarak antara dua firefly harus dicari terlebih dahulu. Ilustrasi perhitungan jarak antar dua buah firefly f1 dan f2 dapat dilihat pada Tabel 3.6.
Tabel 3.6. Perhitungan Jarak Dua Firefly
Firefly
Jarak antar firefly dihitung dengan menjumlahkan selisih kuadrat dari posisi firefly f1 dengan firefly f2 sebanyak dimensi yang ada. Pada Tabel 3.6. dapat dilihat hasil dari selisih kuadrat posisi firefly f1 dan f2 untuk masing-masing dimensi, kemudian hasil selisih kuadrat tersebut dijumlahkan dan dicari akarnya. Contoh
rf1f2 = (0.003+0.008+0.194+0.001+0.444+0.009+0.067+0.537+
0.442+0.037)
= 1.476
= 1.321
Setelah jarak antar firefly diperoleh, maka dilanjutkan dengan menggerakkan firefly f1 mendekati firefly f2 dengan cara mencari posisi baru bagi firefly f1. Posisi awal dari firefly f1 (xf1) diubah menjadi posisi baru (xf1’) dikarenakan intensitas
cahaya firefly f1 lebih kecil daripada intensitas cahaya firefly f2. Contoh perhitungan pergerakan firefly f1 pada dimensi j=1 berdasarkan Persamaan 2.7 dengan nilai
Perhitungan tersebut dilanjutkan sebanyak dimensi j yang ada pada firefly f1. Adapun hasil perhitungan pergerakan firefly f1 untuk setiap dimensi j terdapat pada Tabel 3.7.
Tabel 3.7. Posisi Baru Firefly f1
Firefly