METODE
MULTIPLE-KEY
RSA
SKRIPSI
FAUZANA S
091401031
PROGRAM STUDI S1 ILMU KOMPUTER
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA
2
SKRIPSI
Diajukanuntukmelengkapitugasakhirdanmemenuhisyaratmemperoleh ijazahSarjanaIlmu Komputer
FAUZANA S 091401031
PROGRAM STUDI S1 ILMU KOMPUTER
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
ii
PERSETUJUAN
Judul : ANALISIS DAN PERANCANGAN SISTEM
AUTENTIKASI PENGGUNA PADA WEB MENGGUNAKAN METODE
MULTIPLE-KEY RSA
Kategori : SKRIPSI
Nama : FAUZANA S
Nomor Induk Mahasiswa : 091401031
Program Studi : SARJANA (S1) ILMU KOMPUTER
Departemen : ILMU KOMPUTER
Fakultas : ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, 13 Juni 2013
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
M. Andri Budiman, ST, M.Comp.Sc, MEM Maya Silvi Lydia, B.Sc, M.Sc
NIP.197510082008011011 NIP.197401272002121001
Diketahui/Disetujui oleh
Program Studi S1 Ilmu Komputer Ketua,
PERNYATAAN
ANALISIS DAN PERANCANGAN SISTEM AUTENTIKASI PENGGUNA PADA WEB MENGGUNAKAN METODE
MULTIPLE-KEY RSA
SKRIPSI
Saya menyatakan bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing telah disebutkan sumbernya.
Medan, 12 Juni2013
iv
PENGHARGAAN
Puji dan syukur kehadirat Allah SWT, yang hanya dengan rahmat dan izin-Nya penulis dapat menyelesaikan penyusunan skripsi ini, sebagai syarat untuk memperoleh gelar Sarjana Komputer, pada Program Studi S1 Ilmu Komputer Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara.
Ucapan terima kasih penulis sampaikan kepada:
1. Bapak Dr. Poltak Sihombing, M.Kom selaku Ketua Program Studi S1 Ilmu Komputer Universitas Sumatera Utara.
2. Ibu Maya Silvi Lydia, B.Sc, M.Sc selaku Sekretaris Program Studi
S1IlmuKomputer Universitas Sumatera Utara dan Dosen Pembimbing.
3. Bapak M. Andri Budiman, ST, M.Comp.Sc, MEM selaku Dosen Pembimbing.
4. Bapak Syahriol Sitorus, S.Si, MITdan Ibu Dian Wirdasari, S.Si, M.Kom selaku Dosen Pembanding.
5. Dekan dan Pembantu Dekan Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara, seluruhtenaga pengajar dan pegawai diProgram Studi S1Ilmu Komputer Fasilkom-TIUSU.
6. Ayahanda Sudirman Chaniago dan ibunda Farni Fachruddin, serta kakanda
Muhammad Hasief yang selalu memberikan kasih sayang dan dukungannya kepada penulis.
7. Rekan-rekan kuliah, khususnya Fithri Rizqi Khairani Nasution dan Murni
Novita Sari, serta teman-teman ca8in, Zulwita Hariyati, Fany Fairina Nadyaningrum, Nurul Ulfah Primadini, Uswatun Hasanah, Annissa Fadilla, AuliaAkbar Harahap, dan Idris Siddiq yang selalu memberikan semangat dan dorongan kepada penulisselama menyelesaikan skripsi ini.
Semoga Allah SWT melimpahkan berkahkepada semua pihak yang telah memberikan bantuan, perhatian, serta dukungan kepada penulis dalam menyelesaikan skripsi ini.Akhirnya, semoga skripsi ini bermanfaat bagi pribadi, keluarga, masyarakat, organisasi dan negara.
Medan, 12 Juni 2013
ABSTRAK
Sistem berbasis web dengan banyak pengguna memerlukan proses autentikasi untuk pemberian akses karena setiap pengguna sistem memiliki peran yang berbeda-beda satu sama lainnya. Proses autentikasi dilakukan untuk memeriksa identitas pengguna berdasarkan nama pengguna dan kata sandi. Salah satu mekanisme yang digunakan untuk proses autentikasi ini adalah Multiple-KeyRSA. Algoritma ini membangkitkan satu kunci utama dari seluruh kunci-kunci lainnya. Kunci-kunci dibangkitkan dengan syarat bahwa kunci yang akan dibangkitkan merupakan bilangan ganjil dan relatif prima terhadap kunci-kunci yang telah dibangkitkan sebelumnya. Pembangkitan kunci
menggunakan konsep Strong Prime yang diimplementasikan dengan algoritma
Gordon. Untuk membangkitkan bilangan prima, bilangan dibangkitkan secara acak dan diuji menggunakan algoritma Miller-Rabin. Implementasi sistem menggunakan bahasa pemrograman Python 2.7, framework Flask dan database MongoDB. Sistem diuji dengan kata sandi sepanjang 8 karakter, user sebanyak 2 hingga 10 pengguna dan panjang kunci maksimum 4096 bit dengan interval 512 bit. Hasil penelitian menunjukkan bahwa untuk setiap panjang kunci berbanding lurus terhadap kata sandi yang dienkripsi. Selain itu, setiap bit kunci yang dibangkitkan menggunakan algoritma Gordon akan memiliki digit yang lebih panjang dari yang diharapkan. Rata-rata keseluruhan proses enkripsi adalah 0.404 detik dan dekripsi adalah 0.517 detik dengan kompleksitas waktu enkripsi maupun dekripsi pada kasus terbaik dan rata-rata ialah
Ο(log(�)2) dan pada kasus terburukialah Ο(log(�)3). Kompleksitas waktu algoritma Miller-Rabin ialah Ο(�log3�), dengan �= banyaknya nilai yang diuji atau |�| =
jumlah digit �. Kompleksitas waktu algoritma Gordon ialah Ο(|�| log3�).
vi
ANALYSIS AND DESIGN OF USER AUTHENTICATIONSYSTEM ON THE WEB USING MULTIPLE KEYRSA
ABSTRACT
Web-based system with many users requires authentication process for granting user acces because each user has different role. Authentication process is performed to verify the identity of the user based on username and password. One mechanism that is used for the authentication process is Multiple-Key RSA. These algorithms generate a main key from all other keys. The keys are generated such that the next key is odd number and coprime to the keys that had been generated previously. Key generation use the concept of a Strong Prime that implemented with Gordon algorithm. A number randomly generated and tested using the Miller-Rabin algorithm to generate prime number. System is implemented using Python 2.7 programming language, Flask
framework and MongoDB database. The system was tested with 8
characterspassword, with 2 up to 10 users and 4096 bitsmaximum key length with 512 bit interval. The results show that for each key length and encrypted password is linear ratio. Additionally and occasionally, every bit key generated using algorithms Gordon islonger than expected. Overall average is 0.404 second for encryption process and the decryption is 0.517 second with Ο(log(�)2)time complexity of encryption and decryption in best and average caseand worst case isΟ(log(�)3). Time complexity of Miller-Rabin algorithm is Ο(�log3�), with k = number of tested values or |�| =
numberofdigits. Gordon algorithm time complexity is Ο(|�| log3�).
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak v
Abstract vi
Daftar Isi vii
Daftar Tabel ix
Daftar Gambar x
Daftar Lampiran xi
Bab I Pendahuluan
1.1 Latar Belakang 1
1.2 Rumusan Masalah 2
1.3 Batasan Masalah 2
1.4Tujuan Penelitian 2
1.5 Manfaat Penelitian 2
1.6 Metodologi Penelitian 3
1.7 Sistematika Penulisan 3
BabII Landasan Teori
2.1 Kriptografi 5
2.1.1 Definisi Kriptografi 5
2.1.2 Tujuan Kriptografi 5
2.2 Sistem Kriptografi 6
2.2.1 Sistem Kriptografi Klasik (Simetris) 6
2.2.2 Sistem Kriptografi Modern (Asimetris) 7
2.2.3 Sistem Kriptografi Kunci Publik 7
2.3 Teori Bilangan Integer 8
2.3.1 Faktor Persekutuan Terbesar 8
2.3.2 Algoritma Euclid dan Extended Euclid 8
2.3.3 Invers Modulo 9
2.3.4ϕ˗Euler 9
2.3.5Eksponensial Modulo 10
2.4 Sistem Kriptografi RSA 10
2.4.1 Pembangkitan kunci RSA 10
2.4.2 Enkripsi RSA 11
2.4.3 Dekripsi RSA 11
2.5Sistem Kriptografi Multiple-KeyRSA 11
2.6 Algoritma Miller-Rabin 13
2.7Strong Prime 14
viii
Bab III Analisis dan Perancangan
3.1 Analisis Sistem 15
3.1.1 Analisis Masalah 15
3.1.2 Analisis Kebutuhan 16
3.1.2.1Kebutuhan Fungsional 17
3.1.2.2Kebutuhan Nonfungsional 18
3.1.3Analisis Proses 18
3.2 Perancangan Sistem 19
3.2.1 Flowchart 19
3.2.1.1 Flowchart Pembangkitan Kunci 19
3.2.1.2Flowchart Algoritma Miller-Rabin 21
3.2.1.3Flowchart Algoritma Gordon 22
3.2.2 Data Flow Diagram (DFD) 23
3.2.4.2Status Page 28
3.2.4.3Setting Page 28
3.2.4.4Reset Page 28
3.2.4.5System Page 29
Bab IV Implementasi dan Pengujian
4.1 Implementasi 30
4.1.1 Index Page 30
4.1.2 Status Page 31
4.1.3Setting Page 32
4.1.4 System Page 33
4.1.5 Reset Page 34
4.2 Pengujian 35
4.2.1 Skenario Enkripsi 36
4.2.2 Skenario Pembangkitan Kunci dan Proses Dekripsi 36
4.2.3Pengujian dan Analisis Hasil Enkripsi dan Dekripsi 37
4.2.4Pengujian dan Analisis Waktu Eksekusi
Miller-Rabin Primality Test 40
4.2.5Pengujian dan Analisis Waktu Eksekusi Gordon Strong Prime 41 4.2.6Pengujian dan Analisis Waktu Eksekusi Pembangkitan Kunci 43
Bab V Kesimpulan dan Saran
5.1 Kesimpulan 45
5.2Saran 46
DAFTAR TABEL
Halaman
Tabel 3.1 Kamus Data Keys 27
Tabel 3.2 Kamus Data User_log 27
Tabel 3.3 Kamus Data Users 28
Tabel 4.1 Enkripsi kata sandi 37
Tabel 4.2 Dekripsi kata sandi 37
Tabel 4.3 Pasangan Kata Sandi dan Kunci setiap User 38
Tabel 4.4 Panjang Ciphertext, Rata-rata lama eksekusi proses Enkripsi dan Dekripsi
untuk setiap Panjang Kunci 39
Tabel 4.5 Kode enkripsi pesan 39
Tabel 4.6 Kode dekripsi pesan 40
Tabel 4.7 Rata-rata lama eksekusi Miller-Rabin Primality Test untuk setiap Panjang
Kunci 42
Tabel 4.8 Kode algoritma Miller-Rabin 42
Tabel 4.9 Rata-rata lama eksekusi algoritma Gordon untuk setiap Panjang Kunci 43
Tabel 4.10 Kode Pembangkit Bilangan Prima 44
Tabel 4.11 Kode algoritma Gordon 44
Tabel 4.12 Rata-rata lama eksekusi Pembangkitan Kunci Multiple-Key RSA untuk
x
DAFTAR GAMBAR
Halaman
Gambar 2.1 Skema Sistem Kriptografi Klasik 7
Gambar 2.2 Skema Sistem Kriptografi Kunci Publik 8
Gambar 3.1 Diagram Ishikawa Masalah Penelitian 17
Gambar 3.2 Flowchart Pembangkitan Kunci 21
Gambar 3.3 Flowchart A. Algoritma Miller-Rabin B. Fungsi Witness 22
Gambar 3.4 Flowchart Algoritma Gordon 23
Gambar 3.5 DFD Level 0 24
Gambar 3.6 DFD Level 1 25
Gambar 3.7 DFD Level 2 Proses 1 25
Gambar 3.8 DFD Level 2 Proses 2 26
Gambar 3.9 DFD Level 2 Proses 4 27
Gambar 3.10 Mockup Index page 28
Gambar 3.11 Mockup Status page 29
Gambar 3.12 Mockup Setting page 29
Gambar 3.14 Mockup System page 30
Gambar 4.1 Index Page 32
Gambar 4.2 Status Page 33
Gambar 4.3 Setting Page 34
Gambar 4.4 System Page 35
Gambar 4.5 Reset Page 36
Gambar 4.6 Grafik Panjang Kunci terhadap Panjang Kata Sandi Terenkripsi 39
Gambar 4.7 Grafik Panjang Kunci terhadap lama Proses Enkripsi 40
Gambar 4.8 Grafik Panjang Kunci terhadap lama Proses Dekripsi 40
Gambar 4.9 Grafik Panjang Kunci terhadap lama eksekusi
Miller-Rabin Primality Test untuk setiap Jumlah Pengguna 41
Gambar 4.10 Grafik Panjang Kunci terhadap lama eksekusi
algoritma Gordon untuk Setiap Jumlah Pengguna 43
Gambar 4.11 Grafik Panjang Kunci terhadap lama Pembangkitan Kunci
DAFTAR LAMPIRAN
Halaman
A. Listing Program A-1
v
ABSTRAK
Sistem berbasis web dengan banyak pengguna memerlukan proses autentikasi untuk pemberian akses karena setiap pengguna sistem memiliki peran yang berbeda-beda satu sama lainnya. Proses autentikasi dilakukan untuk memeriksa identitas pengguna berdasarkan nama pengguna dan kata sandi. Salah satu mekanisme yang digunakan untuk proses autentikasi ini adalah Multiple-KeyRSA. Algoritma ini membangkitkan satu kunci utama dari seluruh kunci-kunci lainnya. Kunci-kunci dibangkitkan dengan syarat bahwa kunci yang akan dibangkitkan merupakan bilangan ganjil dan relatif prima terhadap kunci-kunci yang telah dibangkitkan sebelumnya. Pembangkitan kunci
menggunakan konsep Strong Prime yang diimplementasikan dengan algoritma
Gordon. Untuk membangkitkan bilangan prima, bilangan dibangkitkan secara acak dan diuji menggunakan algoritma Miller-Rabin. Implementasi sistem menggunakan bahasa pemrograman Python 2.7, framework Flask dan database MongoDB. Sistem diuji dengan kata sandi sepanjang 8 karakter, user sebanyak 2 hingga 10 pengguna dan panjang kunci maksimum 4096 bit dengan interval 512 bit. Hasil penelitian menunjukkan bahwa untuk setiap panjang kunci berbanding lurus terhadap kata sandi yang dienkripsi. Selain itu, setiap bit kunci yang dibangkitkan menggunakan algoritma Gordon akan memiliki digit yang lebih panjang dari yang diharapkan. Rata-rata keseluruhan proses enkripsi adalah 0.404 detik dan dekripsi adalah 0.517 detik dengan kompleksitas waktu enkripsi maupun dekripsi pada kasus terbaik dan rata-rata ialah
Ο(log(�)2) dan pada kasus terburukialah Ο(log(�)3). Kompleksitas waktu algoritma Miller-Rabin ialah Ο(�log3�), dengan �= banyaknya nilai yang diuji atau |�| =
jumlah digit �. Kompleksitas waktu algoritma Gordon ialah Ο(|�| log3�).
ANALYSIS AND DESIGN OF USER AUTHENTICATIONSYSTEM ON THE WEB USING MULTIPLE KEYRSA
ABSTRACT
Web-based system with many users requires authentication process for granting user acces because each user has different role. Authentication process is performed to verify the identity of the user based on username and password. One mechanism that is used for the authentication process is Multiple-Key RSA. These algorithms generate a main key from all other keys. The keys are generated such that the next key is odd number and coprime to the keys that had been generated previously. Key generation use the concept of a Strong Prime that implemented with Gordon algorithm. A number randomly generated and tested using the Miller-Rabin algorithm to generate prime number. System is implemented using Python 2.7 programming language, Flask
framework and MongoDB database. The system was tested with 8
characterspassword, with 2 up to 10 users and 4096 bitsmaximum key length with 512 bit interval. The results show that for each key length and encrypted password is linear ratio. Additionally and occasionally, every bit key generated using algorithms Gordon islonger than expected. Overall average is 0.404 second for encryption process and the decryption is 0.517 second with Ο(log(�)2)time complexity of encryption and decryption in best and average caseand worst case isΟ(log(�)3). Time complexity of Miller-Rabin algorithm is Ο(�log3�), with k = number of tested values or |�| =
numberofdigits. Gordon algorithm time complexity is Ο(|�| log3�).
BAB I
PENDAHULUAN
1.1 Latar Belakang
Proses autentikasi pengguna sistem berbasis web diperlukan untuk melakukan
verifikasi identitas seorang pengguna untuk memperoleh akses ke sistem atau area
terbatas lainnya. Pada umumnya, proses ini menggunakan nama pengguna dan kata
sandi yang berupa kumpulan karakter. Karena keterbatasan akses ini, kepemilikan
kata sandi harus berada pada tangan yang tepat, di mana kata sandi super user harus dimiliki oleh orang yang berada pada posisi tertinggi dalam hierarki organisasi.
Masing-masing pengguna mempunyai kedudukan, tugas, hak dan kewajiban
yang berbeda satu dengan lainnya. Misalkan dalam dunia akademis, seperti
universitas, jabatan tertinggi dipegang oleh rektor yang selanjutnya dibantu dengan
beberapa pembantu rektor. Pada contoh ini, kekuasaan seorang rektor pada sistem
akan setara dengan seluruh pembantu rektor dalam pembuatan suatu keputusan.
Karena perbedaan kekuatan ini, timbul masalah bagaimana autentikasi masing-masing
entitas terkait agar memberikan kepastian identitas.
RSA merupakan algoritma kriptografi modern yang diperkenalkan oleh Ron
Rivest, Adi Shamir dan Len Adleman. Pada penelitian oleh Indra [8], kecepatan
pemrosesan RSA lebih cepat dibandingkan algoritma kunci publik umumnya.
Berdasarkan outputnya, algoritma RSA menghasilkan ukuran teks cipher yang lebih kecil. Namun dalam hal keamanan, RSA tidak terlalu dominan walaupun pada
dasarnya untuk memecahkan algoritma ini pun sudah sangat sulit.
Algoritma RSA memiliki varian pengembangan yang lebih banyak. Salah
satu pengembangan algoritma RSA ialah konsep multiple-key [10]. Pada
Multiple-KeyRSA, kunci-kunci ditambahkan pada pembangkitan kuncinya yang digunakan
Konsep multiple-keydapat diimplementasikan untuk algoritma asimetris karena dapat meningkatkan kualitas dan kekuatan dari kunci yang sudah ada sebelumnya.
Berdasarkan uraian di atas, maka penulis mengambil tugas akhir dengan judul
“Analisis dan Perancangan Sistem AutentikasiPengguna pada Web Menggunakan
Metode Multiple-Key RSA”.
1.2 Rumusan Masalah
Berdasarkan uraian pada latar belakang, rumusan masalah yang akan dibahas ialah
bagaimana menerapkan sistem kriptografi Multiple-Key RSA untuk melakukan autentikasi pengguna pada web.
1.4 Batasan Masalah
Dalam perancangan prototipe sistem kriptografi Multiple-Key RSA, dilakukan beberapa batasan sebagai berikut:
1. Pembangkit bilangan prima menggunakan konsep Strong Prime. 2. Pengujian bilangan prima menggunakan algoritma Miller-Rabin.
3. Ukuran kunci maksimal adalah 4096 bit.
4. Kriptanalisis tidak dilakukan.
5. Program dibuat dengan bahasa pemrograman Python dan menggunakan
database MongoDB.
1.3 Tujuan Penelitian
Penelitian ini bertujuan untuk membangun sistem yang mampu melakukan autentikasi
pengguna pada web dengan menerapkan sistem kriptografi Multiple-Key RSA.
1.5 Manfaat Penelitian
Penelitian ini diharapkan dapat bermanfaatbagiinstitusi ataupun organisasi yang
3
1.6 Metodologi Penelitian
Metode penelitian yang dilakukan dalam penelitian ini adalah:
1. Studi literatur
Dilakukan peninjauan terhadap buku, jurnal, makalah, serta hasil penelitian yang
membahas tentang kriptografi Multiple-Key RSAdan semua teori yang berkaitan. 2. Analisis dan Perancangan
Berdasarkan rumusan dan batasan masalah, masalahyang ada dianalisis sehingga
dapat dilakukan perancangan dengan baik, seperti pembuatan flowchart, DFD dan mockup.
3. Implementasi
Algoritma Multiple-KeyRSA diimplementasikan sebagai sistem autentikasi pengguna pada web.
4. Pengujian
Pengujian dilakukan terhadap keberhasilan proses yang dilakukan dalam
kriptografi (pembangkitan kunci, enkripsi dan dekripsi).
5. Dokumentasi
Selama analisis dan perancangansistem hingga pengujian, dilakukan
pendokumentasian berupa laporan skripsi.
1.7 Sistematika Penulisan
Sistematikapenulisanskripsiiniterdiri dari beberapa bagian utama, yaitu:
BAB I PENDAHULUAN
Bab ini menjelaskan latar belakang judul skripsi ”Analisis dan
Perancangan Sistem Autentikasi Pengguna pada Web Menggunakan
Metode Multiple-Key RSA”, rumusan masalah, batasan masalah, tujuan penelitian, manfaatpenelitian, metodepenelitian dan sistematika
penulisan.
BAB II LANDASAN TEORI
Bab ini berisi tentang penjelasan singkat mengenai sistem kriptografi
dan teori-teori dasar yang digunakan dalam algoritma RSA, algoritma
BAB IIIANALISIS DAN PERANCANGAN
Bab ini membahas analisis terhadap masalah peelitian dan perancangan
terhadap sistem yang akan dibangun.
BAB IVIMPLEMENTASI DAN PENGUJIAN
Bab ini berisi implementasi algoritma Multiple-Key RSA, skenario pengujian terhadap sistem yang telah dibangun,serta pembahasan hasil
pengujian dan analisisnya.
BAB V KESIMPULAN DAN SARAN
Bab ini memuat kesimpulan dari keseluruhan uraian bab-bab
sebelumnya dan saran berdasarkan hasil pengujian yang diharapkan
BAB II
LANDASAN TEORI
2.1 Kriptografi
2.1.1 Definisi Kriptografi
Secara etimologi, kata kriptografi berasal dari bahasa Yunani, yaitu: kryptos berarti rahasia dan graphein berarti tulisan [18]. Sedangkan secara terminologi, kriptografi adalah ilmu dan seni untuk menjaga kerahasiaan pesan dengan cara menyandikannya
ke dalam bentuk yang tidak dapat dipahami maknanya sehingga tidak dapat dibaca
oleh orang yang tidak berkepentingan.
Dalam kriptografi, setiap orang dimungkinkan untuk bebas memilih metode
untuk merahasiakan pesan. Metode tersebut berbeda-beda (unik) untuk setiap pelaku
kriptografi sehingga penulisan pesan rahasia mempunyai estetika tersendiri. Estetika
penulisan pesan rahasia ini menjadikan kriptografi sebagai sebuah seni. Pada
perkembangan selanjutnya, kriptografi dikenal sebagai disiplin ilmu yang menggunakan
teknik matematika untuk keamanan informasi, seperti privasi dan autentikasi.
2.1.2 Tujuan Kriptografi
Kriptografi bertujuan untuk memberikan layanan keamanan [15] sebagai berikut:
1. Autentikasi (Authentication)
Autentikasi memberikan kepastian terhadap identitas setiap entitas yang terlibat
dan sumber sebuah data.
2. Kerahasiaan (Confidentiality)
Data yang ditransmisikan diproteksi terhadap pengungkapan oleh pihak-pihak
yang tidak berwenang.
3. Keutuhan Data (Data Integrity)
Data yang diterima oleh penerima dipastikan adalah sama dengan data yang
4. Nirpenyangkalan (Non-Repudiation)
Setiap entitas yang berkomunikasi tidak dapat menolak atau menyangkal atas data
yang telah dikirim atau diterima.
2.2 Sistem Kriptografi
Kriptografi membentuk sebuah sistem yang dinamakan sistem
kriptografi(cryptosystem). Cryptosystem adalah lima tuple (P, C, K, E, D), dimana P adalah plaintext,C adalah ciphertext, K adalah himpunan kunci-kunci, E adalah himpunan fungsi enkripsi dan D adalah himpunan fungsi dekripsi [16].Berdasarkan prinsip kerjanya, sistem kriptografi terbagi dua, yaitu sistem kriptografi klasik (simetris)
dan modern (asimetris) [1].
2.2.1 Sistem Kriptografi Klasik (Simetris)
Kriptografi klasik umumnya merupakan teknik penyandian dengan kunci simetris dan
pesan disembunyikan sehingga tidak memiliki arti dengan metode substitusi dan/atau
transposisi. Terdapat lima komponen utama dalam sistem kriptografi klasik, yaitu:
1. Plaintext
Teks asli dapat berupa pesan atau data sebagai input algoritma enkripsi. 2. Kunci Rahasia
Kunci rahasia sebagai penentu output dari algoritma enkripsi. Antar entitas harus saling mengetahui kunci ini agar dapat melakukan enkripsi/dekripsi pesan.
3. Ciphertext
Hasil dari proses algoritma enkripsi di mana teks asli dianggap telah tersembunyi
(tidak memiliki arti).
4. Algoritma Enkripsi
Algoritma enkripsi mengubah teks asli menjadi ciphertext dengan parameter masukan, yaitu teks asli dan kunci rahasia.
5. Algoritma Dekripsi
Algoritma dekripsi mengubahciphertext menjadi teks asli dengan parameter masukan, yaitu ciphertext dan kunci rahasia.
Berdasarkan skema pada gambar 2.1, kriptografi simetris menggunakan
7
satu kunci rahasia tertentu sebelum mereka dapat berkomunikasi dengan aman.
Keamanan kriptografi simetris ini terletak pada kerahasiaan kuncinya [7]. Semua
algoritma kriptografi klasik termasuk dalam algoritma simetri. Contohnya, DES,
Tripel-DES, AES, RC2, RC4 dan sebagainya.
A
Teks Asli
B
Kunci Rahasia
Ciphertext Teks Asli
: Jalur Rahasia Algoritma
Enkripsi
Algoritma Dekripsi
Gambar 2.1 Skema Sistem Kriptografi Klasik
2.2.2 Sistem Kriptografi Modern (Asimetris)
Sistem kriptografi modern juga disebut kriptografi kunci asimetris, memiliki dua jenis
kunci, yaitu kunci enkripsi dan kunci dekripsi yang berbeda. Kunci enkripsi dimiliki oleh
pengirim dan kunci dekripsi dimiliki oleh penerima pesan. Dalam kriptografi kunci
asimetris, hampir semua algoritma kriptografinya menggunakan konsep kunci publik,
seperti RSA, El-Gamal, dan sebagainya. Kecuali algoritma Pohlig ˗Hellman karena kunci
enkripsi maupun kunci dekripsinya bersifat privat.
2.2.3 Sistem Kriptografi Kunci Publik
Sistem kunci kriptografi kunci publik merupakan bagian dari sistem kriptografi modern.
Pada kriptografi kunci publik terdapat dua jenis kunci, kunci pertama ialah kunci tidak
rahasia, yaitu kunci enkripsi (Ke) yang disebut kunci publik (Kpublik). Kunci kedua ialah
kunci dekripsi (Kd) bersifat rahasia (Kprivat) yang ditunjukkan pada gambar 2.2. Berikut
algoritma sistem kriptografi kunci publik [5]:
(Kpublik , Kprivat) PembangkitKunci() …(B)
Ciphertext Enkripsi(Kpublik , Plaintext) …(A)
A
Teks Asli
B
Kpublik B
Ciphertext Teks Asli
Kprivat B
Algoritma Enkripsi
Algoritma Dekripsi
Pembangkit Kunci
Gambar 2.2 Skema Sistem Kriptografi Kunci Publik
2.3 Teori BilanganInteger
Teori bilangan integer (ℤ) memiliki peran yang sangat besar dalam kriptografi pada umumnya serta merupakan pondasi bagi sistem kriptografi kunci publik. Misalnya,
kekuatan sistem kriptografi RSA yang terletak pada sulitnya faktorisasi bilangan
komposit merupakan bagian dari teori bilanganinteger.
2.3.1 Faktor Persekutuan Terbesar (Greatest Common Divisor)
Faktor persekutuan terbesar adalah elemen terbesar pada himpunan divisor dua bilangan integer. Misalnya, divisor 16 = { 1, 2, 4, 8, 16 } dan divisor 24 = { 1, 2, 3, 4, 6, 8, 12, 24 }, maka himpunan divisor kedua bilangan tersebut ialah { 1, 2, 4, 8 } dan yang terbesar ialah 8. Dengan kata lain, faktor persekutuan terbesar 16 dan 24 dapat
dinotasikan sebagai gcd(16, 24) = 8. Apabila ada dua bilangan integer m dan n memiliki gcd(m, n) = 1, maka bilangan m dan n dapat disebut relatif prima.
2.3.2Algoritma Euclid dan Extended Euclid
Salah satu cara untuk menentukan gcd dua bilangan integer a dan b ialah dengan menggunakan algoritma Euclid. Walaupun algoritma ini dijelaskan dalam buku Euclid
yang berjudulElements, para sejarawan meyakini algoritma ini tidak ditemukan oleh Euclid, melainkan telah ada 200 tahun lebih dahulu dari Elements [18]. Algoritma Euclid merupakan algoritma rekursif yang terdapat dua kasus:
I: b = 0 ���(�, 0) =�
9
Algoritma Euclid dikembangkan menjadi kombinasi linear oleh dengan
koefisien integer a dan bdengan dua bilangan integer s dan t sehingga memenuhi persamaan:
��+��= ���(�,�)
Persamaan tersebut merupakan teorema Bézout yang kemudian disebut algoritma
Extended Euclid [16].Berikut pseudocode algoritma Extended Euclid.
extEuclid(aa, bb):
1. lastremainder, remainder = abs(aa), abs(bb)
2. x, lastx, y, lasty = 0, 1, 1, 0 3. while remainder:
4. lastremainder, (quotient, remainder) =
5. remainder, divmod(lastremainder, remainder) 6. x, lastx = lastx - quotient*x, x
7. y, lasty = lasty - quotient*y, y
8. return lastremainder, lastx * (-1 if aa < 0 else 1), 9. lasty * (-1 if bb < 0 else 1)
2.3.3 Invers Modulo
Bilangan n disebut modulo apabila m mod n = r dan ada k, sehingga:
��+�=�
Sedangkan �−1 adalah invers modulo dari � (����), apabila:
�−1∙ � ≡ 1(����)
�(����) memiliki invers modulo jika dan hanya jika m dan n relatif prima. Salah satu cara untuk menemukan invers �(����) ialah dengan menggunakan algoritma Extended Euclid sehingga memenuhi ��+��= ���(�,�) [17]. Karena
���(�,�) = 1 dan �×� ≡0 (����), maka persamaan tersebut menjadi �×�= 1 atau �×� ≡1 (����) sehingga �= �−1.
2.3.4�˗Euler
�˗Euler atau ditulis�(�) adalah fungsi yang mengembalikan jumlah bilangan integer a dalam 0 <� <� dan a relatif prima dengan n (relatif prima jika gcd(a, n) = 1) [16]. Hasil �(�) untuk empat kasus dasar adalah:
1. �(1) = 0.
2. �(�) =� −1apabila � ∈ bilangan prima.
2.3.5 Eksponensial Modulo
Salah satu operasi modulo yang sering digunakan dalam sistem kriptografi adalah
eksponensial. Pada sistem kriptografi RSA, proses enkripsi dan dekripsinya memakai
operasi eksponensial modulo. Operasi eksponensial modulo dinotasikan sebagai
��(����).
Salah satu implementasi penghitungan eksponensial modulo adalah
algoritma Square and Multiply.Algoritma Square and Multiply mengasumsikan eksponen y dalam bentuk biner sehingga
� =� ��2� �−1
�=0
dengan l adalah panjang y dalam biner, xibernilai0 atau 1 untuk 0 ≤ i ≤ l ˗ 1 [17].
Berikut pseudocode algoritma Square and Multiply.
ModEx(x, y, n): 1. y = 1
2.for i = l – 1 downto 0: 3. y = y * y mod n
4. if xi == 1:
5. y = (y * a) mod n 6. return y
2.4 Sistem Kriptografi RSA
Salah satu algoritma kriptografi kunci publik ialah RSA yang dipublikasikan pada
tahun 1977 [11]. RSA dibangun oleh fungsi eksponensial modulo yang terdiri dari tiga
proses utama, yaitu: pembangkitan kunci, enkripsi, dan dekripsi.
2.4.1 Pembangkitan Kunci RSA
Pemilik kunci harus membangkitkan kunci publik dan privat untuk dapat
menggunakan RSA. Kedua kunci ini membutuhkan dua bilangan prima besar agar
sulit untuk difaktorisasi. Berikut variabel-variabel yang dibutuhkan untuk RSA:
11
e kunci enkripsi: bilangan acak dalam rentang 1 < e < ϕ(n), dengan syarat gcd(e, ϕ(n)) = 1
d kunci dekripsi:e-1 mod ϕ(n)
Kpublik = (e, n)
Kprivat = d
P = plain text C = cipher text
2.4.2 Enkripsi RSA
Proses enkripsi RSA menggunakan kunci publik yang telah dibangkitkan sebelumnya.
Enkripsi pada RSA menggunakan fungsi eksponensial modulokunci enkripsi e berikut:
Kpublik = (e, n)
C Pe mod n
2.4.3 Dekripsi RSA
Untuk mengembalikan cipher text menjadi plain text, dekripsi RSA juga berupa fungsi eksponensial modulon dengan menggunakan kunci privat. Berikutproses dekripsi RSA:
Kpublik = (e, n)
Kprivat = d
P Cd mod n
2.5 Sistem Kriptografi Multiple-Key RSA
Kriptografi kunci publik umumnya menggunakan dua kunci untuk masing-masing
proses enkripsi dan dekripsi. Pada 1988, Colin Boyd memperkenalkan konsep
generalisasi RSA sehingga menjadi algoritma Multiple-Key RSA [18]. Dalam fungsi modulo RSA, n merupakan hasil perkalian dua bilangan prima p dan q sehingga
d · e ≡ 1 mod ϕ(n) Untuk konsep ini, dipilih sejumlah t kunci, sehingga
Berikutlangkah-langkah yang terdapat pada Multiple-Key RSA: (p, q)bilangan prima acak besar, p ≠ q
n p · q, sehingga ϕ(n) (p – 1)· (q – 1) t = jumlah kunci enkripsi dan/atau dekripsi
Pembangkitan kunci enkripsi:
Ke1bilangan acak ganjil dalam rentang 1 < Ke1< ϕ(n), gcd(Ke1, ϕ(n)) = 1
Ke2bilangan acak ganjil dalam rentang 1 < Ke2< ϕ(n),
gcd(Ke1 ·Ke2, ϕ(n)) = 1
⁞
Ketbilangan acak ganjil dalam rentang 1 < Ket< ϕ(n),
gcd(Ke1 ·Ke2 · … · Ket, ϕ(n)) = 1
e Ke1 ·Ke2 · … · Ket
Pembangkitan kunci dekripsi:
Kd1bilangan acak ganjil dalam rentang 1 < Kd1< ϕ(n), gcd(Kd1, ϕ(n)) = 1,
Ke1-1 mod ϕ(n)
Kd2bilangan acak ganjil dalam rentang 1 < Kd2< ϕ(n),
gcd(Kd2 ·Kd2, ϕ(n)) = 1, Ke2-1 mod ϕ(n)
⁞
Kdtbilangan acak ganjil dalam rentang 1 < Kdt< ϕ(n),
gcd(Kd1 ·Kd2 · … · Kdt, ϕ(n)) = 1, Ket-1 mod ϕ(n)
d Kd1 ·Kd2 · … · Kdt
Kpublik = (Ke, n) Kprivat = Kd
P = Plain text C = Cipher text
Proses Enkripsi:
Kpublik = (Ke, n)
C PKe mod n
Proses Dekripsi:
Kpublik = (Ke, n), Kprivat = Kd
13
2.6 Algoritma Miller-Rabin
Algoritma Miller-Rabin merupakan algoritma probabilistik pengujian keprimaan
sebuah bilangan berdasarkan pada Fermat’s LittleTheorem dan kepemilikan akar kuadrat [3]. Fermat’s LittleTheorem menyatakan bahwa
��−1 ≡1 ����
apabila n adalah bilangan prima. Sedangkan untuk kepemilikan akar kuadrat, jika n adalah bilangan prima, akar kuadrat modulo
n��2 = 1 (����)�
akan menghasilkan
1 atau ˗1 �(�+ 1)(� −1) = 0 (����)�.
Misalkan � – 1 = 2�� di mana � ∈ ℕ ialah ganjil dan � ∈ ℕ serta n merupakan bilangan integer positif ganjil (n≥ 3) yang akan diuji keprimaannya [13]. Algoritma Miller-Rabin tidak menghitung ��−1���� secara langsung, melainkan
menghitung deret berikut secara berulang: �� ≡ �2� ≡ �22� ≡ ⋯ ≡ �2�−1� ≡
�2��(����). Pada setiap perhitungan �2�� dilakukan pengujian Fermat dan pengujian kepemilikan akar kuadrat. Jika pengujian akar kuadrat ialah positif, n dideklarasikan sebagai bilangan komposit. Jika pengujian Fermat ialah positif, maka n mungkin bilangan prima. Berikut pseudocode algoritma Miler-Rabin:
MillerRabin(n, s): 1. for j = 1 to s: 2. a = Random(1, n-1) 3. if Witness(a, n): 4. return “Composite” 5. return “Prime”
Witness(a, n):
1. let t and u be such that t ≥ 1, u is odd and n – 1 = 2tu
2.x0 = ModularExponentation(a, u, n)
3. for i = 1 to t: 4. �� =��−21(����)
5. if xi == 1 and xi-1 ≠ 1 and xi-1 ≠ n – 1:
6.return True
7. if xt ≠ 1:
2.7 Strong Prime
Bilangan prima p dikatakan strong prime apabila bilangan bulat q, r dan s ada dan memenuhi kondisi berikut [12]:
� −1 mempunyai faktor prima q
�+ 1 mempunyai faktor prima r
� −1 mempunyai faktor prima s
Pada 1984, Gordon memperkenalkan cara menentukan bilangan yang
memenuhi konsep strong prime [10]. Berikut algoritma Gordon untuk membangkitkan bilangan strong prime [14]:
Gordon_StrongPrime():
1. (�,�) large (probable) primes using MillerRabin,
� ≠ � roughly equal bitlength
2.�= 2��+ 1 First prime in {2��+ 1}� ∈ℕ sequence 3. �0≡ ��−1− ��−1(�����)
4.�=�0+ 2��� First prime in {�0+ 2���}�∈ℕ sequence 5.return p
2.7Penelitian yang Relevan
Berikut penelitian tentang kriptografi yang membahas algoritma RSA atau autentikasi:
1. Pada penelitian oleh Sun dan Yang [19], didesain varian RSA dengan nilai d dan e yang seimbang serta p dan q yang juga seimbang sehingga varian ini lebih aman. Berdasarkan varian RSA ini, sebuah aplikasi diimplementasikan untuk autentikasi
entitas sehingga melindungi serangan stolen-secret.
2. Dalam penelitian oleh Brainard, et al [2], konsep vouchingdiperkenalkan sebagai alat autentikasi online. Konsep ini mengubah konsep identifikasi pengguna dari sisi klien dengan mengembangkan autentikasi klasik. Selain memperkenalkan
konsep vouching, model keamanan dirancang untuk menganalisis vouching dan membahas social-engineering dari protokol banyak pengguna.
3. Berdasarkan penelitian oleh Loebenberger dan Nüsken [9], banyaknya definisi
untuk integer RSA mengakibatkan standar substansial yang berbeda-beda. Selain
15
BAB III
ANALISIS DAN PERANCANGAN
3.1 Analisis Sistem
Analisis sistem terdiri dari fase-fase berbeda yang mendeskripsikan pengembangan
sistem. Dalam tugas akhir ini, ada tiga fase analisis yaitu: analisis masalah, analisis
kebutuhan dan analisis proses. Analisis masalah bertujuan untuk memahami
kelayakan masalah. Analisis kebutuhan dilakukan untuk menjelaskan fungsi-fungsi
yang ditawarkan dan mampu dikerjakan sistem. Sedangkan analisis proses untuk
memodelkan tingkah laku sistem.
3.1.1 Analisis Masalah
Dalam model Chain of Trust, terdapat tiga proses utama yang harus
diimplementasikan untuk setiap transaksi elektronik [4], yaitu:
1. Identifikasi
Proses identifikasi membutuhkan identitas yang merupakan hal/fitur unik untuk
mendeskripsikan sesuatu. Misalnya web e-commerce menyimpan identitas berupa nama, e-mail, alamat dan sebagainya.
2. Autentikasi
Autentikasi ialah proses yang membutuhkan credentials yang umumnya berupa nama pengguna dan kata sandi untuk membuktikan validitas pengguna tersebut.
3. Otorisasi
Otorisasi dilakukan untuk mengesahkan bahwa pengguna tersebut memiliki hak
akses untuk sumber daya atau informasi tertentu.
Pada transaksi elektronik, autentikasi merupakan proses mutlak yang harus
17
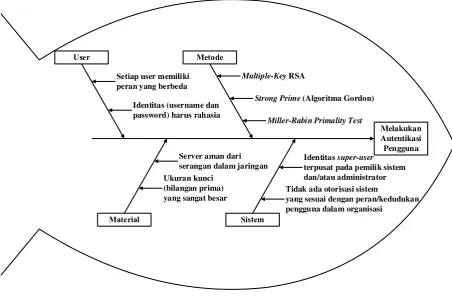
pengguna dengan satu super user. Masalah penelitian ini secara umum ditunjukkan pada gambar 3.1, yaitu diagram Ishikawa (fishbone/cause and effect diagram).
Setiap user memiliki peran yang berbeda
Identitas (username dan password) harus rahasia
Multiple-Key RSA
Strong Prime (Algoritma Gordon)
Miller-Rabin Primality Test
terpusat pada pemilik sistem dan/atau administrator Tidak ada otorisasi sistem
yang sesuai dengan peran/kedudukan pengguna dalam organisasi
Melakukan Autentikasi
Pengguna
Gambar 3.1 Diagram Ishikawa Masalah Penelitian
Berdasarkan gambar 3.1, masalah utama ditunjukkan oleh segi empat paling
kanan (kepala ikan), yaitu melakukan autentikasi pengguna. Sedangkan segi empat
lainnya yang dihubungkan oleh sebuah garis ke tulang utama (garis horizontal yang
terhubung ke kepala ikan) adalah kategori masalah. Garis horizontal selanjutnya yang
ditunjukkan oleh tulang-tulang kecil yang diwakili oleh garis panah yang mengarah ke
tulang-tulang kategori masalah adalah sebab dari masalah yang berada pada kepala
ikan.
3.1.2 Analisis Kebutuhan
Analisis kebutuhan terbagi dua bagian, yaitu kebutuhan fungsional dan kebutuhan
nonfungsional. Kebutuhan fungsional mendeskripsikan aktivitas yang disediakan
suatu sistem. Sedangkan kebutuhan nonfungsional mendeskripsikan fitur, karakteristik
3.1.2.1 Kebutuhan Fungsional
Untuk menerapkan Multiple-KeyRSA, kebutuhan fungsional yang harus dipenuhi antara lain, sebagai berikut:
1. Admin/Super User
Admin hanya dapat melakukan fungsi-fungsi berikut setelah melakukan login. a. Memasuki sistem
Admin dapat memasuki sistem yang aksesnya terbatas untuk role admin. b. Mengubah kata sandi
Admin dapat mengubah kata sandi seperlunya.
c. Mengatur ulang (reset) seluruh pengguna
Admin hanya dapat mengatur ulang (reset) selutuh pengguna tanpa dapat menambah atau mengurangi pengguna yang ada.
d. Melihat status user lainnya
Admin dapat melihat status online seluruh user yang mengakses Status Page.
2. User
User hanya dapat melakukan fungsi-fungsi berikut setelah melakukan login.
a. Melihat status User lainnya
Setelah login, User diarahkan ke Status Page dan dapat melihat status online seluruh user yang mengakses page ini.
b. Memasuki sistem
User dapat memasuki sistem jika dan hanya jika seluruh User (tidak
termasuk super user) online dan mengkakses Status Page. c. Mengubah kata sandi
19
3.1.2.2 Kebutuhan Nonfungsional
Kebutuhan fungsional mencakup karakteristik berikut:
1. Performa
Perangkat lunak yang akan dibangun dapat menunjukkan hasil dari fungsi
kriptografi yang dilakukan oleh sistem.
2. Mudah dipelajari dan digunakan
Perangkat lunak yang akan dibangun memiliki tampilan yang user friendly dan responsif sehingga pengguna mobile dapat mengakses sistem.
3. Hemat biaya
Perangkat lunak yang dibangun akan menggunakan teknologi open source dan bebas digunakan.
4. Dokumentasi
Perangkat lunak yang akan dibangun dapat menyimpan log dan memiliki panduan penggunaan.
5. Manajemen kualitas
Perangkat lunak yang akan dibangun akan memiliki kualitas yang baik yaitu
proses enkripsi dan dekripsi kata sandi serta pembangkitan kunci relatif cepat.
6. Kontrol
Perangkat lunak yang dibangun akan menampilkan pesan error untuk setiap input yang tidak sesuai.
3.1.3 Analisis Proses
Perangkat lunak yang dibangunakan menggunakan tiga metode, yaitu
Multiple-KeyRSA, Miller-Rabin Primality Testdan algoritma Gordon.
Multiple-KeyRSAdigunakan untuk membangkitkan kunci-kunci setiap pengguna dan
melakukan proses enkripsi dan dekripsi. Miller-Rabin Primality Testuntuk menguji
keprimaan bilangan yang akan digunakan sebagai kunci yang
dibangkitkandalamalgoritma Gordon. Sedangkan algoritma Gordon untuk
3.2 Perancangan Sistem
Sistem ini dirancang dengan membuat flowchart, Data Flow Diagram, kamus datasertamockup.
3.2.1 Flowchart
Pada bagian ini, terdapat tiga flowchart, yaitu: flowchartpembangkitan kunci
algoritma Multiple-KeyRSA,flowchartalgoritmaMiller-Rabin dan
flowchartalgoritmaGordon.
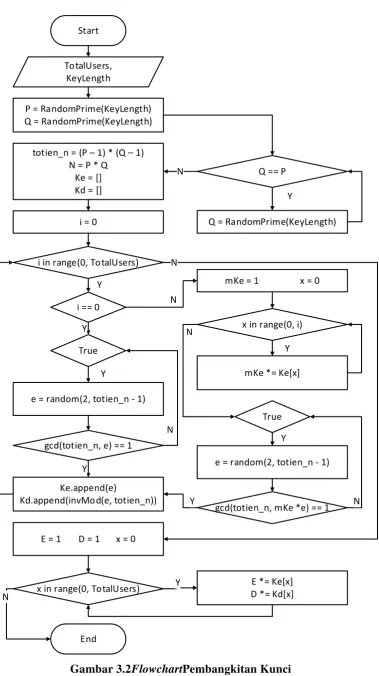
3.2.1.1 Flowchart Pembangkitan Kunci
Proses untuk membangkitkan kunci pada algoritma Multiple-KeyRSAdigambarkan pada Gambar 3.1. Pada proses pembangkitan kunci, terdapat dua paramater masukan,
21
gcd(totien_n, e) == 1
Y
gcd(totien_n, mKe *e) == 1
Y N
i in range(0, TotalUsers)
x in range(0, TotalUsers)
x in range(0, i)
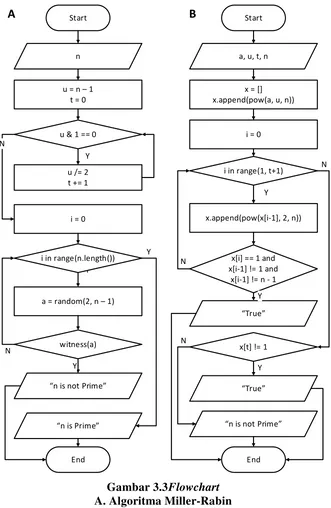
3.2.1.2 Flowchart Algoritma Miller-Rabin
Proses untuk pengujian bilangan prima menggunakan algoritma Miller-Rabin
ditunjukkanpada Gambar 3.2.n merupakan variabel yang akan diuji keprimaannya. t dan umerupakan variabel yang akan memenuhi persamaan � – 1 = 2��. Fungsi witness() diimplementasikan untuk menguji bilangan yang diberikan ialah komposit
dengan menghitung kepemilikan akar kuadrat.
Start A. Algoritma Miller-Rabin
23
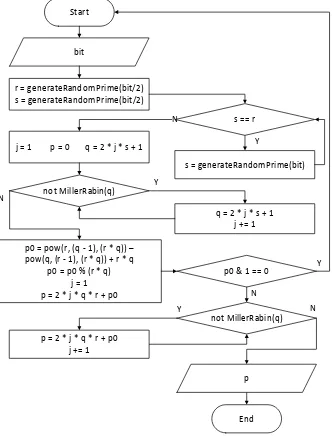
3.2.1.3 Flowchart Algoritma Gordon
Proses untuk pembangkitan bilangan yang memenuhi konsep Strong Prime
menggunakan algoritma Gordon ditunjukkanpada Gambar 3.3.p merupakan bilangan Strong Prime. Algoritma Gordon menggunakan algoritma Miller-Rabin untuk menguji keprimaan setiap deret p dan q yang memenuhi konsep Strong Prime.
Start
bit
r = generateRandomPrime(bit/2) s = generateRandomPrime(bit/2)
s = generateRandomPrime(bit) Y
N
N
p0 = pow(r, (q - 1), (r * q)) – pow(q, (r - 1), (r * q)) + r * q
p0 = p0 % (r * q) j = 1 p = 2 * j * q * r + p0
End j = 1 p = 0 q = 2 * j * s + 1
q = 2 * j * s + 1 j += 1 Y
N
p = 2 * j * q * r + p0 j += 1
p Y
p0 & 1 == 0 Y
N
not MillerRabin(q) not MillerRabin(q)
s == r
3.2.2 Data Flow Diagram (DFD)
Data Flow Diagram ialah suatu model yang menggambarkan aliran data atau proses yang dilakukan pada suatu rancangan sistem. DFD digunakan sebagai perangkat
analisis dan perancangan terstruktur sehingga memungkinkan analis sistem
memahami sistem secara visual yang berupa rangkaian aliran data yang saling
berkaitan.
3.2.2.1 DFD Level 0
DFD Level 0 (diagram konteks) menggambarkan suatu sistem secara keseluruhan, termasuk aliran data masukan (input) ke dalam proses/kegiatan sistem maupun data keluaran (output). Diagram konteks dari aplikasi yang akan dibangun ditunjukkan pada gambar 3.4.
Admin/
Super User User
Data User Jumlah User
Informasi Default User
Daftar Status Users Daftar Status Users Data Admin Sistem Kriptografi RSA
Banyak Kunci (Autentikasi Pengguna pada Web)
0
Gambar 3.5DFD Level 0
Berdasarkan gambar 3.4, terdapat dua entitas, yaitu User dan Admin/Super
User. Untuk memasuki sistem, kedua entitas harus memberikan masukan berupa
password/kata sandi. Kemudian, sistem memberikan keluaran berupa daftar status User. Khusus bagi Admin, dapat memberikan masukan jumlah user ke dalam sistem
untuk mengatur ulang (reset) seluruh User yang ada dan sistem akan memberikan keluaran berupa informasi default User yang terdiri dari nama pengguna dan kata sandi acak.
3.2.2.2 DFD Level 1
Berdasarkan diagram konteks, sistem terbagi menjadi empat aktivitas utama, yaitu:
penggantian kata sandi, update status online/offline seluruh pengguna, pemeriksaan akses ke sistem dan pengaturan ulang seluruh pengguna. Setiap proses memerlukan
25
Data Admin Data User Informasi
Pada proses 1 penggantian kata sandi, proses terbagi menjadi dua, yaitu enkripsi kata
sandi yang diinginkan dan update kata sandi baru pengguna. Pada proses 1.1, kata sandi masing-masing Admin dan User dienkripsi menggunakan kunci e dan n yang terdapat dalam database Keys dan Users. Kemudian, kata sandi terenkripsi disimpan melalui proses 1.2.
Admin/
Super User Enkripsi User
3.2.2.4 DFD Level 2 Proses 2
Pada proses 2, proses update status seluruh pengguna terbagi menjadi dua, yaitu menentukan status Users dan menyimpan status seluruh pengguna. Proses 2.1
membaca isi database User_log untuk memberikan status Users kepada Admin dan
User. Proses 2.2 mendeteksi koneksi User yang login ke dalam sistem dan
menyimpannya ke dalam storage User_log.
Data Status Users Admin/
Super User Data Status Users Menentukan User Status Users
Data Users DataUser Data Status Users
Menyimpan status online/offline seluruh pengguna Data Admin
Data Users 2.1
2.2 User_log
D2
Users D1
Gambar 3.8DFD Level 2 Proses 2
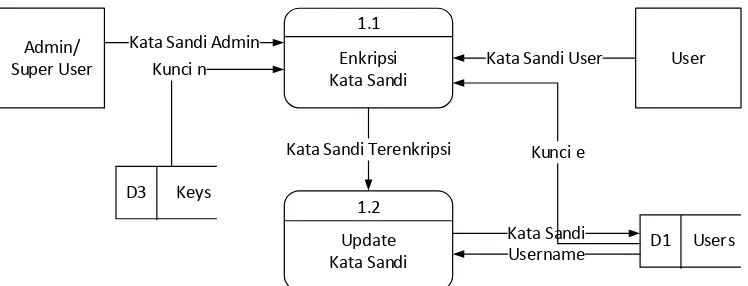
3.2.2.5 DFD Level 2 Proses 4
Pada proses 4, proses pengaturan ulang (reset) seluruh pengguna terbagi menjadi tujuh, yaitu enkripsi kata sandi Admin dan User, dekripsi kata sandi admin,
pemeriksaan kata sandi Admin, pembangkitan kunci setiap pengguna dan kata sandi
User. Kata sandi dienkripsi oleh proses 4.1 dilanjutkan pemeriksaan kesamaan kata
sandi pada proses 4.2. Apabila cocok, kata sandi tersebut didekripsi pada proses 4.3
menggunakan kunci yang telah dibangkitkan pada proses 4.5. Selain
kunci-kunci setiap pengguna dibangkitkan, kata sandi setiap User juga dibangkitkan secara
acak pada proses 4.6 lalu dienkripsi pada proses 4.7. Pasangan kata sandi yang telah
27
Admin/ Super User
Jumlah User
Data Admin +
Kata sandi terenkripsi Pemeriksaan kata sandi Enkripsi kata sandi
Admin
Kata sandi terenkripsi Admin Dekripsi kata sandi
Admin
Pembangkitan kata sandi User Jumlah User
Data Default User Enkripsi kata sandi
Admin
Kata sandi Admin
Kunci Admin
Enkripsi kata sandi User
3.2.3 Kamus Data
Kamus data adalah daftar fakta tentang data dari setiap proses yang terjadi dalam
suatu sistem. Kamus data untuk sistem ini adalah sebagai berikut:
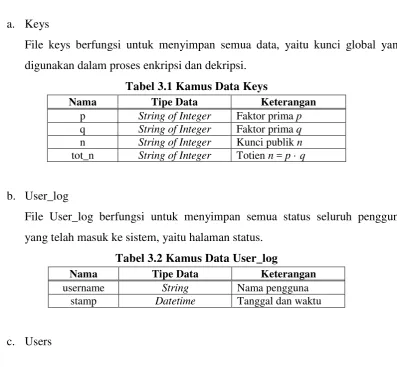
a. Keys
File keys berfungsi untuk menyimpan semua data, yaitu kunci global yang
digunakan dalam proses enkripsi dan dekripsi.
Tabel 3.1 Kamus Data Keys
Nama Tipe Data Keterangan p String of Integer Faktor prima p q String of Integer Faktor prima q n String of Integer Kunci publik n tot_n String of Integer Totien n = p · q
b. User_log
File User_log berfungsi untuk menyimpan semua status seluruh pengguna
yang telah masuk ke sistem, yaitu halaman status.
Tabel 3.2 Kamus Data User_log
Nama Tipe Data Keterangan
username String Nama pengguna
stamp Datetime Tanggal dan waktu
File Users berfungsi untuk menyimpan seluruh identitas setiap pengguna
sistem.
Tabel 3.3 Kamus Data Users
Nama Tipe Data Keterangan
_id String of Integer Nama pengguna
Kd String of Integer Kunci dekripsi
Ke String of Integer Kunci enkripsi
pass String of List Kata sandi pengguna yang telah dienkripsi
3.2.4 Mockup
Mockup adalah rancangan sistem yang berskala kecil dan tidak lengkap serta digunakan sebagai tampilan desain awal. Sistem ini terdapat lima page utama, yaitu Index page, Status page, Setting page, Reset page dan System page.
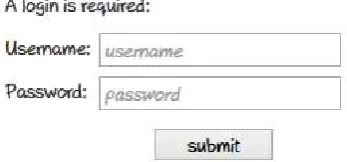
3.2.4.1 Index Page
Tampilan awal sistem ialah Index Page. Di dalam page ini terdapat pilihan navigasi dan form untuk login. Untuk masuk ke dalam sistem, pengguna harus memberikan input berupa username dan password pada form yang tersedia. Rancangan tampilan page ditunjukkan pada gambar 3.9:
29
3.2.4.2 Status Page
Status page ditunjukkan setelah pengguna melakukan login. Page ini menampilkandaftar seluruh pengguna beserta status online/offlinenya. Status masing-masing pengguna memiliki indikator perbedaan warna. Rancangan tampilan page ditunjukkan pada gambar 3.10:
Gambar 3.11Mockup Status page
3.2.4.3 Setting Page
Setting page dapat diakses dengan memilih link setting pada menu navigasi. Dalam page ini, terdapat form input untuk mengubah kata sandi pengguna yang bersangkutan. Rancangan tampilan page ditunjukkan pada gambar 3.11:
Gambar 3.12Mockup Setting page
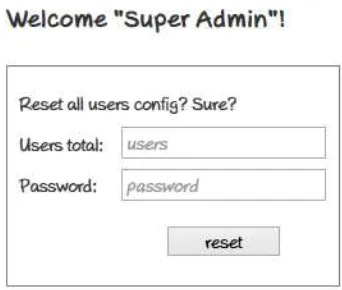
3.2.4.4 Reset Page
Resetpage hanya dapat diakses oleh role admin. Dalam page ini, terdapat form input untuk mengatur ulang jumlah user beserta kata sandi setiap pengguna. Untuk
Gambar 3.13Mockup Reset page
3.2.4.5 System Page
Systempage hanya dapat diakses oleh role admin. Page ini hanya terdapat text yang mengindikasikan bahwa autorisasi pengguna berhasil. Rancangan tampilan page ditunjukkan pada gambar 3.13:
BAB IV
IMPLEMENTASI DAN PENGUJIAN
4.1 Implementasi
Dalam tugas akhir ini, program dibangun menggunakan bahasa pemrograman Python
versi 2.7. Program ini terdiri dari 5 page utama, yaitu: pageindex untuk melakukan login sebelum pengguna masuk ke sistem, page status sebagai gerbang setiap user sebelum memasuki sistem, page setting untuk mengubah kata sandi, pagereset untuk admin mengatur ulang seluruh user beserta kata sandinya dan page system sebagai halaman indikator pengguna sebagai admin/super user.
4.1.1 IndexPage
Gambar 4.1 IndexPage
4.1.2 StatusPage
33
Gambar 4.2StatusPage
4.1.3 SettingPage
Setting Page merupakan page yang dapat digunakan masing-masing pengguna untuk mengubah kata sandi. Kata sandi yang baru akan dienkripsi dan disimpan ke dalam
Gambar 4.3SettingPage
4.1.4 System Page
35
Gambar 4.4System Page
4.1.5 ResetPage
Seperti SystemPage, Reset Page hanya dapat diakses oleh role admin. Page ini berfungsi untuk mengatur ulang seluruh users dan kata sandinya dengan memasukkan total users yang diinginkan serta kata sandi milik super admin. Setelah button Reset ditekan, sistem akan membangkitkan kunci-kunci dan kata sandi milik masing-masing
Gambar 4.5ResetPage
4.2 Pengujian
Pengujian dilakukan terhadap algoritma Multiple-KeyRSA untuk mengukur
keberhasilan sistem dalam melakukan proses pembangkitan kunci, enkripsi dan
dekripsi serta membandingkan waktu yang diperlukan untuk menghasilkan pasangan
kunci untuk setiap pengguna dan panjang kunci. Pengujian dilakukan dengan kriteria
sebagai berikut:
1. Plaintext berupa kata sandi yang terdiri dari karakter ASCII dengan panjang 8 karakter dan dibangkitkan secara acak.
2. Kunci-kunci dibangkitkan secara acak untuk jumlah user 2 hingga 10 pengguna untuk panjang kunci hingga 4096 bit dengan interval 512 bit.
37
4.2.1 Skenario Enkripsi
Misalkan pada page Index, masukan Username = admin dan Password = fauzana5 serta kunci n = 731, e = 185. Kunci yang digunakan ialah pasangan kunci masing-masing pengguna yang disimpan dalam database. Setelah button Login ditekan, kata sandi diproses sebagaimana terlihat pada Tabel 4.1.
Tabel 4.1 Enkripsi kata sandi
�� ������ � ≡ ������
f 102 527
a 97 600
u 117 185
z 122 694
a 97 600
n 110 25
a 97 600
5 53 138
Kemudian, kata sandi yang terenkripsiberupa Python list, yaitu:
[527, 600, 185, 694, 600, 25, 600, 138] akan dicocokkan dengan kata sandi yang terenkripsi pada database. Seperti proses pada page Index, kata sandi yang akan diubah melalui page Setting juga dienkripsi seperti proses yang ditunjukkan pada Tabel 4.1 dan disimpan ke dalam database.
4.2.2 Skenario Pembangkitan Kunci dan Proses Dekripsi
Misalkan pada Page Reset, super user memasukkan User total ( t) = 2 dan Super userpassword = fauzana5 serta kunci n = 731, e = 185 dan d = 425. Mula-mula, kata sandi super user dienkripsi seperti yang ditunjukkan pada Tabel 4.1 dan dicocokkan pada database. Apabila cocok, kata sandi didekripsi seperti Tabel 4.2.
Tabel 4.2Dekripsi kata sandi
� � ≡ ������ �
�
527 102 f
600 97 a
185 117 u
694 122 z
600 97 a
600 97 a
138 53 5
Selanjutnya, kunci-kunci yang baru, �,�,�,�(�) dibangkitkan dengan panjang sekitar 32 bit dan menggunakan algoritma Gordon’s Strong Prime serta algoritma Miller-Rabin Primality Test.
�= 2
�= 47701
�= 10729
�= 511784029
�(�) = 511725600
Kemudian pasangan kunci enkripsi dan dekripsi masing-masing user serta kata sandi acak dibangkitkan.
Tabel 4.3PasanganKata Sandi dan Kunci setiap User
���� ��������� �� ��
����0 ���7� 432276761 324244841
����1 �6��� 134208107 264359843
Dari kunci-kunci user, didapatkan kunci super
user�= 58015045793901427dari hasil perkalian masing-masing kunci Ke dan � = 85717315260319963 dari hasil perkalian masing-masing kunci Kd. Lalu, kata
sandi yang telah didekripsi pada Tabel 4.2 dienkripsi kembali menggunakan kunci
yang baru.
4.2.3 Pengujian dan Analisis Hasil Enkripsi dan Dekripsi
Tujuan dari pengujian ini ialah untuk mengetahui jumlah karakter hasil enkripsi kata
sandisepanjang 8 karakter untuk variasi panjang kunci hingga 4096 bit dengan interval
512 bit serta lama proses enkripsi dan dekripsi. Hasil pengujian divisualisasikan pada
Gambar 4.6, 4.7 dan 4.8. Ringkasan panjang kunci dan panjang kata sandi terenkripsi
serta lama proses enkripsi dan dekripsi diberikan pada Tabel 4.4. Rata-rata
39
Tabel 4.4Panjang Ciphertext, Rata-rata lama eksekusi proses Enkripsi dan Dekripsi untuk setiap Panjang Kunci
Kunci
Gambar 4.6 Grafik Panjang Kunci terhadap Panjang Kata Sandi Terenkripsi
Tabel 4.5 Kode enkripsi pesan
Step Kode
512 1024 1536 2048 2560 3072 3584 4096
P
Gambar 4.7 Grafik Panjang Kunci terhadap lama Proses Enkripsi
Tabel 4.6 Kode dekripsi pesan
Step Kode
Gambar 4.8 Grafik Panjang Kunci terhadap lama Proses Dekripsi
Berdasarkan Tabel 4.4 dan Gambar 4.6, hubungan panjang kunci dan kata
sandi terenkripsi berbanding lurus (linier). Apabila fungsi pada Tabel 4.5 dan 4.6
dieksekusi,hasilnya terdapat pada Gambar 4.7 dan 4.8, yaitu: hubungan panjang kunci
0, 0
512 1024 1536 2048 2560 3072 3584 4096
L
Panj ang Kunci (bit )
0, 0
512 1024 1536 2048 2560 3072 3584 4096
L
41
dan lama proses enkripsi/dekripsi membentuk kurva. Untuk enkripsi maupun dekripsi,
kompleksitas waktu pada kasus terbaik dan rata-rata ialah Ο(log(�)2) dan pada kasus terburukialah Ο(log(�)3) [6].
4.2.4 Pengujian dan Analisis Waktu Eksekusi Miller-Rabin Primality Test
Tujuan dari pengujian ini ialah untuk mengetahui lama eksekusi pengujian bilangan
prima Miller-Rabin untuk setiap 2 hingga 10 pengguna dan variasi panjang kunci
hingga 4096 bit dengan interval 512 bit. Hasil pengujian divisualisasikan pada
Gambar 4.9. Untuk rata-rata pemrosesan setiap panjang kunci, ringkasannya diberikan
pada Tabel 4.7. Untuk pengujian prima Miller-Rabin, kompleksitas waktu ialah
Ο(�log3�), dengan � = banyaknya nilai � yang diuji atau |�| = jumlah digit � [6].
Gambar 4.9 Grafik Panjang Kunci terhadap lama eksekusiMiller-Rabin Primality Testuntuk setiap Jumlah Pengguna
0, 0 1, 0 2, 0 3, 0 4, 0 5, 0 6, 0
512 1024 1536 2048 2560 3072 3584 4096
W
a
k
tu
(
d
e
ti
k
)
Panj ang Kunci (bit )
Tabel 4.7Rata-rata lama eksekusi Miller-Rabin Primality Test untuk setiap Panjang Kunci
Panjang Kunci (bit) Waktu (detik) 512 0.007538211 1024 0.038682747 1536 0.123941353 2048 0.289738589 2560 0.721264308 3072 1.146872587 3586 2.333116841 4096 3.722636829
Tabel 4.8Kode algoritma Miller-Rabin
Step Kode
4.2.5 Pengujian dan Analisis Waktu Eksekusi Gordon Strong Prime
Tujuan dari pengujian ini ialah untuk mengetahui lama eksekusi pembangkitan
bilangan prima menggunakan algoritma Gordon untuk setiap 2 hingga 10 pengguna
dan variasi panjang kunci hingga 4096 bit dengan interval 512 bit. Hasil pengujian
divisualisasikan pada Gambar 4.10. Untuk rata-rata pemrosesan untuk setiap panjang
kunci, ringkasannya diberikan pada Tabel 4.8. Rata-rata keseluruhan pengeksekusian
algoritma Gordon adalah 12.04876388 detik.Untuk algoritma Gordon, kompleksitas
43
Gambar 4.10Grafik Panjang Kunci terhadap lama eksekusi algoritma Gordon untuk Setiap Jumlah Pengguna
Tabel 4.9Rata-rata lama eksekusi algoritma Gordon untuk setiap Panjang Kunci
Panjang Kunci (bit) Waktu (det) 512 0.085000012 1024 0.463611099 1536 1.382944451 2048 4.238222215 2560 8.642666631 3072 15.00533333 3586 27.26494443 4096 39.30738888
0, 00 10, 00 20, 00 30, 00 40, 00 50, 00 60, 00
512 1024 1536 2048 2560 3072 3584 4096
W
a
k
tu
(
d
e
ti
k
)
Panj ang Kunci (bit )
Tabel 4.10Kode Pembangkit Bilangan Prima
Tabel 4.11Kode algoritma Gordon
Step Kode Big O
4.2.6 Pengujian dan Analisis Waktu Eksekusi Pembangkitan Kunci
Tujuan dari pengujian ini ialah untuk mengetahui lama pembangkitan kunci Multiple-Key RSAuntuk setiap 2 hingga 10 pengguna dan variasi panjang kunci hingga 4096 bit dengan interval 512 bit. Hasil pengujian divisualisasikan pada Gambar 4.11. Untuk
rata-rata pemrosesan untuk setiap panjang kunci, ringkasannya diberikan pada Tabel
45
Gambar 4.11Grafik Panjang Kunci terhadap lamaPembangkitan Kunci untuk Setiap Jumlah Pengguna
Tabel 4.12Rata-rata lama eksekusi Pembangkitan Kunci Multiple-KeyRSA untuk setiap Panjang Kunci
Panjang Kunci (bit) Waktu (det) 512 0.253888898 1024 1.304333316 1536 3.551555581 2048 10.73977778 2560 19.69411111 3072 42.8465556 3586 61.54122223 4096 96.33755559
0, 00
512 1024 1536 2048 2560 3072 3584 4096
w
Panj ang Kunci (bit )
BAB V
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Setelah melakukan analisis, prancangan dan pengujian terhadap Sistem Kriptografi
RSA Banyak Kunci untuk Prototipe Autentikasi Pengguna pada Web, diperoleh
kesimpulan sebagai berikut:
1. Proses enkripsi dan dekripsi pada algoritma Multiple-Key RSAdapat digunakan untuk menguji identitas pengguna yang autentik berdasarkan pasangan nama
pengguna (username) dan kata sandi (password).
2. Panjang kunci yang dibangkitkan menggunakan algoritma Gordon’s Strong
Prime dan algoritma Miller-Rabin berbanding lurus terhadap panjang ciphertext (output enkripsi kata sandi). Dari gambar 4.6, semakin panjang kunci yang digunakan, semakin panjang pula kata sandi (ciphertext).
3. Secara implisit, penggunaan Strong Prime tidak efisien dalam pembangkitan bilangan prima karena membutuhkan waktu dan sumber daya lebih banyak.
Berdasarkan tabel 4.7 dan 4.9, eksekusi algoritma Gordon 10 kali lebih lama
daripada algoritma Miller-Rabin. Selain itu, algoritma Gordon membutuhkan
fungsi Miller-Rabin minimal 4 kali untuk kasus terbaik.
4. Berdasarkan tabel 4.4, pembangkitan bilangan prima menggunakan algoritma
47
5.2 Saran
Berikut saran-saran yang dapat dipertimbangkan untuk mengembangkan penelitian
ini:
1. Untuk pengembangan sistem selanjutnya, algoritma digital signature dapat diimplementasikan untuk memenuhi fungsi non-repudiatory, yaitu menjamin semua pihak yang terlibat tidak dapat melakukan penyangkalan atas telah dikirim
atau diterimanya pesan.
2. Sistem ini hanya diuji menggunakan kata sandi sepanjang 8 karakter acak dan
panjang kunci hingga 4096 bit dengan interval 512 bit, sehingga untuk
pengembangan selanjutnya dapat digunakan kata sandi dan kunci yang lebih
panjang.Di sisi lain, poin utama untuk meningkatkan keamanan hanya dengan
membangkitkan kunci (bilangan prima) p dan q yang sangat besar.
3. Kombinasi algoritma Miller-Rabin dan Gordon dalam pembangkitan kunci
kurang efisien, sehingga untuk pengembangan berikutnya dapat dipilih algoritma
yang tepat dalam membangkitkan kunci agar waktu dan penggunaan sumber daya
lebih efisien.
4. Pengukuran waktu eksekusi algoritma disarankan untuk menggunakan
DAFTAR PUSTAKA
[1] Bishop, D. 2003. Introduction to Cryptography with Java Applets. Sudbury: Jones and Bartlett Publishers, Inc.
[2] Brainard, J., et al. 2006. Fourth-Factor Authentication: Somebody You Know.
13th ACM Conference on Computer and Communications Security
(ACM CCS 2006). hal. 168-178.
[3] Cormen, T. H., Leiserson, C. E., Rivest, R. L., Stein, C. 2009. Introduction to Algorithms. Edisi ke-3. Massachusetts: MIT Press.
[4] Evans, J. 2004. PSCIOC/PSSDC Cross-Jurisdictional Identification,
Authentication and Authorization Working Group. Consultation Draft. Government of Ontario.
[5] Ferguson, N., et al. 2010. Cryptography Engineering: Design, Principles, and Practical Applications. Indianapolis: Wiley Publishing, Inc.
[6] Furlani, C. 2009. Digital Signature Standard. Federal Information Processing Standards Publication. National Institute of Standards and Technology.
[7] Hershey, J. E. 2003. Cryptography Demystified: An Unconventional & Painless Way to Aquire the Basic Skills of Cryptography for Applications in Communications. New York: McGraw-Hill.
[8] Indra, N.. 2011. Analisis dan Perbandingan Kecepatan Algoritma RSA dan
Algoritma ElGamal. Makalah. Bandung: Institut Teknologi Bandung.
[9] Loebenberger, D. and Nüsken M. 2011. “Analyzing Standards for RSA
Integers”. Dalam Nitaj, A. dan Pointcheval, D. (eds.). Progress in Cryptology (AFRICACRYPT '11) Proceedings:hal. 260-277. Berlin: Springer-Verlag.
[10] Mollin, R. A. 2002. RSA and Public-Key Cryptography. Florida: Chapman & Hall/CRC.
[11] Mollin, R. A. 2007. An Introduction to Cryptography. Edisi ke-2. Florida: Chapman & Hall/CRC.
[12] Mollin, R. A. 2007. “Recognizing primes”. International Journal of
49
[13] Mollin, R. A. 2008. Fundamental Number Theory with Applications. Edisi ke-2. Florida: Chapman & Hall/CRC.
[14] Mollin, R. A. 2008. “On factoring”. International Journal of Contemporary Mathematics Sciences3(33): hal. 1635-1642.
[15] Paar, C. dan Pelzl, J. 2010. Understanding Cryptography. Berlin: Springer-Verlag.
[16] Rosen, Kenneth H. 2012. Discrete Mathematics and Its Applications. Edisi ke-7. New York: McGraw-Hill.
[17] Sadikin,R. 2012. Kriptografi untukKeamanan Jaringan. Yogyakarta: ANDI. [18] Schneier, B. 1996. Applied Cryptography: Protocols, Algorithms, and Source
Code in C. Edisi ke-2. New Jersey: John Wiley & Sons, Inc.
[19] Sun, H. dan Yang C. 2005. “RSA with Balanced Short Exponents and Its
Application to Entity Authentication”. Dalam Vaudenay, S. (ed.).