DERIVATIVE-FREE TWO STEP ITERATIVE
METHOD USING CENTRAL DIFFERENCE
Riski Amelia, M. Imran and Syamsudhuha
Abstract.This article discusses an iterative method to solve a nonlinear equation, which is free from derivatives by approximating a derivative in the two-step of the method of Xiaojian [Applied Mathematics and Computation, 203: 824-827, 2008] by the method of central difference with one parameterθ. We show analytically that the method is of order four. Numerical experiments show that the new method is comparable with other discussed method.
1. INTRODUCTION
Many problems in the chemistry, economics, marketing and electricity often end in the form of nonlinear equation models [9, p. 4-10],
f(x) = 0. (1)
Many of the numerical methods can be used to solve nonlinear equations, like Newton’s method given by [1, p. 79-80], [3, p. 67]
xn+1=xn−
f(xn)
f′(xn), f
′(xn)6= 0 dan n= 0,1,2,· · ·, (2)
Received 12-01-2016, Accepted 23-03-2016.
2016 Mathematics Subject Classification: 49Mxx, 41A25
Key words and Phrases: Central difference, efficiency index, derivative-free method, order of convergence.
which has quadratically convergence. Using equation (2) and Taylor expan-sion [2, p. 189], Gutierrez and Hernandez [4] obtain the classical Chebyshev-Halley’s method whose form is
xn+1=xn−
1 +1 2
Lf(xn) 1−βLf(xn)
f(xn)
f′(xn), (3)
Lf(xn) =
f′′(xn)f(xn)
(f′(xn))2 , β ∈R, n= 0,1,2,· · ·, (4)
which has third-order convergent [4].
Xiaojian [12] develops the Ostrowski’s method [8] by estimatingf′′(xn)
into (4) using hyperbola one point (xn, f(yn)), which produces
f′′(xn)≈ 2(f′(xn))
2f(yn)
f2(xn)−f(xn)f(yn). (5)
Substituting (5) into (4), we obtain
Lf(xn)≈
2f(yn)
f(xn)−f(yn). (6)
and then substituting (6) into (3), we obtain
yn =xn−
f(xn)
f′(xn),
xn+1 =xn−
f(xn)−f(yn)
f(xn)−2f(yn)
f(xn)
f′(xn),
(7)
which has the fourth-order convergence.
Besides Xiaojian’s method, there are several other methods to solve nonlinear equations like Liu’s method [5] and Ren’s method [7] which have the fourth-order convergence.
2. DERIVATIVE-FREE TWO STEP ITERATIVE METHOD USING CENTRAL DIFFERENCE
Derivative-free iterative method is a method to determine the roots of (1) by estimating f′(x
n) to (7) with central difference one parameterθ
f′(xn)≈ f(xn+θf(xn))−f(xn−θf(xn))
2θf(xn) (8)
If we substitute (8) into (7) then we have, the new iterative method given by
In the following theorem, we show the order of convergence of the iterative method (9).
To obtain 2θf2(xn), squaring the equation (12) and then multiplied it by after simplifying process, we obtain
f(un) = (θf′(α)2−f′(α))e
Using Geometric series and let,
r= 3c2en+ 2c22+c3f′(α)2θ2+ 4c3e2n+ 5c4+· · ·+ 5c2c3
then
Expandingf(yn) using Taylor expansion aboutyn=αuntil the fourth order and ignore the higher order, we have
f(yn) =f(α) +f′(α)(yn−α) +
Substituting equation (22) into (23), after simplifying, we obtain
Applying geometric series to avoid the division of two polynomials, denoted
Substituting equations (22) and (29) into (9),
xn+1 =α+
From the definition of the order of convergence, we see that equation (9) is fourth order. ✷
3. NUMERICAL SIMULATION
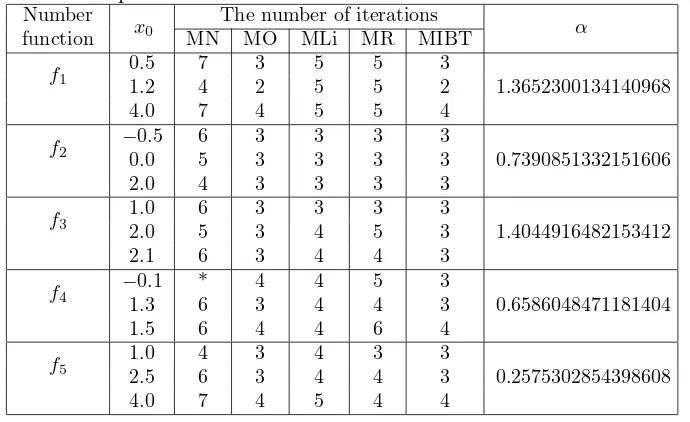
In this section, we compare the number of iterations to obtain an approxi-mated root for Newton’s method (MN), Ostrowski’s method (MO) [8], Liu’s method (MLI) [5], Ren’s method (MR) [7], and derivative-free iterative method (MIBT) given by (9) using five test functions. The computation is carried out using Maple 13. The stopping criteria of the iteration are |xn+1−α| ≤toland |f(xn+1)| ≤tol , where tol≤1.0×10−15. The
maxi-mum iteration allowed is 300.
1. f1(x) =x3+ 4x2−10
2. f2(x) = cos(x)−x
4. f4(x) =x6−10x3+x2−x+ 3
5. f5(x) =x2−ex−3x+ 2
Table 1 presents, the number of iteration needed to obtain the approximated root for several mention methods by varying an initial guess x0. The star
mark∗ indicates that the method converges to a different root.
Table 1: Comparison the number of iteration of discussed iterative methods Number
function x0
The number of iterations
α
MN MO MLi MR MIBT
f1 0.5 7 3 5 5 3
1.3652300134140968
1.2 4 2 5 5 2
4.0 7 4 5 5 4
f2
−0.5 6 3 3 3 3
0.7390851332151606
0.0 5 3 3 3 3
2.0 4 3 3 3 3
f3 1
.0 6 3 3 3 3
1.4044916482153412
2.0 5 3 4 5 3
2.1 6 3 4 4 3
f4
−0.1 * 4 4 5 3
0.6586048471181404
1.3 6 3 4 4 3
1.5 6 4 4 6 4
f5 1
.0 4 3 4 3 3
0.2575302854398608
2.5 6 3 4 4 3
4.0 7 4 5 4 4
The simulation shows that the derivative-free iterative method (MIBT) is sightly better than other methods. Based on the number of iterations,f4
to x0 = −0.1, MIBT has a number of iterations less than MO, MLi, and
MR, while MN converges to the other roots. Therefore this method can be used as an alternative method for solving nonlinear equations.
5. CONCLUSIONS
REFERENCES
1. K. E. Atkinson, Elementary Numerical Analysis, Third Edition, John Wiley & Sons, Inc., New York, 1993.
2. R. G. Bartle & R. D. Sherbert, Introduction to Real Analysis, Fourth Edition, John Wiley & Sons, Inc., New York, 2011.
3. J. D. Faires & R. L. Burden, Numerical Analysis, Seventh Edition, Brooks/Cole, Belmont, 2001.
4. Gutierrez, J. M. & Hernandez, M. A. 1997. A Family of Chebyshev-Halley Type Methods in Banach Spaces. Bulletin Aust. Math. Soc. 55 (1997), 113–130.
5. Z. Liu & Q. Zheng,A variant of Steffensen’s method fourth-order conver-gence and its applications, Applied Mathematics and Computation, 216 (2010), 1978–1983.
6. J. H. Mathews & K. D. Fink, Numerical Methods for Mathematics Sci-ence, and Engineering, Second Edition, Prentice-Hall International Inc., New Jersey, 1987.
7. H. Ren, Q. Wu & W. Bi, A class of two-step Steffensen type methods with fourth-order convergence, Applied Mathematics and Computation, 209 (2009), 206–210.
8. J. F. Traub,Iterative Methods for the Solution of Equations, Prentice-Hall Inc. Englewood Cliffs, 1964.
9. R. Wait,The Numerical Solution of Algebric Equation, Jhon Wiley and Sons, New York, 1979.
10. Cheney, W. & Kincaid, D. 2004. Numerical Methods for Mathematics and Computing, Sixth Edition. Brook/Cole Publishing Company, California
11. S. Weerakoon & T. G. I. Fernando, A variant of Newton’s method with accelerated third order convergence, Applied Mathematics Letters, 13 (2000), 87–93.
12. Z. Xiaojian, Modified Chebyshev-Halley methods free from second deriva-tive, Applied Mathematics and Computation, 203 (2008), 824-827.
RISKI AMELIA: Magister Student, Department of Mathematics, Faculty of
Math-ematics and Natural Sciences University of Riau, Bina Widya Campus, Pekanbaru 28293, Indonesia.
M. IMRAN: Numerical Computing Group, Department of Mathematics, Faculty
of Mathematics and Natural Sciences University of Riau, Bina Widya Campus, Pekanbaru 28293, Indonesia.
E-mail: [email protected]
Syamsudhuha: Numerical Computing Group, Department of Mathematics, Faculty
of Mathematics and Natural Sciences University of Riau, Bina Widya Campus, Pekanbaru 28293, Indonesia.