BAB II
TINJAUAN PUSTAKA
2.1 Perpindahan Kalor
Kalor adalah energi yang diterima oleh benda sehingga suhu benda atau wujudnya
berubah. Ukuran jumlah kalor dinyatakan dalam satuan joule (J). Kalor disebut
juga dengan bahang atau kalor adalah energi yang ditransfer dari satu sistem ke
sistem lain dengan interaksi termal. Berbeda dengan bekerja, kalor selalu disertai
dengan pengalihan entropi. Aliran kalor adalah karakteristik dari objek
makroskopik dan sistem, tetapi sumber dan sifatnya dapat dipahami dari segi
konstituen mikroskopis mereka. Satuan untuk kalor ini adalah joule. Kalor dapat
diukur dengan kalorimeter, atau ditentukan secara tidak langsung dengan
perhitungan berdasarkan jumlah yang lain, bergantung misalnya pada hukum
pertama termodinamika.
Perpindahan kalor dapat terjadi dalam berbagai cara: dengan konduksi,
radiasi, konveksi. Perpindahan kalor mencakup mengenai perpindahan energi
karena perbedaan temperatur diantara dua benda atau material. Di samping itu
perpindahan kalor juga meramalkan laju perpindahan kalor pada kondisi tertentu.
Cara – cara perpindahan kalor dibagi menjadi tiga, yaitu :
1. Konduksi
2. Konveksi
3. Radiasi
2.1.1 Konduksi
Konduksi adalah perpindahan kalor di dalam benda (elemen) padat dari suatu
elemen bertemperatur lebih tinggi ke suatu elemen bertemperatur lebih rendah.
Hal ini dapat dilakukan pada benda – benda padat khususnya dan untuk berbagai
dimensi sebagai berikut :
1. Satu dimensi (mono dimensional) artinya perpindahan kalor secara
(berbeda temperaturnya) dalam elemen yang masih dalam satu bidang datar.
Berlaku perumusan :
̇ = − ¶ (2.1) dengan:
̇ = laju aliran kalor (joule/detik atau watt)
k = koefisien konduktivitas material (W/ m K)
A = luas penampang tegak lurus aliran kalor satu dimensi (m2)
¶ = gradient penurunan temperatur dalam benda padat (K/m)
Persamaan (2.1) disebut hukum Fourier tentang konduksi kalor.
Persamaan tersebut merupakan persaman dasar dari konduktivitas kalor. Tanda
negatif pada persamaan di atas diberikan supaya memenuhi hukum
termodinamika yaitu kalor mengalir ke suhu yang lebih rendah, seperti
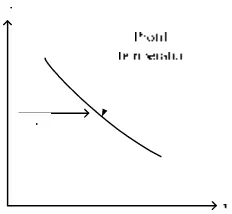
ditunjukkan gambar di bawah ini:
Gambar 2.1 Sketsa yang Menunjukkan Arah Aliran Kalor
Dari gambar di atas dapat diambil kesimpulan, bahwa laju aliran kalor melalui
bidang datar bergantung pada:
a. Beda suhu di antara kedua permukaan ∆T = T1 – T2; makin besar beda
suhu, makin cepat perpndahan kalor.
b. Panjang logam (x); semakin panjang x maka semakin pelan perpindahan
kalor.
c. Luas permukaan A; makin besar luas permukaan, makin cepat
perpindahan kalor.
2. Dua dimensi (dwi dimensional) artinya perpindahan kalor secara perambatan
(konduksi) dalam satu arah (satu garis lurus) atau antara dua titik (berbeda
temperaturnya) bias dalam dua bidang yang berlainan dan dalam satu bidang
datar.
3. Tiga dimensi artinya perpindahan kalor secara perambatan (konduksi) dalam
satu arah (satu garis lurus) atau antara dua titik (berbeda temperaturnya) bias
dalam ruang (bidang tiga) yang berlainan temperaturnya dan berarah lurus
dalam bidang yang berbeda.
2.1.2 Konveksi
Konveksi adalah perpindahan kalor karena perpindahan zat. Peristiwa konveksi
(aliran zat) terjadi pada perubahan suhu suatu zat. Zat cair atau gas yang terkena
kalor molekul-molekulnya bertambah besar dan beratnya tetap. Hal ini akan
menyebabkan massa jenisnya menjadi lebih kecil, sehingga zat cair atau gas yag
terkena kalor tersebut naik ke atas. Posisinya digantikan oleh zat cair atau gas
yang lebih dingin yang massa jenisnya lebih besar. Dari peristiwa aliran inilah,
maka kalor dapat merambat secara konveksi.
Contoh ketika memanaskan air menggunakan kompor, kalor mengalir dari
nyala api (suhu lebih tinggi) menuju dasar wadah (suhu lebih rendah). Karena
mendapat tambahan kalor, maka suhu dasar wadah meningkat. Karena terdapat
perbedaan suhu, maka kalor mengalir dari bagian luar dasar wadah (yang
bersentuhan dengan nyala api) menuju bagian dalam dasar wadah (yang
bersentuhan dengan air). Suhu bagian dalam dasar wadah pun meningkat. Karena
air yang berada di permukaan wadah memiliki suhu yang lebih kecil, maka kalor
mengalir dari dasar wadah (suhu lebih tinggi) menuju air (suhu lebih rendah).
Perpindahan kalor persatuan waktu secara konveksi dapat dinyatakan dengan
persamaan:
̇ = ℎ (T −T ) (2.2) dengan :
h = koefisien perpindahan kalor konveksi (Btu/hr-ft2.oF atau W/m2.K)
Ts = suhu permukaan benda (K)
T∞ = suhu di bagian hulu benda (K)
Hubungan ini dinamakan hukum Newton tentang pendinginan.
Persamaaan ini mendefinisikan koefisien perpindahan kalor konveksi h yang
merupakan konstanta proposional (tetapan kesebandingan) yang menghubungkan
perpindahan kalor per satuan waktu dan satuan luar dengan beda suhu
menyeluruh.
2.1.3 Radiasi
Perpindahan kalor radiasi adalah pengetahuan mengenai transfer energi dalam
bentuk gelombang elektromagnetik. Tidak seperti perpindahan konduksi dan
konveksi, gelombang elektromagnetik tidak memerlukan medium untuk
perambatan energinya. Oleh karena kemampuannya merambat di ruangan vakum,
radiasi kalor menjadi dominan pada transfer kalor di ruang hampa dan di luar
angkasa. Bukti – bukti dari percobaan menunjukkan bahwa perpindahan kalor
radiasi sebanding dengan pangkat empat suhu mutlak, sedangkan konduksi dan
konveksi berbanding lurus dengan beda suhu. Hukum Stefan Boltzman yang
fundamental menyatakan :
̇ = T (2.3) dengan:
̇ =laju aliran kalor (joule/detik atau watt)
T= suhu mutlak (K)
= Konstanta perpindahan kalor radiasi(W/m2.K4)
Sebagai contoh, ketika duduk dan mengelilingi api unggun, maka rasa hangat
2.2 Dasar – Dasar Perpindahan Kalor
2.2.1 Konduktivitas Kalor
Konduktivitas atau keterhantaran kalor, k, adalah suatu besaran intensif bahan
yang menunjukkan kemampuannya untuk menghantarkan kalor. Nilai angka
konduktivitas termal menunjukkan berapa cepat kalor mengalir dalam bahan
tertentu. Pada umumnya konduktivitas termal itu sangat tergantung pada suhu.
Secara umum, konduktivitas termal benda padat lebih besar dari pada gas.
Benda yang memiliki konduktivitas termal (k) besar merupakan penghantar kalor
yang baik (konduktor termal yang baik) dapat disebut dengan konduktor.
Sebaliknya, benda yang memiliki konduktivitas termal yang kecil merupakan
merupakan penghantar kalor yang buruk (konduktor termal yang buruk) dapat
disebut dengan isolator ya ng baik. Setiap materi memiliki lebar batasan dari
konduktivitas kalor. Konsep dasar konduktivitas kalor adalah kecepatan dari
proses difusi energi kinetik molekular pada suatu materi yang menghantarkan
kalor. Faktor – faktor yang mempengaruhi konduktivitas kalor adalah :
Kandungan uap air
Suhu
Berat jenis
Keadaan pori – pori bahan.
2.2.2 Difusivitas Kalor
Suatu variabel dari istilah-istilah yang telah dibahas adalah difusivitas kalor α.
Difusivitas kalor adalah konduktivitas termal dibagi dengan densitas dan kapasitas
kalor spesifik pada tekanan konstan. Difusivitas dapat dinyatakan sebagai:
α ≡ k
C ρ (2.4) dengan:
α = difusivitas kalor (m2/s)
= densitas ( kg/ m3)
k = koefisien konduktivitas kalor (W / m · K)
Makin besar nilai α, makin cepat kalor membaur dalam bahan itu. Nilai α yang besar dapat disebabkan oleh salah satu hal berikut:
1. Nilai konduktivitas kalor yang tinggi menunjukkan laju perpindahan
energi yang pesat.
2. Nilai kapasitas kalor spesifik Cpyang rendah. Nilai kapasitas kalor yang
rendah berarti bahwa energi yang yang berpindah melalui batang itu yang
diserap dan digunakan untuk menaikkan suhu jumlahnya sedikit, jadi
energi yang masih dapat dipindahkan lebih banyak.
2.3 Persamaan Diferensial
Persamaan diferensial adalah hubungan antara sekelompok fungsi dengan turunan-turunannya. Persamaan diferensial muncul secara alami dalam sains fisik,
model matematika, dan dalam matematika itu sendiri. Jika hanya satu variabel
bebasnya, maka persamaannya disebut Persamaan Diferensial Biasa. Sedangkan
jika variabel bebasnya lebih dari satu maka persamaannya disebut persamaan
Diferensial Parsial.
2.3.1 Persamaan Diferensial Linear Order Satu
Salah satu tipe dari persamaan diferensial orde satu yang sering dipakai dalam
aplikasi adalah persamaan linear. Persamaan linear order satu dapat disajikan
dalam bentuk:
( ) + ( )= ( ) (2.5)
dengan ( )≠0, ( ), dan ( ) merupakan fungsi dari x dan y tidak
tergantung pada y.
Jika (2.5) dinyatakan dalam bentuk lain, maka persamaan diferensial linear
ditulis sebagai
atau
interval subset dari R. Persamaan (2.6) dan (2.7) distribusi dengan bentuk standar
dari persamaan linear. Persamaan ini memiliki faktor integrasi yang dapat dibuat
dalam bentuk
( )= ∫ ( ) (2.8)
Faktor integral ( )= ∫ ( ) akan membawa persamaan diferensial
linier order satu berbentuk + ( ) = ( ) menjadi PD eksak. Secara umum
suatu faktor integral adalah faktor μ(x, y) dapat mengubah persamaan diferensial
tidak eksak menjadi persamaan diferensial eksak.
2.3.2 Persamaan Diferensial Parsial
Persamaan diferensial parsial (PDP) adalah persamaan yang di dalamnya terdapat
suku-suku diferensial parsial, yang dalam matematika diartikan sebagai suatu
hubungan yang mengaitkan suatu fungsi yang tidak diketahui, yang merupakan
fungsi dari beberapa variabel bebas, dengan turunan-turunannya melalui
variabel-variabel yang dimaksud. PDP digunakan untuk melakukan formulasi dan
menyelesaikan permasalahan yang melibatkan fungsi-fungsi yang tidak diketahui,
yang merupakan dibentuk oleh beberapa variabel, seperti penjalaran suara dan
kalor, elektrostatika, elektrodinamika, aliran fluida, elastisitas, atau lebih umum
segala macam proses yang terdistribusi dalam ruang, atau terdistribusi dalam
ruang dan waktu. Kadang beberapa permasalahan fisis yang amat berbeda
memiliki formulasi matematika yang mirip satu sama. Bentuk paling sederhana
dari persamaan diferensial adalah
T( , )
Dengan T merupakan suatu fungsi tak diketahui dari x dan t. Hubungan ini
mengisyaratkan bahwa nilai-nilai ( , ) adalah tidak bergantung dari t. Oleh
karena itu solusi umum dari persamaan ini adalah
T( , ) = ( ) (2.10) di mana f adalah suatu fungsi sembarang dari variabel x. Analogi dari persamaan
diferensial biasa untuk persamaan ini adalah
= 0 (2.11) yang memiliki solusi T(t) = c.
2.4 Deret Fourier
Deret Fourier merupakan penguraian fungsi periodik menjadi jumlahan fungsi-
fungsi berosilasi, yaitu fungsi sinus dan kosinus, ataupun eksponensial kompleks.
Studi deret Fourier merupakan cabang analisis Fourier. Deret Fourier
diperkenalkan oleh Joseph Fourier (1768 - 1830) untuk memecahkan
masalah persamaan kalor di lempeng logam.
Persamaan kalor merupakan persamaan diferensial parsial. Sebelum
Fourier, pemecahan persamaan kalor ini tidak diketahui secara umum, meskipun
solusi khusus diketahui bila sumber kalor berperilaku dalam cara sederhana,
terutama bila sumber panas merupakan gelombang sinus atau kosinus. Solusi
sederhana ini kadang-kadang disebut sebagai solusi eigen. Gagasan Fourier adalah
memodelkan sumber kalor ini sebagai superposisi (atau kombinasi linear)
gelombang sinus dan kosinus sederhana, dan menuliskan pemecahannya sebagai
superposisi solusi eigen terkait. Superposisi kombinasi linear ini disebut sebagai
deret Fourier.
Meskipun motivasi awal adalah untuk memecahkan persamaan kalor,
kemudian terlihat jelas bahwa teknik serupa dapat diterapkan untuk sejumlah
besar permasalahan fisika dan matematika. Deret Fourier saat ini memiliki banyak
penerapan di bidang teknik elektro, analisis vibrasi, akustika, optika, pengolahan
2.4.1 Fungsi Genap dan Ganjil
Perhitungan koefisien Fourier seringkali dipermudah jika fungsi f(x) yang
diuraikan memiliki sifat istimewa tertentu, yakni genap atau ganjil terhadap
sumbu x = 0. Keduanya didefenisikan sebagai berikut :
Sebuah fungsi f(x) adalah:
(a) genap, jika berlaku: f(-x) = f(x)
(b) ganjil, jika berlaku: f(-x) = -f(x)
untuk semua x dalam daerah defenisi f(x).
Sebagai contoh, fungsi x2 dan cos x adalah genap, karena menurut defenisi
di atas (-x)2 = x2 dan cos(- x ) = cos x, sedangkan fungsi x dan sin x, misalnya ,
adalah ganjil karena (-x) = -x dan sin(-x) = -sin x. Pada umumnya, fungsi pangkat
genap adalah genap dan fungsi pangkat ganjil adalah ganjil.
Integrasi fungsi genap dan ganjil dalam selang simetris seperti –L < x < L,
ternyata menjadi sederhana. Tinjau misalnya f(x) adalah genap, maka:
( ) = ( ) + ( ) (2.12)
Terhadap integral pertama di ruas kanan, yang dedefenisikan dalam
selang negatif adalah x: -L < x <0, jika dilakukan sisipan variabel integral baru, u
= -x, sehingga f(x) = f(-u). Karena fungsi f adalah genap, maka f(-u) = f(u).
Dengan demikian, jumlah kedua integral di atas menjadi:
f(x)dx =− f(u)du + f(x)dx = f(u)du + f(x)dx (2.13)
Dengan menamakan ulang variabel integrasi u dengan x, diperoleh :
f(x)dx = 2 f(x)dx (2.14)
Uraian Fourier fungsi periodik genap dan ganjil, khususnya perhitungan
koefisien an dan bn yang bersangkutan, menjadi lebih sederhana. Tinjau dahulu
fungsi f(x) adalah ganjil. Karena cos npx genap, maka f(x) cos npx adalah ganjil,
dan f(x) sin npx adalah genap. Dengan demikian, dalam selang simetris –L<x< L,
adalah integral dari suatu fungsi genap dalam selang simetris, karena itu nilainya
adalah dua kali integral dalam selang 0 hingga L. Jadi kita peroleh:
1. Jika f(x) ganjil, maka,
Dalam hal ini , f(x) dikatakan teruraikan dalam deret cosinus.
2.5 Persamaan Kalor
Persamaan kalor merupakan hal yang mendasar dalam berbagai macam bidang
ilmiah. Dalam matematika, persamaan kalor itu persamaan diferensial parsial
prototipe parabola. Dalam teori probabilitas, persamaan kalor dihubungkan
dengan studi gerak Brown melalui persamaan Fokker-Planck. Dalam matematika
keuangan persamaan kalor digunakan untuk memecahkan persamaan diferensial
parsial Black-Scholes. Persamaan difusi, versi yang lebih umum dari persamaan
kalor, muncul sehubungan dengan studi difusi kimia dan proses terkait lainnya.
Persamaan kalor berasal dari hukum Fourier dan konservasi energi maka hukum
Fourier untuk persamaan kalor dapat ditulis:
̇ = − T (2.17)
Persamaan Kalor satu dimensi mempunyai bentuk persamaan diferensial parsial
biasa sebagai berikut:
T − T = 0 (2.18)
Dengan T = T ( , ) yang diturunkan dari rumusan sederhana suatu batangan
sebagai media perambatan kalor.
Sebagaimana telah diketahui bahwa kalor merambat dari temperatur tinggi
ditinjau diisolasi dengan sempurna secara lateral dan dianggap adiabatik (tidak
ada kalor yang masuk maupun keluar secara lateral atau boleh juga dianggap kalor
yang masuk sama dengan kalor yang keluar). Sedangkan, untuk persamaan kalor satu dimensi non homogen dinyatakan
sebagai:
( , ): laju aliran kalor pada batang logam konduktor
2.5.1 Syarat Awal dan Syarat Batas Persamaan Kalor Satu Dimensi
Batang dengan penampang seragam diisolasi secara lateral. Panjang batang = L
dan diletakkan pada sumbu x. Temperatur pada batang pada suatu waktu hanya
X = 0
X = L y
z
x
Gambar 2.2 Pemodelan Aliran Kalor Satu Dimensi
Ada dua macam syarat batas untuk masalah perpindahan kalor konduksi
yaitu kondisi batas (boundary condition) dan kondisi awal (initial condition).
Kondisi batas adalah kondisi pada batas (ujung) batang pada waktu t sembarang.
Kondisi awal adalah temperatur pada x sembarang pada waktu t=0. Syarat batas
untuk perpindahan kalor konduksi 1 dimensi adalah :
1. Jika temperatur awalnya adalah f(x) dan temperatur pada ujung dijaga konstan
pada nol, maka kondisi batasnya :
T(0, ) = 0 (2.25) T( , ) = 0, > 0 (2.26) Syarat awal
( ) = T( , 0) (2.27) 2. Bila batang diisolasi secara keseluruhan, termasuk pada x = 0 dan x = L maka
pada x= 0 dan x = L kalor tidak bisa masuk atau keluar (fluks kalor = 0)
sehingga kondisi batasnya adalah :
= 0 = 0 (2.28)
2.6 Fungsi Green
2.6.1 Mengkonstruksi Fungsi Green Persamaan Diferensial Linear Orde-n Melalui Metode Variasi Parameter
Persamaan diferensial linear tak homogen orde-n:
dengan fungsi f (x) merupakan fungsi yang kontinyu. Solusi umum persamaan
diferensial di atas adalah :
( )= ( )+ ( ) (2.29)
dengan ( ) merupakan solusi umum persamaan diferensial homogen
pautannya dengan ( )merupakan suatu solusi khusus atau solusi partikulirnya.
Untuk menentukan solusi partikulirnya, dapat dilakukan dengan cara
mengkonstruksi fungsi green. Adapun langkah yang dilakukan dalam
mengkontruksi fungsi green adalah sebagai berikut :
1. Menentukan solusi bebas linear persamaan diferensial homogen.
Persamaan diferensial linear tak homogen orde-n di atas dapat di selesaikan
dengan mensubsitusikan = , kemudian menentukan bilangan tepat t
sehingga memenuhi persamaan diferensial linear tak homogen orde-n.
Karena = , ′ = , ′′ = , dan seterusnya hingga = .
Bila disubsitusikan dalam persamaan (2.36) akan didapatkan suatu persamaan
dalam t, yaitu :
( + ( )+ ( )+⋯+ ) = 0
karena etx≠ 0, maka
( + ( )+ ( )+⋯+ ) = 0 (2.30) Persamaan (2.30) tersebut disebut persamaan karakteristik dari persamaan
diferensial linear tak homogen orde-n, dan akar – akar karakteristik. Ada tiga
kemungkinan solusi bebas linear dari persamaan diferensial linear tak homogen
orde-n, yaitu :
a. Bila akar – akarnya real dan berlainan, maka selesian bebasnya yaitu ,
, . . . ,
b. Bila akar – akarnya real dan sama, maka solusi bebas linearnya yaitu
, , . . . ,
c. Bila akar – akarnya kompleks, maka selesain bebas linearnya yaitu
( ) atau ( ) atau ( + )
Apabila solusi bebas linear dari persamaan diferensial homogennya dimisalkan
( ), ( ), . . . , ( ), maka ( ) = ( ) + ( ) +. . . + ( )
2. Memisalkan yp dengan mengganti konstanta , , . . ., dengan fungsi
4. Menentukan uk(x) dengan mengintegralkan uk’(x) terhadap t diperoleh :
( )= ∫ ( ) ( )
[ ( ), ( ),…, ( )] ; k = 1, 2, . . ., n (2.32)
5. Mensubsitusikan persamaan (2.32) pada persamaan (2.31) sehingga diperoleh: ( )= ( )
( ) = ( , ) ( )
Dari langkah – langkah tersebut, maka di dapat fungsi green
( , )= ( ) ( ) ⋯ ( ) ( )
[ ( ), ( ),…, ( )] (2.32)
Jadi solusi umum persamaan diferensial linear tak homogen orde-n adalah :
( ) = ( ) + ∫ ( , ) ( )
solusi persamaan diferensial di atas yang memenuhi kondisi awal
( ) = ′( ) = ′′( ) = ( )( ) = 0
Fungsi green merupakan bagian dari solusi persamaan diferensial non
homogen yang berbentuk :
Dengan ( , )adalah fungsi Green yang menyatakan pengaruh fungsi sumber
f(x) posisi x0dari fungsi sumber pada posisi x.
2.7 Separasi Variabel
Separasi variabel adalah salah satu dari beberapa metode untuk memecahkan
persamaan diferensial biasa dan parsial, di mana aljabar memungkinkan seseorang
untuk menulis ulang persamaan sehingga masing-masing dari dua variabel terjadi
pada sisi yang berbeda dari persamaan .
Salah satu syarat penggunaan metode separasi variabel adalah persamaan
tersebut merupakan persamaan diferensial parsial linear homogen dengan kondisi
batas linier . Dengan menggunakan metode separasi variabel, kondisi awal dari
suatu persamaan diferensial kurang terpenuhi. Metode pemisahan variabel
bergantung pada asumsi bahwa fungsi dari bentuk
T ( , ) = ( ) ( )
Persamaan di atas akan menjadi solusi dari persaan diferensial parsial homogen
linear dalam x dan t . Persamaan tersebut juga harus memiliki kondisi batas yang
homogen dan linear . Namun, seperti disebutkan di atas metode separasi variabel
akan jarang memenuhi kondisi awal.
Tidak semua persamaan diferensial dapat diselesaikan dengan metode ini.
Metode ini hanya dapat dikerjakan pada persamaan yang berbentuk
( ) + ( ) = 0,