PEMODELAN DAN PEMETAAN KASUS DEMAM
BERDARAH
DENGUE
DI PROVINSI JAWA
TIMUR TAHUN 2014 DENGAN
GENERALIZED
POISSON REGRESSION
, REGRESI BINOMIAL
NEGATIF DAN
FLEXIBLY SHAPED SPATIAL
SCAN STATISTIC
NENDY SEPTI ARNIVA NRP 1314 105 007 Dosen Pembimbing Dr. Purhadi M.ScPROGRAM STUDI S1 JURUSAN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH NOPEMBER
MODELING AND MAPPING OF
DENGUE
HEMORRHAGIC FEVER
CASE IN EAST JAVA
2014 USING GENERALIZED POISSON
REGRESSION, NEGATIVE BINOMIAL
REGRESSION AND FLEXIBLY SHAPED
SPATIAL SCAN STATISTIC
NENDY SEPTI ARNIVA NRP 1314 105 007 Supervisor
Dr. Purhadi M.Sc
UNDERGRADUATE PROGRAMME DEPARTMENT OF STATISTICS
FACULTY OF MATHEMATICS AND NATURAL SCIENCES INSTITUT TEKNOLOGI SEPULUH NOPEMBER
vii
TAHUN 2014 DENGAN GENERALIZED POISSON REGRESSION, REGRESI BINOMIAL NEGATIF DAN FLEXIBLY SHAPED SPATIAL SCAN STATISTIC
Nama Mahasiswa : Nendy Septi Arniva
NRP : 1314 105 007
Jurusan : Statistika FMIPA-ITS
Dosen Pembimbing : Dr. Purhadi, M. Sc Abstrak
Salah satu penyakit menular yang menjadi masalah utama kesehatan masyarakat di Indonesia adalah penyakit Demam Berdarah Dengue (DBD). DBD ditularkan oleh vektor nyamuk Aides Aegypti melalui gigitan. Tempat yang paling banyak nyamuk ini berada yaitu di lingkungan yang buruk, lembab. Salah satu Provinsi yang Kasus DBD masih tinggi yaitu Provinsi Jawa Timur. Jumlah kasus DBD di Jawa Timur hingga akhir Januari 2015 sebanyak 1.817 kasus. Dalam penelitian ini dilakukan pemodelan jumlah kasus DBD dengan metode Generalized Poisson Regression (GPR) dan Regresi Binomial Negatif. Metode GPR dan regresi binomial negatif dilakukan untuk menanggani kasus overdispersi pada kasus jumlah DBD di Jawa Timur tahun 2014. Pendeteksian wilayah yang menjadi kantong DBD menggunakan metode Flexibly Shaped Spatial Scan Statistic. Pemodelan menggunakan GPR dan BNR didapatkan variabel berpengaruh terhadap kasus DBD di Jawa Timur Tahun 2014 adalah persentase rumah sehat dan rasio sarana kesehatan per 1000 penduduk. Hasil pendeteksian kantong DBD berdasarkan model GPR dan BNR didapat sepuluh kantong DBD. Kantong dengan nilai resiko tertinggi terdapat pada Kota Surabaya dengan nilai resiko sebesar 3,32 dengan pemodelan GPR, dan 2,84 dengan pemodelan BNR.
Kata kunci : DBD, Flexibly Shaped Spatial Scan Statistic, GPR, Regresi
ix
USING GENERALIZED POISSON REGRESSION, BINOMIAL NEGATIVE REGRESSION AND FLEXIBLY
SHAPED SPATIAL SCAN STATISTIC Student Name : Nendy Septi Arniva
NRP : 1314 105 007
Department : Statistics FMIPA-ITS Supervisor : Dr. Purhadi, M. Sc
Abstract
One of the infectious diseases that became major public health problem in Indonesia is a disease of Dengue Hemorrhagic Fever (DHF). DHF is transmitted by Aides Aegypti mosquito vectors through a bite. The most common places that mosquitoes are located in a bad neighborhood, moist. One province is still high which case DBD East Java Province. Number of DHF cases in East Java until the end of January 2015 as many as 1,817 cases. In this research, modeling the number of DHF cases with Generalized Poisson Regression method (GPR) and Binomial Negative Regression. GPR method and binomial negative regression is done in order to tackle cases of overdispersi the number of dengue cases in East Java in 2014. The detection of regions where there is a DHF using Shaped Flexible Spatial Scan Statistic. Modelling using GPR and BNR obtained variables affect the DHF cases in East Java in 2014 is the percentage of healthy house and the ratio of health facilities per 1000 population. The results of the detection of DHF bags by model GPR and BNR gained ten bags of DHF. Bag with the risk value is highest in the city of Surabaya with the risk value of 3.32 with GPR modeling, and 2.84 with modeling BNR.
Keywords : Binomial Negative Regression, DHF, Flexibly Shaped Spatial
xiii Halaman HALAMAN JUDUL... i LEMBAR PENGESAHAN...v ABSTRAK... vii ABSTRACT ... ix KATA PENGANTAR ... xi
DAFTAR ISI... xiii
DAFTAR GAMBAR ... xvii
DAFTAR TABEL... xix
DAFTAR LAMPIRAN ... xxi
BAB I PENDAHULUAN 1.1 Latar Belakang...1 1.2 Rumusan Permasalahan ...3 1.3 Tujuan Penelitian ...3 1.4 Manfaat Penelitian ...4 1.5 Batasan Masalah ...4
BAB II TINJAUAN PUSTAKA 2.1 Statistik Deskriptif ...5
2.2 Multikolinearitas ...5
2.3 Regresi Poisson...6
2.3.1 Penaksiran Parameter Model Regresi Poisson ...8
2.3.2 Pengujian Parameter Model Regresi Poisson ...11
2.3.3 Deteksi Overdispersi Pada Regresi Poisson ...12
2.4 Generalized Poisson Regression (GPR) ...13
2.4.1 Penaksiran Parameter Model GPR ...14
2.4.2 Pengujian Parameter Model GPR...16
2.5 Regresi Binomial Negatif ...17
2.5.1 Penaksiran Parameter Model Regresi Binomial Negatif ...17
2.5.2 Pengujian Parameter Model Regresi Binomial Negatif ...21
xiv
Hipotesis Monte Carlo...25
2.8 Demam Berdarah Dengue (DBD) ...27
BAB III METODOLOGI PENELITIAN 3.1 Sumber Data ...29
3.2 Variabel Penelitian...29
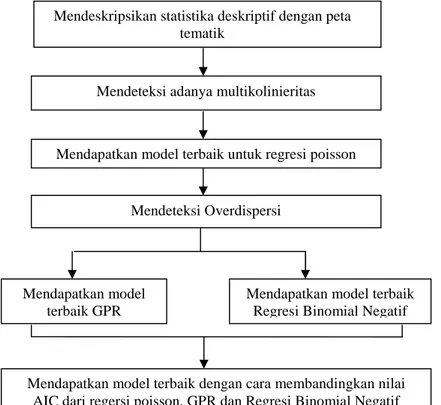
3.3 Langkah Analisis ...32
3.4 Diagram Alir Penelitan ...34
BAB IV ANALISIS DAN PEMBAHASAN 4.1 Deskripsi Kasus Demam Berdarah Dengue dan Faktor-Faktor yang diduga Mempengaruhi ... 35
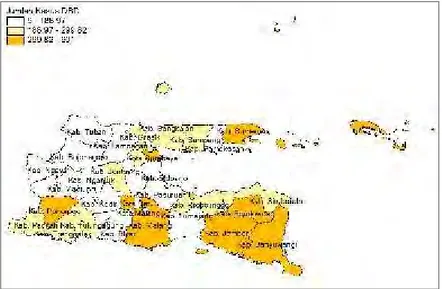
4.1.1 Jumlah Kasus Demam Berdarah Dengue ... 36
4.1.2 Kepadatan Penduduk ... 37
4.1.3iPersentase Rumah Tangga yang Berperilaku Hidup Bersih dan Sehat (PHBS)... 39
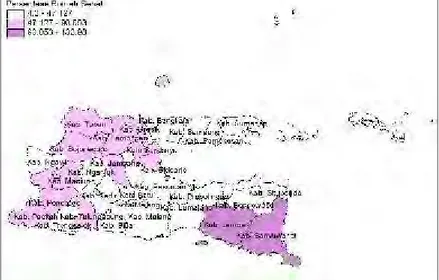
4.1.4iPersentase Rumah Sehat... 40
4.1.5iRasio Sarana Kesehatan per 1000 Penduduk ... 41
4.1.6iRasio Tenaga Kesehatan per 1000 Penduduk... 42
4.2 Pemeriksaan Multikolinearitas... 44
4.3 Pemodelan Jumlah Kasus DBD tiap Kabupaten/ Kota di Jawa Timur Tahun 2014 Menggunakan Regresi Poisson ... 45
4.4 Pemeriksaan Overdispersi... 46
4.5 Pemodelan Jumlah Kasus DBD tiap Kabupaten/ Kota di Jawa Timur Tahun 2014 Menggunakan Generalized Poisson Regression (GPR)... 47
4.6 Pemodelan Jumlah Kasus DBD tiap Kabupaten/ Kota di Jawa Timur Tahun 2014 Menggunakan Regresi Binomial Negatif... 49
4.7 Pemilihan Model Terbaik ... 50
4.8 Pendeteksian Kantong DBD di Jawa Timur Menggunakan Flexibly Shaped Spatial Scan Statistic ... 51
xv BAB V KESIMPULAN DAN SARAN
5.1 Kesimpulan ...55
5.2 Saran ...56
DAFTAR PUSTAKA ...57
xvii
Halaman
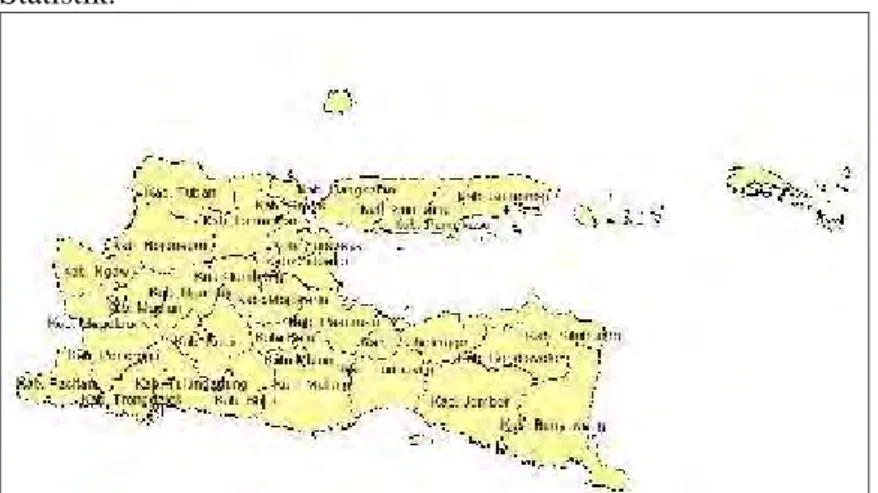
Gambar 3.1 Provinsi Jawa Timur ... 29
Gambar 3.2 Diagram Alir Penelitian ... 34
Gambar 4.1 Penyebaran Jumlah Kasus DBD ... 37
Gambar 4.2 Penyebaran Kepadatan Penduduk ... 38
Gambar 4.3 Penyebaran Persentase Rumah Tangga ber-PHBS ... 39
Gambar 4.4 Penyebaran Persentase Rumah Sehat... 41
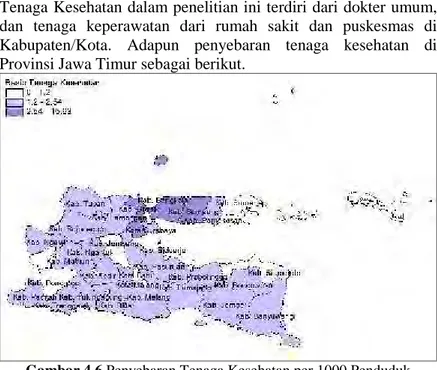
Gambar 4.5 Penyebaran Sarana Kesehatan per 1000 Penduduk... 42
Gambar 4.6 Penyebaran Tenaga Kesehatan per 1000 Penduduk... 43
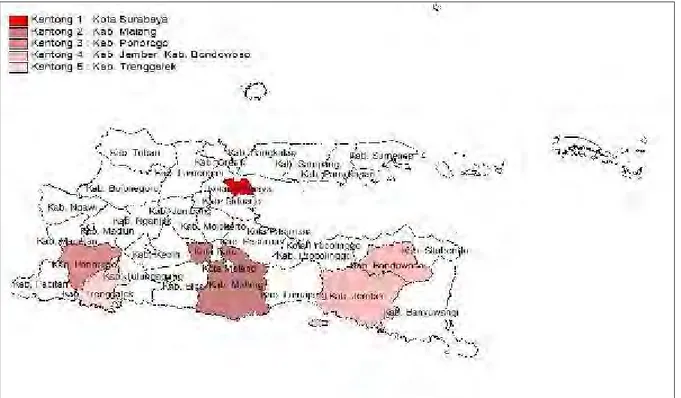
Gambar 4.7 Hasil Pendeteksian Kantong DBD dengan Pemodelan Regresi Binomial Negatif ... 53
xix
Halaman
Tabel 3.1 Variabel Penelitian ... 30
Tabel 4.1 Statistika Deskriptif Variabel Penelitian ... 36
Tabel 4.2 Koefisien Korelasi Antar Variabel Prediktor ... 44
Tabel 4.3 Nilai VIF dari Variabel Prediktor... 44
Tabel 4.4 Estimasi Parameter Model Regresi Poisson ... 45
Tabel 4.5 Nilai Deviance dan Pearson dari Model Regresi Poisson ... 47
Tabel 4.6 Estimasi Parameter Model GPR... 47
Tabel 4.7 Estimasi Parameter Model Regresi Binomial Negatif ... 49
Tabel 4.8 Pemilihan Model Terbaik ... 50
Tabel 4.9 Hasil Deteksi Kantong DBD dengan Pemodelan Regresi Binomial Negatif ... 52
1 1.1 Latar Belakang
Demam Berdarah Dengue (DBD) merupakan masalah utama kesehatan masyarakat di Indonesia dan angka kematian DBD selalu meningkat dari tahun ke tahun. DBD sering muncul sebagai kejadian luar biasa (KLB) dengan angka kematian relatif tinggi. DBD ditularkan oleh vektor nyamuk Aides Aegypti melalui gigitan. Penyakit demam berdarah biasanya didahului dengan adanya demam tinggi, nyeri pada kepala dan otot. Tempat yang paling banyak nyamuk ini berada yaitu di lingkungan yang lembab, curah hujan yang tinggi, genang air di dalam maupun di luar rumah. Faktor lain penyebab DBD ini adalah kepadatan penduduk, sanitasi lingkungan yang buruk, perilaku masyarakat yang tidak sehat.
Departemen Kesehatan Republik Indonesia telah
mengupayakan berbagai strategi dalam mengatasi kasus DBD yang salah satu diantaranya adalah dengan cara Pemberantasan Sarang Nyamuk Demam Berdarah Dengue (PSN DBD), namun ternyata Kasus DBD di Provinsi Jawa Timur masih tinggi. Menurut kementrian kesehatan sebanyak 1.817 kasus demam berdarah dengue (DBD) di Provinsi Jawa Timur hingga akhir Januari 2015. Peningkatan kasus DBD ini hingga 980 kasus dari sebelumnya.
Regresi poisson merupakan analisis regresi nonlinear dari distribusi poisson dan digunakan dalam menganalisis data diskrit (count). Salah satu contoh data diskrit (count) yaitu jumlah kasus demam berdarah dengue di Provinsi Jawa Timur pada penelitian ini. Salah satu permodelan regresi poisson yaitu Generalized Poisson Regresion (GPR), model ini dapat mengatasi masalah dengan varian lebih besar dibandingkan dengan rata-rata yang disebut overdispension, karena tidak mengharuskan nilai mean yang sama dengan nilai varians. Mengatasi overdispersi pada
Regression dapat dilakukan dengan menggunakan pendekatan model regresi Binomial Negatif. Penelitian sebelumnya yang telah dilakukan oleh Rahayu (2012) memperoleh hasil dengan penerapan analisis GPR dan regresi binomial negatif pada pemodelan pengaruh iklim terhadap angka kejadian demam berdarah dengue di Surabaya. Pada penelitian tersebut ditemukan adanya kasus overdispersi pada regresi poisson. Hasil yang diperoleh adalah regresi binomial negatif merupakan model terbaik dalam mengatasi kasus overdipersi pada regresi poisson karena menghasilkan nilai AIC (Akaike Information Criterion) terkecil.
Salah satu strategi untuk mengatasi penyebaran penyakit DBD dengan mengetahui daerah yang menjadi kantong-kantong DBD atau hotspot dengan cara memetakan daerah tersebut. Salah satu metode yang digunakan untuk mendeteksi hotspot yaitu Flexibly Shaped Spatial Scan Statistic. Penelitian sebelumnya yang telah dilakukan oleh Hidayanti (2015) memperoleh hasil
dengan menggunakan Geographically Weighted Negative
Binomial Regression (GWNBR) dan Flexibly Shaped Spatial Scan Statistic menyebutkan bahwa pemodelan jumlah kasus DBD didapatkan sebanyak 12 kelompok, dari hasil proses pendeteksian kantong DBD menunjukkan bahwa terbentuk tiga kantong DBD. Penelitian lain terkait dengan Flexibly Shaped Spatial Scan
Statistic dilakukan oleh Sari (2016) memperoleh hasil
pendeteksian kantong DBD di provinsi Jawa Timur terbentuk 12 kantong DBD, yang mana Kota Surabaya merupakan daerah yang paling rawan terkena DBD.
Untuk mengetahui wilayah yang paling terkena penyakit
Demam Berdarah Dengue (DBD), maka dilakukan penelitian
mengenai pemetaan wilayah di Jawa Timur berdasarkan
penderita Demam Berdarah Dengue (DBD). Penanganan kasus overdispersi dilakukan dengan mengaplikasikan metode Generalized Poisson Regression (GPR) dan Regresi Binomial Negatif untuk mendapatkan model terbaik pada kasus DBD di setiap kabupaten/kota di Provisi Jawa Timur tahun 2014. Untuk
mengetahui kantong-kantong DBD dengan Flexibly Shaped Spatial Scan Statistic, sehingga upaya menangani/ mengatasi wilayah yang paling banyak terjangkit DBD dengan adanya pemetaan wilayah ini, sehingga penangganan lebih efektif dan tepat sasaran dan mengurangi penderita penyakit Demam Berdarah Dengue (DBD).
1.2 Rumusan Masalah
Demam berdarah dengue merupakan salah satu penyakit menular yang mana angka kematian DBD selalu meningkat dan DBD sering muncul sebagai kejadian luar biasa (KLB). Dalam kasus jumlah DBD ini sering terjadi kasus overdispersi maka metode yang digunakan untuk mengatasi overdispersi dan faktor-faktor yang mempengaruhi DBD yaitu dengan membandingkan Generalized Poisson Regression dan regresi binomial negatif. Faktor yang diduga mempengaruhi kasus DBD di Provinsi Jawa Timur tahun 2014 yaitu faktor lingkungan, perilaku kesehatan
masyarakat serta fasilitas kesehatan. Selanjutnya metode yang
digunakan untuk menentukan kantong-kantong DBD di Provinsi Jawa Timur tahun 2014 dengan Flexibly Shaped Spatial Scan Statistic
1.3 Tujuan Penelitian
Tujuan yang ingin dicapai dalam penelitian ini adalah sebagai berikut.
1. Membandingkan analisis GPR dan regresi binomial negatif
dalam mengatasi overdispersi berdasarkan kriteria nilai AIC pada kasus DBD di kabupaten/kota di Jawa Timur tahun 2014.
2. Mengetahui faktor yang berpengaruh terhadap kasus DBD di
Provinsi Jawa Timur tahun 2014.
3. Memetakan Flexibly Shaped Spatial Scan Statistic untuk
mendeteksi kantong DBD tingkat kabupaten/kota di Jawa Timur.
1.4 Manfaat Penelitian
Adapun manfaat yang ingin dicapai dari hasil penelitian ini adalah:
1. Memberikan pengetahuan tentang penyakit DBD serta
memberikan pemahaman tentang mengatasi kasus
overdispersi pada regresi poisson dengan menggunakan analisis GPR dan regresi binomial negatif. Serta pemetaan berdasarkan kantong-kantong DBD yang terbentuk di kabupaten/kota di Jawa Timur dengan metode Flexibly Shaped Spatial Scan Statistic.
2. Membantu Dinas Kesehatan dan masyarakat dalam
pencegahan meluasnya penyakit DBD di kabupaten/kota di Jawa Timur dari daerah yang paling terjangkit DBD dan rawan terkena DBD.
1.5 Batasan Masalah
Penelitian ini menggunakan data jumlah kasus DBD di Provinsi Jawa Timur tahun 2014 dengan unit penelitian adalah tiap kabupaten/kota untuk mendapatkan wilayah yang paling banyak terkena DBD dan mendapatkan model dengan menggunakan analisis GPR dan regresi binomial negatif dan pembentukan kantong DBD dengan metode Flexibly Shaped Spatial Scan Statistic.
5
Pada bab ini akan dibahas mengenai konsep dan teori dari metode yang digunakan dalam melakukan analisis untuk menjawab perumusan masalah dari kasus DBD di Provinsi jawa Timur. Metode yang digunakan diantaranya adalah statistika
deskriptif, analisis regersi poisson, Generalized Poisson
Regression (GPR) dan regresi binomial negatif, serta untuk melihat kantong DBD yang terbentuk menggunakan Flexibly Shaped Spatial Scan Statistic. Pembahasan mengenai konsep dan teori yang digunakan dalam analisis disajikan sebagai berikut.
2.1 Statistika Deskriptif
Statistika deskriptif merupakan bagian statistika yang membahas tentang metode-metode dengan pengumpulan dan penyajian data sehingga menarik dan memberikan informasi. Data dapat didefinisikan menjadi dua, yaitu dideskripsikan menjadi grafik atau tabel dan dideskripsikan secara numerik. Penyajian data dalam bentuk grafik atau tabel memberikan informasi dengan tampilan yang menarik, seperti diagram batang (bar chart), diagram lingkaran (pie chart), histogram, scatter plot dan lainnya. Penyajian data dalam bentuk deskriptif secara numerik memberikan informasi berupa ukuran pemusatan, penyebaran data, serta kecenderungan suatu gugus data seperti rata-rata (mean), standar deviasi, nilai maksimum, nilai minimum, serta modus. Mean (rataan) didefinisikan sebagai jumlah data dibagi dengan banyaknya data (Walpole, 1995). Varians adalah suatu angka yang menunjukkan ukuran varibilitas yang dihitung dengan jalan mengkuadratkan standar deviasi.
2.2 Multikolinieritas
Multikolinearitas adalah kondisi terdapatnya hubungan linier atau korelasi yang tinggi antara masing-masing variabel independen dalam model regresi. Menurut Draper dan Smith (1992) multikolinearitas biasanya terjadi ketika sebagian besar
variabel yang digunakan saling terkait dalam suatu model regresi. Oleh karena itu masalah multikolinearitas tidak terjadi pada regresi linier sederhana yang hanya melibatkan satu variabel independen. Menurut Hocking (1996) pendeteksian adanya kasus multikolinieritas dapat dilihat melalui.
1. Variance Inflation Factors (VIF) > 10 VIF dinyatakan sebagai berikut :
2 1 1 j VIF R (2.1) 2 j
R merupakan nilai koefisien determinasi antara variabel xj
dengan variabel prediktor lainnya. Nilai VIF yang lebih besar dari 10 menunjukkan adanya kasus multikolinieritas antar variabel prediktor.
2. Nilai koefisien korelasi Pearson (rij) antar variabel-variabel
prediktor. Mengindikasikan adanya multikolinieritas dengan melihat nilai koefisien korelasi Pearson antar variabel prediktor cukup besar (lebih dari 0,95).
Multikolinieritas dapat diatasi dengan mengeluarkan salah satu variabel independen yang berkorelasi tinggi dengan variabel
independen yang lain. Pengeluaran variabel ini dapat
dilakukan secara manual ataupun otomatis melalui metode stepwise.
2.3 Regresi Poisson
Regresi poisson merupakan salah satu regresi yang menggambarkan hubungan antara variabel respon (Y) dan variabel prediktor (X) dengan mengasumsikan variabel Y berdistribusi poisson. Menurut Walpole (1995) distribusi poisson menyatakan banyak sukses yang terjadi dalam suatu selang waktu atau daerah tertentu. Menurut Myers (1990) fungsi peluang dari distribusi poisson dapat dinyatakan sebagai berikut.
,... 2 , 1 , 0 , ! ) , ( y y e y f y (2.2)
Dengan merupakan rata-rata variabel random Y yang
berdistribusi poisson dimana nilai rata-rata dan varians mempunyai nilai lebih dari nol. Distribusi poisson adalah suatu distribusi yang paling sederhana dalam pemodelan data yang
berupa jumlah (count). Menurut Agresti (2002) yang
menunjukkan bahwa Generalized Linear Model (GLM)
merupakan pengembangan dari model linear klasik khususnya dalam mengatasi kendala variabel respon yang tidak normal. GLM terdiri dari 3 komponen yaitu komponen random, komponen sistematik, dan link function. Komponen random merupakan variabel dependen yaitu variabel Y. Variabel y
merupakan vektor yang terdiri dari [y1,y2,...,yn]T. Komponen
random dari GLM termasuk ke dalam keluarga eksponensial yang fungsi peluang dapat dinyatakan sebagai berikut.
)) ( exp( ) ( ) ( ) , (yi i a i b yi yiQ i f (2.3)
Komponen sistematik yaitu vektor η yang terdiri dari
T n]
,..., ,
[12 menghubungkan dengan variabel X atau sebagai
variabel prediktor, sehingga untuk bentuk umum dari η = Xβ
dimana X merupakan suatu matriks dengan elemen yang terdiri
variabel prediktor dan dinyatakan dengan
k n n k x x x x X , 1 , , 1 1 , 1 1 1 ,
sedangkan β merupakan bentuk vektor dari parameter-parameter
model. Masing-masing dari elemen η dapat dinyatakan dengan
k j ij j i x 0 merupakan kombinasi linier dari variabel prediktor
disebut dengan linear prediktor.
Komponen link function yang menghubungkan antara komponen random dan komponen sistematik. Berdasarkan
Agresti (2002) dimisalkan
i = E(Yi) dimana i=1,2,...,n. Modeluntuk menghubungkan
i dengan
i oleh g(i)i, dimanag(.) adalah fungsi yang diturunkan. Sehingga g(.)
menghubungkan E(Yi) dengan variabel prediktor, dan
diformulasikan sebagai berikut.
ik k i i ij k j j i x x x g
... ) ( 0 1 2 0 (2.4)Link function yang digunakan dalam regresi poisson
adalah ln, sehingga ln(
i) =
i. Dengan demikian regresipoisson dapat dinyatakan sebagai berikut.
n 1,2,..., i , ) ln( 1 0
ij k j j i x dimana
k j ij j i i x 1 0 exp ) ( xi (2.5)2.3.1 Penaksiran Parameter Model Regresi Poisson
Penaksiran parameter model regresi poisson dilakukan dengan menggunakan metode Maximum Likelihood Estimation (MLE) yaitu dengan cara memaksimumkan fungsi likelihood (Myers, 1990). Fungsi likelihood dari regresi poisson yaitu.
n i i y i i y L i 1 ! ) exp( ln ) ( ln β
n i i y i i y i 1 ! ) exp( ln
n i i n i i n i y y e 1 1 1 ) ! ln( β xiT β xiT (2.6) dimana T ik i i x x x ] 1 [ 1 2 i xT k]
[0 1 2
β
Taksiran maksimum Likelihood untuk parameter βj
dinyatakan dengan ˆjyang merupakan penyelesaian dari turunan
pertama fungsi logaritma natural dari likelihood. Selanjutnya
persamaan (2.6) diturunkan terhadap βT menjadi turunan kedua
sebagai berikut.
1 1 ln exp n n i i i L y T i i i T β x x β x β (2.7)Selanjutnya persamaan (2.7) disamakan dengan nol untuk mendapatkan penyelesaiannya. Tetapi penyelesaian dengan cara tersebut sering kali tidak mendapatkan hasil yang eksplisit sehingga alternatif yang bisa digunakan untuk mendapatkan penyelesaian dari MLE adalah dengan metode iterasi numerik Newton-Raphson. Dalam metode iterasi Newton diperlukan turunan kedua dari fungsi likelihood untuk pembentukan matriks hessian, turunan kedua tersebut adalah
n i e L 1 2 ln T x β i i T T i x x β β βMenurut Cameron dan Travedi (1998) algoritma untuk optimalisasi metode Newton-Raphson adalah sebagai berikut.
1. Menentukan nilai taksiran awal parameter
βˆ 0 yangdiperoleh dengan metode Ordinary Least Square (OLS) yaitu
ˆ T -1 T 0 β = X X X Y (2.8) dimana nk n k k x x x x x x 1 2 21 1 11 1 1 1 X dan y
Y1 Y2 Yn
T2. Membentuk vektor gradien g, ) ( . ) ( 1 1 1 i i n i n i i i n i y y g
i i i x x x ) ( 2 1 0 1 ) 1 ( ) ( ln ... ) ( ln ) ( ln ) ( ln m k x k L L L L ) (β g (m) Tdimana k adalah banyaknya parameter yang ditaksir.
3. Membentuk matriks Hessian H.
Matriks Hessian ini disebut juga matriks informasi.
T n i i i T n i H
xi.xi
xi.xi 1 1 . . ) ( ) ( 2 2 1 2 2 1 2 0 2 1 0 2 2 0 2 ) 1 ( ) 1 ( ) ( ln ) ( ln ) ( ln ) ( ln ) ( ln ) ( ln m k k k k x k L L L L L L ) H(β(m)
H β
β) 1 ˆ ( E Var4. Memasukkan nilai βˆ(0) ke dalam elemen-elemen vektor g
dan matriks H, sehingga diperoleh vektor g(βˆ(0)) dan
matriks H(βˆ(0)).
5. Melakukan iterasi pada persamaan
) ( ( ) ( ) ) ( 1) m m m (m β H β )g(β β 1
Dimulai dari m=0, dengan nilai (m)
β merupakan sekumpulan
penaksir parameter yang konvergen pada iterasi ke-m.
6. Penaksir parameter dikatakan konvergen ketika nilai
) ( ) 1 (m βm
β dimana merupakan suatu bilangan yang
sangat kecil sekali. Sehingga hampir tidak ada perbedaan
antara β(m1) dan β(m). Jika belum didapatkan penaksir
parameter yang konvergen, maka dilanjutkan kembali langkah 5 hingga iterasi ke m* = m+1.
2.3.2 Pengujian Parameter Model Regresi Poisson
Menguji kelayakan model regresi Poisson, terlebih dahulu ditentukan dua buah fungsi likelihood yang berhubungan dengan model regresi yang diperoleh. Fungsi-fungsi likelihood yang
dimaksud adalah ( )
L yaitu nilai likelihood untuk model
lengkap dengan melibatkan variabel prediktor dan ( )
L yaitu
nilai likelihood untuk model sederhana tanpa melibatkan variabel prediktor. Salah satu metode yang digunakan untuk menentukan statistik uji dalam pengujian parameter model regresi poisson adalah dengan menggunakan metode Maximum Likelihood Rasio Test (MLRT) dengan hipotesis.
H0: β1= β2= ... = βk= 0
H1: paling sedikit ada satu βj≠0 ; j=1,2,...,k
Statistik uji untuk kelayakan model regresi poisson adalah sebagai berikut.
ln( (ˆ)) ln( (ˆ))
2 ) ˆ ( ) ˆ ( ln 2 ) ˆ ( L L L L D β
n i i i i i i i y y y y 1 ) ln( ln 2 (2.9) dimana
n e yi yi L 1 i T i β x β x T i ln( !) ) ˆ ( ln
n i i i y y e L 1 0 ln( !) ) ˆ ( ln 0 Kriteria penolakan: tolak H0 jika
2 ) ; ( β) ( k D dengan k adalah banyaknya parameter model dibawah populasi dikurangi
dengan banyaknya parameter dibawah H0. Parameter model
regresi poisson yang telah dihasilkan dari estimasi parameter belum tentu mempunyai pengaruh yang signifikan terhadap model. Untuk itu perlu dilakukan pengujian terhadap parameter model regresi poisson secara individu. Dengan menggunakan hipotesis sebagai berikut.
H0: βj= 0 (pengaruh variabel ke-j tidak signifikan)
H1: βj≠ 0 (pengaruh variabel ke-j signifikan)
Statistik uji yang digunakan adalah:
) ˆ ( ˆ j j se z (2.10) ) ˆ ( j
se adalah nilai standar error atau tingkat kesalahan
dari parameterβj,didapat dari akar elemen diagonal ke-(j+1) dari
)
ˆ
r aˆ
v (β dengan vaˆr(βˆ)E(H1(βˆ)) . Kriteria penolakan tolak H0
jika
2 hit
z z dimanaαadalah tingkat signifikansi.
2.3.3 Deteksi Overdispersi Pada Regresi Poisson
Metode regresi poisson mensyaratkan kondisi dimana nilai varians dan mean variabel respon bernilai sama atau kondisi equidispersion (Khoshgotaar et al, 2004). Sedangkan, regresi poisson dikatakan overdispensi apabila nilai variansnya lebih besar dari nilai meannya. Overdispensi memiliki dampak yang sama dengan pelanggaran asumsi. Dampak ini terlihat pada nilai
standar error yang menjadi under estimate, sehingga
kesimpulannya tidak valid. Menurut McCullagh dan Nelder
(1983), kondisi overdispensi dapat ditulis Var(Y) >E(Y). Misal θ
merupakan parameter dispersi maka jika θ=0 artinya tidak terjadi kasus overdispersi, jika θ>0 artinya terjadinya kasus overdispersi,
dan jika θ<0 artinya terjadi kasus underdispersi. Kondisi
overdispersi dapat terjadi karena adanya sumber keragaman yang tidak teramat (Cameron dan Trivedi, 1998). Overdispersi dapat terjadi juga karena adanya pengamatan yang missing value pada variabel prediktor, adanya pencilan pada data, variabel prediktor perlu ditranformasi atau kesalahan spesifik link function dan perlunya iteraksi dalam model (Hardin dan Hilbe, 2007). Overdispersion merupakan nilai dispersi pearson chi-square dan deviance yang dibagi dengan derajat bebasnya, diperoleh nilai lebih besar dari 1.
2.4 Generalized Poisson Regression (GPR)
Model GPR merupakan suatu model yang sesuai digunakan untuk data count dimana terjadi over/under dispersion. Sehingga
selain parameter µ juga terdapat
sebagai parameter dispersi.GPR hampir mirip dengan regresi poisson yaitu merupakan suatu model GLM. Akan tetapi pada model GPR mengasumsikan bahwa komponen randomnya berdistribusi Generalized Poisson (GP). Misal, y=0,1,2,... merupakan variabel respon. Distribusi GPR diberikan Famoye, Wulu, dan Singh (2004) sebagai berikut.
1
-1
1
; ; exp , 0,1, 2, 1 ! 1 y y y y f y y y (2.11)Mean dan varians model GPR adalah sebagai berikut.
2 ) 1 ( ) var( dan ) (Y Y E
Apabila
0
maka model GPR akan menjadi regresipoisson biasa, apabila
0
maka model GPR merepresentasikandata count yang overdispersion, dan jika
0
maka GPRmerepresentasikan data count yang underdispersion. Model GPR memiliki bentuk yang sama dengan model regresi poisson yaitu sebagai berikut.
ln(µi) = xi
T
µi= exp (xi T β), i=1,2, ..., n (2.12) dimana T ik i i x x x ] 1 [ 1 2 i x T k] [0 1 2 β
2.4.1 Penaksir Parameter Model Generalized Poisson Regression (GPR)
Penaksir parameter model GPR pada persamaan (2.12) dilakukan dengan metode MLE (Maximum Likelihood Estimator). Fungsi likelihood untuk model GPR adalah sebagai berikut.
n i i i i n i i y i n i y i i n i i i i y y i i n i y y y L y y y L f L i i i i 1 1 _) 1 ( 1 1 1 ) 1 ( 1 1 1 ) 1 ( exp ! ) 1 ( 1 ) , ( 1 ) 1 ( exp ! 1 1 ) , ( ) , ( ) , ( β β β β (2.13) (2.12)Selanjutnya persamaan (2.13) diubah dalam bentuk fungsi logaritma natural menjadi.
n i i i i i i i n i i i i n i i y i n i y i i y y y y L y y y L i ii 1 1 1 _) 1 ( 1 ) 1 ln( ) 1 ( ) 1 ln( ) ln( ) , ( ln 1 ) 1 ( exp ! ) 1 ( 1 ln ) , ( ln β β dimana i i i i y y 1 ) 1 ( ) ! ln(dengan mensubtitusikan nilai i exp
xTiβ maka diperoleh,
n i i i i y y y L 1 ) ! ln( )) exp( 1 ln( )) ln(exp( ) , ( ln β xiTβ xiTβdimana ) exp( 1 ) 1 )( exp( ) 1 ln( ) 1 ( β x β x T i T i i i i y y y
n i i i i i y y y y L 1 * ) 1 ln( ) 1 ( )) exp( 1 ln( ) , ( ln β xiTβ xiTβ dimana 1 )) exp( 1 )( 1 ))( exp( ( ) ! ln( * x β xiTβ T i i i y yKemudian persamaan logaritma natural dari fungsi
likelihood diturunkan terhadap
β
Tdan disamakan dengan noluntuk mendapatkan parameter βˆ. Bentuk turunan persamaan
logaritma natural dari likelihood terhadap
β
Tyaitu.
1 1 )) exp( 1 )( exp ) , ( ln β x β (x x x β β T i T i i i i n i i T y y L dimana (1yi)
xiexp(xiTβ)(1(xiTβ))1*
dan 2 2 )) ( 1 ( )) (exp( * xi xiTβ xiTβJika ingin mendapatkan penaksir parameter
ˆ
makapersamaan tersebut diturunkan terhadap
dan disamakan dengannol. Hasil turunan terhadap
dinyatakan sebagai berikut.
n i i i i i y y y y L 1 1 1 ) 1 )( 1 ( )) exp( 1 )( exp( ) , ( ln β x β x β T i T i dimana
exp(xiTβ) yi(1 exp(xiTβ)1 *dan *(1 )exp(x β)(1 exp(x Tβ))2
i T
i
yi
Penurunan fungsi ln-likelihood terhadap
β
Tdan
seringkali menghasilkan persamaan yang implisit, sehingga digunakan iterasi Newton-Raphson sampai didapatkan penaksir parameter yang konvergen seperti pada subbab 2.3.1.
2.4.2 Pengujian Parameter Model GPR
Pengujian parameter GPR dilakukan dengan metode Maximum Likelihood Ratio Test (MLRT). Hipotesis yang digunakan adalah sebagai berikut.
H0: β1= β2= ... = βk= 0
H1: paling sedikit ada satu βj≠0; j=1,2,...,k
Statistik uji:
ln (ˆ) ln (ˆ)
2 ) ˆ ( ) ˆ ( ln 2 ln 2 ) ˆ ( L L L L D β (2.14) Dimana
n i i i i i y y y y L 1 * ) 1 ln( ) 1 ( )) exp( 1 ln( ) ˆ ( ln x β xiTβ T i 1 * ln( !)(exp( ))(1 )(1 exp( )) yi xiTβ yi xiTβ
n i i i i i y y y y L 1 * * 0 0 ln(1 exp( )) ( 1)ln(1 ) ) ˆ ( ln 1 0 0 * * )) exp( 1 )( 1 ))( exp( ( ) ! ln( yi yi Kriteria penolakan: Tolak H0 jika nilai
2 ) ; ( ˆ k Dβ Jika H0ditolak berarti paling sedikit ada satu βj≠ 0 yang menunjukkan
bahwa Xj berpengaruh secara signifikan terhadap model.
Pengujian dilanjutkan dengan uji secara parsial dengan hipotesis sebagai berikut.
H0: βj= 0 (pengaruh variabel ke-j tidak signifikan)
H1: βj≠ 0 (pengaruh variabel ke-j signifikan)
Statistik uji yang digunakan adalah:
) ˆ ( ˆ j j se z (2.15) ) ˆ ( j
se adalah nilai standar error atau tingkat kesalahan dari
)
ˆ
r( aˆ
v β dengan vaˆr(βˆ)E(H1(βˆ)) . Kriteria penolakan tolak H0
jika
2 hit
z z dimanaαadalah tingkat signifikansi.
2.5 Regresi Binomial Negatif
Penanganan overdispersi pada regresi poisson selain menggunakan Generalized Poisson Regression dapat dilakukan dengan menggunakan pendekatan model regresi Binomial Negatif. Masalah overdispersi dapat menyebabkan kesalahan inferensi mengenai estimasi parameter.
Menurut Cameron dan Trivedi (1998), distribusi Binomial Negatif yang mengakomodasi overdispersi memiliki fungsi densitas sebagai berikut.
,... 2 , 1 , 0 , 0 , 1 ) , ; ( 1 1 1 1 1 1 i y i i i i i i i y y y y f i (2.16)dengan (.) adalah fungsi Gamma. Distribusi Binomial Negatif
memiliki mean dan varians sebagai berikut. ) exp( ) | (yi xi i xiTβ E dan var(yi|xi)i i2,
jika θ menuju nol maka var(Yi) menuju µi sehingga Binomial
Negatif akan konvergen menuju Poisson. Model regresi Binomial Negatif memiliki bentuk yang sama dengan model regresi Poisson yaitu pada persamaan (2.5) sebagai berikut.
ik k i i i x x x ) 0 1 1 2 2 ln( dengan, ) exp( ) | (yi xi i xiTβ E ) exp( 0 1 i1 2 i2 k ik i x x x
2.5.1 Penaksiran Parameter Model Regresi Binomial Negatif
Penaksiran parameter regresi Binomial Negatif dilakukan dengan metode Maximum Likelihood Estimation (MLE) dengan
prosedur Newton Rhapron. Metode ini membutuhkan turunan
pertama dan kedua dari fungsi likelihood. Yi mempunyai fungsi
massa probabilitas distribusi binomial negatif seperti berikut.
i y i i i i i i i y y y f 1 1 1 1 1 1 ) , | ( 1 (2.17) dengan yi= 0,1,2,...Karena fungsinya saling bebas, akan fungsi likelihood adalah:
i y i i i n i i i y y L
1 1 1 1 1 1 ) , ( 1 1 β dengan
1 1 1 1 1 yi r i r y
y i i i i n i y r y r L i
1 1 1 ! 1 ) , ( 1 1 1 1 1 β
) ln , , (β lβ L
n i i i i i i y r y y y r i 1 1 1 1 1 ) 1 ln( ) ( ) ln( ) ! ln( ) ln( (2.18) Turunan pertama dari fungsi likelihood terhadap koefisien regresiβadalah
0 1 1 ) , ( 1 1 1 0
n i i i i n i i i i i y y y L β
n i i ip i i ip i p x y x y L 1 1 1 ) , ( β
n i i ip i i x y 1 1
0 1 1
n i i ip i i i i y x bentuk persamaan matriks dari turunan pertama fungsi likelihood
terhadap parameter β yaitu:
q
X
TWz
, dengan X adalahmatriks (n x c) dari variabel prediktor, W adalah matriks weight diagonal ke-i dan z adalah vektor matriks dengan baris ke-i, dnegan masing-masing elemenya adalah:
i i i w 1 dan
i i i i y z turunan pertama dari fungsi log-likelihood terhadap parameter
dispersi θ adalah
0 1 ) 1 ln( ) ( 1 ) , ( ) ( ' 1 1 0 1 2 1 2
n i y r i i i i i t y y r L f β
0 1 ) 1 ln( ) ( 1 ) , ( ) ( ' 1 1 0 2 1 2
n i y r i i i i i y r L f βTurunan parsial kedua fungsi likelihood terhadap parameter
koefisien regresiβadalah
n i i i i y L 1 2 2 0 2 1 1 ) , ( β
n i i i ij i i i ij i j x y x L 1 2 0 2 1 1 ) , ( β
n i i i ij i j x y L 1 2 0 2 1 1 ) , ( βMisalkan turunan parsial pertama dari L(β,) terhadap j,j p
adalah
0 1 ) , ( 1
n i i ij i i p x y L β
n i i i ij iu i i i ij iu i j u x x y x x L 1 2 2 1 ) )( ( ) 1 ( ) , ( β (2.19)
n i i i i ij iu j u y x x L 1 2 2 1 ) 1 ( ) , ( βEkspetasi dari turunan kedua log-likelihood adalah
n i i i ij iu j u x x L E 1 2 1 ) , ( β (2.20)Jika persamaan (2.20) dinyatakan dalam matriks I (matriks informasi) yaitu matriks yang mengandung ekspektasi negatif dari turunan kedua log-likelihood maka.
I=XTWX
Dengan X adalah matriks dari variabel prediktor, W adalah
matriks weight diagonal ke-i dengan elemen:
i i i w 1
Turunan kedua fungsi likelihood terhadap parameter dispersi θ
adalah ] ) ( ) 2 1 )( ( ) 1 ( ) 1 ln( 2 ) ( ) 2 ( [ ) , ( ) ( " 2 2 2 1 1 0 3 2 1 1 3 2 2 i i i i i i n i y r i y r r L f i
βLangkah-langkah estimasi parameter regresi binomial negatif dilakukan dengan langkah sebagai berikut:
1. Menentukan estimasi awal θ, misalˆ1 0,1
2. Menentukan estimasi maksimum likelihooddari parameter β
menggunakan prosedur iterasi Fisher scoring dengan asumsi
1 ˆ i i T 1 i T i 1 i β (X W X) X W z β ˆ ˆ
3. Menggunakan βˆ untuk menghasilkan estimasi dari
perameter θ dengan menggunakan prosedur iterasi Newton -Raphson satu variabel, iterasi berakhir jika diperoleh
ˆi ˆi 1 ) ( ) ( ˆ ˆ '' ' 1 i i i i f f
4. Jika ˆi1ˆi selesai; bila tidak, gunakan parameter
1 ˆ
i
dan kembali ke langkah 2, nilai merupakan
bilangan positif yang sangat kecil.
2.5.2 Pengujian Parameter Model Regresi Binomial Negatif
Uji kesesuaian model regresi binomial negatif dengan uji deviansi sebagai berikut.
Hipotesis:
H0: β1= β2= ... = βk= 0
H1: paling sedikit ada satu βj≠ 0, j=1,2,...,k
Statistik Uji: )) ˆ ( ln ) ˆ ( (ln 2 ) ˆ ( ) ˆ ( ln 2 ln 2 ) ˆ ( L L L L D
n i i i i i i i y y y y 1 1 1 ln 1 ln 2 (2.21) dimana
n i i i i y r a y y r L i 1 1 1 1 ) ln( ) ! ln( ) ln( ) ˆ ( ln dimana ) 1 ln( ) ( 1 yi i a
n i i i y r b y y r L i 1 0 1 1 1 ) ˆ exp( ln( ) ! ln( ) ln( ) ˆ ( ln dimana ) ˆ exp( 1 ln( ) ( 0 1 i y bKriteria penolakan: tolak H0jika statistik uji D(ˆ)2;k
Uji signifikasi individu variabel prediktornya dengan menggunakan uji z dengan hipotesis sebagai berikut.
H0: βj= 0 (pengaruh variabel ke-j tidak signifikan)
H1: βj≠0 (pengaruh variabel k-j signifikan)
Statistik uji yang digunakan adalah:
) ˆ ( ˆ j j se z (2.22)
Kriteria penolakan: tolak H0 jika nilai zhitung >
2
z
dimana α adalah tingkat signifikasi yang digunakan.
2.6 Pemilihan Model Terbaik
Beberapa metode dalam menentukan model terbaik, salah
satunya adalah Akaike Information Criterion (AIC). AIC
merupakan kriteria kesesuaian model dalam mengestimasi model
secara statstik. Kriteria AIC biasanya digunakan apabila
pembentukan model regresi bertujuan untuk mendapatkan faktor-faktor yang berpengaruh terhadap model bukan untuk melakukan suatu prediksi.
Besarnya nilai AIC sejalan dengan nilai devians dari model. Semakin kecil nilai devians maka akan semakin kecil pula tingkat kesalahan yang dihasilkan model sehingga model yang diperoleh menjadi semakin tepat. Oleh karena itu, model terbaik adalah model yang mempunyai nilai AIC terkecil. Menurut Bozdogan (2000) rumus AIC didefinisikan sebagai berikut.
k L
dimana L(βˆ)adalah nilai likelihood yang didapat dari persamaan (2.6) untuk regresi poisson persamaan (2.13) untuk genelized poisson regression dan persamaan (2.18) untuk regresi binomial negatif dan k adalah jumlah parameter.
2.7 Metode Flexibly Shaped Spatial Scan Statistic
Spatial Scan Statistic merupakan salah satu metode statistik yang digunakan untuk mendeteksi cluster pada sebuah lokasi yang berupa titik maupun data agregat. Menurut Tango dan
Takahashi (2005) metode Flexibly Spatial Scan Statistic
mempunyai power lebih tinggi daripada metode Circular Spatial Scan Statistic saat cluster yang dideteksi adalah non-circular dan fleksibel terhadap bentuk kantong yang dihasilkan sehingga tidak terbatas pada bentuk lingkaran saja. Untuk mendeteksi hotspot dengan metode Flexibly Spatial Scan Statistic, pada awalnya suatu daerah dibagi menjadi n daerah seperti kabupaten dan sebagainya. Jumlah kasus yang ada di wilayah i dilambang dengan Yi dengan nilai yang diamati i = 1,2,...,n diasumsikan saling bebas dan mengikuti sebaran poisson dengan fungsi peluang seperti persamaan (2.2). Untuk menentukan letak geografis masing-masing daerah digunakan titik koordinat pusat penduduk administrasi.
Pada awalnya, Flexibly Scan Statistic ditempatkan pada kantong yang tidak teratur (irregularly shaped) pada setiap
wilayah. Window ke-i dilambangkan dengan Wiyang merupakan
kumpulan wilayah i dan wilayah-wilayah yang berbatasan dengan wilayah i yang kemudian disusun himpunan Z yang bentuknya tidak teratur dengan panjang l pada setiap wilayah, terdiri atas l wilayah. Untuk menghindari pendeteksian kantong yang bentuknya aneh (unlikely peculiar shape), wilayah yang berbatasan dibatasi sebagai himpunan bagian dari wilayah i dan (L-1) wilayah sekitar yang terdekat dengan wilayah i dimana L adalah pre-specified maximum length dari cluster. Selanjutnya akan berbentuk Z yang berbeda-beda dan saling overlapping
ke-m yang merupakan himpunan l wilayah yang berhubungan
dimulai dari wilayah i, dimana mil adalah jumlah m yang
memenuhi Zil(m) Zil untuk l = 1,2,...,L. Kemudian semua yang
diperiksa dimasukkan dalam himpunan berikut.
} 1 , 1 , 1 {Zil(m) i n l L m mil Z (2.24)
Algoritma yang digunakan untuk mendapatkan Z dengan pre-specified maximum length L (Tango dan Takahashi, 2005) adalah sebagai berikut.
1. Pertama, membuat sebuah matriks A = (aih) berukuran n x n
sedemikian hingga lainnya untuk , 0 contiguity atau an bersebelah h dan i wilayah jika , 1 ih a
dan set Z2=Ø dan i0= 0
2. Misalkan
i
0
i
0
1
dani
0 (=1,2,…,m) menjadi wilayahawal. Kemudian dibentuk Wi0 yang terdiri dari (L-1) nearest
neighbours ke wilayah awal i0 dan i0 sendiri, sebagai contoh
Wi0
i0,i1,...,iL1
dimana il adalah l wilayah ke-l terdekatterhadap i0.
Misalkan wilayah seperti berikut.
1 2
3 4 5
Wi= {1,2,3,4} dimana wilayah awal berada di satu.
3. Pertimbangkan semua himpunan Z
Wi0, dimana termasukwilayah awal i0. Untuk himpunan Z lainnya, ulangi langkah
4-7. Dimana nilai Z diperoleh dari anggota himpunan Wi,
sehingga Zi = {1,2} {1,3} [1,4} {1,2,3} {1,2,4} dan begitu
untuk tiga dan empat anggota himpunan lainnya.
4. Bagi himpunan Z menjadi dua disjoint : Z0={i0} dan Z1
dimana berisi wilayah lain yang terdapat dalam Z.
5. Buat dua himpunan baru Z’0 dan Z
’
1. Z
’
0terdiri dari wilayah
dari wilayah Z1 yang tidak berbatasan dengan wilayah Z0.
Kemudian, ganti Z0dan Z1dengan Z’0dan Z’1.
Untuk langkah ini dimisalkan Z = {1,2,3} maka Z0= {1}, Z1
={2,3}. Di bentuk himpunan baru Z’0= {2,3} dan Z’1=ϕ. Z’1
himpunan kosong karena tidak ada wilayah lain dari anggota dari Z yang tidak berdekatan dengan wilayah 1.
6. Ulangi langkah 5 secara rekursif sampai Z0 dan Z1 menjadi
himpunan kosong.
7. Buat kesimpulan sebagai berikut.
Z dikatakan berhubungan (connected) ketika Z1 menjadi
himpunan kosong terlebih dahulu dan tidak berhubungan
ketika Z0 menjadi himpunan kosong terlebih dahulu, maka Z
dimasukkan dalam set Z. Jika Z tidak berhubungan maka Z dibuang.
8. Ulangi langkah 2-7 sampai pada akhirnya diperoleh himpunan Z yang terdiri dari Z berbentuk tertentu dengan maximum length adalah L.
2.7.1 Likelihood Ratio Test dan Pengujian Hipotesis Monte Carlo
Untuk setiap wilayah i dan panjang dari scanning window, hipotesis alternatifnya adalah minimal ada satu window Z yang mempunyai peluang resiko lebih tinggi (elevated risk) daripada di luar window. Dengan kata lain, hipotesis yang digunakan adalah sebagai berikut.
H0: E(Y(Z)) = µ(Z) untuk semua Z
H1: E(Y(Z))> µ(Z) untuk beberapa Z
dimana Y(.) melambangkan jumlah kasus yang random dan µ(.) merupakan nilai harapan dari kasus window tertentu.
Pada setiap window, dapat dihitung likelihood untuk mengetahui jumlah kasus di dalam dan di luar window. Persamaan likelihood untuk setiap window mengikuti dengan asumsi Poisson, uji statistik yang disusun dengan likelihood ratio test (Kulldorff, 1997) adalah sebagai berikut.
) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( sup ( ) ( ) c c Z n c c Z n y y I y y Z c Z Z Z Z Z Z Z Z z (2.25)
dimana Zc melambangkan semua wilayah di luar window Z, dan
y(.) melambangkan jumlah kasus dalam window yang ditentukan dan I(.) merupakan fungsi indikator. Ketika memeriksa kantong
dengan high rates, maka I(.) bernilai 1 jika y(Zc) dibagi (Zc)
memiliki peluang lebih besar .
Uji statistik yang dilakukan menggunakan pengujian hipotesis Monte Carlo. P-value diperoleh dengan membandingkan rank dari likelihood yang maksimal dari data yang sebenarnya dengan likelihood yang maksimal dari himpunan data acak. Jika rank dilambangkan dengan R maka p-value = R/(1+#simulasi) dimana #simulasi menunjukkan banyaknya replikasi yang digunakan.
Prosedur untuk mendapatkan p-value dengan pendekatan Monte Carlo adalah sebagai berikut.
1. Hitung penjumlahan nilai log likelihood ratio tertinggi t0untuk
data riil.
2. Membangun data acak yang ukurannya sama dengan data riil
yang dibangun di bawah kondisi H0.
3. Melakukan proses pembentukan scanning window Z dari data
acak yang dibangun berdasarkan kondisi H0.
4. Mencari nilai log likelihood ratio dari setiap scanning window, dan dicatat apakah jumlah kasus yang diamati lebih besar atau lebih kecil dari yang diestimasi, kemudian menjumlahkan nilai log likelihood ratio yang jumlah kasusnya lebih besar dari jumlah yang diestimasi, untuk setiap scanning window. Langkah selanjutnya, mendapatkan penjumlahan nilai log likelihood ratio yang tertinggi dari simulasi pertama pembangunan data acak tersebut.
5. Mengulang langkah 2, 3, dan 4 sebanyak m kali
pengulangan/simulasi, sehingga memperoleh m penjumlahan nilai log likelihood ratio tertinggi dari data acak dan data riil.
6. Hitung p-value,
1 ) ( banyaknya 0 m t y T pt0menyatakan penjumlahan nilai log likelihood ratio tertinggi
yang dimiliki suatu scanning window Z dari data riil. T(y) adalah penjumlahan nilai log likelihood ratio dari data acak
yang dibangun di bawah kondisi H0. m adalah banyaknya
simulasi untuk membangun data di bawah kondisi H0.
Kantong-kantong yang terbentuk (window Z) diurutkan berdasarkan nilai likelihood-nya dan window Z yang memiliki nilai likelihood lebih besar daripada yang lain dan nyata pada tingkat signifikansi tertentu akan membentuk hotspot.
2.8 Demam Berdarah Dengue (DBD)
Demam Berdarah Dengue (DBD) adalah penyakit menular yang disebabkan oleh infeksi virus DEN-1, DEN-2, DEN-3, atau DEN-4 yang ditularkan melalui gigitan nyamuk Aedes Aegypti atau aedes albopictus yang sebelumnya telah terinfeksi oleh virus dengue dari penderita DBD lainnya.
Ginanjar (2007) Masa inkubasi penyakit DBD, yaitu
periode sejak virus dengue menginfeksi manusia hingga
menimbulkan gejala klinis, antara 3-14 hari, rata-rata antara 4-7 hari. Penyakit DBD tidak ditularkan langsung dari orang ke orang. Penderita menjadi infeksif bagi nyamuk pada saaat viremia yaitu beberapa saat menjelang timbulnya demam hingga saat masa demam berakhir. Nyamuk aedes aegypti merupakan penyebar penyakit DBD yang paling efektif an utama karena tinggal di sekitar permukiman penduduk. Adapun nyamuk aedes albopictus, banyak terdapat di daerah perkebunan dan semak-semak.
Penyakit DBD pertama kali di Surabaya pada tahun 1968. Pada tahun 1994 DBD telah menyebar ke seluruh provinsi (pada waktu itu berjumlah 27 provinsi) di Indonesia. Penyakit DBD mesti mendapatkan perhatian serius dari semua pihak, mengingat jumlah kasusnya yang cenderung meningkat setiap tahun. Menurut data Depaetemen Kesehatan Republik Indonesia, pada
awal 2007 jumlah penderita DBD telah mencapai 16.803 orang dan 267 orang yang diantaranya meninggal dunia. Jumlah orang yang meninggal tersebut jauh lebih banyak dibandingkan kasus kematian manusia karena flu burung.
Penularan penyakit DBD ini juga dipengaruhi oleh interaksi tiga faktor, yaitu sebagai berikut.
a. Faktor penjamu (Target penyakit, inang), dalam hal ini adalah manusia yang rentan tertular penyakit DBD. Adapun indikator yang termasuk faktor penjamu ini adalah kepadatan penduduk. b. Faktor penyebar (vektor) dan penyebab penyakit (agen), dalam hal ini adalah virus DEN tipe 1-4 sebagai agen penyebab penyakit, sedangkan nyamuk Aedes Aegypti dan Aedes albopictus yang berperan sebagai vektor penyebar penyakit DBD. Adapun indikator yang termasuk faktor penyebab ini adalah jentik nyamuk.
c. Faktor lingkungan yaitu lingkungan yang memudahkan terjadinya kontak penularan penyakit DBD. Adapun indikator yang termasuk faktor lingkungan ini adalah rumah tangga berperilaku hidup bersih dan sehat.
Berbagai upaya untuk memutus mata rantai penularan penyakit DBD dapat ditempuh dengan cara memodifikasi faktor-faktor yang terlibat di dalamnya. Perbaikan kualitas kebersihan (sanitasi) lingkungan, serta pencegahan penyakit dan pengobatan segera bagi penderita penyakit DBD. Namun, yang paling penting diperhatikan adalah peningkatan pemahaman, kesadaran, sikap dan perubahan perilaku masyarakat terhadap penyakit DBD ini, sakan sangat mendukung percepatan upaya memutuskan mata rantai penularan penyakit DBD.
29 3.1 Sumber Data
Data yang digunakan dalam penelitian ini adalah data sekunder yaitu data variabel respon (jumlah penderita penyakit Demam Berdarah Dengue (DBD) tiap kabupaten/kota di Provinsi Jawa Timur tahun 2014) diperoleh dari profil kesehatan Dinas Kesehatan Provinsi Jawa Timur. Sedangkan untuk variabel
prediktor diperoleh dari profil kesehatan Dinas Kesehatan
Provinsi Jawa Timur dan Jawa Timur Dalam Angka Badan Pusat Statistik.
Gambar 3.1 Provinsi Jawa Timur 3.2 Variabel Penelitian
Variabel yang digunakan dalam penelitian terdiri dari satu variabel respon (Y) yaitu jumlah kasus DBD dan tujuh variabel
prediktor (X).Variabel yang digunakan dalam penelitian ini dapat