PEMBELAJARAN KONVERGENSI BARISAN BILANGAN DAN FUNGSI REAL DENGAN MATLAB dan GEOGEBRA

(1)

Parhusip, H.A Pembelajaran Konvergensi Barisan Bilangan Dan Fungsi Real Dengan Matlab Dan Geogebra, prosiding Seminar Nasional Matematika VII UNNES 26 Oktober 2013, ISBN 978-602-14724-7-7.l

Bidang Kajian : Pendidikan Matematika

PEMBELAJARAN KONVERGENSI BARISAN BILANGAN DAN

FUNGSI REAL DENGAN MATLAB dan GEOGEBRA

H.A. Parhusip

Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana

Abstrak

Paper ini memberikan petunjuk untuk memulai belajar analisa real dengan menggunakan visualisasi MATLAB dan GEOGEBRA. Studi konvergensi dapat dengan mudah dilakukan jika barisan bilangan real dan barisan fungsi real divisualisasikan dalam suatu grafik. Ilustrasi dapat dilakukan secara langsung untuk beberapa nilai n sekalipun kita menghendaki untuk mempelajari konvergnsi barisan untuk n menuju tak hingga.

Beberapa contoh barisan real ditunjukkan dengan bukti formal secara lengkap menggunakan definisi dan visualisasi dengan MATLAB. Sedangkan barisan fungsi ditunjukkan dengan visualisasi grafik menggunakan GEOGEBRA. Makalah ini juga membantu pembaca untuk menuliskan pembuktian analisa real lebih mudah untuk disampaikan kepada siswa/mahasiswa karena didukung dengan grafik.

Kata kunci: konvergensi, divergensi, terbatas

A. Pendahuluan

Cara memahami dan menuliskan kembali bukti dalam matematika merupakan masalah yang umum bagi siswa, mahasiswa maupun pengajar. Selama ini seringkali siswa diajar dengan teknik berhitung sedangkan cara menuangkan alasan secara matematis sangat minim diajarkan. Demikian pula mengkomunikasikan hasil hitungan secara formal dan saintifik (mengikuti kaidah matematika) juga sangat mungkin belum dialami siswa sehingga ketika menjadi mahasiswa matematika hal itu menjadi kendala yang sangat besar. Khususnya dalam memberikan pembuktian pada analisa real diperlukan tata bahasa analisis yang formal sesuai definisi. Kemampuan mengungkapkan alasan dalam analisis sangat diperlukan.

Literatur analisa real (Royden,1988;Trench,2003;Web1) umumnya sangat formal (secara matematis) sebagaimana penulis amati dimana visualisasi sangat jarang dilakukan. Untuk itulah kemampuan ini perlu dikaji dan dikembangkan. Terlebih lagi adanya penggunaan komputer, maka analisis sangat terbantu untuk mengungkapkan fenomena umum dari suatu kasus yang dipelajari.

Tulisan ini menginspirasi bagaimana menuliskan pembuktian secara formal dalam analisa real khususnya tentang konvergensi atau divergensi suatu barisan bilangan real. Kasus yang dipelajari sangat sederhana yaitu barisan

(a). 2 1 3    n n an (b). 1 2 4 2    n n an (c). n n n e a 2  .

Dari ketiga kasus yang dipelajari sebagai contoh maka diharapkan mahasiswa dapat mengolah soal jawab yang terkait dengan pembuktian tersebut.

(2)

B. Pembuktian Konvergensi dan Divergensi Barisan dan Visualisasinya Kasus 1. n n n n an / 2 1 / 1 3 2 1 3     

 . Untuk n maka 1/n 0 dan 2/n 0 .

Oleh karena itu 3/1 3.

/ 2 1 / 1 3 lim lim          _n n a n n

n Jelas barisan konvergen ke 3.

Biasanya mahasiswa menulis hanya berhenti sampai disini. Secara formal matematis, maka perlu ditulis lebih ’elegant’. Secara formal , suatu barisan bilangan real dikatakan konvergen (punya limit) dengan definisi berikut.

Definisi 1. (Goldberg,1976)

Suatu barisan bilangan real

 

a_n dikatakan mempunyai limit L, atau barisan tersebut konvergen ke L ditulis a_n L

n 

lim artinya untuk sembarang  0, pertidaksamaan





L

a_n harus dipenuhi untuk semua nilai n N. Dengan kata lain a_n L  harus dipenuhi untuk semua nilai n, kecuali paling banyak pada bilangan berhingga n, sebutlah pada n =1,2,…,N-1. Untuk memahami definisi tersebut kita akan membahas barisan

2 1 3    n n

a_n dan akan membuktikan dengan menuliskan secara formal bahwa

. 3 1 / 3 / 2 1 / 1 3 lim lim          _n n a n n n

Cara ini yang biasa digunakan siswa. Akan tetapi pada tingkat universitas masih perlu dibuktikan bahwa lim 3



 n

n a . Artinya untuk sembarang  0, pertidaksamaan



 3 n

a harus dipenuhi untuk semua nilai n, kecuali paling banyak pada bilangan berhingga n, sebutlah pada n=1,2,…,N-1. Sedangkan pada n=N berlaku dan N pada umumnya tergantung pada nilai . Kita dapat mempelajari hal ini dengan mendaftar sebagai tahap observasi. Agar membuat daftar dengan mudah, kita dapat menggunakan MATLAB sebagai alat bantu. Program tentang ini dan hasil keluaran ditunjukkan pada Tabel 1 dan Gambar 1.

Tabel 1a. Daftar Program untuk menggambar n n n n a_n / 2 1 / 1 3 2 1 3       . __________________________ clear close all n=[1:100]'; a=inline('(3*n +1)./(n+2)','n'); an=a(n); figure(1) plot(n,an,'o'); epsku=3-an; Daftar=[n an epsku]

Tabel 1b. Daftar Program untuk mendaftar

n n n n a_n / 2 1 / 1 3 2 1 3       untuk n merupakan

kelipatan 10 (buat sebagai kelanjutan Tabel 1a) __________________________ n=10;j=1; while n<=100 gn=g(n); epsku=3-gn; Daftar=[n gn epsku] Simpan(j,:)=Daftar j=j+1 n=j*10; end

(3)

Gambar 1 membantu intuisi kita untuk mendapatkan pemahaman sifat konvergen barisan tersebut yaitu 3. Yang menjadi masalah berapakah n = N sehingga kita dapat menjamin limit barisan tersebut 3?. Jikalau hasil Gambar 1 didaftar untuk beberapa n (misalnya kelipatan 10) maka kita dapat mendaftar setiap n dan nilai

2 1 3    n n a_n serta  yang diperoleh. Kita dapat menambahkan perintah pada program sebagaimana ditunjukkan pada Tabel 1b. Gambar 1. Visualisasi n n n n a_n / 2 1 / 1 3 2 1 3       untuk beberapa n

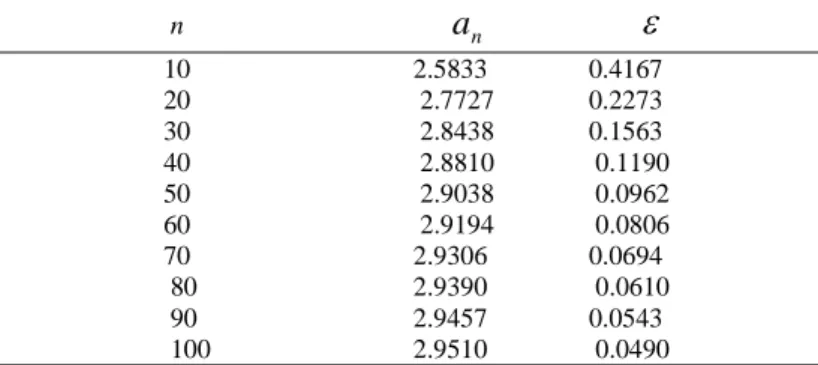
Tabel 2. Daftar n, nilai barisan tiap n dan nilai  untuk tiap n. n a_n  10 2.5833 0.4167 20 2.7727 0.2273 30 2.8438 0.1563 40 2.8810 0.1190 50 2.9038 0.0962 60 2.9194 0.0806 70 2.9306 0.0694 80 2.9390 0.0610 90 2.9457 0.0543 100 2.9510 0.0490

Secara analitik, umumnya kita tetapkan , kemudian kita dapat mendapatkan nilai

n=N yang sesuai dengan  yang dipilih. Dengan kata lain kita perlu memformulasikan untuk suatu n=N yang umumnya tergantung pada . Sedangkan Tabel 2 diperoleh dengan menetapkan nilai n terlebih dahulu sehingga nilai  diperoleh merupakan selisih nilai a_n dengan 3 (yang sudah kita klaim sebagai limit barisan). Secara komputasi, maka nilai n lebih mudah ditetapkan terlebih dahulu. Sedangkan prosedur analitik menjelaskan bahwa kita tetapkan terlebih dahulu. Kita dapat menetapkan misalkan  sekitar 0.1 maka berdasarkan Tabel 2, kita dapat memperoleh n=N sekitar 40. Nampaknya cara analitik lebih susah tetapi hal itu diperlukan untuk proses pembuktian umum bahwa barisan tersebut konvergen pada 3. Kita coba dengan proses ini.

Dengan proses berikut ini ternyata salah. Kita akan mencari batas N dengan cara mencari batas paling atas yaitu  sehingga

(4)

Parhusip, H.A Pembelajaran Konvergensi Barisan Bilangan Dan Fungsi Real Dengan Matlab Dan Geogebra, prosiding Seminar Nasional Matematika VII UNNES 26 Oktober 2013, ISBN 978-602-14724-7-7.l   3 n a atau -< 3 2 1 3 _   n n _<__.

Dengan menggunakan batas atas, sebutlah

3 2 1 3    n n = atau 3n +1 -3n -6 =n +2. atau -5-2 = n atau n= N = _  _   2 5 . (*)

Notasi



. menyatakan bilangan bulat terbesar yang lebih kecil atau sama dengan argumen didalamnya. Jelas bernilai bulat negatif, padahal n harus positif bulat. Jika dipilih batas bawah

-n-2= -5 atau n=N= _  _   2 5 (**)

Dari kedua batas ini kita belum mendapatkan secara eksplisit untuk nilai n terkecil yang diijinkan sehingga kita dapat mengatakan bahwa dimulai dari n=N maka limit barisan tersebut adalah 3. Cara menentukan n=N dapat lebih praktis dengan cara sebagai berikut. Coba -< 3 2 1 3    n n

< ditulis sebagai a_n 3  yaitu

2 6 3 2 1 3      n n n n < atau 2 5  

n <. Karena  bilangan positif kecil dan n bilangan asli maka kita dapat memilih

2 5  n < atau 5 < n+2 atau n    2 5

. Jadi kita dapat memilih N >

  2 5

agar barisan konvergen pada 3. Perhatikan bahwa dengan kondisi ini kita dapat memilih N dengan menetapkan  terlebih dahulu. Hal ini ditunjukkan pada Tabel 3. Jadi dengan cara ini kita dapat memperoleh bukti bahwa a_n 3  untuk n Ndengan N 

  2 5

. Perhatikan bahwa N bilangan asli (bulat), padahal

  2 5

dapat tidak bulat. Untuk itu kita perlu menuliskan kondisi N 

  2 5 menjadi N         2 5

. Jadi dari tata cara menulis



 3 n

a sangat menentukan dalam mendapatkan kondisi N 

  2 5

. Hal ini ditunjukkan pada program pada Tabel 3 serta ilustrasi untuk a_n,a_n ,dan a_n  pada Gambar 2. Sedangkan untuk data tiap n untuk n=N 

       2 5 . a_n,a_n ,dan a_n 

dengan nilai  ditetapkan terlebih dahulu ditunjukkan pada Tabel 4.

Tabel 3. Program untuk

2 1 3    n n

a_n dengan menetapkan  terlebih dahulu. clear close all epsku=[0.2 0.1 0.05 0.025 0.01 0.005 ]; n=round((5-2*epsku)./epsku); a=inline('(3*n +1)./(n+2)','n'); an=a(n);

(5)

anminuseps=an-epsku; anpluseps=an+epsku; figure(1)

plot(n,an,'o',n,anminuseps,'*',n,anpluseps,'.-'); Daftar=[epsku' n' anminuseps' an' anpluseps']

Tabel 4. Daftar nilai berbagai

2 1 3    n n

an untuk berbagai  yang ditetapkan

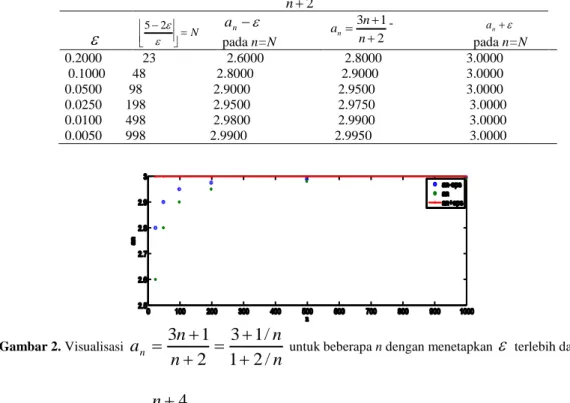
 N        2 5 an  pada n=N 2 1 3    n n an - an pada n=N 0.2000 23 2.6000 2.8000 3.0000 0.1000 48 2.8000 2.9000 3.0000 0.0500 98 2.9000 2.9500 3.0000 0.0250 198 2.9500 2.9750 3.0000 0.0100 498 2.9800 2.9900 3.0000 0.0050 998 2.9900 2.9950 3.0000 Gambar 2. Visualisasi n n n n a_n / 2 1 / 1 3 2 1 3     

 untuk beberapa n dengan menetapkan  terlebih dahulu. Kasus 2. Pelajari 1 2 4 2    n n an . Bagaimana n na lim ?

Jawab : Barisan tersebut berbentuk fungsi rasional dalam n dengan pembilang n + 4 dan penyebut bentuk kuadrat. Untuk n yang membesar maka penyebut akan lebih cepat membesar daripada pada bagian pembilang. Oleh karena itu kita dapat menyimpulkan intuisi tersebut bahwa _n

na

lim =0. Untuk memberikan penjelasan yang lebih kreatif kita dapat memvisualisasikan barisan tersebut untuk berbagai n. Kita dapat mengubah program pada Tabel 1 dengan menggantikan definisi barisan. Akan tetapi perlu diperhatikan bahwa untuk n yang kecil (sekitar mulai dari n=10, maka barisan sudah mendekati 0 sehingga kita tidak perlu menggunakan n yang terlalu besar. Hasil keluaran pada Gambar 3 yang menunjukkan bahwa untuk n membesar maka nilai barisan menuju ke 0.

Tabel 5. Program untuk mengilustrasikan dan mendaftar

1 2 4 2_   n n an Clear close all n=[1:10]'; a=inline('(n +4)./(2*n.^2+1)','n'); an=a(n); figure(1) plot(n,an,'o'); epsku=abs(0-an); Daftar=[n an epsku]

(6)

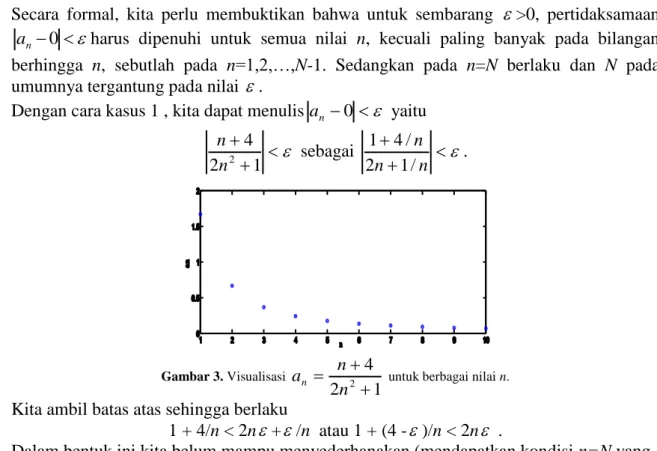
Secara formal, kita perlu membuktikan bahwa untuk sembarang >0, pertidaksamaan



 0 n

a harus dipenuhi untuk semua nilai n, kecuali paling banyak pada bilangan berhingga n, sebutlah pada n=1,2,…,N-1. Sedangkan pada n=N berlaku dan N pada umumnya tergantung pada nilai .

Dengan cara kasus 1 , kita dapat menulisa_n 0  yaitu

    1 2 4 2 n n sebagai    n n n / 1 2 / 4 1 . Gambar 3. Visualisasi 1 2 4 2    n n

a_n untuk berbagai nilai n.

Kita ambil batas atas sehingga berlaku

1 + 4/n < 2n+/n atau 1 + (4 -)/n < 2n .

Dalam bentuk ini kita belum mampu menyederhanakan (mendapatkan kondisi n=N yang tergantung . Kita ubah dengan cara lain berikut ini. Jelas bahwa

       ₂ ₂ 2 2 4 1 2 4 2 4 n n n n n . (a1)

Perhatikan bahwa pertidaksamaan tersebut dicari sedemikian rupa sehingga kita mendapatkan suatu n=N yang hanya tergantung . Untuk mendapatkan urutan pertidaksamaan yang benar kita dapat menggunakan program MATLAB untuk membantu kita dalam menvisualisasikan.

Tabel 6. Menggambar berbagai barisan pada

pertidaksamaan (a1). clear close all n=linspace(1,10,20); an1=(n +4)./(2*n.^2+1); an2=(n +4)./(2*n.^2); an3=4./(2*n.^2); plot(n,an1,’*’,n,an2,’o’,n,an3,’.’) Gambar 4. Visualisasi 2 2 4 n (bertanda .), 1 2 4 2_  n n (bertanda *) dan 2 2 4 n

(7)

Jadi kita dapat menggunakan batas ₂ 2₂

2 4

n

n  <  untuk mencari N. Dengan

menggunakan notasi n = N pada 2₂

n diperoleh 2 < 2 N  atau N  2

. Marilah kita daftar untuk berbagai nilai  yang kita tetapkan dengan mengambil nilai N yang memenuhi

N





2

dan menyelidiki nilai barisan untuk setiap N yang dipilih. Kita dapat mendaftarnya dengan MATLAB. Perhatikan bahwa



2

tidak bulat maka kita perlu membulatkan dengan fungsi floor pada MATLAB. Program ditunjukkan pada Tabel 7 dan hasil keluaran program ditunjukkan dengan daftar Tabel 8 agar kita dapat melihat seberapa besar nilai barisan untuk tiap  dan N yang dipilih.

Tabel 7. Program MATLAB untuk membuat daftar nilai  dan



2

serta nilai barisannya. epsku=[0.2 0.15 0.1 0.05 0.025 0.02 0.01 0.005 0.0025 0.001]

batasn=round(sqrt(2./epsku)); Daftar=[epsku’ batasn’]; siN=batasn + 1;

an=(siN +4)./(2*siN.^2+1); Daftark=[epsku’ batasn’ siN’ an’]

Tabel 8. Daftar  yang ditetapkan dan nilai N dan barisan yang diperoleh

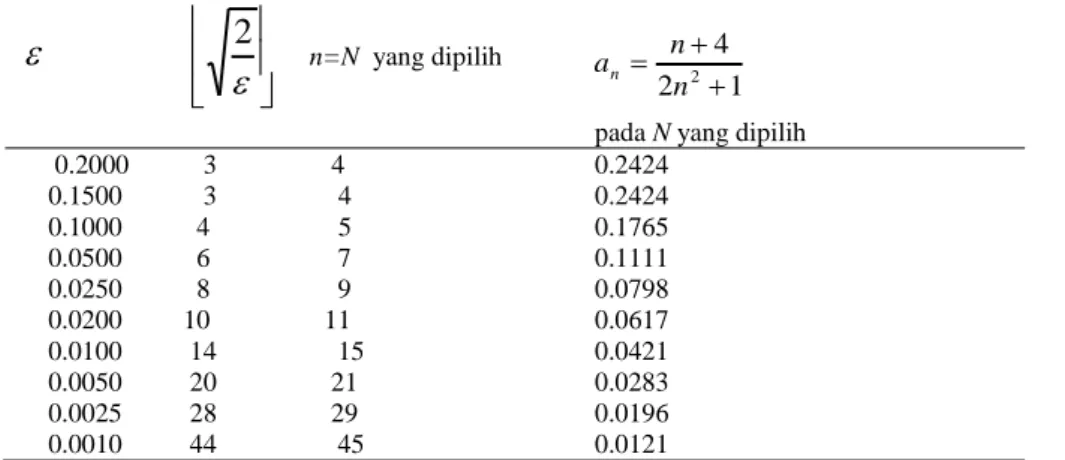
        2 n=N yang dipilih 1 2 4 2 _   n n a_n

pada N yang dipilih 0.2000 3 4 0.2424 0.1500 3 4 0.2424 0.1000 4 5 0.1765 0.0500 6 7 0.1111 0.0250 8 9 0.0798 0.0200 10 11 0.0617 0.0100 14 15 0.0421 0.0050 20 21 0.0283 0.0025 28 29 0.0196 0.0010 44 45 0.0121

Bagaimana menuliskan bukti formal bahwa 0?

1 2 4 lim lim ₂         _n n a n n n .

Hal ini ditunjukkan berikut ini berdasarkan tahap observasi di atas.

0 1 2 4 lim lim ₂         _n n a n n

n artinya untuk setiap sembarang > 0 maka perlu ditunjukkan

     0 1 2 4 2 n n

untuk n N. Dengan mengetahui bahwa       ₂ ₂ 2 2 4 1 2 4 2 4 n n n n n

kita dapat memilih ₂ 2₂

2 4

n

n  <  untuk mencari N. Dengan menggunakan notasi n = N

pada 2₂ n <  diperoleh 2 < 2 N  atau  N  2 .

(8)

Kasus 3. Bagaimana dengan ?

2 lim lim _n n n n n e a     

Sebagaimana pada kasus 1 dan 2, untuk mendapatkan intuisi tentang sifat barisan untuk n membesar, maka kita dapat membuat gambar atau mendaftar a_nuntuk berbagai nilai n. Karena pembilang dan penyebut membesar dengan cepat untuk nilai n yang diberikan, kita menggunakan n yang tidak terlalu besar. Kita hanya mengedit program Tabel 1 yang ditunjukkan pada Tabel 9 dan hasil keluaran ditunjukkan pada Gambar 5.

Tabel 9. Program MATLAB untuk

menggambar barisan n n e 2 clear close all n=[1:10]'; a=inline('exp(n)./(2.^n)','n'); an=a(n); figure(1) plot(n,an,'o'); Daftar=[n an]

Tabel 10. Daftar nilai n dan _n

n e 2 n n n e 2 1 1.3591 2 1.8473 3 2.5107 4 3.4124 5 4.6379 6 6.3036 7 8.5674 8 11.6444 9 15.8263 10 21.5102

Gambar 5. Ilustrasi barisan _n n

e

2

Daftar nilai n dan barisan terkait ditunjukkan pada Tabel 10. Hasil grafik menunjukkan bahwa untuk n yang membesar maka kita peroleh _n

n

e

2 yang membesar juga. Kita tidak

dapat menyimpulkan : berapakah n=N sehingga untuk setiap n>N maka ada bilangan berhingga yang dekat dengan nilai barisan pada n=N. Barisan demikian kita sebut barisan divergen. Untuk itu kita perlu membuktikan bahwa barisan tersebut divergen (tidak ada suatu nilai berhingga yang dapat dipilih). Kita menuliskan an  untuk n. Secara formal ditulis suatu barisan dikatakan divergen dalam definisi berikut.

Definisi 2 (barisan divergen) (Goldberg,1976)

Suatu barisan bilangan real

 

an mendekati tak hingga (divergen) untuk n mendekati tak hingga jika untuk sembarang bilangan real M >0, terdapat suatu bilangan positif bulat N sedemikian hingga berlaku

M

a_n  ,



nN



. (a2)

Ekspresi (a2) menjelaskan bahwa jika kita menetapkan bahwa limit barisan adalah M , maka nilai barisan akan selalu lebih besar dari M pada suatu n=N. Kita akan bahas pada kasus 3.

(9)

Parhusip, H.A Pembelajaran Konvergensi Barisan Bilangan Dan Fungsi Real Dengan Matlab Dan Geogebra, prosiding Seminar Nasional Matematika VII UNNES 26 Oktober 2013, ISBN 978-602-14724-7-7.l Diberikan suatu M > 0, _n n e 2 > M atau M e n _       2 atau M e n ln 2 ln       atau 2 ln 1 ln 2 ln ln ln 2 ln ln            M e M e M n . Jadi dipilih ) ( 2 ln 1 ln N n M n    . (b)

Jadi jika dipilih

2 ln 1 ln   M

N maka (b) dipenuhi atau berarti barisan tersebut divergen. Ekspresi 2 ln 1 ln  M

bisa tidak bulat sedangkan N harus bulat positif (karena sebagai indeks). Maka kita dapat menuliskan (b) dengan

) ( , 2 ln 1 ln N n M n        ©

Kita dapat melakukan observasi menggunakan kondisi (c) dengan menetapkan M dan memilih N, serta mendaftar nilai barisan pada tiap N. Perintah untuk melakukan hal ini ditunjukkan pada Tabel 11 dan keluarannya ditunjukkan pada Tabel 12.

Tabel 11. Program MATLAB dengan input M dan mencari batas (c) dan nilai barisan

Clear close all M=[5 10 15 20 30 50 60 70 80]; batasN=log(M)./(1 -log(2)) Npilih=floor(batasN)+1; aNpilih=exp(Npilih)./(2.^Npilih); DaftarMNan=[M' batasN' Npilih' aNpilih']

Tabel 12.Daftar M, 2 ln 1 ln  M

, dan N serta nilai barisan _n

n e 2 M 2 ln 1 ln  M N yang dipilih n n e 2 100 15 16 136 200 17 18 250 300 19 19 340 400 20 20 463 500 20 21 629 600 21 21 629 700 21 22 855

Perhatikan bahwa pada kasus ini kita berharap bahwa ada suatu limit sebutlah M sehingga untuk N yang dipilih maka hasil nilai barisan akan cukup saling berdekatan atau berbeda cukup kecil (kurang dari 1) untuk N yang berturutan. Mungkin kita mencurigai hasil tersebut karena N masih kecil. Kita dapat menguji program dengan menggunakan program Tabel 8 untuk M yang jauh lebih besar.

Berikut ini kita dapat pula menggunakan Geogebra untuk menjelaskan konvergensi barisan fungsi real.

(10)

Geogebra mempunyai fasilitas Excel yang memungkinkan kita dapat membuat barisan fungsi secara cepat dan fungsi slider yang memungkinkan kita dapat melakukan animasi.

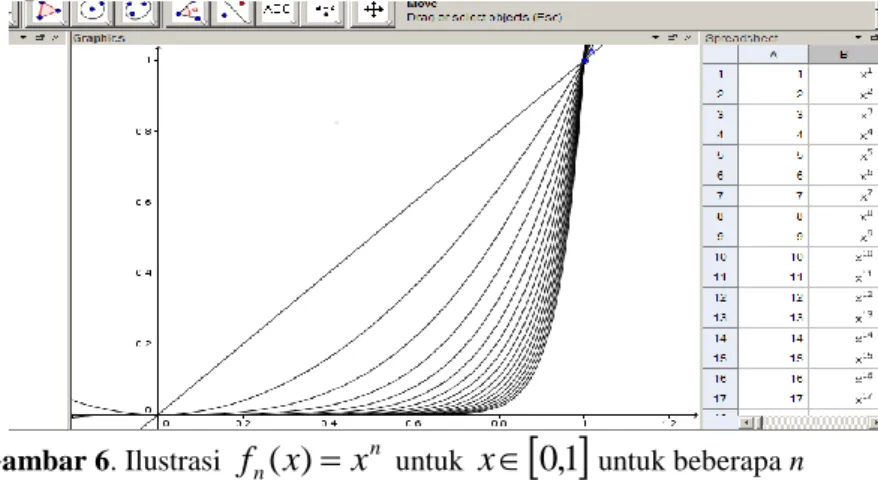
Contoh 1. Perhatikan f_n(x)xn untuk x

 

0,1.

Kita tidak perlu menggunakan n sebagai parameter dalam fungsi slider, karena gambar akan diperoleh 1 grafik saja jika menggunakan slider untuk n. Yang kita perlukan adalah ilustrasi grafik untuk berbagai n. Oleh karena itu kita menggunakan Excel dalam Geogebra. Berbeda dengan Excel pada Microsoft, Excel pada Geogebra memungkinkan untuk menuliskan fungsi f(x) secara eksplisit tanpa mendefinisikan titik-titik x yang digunakan. Tahapan yang dilakukan ditunjukkan berikut ini.

Tahap 1. Klik spreadsheet , buat daftar n pada kolom A1, ketik 1. Baris kedua ditulis =A1 + 1. Drag untuk baris selanjutnya sehingga diperoleh n=1,2,...16 (boleh lebih).

Tahap 2. Ketik pada B1 =x^A1 maka akan muncul grafik yang dikehendaki. Tahap 3. Buat grafik lain dengan menggunakan drag.

Tahap 4. Atur sumbu x, dengan klik sumbu->Graphics-> atur jendela sumbu x dan sumbu y. Diperoleh Gambar 6.

Gambar 6. Ilustrasi f_n(x)xn untuk x

 

0,1 untuk beberapa n

Catatan : Dapat juga hanya mengcopy Gambar, dengan fasilitas :

File ->Export -> Graphic View to Clipboard , maka akan diperoleh grafik saja.

Analisis yang biasa diperlukan untuk barisan f_n(x)xnadalah konvergensi barisan tersebut : apakah konvergen pada suatu fungsi kontinu pada setiap x

 

0,1?. Secara visual pada Gambar 6 ditunjukkan bahwa pada persekitaran x=0 dan x=1 barisan tersebut konvergen pada nilai fungsi yang berbeda. Hal ini menunjukkan perlunya definisi konvergensi yang tergantung pada titik yang dipilih (disebut konvergen titik) dan konvergensi yang tergantung pada interval yang dipilih (disebut konvergen seragam). Jelas bahwa fn(x)xn menjadi tidak konvergen seragam pada setiap x

 

0,1 karena ada 2 titik yang melanggar (punya limit berbeda) pada interval tersebut.

Contoh 2. Perhatikan fungsi f_n pada

 

0, yang diberikan oleh

nx n x fn sin 1 ) (  .

Tahap 1. Klik spreadsheet , buat daftar n pada kolom A1, ketik 1. Baris kedua ditulis =A1 + 1. Drag untuk baris selanjutnya sehingga diperoleh n=1,2,...16 (boleh lebih).

(11)

Tahap 2. Ketik pada B1 ‘=sin(A1x)/A1 maka akan muncul grafik yang dikehendaki. Tahap 3. Buat grafik lain dengan menggunakan drag.

Tahap 4. Atur sumbu x, dengan klik sumbu->Graphics-> atur jendela sumbu x dan sumbu

y. Diperoleh Gambar 7.

Gambar 7. Jendela Geogebra untuk nx n x

f_n( ) 1sin

Selanjutnya kita dapat melakukan analisa sebagaimana pada materi kuliah reguler. Perhatikan bahwa untuk n(ditunjukkan untuk n =1 hingga 9) maka perilaku barisan fungsi berosilasi di sekitar sumbu x atau sebagai fungsi y=0. Jadi dugaan limit barisan untuk membuktikan secara formal ditulis perlu dibuktikanlim ( )lim1sin 0.

    fn x n _n nx n Ditulis :  0, 1sinnx0  n , nN (*) Jelas bahwa nx  nsin 1

. Karena sinnx 1 maka

n nx n 1 sin 1  . Karena n bilangan

asli maka kita dapat membuang tanda absolut pada ruas kanan sehingga  

n nx n 1 sin 1 . Jadi kita dapat memilih _ _n N

 1

agar persamaan (*) terpenuhi. Terbukti

. 0 sin 1 lim ) ( lim       fn x n _n nx n

Contoh 3. Diberikan fn x xne nx





)

( untuk semua x0 dan n1.

Visualisasi dapat dilakukan dengan cara yang sama pada Contoh 1 dan Contoh 2 sehingga dapat diperoleh Gambar 8.

(12)

Sekalipun kurva pada sekitar 0< x<0.5 bernilai sekitar 0.4 , kurva-kurva tersebut cenderung menuju ke y=0 untuk n besar dimulai dari x > 0.5. Jadi klaim fungsi sebagai limit adalah lim ( )lim ( )  0.

    x n n n n n f x f x xne

Contoh 4. Diberikan f_n(x)nx



1x2



n pada [0,1] untuk n1 yang ditunjukkan pada Gambar 9.

Gambar 9. Ilustrasi f_n(x)nx



1x2



n pada [0,1] untuk n1

Pada grafik ini kita melihat bahwa untuk n membesar (misal diambil n=13) maka barisan fungsi bersifat menuju kurva parabola pada 0<x<0.5 sedangkan pada [0.5,1] maka kurva mendekati y=0. Akan tetapi jika n semakin membesar maka terlihat kurva semakin dekat ke y=0 pada seluruh interval [0,1]. Hal ini memperjelas bahwa konvergen seragam ke y=0 pada [0,1]. Dapat ditulis  0, f_n(x)0  , untuk nNdan x

 

0,1.

Pernyataan  























 n n n n x nx x nx x nx x f ( ) 0 1 2 1 2 1 2 _{berlaku jika}





n x x x N n 2 1      _dimana x 1

. dimana n=N harus bulat positif. Jadi disimpulkan konvergen.

Contoh 5. Beberapa barisan yang lain selanjutnya dapat dengan mudah divisualisasikan

sebagaimana ditunjukkan pada Gambar 10-15.

Gambar 10.Barisan ( ) 1 nx2 x x fn  _ Gambar 11. n nx x f_n( )arctan( )

(13)

Gambar 12. fn(x)nsin(x/n)

Gambar 13a. Grafik

n n n x x x f               1 2 ) ( untuk n =1 Gambar 13b. n n n x x x f               1 2 ) ( untuk berbagai n. Gambar 14. Grafik nx nx x gn 5 2 ) (  

Gambar 15. Grafik f_n(x)arctan(nx)/ n

D. Penutup

Pada tulisan ini telah ditunjukkan bagaimana menggantikan intuisi dalam me nentukan barisan konvergen atau divergen dalam bentuk grafik dengan bantuan program

(14)

MATLAB dan Geogebra. Beberapa kasus barisan bilangan real diprogram dengan MATLAB sedangkan barisan fungsi real dengan Geogebra. Visualisasi tersebut untuk membantu dugaan limit yang dicari. Sedangkan pembuktian umum tetap perlu menggunakan kaidah penulisan bukti secara formal.

Sangat sedikit (bahkan belum ditemukan) literatur yang menjelaskan pengajaran analisa real dengan visualisasi baik dalam bahasa Inggris maupun bahasa Indonesia. Jadi materi ini dapat membantu kebutuhan mahasiswa dalam memulai belajar analisa real.

DAFTAR PUSTAKA

Goldberg, R.R., 1976. Methods of Real Analysis, John Wiley & Sons, Inc, Second Edition, New York.

Royden, H.L,1988, Real Analysis, Prentice Hall, Inc,fourth edition, USA. Trench,W.F.,2003. IntroductionTo Real Analysis, Pearson Education, Web1. http://math.louisville.edu/~lee/ira/