KRISTALOGRAFI BIDANG DATAR BATIK CAP

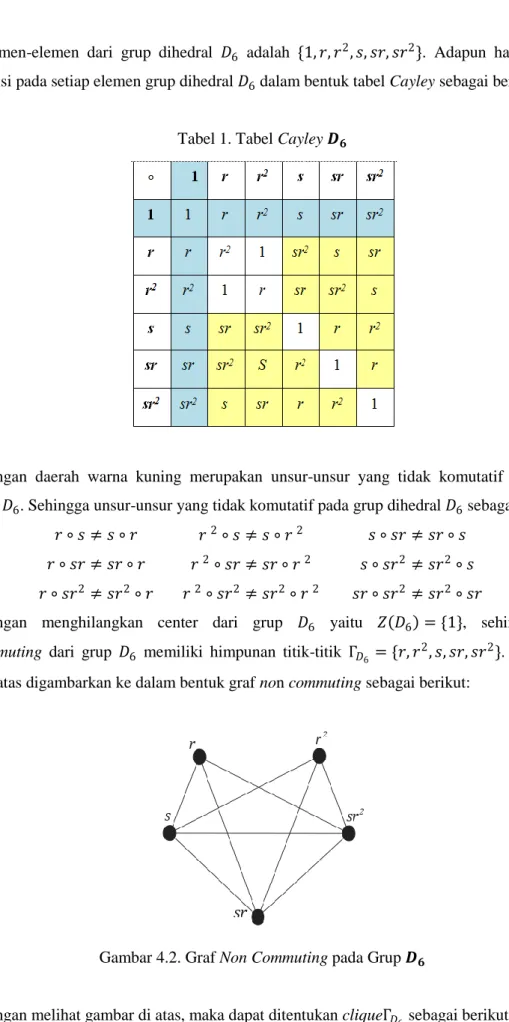
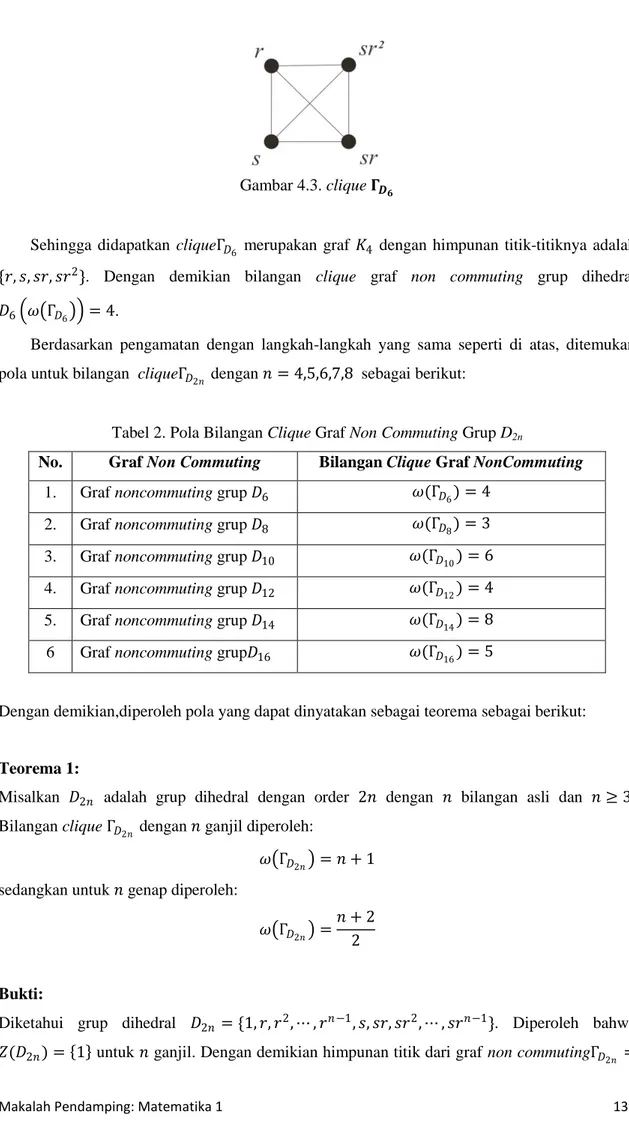
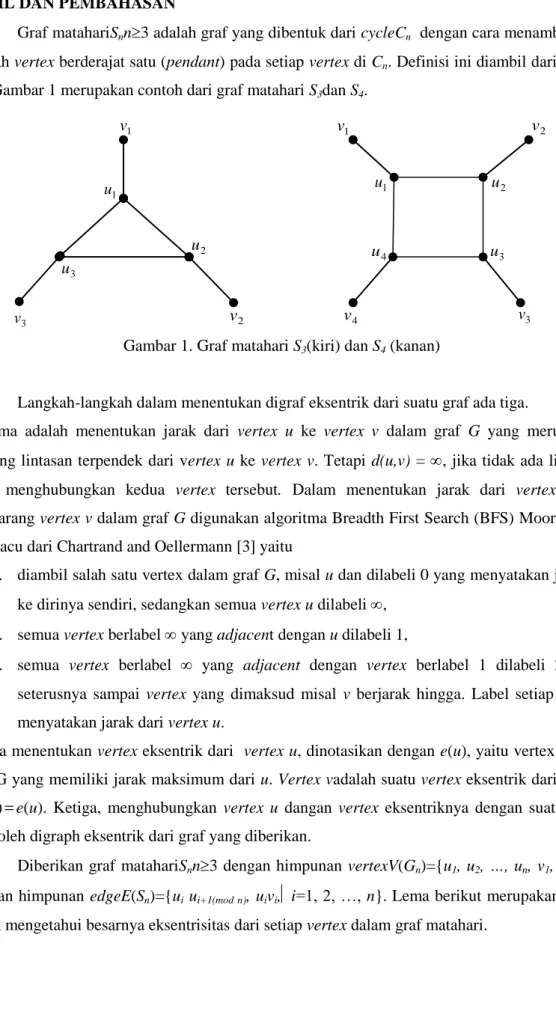
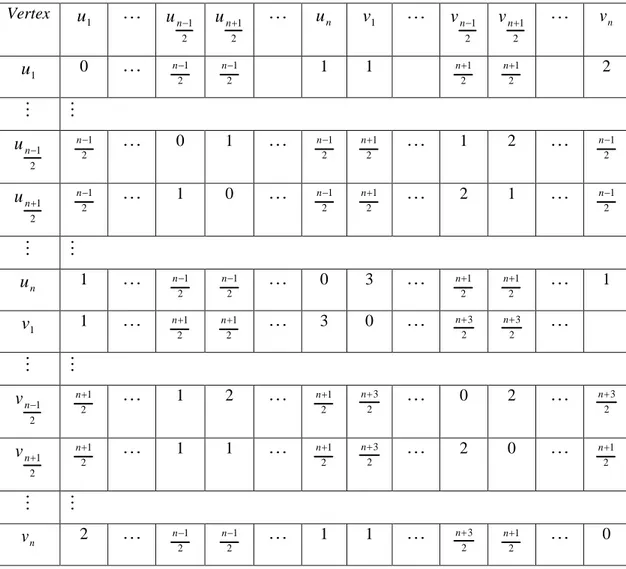
KRISTALOGRAFI BIDANG DATAR BATIK CAP

Kartono1), R.Heri Sulistyo Utomo2), Priyo Sidik S3)

1) , 2) Jurusan Matematika FMIPA UNDIP 3) Jurusan Informatika FMIPA UNDIP

Jl. Prof. H.Soedarto, SH Tembalang Semarang, e-mail: kartonoundip@gmail.com Abstrak

Pembuatan kain batik cap yang beragam corak memerlukan banyak cap, sehingga modal awal yang dibutuhkannya cukup besar. Di lain fihak, kain batik cap mendapat persaingan yang keras dari tekstil printing bermotif batik di pasaran, Kedua hal inilah yang memicu semakin tertekannya produksi kain batik cap, sehingga diperlukan suatu inovasi dalam pembuatannya untuk menekan biaya produksinya. Penelitian ini menjawab permasalahan tersebut dengan melakukan inovasi desain motif dan metode pengecapannya, yang dengan satu cap dapat dihasilkan beragam corak. Inovasi ini didasarkan pada teori grup simetri dan kristalografi dua dimensi, sehingga kain batik cap yang dihasilkan ini merupakan grup kristalografi dua dimensi. Metode pengecapan ini mampu menghasilkan beragram corak sebanyak 13 kain batik cap dari satu cap saja, sehingga cap ini disebut ajaib (magic). Hasil penelitian ini bermanfaat dalam mendukung program penguatan sistem inovasi daerah dalam mengembangkan potensi unggulan daerah, dan pembelajaran matematika yang kreatif, inovatif dan produktif.

Kata Kunci: batik cap, cap ajaib, motif, corak, kristalografi, simetri

PENDAHULUAN

Penguatan sistem inovasi daerah dalam mengembangkan potensi unggulan daerah digalakkan oleh pemerintah, termasuk pemerintah Kota Surakarta dengan unggulan batik. Perkembangan batik diawali dengan adanya batik tulis, yang kemudian diikuti dengan batik cap. Perkembangan batik pada masa sekarang cukup menggembirakan, permintaan batik tulis maupun batik cap cukup tinggi, walaupun kebutuhan pasar batik sekarang sebagian sudah dipenuhi dengan tekstil bermotif batik, bahkan telah dibanjiri produk import.

Batik cap membutuhkan modal awal yang cukup mahal karena bergantung pada harga tembaga sebagai bahan utama pembuatan capnya. Untuk membuat batik cap yang beragam motif maka diperlukan banyak cap, sementara harga satu cap relatif lebih mahal dari harga canting. Harga cap pada kondisi sekarang dengan ukuran 20 cm X 20 cm berkisar Rp. 750.000,- hingga Rp. 1.250.000,-/motif tergantung kerumitan motifnya. Selain proses pelukisan motif batik yang menggunakan cap, proses selanjutnya dilakukan dengan cara yang hampir sama seperti saat membuat batik tulis, misalnya dari proses pewarnaannya yang harus berulang-ulang untuk mendapatkan warna yang diinginkan, atau dari proses nglorodnya.

Pembuatan batik cap membutuhkan ketelitian yang tinggi. Kualitas batik cap sering dilihat dari kehalusannya yaitu presisi peletakan cap di sekujur bidang kain, tidak ada garis sambungan yang meleset atau semuanya pas. Tukang cap harus memastikan agar menyambungnya pas, sehingga tidak ada garis-garis yang menebal atau malamnya menggumpal di kain. Celakanya, ketidaksempurnaan ini seringkali baru terlihat setelah proses pewarnaan. Batik cap pun membutuhkan satu feeling dalam pengerjaannya. Hanya dengan komitmen untuk

mendapatkan yang terbaiklah, tercipta karya batik cap yang berkualitas. Bentuk gambar/desain motif pada batik cap selalu ada pengulangan yang jelas, sehingga gambar nampak berulang dengan bentuk yang sama, dengan ukuran garis motif relatif lebih besar dibandingkan dengan batik tulis.

Pengembangan desain motif batik cap, yang dari satu cap dapat menghasilkan beragam corak, merupakan permasalahan yang diselesaikan dalam penelitian ini. Permasalahan ini diselesaikan dengan menerapkan konsep grup simetri dan kristalografi berdimensi dua untuk menghasilkan motif dan juga cap ajaib (magic stamp). Cap ini disebut ajaib (magic) karena dengan satu cap yang didesain berdasarkan motif tersebut dapat menghasilkan beragam corak batik cap melalui inovasi metode pengecapannya, yang didasarkan pada generator dalam grup simetri (translasi, refleksi, rotasi, dan glide-refleksi).

Seperti yang telah diuraikan dalam latar belakang, para pengrajin batik cap menghadapi kendala mahalnya harga sebuah cap, padahal satu cap biasanya hanya menghasilkan satu corak batik cap, sedangkan harga jualnya lebih murah daripada batik tulis. Dalam kondisi seperti ini maka sangat perlu dan urgen untuk mengembangkan desain motif dalam cap, yang dapat menghasilkan banyak corak, artinya, dari satu desain motif dalam cap dapat menghasilkan lebih dari satu corak batik cap. Pengembangan motif yang demikian akan dapat memperkecil modal awal dan memberikan banyak pilihan corak batik bagi konsumen, sehingga akan meningkatkan daya saing batik cap. Hal inilah yang merupakan fokus tujuan penelitian ini dilaksanakan.

Penelitian ini diharapkan dapat berkontribusi secara nyata dalam pengembangan ilmu pengetahuan, teknologi dan seni (Kategori Penelitian I) yakni mengembangkan penerapan teori grup simetri dan konsep kristalografi berdimensi dua untuk mendesain motif batik cap. Disisi lain, pelaksanaan penelitian ini dimaksudkan dapat berkontribusi dalam pemecahan masalah pembangunan dengan meningkatkan daya saing kain batik cap dan mendukung pengembangan cluster unggulan potensi daerah, sekaligus meningkatkan kemampuan masyarakat (pengrajin/ produsen) dalam menerapkan teori tepat guna (Kategori Penelitian II). Dari sudut pandang pengembangan kelembangaan (Kategori Penelitian III), penelitian ini dimaksudkan untuk memperkuat Jurusan Matematika Fakultas Sains dan Matematika (FSM) Universitas Diponegoro Semarang, khususnya Laboratorium Matematika Terapan (Bengkel Desain Motif Simetris) dapat bermitra dengan fihak UMKM dalam rangka mengembangkan industri kreatif. Metode pengecapan yang ditemukan dapat dimanfaatkan dalam pengembangan pembelajaran matematika (grup simetri dan kristalografi) secara kreatif, inovatif dan produktif.

Penelitian ini dilakukan atas dorongan untuk dapat menciptakan (mengembangkan) motif batik cap dan inovasi produk derivatifnya, dengan menerapkan teori grup simetri dan kristalografi berdimensi dua dalam mendesain motifnya. Metode pengecapan motif dasar pada selembar kain melalui formulasi-formulasi matematis menghasilkan banyak corak. Pengecapan ini dilakukan tanpa adanya tumpang tindih yang satu dengan yang lain, dan secara

berulang-ulang menurut komposisi yang cocok dari rotasi, translasi dan refleksi. Hasil pengecapan yang berdasarkan operasi rotasi, translasi atau refleksi dan komposisinya berasosiasi dengan sebuah grup simetri.(Durbin, 1985).

Salah satu aplikasi grup simetri yang sangat menarik adalah dikenal sebagai kristalografi berdimensi dua maupun tiga. Permasalahan tentang mengisi secara penuh suatu bidang datar dengan poligon yang kongruen tanpa tumpang tindih kecuali pada sisi-sisinya merupakan permasalahan yang dapat diselesaikan dengan teori kristalografi berdimensi dua. Poligon-poligon kongruen yang mengisi penuh suatu bidang datar dengan mengoperasikan gerakan (translasi, rotasi, refleksi atau glide-refleksi) dari satu poligon tersebut dikenal dengan poligon fondamental. Hasil pengisian yang diperoleh berasosiasi dengan grup simetri dari gambar yang dibentuk oleh sisi-sisi dari semua poligon tersebut. Hal ini merupakan fakta yang mengaitkan antara teori grup dan kristalografi berdimensi dua, sehingga dinamakan grup kristalografi berdimensi dua (Durbin, 1985).

Sekarang pandang bidang datar (kain mori) akan dipenuhi oleh poligon-poligon yang berbentuk bujur sangkar yang memuat sebuah motif dasar yang tidak saling tumpang tindih kecuali pada sisi-sisinya saling adjacent. Dengan menggerakkan poligon ini sesuai dengan komposisi generator-generator rotasi, refleksi, translasi maupun refleksi-glide yang cocok akan diperoleh suatu corak hasil pengecapan. Dengan memulai pada poligon dasar dan secara periodik menggerakkan poligon dasar menurut generator yang dipilih maka keseluruhan bidang datar (kain mori) akan terpenuhi oleh poligon-poligon dasar sehingga corak baru dapat diperoleh.

Pengembangan motif batik cap yang didasarkan pada teori grup simetri, juga telah digunakan untuk mengembangkan desain motif batik simetris. Pada tahun 1999-2000, Kartono dkk pernah melakukan penelitian dengan judul ”Grup simetri untuk pengembangan desain motif batik simetris” . Pengembangan desain motif batik simetris dengan menerapkan konsep teori grup simetri dan periodesasi telah berhasil dari satu buah desain motif dasar dapat menghasilkan 14 corak. (Kartono et al, 2000). Keempatbelas corak tersebut dihasilkan dengan menggunakan bermacam-macam bentuk poligon seperti bujur sangkar, persegi panjang, segitiga siku-siku, segitiga sama kaki, segitiga sama sisi bahkan segitiga dengan sudut-sudut yang ditentukan sesuai dengan keinginan, sedangkan dalam pembuatan motif batik cap ini hanya menggunakan poligon yang berbentuk bujur sangkar saja.

Kartono dkk (2011) menerapkan teori yang sama untuk menguak pola (motif) geometris crop circle yang muncul di Berbah Sleman Daerah Istemewa Yogyakarta. Penelitian ini menghasilkan motif lingkaran sebagai motif dasar, dan ternyata bentuk crop circle tersebut dihasilkan melalui operasi translasi, rotasi, maupun glide-refleksi dari motif dasar lingkaran. Penelitian itu berhasil menemukan pola geometrisnya yang tersusun dari 12 lingkaran utama, 2 lingkaran lain di luarnya dengan 11 titik pusat lingkaran (Kartono et al, 2011).

Pada awal tahun 2012, teori yang sama dipakai untuk mengembangkan pemanfaatan limbah kayu sebagai bahan pembuat ukiran bergerak berbasis transformasi oleh Nurhilaliah dan Ulfia Azmi dengan Kartono sebagai pembimbing, dalam rangka mengikuti Indonesian Science Project Olympiad (ISPO) 2012.

Dari penelitian-penelitian ini dapat disimpulkan bahwa, motif yang dihasilkan dapat dikategorikan ke dalam bentuk karya seni generatif. Dari sudut pandang seni generatif, selalu dapat dihubungkan dengan keindahan yang selalu melekat pada karya seni itu. Penelitian-penelitian ini semakin meyakinkan peneliti, bahwa motif dalam karpet maupun hiasan dinding bordir yang dihasilkan juga mengandung unsur keindahan sebagai karya seni generatif.

Pada tahun 2012, Kartono dkk melaksanakan penelitian Riset Unggulan Daerah (RUD) Balitbang Provinsi Jawa Tengah tahun 2012 dengan judul ”Pemberdayaan Ekonomi Lokal melalui Pengembangan Inovasi Jenis Produk Bordir di Kabupaten Kudus”(Kartono et al, 2012). Inovasi jenis produk yang dimaksud adalah karpet dan hiasan dinding bordir. Pembuatan desain motif dasarnya juga berbasis pada teori grup simetri dan kristalografi berdimensi dua. Dari penelitian-penelitian ini dapat disimpulkan bahwa, baik desain motif batik simetris, crop circle, ukiran kayu bergerak, maupun bordir tersebut dapat dikategorikan ke dalam bentuk karya seni generatif, yang dapat dihubungkan dengan keindahan yang selalu melekat pada karya seni itu. Unsur keindahan merupakan salah satu bagian penting dalam usaha pengembangan industri kreatif.

METODE PENELITIAN Jenis Penelitian

Penelitian ini merupakan penelitian eksperimental .

Waktu dan Tempat Penelitian

Jangka waktu penelitian ini selama sembilan bulan di Bengkel Desain Motif Simetris Laboratorium Matematika Terapan, Laboratorium Komputasi Jurusan Matematika FMIPA UNDIP, dan bekerjasama dengan Batik Adityan Laweyan Surakarta.

Target/Subjek Penelitian

Target penelitian iniadalah penemuan atau inovasi desain motif dalam cap dan formulasi matematis pengecapannya, sehingga dari satu motif dalam cap tersebut dapat menghasilkan banyak corak batik. Wujud hasil penelitian ini adalah cap ajaib (magic stamp), prototipe kain batik cap yang siap diproduksi massal.

Prosedur

1. Membuat poligon dasar (poligon fondamental) berbentuk persegi ukuran 12 cm x 12 cm pada kertas gambar.

2. Mendesain motif dasar dengan mempertimbangkan nilai keindahannya dan generator-generator pada teori grup simetri yang dipakai. Pada tahapan ini, telah dipilih satu desain motif yang akan dibuatkan capnya.

3. Melakukan simulasi penataan motif.

4. Motif dasar ini kemudian discan, dan diperbaiki di studio gambar milik pengrajin batik di Laweyan Surakarta. Perbaikan ini dilakukan untuk mendapatkan motif yang akurat dan mencoba beberapa kombinasi warna. Hasil perbaikan inilah yang menjadi motif yang dipakai untuk membuat cap, dan pemesanan cetakan/ cap ajaib (magic stamp) dengan motif yang terpilih.

5. Membuat formulasi pergerakan/pergeseran poligon dasar ini berdasarkan kombinasi generator pada grup simetri (rotasi, refleksi, translasi maupun refleksi-glide) dan periodesasinya. Formulasi ini dibuat berdasarkan kombinasi yang diinginkan dan kemudian dipilih formula yang menghasilkan corak hasil penyusunan yang indah. Formulasi inilah yang kemudian dinamakan formula metode penataan motif dasar simetris yang ditemukan itu.

6. Dengan menerapkan formula yang dipilih ini dan konsep periodesasi maka keseluruhan poligon dasar akan terpenuhi oleh motif dasar tersebut. Dari sinilah keindahan dari hasil penataan motif dasar simetris yang ditentukan itu akan dinilai.

7. Melakukan simulasi komputer dan pengecapan berdasarkan formulasi gerakan

pengecapan yang telah diperoleh pada langkah (5). Hasil pengecapan ini akan menghasilkan corak-corak batik cap dari satu motif tersebut. Formulasi matematis yang disimulasikan ini yang akan dipakai sebagai aturan gerakan pengecapan/ pembuatan kain batik cap oleh pengrajin. Sampai pada penulisan laporan kemajuan ini, pembuatan cap masih dilakukan, sehingga pembuatan kain batiknya belum dilaksanakan.

HASIL PENELITIAN DAN PEMBAHASAN Hasil Penelitian

Penelitian ini berhasil membuat cap ajaib bermotif dengan tema Crop Circle dan 13 corak kain batik cap (Lampiran.1) berdasarkan teori grup symetri dan kristalografi berdimensi dua. Ketigabelas corak kain batik cap yang berhasil dibuat ini merupakan penerapan dari 13 buah formulasi matematis gerakan pengecapan yang berhasil dirumuskan pada penelitian ini. Inilah keunggulan dari hasil penelitian ini, dari satu cap dapat diciptakan beragam corak kain batik cap, sehingga wajar kalau cap ini disebut cap ajaib (magic stamp).

Pembahasan

Formulasi pengecapan yang berhasil dirumuskan dalam penelitian ini dapat menghasilkan 13 corak kain batik cap, yang variasi coraknya tidak sebanyak jika dibandingkan dengan desain batik simetris (Kartono et al, 2000). Hal ini dikarenakan polygon bermotif dasar

yang digunakan dalam desain motif batik cap ini hanyalah berbentuk persegi tidak seperti pada desain batik simetris yang menggunakan polygon persegi, persegi panjang, maupun segitiga.

Tema motif dasar pada cap (polygon persegi) yang dibuat terinspirasi oleh adanya kemunculan crop circle di Berbah Sleman pada tahun 2011 (Kartono et al, 2011). Motif dasar pada cap didesain terdiri dari lingkaran-lingkaran dengan beragam koordinat pusat dan jari-jarinya. Bidang datar (selembar kain mori) diisi penuh oleh polygon-poligon kongruen (cap bermotif dasar) melalui pengoperasian generator gerakan (translasi, refleksi, rotasi, atau glide-refleksi), sehingga menghasilkan suatu corak batik cap. Dengan memulai pada polygon fundamental dan mengulanginya secara berulang-ulang menurut gerakan yang diperintahkan oleh generator gerakan maka keseluruhan bidang datar (selembar kain mori) dapat terisi penuh. Menurut Durbin (1985), corak batik cap yang dihasilkan ini merupakan grup simetri dari gambar yang dibentuk oleh sisi-sisi semua polygon (cap bermotif dasar) dan ketigabelas corak batik cap yang dihasilkan ini merupakan kristalografi berdimensi dua.

Kain batik cap ini dapat dipandang sebagai sebuah obyek estetika berpola yang memiliki tata aturan penggambaran pseudo-algoritmik yang dapat diperlakukan sebagai bentuk seni generatif yang memiliki kegunaan memberikan inspirasi kepada peradaban umat manusia, khususnya dalam bidang perkembangan seni generatif itu sendiri. Seni generatif pada batik cap ini, selalu dapat dihubungkan dengan keindahan yang selalu melekat pada karya seni itu, yaitu berbagai bentuk keselarasan (harmoni) dari berbagai cara pengecapan secara berulang tersebut. Jadi sangat masuk akal kalau kain batik cap tersebut dikategorikan dalam suatu karya seni rupa generatif karena pola tersebut merupakan pola iteratif (berulang) yang digenerateoleh motif dasar. Ciri khas corak kain batik cap ini adalah pola iteratif yang terbentuk selalu mengawetkan keterhubungan (konektifitas).

Dalam proses pembuatan kain batik cap ini, pengrajin mengeluh kesulitan dalam melakukan pengecapan yang dapat mengawetkan keterhubungan tersebut. Ketigabelas corak kain batik cap yang dihasilkan oleh pengrajin ini masih memperlihatkan adanya sambungan yang tidak sempurna, walaupun dalam pengerjaannya telah dilakukan dengan sabar dan penuh konsentrasi. Kesulitan lainnya adalah membuat seragam ketebalan tekstur kurvanya, namun ketidaksempurnaan inilah yang akan menjadi pembeda dengan produk tekstil bermotif batik (batik printing/ sablon).

Jelaslah bahwa pola berulang (iteratif) dari motif dasar yang membentuk beragram corak akan menghasilkan bentuk fraktal sebagaimana pola berulang aritmatik sederhana dapat menghasilkan pola chaos. Seiring dengan perkembangan teknologi komputasi, sebagaimana dapat diterapkan untuk melihat pola aritmatika sederhana yang menghasilkan chaos dapat pula diterapkan untuk melihat pola geometri sederhana (motif dasar) yang menghasilkan fraktal. Upaya melihat fenomena fraktal pada corak batik cap yang dihasilkan ini akan memperluas pula khazanah dan peluang apresiasi yang lebih baik pada produk ini.

Penerapan teori grup simetri dan kristalografi berdimensi dua pada pembuatan motif dan kain batik cap ini juga dapat dipakai sebagai alat edukasi secara kreatif, inovatif, dan produktif dalam mempelajari transformasi geometris bidang, atau teori grup simetri dan kristalografi berdimensi dua. Titik atau bentuk obyek di bidang datar yang biasanya ditransformasikan dengan generator translasi, rotasi, refleksi, atau glide-refleksi diganti dengan motif batik. Pembelajaran matematika secara kreatif seperti ini akan sangat menyenangkan karena disamping belajar, peserta didik akan tahu manfaat nyata dari proses pembelajaran. Sambil bermain, juga belajar tentang transformasi bidang. bisa digunakan sebagai sarana permainan kreatifitas seperti bermain puzzle. Karena sistem kerja pengecapan yang berulang-ulang ini seperti menggunakan puzzle maka pembelajarannya lebih menyenangkan dan tidak membosankan. Sifat inovatif dalam pembelajaran ini terlihat pada motif batik cap yang didesain dengan melakukan inovasi dari satu motif dapat menghasilkan beragam corak. Pembelajaran ini juga bersifat produktif karena hasil proses pembelajaran ini tidak berhenti di atas kertas tetapi betul-betul diterapkan dan menghasilkan produk nyata. Proses pembelajaran seperti inilah yang diharapkan mampu melahirkan teknoprenuer, seperti yang diinginkan oleh Kurikulum SMA 2013.

Diskusi dengan para pengrajin batik cap di Laweyan Surakarta menyarankan bahwa hasil penelitian ini masih perlu penyempurnaan produk dan perencanaan produksi yang cermat agar dapat menekan biaya produksi. Inovasi motif batik cap perlu dilakukan secara berkelanjutan dalam rangka pengembangan keanekaragaman motif karya seni generatif. Upaya-upaya inilah yang harus selalu dilakukan sebagai langkah nyata dalam memberdayakan ekonomi lokal, mengembangkan potensi unggulan daerah dalam rangka meningkatkan kesejahteraan masyarakat.

SIMPULAN DAN SARAN Simpulan

Penerapan teori grup simetri dan kristalografi berdimensi dua, khususnya transformasi geometris bidang datar (motif dasar bertema Crop Circle) dapat menghasilkan motif simetris batik cap dan beragam coraknya melalui pengecapan yang berulang. Penelitian ini berhasil membuat 13 formula pengecapan berulang yang menghasilkan 13 corak kain batik cap, Keseluruhan proses pembuatan kain batik cap ini merupakan media edukasi yang kreatif, inovatif dan produktif.

Hasil penelitian dapat diimplikasikan untuk mendukung pengembangan keanekaragaman motif maupun metode pengecapan batik cap, dan potensi unggulan daerah, yang diharapkan dapat menciptakan lapangan kerja baru sehingga dapat mendukung upaya mempercepat pengentasan kemiskinan dan meningkatkan kesejahteraan masyarakat. Pelibatan

pengrajin dalam keseluruhan proses penelitian ini semakin memperkaya pengetahuan dan keahliannya dalam menghasilkan produk kain batik cap.

Saran

Prototip kain batik cap yang dihasilkan pada penelitian ini (dibukukan dalam product knowledge booklet) dapat ditindaklanjuti sebagai peningkatan daya saing dan perluasan pangsa pasar produk kain batik cap dalam rangka pemberdayaan ekonomi lokal. Peningkatan keahlian pengrajin dalam pengembangan moif, yang berbasis pada perkembangan ilmu pengetahuan, teknologi dan seni ini dapat menjadi inspirator dalam upaya mengembangkan teknoprener-teknoprener baru di industri kreatif batik cap atau merevitalisasi UMKM inovatif, yang merupakan salah satu pilar utama dalam pengembangan SIDa (Sistem Inovasi Daerah).

DAFTAR PUSTAKA

1. Durbin, J.R, (1985), Modern Algebra : an Introduction, Second Edition, New York:John Willey & Sons

2. Kartono, R. Heri Soelistyo Utomo, Harjito, (2000), Grup Simetri untuk Pengembangan Desain Motif Batik Simetris, Laporan penelitian dosen muda dengan nomor: 015/P2IPT/DM/VI/1999.

3. Kartono, Priyono, Budi Warsito, (2011), Menguak Misteri Crop Circle di Indonesia, Yogyakarta: Graha Ilmu, pp.41-53

4. Kartono, R.Heri Soelistyo Utomo, (2012),Pemberdayaan Ekonomi Lokal melalui Pengembangan Inovasi Jenis Produk Bordir di Kabupaten Kudus, Laporan RUD Balitbang Provinsi Jawa Tengah

5. Nurhilaliah, Ulfia Azmi, Kartono (Pembimbing), (2012), Pemanfaatan Limbah Kayu Sebagai Bahan Pembuatan Ukiran Bergerak Berbasis Transformasi , Artikel Ilmiah ISPO 2012

UCAPAN TERIMA KASIH

Artikel ini merupakan sebagian dari hasil penelitian Hibah Bersaing Desentralisasi DIKTI tahun 2013, oleh karena itulah penulis mengucapkan terima kasih atas kesempatan penelitian yang diberikan. Ucapan terima kasih juga disampaikan kepada Batik Adityan Laweyan Surakarta yang telah bekerjasama dengan baik untuk menyelesaikan proses pembuatan cap dan kain batiknya.

Eksistensi dan Karakterisasi Kontrol Optimal Vaksinasi Model Epidemi S I R

dengan Laju Insidensi Jenuh yang Termodifikasi

Rubono Setiawan

Prodi Pendidikan Matematika

Jurusan P.MIPA, F.KIP, Universitas Sebelas Maret Gedung D Lantai 3 Komplek Gedung F.KIP Kampus Kentingan

Jalan Ir.Sutami No.36 A Kentingan Surakarta e-mail : rubono.matematika@gmail.com

Abstrak

Dalam paper ini digunakan model epidemi S I R ( Susceptible Invected Recovered) dasar ( Kermack & Mc. Kendrick ) dengan laju insidensi jenuh termodifikasi dan dengan beberapa asumsi tambahan lain. Strategi vaksinasi optimal dilakukan untuk meminimalkan jumlah individu pada kelompok individu rentan dan terinfeksi untuk kemudian memaksimalkan jumlah individu pada kelompok sembuh. Permasalahan optimasi yang dibentuk adalah meminimalkan fungsional tujuan yang memuat variabel kontrol, serta sistem persamaan diferensial yang dalam hal ini adalah model S I R sebagai kendala dalam permasalahan optimasi tersebut. Hamiltonian disusun berdasarkan Lagrangian dari permasalahan optimasi dan digunakan untuk membuktikan eksistensi serta menentukan kontrol yang optimal dari permasalahan optimasi. Kriteria minimum Pontryagin digunakan sebagai alat utama untuk menentukan kontrol yang optimal dan sistem yang optimal.

Kata Kunci : Kontrol Optimal, Model S I R , Vaksinasi Optimal, Hamiltonian, Pontryagin

1. PENDAHULUAN

Pembelajaran tentang dinamika penyakit menular merupakan bagian yang sangat penting dalam bidang matematika epidemiologi. Dengan mengerti lebih dalam tentang karakteristik dari penyebaran penyakit menular dalam suatu kelompok, daerah, masyarakat atau bahkan suatu negara, maka dapat ditemukan cara cara yang lebih baik dan sesuai untuk menekan penyebaran penyakit tertentu tersebut. Cara yang umum dikenal adalah dengan program vaksinasi yang sesuai dan program proteksi atau karantina.

Model penyebaran penyakit telah banyak dipelajari oleh banyak penulis 1 , 2 , 3 , 5 , 6 . Cukup banyak diantaranya yang tertarik menggunakan bentuk laju insidensi jenuh dalam formulasi modelnya, seperti 6 , 5 , 3 . Bentuk laju insidensi jenuh dapat digolongkan menjadi bentuk laju insidensi nonlinear. Salah satu kelebihan dari bentuk laju insidensi ini adalah adanya faktor jenuh yang ditentukan berdasarkan pengendalian epidemi. Pengendalian epidemi yang dimaksud adalah berdasarkan ukuran pencegahan yang sesuai terhadap penyakit atau pembawa ( vektor ) penyakit yang bersangkutan. Dalam hal ini pencegahan ataupun pengendalian dapat dilakukan oleh dan atau terhadap individu dalam kelompok individu rentan penyakit ataupun yang telah terjangkit penyakit. Bila hanya ada satu ukuran pencegahan misalnya dilakukan oleh individu rentan penyakit maka digunakan bentuk insidensi jenuh dengan satu faktor insidensi jenuh yang menunjukkan ukuran ukuran pencegahan atau tindakan-tindakan prefentif yang sesuai dari individu sehat yang rentan terkena penyakit , seperti yang telah digunakan dan dibahas oleh Zhang, dkk., 6 dan Setiawan,

R., 5 yaitu berbentuk 𝛽 𝑆𝐼

1+𝛼1𝑆. Kemudian juga terdapat bentuk laju insidensi yang lain yaitu 𝛽 𝑆𝐼

1+𝛼2𝐼, dalam bentuk insidensi ini menunjukkan bahwa jumlah kontak infektif antara individu rentan dan individu terinfeksi dapat mengalami jenuh pada level infeksi yang tinggi karena tingkat kepadatan individu yang tinggi dalam kelompok terinfeksi atau karena ukuran ukuran proteksi yang dilakukan oleh kelompok individu rentan penyakit. Dalam paper ini akan digunakan bentuk insidensi jenuh yang dimodifikasi yang berbentuk 𝛽𝑆 𝑡 𝐼 𝑡

1+𝛼1𝑆 𝑡 +𝛼2𝐼(𝑡). Dalam laju

insidensi tersebut memuat dua faktor insidensi jenuh yang tentunya mengakomodasi ukuran ukuran tindakan pencegahan, proteksi dan kejenuhan yang terjadi karena tingkat kepadatan penduduk yang tinggi.

Model dasar yang digunakan pada makalah ini nantinya adalah model S I R ( Susceptible Invected Recovered ) dasar dengan beberapa asumsi- asumsi tambahan. Kemudian akan dibentuk suatu permasalahan optimasi yang melibatkan model berbentuk sistem persamaan diferensial sebagai kendala dari fungsi kontrol opimal vaksinasi yang merupakan fungsi tujuan ( biaya) dari permasalahan kontrol optimal tersebut. Dalam hal untuk menjabarkan permasalahan tersebut maka makalah ini ditulis dalam beberapa bab yang dimulai dengan materi pendukung tentang kontrol optimal sistem dinamik kontinu, fungsi biaya sebagai fungsi kontrol optimal vaksinasi. Kemudian dilajutkan dengan bab hasil dan pembahasan yang berisi tentang eksistensi kontrol optimal dan karakterisasi dari kontol optimal tersebut.

2. METODE PENELITIAN

Metode penelitian untuk mendapatkan hasil dalam makalah ini adalah metode literatur dengan mengkaji makalah-makalah yang membahas penggunaan teori kontrol optimal pada model penyebaran penyakit. Model dasar yang digunakan adalah model S I R yang digunakan oleh Laarabi, dkk. 3 . Penelitian pengembangan dilakukan dengan menggunakan model yang menggunakan angka kematian yang berbeda pada tiap subkelas populasi.

3. MATERI DAN TEORI PENDUKUNG

3.1. Bentuk Permasalahan Optimasi Kontol Optimal Sistem Dinamik Kontinu

Tanpa mengurangi keumuman, akan dijelaskan bentuk umum permasalahan optimasi sistem dinamik kontinu untuk masalah minimasi fungsional kontrol. Misalkan diketahui 𝑥 adalah keadaan (state) dari sistem dinamik kontinu bersyarat awal 𝑥0 dan dengan input kontrol u

sedemkian sehingga

𝑥 = 𝑓 𝑥, 𝑢 , 𝑥 0 = 𝑥0, 𝑢 𝑡 ∈ 𝒰, 𝑡 ∈ 0, 𝑇 (3.1.1)

dengan 𝒰 adalah himpunan kontrol admissible, T adalah waktu final / akhir dari sistem. Dalam hal ini kontrol 𝑢 ∈ 𝒰 haruslah dipilih untuk semua 𝑡 ∈ 0, 𝑇 untuk meminimalkan fungsional

tujuan J yang didefinisikan berdasarkan permasalahan nyata dalam aplikasi dan dapat diabstraksikan sebagai

𝐽 = Ψ 𝑥 𝑇 + 𝐿 𝑥 𝑡 , 𝑥(𝑡) 𝑑𝑡 (3.1.2)

𝑇

0

dengan L adalah Lagrangian. Kemudian kendala dalam sistem dinamik dapat digabung dengan Lagrangian L untuk mendapatkan vektor pengali Langrange 𝜆 yang sesuai dan nilainya berubah terhadap waktu, dimana masing – masing anggota 𝜆 disebut sebagai keadaan bersama (costate) dari sistem. Pengertian – pengertian tersebut sebagai dasar untuk mengkontruksi HamiltonianH yang didefinisikan untuk setiap 𝑡 ∈ 0, 𝑇 sebagai

𝐻 𝜆 𝑡 , 𝑥 𝑡 , 𝑢 𝑡 , 𝑡 = 𝐿 𝑥 𝑡 , 𝑢(𝑡) + 𝜆𝑇𝑓 𝑥 𝑡 , 𝑢(𝑡) (3.1.3)

dengan 𝜆𝑇adalah transpose dari 𝜆. Selanjutnya Hamiltonian tersebut memengang peranan yang sangat penting untuk membuktikan eksistensi adanya kontrol yang optimal dan menentukannya dengan menggunakan prinsip minimum Pontryagin yang akan dijelaskan pada subbab selanjutnya.

3.2. Permasalahan Optimasi Kontrol Optimal Model Penyebaran Penyakit

Dalam masalah penyebaran penyakit, hal yang pasti ingin diminimumkan adalah jumlah individu rentan dan individu terinfeksi penyakit sehingga jumlah individu sembuh dapat dimaksimumkan. Dalam usaha untuk mengendalikan penyebaran penyakit tersebut, salah satu cara yang umum dilakukan adalah vaksinasi, yaitu vaksinasi terhadap individu rentan ( pasif ) dan atau individu terinfeksi penyakit ( aktif ). Vaksinasi tersebut dapat diasosiasikan dengan suatu variabel kontrol u dan ditambahkan ke dalam model penyebaran penyakit yang bersangkutan. Dalam hal membentuk permasalahan optimasi kontrol optimal, jumlah individu rentan dan terinfeksi yang dikalikan dengan angka penyeimbang yang sesuai serta ditambah dengan fungsi biaya yang dibutuhkan dalam kegiatan vaksinasi akan diformulasikan menjadi fungsional tujuan yang akan diminimumkan, sedangkan model penyebaran penyakit yang berbentuk sistem persamaan diferensial nonlinear yang memuat variabel kontrol akan menjadi kendala ( constraint ) dalam permasalahan optimasi kontrol optimal tersebut.

3.3. Prinsip Minimum Pontryagin

Prinsip-prinsip minimum Pontryagin diturunkan dari aslinya yaitu prinsip- prinsip maksimum Pontryagin. Prinsip tersebut ( baik maksimum maupun minimum) digunakan dalam teori kontrol optimal untuk menentukan kemungkinan kontrol terbaik untuk sistem dinamik yang telah ditentukan, dari keadaan satu ke keadaan yang lain, lebih khusus lagi apabila munculnya kendala-kendala untuk keadaan atau input kontrolnya. Prinsip tersebut pertama kali

diperkenalkan pada tahun 1956 oleh matematikawan Rusia Lev Semenovic Pontryagin dan murid-muridnya V.G. Boltyanskii, R.V. Gamkrelidze, 7 .Prinsip tersebut mempunyai bentuk khusus persamaan Euler dan Lagrange dari kalkulus variasi.

Inti dari prinsip tersebut mengatakan bahwa Hamiltonian H yang dibentuk dari permasalahan optimasi ( dalam hal ini tanpa mengurangi keumuman diambil kasus untuk minimasi) kontrol optimal haruslah diminimumkan atas U, yaitu himpunan admissible control. Jika 𝑢∗_{∈ 𝑈 adalah kontrol yang optimal dari permasalahan optimasi, maka prinsip minimum}

Pontryagin mengatakan

𝐻 𝑥∗ _{𝑡 , 𝑢}∗ _{𝑡 , 𝜆}∗ _{𝑡 , 𝑡 ≤ 𝐻 𝑥}∗ _{𝑡 , 𝑢(𝑡), 𝜆}∗ _{𝑡 , 𝑡 , ∀𝑢 ∈ 𝑈, 𝑡 ∈ 𝑡}

0, 𝑡𝑒𝑛𝑑 , (3.3.1)

dengan 𝑥∗∈ 𝐶1 𝑡₀, 𝑡𝑒𝑛𝑑 adalah trayektori keadaan (state) yang optimal, sedangkan 𝜆∗∈

𝐵𝑉 𝑡0, 𝑡𝑒𝑛𝑑 ( Fungsi bervariasi terbatas pada 𝑡0, 𝑡𝑒𝑛𝑑 ) adalah trayektori costate yang optimal.

Kemudian prinsip tersebut juga diturunkan untuk kondisi khusus dari Hamiltonian, yaitu apabila waktu akhir 𝑡𝑒𝑛𝑑 ditentukan dan Hamiltonian tidak bergantung secara eksplisit terhadap waktu (

kondisi ekuilibrium terhadap waktu , 𝜕𝐻

𝜕𝑡 ≡ 0 ), maka prinsip minimum Pontryagin – nya adalah

𝐻 𝑥∗ 𝑡 , 𝑢∗ _{𝑡 , 𝜆}∗ _{𝑡 ≡ konstan, (3.3.2)}

dan kemudian jika waktu akhir tidak ada maka

𝐻 𝑥∗ 𝑡 , 𝑢∗ _{𝑡 , 𝜆}∗ _{𝑡 ≡ 0. (3.3.3)}

Selanjutnya akan dijelaskan syarat perlu untuk masalah minimasi kontrol optimal berdasar prinsip minimum Pontryagin. Berdasarkan bentuk formal dari permasalahan minimasi kontrol optimal (3.1.2) dengan kendala (3.1.1), maka prinsip minimum Pontryagin mengatakan bahwa trayektori keadaan (state) optimal 𝑥∗, kontrol optimal 𝑢∗dan vektor pengali Lagrange 𝜆∗ yang sesuai haruslah meminimalkan Hamiltonian H sedemikian sehingga

i. 𝐻 𝑥∗ _{𝑡 , 𝑢}∗ _{𝑡 , 𝜆}∗ _{𝑡 , 𝑡 ≤ 𝐻 𝑥}∗ _{𝑡 , 𝑢(𝑡), 𝜆}∗ _{𝑡 , 𝑡 , ∀𝑢 ∈ 𝑈, 𝑡 ∈ 𝑡} 0, 𝑡𝑒𝑛𝑑 dan haruslah memenuhi kondisi ii. Ψ𝑇 𝑥 𝑇 + 𝐻 𝑇 = 0, dengan Ψ𝑇 𝑥 𝑇 = 𝜕Ψ 𝑥 𝜕𝑇 _{𝑥=𝑥 𝑇} ,

sebagai tambahan persamaan keadaan bersama ( costate ) iii. −𝜆 𝑇 _{𝑡 = 𝐻}

𝑥 𝑥∗ 𝑡 , 𝑢∗ 𝑡 , 𝜆∗ 𝑡 , 𝑡 = 𝜆𝑇 𝑡 𝑓𝑥 𝑥∗ 𝑡 , 𝑢∗ 𝑡 + 𝐿𝑥 𝑥∗ 𝑡 , 𝑢∗ 𝑡 harus

juga dipenuhi, dengan 𝐻𝑥 𝑥∗, 𝑢∗, 𝜆∗ = 𝜕𝐻 𝜕𝑥1 _𝑥=𝑥∗_,𝑢=𝑢∗_,𝜆=𝜆∗ … 𝜕𝐻 𝜕𝑥𝑛 _𝑥=𝑥∗_,𝑢=𝑢∗_,𝜆=𝜆∗ 𝐿𝑥 𝑥∗, 𝑢∗ = 𝜕𝐿 𝜕𝑥1 _𝑥=𝑥∗_,𝑢=𝑢∗ … 𝜕𝐿 𝜕𝑥𝑛 _𝑥=𝑥∗_,𝑢=𝑢∗

𝑓𝑥 𝑥∗, 𝑢∗ = 𝜕𝑓1 𝜕𝑥1 _𝑥=𝑥∗_,𝑢=𝑢∗ … 𝜕𝑓1 𝜕𝑥𝑛 _𝑥=𝑥∗_,𝑢=𝑢∗ ⋮ ⋱ ⋮ 𝜕𝑓𝑛 𝜕𝑥1 _𝑥=𝑥∗_,𝑢=𝑢∗ … 𝜕𝑓𝑛 𝜕𝑥𝑛 _𝑥=𝑥∗_,𝑢=𝑢∗

Jika waktu akhir / final 𝑥(𝑇) tidak diketahui nilainya secara pasti (𝜕𝐻

𝜕𝑡 ≠ 0) maka haruslah

berlaku

iv. 𝜆𝑇 𝑇 = Ψ_𝑥 𝑥 𝑇 .

Keempat kondisi di atas merupakan syarat perlu untuk adanya kontrol optimal, tetapi syarat ke empat hanya digunakan ketika sistem tidak memiliki 𝑥 𝑇 . Jika 𝑥 𝑇 nilainya diketahui pasti (fixed) maka kondisi ke empat bukanlah kondisi perlu untuk adanya kontrol optimal.

4. HASIL DAN PEMBAHASAN

4.1. Formulasi Model SIR dengan Laju Insidensi Jenuh Termodifikasi

Dalam subbab ini akan diformulasikan model SIR dengan beberapa asumsi tambahan baru, dinama berdasarkan modelSIR tersebut akan dianalisa eksistensi dan karakterisasi kontrol optimal tindakan vaksinasi. Model SIR yang digunakan adalah model SIR berdasarkan model SIR yang ditulis oleh Laarabi, dkk. 3 , tetapi dengan modifikasi pada angka kematian alami pada tiap kelas. Jika model SIR dalam 3 digunakan laju kematian alami yang pasti sama pada tiap kelas, maka pada model di paper ini digunakan laju kematian alami yang memungkinkan berbeda pada tiap kelas individu. Model SIR tersebut menggunakan laju insidensi jenuh yang menggunakan dua faktor insidensi jenuh. Berikut ini model SIR selengkapnya yang disajikan dalam sistem persamaan diferensial autonomos

𝑆 = 𝐴 − 𝛽𝑆𝐼 1 + 𝛼1𝑆 + 𝛼2𝐼 − 𝜇1𝑆 𝐼 = 𝛽𝑆𝐼 1 + 𝛼1𝑆 + 𝛼2𝐼 − 𝛿 + 𝜇2+ 𝛾 𝐼 (4.1.1) 𝑅 = 𝛾𝐼 − 𝜇3𝑅 𝑁 = 𝑆 + 𝐼 + 𝑅

dengan syarat awal 𝑆 0 = 𝑆0≥ 0, 𝐼 0 = 𝐼0≥ 0, 𝑅 0 = 𝑅0≥ 0. Dalam model SIR tersebut

di atas konstanta A adalah angka masukan (recruitment) populasi, 𝛽 adalah angka kontak (transmisi), 𝜇1, 𝜇2, 𝜇3 masing – masing adalah angka kematian alami individu pada kelas rentan

(S), kelas terinfeksi (I) dan kelas sembuh (R), sedangkan 𝛿 adalah angka kematian akibat pengaruh penyakit, kemudian yang terakhir adalah konstanta 𝛾 adalah angka kesembuhan dari individu – individu yang terinfeksi.

4.2. Formulasi Model dengan Kontol Optimal Vaksinasi

Teknik kontrol optimal adalah cara yang banyak digunakan dalam hal mengembangkan strategi untuk mengontrol berbagai jenis penyakit. Salah satu strategi tersebut adalah strategi vaksinasi yang optimal. Tujuan utama dari strategi tersebut adalah untuk mengurangi jumlah individu rentan dan individu terinfeksi penyakit serta meningkatkan jumlah individu yang sembuh.

Guna merumuskan permasalahan kontrol optimal maka akan dibutuhkan variabel kontrol 𝑢 𝑡 ∈ 𝑈𝑘𝑜𝑛𝑡𝑟𝑜𝑙 yang merupakan persentase dari individu – individu yang telah tervaksinasi per

satuan waktu. Kemudian 𝑈𝑘𝑜𝑛𝑡𝑟𝑜𝑙 didefinisikan dalam bentuk himpunan admissible control (

lihat 1 ) sebagai berikut :

𝑈𝑘𝑜𝑛𝑡𝑟𝑜𝑙 = 𝑢 𝑢 𝑡 terukur, 0 ≤ 𝑢 𝑡 ≤ 𝑢𝑚𝑎𝑥 < ∞, 𝑡 ∈ 0, 𝑡𝑒𝑛𝑑 (4.2.1)

Dalam tulisan ini diasumsikan adanya penyederhanaan pada variable kontrol yaitu 0 ≤ 𝑢(𝑡) ≤ 𝑢𝑚𝑎𝑥 7 . Hal tersebut menurut Laarabi, dkk. 3 . Dikarenakan tidak mungkin untuk melakukan

vaksinasi untuk semua individu yang masuk kelas rentan penyakit dalam satu waktu. Kemudian arti fisik dari variabel kontrol dalam masalah ini adalah jika jumlah individu rentan dan terinfeksi mencapai level yang redah, maka jumlah individu sembuh akan meningkat. Berdasarkan uraian tersebut di atas maka tujuan dari permasalahan optimasi yang akan dibentuk adalah menimalkan jumlah individu rentan dan terinfeksi untuk meningkatkan jumlah individu sembuh.

Setelah menentukan formulasi model SIR di atas, maka selanjutnya akan ditentukan permasalahan optimasi dengan melibatkan model SIR dengan laju insidensi jenuh sebagai kendala dan kontrol optimal vaksinasi sebagai fungsi tujuan untuk meminimalkan jumlah individu terinfeksi dan juga individu rentan yang kemudian memaksimalkan jumlah individu sembuh, yang dalam hal ini individu yang tervaksinasi akan langsung masuk ke dalam kelas sembuh. Kontrol optimal yang digunakan dalam paper ini menggunakan kontrol optimal yang digunakan oleh Laarabi, dkk. 3 . Berikut permasalahan optimasi selengkapnya.

Meminimalkan 𝐽 𝑢 = 𝐴1𝑆 𝑡 + 𝐴2𝐼 𝑡 + 1 2𝜏𝑢 2 _𝑡 𝑡_𝑒𝑛𝑑 0 𝑑𝑡 (4.2.2) dengan kendala 𝑆(𝑡)= 𝐴 − 𝜇1+ 𝑢 𝑡 𝑆(𝑡) − 𝛽𝑆 𝑡 𝐼(𝑡) 1 + 𝛼1𝑆(𝑡) + 𝛼2𝐼(𝑡)

𝐼(𝑡) = 𝛽𝑆 𝑡 𝐼(𝑡) 1 + 𝛼1𝑆(𝑡) + 𝛼2𝐼(𝑡)

− 𝛿 + 𝜇2+ 𝛾 𝐼(𝑡) (4.2.3)

𝑅(𝑡)= 𝛾𝐼 𝑡 − 𝜇3𝑅 𝑡 + 𝑢 𝑡 𝑆(𝑡)

dan dengan syarat awal 𝑆 0 = 𝑆0≥ 0, 𝐼 0 = 𝐼0≥ 0, 𝑅 0 = 𝑅0≥ 0. Dalam Persamaan

fungsi tujuan (4.2.2) suku 𝑆(𝑡) dan 𝐼 𝑡 merepresentasikan hasil capaian 𝑆(𝑡) dan 𝐼(𝑡) yang ingin dikurangi, kemudian konstanta – konstanta positif 𝐴1 dan 𝐴2 masing – masing

dimaksudkan untuk menjaga keseimbangan besar 𝑆(𝑡) dan 𝐼 𝑡 . Dalam banyak kontrol optimal yang terjadi membutuhkan biaya, tetapi dalam hal ini kita tidak mempunyai data yang cukup untuk menentukan biaya secara pasti yang berhubungan dengan kontrol vaksinasi, oleh karena itu dalam tulisan ini difokuskan dalam hal penggunaan “ biaya relatif ” (relative cost) untuk kontrol. Dalam Persamaan (4.2.1) digunakan suku kuadrat 1

2𝜏𝑢

2_{, dimana konstanta 𝜏 adalah}

angka beban yang berkaitan dengan kontrol 𝑢(𝑡) dan dalam hal ini kontrol kuadrat mencerminkan tingkat keparahan efek samping dari vaksinasi (Joshi, 2 , dalam Laarabi, dkk. 3 .)

4.3. Eksistensi Penyelesaian

Dalam subbab ini akan dianalisa eksistensi penyelesaian dari Sistem (4.2.3). Pertama, Sistem (4.2.3) akan ditulis dalam sistem nonlinear dengan koefisien terbatas adalah :

𝜙𝑡 = 𝐵𝜙 + 𝐹 𝜙 (4.3.1) dengan 𝜙 = 𝑆 𝑡 𝐼 𝑡 𝑅(𝑡) 𝑇_; 𝐵 = − 𝜇1+ 𝑢 𝑡 0 0 0 − 𝛿 + 𝜇2+ 𝛾 0 𝑢 𝑡 𝛾 −𝜇3 , 𝐹 𝜙 = 𝐴 − 𝛽𝑆 𝑡 𝐼(𝑡) 1 + 𝛼1𝑆(𝑡) + 𝛼2𝐼(𝑡) 𝛽𝑆 𝑡 𝐼(𝑡) 1 + 𝛼1𝑆(𝑡) + 𝛼2𝐼(𝑡) 0

dan 𝜙𝑡 adalah turunan dari 𝜙 terhadap waktu t . Kemudian dibentuk operator D dengan definisi

sebagai berikut

𝐷 𝜙 = 𝐵𝜙 + 𝐹 𝜙

Diambil sebarang 𝜙1 dan 𝜙2 anggota himpunan penyelesaian dari Sistem kemudian

𝐹 𝜙₁ − 𝐹 𝜙₂ = 2𝛽𝑆2𝐼2 1 + 𝛼1𝑆1+ 𝛼2𝐼1 − 𝑆1𝐼1 1 + 𝛼1𝑆2+ 𝛼2𝐼2 1 + 𝛼₁𝑆1+ 𝛼2𝐼1 1 + 𝛼1𝑆2+ 𝛼2𝐼2 = 2𝛽 𝑆2𝐼2 1 + 𝛼1𝑆1+ 𝛼2𝐼1 − 𝑆1𝐼1 1 + 𝛼1𝑆2+ 𝛼2𝐼2 1 + 𝛼₁𝑆1+ 𝛼2𝐼1 1 + 𝛼1𝑆2+ 𝛼2𝐼2

≤ 2𝛽 𝑆2𝐼2 1 + 𝛼1𝑆1+ 𝛼2𝐼1 − 𝑆1𝐼1 1 + 𝛼1𝑆2+ 𝛼2𝐼2 ≤ 2𝛽 𝑆2𝐼2+ 𝛼1𝑆1𝑆2𝐼2+ 𝛼2𝐼1𝑆2𝐼2− 𝑆1𝐼1− 𝛼1𝑆2𝑆1𝐼1− 𝑆1𝐼1𝛼2𝐼2 ≤ 2𝛽 𝛼1𝑆1𝑆2 𝐼2− 𝐼1 + 𝛼2𝐼1𝐼2 𝑆2− 𝑆1 + 𝑆2𝐼2− 𝑆1𝐼1 ≤ 2𝛽 𝛼1𝑆1𝑆2 𝐼2− 𝐼1 + 𝛼2𝐼1𝐼2 𝑆2− 𝑆1 + 𝑆2 𝐼2− 𝐼1 + 𝐼1 𝑆2− 𝑆1 ≤ 2𝛽 𝛼1𝑆1𝑆2 𝐼2− 𝐼1 + 𝛼2𝐼1𝐼2 𝑆2− 𝑆1 + 𝑆2 𝐼2− 𝐼1 + 𝐼1 𝑆2− 𝑆1 (∗) ≤ 2𝛽 𝛼1 𝐴 𝜇1 2 𝐼2− 𝐼1 + 𝛼2 𝐴 𝜇1 2 𝑆2− 𝑆1 + 𝐴 𝜇1 𝐼2− 𝐼1 + 𝐴 𝜇1 𝑆2− 𝑆1 ∗∗ ≤ 𝑀 𝑆2− 𝑆1 + 𝐼2− 𝐼1 (4.3.2) dengan 𝑀 = 2𝛽max 𝛼1 𝐴 𝜇₁ 2 +_𝜇𝐴 1 , 𝛼2 𝐴 𝜇₁ 2 +_𝜇𝐴 1 .

Dalam pertidaksamaan (4.3.2), berdasarkan (*) apabila dicari penyelesaian untuk dinamika S sebelum dikurangi dengan suku insidensi dan penyelesaian tersebut diambil untuk 𝑡 → ∞ maka akan diperoleh kesimpulan bahwa jumlah individu S terbatas pada 𝐴

𝜇₁, lebih lanjut jumlah

individu I juga pasti tidak akan lebih dari 𝐴

𝜇₁. Berdasarkan Pertidaksamaan (4.3.2) akan

didapatkan hubungan :

𝐷 𝜙₁ − 𝐷 𝜙₂ ≤ 𝐾 𝜙₁− 𝜙2 (4.3.3)

dengan 𝐾 = max 𝑀, 𝐵 < ∞. Berdasarkan Pertidaksamaan (4.3.3) D adalah kontinu Lipschitz seragam, lebih lanjut ditambah dengan definisi dari kontrol 𝑢(𝑡) serta pembatasan pada 𝑆 𝑡 , 𝐼 𝑡 , 𝑅 𝑡 ≥ 0, maka dapat kita simpulkan bahwa penyelesaian dari Sistem (4.3.1) ada.

4.4. Eksistensi Kontrol yang Optimal

Setelah memuktikan eksistensi penyelesaian dari Sistem (4.3.2), selanjutnya akan dibuktikan eksistensi dari kontrol optimal. Sebelumnya akan ditentukan terlebih dahulu Lagrangian dan Hamiltonian dari permasalahan optimasi (4.2.2) – (4.2.3). Langrangian dari permasalahan optimasi tersebut adalah

𝐿 𝑆, 𝐼, 𝑢 = 𝐴1𝑆 𝑡 + 𝐴2𝐼 𝑡 +

1 2𝜏𝑢

Selanjutnya untuk mencari nilai minimum dari Lagrangian (4.4.1) maka dibentuklah Hamiltonian H untuk permasalahan kontrol optimal. Hamiltonial dari permasalahan optimasi (4.2.2) – (4.2.3) adalah

𝐻 𝑥 𝑡 , 𝑢 𝑡 , 𝜆 𝑡 , 𝑡 = 𝑓 𝑥 𝑡 , 𝑢 𝑡 , 𝑡 + 𝜆 𝑡 𝑔 𝑥 𝑡 , 𝑢 𝑡 , 𝑡 (4.4.2)

dengan 𝑓 𝑡, 𝑥 𝑡 , 𝑢(𝑡) adalah integran fungsi tujuan, 𝜆(𝑡) adjoint dan 𝑔 𝑡, 𝑥 𝑡 , 𝑢 𝑡 adalah ruas kanan dari sistem persamaan diferensial biasa yang sebagai model S I R. Bentuk (4.4.2) apabila disesuaikan dengan model yang telah terformulasikan maka dapat ditulis sebagai

𝐻 𝑆, 𝐼, 𝑅, 𝑢, 𝜆1, 𝜆2, 𝜆3, 𝑡 = 𝐿 𝑆, 𝐼, 𝑢 + 𝜆1 𝑑𝑆(𝑡) 𝑑𝑡 + 𝜆2 𝑑𝐼(𝑡) 𝑑𝑡 + 𝜆3 𝑑𝑅(𝑡) 𝑑𝑡 (4.4.3) dalam hal ini 𝜆1, 𝜆2 dan 𝜆3 adalah fungsi-fungsi adjoint yang sesuai.

Untuk penjaminan adanya kontrol optimal dari permasalahan optimasi (4.2.2) – (4.2.3), akan dijelaskan lewat teorema berikut :

Teorema 4.4.1.Terdapat suatu kontrol optimal 𝑢∗ 𝑡 sedemikian sehingga 𝐽 𝑢∗ 𝑡 = 𝑚𝑖𝑛

𝑢∈𝑈 𝐽 𝑢(𝑡)

dengan kendala Sistem (4.2.3) dengan syarat awal.

Bukti :

Variabel kontrol dan variabel keadaan (state variable) dari sistem semuanya bernilai tak negatif. Kemudian suku 𝑢(𝑡) pada fungsional fungsi tujuan bersifat konvek yang merupakan syarat perlu untuk masalah minimasi. Berdasarkan definisi dari ruang kontrol sendiri maka ruang kontrol (4.2.1) juga konvek dan tertutup. Karena sistem optimal (4.2.3) terbatas maka juga memenuhi sifat kekompakan yang diperlukan untuk eksistensi kontrol yang optimal. Selain itu integran dalam fungsional (4.2.2) , 𝐴1𝑆 𝑡 + 𝐴2𝐼 𝑡 +

1

2𝜏𝑢

2 _{𝑡 juga konveks pada suku kontrol}

𝑢(𝑡). Kemudian dapat dengan dibuktikan bahwa terdapat konstanta 𝜌 > 1, bilangan positif 𝜔1

dan 𝜔2 sedemikian sehingga

𝐽 𝑢(𝑡) ≥ 𝜔2+ 𝜔1 𝑢 2 𝜌

2_.

Berdasarkan uraian tersebut dapat disimpulkan bahwa terdapat kontrol optimal untuk permasalahan optimasi (4.2.2) – (4.2.3). Q.E.D.

4.5. Karakterisasi dan Penentuan Kontrol yang Optimal

Eksistensi adanya kontrol yang optimal dari permasalahan optimasi (4.2.2) – (4.2.3) telah dibuktikan pada subbab sebelumnya, kemudian untuk menentukan kontrol yang optimal

tersebut akan digunakan prinsip minimum Pontryagin pada Hamiltonian (4.4.2). Jika 𝑥∗ 𝑡 , 𝑢∗ _{𝑡 adalah solusi optimal dari permasalahan optimasi kontrol optimal, maka terdapat}

fungsi vektor nontrivial 𝜆 𝑡 = 𝜆1 𝑡 , 𝜆2 𝑡 , … , 𝜆𝑛 𝑡 𝑡 yang memenuhi persamaan –

persamaan berikut : 𝑥′ 𝑡 =𝜕𝐻 𝑥 ∗ _{𝑡 , 𝑢}∗ _{𝑡 , 𝜆 𝑡 , 𝑡} 𝜕𝜆 4.5.1 0 =𝜕𝐻 𝑥 ∗ _{𝑡 , 𝑢}∗ _{𝑡 , 𝜆 𝑡 , 𝑡} 𝜕𝑢 4.5.2 𝜆′ 𝑡 = −𝜕𝐻 𝑥 ∗ _{𝑡 , 𝑢}∗ _{𝑡 , 𝜆 𝑡 , 𝑡} 𝜕𝑥 (4.5.3) Berdasarkan sifat dari ruang kontrol

𝑢∗ _{𝑡 = 0, jika}𝜕𝐻 𝜕𝑢 < 0 𝑢∗ 𝑡 ∈ 0, 𝑢_𝑚𝑎𝑥 , jika𝜕𝐻 𝜕𝑢 = 0 𝑢∗ _{𝑡 = 𝑢} 𝑚𝑎𝑥, jika 𝜕𝐻 𝜕𝑢 > 0 4.5.4 dan hasil dalam Persamaan (4.5.2) maka 𝑢∗ 𝑡 ∈ 0, 𝑢_𝑚𝑎𝑥 .

Teorema 4.5.1.Jika 𝑆∗ _{𝑡 , 𝐼}∗ _{𝑡 dan 𝑅}∗_{(𝑡) adalah keadaan optimal yang berhubungan dengan}

variabel kontrol yang optimal 𝑢∗ _{𝑡 dari permasalahan optimasi (4.2.2) – (4.2.3), maka}

terdapat variabel adjoint ( pengali Lagrange) 𝜆1, 𝜆2 dan 𝜆3 yang sesuai dan memenuhi

𝑑𝜆1 𝑡 𝑑𝑡 = −𝐴1+ 𝜆1 𝑡 𝜇1+ 𝑢 𝑡 + 𝜌1 − 𝜆2 𝑡 𝜌1− 𝜆3 𝑡 𝑢 𝑡 , 𝑑𝜆2 𝑑𝑡 = −𝐴2+ 𝜆1 𝑡 𝜌2− 𝜆2 𝑡 𝜌2− 𝛿 + 𝜇2+ 𝛾 − 𝜆3 𝑡 𝛾, 𝑑𝜆3 𝑡 𝑑𝑡 = 𝜆3 𝑡 𝜇3, dengan 𝜌1= 𝛽𝐼 1 + 𝛼2𝐼 1 + 𝛼1𝑆 + 𝛼2𝐼 2 , 𝜌2= 𝛽𝑆 1 + 𝛼2𝑆 1 + 𝛼1𝑆 + 𝛼2𝐼 2 ,

dan kondisi transversal

𝜆𝑖 𝑡𝑒𝑛𝑑 = 0, 𝑖 = 1,2,3.

𝑢∗ _{𝑡 = 𝑚𝑎𝑥 𝑚𝑖𝑛} 𝜆1 𝑡 − 𝜆3 𝑆

∗ _𝑡

𝜏 , 𝑢𝑚𝑎𝑥 , 0 .

Bukti

Akan digunakan persamaan Hamiltonian (4.4.3) untuk membuktikan persamaan – persamaan adjoint dan kondisi transversal. Jika diambil 𝑆 𝑡 = 𝑆∗ 𝑡 , 𝐼 𝑡 = 𝐼∗ _{𝑡 ,}

𝑅 𝑡 = 𝑅∗ 𝑡 dan kemudian melakukan diferensiasi terhadap Hamiltonian H terhadap S, I dan R, serta berdasarkan syarat perlu ( syarat iii ) untuk prinsip minimum Pontryagin maka akan didapat 𝑑𝜆1 𝑡 𝑑𝑡 = − 𝜕𝐻 𝜕𝑆 = −𝐴1+ 𝜆1 𝑡 𝜇1+ 𝑢 𝑡 + 𝜌1 − 𝜆2 𝑡 𝜌1− 𝜆3 𝑡 𝑢 𝑡 𝑑𝜆2 𝑡 𝑑𝑡 = − 𝜕𝐻 𝜕𝐼 = −𝐴2+ 𝜆1 𝑡 𝜌2− 𝜆2 𝑡 𝜌2− 𝛿 + 𝜇2+ 𝛾 − 𝜆3 𝑡 𝛾 𝑑𝜆3 𝑡 𝑑𝑡 = − 𝜕𝐻 𝜕𝑅= 𝜆3 𝑡 𝜇3 dengan 𝜌1= 𝛽𝐼 1 + 𝛼2𝐼 1 + 𝛼₁𝑆 + 𝛼2𝐼 2 , 𝜌2= 𝛽𝑆 1 + 𝛼2𝑆 1 + 𝛼₁𝑆 + 𝛼2𝐼 2

Selanjutnya dengan menggunakan kondisi optimal untuk Hamiltonian, maka akan didapat hubungan 𝜕𝐻 𝜕𝑢 = 0 ⇔𝜕𝐻 𝜕𝑢 = 𝜏𝑢 ∗ _{𝑡 − 𝜆} 1 𝑡 𝑆∗+ 𝜆3 𝑡 𝑆∗ 𝑡 = 0, di 𝑢 = 𝑢∗ 𝑡 , dan dihasilkan 𝑢∗ 𝑡 = 𝜆1 𝑡 − 𝜆3 𝑆 ∗ _𝑡 𝜏 .

Kemudian jika menggunakan sifat dari ruang kontrol, akan didapatkan hubungan

𝑢∗ 𝑡 = 0, jika 𝜆1 𝑡 − 𝜆3 𝑆 ∗ _𝑡 𝜏 ≤ 0 𝑢∗ _{𝑡 =} 𝜆1 𝑡 − 𝜆3 𝑆 ∗ _𝑡 𝜏 , jika 0 < 𝜆₁ 𝑡 − 𝜆₃ 𝑆∗ _𝑡 𝜏 < 𝑢𝑚𝑎𝑥 𝑢∗ 𝑡 = 𝑢𝑚𝑎𝑥, jika 𝜆₁ 𝑡 − 𝜆₃ 𝑆∗ _𝑡 𝜏 > 0

Jadi, kontrol yang optimal dari permasalahan optimasi (4.2.2) – (4.2.3) dapat dikarakterisasi sebagai

𝑢∗ _{𝑡 = 𝑚𝑎𝑥 𝑚𝑖𝑛} 𝜆1 𝑡 − 𝜆3 𝑆

∗ _𝑡

𝜏 , 𝑢𝑚𝑎𝑥 , 0 .

Q.E.D.

Suatu sistem yang optimal dari permasalahan optimasi kontrol otpimal terdiri atas keadaan dari sistem ( state sytem ) yang berpasangan dengan adjoint dari sistem ( vektor pengali Lagrange ) dengan kondisi awal dan kondisi transversal bersama beserta karakterisasi dari kontrol optimal tersebut. Berdasarkan karakterisasi dari kontrol optimal yang telah dijelaskan dalam Teorema (4.5.1) maka didapat sistem optimal dari permasalahan optimasi (4.2.2) – (4.2.3)

𝑆 ∗= 𝐴 − 𝜇1+ 𝑢∗ 𝑆∗− 𝛽𝑆∗𝐼∗ 1 + 𝛼1𝑆∗+ 𝛼2𝐼∗ 𝐼 ∗₌ 𝛽𝑆 ∗_𝐼∗ 1 + 𝛼1𝑆∗+ 𝛼2𝐼∗ − 𝛿 + 𝜇2+ 𝛾 𝐼∗ 𝑅 ∗_{= 𝛾𝐼}∗_{− 𝜇} 3𝑅∗+ 𝑢∗𝑆∗ 𝜆1 = −𝐴1+ 𝜆1 𝜇1+ 𝑢∗+ 𝛽𝐼∗ _{1 + 𝛼} 2𝐼∗ 1 + 𝛼₁𝑆∗_{+ 𝛼} 2𝐼∗ 2 − 𝜆2 𝛽𝐼∗ _{1 + 𝛼} 2𝐼∗ 1 + 𝛼₁𝑆∗_{+ 𝛼} 2𝐼∗ 2 − 𝜆3𝑢∗ 𝜆2 = −𝐴2+ 𝜆1 𝛽𝑆∗ 1 + 𝛼₂𝑆∗ 1 + 𝛼1𝑆∗+ 𝛼2𝐼∗ 2 − 𝜆2 𝛽𝑆∗ 1 + 𝛼₂𝑆∗ 1 + 𝛼1𝑆∗+ 𝛼2𝐼∗ 2 − 𝛿 + 𝜇2+ 𝛾 − 𝜆3𝛾 𝜆3 = 𝜆3𝜇3 4.5.5 5. PENUTUP

Berdasarkan uraian dan penjelasan pada bab hasil dan pembahasan dapat diambil kesimpulan terdapat suatu kontrol optimal untuk permasalahan optimasi (4.2.2) – (4.2.3) dan untuk menentukannya digunakan prinsip-prinsip minimum Pontryagin pada Hamiltonian yang terbentuk. Dengan ditemukannya kontrol optimal tersebut, maka juga ditemukan keadaan sistem persamaan diferensial ( model S I R ) dan vektor pengali Langrange yang sesuai untuk terpenuhinya fungsi tujuan yang minimum yaitu meminimumkan jumlah individu rentan dan terifeksi sehingga otomatis akan memaksimumkan jumlah individu yang sembuh, selain itu juga meminimukan biaya ( cost ) relatif dari tindakan vaksinasi, sehingga pada akhirnya akan ditemukan sistem yang optimal dari permasalahan optimasi (4.2.2) – (4.2.3) yaitu Sistem (4.5.5)

6.DAFTAR PUSTAKA

1 Chachuat, B., Optimal Control Lecture 17-18 : Problem Formulation, Department of Chemical Engineering, McMaster University, (2009)., diakses pada 12 september 2013.

2 Joshi, H.R., “ Optimal Control of An HIV Immunology Model “, Optim. Control Appl. Methods, 23, pp. 199 – 213, (2002).

3 Laarabi, H.,Labriji, E.H.,Rachik, M.,Kaddar, A.,”Optimal Control of An Epidemic Model with A Saturated Incidence Rate”, Nonlinear Analysis : Modelling and Control, Vol.17, No.4, pp. 448 – 459, (2012).

4 Luenberger, D.G., Optimization by Vector Space Methods, John Wiley and Sons, Inc., USA, (1969)

5 Setiawan, R., Widodo, Aryati, L.,” Stability Analysis of Delayed S I R Epidemic Model With Saturated Incidence”, Presented on International Conference on Algebra (ICA) UGM Yogyakarta,Yogyakarta, Indonesia, (2010).

6 Zhang, J-Z. ; Jin,Z. ; Liu, Q –X. ; dan Zhang, Z-Y., Analysis of a Delayed SIR Model with Nonlinear Incidence , Discrete Dynamics in Nature and Society, Hindawi Publishing Corporation , Vol. 2008, Article ID 636153, (2008).

7 ---, Pontryagin’s Minimum Principle, Wikipedia the free encyclopedia, diakses di

ANALISIS KAPASITAS MAKSIMUM LINTASAN

DENGAN PENDEKATAN ALJABAR MAX-MIN

M. Andy Rudhito1)

1) Program Studi Pendidikan Matematika FKIP Universitas Sanata Dharma Kampus III USD Paingan Maguwoharjo Yogyakarta,

e-mail: arudhito@gmail.com

Abstract

Artikel ini membahas suatu metode analisis kapasitas maksimum lintasan dalam suatu jaringan dengan menggunakan pendekatan aljabar max-min. Pembahasan merupakan hasil kajian teoritis yang didasarkan literatur dan suatu perhitungan menggunakan program MATLAB. Hasil pembahasan menunjukkan bahwa jaringan yang memuat kapasitas, dapat dimodelkan sebagai graf berarah terbobot, di mana bobotnya adalah kapasitas dalam jaringan. Graf berarah terbobot di atas dapat dinyatakan dalam matriks atas aljabar max-min. Dengan menggunakan operasi perpangkatan max-min untuk matriks di atas, dapat ditentukan kapasitas maksimum lintasan antara dua buah titik dalam jaringan. Selanjutnya diberikan program MATLAB untuk menghitung perpangkatan matriks atas aljabar max-min yang dapat digunakan untuk membantu menentukan kapasitas maksimum lintasan dalam jaringan tersebut..

Keywords:aljabar max-min, matriks, lintasan, kapasitas maksimum.

PENDAHULUAN

Aljabar max-plus (himpunan R{}, dengan R adalah himpunan semua bilangan real, yang dilengkapi dengan operasi maximum dan penjumlahan) telah digunakan untuk memodelkan dan menganalisis sistem produksi sederhana, dengan fokus analisa pada masalah input-output sistem (Baccelli et.al, 2001 dan Rudhito, 2003). Pemodelan dan analisis sifat-sifat suatu jaringan antrian juga telah dilakukan dengan pendekatan aljabar max-plus, seperti dalam Krivulin (2000) dan Rudhito (2011). Penerapan aljabar max-plus pada masalah analisis lintasan kritis juga telah dibahas dalam Rudhito (2010). Pemodelan dan analisa suatu jaringan dengan pendekatan aljabar max-plus ini dapat memberikan hasil analitis dan lebih mudah pada komputasinya.

Selain aljabar max-plus, dalam Baccelli et.al. (2001), Gondran and Minoux (2008) dan John and George (2010) telah disinggung beberapa varian aljabar yang serupa dengan aljabar max-plus, seperti aljabar min-plus (dengan operasi minimum dan penjumlahan) dan aljabar max-min (dengan operasi maximum dan minimum). Diberikan pula dalam referensi di atas, beberapa gambaran singkat mengenai ilustrasi penerapannya yang terkait dengan masalah-masalah dalam teori graf, seperti masalah-masalah lintasan terpendek dan masalah-masalah kapasitas maksimum suatu lintasan dalam jaringan. Seperti halnya dalam aljabar max-plus, dengan pendekatan aljabar yang serupa diharapkan masalah-masalah yang terkait dapat dimodelkan dan perhitungan-perhitungan masalah-masalah yang terkait dapat dilakukan secara lebih analitis.

Makalah ini akan membahas analisis penentuan kapasitas maksimum suatu lintasan dalam jaringan dengan menggunakan pendekatan aljabar max-min. Untuk memudahkan dalam

perhitungan numeriknya, akan disusun pula suatu program komputer dengan menggunakan MATLAB. Dari hasil pembahasan makalah ini diharapkan sebagai langkah awal untuk ke masalah berikutnya yang lebih kompleks, seperti menentukan aliran (flow) maksimum dalam suatu jaringan.

ALJABAR MAX-MIN DAN MATRIKS

Dalam bagian ini dibahas konsep-konsep dasar aljabar max-min dan matriks atas aljabar max-min. Pembahasan lebih lengkap dapat dilihat pada Rudhito (20011), Rudhito (2013a) dan Rudhito (2013b).

Diberikan R_:=

R

{} dengan

R

adalah himpunan semua bilangan real nonnegatip dan  : = +. Pada R_didefinisikan operasi berikut:

a,b R_, ab := max(a, b) danab : = min(a, b) .

Dapat ditunjukkan bahwa (R_, , ) merupakan semiring idempoten komutatif dengan elemen

netral 0 = 0 dan elemen satuan = +. Kemudian (R_, , ) disebut dengan aljabar max-min,

yang selanjutnya cukup dituliskan dengan R_. Dalam hal urutan pengoperasian (jika tanda kurang tidak dituliskan), operasimempunyai prioritas yang lebih tinggi dari pada operasi. Karena (R_, ) merupakan semigrup komutatif idempoten, maka relasi“ ” yang didefinisikan padaR_denganx yxy = y merupakan urutan parsial padaR_.Lebih lanjut relasi ini merupakan urutan total padaR_. Karena R_ merupakan semiring idempoten, maka operasi  dan konsisten terhadap urutan , yaitu a, b, c R_, jika a b , maka ac bc, dan ac b c. Aljabar max-min R_tidak memuat pembagi nol yaitu  x, y R_

berlaku: jika x y = min(x, y) = 0,maka x =0atau y = 0. Operasi  dan  pada 



R dapat diperluas untuk operasi-operasi matriks dalam mn



R

: = {A = (Aij)AijR_, untuk i = 1, 2, ..., m dan j = 1, 2, ..., n}. Untuk R_, dan A, B

n m

 

R didefinisikan A, dengan (A)ij = Aij dan AB, dengan (AB)ij = AijBij untuk i = 1, 2, ..., m dan j = 1, 2, ..., n. Untuk A mp



R , BR_pndidefinisikan AB, dengan

(AB)ij = ik kj p k

B

A





1 . Matriks A, B mn 

R dikatakan samajikaAij = Bijuntuk setiapidanj. Didefinisikan matriks matriks O mn



R , di mana (O)ij := 0, untuk setiap i dan j, dan matriks

E  nn  R , di mana (E )ij :=











j

i

j

i

jika

,

0

jika

,



. Dapat ditunjukkan bahwa ( nn



R , , )

merupakan semiring idempoten dengan elemen netral matriks O dan elemen satuan matriks E.

m  m  m  _m m  _m

Sedangkan mn



R merupakan semimodul atas R_ . Pangkat k darimatriks A nn



R dalam

aljabar max-plus didefinisikan dengan: A0 = En dan k A = AAk1 untuk k = 1, 2, ... . Contoh 1. i)

_











3

2

1







_









7

1

5

0

=

_



















7

3

1

5

2

0

1



=

 

 

 

 













7

3,

max

1

,

max

5

2,

max

0

1,

max



=



_









7

5

1



. ii)

_











2

3

8

0

1

























4

2

0

6

1



=

_



















































4

2

0

3

1

2

2

6

3

4

8

0

0

1

1

2

8

6

0

1









=

_





_



_

_















2

0,

,

1

max

2

3,

,

max

4

0,

1,

max

2

0,

,

1

max



=



_









2

3

4

2

.

ANALISIS KAPASITAS MAKSIMUM LINTASAN

Konsep-konsep dalam aljabar max-plus sangat terkait dengan konsep-konsep dalam teori graf. Untuk itu dalam bagian ini akan diawali dengan meninjau kembali beberapa konsep dalam teori graf.

Suatu graf berarah G didefinisikan sebagai suatu pasangan G = (V, A) dengan V adalah suatu himpunan berhingga tak kosong yang anggotanya disebut titik dan A adalah suatu himpunan pasangan terurut titik-titik. Anggota A disebut busur. Suatu lintasan dalam graf berarah G adalah suatu barisan berhingga busur (i1, i2), (i2, i3), ... , (il1, il) dengan (ik, ik+1)  A untuk suatu l N(= himpunan semua bilangan asli) dank = 1, 2, ..., l  1. Suatu lintasan disebut sirkuit jika titik awal dan titik akhirnya sama. Diberikan graf berarah G = (V, A) dengan V = {1, 2, ... ,p}. Graf berarah G dikatakan berbobot jika setiap busur (j, i)  A dikawankan dengan suatu bilangan real Aij. Bilangan real Aij disebut bobot busur (j, i), dilambangkan dengan w(j, i). Graf preseden dari matriks A  nn



R adalahgraf berarah berbobot G(A) = (V, A) denganV = {1, 2, ... ,n} dan A = {(j, i) | w(i, j) = Aij 0}. Sebaliknya untuk setiap graf

berarah berbobot G = (V, A) selalu dapat didefinisikan suatu matriks A Rn_maxn dengan Aij =

     . ) ( jika ) ( jika ) ( A , , A , , , i j i j i j w

 , yang disebut matriks bobot graf G.

Dalam masalah lintasan kapasitas maksimum, untuk suatu graf berarah berbobot dengan matriks bobotnya A nn



R , Aijadalah bilangan real nonnegatif dan merupakan kapasitasbusur (j, i), yaitu aliran maksimum yang dapat melalui busur (j, i). Diberikan A

n n

 

st k A ) (  = n i i i _k  1,2, 1 1 max (min(

A

s,ik1, ... ,Ai2,i1, Ai1,t)) = n i i i k  1,2, 1

1 max (min( Ai1,t,Ai2,i1, ... ,

A

s,ik1)) , untuk setiap s, t.

Karena min( A_i,t

1 ,Ai2,i1, ... ,

A

s,ik1) adalah kapasitas lintasan dengan panjang k dengan t

sebagai titik awal dan s sebagai titik akhirnya dalam G(A), maka _(Ak_)stadalah kapasitas maksimumsemua lintasan dalam G(A) dengan panjang k, dengan t sebagai titik awal dan s sebagai titik akhirnya. Jika tidak ada lintasan dengan panjang k dari t ke s, maka kapasitas bobot maksimum didefinisikan sama dengan 0.

Teorema 1. DiberikanA nn  R . pn , Ap



mEA ...  1  n A .

Bukti: Karena banyak titik dalam G(A) adalah n maka semua lintasan dengan panjang pn tersusun setidaknya oleh sebuah sirkuit, sehingga kapasitas maksimum sirkuit tersebut lebih kecil atau sama dengan kapasitas maksimum lintasan yang panjangnya kurang dari n. Akibatnya

p

A



_mA ... An1, p n. Karena untuk setiap A nn

 R berlaku A



_mEA, maka p A



mE A ...  1  n A , pn. ∎

Berdasarkan Teorema 1 di atas didefinisikan operasi bintang (*) berikut.

Definisi 1. DiberikanA nn



R . DidefinisikanA* : = E A ... AnAn1... .

Mengingat Teorema 1 diperoleh bahwa A* : = E A ... An1. Berdasarkan penjelasan tentang kapasitas dan pangkat matriks di atas dapat disimpukan bahwa unsur (A*)ij merupakan kapasitas maksimum lintasan dengan ujung titik j dan pangkal titik i . Dari uraian di atas diperoleh Teorema 2 berikut, dengan bukti seperti pada uraian di atas.

Teorema 2. Jika A nn



R merupakan matriks bobot suatu graf berarah berbobot, makaunsur (A*)ij merupakan kapasitas maksimum lintasan dengan ujung titikj dan pangkal titik i .

Contoh 2. Diberikan suatu jaringan berkapasitas seperti pada Gambar 1 di bawah ini.

4 5 3 6 7 1 7 2 2 5 6 5 7 6 2 4 3

Gambar 1. Suatu Jaringan Berkapasitas 5