Contoh Soal Metode Simpleks Max dan Min

(1)

contoh soal metode simplex dengan

minimum

Perusahaan Maju Terus merencanakan untuk menginvestasikan uang paling banyak $ 1.200.000.

uang ini akan ditanamkan pada 2 buah cabang usaha yaitu P dan Q. setiap unit P memerlukan

uang sebesar $50 dan dapat memberikan rate of return per unitnya per tahun sebesar 10%

sedangkan untuk setiap unit Q memerlukan uang sebesar $100, namun memberikan rate of return

per unit per tahunnya sebesar 4%. Perusahaan tersebut telah mempertimbangkan bahwa target

rate of return dari kedua usaha tersebut paling sedikit adalah $60.000 per tahunnya.

Kemudian hasil analisis perusahaan memperoleh data bahwa setiap unit P dan Q mempunyai

index risiko masing-masing 8 dan 3. Padahal perusahana ini tidak mau menanggung resiko yang

terlalu besar. Kebijakan lainnya yang diinginkan oleh pemimpin khususnya untuk cabang usaha

P ditargetkan paling sedikit jumlah investasinya adalah $3.0000.

Bagaimana penyelesaian persoalan diatas apabila perusahaan bermaksud untuk tetap melakukan

investasi tetapi dengan menekan atau meminimasi resiko sekecil mungkin. Berapa unit

masing-masing usaha dapat diinvestasikan ?(metode grafis dan metode simpleks)

JAWABAN

1. Metode Grafis

Fungsi Tujuan : z = 8x + 3y

Fungsi Pembatas : 50x + 100y ≤ 1.200.000

50x ≥ 3.000

5x + 4y ≥ 60.000

Grafisnya :

50x + 100y ≤ 1.200.000

50x + 100y = 1.200.000

Jika x = 0 maka y = 12.000, jadi koordinatnya (0,12.000)

Jika y = 0 maka x = 24.000, jadi koordinatnya (24.000,0)

50x ≥ 3.000

(2)

50x = 3.000

x = 60

5x + 4y ≥ 60.000

5x + 4y = 60.000

Jika x = 0 maka y = 15.000, jadi koordinatnya (0,15.000)

Jika y = 0 maka x = 12.000, jadi koordinatnya (12.000,0)

Jadi Solusi yang ditawarkan :

x y Z = 8x + 3y Keterangan 12.00 0 0 96.000 24.00 0 0 192.000 4.000 10.000 62.000 * Minimum

1. Metode Simpleks

Fungsi Tujuan : z = 8x + 3y

Fungsi Pembatas : 50x + 100y ≤ 1.200.000

50x ≥ 3.000

5x + 4y ≥ 60.000

Bentuk baku diperoleh dengan menambahkan variabel slack pada

kendala pertama, mengurangkan variabel surplus pada kendala kedua.

Sehingga diperoleh :

Minimumkan : Z = 8x + 3y + 0S1 + 0S2 + 0S3 +MA1 + MA2

50x + 100y + S1 = 1.200.000

50x - S2 + A1 = 3.000

(3)

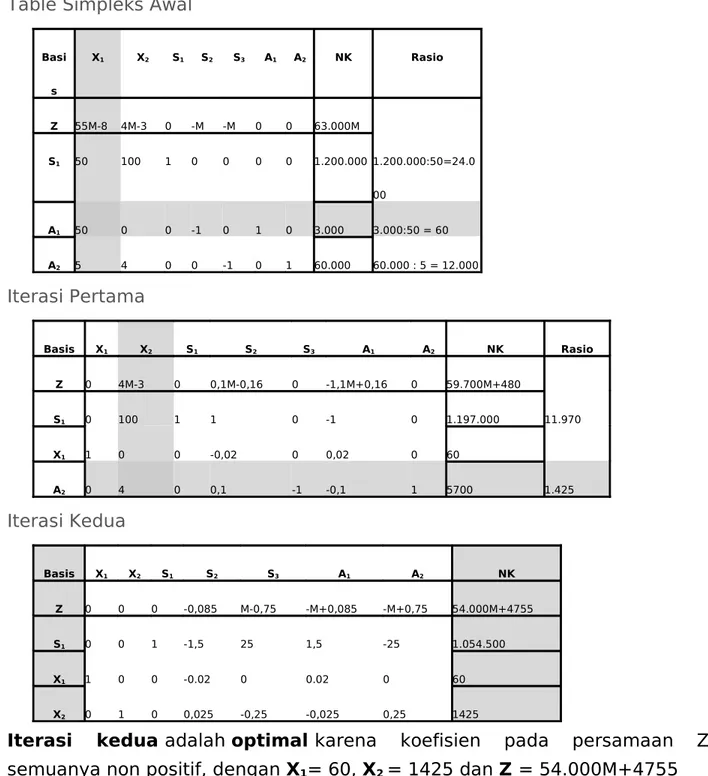
Table Simpleks Awal

Basi s X1 X2 S1 S2 S3 A1 A2 NK Rasio Z 55M-8 4M-3 0 -M -M 0 0 63.000M S1 50 100 1 0 0 0 0 1.200.000 1.200.000:50=24.0 00 A1 50 0 0 -1 0 1 0 3.000 3.000:50 = 60 A2 5 4 0 0 -1 0 1 60.000 60.000 : 5 = 12.000

Iterasi Pertama

Basis X1 X2 S1 S2 S3 A1 A2 NK Rasio Z 0 4M-3 0 0,1M-0,16 0 -1,1M+0,16 0 59.700M+480 S1 0 100 1 1 0 -1 0 1.197.000 11.970 X1 1 0 0 -0,02 0 0,02 0 60 A2 0 4 0 0,1 -1 -0,1 1 5700 1.425

Iterasi Kedua

Basis X1 X2 S1 S2 S3 A1 A2 NK Z 0 0 0 -0,085 M-0,75 -M+0,085 -M+0,75 54.000M+4755 S1 0 0 1 -1,5 25 1,5 -25 1.054.500 X1 1 0 0 -0.02 0 0.02 0 60 X2 0 1 0 0,025 -0,25 -0,025 0,25 1425

Iterasi kedua adalah optimal karena koefisien pada persamaan Z

(4)

2.Persamaan matematis suatu program linier adalah sebagai berikut : Minimasi : Z = 6X1 + 7,5X2 Dengan pembatas : 7X1 + 3X2 ≥ 210 6X1 + 12X2 ≥ 180 4X2 ≥ 120 X1, X2 ≥ 0

Carilah harga X1 dan X2 ?

JAWABAN

Pada kasus ini kita akan menggunakan metode simplex M (BIG – M), hal ini dikarenakan pada kasus ini pertidk samaan pembatasnya menggunakan ≥ (lebih dari sama dengan).

Persamaan Tujuan : Z - 6x1 - 7,5X2 - 0S1 - 0S2 - 0S3 = 0 Baris 0

Persamaan Kendala : 7x1 + 3x2 - S1 +A1 = 210 Baris 1

6x1 + 12x2 - S2 +A2 = 180 Baris 2

(5)

Bagi kendala pertidaksamaan jenis ≤, maka variabel slack ditambahkan untuk menghabiskan sumber daya yang digunakan dalam kendala. Cara ini tidak dapat diterapkan pada kendala pertidaksamaan jenis ≥ dan kendala persamaan (=) persamaan diatas diperoleh karena tanda ≥ harus mengurangi variable surplus.

Untuk mengarahkan artifisial variabel menjadi nol, suatu biaya yang besar ditempatkan pada A1, A2, dan A3 sehingga fungsi tujuannya menjadi :

Z = 6x1 + 7,5X2 + 0S1 + 0S2 + 0S3 + MA1 + MA2 + MA3

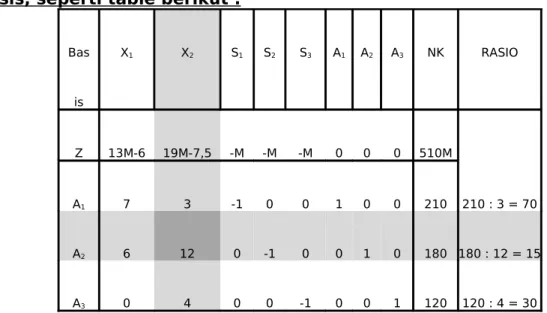
Table simplex awal dibentuk dengan A1, A2, dan A3 sebagai variable

basis, seperti table berikut :

Bas is X1 X2 S1 S2 S3 A1 A2 A3 NK RASIO Z 13M-6 19M-7,5 -M -M -M 0 0 0 510M A1 7 3 -1 0 0 1 0 0 210 210 : 3 = 70 A2 6 12 0 -1 0 0 1 0 180 180 : 12 = 15 A3 0 4 0 0 -1 0 0 1 120 120 : 4 = 30

Dari table diatas kita ketahui bahwa semua BFS belum optimal. Hal ini dikarenakan seluruh NBV masih mempunyai koefisien yang berharga positif. Oleh karena itu Untuk x2 terpilih sebagai entry variable karena x2 memiliki nilai

(6)

koefisien positif yang paling besar, dan A3 menjadi Leaving Variable. Dan yang akan menjadi pivot adalah baris 2 karena memiliki rasio paling kecil.

Langkah-langkah ERO Iterasi Pertama :

ERO 1 : Menjadikan nilai koefisien x2 berharga 1 pada baris 2

½ x1 + x2 - 1/12 S2 +1/12 A2 = 15

ERO 2 : Menjadikan nilai koefisien x2 berharga 0 pada baris 0 Z = 9_/

4 x1 + 0S1 + 15/24 S2 + 0S3 + MA1 + [ M - 15/24]A2 + MA3 + 112,5

ERO 3 : Menjadikan nilai koefisien x2 berharga 0 pada baris 1 11_/

2 x1 + ¼ S2 + A1 - 1/4 A2= 165

-2x1 + 1/3 S2 - S3 - 1/3 A2 + A3 = 60

Konversi bentuk standard iterasi Pertama :

Z = 9_/ 4 x1 + 0S1 + 15/24 S2 + 0S3 + MA1 + [ M - 15/24]A2 + MA3 + 112,5 11_/ 2 x1 + ¼ S2 + A1 - 1/4 A2 = 165 -2x1 + 1/3 S2 - S3 - 1/3 A2 + A3 = 60 ½ x1 + x2 - 1/12 S2 +1/12 A2 = 15

Tabel Iterasi Pertama

Bas

is

(7)

Z -13_/ 2M-6 0 0 7/12 -15/24 -M 0 1/24 - M 0 225M – 112,5 * A1 11/2 0 0 1/4 0 1 -1/4 0 165 165 : 5,5 = 30 A3 -2 0 0 1/3 -1 0 -1/3 1 60 * X2 ½ 1 0 -1/12 0 0 1/12 0 15 15 : 0,5 = 30

Pada fungsi tujuan masih terdapat variable dengan nilai koefisien positif, oleh karena itu lakukan iterasi kedua.

Langkah-langkah ERO Iterasi Kedua:

x1 + 1/22 S2 + 2/11A1 - 1/22 A2 = 30

Z = 0S1 + 0,725S2 + 0S3 + MA1 -0,4A1 + [ M – 0,725]A2 + MA3 + 180 ERO 3 : Menjadikan nilai koefisien x1 berharga 0 pada baris 2

0.5 A2 = 0

0,39 S2 - S3 +0,36A1 + 0,21 A2 + A3 = 120

Konversi bentuk standard iterasi kedua :

Z = 0S1 + 0,725S2 + 0S3 + [M -0,4]A1 + [ M – 0,725]A2 + MA3 + 180

(8)

0.5 A2 = 0

0,39 S2 - S3 + 0,36A1 + 0,21 A2 + A3 = 120

Tabel Iterasi Kedua

Bas is X1 X2 S1 S2 S3 A1 A2 A3 NK Z 0 0 0 -0,725 0 -M+0,4 -1_/ 2M+0,725 M -180 x1 1 0 0 1/22 0 2/11 -1/22 0 30 A3 0 0 0 0 0 0 ½ 0 0 X2 0 0 0 0,39 -1 0,36 0,21 1 120

Iterasi kedua adalah optimum karena koefisien pada persamaan Z semuanya

non positif, dengan x1 = 30, x2 = 120 dan z=-180.

3.PT Unilever bermaksud membuat 2 jenis sabun, yakni sabun bubuk dan sabun batang. Untuk itu dibutuhkan 2 macam zat kimia, yakni A dan B. jumlah zat kimia yang tersedia adalah A=200Kg dan B=360Kg.

Untuk membuat 1Kg sabun bubuk diperlukan 2 Kg A dan 6 Kg B. untuk membuat 1 Kg sabun batang diperlukan 5 Kg A dan 3 Kg B. bila keuntungan yang akan diperoleh setiap membuat 1Kg sabun bubuk = $3 sedangkan setiap 1 Kg sabun batang = $2, berapa Kg jumah sabun bubuk dan sabun batang yang sebaiknya dibuat ?

(9)

JAWABAN

Pemodelan matematika : Maksimumkan : Z = 3x1 + 2x2

Pembatas : 2x1 + 5x2 = 200

6x1 + 3x2 = 360

Persamaan Tujuan : Z - 3x1 - 2x2 = 0 Baris 0

Persamaan Kendala : 2x1 + 5x2 + A1 = 200 Baris 1

6x1 + 3x2 + A2 = 360 Baris 2

Untuk mengarahkan artifisial variabel menjadi nol, suatu biaya yang besar ditempatkan pada A1, A2, dan A3 sehingga fungsi tujuannya menjadi :

Z = 3x1 - 2X2 + MA1 + MA2

Basis x1 x2 A1 A2 NK Rasio

Z 8M-3 8M+2 0 0 560M

A1 2 5 1 0 200 200:5=40

A2 6 3 0 1 360 360:3=120

Dari table diatas kita ketahui bahwa semua BFS belum optimal. Hal ini dikarenakan belum seluruhnya NBV mempunyai koefisien yang berharga positif. Oleh karena itu Untuk x2terpilih sebagai entry variable karena x2 memiliki nilai

(10)

koefisien negatif, dan A1 menjadi Leaving Variable. Dan yang akan menjadi pivot adalah baris 1 karena memiliki rasio paling kecil.

Langkah-langkah ERO Iterasi Pertama :

0,4x1 + x2 + 0,2A1 = 40

ERO 2 : Menjadikan nilai koefisien x2 berharga 0 pada baris 0 Z = 3,8x1 + [M-0,4]A1 + MA2 - 80

4,8x1 – 0,6A1 + A2 = 240

Konversi bentuk standard iterasi pertama :

Z = 3,8x1 + [M-0,4]A1 + MA2 - 80 0,4x1 + x2 + 0,2A1 = 40 4,8x1 – 0,6A1 + A2 = 240 Basis x1 x2 A1 A2 NK Rasio Z 4,8M-3,8 0 0,4-0,4M 0 240M+80 X2 0,4 1 0,2 0 40 A2 4,8 0 0,6 1 240

Iterasi pertama adalah optimum karena koefisien pada persamaan Z