contoh soal metode simplex dengan
minimum
Perusahaan Maju Terus merencanakan untuk menginvestasikan uang paling banyak $ 1.200.000.
uang ini akan ditanamkan pada 2 buah cabang usaha yaitu P dan Q. setiap unit P memerlukan
uang sebesar $50 dan dapat memberikan rate of return per unitnya per tahun sebesar 10%
sedangkan untuk setiap unit Q memerlukan uang sebesar $100, namun memberikan rate of return
per unit per tahunnya sebesar 4%. Perusahaan tersebut telah mempertimbangkan bahwa target
rate of return dari kedua usaha tersebut paling sedikit adalah $60.000 per tahunnya.
Kemudian hasil analisis perusahaan memperoleh data bahwa setiap unit P dan Q mempunyai
index risiko masing-masing 8 dan 3. Padahal perusahana ini tidak mau menanggung resiko yang
terlalu besar. Kebijakan lainnya yang diinginkan oleh pemimpin khususnya untuk cabang usaha
P ditargetkan paling sedikit jumlah investasinya adalah $3.0000.
Bagaimana penyelesaian persoalan diatas apabila perusahaan bermaksud untuk tetap melakukan
investasi tetapi dengan menekan atau meminimasi resiko sekecil mungkin. Berapa unit
masing-masing usaha dapat diinvestasikan ?(metode grafis dan metode simpleks)
JAWABAN
1. Metode Grafis
Fungsi Tujuan : z = 8x + 3y
Fungsi Pembatas : 50x + 100y ≤ 1.200.000
50x ≥ 3.000
5x + 4y ≥ 60.000
Grafisnya :
50x + 100y ≤ 1.200.000
50x + 100y = 1.200.000
Jika x = 0 maka y = 12.000, jadi koordinatnya (0,12.000)
Jika y = 0 maka x = 24.000, jadi koordinatnya (24.000,0)
50x ≥ 3.000
50x = 3.000
x = 60
5x + 4y ≥ 60.000
5x + 4y = 60.000
Jika x = 0 maka y = 15.000, jadi koordinatnya (0,15.000)
Jika y = 0 maka x = 12.000, jadi koordinatnya (12.000,0)
Jadi Solusi yang ditawarkan :
x y Z = 8x + 3y Keterangan 12.00 0 0 96.000 24.00 0 0 192.000 4.000 10.000 62.000 * Minimum
1.
Metode Simpleks
Fungsi Tujuan : z = 8x + 3y
Fungsi Pembatas : 50x + 100y ≤ 1.200.000
50x ≥ 3.000
5x + 4y ≥ 60.000
Bentuk baku diperoleh dengan
menambahkan variabel slack
pada
kendala pertama,
mengurangkan variabel surplus
pada kendala kedua.
Sehingga diperoleh :
Minimumkan : Z = 8x + 3y + 0S1 + 0S2 + 0S3 +MA1 + MA2
50x + 100y + S1 = 1.200.000
50x - S2 + A1 = 3.000
Table Simpleks Awal
Basi s X1 X2 S1 S2 S3 A1 A2 NK Rasio Z 55M-8 4M-3 0 -M -M 0 0 63.000M S1 50 100 1 0 0 0 0 1.200.000 1.200.000:50=24.0 00 A1 50 0 0 -1 0 1 0 3.000 3.000:50 = 60 A2 5 4 0 0 -1 0 1 60.000 60.000 : 5 = 12.000Iterasi Pertama
Basis X1 X2 S1 S2 S3 A1 A2 NK Rasio Z 0 4M-3 0 0,1M-0,16 0 -1,1M+0,16 0 59.700M+480 S1 0 100 1 1 0 -1 0 1.197.000 11.970 X1 1 0 0 -0,02 0 0,02 0 60 A2 0 4 0 0,1 -1 -0,1 1 5700 1.425Iterasi Kedua
Basis X1 X2 S1 S2 S3 A1 A2 NK Z 0 0 0 -0,085 M-0,75 -M+0,085 -M+0,75 54.000M+4755 S1 0 0 1 -1,5 25 1,5 -25 1.054.500 X1 1 0 0 -0.02 0 0.02 0 60 X2 0 1 0 0,025 -0,25 -0,025 0,25 1425Iterasi kedua
adalah
optimal
karena koefisien pada persamaan Z
2.Persamaan matematis suatu program linier adalah sebagai berikut : Minimasi : Z = 6X1 + 7,5X2 Dengan pembatas : 7X1 + 3X2 ≥ 210 6X1 + 12X2 ≥ 180 4X2 ≥ 120 X1, X2 ≥ 0
Carilah harga X1 dan X2 ?
JAWABAN
Pada kasus ini kita akan menggunakan metode simplex M (BIG – M), hal ini dikarenakan pada kasus ini pertidk samaan pembatasnya menggunakan ≥ (lebih dari sama dengan).
Persamaan Tujuan : Z - 6x1 - 7,5X2 - 0S1 - 0S2 - 0S3 = 0 Baris 0
Persamaan Kendala : 7x1 + 3x2 - S1 +A1 = 210 Baris 1
6x1 + 12x2 - S2 +A2 = 180 Baris 2
Bagi kendala pertidaksamaan jenis ≤, maka variabel slack ditambahkan untuk menghabiskan sumber daya yang digunakan dalam kendala. Cara ini tidak dapat diterapkan pada kendala pertidaksamaan jenis ≥ dan kendala persamaan (=) persamaan diatas diperoleh karena tanda ≥ harus mengurangi variable surplus.
Untuk mengarahkan artifisial variabel menjadi nol, suatu biaya yang besar ditempatkan pada A1, A2, dan A3 sehingga fungsi tujuannya menjadi :
Z = 6x1 + 7,5X2 + 0S1 + 0S2 + 0S3 + MA1 + MA2 + MA3
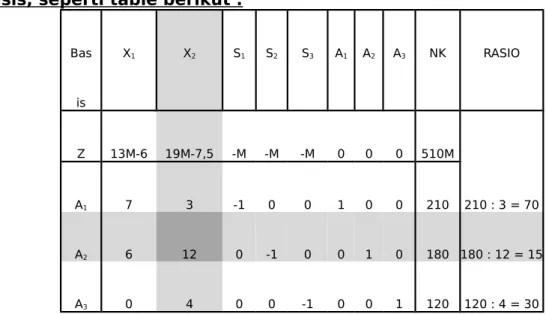
Table simplex awal dibentuk dengan A1, A2, dan A3 sebagai variable
basis, seperti table berikut :
Bas is X1 X2 S1 S2 S3 A1 A2 A3 NK RASIO Z 13M-6 19M-7,5 -M -M -M 0 0 0 510M A1 7 3 -1 0 0 1 0 0 210 210 : 3 = 70 A2 6 12 0 -1 0 0 1 0 180 180 : 12 = 15 A3 0 4 0 0 -1 0 0 1 120 120 : 4 = 30
Dari table diatas kita ketahui bahwa semua BFS belum optimal. Hal ini dikarenakan seluruh NBV masih mempunyai koefisien yang berharga positif. Oleh karena itu Untuk x2 terpilih sebagai entry variable karena x2 memiliki nilai
koefisien positif yang paling besar, dan A3 menjadi Leaving Variable. Dan yang akan menjadi pivot adalah baris 2 karena memiliki rasio paling kecil.
Langkah-langkah ERO Iterasi Pertama :
ERO 1 : Menjadikan nilai koefisien x2 berharga 1 pada baris 2
½ x1 + x2 - 1/12 S2 +1/12 A2 = 15
ERO 2 : Menjadikan nilai koefisien x2 berharga 0 pada baris 0
Z = 9/
4 x1 + 0S1 + 15/24 S2 + 0S3 + MA1 + [ M - 15/24]A2 + MA3 + 112,5
ERO 3 : Menjadikan nilai koefisien x2 berharga 0 pada baris 1
11/
2 x1 + ¼ S2 + A1 - 1/4 A2= 165
ERO 4 : Menjadikan nilai koefisien x2 berharga 0 pada baris 3
-2x1 + 1/3 S2 - S3 - 1/3 A2 + A3 = 60
Konversi bentuk standard iterasi Pertama : Z = 9/ 4 x1 + 0S1 + 15/24 S2 + 0S3 + MA1 + [ M - 15/24]A2 + MA3 + 112,5 11/ 2 x1 + ¼ S2 + A1 - 1/4 A2 = 165 -2x1 + 1/3 S2 - S3 - 1/3 A2 + A3 = 60 ½ x1 + x2 - 1/12 S2 +1/12 A2 = 15
Tabel Iterasi Pertama
Bas
is
Z -13/ 2M-6 0 0 7/12 -15/24 -M 0 1/24 - M 0 225M – 112,5 * A1 11/2 0 0 1/4 0 1 -1/4 0 165 165 : 5,5 = 30 A3 -2 0 0 1/3 -1 0 -1/3 1 60 * X2 ½ 1 0 -1/12 0 0 1/12 0 15 15 : 0,5 = 30
Pada fungsi tujuan masih terdapat variable dengan nilai koefisien positif, oleh karena itu lakukan iterasi kedua.
Langkah-langkah ERO Iterasi Kedua:
ERO 1 : Menjadikan nilai koefisien x1 berharga 1 pada baris 1
x1 + 1/22 S2 + 2/11A1 - 1/22 A2 = 30
ERO 2 : Menjadikan nilai koefisien x1 berharga 0 pada baris 0
Z = 0S1 + 0,725S2 + 0S3 + MA1 -0,4A1 + [ M – 0,725]A2 + MA3 + 180
ERO 3 : Menjadikan nilai koefisien x1 berharga 0 pada baris 2
0.5 A2 = 0
ERO 4 : Menjadikan nilai koefisien x1 berharga 0 pada baris 3
0,39 S2 - S3 +0,36A1 + 0,21 A2 + A3 = 120
Konversi bentuk standard iterasi kedua :
Z = 0S1 + 0,725S2 + 0S3 + [M -0,4]A1 + [ M – 0,725]A2 + MA3 + 180
0.5 A2 = 0
0,39 S2 - S3 + 0,36A1 + 0,21 A2 + A3 = 120
Tabel Iterasi Kedua
Bas is X1 X2 S1 S2 S3 A1 A2 A3 NK Z 0 0 0 -0,725 0 -M+0,4 -1/2M+0,725 M -180 x1 1 0 0 1/22 0 2/11 -1/22 0 30 A3 0 0 0 0 0 0 ½ 0 0 X2 0 0 0 0,39 -1 0,36 0,21 1 120
Iterasi kedua adalah optimum karena koefisien pada persamaan Z semuanya non positif, dengan x1 = 30, x2 = 120 dan z=-180.
3.PT Unilever bermaksud membuat 2 jenis sabun, yakni sabun bubuk dan sabun
batang. Untuk itu dibutuhkan 2 macam zat kimia, yakni A dan B. jumlah zat kimia yang tersedia adalah A=200Kg dan B=360Kg.
Untuk membuat 1Kg sabun bubuk diperlukan 2 Kg A dan 6 Kg B. untuk membuat 1 Kg sabun batang diperlukan 5 Kg A dan 3 Kg B. bila keuntungan yang akan diperoleh setiap membuat 1Kg sabun bubuk = $3 sedangkan setiap 1 Kg sabun batang = $2, berapa Kg jumah sabun bubuk dan sabun batang yang sebaiknya dibuat ?
JAWABAN
Pemodelan matematika : Maksimumkan : Z = 3x1 + 2x2
Pembatas : 2x1 + 5x2 = 200
6x1 + 3x2 = 360
Persamaan Tujuan : Z - 3x1 - 2x2 = 0 Baris 0
Persamaan Kendala : 2x1 + 5x2 + A1 = 200 Baris 1
6x1 + 3x2 + A2 = 360 Baris 2
Untuk mengarahkan artifisial variabel menjadi nol, suatu biaya yang besar ditempatkan pada A1, A2, dan A3 sehingga fungsi tujuannya menjadi :
Z = 3x1 - 2X2 + MA1 + MA2
Basis x1 x2 A1 A2 NK Rasio
Z 8M-3 8M+2 0 0 560M
A1 2 5 1 0 200 200:5=40
A2 6 3 0 1 360 360:3=120
Dari table diatas kita ketahui bahwa semua BFS belum optimal. Hal ini dikarenakan belum seluruhnya NBV mempunyai koefisien yang berharga positif. Oleh karena itu Untuk x2terpilih sebagai entry variable karena x2 memiliki nilai
koefisien negatif, dan A1 menjadi Leaving Variable. Dan yang akan menjadi pivot adalah baris 1 karena memiliki rasio paling kecil.
Langkah-langkah ERO Iterasi Pertama :
ERO 1 : Menjadikan nilai koefisien x2 berharga 1 pada baris 1
0,4x1 + x2 + 0,2A1 = 40
ERO 2 : Menjadikan nilai koefisien x2 berharga 0 pada baris 0
Z = 3,8x1 + [M-0,4]A1 + MA2 - 80
ERO 3 : Menjadikan nilai koefisien x2 berharga 0 pada baris 2
4,8x1 – 0,6A1 + A2 = 240
Konversi bentuk standard iterasi pertama : Z = 3,8x1 + [M-0,4]A1 + MA2 - 80 0,4x1 + x2 + 0,2A1 = 40 4,8x1 – 0,6A1 + A2 = 240 Basis x1 x2 A1 A2 NK Rasio Z 4,8M-3,8 0 0,4-0,4M 0 240M+80 X2 0,4 1 0,2 0 40 A2 4,8 0 0,6 1 240
Iterasi pertama adalah optimum karena koefisien pada persamaan Z semuanya positif, dengan x1 = 40, x2 = 240 dan z=240M+80.
RISET OPERASI contoh soal
BAB I
PENDAHULUAN
1.1
Latar Belakang
Riset operasional merupakan serangkaian kegiatan analisis dan pemodelan matematik
untuk keperluan pengambilan keputusan. Banyak persoalan manajerial di suatu
organisasi/perusahaan yang senantiasa dikaitkan dengan proses pengambilan keputusan.
Walaupun tujuan utamanya adalah untuk mendapatkan solusi, namun dalam prakteknya lebih
dipentingkan solusi yang memuaskan. Analisis kuantitatif dan sistematik tetap dibutuhkan
sebagai dasar argumentasi yang dapat dipertanggungjawabkan secara rasional.
Makalah ini dimaksudkan sebagai sebuah contoh panduan untuk beberapa penyelesaian
persoalan riset operasi yang dilengkapi dengan jawaban dan penyelesaian.
1.2
Rumusan Masalah
Rumusan masalah yang akan dibahas dalam makalah ini yakni metode penyelesaian
persoalan riset operasinal dengan 5 bentuk metode penyelesaian yaitu:
a)
Metode Grafik
b)
Metode OBE
c)
Metode Simpleks
d)
Metode Dua Fasa
e)
Metode Primal Dual
BAB II
PEMBAHASAN
a.)
Metode Grafik
Perusahaan sepatu membuat 2 macam sepatu. Sepatu yang pertama merk logo dengan karet sol
karet dan merk sugu dengan sol kulit. Diperlukan 3 macam mesin. Mesin 1 membuat sol karet,
mesin 2 membuat sol kulit dan mesin 3 membuat bagian atas sepatu dengan melakukan
assembling bagian atas dengan sol. Setiap lusin sepatu merk sogo, mula-mula dikerjakan dimesin
1 selama 2 jam, kemudian tanpa melalui mesin 2 terus dikerjakan dimesin 3 selama 6 jam.
Sedangkan untuk sepatu merk sugu tidak diproses dimesin 1, tetapi pertama kali dikerjakan
dimesin 2 selama 3 jam kemudian dimesin 3 selama 5 jam. Jam kerja maksimum setiap hari
mesin 1 adalah 8 jam, mesin 2 adalah 15 jam dan mesin 3 adalah 30 jam. Laba untuk setiap lusin
sepatu merk logo = Rp. 30.000 dan sepatu merk sugu Rp. 50.000. Masalahnya adalah
menentukan berapa lusin sebaiknya sepatu merk logo dan sugu yang dibuat agar bias mencapai
keuntungan maksimal.
Penyelesaian:
1.
Tentukan Variabel
X= Logo
Y= Sugu
1.
Fungsi Tujuan
Zmax = 30.000X + 50.000Y
2.
Fungsi Kendala/ Batasan
a). 2 X
≤ 8
b). 3 Y ≤ 15
c). 6X + 5Y ≤ 30
d). Membuat Grafik
1.
2X = 8
X = 8/2
X = 4
Maka titik 6
1=(4,0)
2.
3Y = 15
Y = 15/3
Y =5
Maka titik 6
2=(0.5)
3.
6x + 5y = 30
x=0 y =0
6(0)+5y=30 6x+5(0) = 30
5y=30 6x = 30
y=30/5 x = 30/6
y=6 x = 5
maka titik 6
3= (5,6)
Cara menepatkansolusi optimal dengan cara mencari nilai Z setiap titik ekstrim
Titik A
X = 0 , Y = 5
Mesin Logo
Sugu
Kapasitas
Max
1
2
0
8
2
0
3
15
Maka Zmax = 30.000x + 50.000y
=30.000(0) + 50.000(5)
=250.000
Titik B
Mencari titik potong 6
2dan 6
33y = 15 x5
6x + 5y = 30 x3
15y =75
18x + 15 y = 90
18x = 15
X = 5/6 , Y=5
Maka Zmax = 30.000 x + 50.000 y
= 30.000(5/6) + 50.000 (5)
= 25.000 + 250.000
= 257.000
Titik C
Mencari titik potong 6
1dan 6
32x = 8 x3
6x + 5y = 30 x1
6x = 24
6x + 5y = 30
5y= 6
y=6/5, x = 4
maka Zmax = 30.000x + 50.000y
=30.000(4) + 50.000(6/5)
= 120.000 + 60.000
=180.000
Titik D
X = 4 , Y = 0
Maka Zmax = 30.000x + 50.000y
30.000(4) + 50.000 (0)
=120.000
Kesimpulan: untuk memperoleh keuntungan optimal, dengan X=5/6, dan Y = 5 akan
menghasilkan keuntungan sebesar 275.000 makan, perusahaan sepatu tersebut harus
memproduksi setidak-tidaknya 1 buah (pembulatan ke atas) sepatu merk logo dan 5 buah sepatu
merk sugu setiap harinya agar diperoleh hasil yang optimal.
C4t4l4n1
Soal 1 (Minimalisasi)
Seorang ahli penata diet merencanakan untuk memnbuat 2 jenismakanan yaitu
makanan A dan makanan B. Kedua jenis makanan tersebut mengandung
vitamin dan protein. Jenis makanan A palingsedikit diproduksi 2 unit dan jenis
makanan B paling sedikitdiproduksi 1 unit. Tabel berikut menunjukkan jumlah
vitamin dan protein dalam setiap jenis makanan.
Jenis Makanan
Vitamin
(Unit)
Protein
(Unit)
Biaya per unit(Rp.)
B
1
3
80
Minimum Kebutuhan
8
12
Bagaimana menentukan kombinasi kedua jenis makanan, agar menimumkan biaya, selesaikan persoalan ini menggunakan metode grafik ?
Jawab : 1.Variabel X1 = A X2 = B 2.Fungsi Tujuan
Zmin = 100X
1+ 80X
2 3.Fungsi Kendala a.2X1 + X2 ≥ 8 (vitamin) b.2X1 + 3X2≥12 (protein) c.X1 ≥2 d.X2 ≥1 4.Grafik a.2X1 + X2 = 8 (vitamin) X1 =0 , X2 =8 X2 =0 , X1 = 4 b.2X1 + 3X2 = 12 (protein) X1 =0 , X2 =4 X2 =0 , X1 = 6 c.X1 = 2d.X2= 1
Kendala (a) dan (b) 2X1 + X2 = 8
2X1 + 3X2 = 12 _
-2X2 = -4
X2 = 2
Masukkan X2 kekendala (a)
2X1 + X2 = 8
2X1 + 2= 8
2X1 = 6
X1 = 3
Subtitusi X1 dan X2 kedalam Z (Fungsi Tujuan)
Zmin = 100X
1+ 80X
2= 100.3 + 80.2
= 300 + 160
= 460
Soal 2 (Minimalisasi)
Sebuah toko “TO MING SE” menyediakan dua merk pupuk, yaitu Standard dan Super.
Setiap jenis mengandung campuran bahan nitrogen dan fosfat dalam jumlah tertentu.
Jenis
Kandungan Bahan Kimia
Nitrogen (kg/sak)
Fosfat (kg/sag)
Standar
2
4
Seorang petani membutuhkan paling sedikit 16 kg nitrogen dan 24 kgfosfat untuk
lahan pertaniannya. Harga pupuk Standar dan Super masing-masing $3 dan $6. Petani
tersebut ingin mengetahui berapa sak masingmasing jenis pupuk harus dibeli agar total
harga pupuk mencapaiminimum dan kebutuhan pupuk untuk lahannya terpenuhi.
Jawab : 1.Variabel X1 = Standar X2 = Super 2.Fungsi Tujuan
Zmin = 6X
1+ 3X
2 3.Fungsi Kendala a.2X1 + 4X2 ≥ 16 b.4X1 + 3X2 ≥ 24 X1 , X2 ≥ 0 4.Grafik a.2X1 + 4X2 ≥ 16 X1 =0 , X2 =4 X2 =0 , X1 = 8 b.4X1 + 3X2 ≥ 24 X1 =0 , X2 =8 X2 =0 , X1 = 6 (a) 2X1 + 4X2 ≥ 16 | x 3 (b) 4X1 + 3X2 ≥ 24 _ | x 4 6X1 + 12X2 ≥ 4816X1 + 12X2 ≥ 96 _
-10X1 = -48
X1 = 4,8
Subtitusi X1 kedalam (a)
(a)2X1 + 4X2 ≥ 16 2(4,8) + 4X2 ≥ 16 9,6 + 4X2 = 16 4X2 = 16-9,6 X2 = 1,6
Zmin = 6X
1+ 3X
2 Z = 6.(4,8) + 3.(1,6) = $138.24Soal 3 (Maksimasi)
HMJ Teknik Informatika UNCP akan memproduksi dua jenis jaket, yaitu jaket Standard dan jaket super. setiap jenis jaket menggunakan sumber daya sebagai berikut :
Sumber daya
Jenis jaket
Kapasitas
Standar
Super
Bahan baku
4
6
1200
Jumlah jam
4
2
800
Diperkirakan permintaan Produk standard maksimum 250 unit per bulan, sedang produk super 300 unit per bulan. Sumbangan keuntungan untuk produk standard sebesar Rp 400 per unit sedangkan produk Super Rp 300 per unit. Berapa kapasitas produksi optimum untuk kedua jenis produk tersebut supaya diperoleh keuntungan maksimum ?
Jawab :
1.Variabel
X2 = Jumlah Jam 2.Fungsi Tujuan Z=400X1+300X2 3.Fungsi Kendala a.4X1 + 6X2 ≤ 1200 b.4X1 + 2X2 ≤ 800 4.Grafik a.4X1 + 6X2 ≤ 1200 X1 =0 , X2 =600 X2 =0 , X1 = 300 b.4X1 + 2X2 ≤ 800 X1 =0 , X2 =400 X2 =0 , X1 =200
Soal 4 (Maksimasi)
Sebuah industri kramik membuat jenis produk unggulan A dan B. Untuk menghasilkan satu jenis A di perlukan waktu pengerjaan 1 jam dan bahan baku 4 kg, sedangkan jenis B membutuhkan waktu 2 dua jam dan bahan baku 3 kg, waktu dan bahan baku yeng tersedia masing-masing 40 Jam dan 120 kg. keuntungan tiap unit A dan B masing-masing 40$ dan 50$
a.Tentukan model program linier untuk persoalan diatas
b.Tentukan dengan metode grafik berupa jumlah yang harus diproduksi untuk masing-masing
jenis produk , sehingga keuntungan mencapai maksimum.
Jawab :
1.Variabel :
X2 = Jumlah Produksi jenis B 2.Fungsi : ZMaks40X1 + 50X2 3.Kendala : a.X1 + 2X2 ≤ 40 b.4X1 + 3X2 ≤ 120
a. Model program linier
a.X1 + 2X2 ≤ 40 X1 =0 , X2 =20 X2 =0 , X1 = 40 b.4X1 + 3X2 ≤ 120 X1 =0 , X2 =40 X2 =0 , X1 = 30
Pada Titik fesible Titik (0,0) = 0 Titik (0,20) = Z=40X1 + 50X2 Z=40.0 + 50.20=$1000 Titik (30,0) = Z=40X1 + 50X2 Z=40.30 + 50.0 =$1200 X1 + 2X2 = 40 | x 4 4X1 + 2X2 = 160 4X1 + 3X2 = 120 _ | x 1 4X1 + 3X2 = 120 _ 5X2 = 40
X2 = 8 X1 + 2X2 = 40 X1 + 2(8)= 40 X1 = 40-16 X1 = 24 Titik optimal (24,8) = Z=40X1 + 50X2 Z=40.24 + 50.8 = $1360
a. Garafik
jumlah yang harus diproduksi untuk masing-masing jenis produk
Produksi Jenis A = 24 , Produksi Jenis B = 8 Keuntungan Makzimum yang diperoleh $1360
Soal 5 (Maksimasi)
Sebuah Industri kerajinan kulit membuat tas yeng terdiri dari jenis A dan B keuntungan masing – masing jenis Tas adalah $400 dan $200 perunit. Industri mendapat kontrak pesanan dari tokoh sebesar 30 (A dan B) buah perbulan suplay bahan kulit paling sedikit 80 lembar perbulan, dan industri kerajinan ini harus memesan paling tidak 80 lembar perbulan . setiap barang A membutuhkan 2 lembar kulit sedangkan barang B membutuhkan 8 lembar. Dari pengalaman sebelumnya industri ini tidak biasa membuat barang jenis A lebih dari 20 buah perbulan. Mereka ingin mengetahui berapa jumlah masing masing jenis A dan B yang harus dibuat supaya keuntungan yang didapat maksimum.
a.Formulasi Model
X1 = Jenis A
X2 = Jenis B
b.Dimana Model Liniernya Max Z=400X1 + 200X2
c.Batasan/Kendala
2X1 + 8X2 ≥80
X1 ≤ 20
X1, X2 ≥ 0
Selesaikan persoalan ini dengan metode grafik serta titik optimum dari titik sudut yang dibentuk oleh daerah pungsinya? Jawab : a. X1 + X2 = 30 X1 =30 X2=30 b. 2X1 + 8X2 ≥80 X1 =0 , X2 =10 X2 =0 , X1 = 40 c. X1 ≤ 20 X1 = 20 d. X1, X2 ≥ 0
Pada Titik fesible
Titik (0,10) = Z=400X1 + 200X2 Z=400.0 + 200.10=2000 Titik (0,30) = Z=400X1 + 200X2 Z=400.0 + 200.30=6000 Titik (20,0) = Z=400X1 + 200X2 Z=400.20 + 200.0=8000 Titik (20,10) = Z=400X1 + 200X2 Z=400.20 + 200.10=10000
Titik (20,5) = Z=400X1 + 200X2
Z=400.20 + 200.5=9000
Jadi jumlah yang harus diproduksi untuk masing-masing jenis produk
Produksi Jenis A = 20, Produksi Jenis B = 10 dengan Keuntungan Makzimum