i
LUAS PADA GEOMETRI HIPERBOLIK
MENGGUNAKAN MODEL SETENGAH BIDANG ATAS ℍ
SKRIPSIDiajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Oleh : DEDY LUCKY
121414121
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
SKRIPSI
LUAS PADA GEOMETRI HIPERBOLIK
MENGGUNAKAN MODEL SETENGAH BIDANG ATAS ℍ
Oleh : Dedy Lucky NIM : 121414121
Telah disetujui oleh :
Dosen Pembimbing,
iii
SKRIPSI
LUAS PADA GEOMETRI HIPERBOLIK
MENGGUNAKAN MODEL SETENGAH BIDANG ATAS ℍ
Dipersiapkan dan ditulis oleh : Dedy Lucky
NIM : 121414121
Telah dipertahankan di depan panitia penguji pada tanggal 31 Agustus 2016 dan dinyatakan memenuhi syarat
Susunan Panitia Penguji
Nama Lengkap Tanda Tangan
Ketua : Dr. Marcellinus Andy Rudhito, S.Pd. ... Sekretaris : Dr. Hongki Julie, M.Si. ... Anggota : 1. Beni Utomo, M.Sc. ... 2. Dra. Haniek Sri Pratini, M.Pd. ... 3. Febi Sanjaya, M.Sc ...
Yogyakarta, 31 Agustus 2016
Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma
Dekan,
iv
PERSEMBAHAN
“ Berbagai hal ada di luar sana,
hanya menunggu untuk
ditemukan... ” (Anonymous)
Untuk Tuhan, Keluarga, Para Pendidik, Teman, Ilmu
Pengetahuan, Pembaca & Almamaterku
v
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka sebagaimana layaknya karya ilmiah.
Yogyakarta,
vi
LEMBAR PERNYATAAN PERSETUJUAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIK
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma : Nama : Dedy Lucky
NIM : 121414121
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma sebuah karya ilmiah yang berjudul :
LUAS PADA GEOMETRI HIPERBOLIK
MENGGUNAKAN MODEL SETENGAH BIDANG ATAS ℍ
Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma untuk menyimpannya, mengalihkan dalam bentuk media lain, mengolahnya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikan di internet atau media lain demi kepentingan akademis tanpa meminta jin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Yogyakarta, 18 Agustus 2016 Yang menyatakan,
vii
ABSTRAK
Dedy Lucky, 2016. Luas pada Geometri Hiperbolik Menggunakan Model Setengah Bidang Atas ℍ. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Geometri hiperbolik dibangun dari postulat kesejajaran yang menyatakan bahwa “Diberikan suatu garis hiperbolik ℓ dan titik p di luar garis ℓ, maka terdapat minimal dua garis hiperbolik yang melalui p dan sejajar ℓ”. Model setengah bidang atas ℍ adalah model yang dapat merepresentasikan objek-objek pada bidang hiperbolik ke bidang datar.
Penelitian ini bertujuan untuk mendeskripsikan objek-objek geometri hiperbolik serta luas geometri hiperbolik pada model bidang setengah atas ℍ.
Penelitian ini menggunakan metode studi pustaka dari beberapa bahasan seperti Geometri Euclides, Geometri Hiperbolik, dan Transformasi M𝑜̈bius.
Titik dan sudut hiperbolik di ℍ didefinisikan sama dengan titik dan sudut pada geometri Euclides. Titik ideal adalah titik di tak hingga, atau titik pada sumbu real. Garis hiperbolik di ℍ berupa garis Euclides tegak lurus sumbu real atau busur lingkaran dengan pusat di sumbu real. Poligon hiperbolik dibatasi oleh segmen garis hiperbolik, sinar garis hiperbolik, atau garis hiperbolik. Terdapat empat jenis segitiga hiperbolik yang ditentukan berdasarkan letak titik sudutnya.
Panjang hiperbolik di ℍ ditentukan oleh elemen panjang busur yaitu 1
𝐼𝑚(𝑧) |𝑑𝑧|.
Luas hiperbolik suatu daerah 𝑋 di ℍ didefinisikan sebagai hasil integral dari
𝑎𝑟𝑒𝑎ℍ(𝑋) = ∫
1
(𝐼𝑚(𝑧))2 𝑑𝑥 𝑑𝑦
𝑋
.
Luas segitiga hiperbolik ditentukan oleh defeknya, dengan defek segitiga hiperbolik adalah selisih antara 𝜋 dengan jumlah sudut segitiga hiperbolik. Luas poligon hiperbolik P konvek (sudut dalam poligon tak lebih dari 𝜋) dengan besar sudut
𝛼1, … , 𝛼𝑛 dapat diperoleh dari
𝑎𝑟𝑒𝑎ℍ(𝑃) = (𝑛 − 2)𝜋 − ∑ 𝛼𝑘 𝑛 𝑘=1
.
Kata kunci : Luas Hiperbolik, Setengah Bidang Atas, Segitiga Hiperbolik, Poligon Hiperbolik
viii
ABSTRACT
Dedy Lucky, 2016. Hyperbolic Geometry Area with Upper Half Plane Model ℍ. Thesis. Mathematics Education Study Program, Mathematics and Science Education Deparment, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
Hyperbolic geometry built from parallel postulate states that "Given a hyperbolic line ℓ and a point 𝑝 outside the line ℓ, then there is a minimum of two hyperbolic lines through 𝑝 and parallel ℓ". The upper half plane ℍ is a model that can represent the objects in the field of hyperbolic onto a flat surface.
This study aimed to describe the objects of hyperbolic geometry and the area of hyperbolic geometry on the upper half plane ℍ. This research was conducted by literature study of some discussion as Euclidean Geometry, Hyperbolic Geometry, and Transformation M𝑜̈bius.
Hyperbolic point and angle in ℍ defined with the point and angle in Euclidean geometry. Ideal point is the point at infinity, or points on the real axis. Hyperbolic lines in ℍ is a Euclides line perpendicular to the real axis or arc of a circle with its center at the real axis. Hyperbolic polygons bounded by hyperbolic line segments, rays hyperbolic lines, or lines hyperbolic. There are four types of hyperbolic triangle defined by the location of the vertex.
Hyperbolic length in ℍ determained by element of arc length 1
𝐼𝑚(𝑧) |𝑑𝑧|.
Hyperbolic area of a region 𝑋 in ℍ is given by integrating
𝑎𝑟𝑒𝑎ℍ(𝑋) = ∫
1
(𝐼𝑚(𝑧))2 𝑑𝑥 𝑑𝑦
𝑋
.
Hyperbolic triangle area defined by the defect, the defect hyperbolic triangle is the difference between 𝜋 by the sum of angle hyperbolic triangles. 𝑃 is hyperbolic convex polygon (angles in polygons less than π) with interior angles 𝛼1, … , 𝛼𝑛, then area of P is
𝑎𝑟𝑒𝑎ℍ(𝑃) = (𝑛 − 2)𝜋 − ∑ 𝛼𝑘 𝑛 𝑘=1
.
Keywords: Hyperbolic Area, Upper Half Plane, Hyperbolic Triangle, Hyperbolic Polygons
ix
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa, atas segala berkat dan rahmat-Nya penulis dapat menyelesaikan skripsi yang berjudul “Luas Geometri Hiperbolik Menggunakan Model Setengah Bidang Atas ℍ” ini dengan baik.
Banyak masalah dan hambatan yang penulis temui selama dinamika penyusunan skripsi ini. Namun, dengan dukungan, bantuan, dan doa dari berbagai pihak telah memberikan motivasi berlebih kepada penulis untuk terus bersemangat dalam menyelesaikan skripsi ini. Pada kesempatan kali ini, tak lupa penulis mengucapkan terima kasih dengan sepenuh hati kepada beberapa pihak, di antaranya:
1. Pemerintahan Kabupaten Kutai Barat yang telah memberikan penulis kesempatan untuk berkuliah di Universitas Sanata Dharma.
2. Dinas Pendidikan Kabupaten Kutai Barat yang telah membiayai perkuliahan, dan akomodasi penulis selama ini.
3. Bapak Rohandi, Ph.D. selaku dekan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.
4. Bapak Dr. Hongki Julie, M.Si. selaku Ketua Program Studi Pendidikan Matematika, Universitas Sanata Dharma.
5. Bapak Beni Utomo, M.Sc. selaku dosen pembimbing dan wali penulis di prodi Pendidikan Matematika yang telah banyak memberikan masukan dan
x
nasihat kepada penulis selama menyusun skripsi maupun selama penulis berkuliah.
6. Bapak Prof. Dr. St. Suwarsono selaku dosen pembimbing akademik yang telah banyak membimbing dan memberikan nasihat kepada penulis.
7. Bapak Febi Sanjaya, M.Sc. yang sering menjadi tempat bertanya masalah-masalah seputar matematika dan selalu bisa meluangkan waktu untuk membantu penulis.
8. Seluruh dosen Pendidikan Matematika yang telah memberikan ilmu selama penulis berkuliah di Universitas Sanata Dharma.
9. Seluruh staf sekretariat JPMIPA, Ibu Tari, Bapak Sugeng, Mas Arif, dan Mas Made yang telah banyak membantu memberikan pelayanan kesekretariatan selama ini.
10. Bapak, Ibu, Kakak, dan Keluarga yang selalu mendukung, memberi semangat, dan berdoa untuk penulis.
11. Teman-teman seperjuangan Dennis, Anton, Yopek, Edith, Winda, Grace, Riris, Sasi, Selly, Dian, Asri, Selpa, Tya, dan Yosep yang selama ini memberi dukungan, semangat, motivasi, serta hal-hal luar biasa lainnya yang akan selalu diingat penulis.
12. Teman-teman Pendidikan Matematika Kelas C yang sudah berproses, berbagi suka dan duka bersama selama empat tahun ini.
13. Teman-teman Pendidikan Matematika angkatan 2012 yang sudah berproses bersama selama empat tahun ini.
xi
14. Teman mencari Pokemon, Devi, Rian, Santo, dan Ocha yang selama ini membantu mengurangi kejenuhan penulis.
15. Teman-teman Kos Kantil yang telah menjadi teman main, ngumpul, dan mengomentari hal-hal yang kurang penting bersama.
16. Semua pihak yang telah membantu dan tidak dapat disebutkan satu persatu. Semoga tulisan ini dapat memberikan manfaat dan wawasan kepada setiap pembaca.
Yogyakarta, 18 Agustus 2016
xii
DAFTAR ISI
HALAMAN JUDUL...i
HALAMAN PERSETUJUAN PEMBIMBING...ii
HALAMAN PENGESAHAN...iii
HALAMAN PERSEMBAHAN ... iv
HALAMAN KEASLIAN KARYA ... v
HALAMAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xii
DAFTAR SIMBOL ... xiv
DAFTAR GAMBAR ... xvi
BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 6 C. Pembatasan Masalah ... 6 D. Batasan Istilah ... 7 E. Tujuan Penelitian ... 8 F. Manfaat Penelitian ... 8 G. Metode Penelitian ... 9 H. Sistematika Penulisan ... 10
BAB II LANDASAN TEORI ... 11
xiii
B. Bidang Kompleks ℂ... 14
C. Garis dan lingkaran Euclides dalam bidang kompleks ℂ ... 19
D. Elemen Panjang dalam bidang kompleks ℂ ... 20
E. Sudut pada Bidang Kompleks ℂ ... 22
F. Transformasi Konformal pada Bidang Kompleks ℂ ... 28
G. Riemann Sphere ℂ ... 31
H. Inversi ... 32
I. Transformasi M𝒐bius dan Cross Rasio ... 38
BAB III MODEL BIDANG HIPERBOLIK ... 42
A. Setengah Bidang Atas (ℍ)... 42
B. Hubungan Geometri Euclides dan Geometri Hiperbolik ... 44
C. Kesejajaran dalam geometri hiperbolik ... 49
D. Jarak Hiperbolik ... 54
E. Transformasi M𝒐bius di ℍ ... 58
BAB IV LUAS PADA GEOMETRI HIPERBOLIK MENGGUNAKAN MODEL SETENGAH BIDANG ATAS H ... 64
A. Definisi Konvek pada Geometri Hiperbolik ... 64
B. Segitiga Hiperbolik dan Poligon Hiperbolik ... 68
C. Definisi Luas Hiperbolik ... 84
D. Luas Poligon Hiperbolik ... 90
BAB V PENUTUP ... 102
A. Kesimpulan ... 102
B. Saran ... 104
xiv
DAFTAR SIMBOL
ℝ : Himpunan semua bilangan real.
ℂ : Himpunan semua bilangan kompleks.
~ : pendekatan atau aprokmasi.
∞ : notasi tak hingga.
𝑅𝑒(𝑧) : 𝑥, bagian real dari bilangan kompleks 𝑧 = 𝑥 + 𝑖𝑦.
𝐼𝑚(𝑧) : 𝑦, bagian imajiner dari bilangan kompleks 𝑧 = 𝑥 + 𝑖𝑦. 𝑧̅ : 𝑥 − 𝑖𝑦, konjugat dari bilangan kompleks 𝑧 = 𝑥 + 𝑖𝑦.
|𝑧| : √(𝑅𝑒(𝑧))2+ (𝐼𝑚(𝑦))2, modulus dari bilangan kompleks z.
ℍ : {𝑧 ∈ ℂ| 𝐼𝑚(𝑧) > 0}, setengah bidang atas di ℂ.
ℂ̅ : ℂ ∪ {∞}, Riemann sphere.
ℝ3 : {(𝑥, 𝑦, 𝑧) ∈ ℝ3|𝑥, 𝑦, 𝑧 ∈ ℝ}, ruang dimensi tiga.
𝕊2 : Bola satuan di ℝ3.
ℝ̅ : ℝ ∪ {∞}, sumbu real yang diperpanjang.
𝑙𝑒𝑛𝑔𝑡ℎ(𝑓) : panjang lintasan f.
xv
𝑧, 𝑣, 𝑐, 𝑑, … : titik-titik pada bidang kompleks ℂ.
𝑇, 𝑋, 𝐿, … : garis-garis Euclides pada bidang kompleks ℂ.
ℓ, 𝓂, 𝓀, … : garis-garis hiperbolik pada setengah bidang atas ℍ.
𝑇𝑧1𝑧2 : segmen garis Euclides dengan pangkal di 𝑧1 dan ujung di 𝑧2. 𝑇𝑧1 : sinar garis Euclides dengan pangkal di 𝑧1.
ℓ𝑧1𝑧2 : segmen garis hiperbolik dengan pangkal di 𝑧1 dan ujung di 𝑧2. ℓ𝑧1 : sinar garis hiperbolik dengan pangkal di 𝑧1.
∠(𝐶1, 𝐶2) : sudut antara kurva 𝐶1 dan 𝐶2.
∠𝑧1𝑧2𝑧3 : sudut 𝑧1𝑧2𝑧3.
𝑙𝑒𝑛𝑔𝑡ℎℍ(𝑓) : panjang hiperbolik lintasan f di setengah bidang atas ℍ.
𝑑(𝑧1, 𝑧2) : jarak Euclides dari titik 𝑧1 ke 𝑧2.
𝑑ℍ(𝑧1, 𝑧2) : jarak hiperbolik dari titik 𝑧1 ke 𝑧2 di setengah bidang atas ℍ.
𝑎𝑟𝑒𝑎ℍ(𝑋) : luas hiperbolik dari himpunan 𝑋 di ℍ.
Φ : defek segitiga.
xvi
DAFTAR GAMBAR
Gambar 1.1 Tablet Babilonia, Plimpton 322...1
Gambar 2.1 Ilustrasi Proposisi 2.1...12
Gambar 2.2 Ilustrasi Proposisi 2.2...13
Gambar 2.3 Ilustrasi Proposisi 2.3...13
Gambar 2.4 Representasi Bilangan Kompleks ke Titik pada Bidang Kompleks...17
Gambar 2.5 Bilangan Kompleks z dalam Koordinat Polar...18
Gambar 2.6 Ilustrasi Definisi 2.4...22
Gambar 2.7 Ilustrasi Proposisi 2.5...24
Gambar 2.8 Ilustrasi Sudut Tipe I...26
Gambar 2.9 Ilustrasi Sudut Tipe II...27
Gambar 2.10 Ilustrasi Sudut Tipe III...28
Gambar 2.11 Proyeksi Stereografi...32
Gambar 3.1 Model Bidang pada Geometri Hiperbolik...42
Gambar 3.2 Garis Hiperbolik di ℍ...46
Gambar 3.3 Garis Hiperbolik melalui Dua Titik Berbeda...47
Gambar 3.4 Sudut antara Dua Garis Hiperbolik...48
Gambar 3.5 Dua Garis Sejajar pada Geometri Euclides...49
Gambar 3.6 Garis-garis Hiperbolik yang Sejajar melalui Sebarang Titik...51
Gambar 3.7 Ilustrasi Sejajar untuk Kasus Pertama...52
Gambar 3.8 Ilustrasi Sejajar untuk Kasus Kedua...53
xvii
Gambar 4.1 Segmen-segmen Garis pada X di ℍ...65
Gambar 4.2 (a) Garis Hiperbolik di ℍ, (b) Sinar Garis Hiperbolik di ℍ, dan (c) Segmen Garis Hiperbolik di ℍ...66
Gambar 4.3 (a) Contoh Poligon Hiperbolik Konkaf; (b) Contoh Poligon Hiperbolik Konvek ...67
Gambar 4.4 Jenis-jenis Segitiga Hiperbolik di ℍ...68
Gambar 4.5 (a) Segitiga Hiperbolik pada Posisi Standar; (b) Ilustrasi Segitiga Hiperbolik Kasus I Proposisi 4.4; (c) Ilustrasi Segitiga Hiperbolik Kasus II Proposisi 4.4; (d) Ilustrasi Segitiga Hiperbolik Kasus III Proposisi 4.4...70
Gambar 4.6 Ilustrasi Segitiga Hiperbolik Siku-siku di i...74
Gambar 4.7 Tinggi dari Sembarang Segitiga Hiperbolik...76
Gambar 4.8 Ilustrasi dari Teorema 4.7...78
Gambar 4.9 Ilustrasi Poligon Hiperbolik Berdasarkan Definisi...84
Gambar 4.10 Ilustrasi Contoh 4.1...89
Gambar 4.11 Segitiga Hiperbolik dengan 𝑣1 di ∞...91
Gambar 4.12 Ilustrasi Teorema 4.12...93
Gambar 4.13 Segitiga Hiperbolik P pada Contoh 4.3...95
Gambar 4.14 Ilustrasi Teorema 4.13...97
1
BAB I
PENDAHULUAN
A. Latar Belakang
Ilmu pengetahuan adalah salah satu cipta manusia dalam rangka memahami, mengolah, mengeksplorasi, dan memprediksi segala fenomena yang terjadi di alam semesta. Perkembangan ilmu pengetahuan terus berlangsung dari awal peradaban manusia sampai kelak berakhirnya peradaban itu sendiri. Sebagai bentuk nyata dari perkembangan ilmu pengetahuan adalah dengan munculnya berbagai macam disiplin ilmu, mulai dari ilmu tentang manusia, gejala fenomena alam, sampai ilmu tentang galaksi dan alam semesta. Salah satu cabang ilmu tertua yang dipelajari manusia adalah matematika, hal ini terbukti dengan ditemukannya tulisan matematika tertua berupa tablet tanah liat yang disebut Plimpton 322 (Gambar 1.1) sekitar 1900 SM di Babilonia (Burton, 2011: 74).
Pada masa silam matematika sering digunakan untuk mengatasi persoalan-persoalan sehari-hari, seperti yang dilakukan oleh bangsa Mesir dalam menentukan batas-batas tanah yang hilang tersapu banjir sungai Nil.
Bangsa Mesir menggunakan teknik-teknik tertentu dalam menentukan batas bidang tanah yang terhapus. Salah satu cabang ilmu matematika yang mampu menjawab permasalahan ini adalah geometri. Kata “geometri” berasal dari kata Yunani yaitu “geometrien” (geo berarti bumi, dan metrein berarti ukuran) yang memiliki arti ilmu ukur bumi (Burton, 2011: 53).
Euclides (325-265 SM), seorang matematikawan bangsa Yunani yang dianggap sebagai pelopor pembentuk geometri aksiomatis membawa perubahan besar terhadap bidang kajian geometri. Buku yang berjudul The Elements adalah salah satu buku karya Euclides yang paling fenomenal karena telah berhasil menyusun dasar-dasar geometri secara sistematis dan tetap digunakan sebagai acuan hingga saat ini. Buku tersebut memuat 23 definisi, 5 aksioma, dan 5 postulat. Euclides menggunakan istilah postulat yang merupakan aksioma khusus digunakan pada bidang geometri. Lima postulat Euclides yang telah dinyatakan dengan arti yang sama oleh Kline (1972) dalam buku Hyperbolic Geometry karya James W. Cannon sebagai berikut.
1. Each pair of points can be joined by one and only one straight line segment.
2. Any straight line segment can be indefinitely extended in either direction.
3. There is exactly one circle of any given radius with any given center. 4. All right angles are congruent to one another.
5. If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if extended indefinitely, meet on that side on which the angles are less than two right angles.
Diterjemahkan dalam bahasa Indonesia dengan makna kurang lebih sebagai berikut.
1. Sepasang titik dapat dihubungkan dengan tepat satu segmen garis lurus. 2. Setiap segmen garis lurus dapat diperpanjang tanpa batas pada kedua
arah.
3. Terdapat tepat satu lingkaran dari sebarang jari-jari yang diberikan dengan sebarang titik pusat yang diberikan.
4. Semua sudut siku-siku memiliki besar sudut yang sama.
5. Jika sebuah garis lurus memotong dua garis yang lain, maka akan terbentuk sudut dalam pada sisi-sisinya besarnya kurang dari dua sudut siku-siku, kedua garis lurus tersebut jika diteruskan sampai tak hingga akan bertemu pada sisi yang sudutnya kurang dari dua sudut siku-siku. Kelima postulat tersebut adalah fondasi dari berbagai teorema dalam geometri Euclides. Dari kelima postulat tersebut, postulat kelima adalah yang paling rumit dan tidak wajar. Postulat tersebut sebenarnya ekuivalen dengan postulat kesejajaran yaitu “ Diberikan sebuah garis dan sebuah titik di luar garis, ada tepat satu garis yang melalui titik tersebut dan sejajar dengan garis yang diberikan”. Para matematikawan memandang bahwa postulat kelima Euclides bukanlah suatu postulat melainkan teorema yang dapat
dibuktikan. Selama dua ribu tahun banyak matematikawan mencoba untuk membuktikan postulat tersebut namun tidak dapatkan hasil yang memuaskan. “Out of nothing I have created a strange new universe”, merupakan potongan kalimat yang diambil dari salah satu surat János Bolyai (1802-1860) untuk ayahnya ketika ia mencoba memecahkan pembuktian postulat kelima Euclides (Greenberg, M.J. 1980: 140). “Alam semesta baru yang aneh” yang dimaksudkan oleh János Bolyai merupakan cabang ilmu geometri baru yang sering disebut Geometri non-Euclid atau Geometri Hiperbolik. Salah satu dasar utama geometri hiperbolik adalah negasi dari postulat kesejajaran beserta keempat postulat Euclides sebelumnya. Tokoh lain dari munculnya geometri hiperbolik adalah Carl Friedrich Gauss (1777-1855), dan Nikolai Ivanovich Lobachevsky (1792-1856). Dilihat dari kemunculannya, geometri hiperbolik merupakan kajian ilmu yang relatif baru dan terus berkembang hingga saat ini. Selain geometri hiperbolik, ada beberapa cabang geometri lainnya seperti geometri netral, geometri eliptik, hingga geometri fraktal yang dikembangkan dengan merubah maupun membentuk postulat-postulat baru dari geometri Euclides.
Henri Poincaré (1854-1912) adalah salah satu tokoh dalam perkembangan geometri hiperbolik yang berkontribusi menemukan model bidang hiperbolik yang disebut Model Poincaré (Greenberg, 1980: 187). Model Poincaré digunakan untuk merepresentasikan objek-objek geometri seperti titik, sudut, garis, dan bentuk-bentuk poligon. Selain model Poincaré, ada model lain dalam merepresentasikan objek-objek geometri yaitu model
setengah bidang atas, dan model Beltrami-Klein. Model-model tersebut memiliki sifat, definisi, dan teorema-teorema yang berbeda serta memiliki kekhasannya masing-masing.
Wicaksono (2015) telah membedah secara teoritis mengenai geometri hiperbolik terutama pada bagian luas hiperbolik. Teori yang digunakan beracu pada postulat-postulat pada geometri Euclides dan postulat kesejajaran untuk geometri hiperbolik. Pada tugas akhir ini telah dijelaskan tentang bangun-bangun datar pada geometri hiperbolik seperti jumlah sudut dalam segitiga kurang dari 𝜋 serta luas segitiga yang ternyata diperoleh dari selisih 𝜋 dengan jumlah sudut dalam segitiga hiperbolik. Hal-hal yang belum dibahas pada tugas akhir ini adalah belum ditampilkannya bentuk-bentuk objek geometri hiperbolik di suatu bidang datar sehingga teori tersebut dapat didukung dengan lebih mendalam. Belum adanya bidang yang mempresentasikan bangun datar pada geometri hiperbolik juga berdampak pada sukarnya abstraksi atau penghitungan dalam aplikasi langsung, seperti menghitung luas sembarang segitiga hiperbolik, mengukur sudut di antara dua garis hiperbolik berpotongan, menghitung jarak dua titik berbeda, dan adakah transformasi dalam geometri hiperbolik. Kekurangan ini dapat dilengkapi dengan menambahkan suatu model bidang hiperbolik yang sesuai untuk model tersebut serta menyajikan proposisi-proposisi yang berlaku pada model tersebut untuk memahami konsep luas pada geometri hiperbolik lebih mendalam.
Berdasarkan pernyataan-pernyataan di atas, peneliti meyakini bahwa geometri terus berkembang dan layak untuk dipelajari. Salah satunya adalah mengenai geometri hiperbolik yang merupakan dunia baru dalam geometri. Dengan berbagai bentuk model berbeda dalam merepresentasikan objek geometri pada geometri hiperbolik, akan menjadi menarik untuk mengetahui bentuk-bentuk poligon pada suatu model bidang hiperbolik. Area atau luas dari setiap bentuk poligon pada geometri hiperbolik juga merupakan hal yang menarik untuk diteliti. Selain itu, juga dapat melengkapi konsep pada luas hiperbolik jika disajikan dalam bidang hiperbolik. Oleh karena itu, peneliti ingin melakukan penelitian mengenai luas pada geometri hiperbolik menggunakan model setengah bidang atas.
B. Rumusan Masalah
1. Bagaimana objek-objek geometri hiperbolik direpresentasikan pada model setengah bidang atas ℍ?
2. Bagaimana konsep-konsep dasar seperti panjang, jarak, dan sudut hiperbolik yang disajikan pada model setengah bidang atas ℍ?
3. Bagaimana luas pada geometri hiperbolik dan luas hiperbolik untuk poligon hiperbolik yang disajikan pada model setengah bidang atas ℍ? C. Pembatasan Masalah
Penelitian ini dibatasi pada model setengah bidang atas ℍ dan hanya membahas mengenai objek-objek bidang datar untuk geometri hiperbolik.
D. Batasan Istilah
Berdasarkan latar belakang, untuk menghindari kesalahpahaman dalam memahami hasil penelitian ini, maka diperlukan batasan istilah sebagai berikut.
1. Aksioma adalah suatu pernyataan yang nilai kebenarannya mutlak sebagai suatu kejelasan ataupun asumsi.
2. Postulat adalah aksioma khusus pada bidang geometri.
3. Teorema adalah suatu pernyataan yang nilai kebenarannya masih perlu untuk dibuktikan.
4. Proposisi adalah suatu pernyataan yang diturunkan langsung dari suatu aksioma atau postulat dan nilai kebenarannya masih perlu untuk dibuktikan.
5. Geometri Euclides adalah ranah kajian matematika yang berkaitan dengan studi geometri berdasarkan definisi dan aksioma yang ditetapkan dalam buku Euclides “The Element”.
6. Geometri hiperbolik adalah ranah kajian matematika yang berkaitan dengan studi geometri berdasarkan definisi, postulat Euclides dan postulat kesejajaran hiperbolik.
7. Setengah bidang atas adalah bagian dari bidang kompleks yang memenuhi 𝑦 = 𝐼𝑚(𝑧) > 0.
8. Tititk ideal adalah titik di tak hingga yang terdapat pada sumbu real dalam setengah bidang atas.
9. Panjang hiperbolik adalah ukuran panjang yang digunakan untuk mengukur panjang suatu kurva pada setengah bidang atas ℍ.
10.Jarak hiperbolik adalah jarak antara dua titik pada setengah bidang atas
ℍ.
11.Sudut hiperbolik adalah ukuran sudut antara dua kurva pada setengah bidang atas ℍ.
12.Luas hiperbolik adalah luas suatu daerah pada setengah bidang atas ℍ.
13.Poligon hiperbolik adalah bangun segi banyak yang terdapat pada setengah bidang atas ℍ.
E. Tujuan Penelitian
Penelitian ini bertujuan untuk:
1. Mendeskripsikan objek-objek geometri hiperbolik yang direpresentasikan pada model setengah bidang atas ℍ.
2. Mendeskripsikan konsep-konsep dasar seperti panjang, jarak, dan sudut hiperbolik yang disajikan pada model setengah bidang atas ℍ.
3. Menentukan luas pada geometri hiperbolik dan luas hiperbolik untuk poligon hiperbolik yang disajikan pada model setengah bidang atas ℍ. F. Manfaat Penelitian
Manfaat yang dapat diperoleh dari penelitian ini adalah: 1. Bagi Pembaca
Pembaca dapat menambah pengetahuan tentang model bidang hiperbolik dan luas poligon hiperbolik pada geometri hiperbolik.
2. Bagi Penulis
Penulis dapat menambah pengetahuan tentang model bidang hiperbolik dan luas poligon hiperbolik pada geometri hiperbolik.
3. Bagi Universitas
Universitas dapat menambah koleksi skripsi dalam bidang geometri. G. Metode Penelitian
Metode penelitian yang digunakan dalam skripsi ini adalah metode studi pustaka, yaitu dengan membaca referensi-referensi mengenai geometri hiperbolik. Pembahasan dalam skripsi ini banyak mengacu pada buku Hyperbolic Geometry Second Edition, karangan James W. Anderson (2005) dan buku A Gateway to Modern Geometry: The Poincare Half-Plane, karangan Saul Stahl (1993).
Langkah-Langkah yang dilakukan dalam penelitian ini adalah
1. Membaca berbagai referensi mengenai topik geometri hiperbolik dan model bidang hiperbolik.
2. Menyajikan kembali definisi, proposisi, postulat, dan teorema yang menjadi dasar dalam merepresentasikan geometri hiperbolik ke dalam model bidang hiperbolik, khususnya model setengah bidang atas ℍ
dengan bahasan luas hiperbolik.
3. Menyusun seluruh materi yang telah dikumpulkan secara runtut agar memudahkan pembaca dalam memahaminya.
H. Sistematika Penulisan
Bab pertama berupa pendahuluan. Pendahuluan ini berisi tentang latar belakang, rumusan masalah, pembatasan masalah, batasan istilah, tujuan, manfaat, metode penelitian, dan sistematika penulisan.
Bab dua berisi tentang dasar-dasar yang akan digunakan dalam membahas model bidang hiperbolik dan luas hiperbolik seperti: dasar-dasar geometri Euclides, bidang kompleks ℂ, garis dan lingkaran dalam bidang kompleks ℂ, elemen panjang dalam bidang kompleks ℂ, sudut pada bidang kompleks ℂ, transformasi konformal, Riemann sphere, inversi, transformasi M𝑜̈bius, dan cross ratio.
Bab tiga membahas tentang model bidang hiperbolik, yaitu setengah bidang atas ℍ. Selanjutnya dibahas mengenai hubungan geometri Euclides dan geometri hiperbolik berdasarkan objek-objek dasarnya (titik, garis, dan sudut). Pada bab ini juga dibahas mengenai postulat kesejajaran dalam geometri hiperbolik, jarak hiperbolik, dan transformasi M𝑜̈bius pada setengah bidang atas ℍ.
Bab empat membahas tentang kekonvekan, segitiga hiperbolik dan poligon hiperbolik, definisi luas hiperbolik, serta luas poligon hiperbolik. Materi yang dibahas mengenai definisi, teorema, dan sifat-sifat terkait kekonvekan, poligon hiperbolik, dan luas hiperbolik di setengah bidang atas
ℍ, serta dilengkapi contoh soal untuk memperjelas materi yang dibahas. Bab lima membahas tentang kesimpulan terkait pembahasan pada bab sebelumnya dan saran kepada pembaca tentang keberlanjutan penelitian.
11
BAB II
LANDASAN TEORI
A. Dasar-Dasar Geometri Euclides
Pada skripsi ini akan mengacu pada beberapa teori yang terdapat pada geometri Euclides antara lain sebagai berikut.
1. Common Notions (Pengertian Umum)
Euclides mengasumsikan Common Notions (Pengertian Umum) sebagai dasar atau syarat tak tertulis dari berbagai objek geometris seperti panjang, luas, volume, dan ukuran sudut (Stahl, 1993: 8). Euclides menuangkan Common Notions pada buku pertama The Elements sebagai berikut.
a. Benda-benda (ukuran-ukuran) sama terhadap benda (ukuran) yang sama adalah sama antara yang satu terhadap yang lain.
b. Jika benda (ukuran-ukuran) sama, ditambah dengan benda-benda (ukuran-ukuran) sama, semuanya adalah sama.
c. Jika benda-benda (ukuran-ukuran) sama, dikurangi benda-benda (ukuran-ukuran) sama, semua sisanya adalah sama.
d. Benda-benda (ukuran-ukuran) yang serupa satu sama lain adalah sama antara yang satu terhadap yang lain.
2. Kekongruenan segitiga
Kekongruenan segitiga yang dikemukakan Euclides dalam buku pertama The Elements digunakan sebagai dasar acuan untuk menentukan kekongruenan segitiga hiperbolik. Syarat kekongruenan segitiga terbagi dalam beberapa Proposisi sebagai berikut.
Proposisi 2.1 (Stahl, 1993: 13)
Jika dua segitiga mempunyai dua sisi yang bersesuaian sama panjang, dan sudut yang diapit sisi tersebut sama besar, maka sisi bersesuaian yang tersisa sama panjang dan sudut-sudut lain yang lain bersesuaian sama besar sehingga dua segitiga tersebut sama.
Proposisi 2.1 lebih dikenal sebagai syarat kekongruenan segitiga yang mengacu pada sisi-sudut-sisi (SS, SD, SS).
Gambar 2.1 Ilustrasi Proposisi 2.1 Proposisi 2.2 (Stahl, 1993: 15)
Jika dua segitiga mempunyai tiga sisi yang bersesuaian sama panjang, sehingga sudut-sudut yang bersesuaian sama besar, maka segitiga tersebut sama.
Proposisi 2.2 lebih dikenal sebagai syarat kekongruenan segitiga yang mengacu pada sisi-sisi-sisi (SS, SS, SS).
Gambar 2.2 Ilustrasi Proposisi 2.2
Proposisi 2.3 (Stahl, 1993: 19)
Jika dua segitiga mempunyai dua sudut yang bersesuaian sama besar, dan sebuah sisi yang diapit dua sudut tersebut sama panjang, maka panjang sisi-sisi yang bersesuaiannya sama panjang, maka segitiga tersebut sama. Proposisi 2.3 lebih dikenal sebagai syarat kekongruenan segitiga yang mengacu pada sudut-sisi-sudut (SD, SS, SD).
Gambar 2.3 Ilustrasi Proposisi 2.3
Dasar teori yang diambil dari geometri Euclides akan digunakan untuk membuktikan proposisi-proposisi pada geometri hiperbolik dalam model bidang hiperbolik. Sebelum membahas model bidang untuk geometri
hiperbolik akan terlebih dahulu akan dibahas mengenai model bidang untuk geometri Euclides.
B. Bidang Kompleks ℂ
Brown dan Churchill (1990) menyatakan bilangan kompleks 𝑧
didefinisikan sebagai
𝑧 = 𝑥 + 𝑖𝑦 (2.1)
atau dapat pula didefinisikan sebagai pasangan bilangan real yaitu
𝑧 = (𝑥, 𝑦) (2.2)
dengan x dan y adalah bilangan real, dan 𝑖 adalah bilangan imajiner murni
(√−1). Pada persamaan (2.1) dan persamaan (2.2), x dan y berturut-turut disebut bagian real dan imajiner dari z, dan dapat dituliskan sebagai
𝑅𝑒(𝑧) = 𝑥, dan 𝐼𝑚(𝑧) = 𝑦.
Sifat aljabar pada bilangan kompleks sama dengan sifat aljabar pada bilangan real. Selanjutnya akan ditunjukkan beberapa sifat aljabar pada bilangan kompleks sebagai berikut (Brown dan Churchill, 1990: 2):
1. Sifat komutatif
Misalkan 𝑧1 = 𝑥1+ 𝑖𝑦1, 𝑧2 = 𝑥2+ 𝑖𝑦2
a. 𝑧1 + 𝑧2 = 𝑧2+ 𝑧1
b. 𝑧1𝑧2 = 𝑧2𝑧1
2. Sifat asosiatif
Misalkan 𝑧1 = 𝑥1+ 𝑖𝑦1, 𝑧2 = 𝑥2+ 𝑖𝑦2, dan 𝑧3 = 𝑥3+ 𝑖𝑦3, diperoleh a. (𝑧1+ 𝑧2) + 𝑧3 = 𝑧1+ (𝑧2+ 𝑧3)
b. (𝑧1𝑧2) 𝑧3 = 𝑧1(𝑧2𝑧3)
3. Sifat distributif
Misalkan 𝑧1 = 𝑥1+ 𝑖𝑦1, 𝑧2 = 𝑥2+ 𝑖𝑦2, dan 𝑧 = 𝑥 + 𝑖𝑦, maka
𝑧(𝑧1+ 𝑧2) = 𝑧𝑧1+ 𝑧𝑧2
4. Sifat identitas
Misalkan 𝑧 = 𝑥 + 𝑖𝑦, 0 ∈ ℝ merupakan unsur identitas pada penjumlahan, dan 1 ∈ ℝ adalah unsur identitas pada perkalian maka
a. 𝑧 + 0 = 𝑧
b. 𝑧. 1 = 𝑧
Pada bilangan kompleks terdapat beberapa konsep yang tidak terdapat pada bilangan real yaitu modulus dan konjugat kompleks (Brown, 1990: 7). Definisi modulus atau disebut sebagai nilai mutlak pada bilangan kompleks
𝑧 = 𝑥 + 𝑖𝑦 adalah bilangan real tak negatif √𝑥2+ 𝑦2 dengan notasi |𝑧|
sehingga
|𝑧| = √𝑥2+ 𝑦2 ; (2.3)
Sedangkan konjugat kompleks atau disebut konjugat dari bilangan kompleks
𝑧 = 𝑥 + 𝑖𝑦 adalah bilangan kompleks 𝑥 − 𝑖𝑦 dengan notasi 𝑧̅ sehingga
𝑧̅ = 𝑥 − 𝑖𝑦. (2.4)
Berdasarkan persamaan (2.3) dan persamaan (2.4) diperoleh bahwa |𝑧̅| = |𝑧|
dan 𝑧̿ = 𝑧 untuk setiap z. Jika 𝑧1 = 𝑥1 + 𝑖𝑦1 dan 𝑧2 = 𝑥2+ 𝑖𝑦2 maka
𝑧1+ 𝑧2
̅̅̅̅̅̅̅̅̅ = (𝑥̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = (𝑥1+ 𝑖𝑦1) + (𝑥2+ 𝑖𝑦2) ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅1+ 𝑥2) + 𝑖(𝑦1+ 𝑦2)
= (𝑥1− 𝑖𝑦1) + (𝑥2− 𝑖𝑦2) = 𝑧̅ + 𝑧1 ̅ 2
sehingga konjugat dari penjumlahan sama dengan jumlahan konjugat.
Dengan cara serupa dapat ditunjukkan bahwa untuk 𝑧1 = 𝑥1 + 𝑖𝑦1 dan 𝑧2 =
𝑥2+ 𝑖𝑦2 maka a. ̅̅̅̅̅̅̅̅̅ = (𝑥𝑧1− 𝑧2 ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = (𝑥1 + 𝑖𝑦1) + (𝑥2+ 𝑖𝑦2) ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅1− 𝑥2) + 𝑖(𝑦1− 𝑦2) = (𝑥1− 𝑥2) − 𝑖(𝑦1− 𝑦2) = (𝑥1− 𝑖𝑦1) − (𝑥2 − 𝑖𝑦2) = 𝑧̅ − 𝑧1 ̅2 b. 𝑧̅̅̅̅̅̅ = (𝑥1𝑧2 ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅1𝑥2− 𝑦1𝑦2) + 𝑖(𝑥1𝑦2+ 𝑥2𝑦1) = (𝑥1𝑥2− 𝑦1𝑦2) + 𝑖(𝑥1𝑦2+ 𝑥2𝑦1) = (𝑥1− 𝑖𝑦1)(𝑥2− 𝑖𝑦2) = 𝑧̅ 𝑧1̅2
c. Untuk 𝑧2 ≠ 0 maka dapat diperoleh
(𝑧1 𝑧2) ̅̅̅̅̅̅ = (𝑥1+ 𝑖𝑦1 𝑥2 + 𝑖𝑦2) ̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = ((𝑥1+ 𝑖𝑦1)(𝑥2− 𝑖𝑦2) (𝑥2+ 𝑖𝑦2)(𝑥2 − 𝑖𝑦2)) ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = ((𝑥1𝑥2+ 𝑦1𝑦2 + 𝑖(−𝑥1𝑦2 + 𝑥2𝑦1)) 𝑥22+ 𝑦22 ) ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = ((𝑥1𝑥2 + 𝑦1𝑦2− 𝑖(−𝑥1𝑦2+ 𝑥2𝑦1)) 𝑥22+ 𝑦 22 ) = (𝑥1− 𝑖𝑦1)(𝑥2+ 𝑖𝑦2) (𝑥2+ 𝑖𝑦2)(𝑥2− 𝑖𝑦2) = 𝑧̅1 𝑧̅2.
Salah satu relasi penting antara konjugat bilangan kompleks 𝑧 = 𝑥 + 𝑖𝑦
𝑧𝑧̅ = (𝑥 + 𝑖𝑦)(𝑥 − 𝑖𝑦) = 𝑥2− 𝑖2𝑦2 = 𝑥2+ 𝑦2 = |𝑧|2.
Selain itu juga terdapat sifat yang menarik dari dua bilangan kompleks dan konjugatnya. Misalkan 𝑧1 = 𝑥1+ 𝑖𝑦1 dan 𝑧2 = 𝑥2+ 𝑖𝑦2 diperoleh
𝑧1𝑧2+ 𝑧̅1𝑧̅2 = (𝑥1+ 𝑖𝑦1)(𝑥2+ 𝑖𝑦2) + (𝑥1 − 𝑖𝑦1)(𝑥2− 𝑖𝑦2) = 𝑥1𝑥2 + 𝑖𝑥1𝑦2+ 𝑖𝑦1𝑥2− 𝑦1𝑦2+ 𝑥1𝑥2− 𝑖𝑥1𝑦2− 𝑖𝑦1𝑥2+ 𝑦1𝑦2
= 2𝑥1𝑥2 = 2𝑅𝑒(𝑧1𝑧2) .
Jadi diperoleh
𝑧1𝑧2+ 𝑧̅1𝑧̅2 = 2𝑅𝑒(𝑧1𝑧2) (2.5)
Setiap bilangan kompleks berkorespondensi dengan satu titik pada bidang datar, seperti bilangan −2 + 𝑖 dapat direpresentasikan sebagai titik dengan koordinat (−2,1). Bilangan z juga dapat dianggap sebagai vektor dari titik asal (0,0) ke titik (𝑥, 𝑦) (Gambar 2.4).
Gambar 2.4 Representasi Bilangan Kompleks ke Titik pada Bidang Kompleks
Bidang yang digunakan digunakan untuk merepresentasikan bilangan kompleks tersebut disebut bidang xy, bidang z atau bidang kompleks. Himpunan semesta bilangan kompleks atau bidang kompleks dinotasikan dengan ℂ. Sumbu x disebut sumbu real dan sumbu y disebut sumbu imajiner (Brown dan Churchill, 1990: 6-7).
Gambar 2.5 Bilangan Kompleks z dalam Koordinat Polar
Letak titik (𝑥, 𝑦) dapat disajikan dalam koordinat polar (𝑟, 𝜃), sehingga untuk bilangan kompleks z dapat disajikan dalam bentuk polar. Misalkan r dan
𝜃 adalah koordinat polar yang dari titik (𝑥, 𝑦) yang berkorespondensi dengan bilangan kompleks 𝑧 = 𝑥 + 𝑖𝑦 (Gambar 2.5), diperoleh
𝑥 = 𝑟 cos 𝜃 dan 𝑦 = 𝑟 sin 𝜃
Sehingga z direpresentasikan dalam bentuk polar sebagai
𝑧 = 𝑟 (cos 𝜃 + 𝑖 sin 𝜃), (2.6)
dengan r tak negatif. Nilai 𝜃 disebut sebagai argumen dari z, dan ditulis sebagai
𝜃 = arg 𝑧 (Brown dan Churchill, 1990: 12). Selain dalam bentuk polar, bilangan kompleks z dapat dibentuk dalam bentuk eksponensial menggunakan formula Euler sebagai
𝑒𝑖𝜃 = cos 𝜃 + 𝑖 sin 𝜃.
Berdasarkan persamaan (2.6) maka z dapat direpresentasikan dalam bentuk eksponensial sebagai
𝑧 = 𝑟𝑒𝑖𝜃. (2.7)
Setelah membahas bilangan kompleks dan bidang kompleks ℂ, akan dilanjutkan dengan membahas persamaan garis dan lingkaran Euclides pada bidang datar disajikan dalam bidang kompleks ℂ.
C. Garis dan lingkaran Euclides dalam bidang kompleks ℂ
Purcell dan Varberg (1987) menyatakan bahwa persamaan garis Euclides dalam koordinat kartesius dapat dibentuk sebagai
𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0. (2.8)
Pada persamaan (2.8), x dan y dapat dinyatakan dalam z dan 𝑧̅. Diberikan 𝑧 = 𝑥 + 𝑖𝑦 dan 𝑧̅ = 𝑥 − 𝑖𝑦 diperoleh
𝑥 = 𝑅𝑒(𝑧) =1
2(𝑧 + 𝑧̅) (2.9) 𝑦 = 𝐼𝑚(𝑧) = −𝑖
2(𝑧 − 𝑧̅) (2.10)
Subsitusikan persamaan (2.9) dan (2.10) ke persamaan (2.8) diperoleh
𝑎 (1 2(𝑧 + 𝑧̅)) + 𝑏 (− 𝑖 2(𝑧 − 𝑧̅)) + 𝑐 = 0 1 2(𝑎 − 𝑖𝑏)𝑧 + 1 2(𝑎 + 𝑖𝑏)𝑧̅ + 𝑐 = 0 Misalkan 𝛽 =1 2(𝑎 − 𝑖𝑏) maka 𝛽𝑧 + 𝛽̅𝑧̅ + 𝑐 = 0
Sehingga persamaan garis Euclides dalam bidang kompleks adalah
𝛽𝑧 + 𝛽̅𝑧̅ + 𝑐 = 0 (2.11)
dengan 𝛽 ∈ ℂ dan 𝑐 ∈ ℝ (Anderson, 2005: 217).
Purcell dan Varberg (1987) menyatakan bahwa persamaan lingkaran Euclides dalam koordinat kartesius dengan jari-jari r dan pusat di (ℎ, 𝑘) dapat dibentuk sebagai
(𝑥 − ℎ)2+ (𝑦 − 𝑘)2 = 𝑟2. (2.12)
Pada persamaan (2.12), x dan y dapat dinyatakan dalam z dan 𝑧̅, serta (ℎ, 𝑘)
diwakili oleh suatu bilangan kompleks tertentu. Diberikan 𝑧0 = ℎ + 𝑖𝑘 adalah titik pusat lingkaran maka dapat dibentuk
𝑧 − 𝑧0 = (𝑥 + 𝑖𝑦) − (ℎ + 𝑖𝑘) = (𝑥 − ℎ) + 𝑖(𝑦 − 𝑘),
sehingga diperoleh
(𝑥 − ℎ)2+ (𝑦 − 𝑘)2 = |𝑧 − 𝑧
0|2 = 𝑟2,
dengan fakta bahwa |𝑧|2 = 𝑧𝑧̅ maka
|𝑧 − 𝑧0|2 = (𝑧 − 𝑧
0)(𝑧̅ − 𝑧̅ ) = 𝑧𝑧̅ − 𝑧0 0𝑧̅ − 𝑧̅ 𝑧 + |𝑧0 0|2= 𝑟2. (2.13)
Misalkan 𝛼 ∈ ℝ, 𝛽 = −𝛼𝑧̅0 dan 𝛾 = 𝛼(|𝑧|2− 𝑟2) persamaan (2.13) dapat dibentuk menjadi
𝛼𝑧𝑧̅ + 𝛽𝑧 + 𝛽̅𝑧̅ + 𝛾 = 0 (2.14)
dengan 𝛽 ∈ ℂ dan 𝛾 ∈ ℝ (Anderson, 2005: 217). D. Elemen Panjang dalam bidang kompleks ℂ
Pada bagian ini akan dibahas mengenai elemen panjang pada bidang kompleks ℂ, namun sebelumnya akan diberikan definisi mengenai busur pada
bidang kompleks ℂ. Himpunan titik 𝑧 = (𝑥, 𝑦) pada bidang kompleks ℂ
disebut sebagai busur jika
𝑥 = 𝑥(𝑡), dan 𝑦 = 𝑦(𝑡)
dengan 𝑡 pada interval [𝑎, 𝑏], serta 𝑥(𝑡) dan 𝑦(𝑡) adalah fungsi kontinu pada parameter real 𝑡, sehingga sebuah busur 𝐶1 pada bidang kompleks ℂ dapat disajikan dengan persamaan sebagai
𝑧(𝑡) = 𝑥(𝑡) + 𝑖𝑦(𝑡) (2.15)
(Brown, 1990: 89). Jika 𝑥′(𝑡) dan 𝑦′(𝑡) untuk persamaan (2.15) ada dan kontinu maka turunan dari persamaan (2.15) adalah sebagai berikut:
𝑧′(𝑡) = 𝑥′(𝑡) + 𝑖𝑦′(𝑡). (2.16)
Sebuah busur yang memenuhi syarat dari persamaan (2.15) dan persamaan (2.16) disebut busur deferensiabel (Brown, 1990: 90).
Setelah membahas mengenai busur deferensiabel pada bidang kompleks
ℂ, akan dilanjutkan untuk elemen panjang busur pada bidang kompleks ℂ.
Misalkan f adalah busur deferensiabel pada bidang kompleks ℂ dalam interval
[𝑎, 𝑏], berdasarkan persamaan (2.15) dan persamaan (2.16) diperoleh
𝑓(𝑡) = 𝑥(𝑡) + 𝑖𝑦(𝑡), dan 𝑓′(𝑡) = 𝑥′(𝑡) + 𝑖𝑦′(𝑡). Modulus untuk 𝑓′(𝑡) adalah
|𝑓′(𝑡)| = √(𝑥′(𝑡))2+ (𝑦′(𝑡))2, sehingga panjang Euclides f adalah
𝑙𝑒𝑛𝑔𝑡ℎ(𝑓) = ∫ √(𝑥′(𝑡))2+ (𝑦′(𝑡))2 𝑑𝑡 𝑏 𝑎 = ∫ |𝑓′(𝑡)| 𝑏 𝑎 𝑑𝑡
atau biasanya dinotasikan sebagai
𝑙𝑒𝑛𝑔𝑡ℎ(𝑓) = ∫ |𝑓′(𝑡)|
𝑏 𝑎
𝑑𝑡 = ∫ |𝑑𝑧|
dengan |𝑑𝑧| = |𝑓′(𝑡)|𝑑𝑡 adalah elemen panjang-busur pada ℂ (Anderson,
2005: 74).
E. Sudut pada Bidang Kompleks ℂ
Sudut antar kurva 𝐶1 dan 𝐶2 pada bidang kompleks ℂ yang berpotongan
di 𝑧0 diperoleh dari sudut antara garis singgung kurva 𝐶1 dan 𝐶2 di 𝑧0 . Definisi untuk sudut antar kurva di bidang kompleks ℂ didefinisikan sebagai berikut. Definisi 2.4 (Anderson, 2005: 53)
Diberikan dua kurva smooth 𝐶1 dan 𝐶2 di ℂ yang berpotongan di 𝑧0,
didefinisikan ∠(𝐶1, 𝐶2) sudut antara 𝐶1 dan 𝐶2 di 𝑧0 adalah sudut antara garis
singgung 𝐶1 dan 𝐶2 di 𝑧0, besar sudut diukur dari 𝐶1 ke 𝐶2 (Gambar 2.6).
Gambar 2.6 Ilustrasi Definisi 2.4
Pengukuran sudut yaitu dengan berlawanan arah jarum jam untuk sudut positif dan searah jarum jam untuk sudut negatif. Berdasarkan definisi diperoleh bahwa
Berdasarkan definisi 2.4 maka dapat dicari besar sudut antar dua kurva menggunakan garis singgung pada titik perpotongan. Besar sudut antara dua garis singgung dapat dicari menggunakan selisih antara arctan dari tiap kemiringan garisnya.
Misalkan 𝑋1 dan 𝑋2 adalah dua garis Euclides di ℂ yang berpotongan di sebuah titik 𝑧0, misalkan 𝑧𝑘 adalah titik di 𝑋𝑘 dan bukan 𝑧0, dan misalkan kemiringan
garis (gradien) 𝑋𝑘 adalah 𝑠𝑘. Gradien garis 𝑋𝑘 dapat diperoleh dari
𝑠𝑘=
𝐼𝑚(𝑧𝑘− 𝑧0) 𝑅𝑒(𝑧𝑘− 𝑧0)
Misalkan 𝜃𝑘 adalah sudut yang terbentuk antara garis 𝑋𝑘 dan sumbu real, maka
diperoleh
𝑠𝑘= tan(𝜃𝑘)
Secara khusus besar sudut yang terbentuk antara 𝑋1 dan 𝑋2 adalah
𝑎𝑛𝑔𝑙𝑒(𝑋1, 𝑋2) = arctan(𝑠2) − arctan(𝑠1) = 𝜃2− 𝜃1
Berikut akan diberikan proposisi mengenai sudut antar busur lingkaran berpusat di sumbu real pada bidang kompleks ℂ :
Proposisi 2.5 (Stahl, 1993: 95)
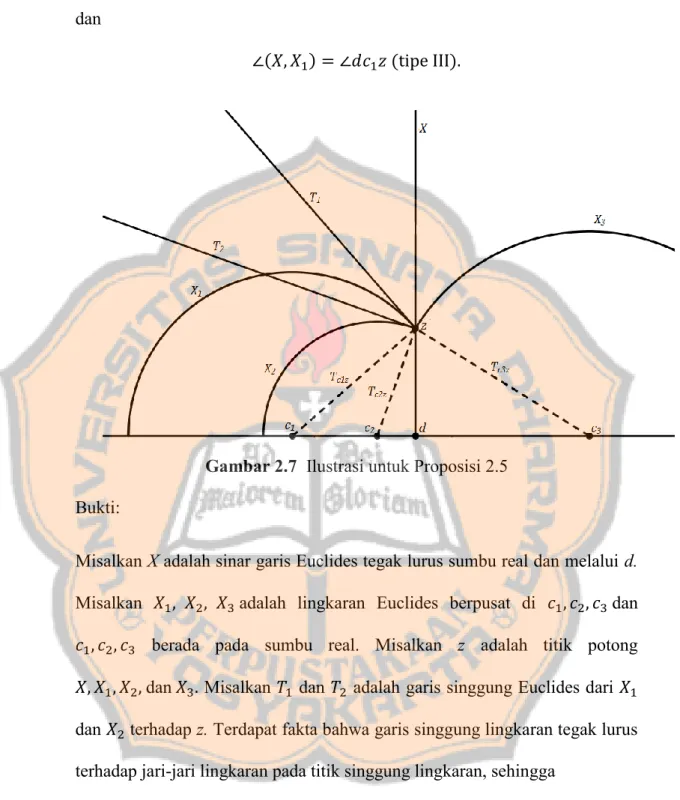
Diberikan sembarang titik z, misalkan X adalah sinar garis Euclides dan misalkan 𝑋1, 𝑋2, 𝑋3 adalah lingkaran Euclides yang berpusat di 𝑐1, 𝑐2, 𝑐3
(Gambar 2.7), maka
∠(𝑋1, 𝑋2) = ∠(𝑇𝑐1𝑧, 𝑇𝑐2𝑧) (tipe I), ∠(𝑋3, 𝑋1) = 𝜋 − ∠(𝑇𝑐1𝑧, 𝑇𝑐3𝑧) (tipe II),
dan
∠(𝑋, 𝑋1) = ∠𝑑𝑐1𝑧 (tipe III).
Gambar 2.7 Ilustrasi untuk Proposisi 2.5 Bukti:
Misalkan X adalah sinar garis Euclides tegak lurus sumbu real dan melalui d. Misalkan 𝑋1, 𝑋2, 𝑋3adalah lingkaran Euclides berpusat di 𝑐1, 𝑐2, 𝑐3dan
𝑐1, 𝑐2, 𝑐3 berada pada sumbu real. Misalkan z adalah titik potong
𝑋, 𝑋1, 𝑋2, dan 𝑋3. Misalkan 𝑇1 dan 𝑇2 adalah garis singgung Euclides dari 𝑋1
dan 𝑋2 terhadap z. Terdapat fakta bahwa garis singgung lingkaran tegak lurus
terhadap jari-jari lingkaran pada titik singgung lingkaran, sehingga
∠(𝑋1, 𝑋2) = ∠(𝑇1, 𝑇2) = ∠(𝑇1, 𝑇𝑐1𝑧) − ∠(𝑇2, 𝑇𝑐2𝑧) =𝜋
2− ∠(𝑇2, 𝑇𝑐1𝑧) = ∠(𝑇2, 𝑇𝑐2𝑧) − ∠(𝑇2, 𝑇𝑐1𝑧) = ∠(𝑇𝑐1𝑧, 𝑇𝑐2𝑧)
∠(𝑋, 𝑋1) = ∠(𝑋, 𝑇1) = 𝜋 − ∠(𝑇1, 𝑇𝑐1𝑧) − ∠(𝑇𝑐1𝑧, 𝑋) = 𝜋
2− ∠(𝑇𝑐1𝑧, 𝑋) = ∠𝑑𝑐1𝑧
dan
∠(𝑋3, 𝑋1) = ∠(𝑋3, 𝑋) + ∠(𝑋, 𝑋1) = ∠𝑧𝑐3𝑑 + ∠𝑑𝑐1𝑧 = 𝜋 − ∠(𝑇2, 𝑇𝑐1𝑧).
Terbukti untuk Proposisi 2.5. QED.
Berikut akan diberikan cara untuk menghitung besar sudut menurut Proposisi 2.5 :
a. Tipe I
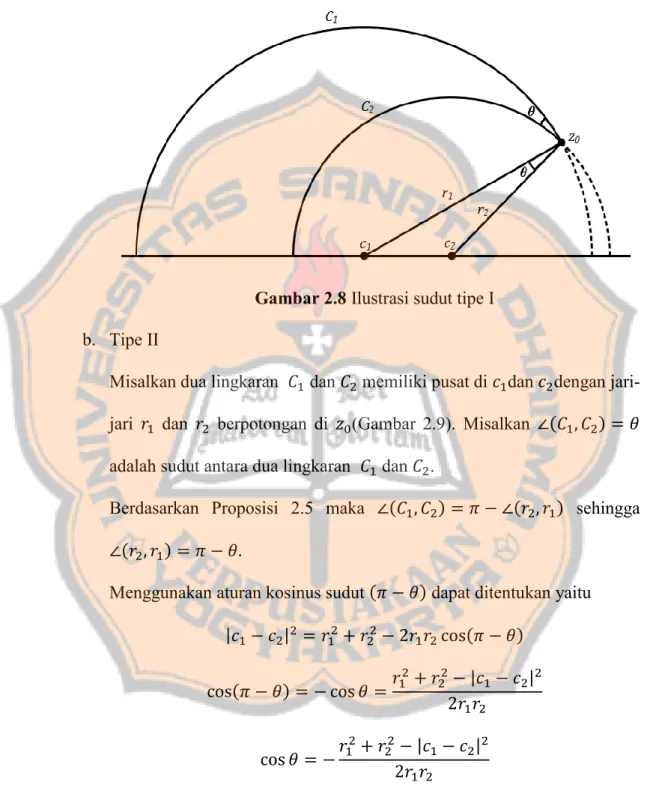
Misalkan dua lingkaran 𝐶1 dan 𝐶2 memiliki pusat di 𝑐1dan 𝑐2dengan
jari-jari 𝑟1 dan 𝑟2 berpotongan di 𝑧0(Gambar 2.8). Misalkan ∠(𝐶1, 𝐶2) = 𝜃
adalah sudut antara dua lingkaran 𝐶1 dan 𝐶2.
Berdasarkan Proposisi 2.5 maka ∠(𝐶1, 𝐶2) = ∠(𝑟2, 𝑟1) sehingga
∠(𝑟2, 𝑟1) = 𝜃.
Menggunakan aturan kosinus sudut 𝜃 dapat ditentukan yaitu
|𝑐1− 𝑐2|2 = 𝑟12+ 𝑟22− 2𝑟1𝑟2cos 𝜃
cos 𝜃 = 𝑟1
2+ 𝑟
22− |𝑐1− 𝑐2|2
sehingga sudut 𝜃 dapat ditentukan dari arccos 𝜃.
Gambar 2.8 Ilustrasi sudut tipe I b. Tipe II
Misalkan dua lingkaran 𝐶1 dan 𝐶2 memiliki pusat di 𝑐1dan 𝑐2dengan jari-jari 𝑟1 dan 𝑟2 berpotongan di 𝑧0(Gambar 2.9). Misalkan ∠(𝐶1, 𝐶2) = 𝜃
adalah sudut antara dua lingkaran 𝐶1 dan 𝐶2.
Berdasarkan Proposisi 2.5 maka ∠(𝐶1, 𝐶2) = 𝜋 − ∠(𝑟2, 𝑟1) sehingga
∠(𝑟2, 𝑟1) = 𝜋 − 𝜃.
Menggunakan aturan kosinus sudut (𝜋 − 𝜃) dapat ditentukan yaitu
|𝑐1− 𝑐2|2 = 𝑟 12+ 𝑟22− 2𝑟1𝑟2cos(𝜋 − 𝜃) cos(𝜋 − 𝜃) = − cos 𝜃 =𝑟1 2+ 𝑟 22− |𝑐1− 𝑐2|2 2𝑟1𝑟2 cos 𝜃 = −𝑟1 2+ 𝑟 22− |𝑐1− 𝑐2|2 2𝑟1𝑟2
sehingga sudut 𝜃 dapat ditentukan dari arccos 𝜃.
Gambar 2.9 Ilustrasi Tipe II c. Tipe III
Misalkan garis 𝑋1 adalah garis yang melalui di 𝑐1 dan tegak lurus X. Misalkan lingkaran 𝐶1 memiliki pusat di 𝑐1 dengan jari-jari 𝑟1, dan garis
𝑋1 tegak lurus garis X berpotongan di 𝑑1. Lingkaran 𝐶1 berpotongan
dengan garis X di 𝑧0 (Gambar 2.10).
Misalkan ∠(𝐶1, 𝑋) adalah sudut antara lingkaran 𝐶1 dan garis X dengan besar sudut 𝜃. Berdasarkan Proposisi 2.5 maka ∠(𝐶1, 𝑋) = ∠𝑧0𝑐1𝑑1
sehingga ∠𝑧0𝑐1𝑑1memiliki besar sudut 𝜃. Karena titik 𝑐1, 𝑑1, dan 𝑧0
membentuk segitiga siku-siku di 𝑑1, sehingga sudut 𝜃 dapat diperoleh dari
cos 𝜃 = 𝑟1 |𝑑1 − 𝑐1|
sehingga sudut 𝜃 dapat ditentukan dari arccos 𝜃.
Gambar 2.10 Ilustrasi Tipe III
F. Transformasi Konformal pada Bidang Kompleks ℂ
Terdapat beberapa transformasi dalam bidang kompleks ℂ yang memiliki sifat konformal yaitu transformasi yang mempertahankan sudut. Transformasi affine adalah salah satu transformasi konformal. Transformasi ini adalah komposisi dari beberapa transformasi sederhana seperti dilatasi, rotasi, dan translasi dalam bidang kompleks ℂ (Olsen, 2010: 2). Dilatasi, rotasi, dan translasi sederhana dalam bidang kompleks ℂ didefinisikan sebagai berikut.
i. Dilatasi : 𝑓(𝑧) = 𝑐𝑧, dengan 𝑐 ∈ ℝ
ii. Translasi : 𝑓(𝑧) = 𝑧 + 𝛽, dengan 𝛽 ∈ ℂ
iii. Rotasi : 𝑓(𝑧) = 𝛼𝑧, dengan 𝛼 = 𝑒𝑖𝜃.
Olsen (2010) menyatakan transformasi affine didefinisikan sebagai berikut.
Definisi 2.6 (Olsen, 2010: 2)
Transformasi affine adalah kombinasi dari (i), (ii), dan (iii) dengan pemetaan
𝑇(𝑧) = 𝛼𝑧 + 𝛽 dengan 𝛼, 𝛽 ∈ ℂ dan 𝛼 ≠ 0.
Sifat-sifat dalam transformasi affine seperti mempertahankan garis dan lingkaran Euclides, serta sudut, ditunjukkan oleh beberapa teorema berikut. Teorema 2.7 (Olsen, 2010: 3)
Transformasi affine mempertahankan lingkaran dan garis Euclides. Bukti:
Misalkan diberikan suatu transformasi affine 𝑇(𝑧) = 𝐴𝑧 + 𝐵 dan persamaan garis Euclides 𝛽𝑧 + 𝛽̅𝑧̅ + 𝑐 = 0 dengan 𝐴, 𝐵, 𝛽 ∈ ℂ dan 𝑐 ∈ ℝ. Menggunakan cara substitusi diperoleh
𝛽(𝐴𝑧 + 𝐵) + 𝛽̅(𝐴𝑧 + 𝐵)̅̅̅̅̅̅̅̅̅̅̅̅ + 𝑐 = 0 𝛽𝐴𝑧 + 𝛽𝐵 + 𝛽𝐴̅̅̅̅𝑧̅ + 𝛽̅𝐵̅ + 𝑐 = 0
𝛽𝐴𝑧 + 𝛽𝐴̅̅̅̅𝑧̅ + (𝛽𝐵 + 𝛽̅𝐵̅) + 𝑐 = 0 (2.17)
Kita tahu bahwa 𝛽𝐵 + 𝛽̅𝐵̅ = 2𝑅𝑒(𝛽𝐵) sehingga persamaan (2.17) merupakan persamaan garis.
Dengan transformasi yang sama dan misalkan diberikan persamaan lingkaran Euclides 𝛼𝑧𝑧̅ + 𝛽𝑧 + 𝛽̅𝑧̅ + 𝛾 = 0 dengan 𝛼, 𝛾 ∈ ℝ. Menggunakan cara yang sama diperoleh
𝛼(𝐴𝑧 + 𝐵)(𝐴𝑧 + 𝐵)̅̅̅̅̅̅̅̅̅̅̅̅ + 𝛽(𝐴𝑧 + 𝐵) + 𝛽̅(𝐴𝑧 + 𝐵)̅̅̅̅̅̅̅̅̅̅̅̅ + 𝛾 = 0 𝛼𝐴𝐴̅𝑧𝑧̅ + (𝐴𝐵̅ + 𝛽𝐴)𝑧 + (𝐴̅𝐵 + 𝛽𝐴̅̅̅̅)𝑧̅ + 𝛽𝐵 + 𝛽̅𝐵̅ + 𝛾 = 0
misalkan 𝐷 = 𝐴𝐵̅ + 𝛽𝐴 maka diperoleh
Persamaan (2.18) merupakan persamaan lingkaran. Jadi Teorema 2.7 terbukti. QED.
Teorema 2.8 (Olsen, 2010: 4)
Transformasi affine adalah konformal. Bukti:
Misalkan 𝑋1 dan 𝑋2 adalah dua garis Euclides di ℂ yang berpotongan di sebuah titik 𝑧0. Misalkan 𝑇(𝑧) = 𝛼𝑧 + 𝑏 dengan 𝛼, 𝑏 ∈ ℂ, 𝛼 ≠ 0, dan 𝛼 = 𝜌𝑒𝑖𝛽.
Misalkan ∠(𝑋1, 𝑋2) = 𝜃2− 𝜃1 dengan 𝜃1 dan 𝜃2 adalah sudut kemiringan
garis 𝑋1 dan 𝑋2.
Berdasarkan Teorema 2.6 maka 𝑇(𝑋1) dan 𝑇(𝑋2) adalah garis Euclides juga. Karena 𝑇(𝑋𝑘) melalui 𝑇(𝑧0) dan 𝑇(𝑧𝑘) sehingga kemiringan 𝑡𝑘 dari garis
𝑇(𝑋𝑘) adalah 𝑡𝑘 =𝐼𝑚(𝑇(𝑧𝑘) − 𝑇(𝑧0)) 𝑅𝑒(𝑇(𝑧𝑘) − 𝑇(𝑧0)) = 𝐼𝑚(𝛼(𝑧𝑘− 𝑧0)) 𝑅𝑒(𝛼 (𝑧𝑘− 𝑧0)) = 𝐼𝑚 (𝑒 𝑖𝛽(𝑧 𝑘− 𝑧0)) 𝑅𝑒 (𝑒𝑖𝛽(𝑧 𝑘− 𝑧0)) = tan(𝛽 + 𝜃𝑘),
secara khusus diperoleh bahwa
∠(𝑇(𝑋1), 𝑇(𝑋2)) = arctan(𝑡2) − arctan(𝑡1) = (𝛽 + 𝜃2) − (𝛽 + 𝜃1)
= 𝜃2− 𝜃1 = ∠(𝑋1, 𝑋2).
G. Riemann Sphere ℂ̅
Bidang lengkung atau permukaan lengkung sukar bila disajikan ke dalam bidang datar, misalkan permukaan bola atau permukaan hiperbolik. Salah satu cara untuk memproyeksikan permukaan bola adalah dengan menggunakan proyeksi stereografi. Proyeksi tersebut memungkinkan untuk memetakan permukaan bola ke dalam suatu bidang datar (Olsen, 2010: 7). Misalkan diberikan bola satuan 𝕊2 di ℝ3dengan 𝕊2 = {(𝑢, 𝑣, 𝑤) ∈ ℝ3|𝑢2+
𝑣2+ 𝑤2 = 1} berpusat di 𝑂(0,0,0), 𝑁 adalah kutub utara dengan koordinat
di (0,0,1), dan bidang kompleks ℂ adalah bidang yang terbentuk saat 𝑤 = 0.
Untuk setiap titik 𝑃 ∈ 𝕊2, terdapat tepat satu segmen garis yang menghubungkan N ke P. Garis tersebut menembus bidang kompleks ℂ tepat di satu titik z (Gambar 2.11). Titik P yang merupakan titik tembus segmen garis terhadap bola satuan disebut proyeksi stereografi dari titik z. Oleh karena itu, proyeksi stereografi dari titik di tak hingga {∞} bersesuaian dengan kutub utara N dari bola. Dengan demikian bidang kompleks ℂ ditambahkan dengan titik ditak hingga {∞} “sebenarnya” merupakan bola dan disebut sebagai Reimaan sphere (Krantz, 1999: 83).
Reimaan sphere atau disebut juga sebagai bidang kompleks yang diperluas, didefinisikan sebagai himpunan
dengan kata lain adalah bidang kompleks yang ditambahkan sebuah titik yang tak terdapat di ℂ yang dinotasikan dengan ∞. (Anderson, 2005: 9).
Gambar 2.11 Proyeksi Stereografi
Lingkaran pada 𝕊2 yang melalui 𝑁 diproyeksikan menjadi garis Euclides
pada bidang kompleks ℂ dan sebuah titik di tak hingga ∞, sedangkan untuk lingkaran yang tidak melalui 𝑁 diproyeksikan menjadi lingkaran Euclides pada bidang ℂ. Pada Riemann sphere lingkaran didefinisikan sebagai berikut. Definisi 2.9 (Anderson, 2005: 12)
Lingkaran pada ℂ̅ adalah lingkaran Euclides di ℂ atau gabungan garis Euclides di ℂ dengan {∞}.
Setelah didefinisikannya Riemann sphere ℂ̅ dan lingkaran di dalamnya, akan diberikan suatu transformasi yang terdapat pada Riemann sphere ℂ̅.
H. Inversi
Inversi adalah salah satu transformasi dalam bidang kompleks ℂ dan merupakan transformasi pula dalam bidang kompleks ℂ̅ yang didefinisikan sebagai berikut.
Definisi 2.10 (Anderson, 2005: 26)
Inversi didefinisikan sebagai fungsi 𝐽 ∶ ℂ̅ → ℂ̅ dengan syarat
𝐽(𝑧) =1
𝑧, 𝐽(0) = ∞, 𝐽(∞) = 0
untuk 𝑧 ∈ ℂ − {0}.
Beberapa sifat tentang inversi disajikan dalam teorema berikut: Teorema 2.11 (Olsen, 2010:9)
Inversi mempertahankan lingkaran di ℂ̅. Bukti:
Berdasarkan definisi 2.9, lingkaran di ℂ̅ dapat disajikan sebagai
𝐿̅ = {𝛽𝑧 + 𝛽̅𝑧̅ + 𝑐 = 0} ∪ {∞}
atau
𝐴 = {𝛼𝑧𝑧̅ + 𝛽𝑧 + 𝛽̅𝑧̅ + 𝛾 = 0}
dengan 𝛼, 𝑐, 𝛾 ∈ ℝ dan 𝛽 ∈ ℂ.
Misalkan suatu inversi 𝐽 ∶ ℂ̅ → ℂ̅ dengan 𝐽(𝑧) =1
𝑧, 𝐽(0) = ∞, 𝐽(∞) = 0
a. Kasus pertama untuk garis Eulides di ℂ dengan {∞} serta melewati 𝑧 = 0, diperoleh 𝐿̅ = {𝛽𝑧 + 𝛽̅𝑧̅ = 0} ∪ {∞}. Inversi 𝐽(𝐿̅) menjadi 𝛽1 𝑧+ 𝛽̅ 1 𝑧̅= 0 𝛽𝑧̅ + 𝛽̅𝑧 = 0 serta 𝐽(0) = ∞, 𝐽(∞) = 0 sehingga
𝐽(𝐿̅) = {𝛽𝑧̅ + 𝛽̅𝑧 = 0} ∪ {0} ∪ {∞}
Akibatnya 𝐽(𝐿̅) adalah garis Euclides di ℂ dengan {∞}, sehingga 𝐽(𝐿̅)
lingkaran di ℂ̅.
b. Kasus kedua untuk garis Eulides di ℂ dengan {∞} serta melewati 𝑧 ≠ 0, diperoleh 𝐿̅ = {𝛽𝑧 + 𝛽̅𝑧̅ + 𝑐 = 0} ∪ {∞}. Inversi 𝐽(𝐿̅) menjadi 𝛽1 𝑧+ 𝛽̅ 1 𝑧̅+ 𝑐 = 0 𝛽𝑧̅ + 𝛽̅𝑧 + 𝑐𝑧𝑧̅ = 0
Persamaan tersebut akan menjadi persamaan lingkaran Eucllides di ℂ jika digabung dengan {0}. Karena 𝐽(∞) = 0 sehingga
𝐽(𝐿̅) = {𝛽𝑧̅ + 𝛽̅𝑧 + 𝑐𝑧𝑧̅ = 0} ∪ {0}
Akibatnya 𝐽(𝐿̅) adalah lingkaran Euclides di ℂ sehingga 𝐽(𝐿̅) lingkaran di
ℂ̅.
c. Kasus ketiga untuk lingkaran Euclides di ℂ serta melewati 𝑧 = 0, diperoleh 𝐴 = {𝛼𝑧𝑧̅ + 𝛽𝑧 + 𝛽̅𝑧̅ = 0}. Inversi 𝐽(𝐴) menjadi 𝛼1 𝑧 1 𝑧̅ + 𝛽 1 𝑧+ 𝛽̅ 1 𝑧̅ = 0 𝛼 + 𝛽𝑧̅ + +𝛽̅𝑧 = 0
Karena 𝛼 ∈ ℝ serta 𝐽(0) = ∞ sehingga
Akibatnya 𝐽(𝐴) adalah garis Euclides di ℂ dengan {∞}, sehingga 𝐽(𝐴)
lingkaran di ℂ̅.
d. Kasus empat untuk lingkaran Euclides di ℂ dengan 𝑧 ≠ 0, diperoleh
𝐴 = {𝛼𝑧𝑧̅ + 𝛽𝑧 + 𝛽̅𝑧̅ = 0} Inversi 𝐽(𝐴) menjadi 𝛼1 𝑧 1 𝑧̅ + 𝛽 1 𝑧+ 𝛽̅ 1 𝑧̅+ 𝛾 = 0 𝛼 + 𝛽𝑧̅ + +𝛽̅𝑧 + 𝛾𝑧𝑧̅ = 0 Karena 𝛼, 𝛾 ∈ ℝ sehingga 𝐽(𝐴) = {𝛾𝑧𝑧̅ + 𝛽𝑧̅ + 𝛽̅𝑧 + 𝛼 = 0}.
Akibatnya 𝐽(𝐴) adalah lingkaran Euclides di ℂ, sehingga 𝐽(𝐴) lingkaran di ℂ̅.
Berdasarkan kasus pertama sampai empat maka Teorema 2.11 terbukti. QED. Inversi merupakan transformasi konformal atau mempertahankan besar sudut. Hal tersebut termuat dalam teorema berikut:
Teorema 2.12 (Olsen, 2010: 4) Inversi adalah konformal. Bukti:
Berdasarkan definisi 2.9, lingkaran di ℂ̅ dapat disajikan sebagai
𝐿̅ = {𝛽𝑧 + 𝛽̅𝑧̅ + 𝑐 = 0} ∪ {∞}
atau
𝐴 = {𝛼𝑧𝑧̅ + 𝛽𝑧 + 𝛽̅𝑧̅ + 𝛾 = 0}
Misalkan suatu inversi 𝐽 ∶ ℂ̅ → ℂ̅ dengan 𝐽(𝑧) =1
𝑧, 𝐽(0) = ∞, 𝐽(∞) = 0
Akan ditunjukkan bahwa lingkaran yang berpotongan dalam ℂ̅ akan tetap berpotongan bila diinversikan.
a. Dua garis Euclides di ℂ berpotongan di 𝑧0 = 0.
Berdasarkan pembuktian Teorema 2.7, J memetakan garis Euclides yang melalui titik 𝑧0 menjadi garis Euclides yang melalui titik 𝑧0 juga, sehingga kedua garis tetap berpotongan.
b. Dua garis Euclides di ℂ berpotongan di 𝑧0 = 𝑎, 𝑎 ≠ 0.
Berdasarkan pembuktian Teorema 2.7, J memetakan garis Euclides yang melalui titik 𝑧0 menjadi lingkaran Euclides yang melalui titik 𝐽(𝑧0) =
1 𝑎
, sehingga kedua garis tetap berpotongan.
c. Garis Euclides dan lingkaran Euclides di ℂ berpotongan di 𝑧0 = 0 dan
𝑧1 = 𝑎, 𝑎 ≠ 0.
Berdasarkan pembuktian Teorema 2.7, J memetakan garis Euclides yang melalui titik 𝑧0 menjadi garis Euclides yang melalui titik 𝑧0 juga, dan memetakan lingkaran Euclides yang melalui titik 𝑧0 menjadi garis Euclides. kedua garis tersebut berpotongan di 𝐽(𝑧1) =
1
𝑎 sehingga kedua
garis tetap berpotongan.
d. Garis Euclides dan lingkaran Euclides di ℂ berpotongan di 𝑧0 = 𝑎 dan
𝑧1 = 𝑏, 𝑎, 𝑏 ≠ 0, 𝑎 ≠ 𝑏.
Menggunakan alasan yang sama kedua garis tetap berpotongan di
e. Dua lingkaran Euclides di ℂ berpotongan di 𝑧0 = 0 dan 𝑧1 = 𝑎, 𝑎 ≠ 0. Menggunakan alasan yang sama kedua garis tetap berpotongan di
𝐽(𝑧1) = 1 𝑎
f. Dua lingkaran Euclides di ℂ berpotongan di 𝑧0 = 𝑎 dan 𝑧1 = 𝑏, 𝑎, 𝑏 ≠ 0, 𝑎 ≠ 𝑏.
Menggunakan alasan yang sama kedua garis tetap berpotongan di
𝐽(𝑧1) = 1
𝑎 .
Berdasarkan Definisi 2.9 dan fakta yang telah ditunjukkan sebelumnya, maka hanya akan ditunjukkan bahwa inversi mempertahankan sudut antar dua garis berpotongan.
Misalkan 𝑋1 dan 𝑋2 adalah dua garis Euclides di ℂ yang berpotongan di sebuah titik 𝑧0. Misalkan 𝐽(𝑧) =1
𝑧. Misalkan ∠(𝑋1, 𝑋2) = 𝜃2 − 𝜃1 dengan 𝜃1 dan 𝜃2
adalah sudut kemiringan garis 𝑋1 dan 𝑋2.
Misalkan 𝑧𝑘 = 𝑟1(cos 𝛼 + 𝑖 sin 𝛼) dan 𝑧0 = 𝑟2(cos 𝛽 + 𝑖 sin 𝛽) diperoleh
𝑧𝑘− 𝑧0 = 𝑟1(cos 𝛼 + 𝑖 sin 𝛼) − 𝑟2(cos 𝛽 + 𝑖 sin 𝛽)
= (𝑟1cos 𝛼 − 𝑟2cos 𝛽) + 𝑖(𝑟1sin 𝛼 − 𝑟2sin 𝛽).
Untuk 1
𝑧𝑘= 𝑟1(cos 𝛼 − 𝑖 sin 𝛼) dan
1
𝑧0 = 𝑟2(cos 𝛽 − 𝑖 sin 𝛽) 1
𝑧𝑘 − 1
𝑧0 = 𝑟1(cos 𝛼 − 𝑖 sin 𝛼) − 𝑟2(cos 𝛽 − 𝑖 sin 𝛽) = (𝑟1cos 𝛼 − 𝑟2cos 𝛽) − 𝑖(𝑟1sin 𝛼 − 𝑟2sin 𝛽)
𝑠𝑘 = 𝐼𝑚(𝑧𝑘− 𝑧0) 𝑅𝑒(𝑧𝑘− 𝑧0) = 𝑟1sin 𝛼 − 𝑟2sin 𝛽 𝑟1cos 𝛼 − 𝑟2cos 𝛽 = tan(𝜃𝑘).
Berdasarkan Teorema 2.5, maka 𝐽(𝑋1) dan 𝐽(𝑋2) adalah garis Euclides atau lingkaran Euclides. Karena 𝐽(𝑋𝑘) tetap melalui 𝐽(𝑧0) dan 𝐽(𝑧𝑘) maka
kemiringan 𝑡𝑘 dari garis 𝐽(𝑋𝑘) adalah
𝑡𝑘 = 𝐼𝑚(𝐽(𝑧𝑘) − 𝐽(𝑧0)) 𝑅𝑒(𝐽(𝑧𝑘) − 𝐽(𝑧0)) = 𝐼𝑚 (𝑧1 𝑘− 1 𝑧0 ) 𝑅𝑒 (𝑧1 𝑘− 1 𝑧0 ) = − 𝐼𝑚(𝑟1sin 𝛼 − 𝑟2sin 𝛽) 𝑅𝑒 (𝑟1cos 𝛼 − 𝑟2cos 𝛽) = − tan(𝜃𝑘) = tan(−𝜃𝑘).
Secara khusus diperoleh bahwa
∠(𝑇(𝑋1), 𝑇(𝑋2)) = arctan(𝑡2) − arctan(𝑡1) = −𝜃2+ 𝜃1 = −(𝜃2 − 𝜃1)
= −∠(𝑋1, 𝑋2) = ∠(𝑋1, 𝑋2)
Teorema 2.12 terbukti. QED.
Bersama dengan transformasi affine, inversi merupakan komposisi dari transformasi M𝑜̈bius pada Riemann sphere ℂ̅.
I. Transformasi M𝒐̈bius dan Cross Rasio
Transformasi M𝑜̈bius adalah suatu transformasi yang juga disebut linear fractional transformations atau transformasi bilinear. Transformasi ini definisikan sebagai suatu fungsi pada Riemann sphere ℂ̅. Definisi transformasi M𝑜̈bius di ℂ̅ adalah sebagai berikut.
Definisi 2.13 (Olsen, 2010: 11)
Transformasi M𝑜̈bius adalah pemetaan 𝑓: ℂ̅ → ℂ̅ yaitu
𝑓(𝑧) =𝑎𝑧 + 𝑏 𝑐𝑧 + 𝑑
dengan 𝑎, 𝑏, 𝑐, 𝑑 ∈ ℂ dan 𝑎𝑑 − 𝑏𝑐 ≠ 0.
Sifat-sifat transformasi M𝑜̈bius disajikan dalam teorema berikut. Teorema 2.14 (Olsen, 2010: 11)
Misalkan f sembarang transformasi M𝑜̈bius, maka
i. 𝑓 dapat diubah dalam komposisi transformasi affine dan inversi ii. 𝑓 memetakan lingkaran di ℂ̅ ke lingkaran di ℂ̅
iii. 𝑓 konformal. Bukti:
i. Diberikan f sebagai
𝑓(𝑧) =𝑎𝑧 + 𝑏
𝑐𝑧 + 𝑑, 𝑎, 𝑏, 𝑐, 𝑑 ∈ ℂ, 𝑎𝑑 − 𝑏𝑐 ≠ 0
Jika dimisalkan 𝑤1, 𝑤2, dan 𝑤3 dengan 𝑤1 = 𝑐𝑧 + 𝑑, 𝑤2 = 1
𝑤1, dan 𝑤3 = (𝑏 −
𝑎𝑑 𝑐 ) 𝑤2+
𝑎
𝑐. Kita tahu bahwa 𝑤1, dan 𝑤3 adalah
transformasi affine dan 𝑤2 adalah inversi. Akan ditunjukkan bahwa f adalah komposisi dari 𝑤1, 𝑤2, dan 𝑤3.
𝑤3∘ 𝑤2∘ 𝑤1 =𝑎 𝑐 + 𝑏 −𝑎𝑑𝑐 𝑐𝑧 + 𝑑 = 𝑎 𝑐(𝑐𝑧 + 𝑑) − 𝑎𝑑 𝑐 + 𝑏 𝑐𝑧 + 𝑑 = 𝑎𝑐𝑧 + 𝑎𝑑 − 𝑎𝑑 + 𝑏𝑐 𝑐 𝑐𝑧 + 𝑑 = 𝑎𝑧 + 𝑏 𝑐𝑧 + 𝑑 = 𝑓(𝑧).