Bab 2
Tinjauan Pustaka
2.1
Penelitian Sebelumnya
Dalam skripsi penelitian yang berjudul “Pemodelan dinamis pola tanam berbasis metode LVQ (Learning Vector Quantization)” (Bursa, 2010), menghasilkan sistem informasi pola tanam pada suatu daerah dengan menggabungkan data klimatologi, data koordinat dan ketinggian wilayah pada citra landsat menggunakan data raster dan diolah dengan metode LVQ (Learning Vector Quantization).
Judul penelitian hibah bersaing “Penyusunan Model Pranata Mangsa Baru dengan Menggunakan Teknologi Map Server” (Simanjuntak, 2010), hasil penelitian tersebut adalah penyediaan fasilitas diseminasi pembelajaran mandiri terhadap kelompok penyuluh pertanian lapangan (PPL) untuk penataan pola tanam komoditas pertanian menggunakan perangkat Pranata Mangsa Baru yang disusun dengan pendekatan agrometeorologi.
Perbedaan dari penelitian ini adalah selain menggabungkan data klimatologi dan agrometeorologi yang akurat, penelitian ini dilengkapi dengan peramalan cuaca. Sehingga sistem ini akan memperkirakan tanaman yang cocok untuk ditanam pada masa yang ditentukan oleh
user.
2.2
Identifikasi Iklim di Jawa Tengah
Letak geografis propinsi Jawa Tengah terletak pada 5o40' Lintang Utara dan 8o30' Lintang Selatan dan antara 108o30' Bujur Barat dan 111o30' Bujur Timur (termasuk Pulau Karimunjawa). Secara administratif propinsi Jawa Tengah terbagi menjadi 29 Kabupaten dan 6 Kota. Luas Wilayah Jawa Tengah sebesar 3.250.000 hektar atau sekitar 25,04% dari luas pulau Jawa (1,70% luas Indonesia). Luas yang ada terdiri dari 1.000.000 hektar (30,80%) lahan sawah dan 2.250.000 hektar (69,20%) bukan lahan sawah (BPS Provinsi Jawa Tengah, 2011).
Menurut penggunaannya, luas lahan sawah terbesar berpengairan teknis (38,26 persen), selainnya berpengairan setengah teknis, tadah hujan dan lain-lain. Dengan teknik irigasi yang baik, potensi lahan sawah yang dapat ditanami padi lebih dari dua kali sebesar 69,56%. Lahan kering yang dipakai untuk tegalan/kebun/ladang/huma sebesar 34,36% dari total bukan lahan sawah (DINHUBKOMINFO, 2009).
2.3
Analisis Abnormalitas Cuaca pada Curah Hujan
dan Pola Tanam
Kondisi iklim di Indonesia pada dasarnya dipengaruhi oleh sirkulasi monsoon yang menimbulkan perbedaan iklim antara musim hujan dan musim kemarau. Besarnya curah hujan akan sangat tergantung pada sirkulasi monsoon. Sirkulasi monsoon akan dipengaruhi oleh kejadian ENSO (El Nino Southern Oscillation) yang secara meteorologis diekspresikan dalam nilai Southern Oscillation Index (SOI). Berdasarkan hal tersebut maka fluktuasi curah hujan sangat berkorelasi dengan fluktuasi SOI. Kejadian El Nino dapat berdampak pada penurunan curah hujan, dan kejadian La Nina dapat menimbulkan peningkatan curah hujan. Pola produksi tanaman pangan umumnya berbeda pada musim kemarau dan musim hujan. Musim hujan dimulai manakala curah hujan pada hari tertentu telah mencapai antara 200 - 350 mm. Definisi dari Badan Meteorologi dan Geofisika, awal musim hujan curah hujan harian sebesar 50 mm selama 10 hari berturur-turut yang kemudian diikuti dengan curah hujan diatas 50 mm pada 10 hari berikutnya. Dengan menggunakan batasan curah hujan tersebut periode musim hujan di wilayah Indonesia bervariasi menurut lokasi tetapi umumnya berlangsung antara bulan September/Oktober hingga bulan Maret/April (Irawan, 2006).
normal sedangkan akhir musim kemarau lebih lambat 2-4 dasarian, sehingga musim kemarau menjadi lebih panjang dari yang biasanya sekitar 8-20 dasarian menjadi 14-25 dasarian. Musim kemarau yang semakin panjang juga terjadi di Provinsi Jawa Barat dan Jawa Tengah sekitar 7-9 dasarian menurut daerah (Irawan, 2006).
Peristiwa El Nino dan La Nina dapat menimbulkan variasi besarnya dampak yaitu : besarnya dampak yang ditimbulkan oleh anomali iklim terhadap situasi iklim lokal atau curah hujan lokal, dan kemampuan petani dalam mencegah penurunan produksi yang disebabkan oleh anomali iklim di setiap daerah. Kedua faktor tersebut menyebabkan penurunan curah hujan yang tergolong besar di suatu daerah, dapat saja tidak menimbulkan dampak serius terhadap produksi pangan jika penurunan suplai air akibat El Nino dapat ditanggulangi. Sebaliknya,daerah yang mengalami penurunan curah hujan relatif kecil dapat mengalami dampak penurunan produksi yang tinggi, jika petani tidak mampu melakukan adaptasi dan antisipasi yang diperlukan (Irawan, 2006).
Sistem usaha tani memiliki ketergantungan yang sangat besar terhadap faktor klimatologi, sebagaimana digambarkan oleh Gambar 2.1. Bentuk resiko iklim pada pola tanam lahan sawah adalah sebagaimana berikut ini :
− Bulan Januari – Februari komoditas padi (padi 1) beresiko terkena banjir di beberapa daerah.
− Komoditas padi 2 resiko terkena kekeringan (awal musim kemarau lebih cepat).
Gambar 2.1 Pengaruh curah huja
Bentuk resiko iklim pada pola t berikut ini:
− Jagung/kacang–kacangan panjang awal musim hujan da
− Jagung resiko terkena ang
2.4
Pemodelan
Konsep dan teknik anal para ahli militer untuk kepe keseluruhan implikasi yang strategi militer. Pendekatan ini yang luas dan sistematik unt penelitian yang kompleks. O suatu sistem dengan kerumit
ujan terhadap sistem usaha tani (Boer, 2004)
a tanam lahan kering adalah sebagaimana
gan resiko terkena kekeringan (hari kering hujan dan awal musim kering lebih cepat).
ngin kencang (bulan Januari – Februari).
sehingga memerlukan pengabstraksian. Dalam hubungan inilah dikenal istilah "model dan pemodelan".
Istilah pemodelan adalah terjemahan bebas dari istilah "modelling". Untuk menghindari berbagai pengertian atau penafsiran yang berbeda-beda, maka istilah "pemodelan" dapat diartikan sebagai suatu rangkaian aktivitas pembuatan model (Soemarno, 2003).
Model adalah suatu representasi atau formalisasi dalam bahasa tertentu dari suatu sistem nyata. Pemodelan merupakan tahapan dalam membuat model darisuatu sistem. Tujuan dari pemodelan adalah menentukan informasi (variabel dan parameter) yang dianggap penting untuk dikumpulkan, sehingga tidak ada model yang unik. Model yang dibuat dapat berfungsi sebagai :
• Pembantu untuk berpikir
• Pembantu untuk berkomunikasi
• Alat dan latihan
• Alat prediksi
• Pembantu dalam percobaan
Kriteria model yang baik antara lain:
• Mudah dimengerti pemakainya
• Harus mempunyai tujuan yang jelas
• Dinyatakan secara jelas dan lengkap
• Mudah dikontrol dan dimanipulasi oleh pemakainya
• Mengandung pemecahan masalah yang penting dan jelas
• Mudah diubah, mempunyai prosedur modifikasi
Adapun hubungan model denga Gambar 2.2 (Hasanah, 2010).
Gambar 2.2 Hubungan Model
2.5
Produksi
Para ahli ekonomi “menghasilkan kekayaan me sumber-sumber kekayaan lingkun konvensional, produksi adalah nilai guna suatu barang atau ja yang ada. Produksi tidak berarti tidak ada, karena tidak seoran (Choir, 2010).
2.6
Tanaman Pangan
Pangan diartikan sebaga sumber hayati dan air, baik ya Batasan untuk tanaman panga karbohidrat dan protein. Seca
dengan sistem nyata dapat dilihat pada
del dengan Sistem Nyata(Hasanah, 2010)
i mendefinisikan produksi sebagai melalui eksploitasi manusia terhadap ngkungan.” Atau bila kita artikan secara ah proses menghasilkan atau menambah u jasa dengan menggunakan sumber daya arti menciptakan secara fisik sesuatu yang ang pun yang dapat menciptakan benda
tanaman sumber karbohidrat tanpa dibatasi pada kelompok tanaman semusim (Purwono, 2003).
Pada penelitian ini tanaman pangan yang digunakan adalah jagung, padi dan kedelai. Alasan pemilihan komoditas tersebut adalah peranannya sebagai sumber karbohidrat dan sumber protein bagi sebagian besar masyarakat Indonesia sehingga disebut sebagai tanaman pangan utama.
2.7
Data Spasial
Data spasial mempunyai pengertian sebagai suatu data yang mengacu pada posisi, obyek, dan hubungan diantaranya dalam ruang bumi. Data spasial merupakan salah satu item dari informasi, dimana didalamnya terdapat informasi mengenai bumi termasuk permukaan bumi, dibawah permukaan bumi, perairan, kelautan dan bawah atmosfir (Rajabidfard, 2000).
Karakteristik utama dari data spasial adalah bagaimana mengumpulkannya dan memeliharanya untuk berbagai kepentingan. Selain itu juga ditujukan sebagai salah satu elemen yang kritis dalam melaksanakan pembangunan sosial ekonomi secara berkelanjutan dan pengelolaan lingkungan. Berdasarkan perkiraan hampir lebih dari 80% informasi mengenai bumi berhubungan dengan informasi spasial (Wulan, 2002).
2.7.1 Metode Data Spasial
representasi hubungan antara dunia nyata dengan data spasial (Economic and Social Comminssion for Asia and the Pasific, 1996).
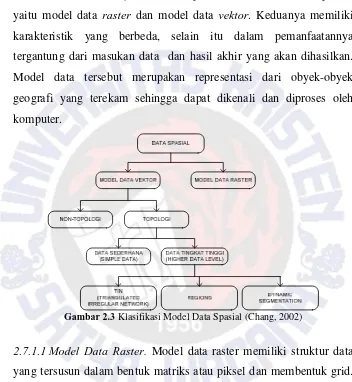
Gambar 2.3 menjelaskan terdapat 2 model dalam data spasial, yaitu model data raster dan model data vektor. Keduanya memiliki karakteristik yang berbeda, selain itu dalam pemanfaatannya tergantung dari masukan data dan hasil akhir yang akan dihasilkan. Model data tersebut merupakan representasi dari obyek-obyek geografi yang terekam sehingga dapat dikenali dan diproses oleh komputer.
Gambar 2.3 Klasifikasi Model Data Spasial (Chang, 2002)
Gambar 2.4 Struktur M
2.7.1.2 Model Data Vektor. Mode yang paling banyak digunaka (points) dengan nilai koordina spasialnya. Obyek yang dibang yaitu berupa titik (point), gar ditunjukkan pada Gambar 2.5 (
• Titik (Point)
Titik merupakan represent suatu obyek. Titik tidak mempun dalam bentuk simbol baik pada Contoh : Lokasi Fasilitasi Keseha
• Garis (Line)
Garis merupakan bentuk lebih titik dan merepresentasika Jalan, Sungai, dll.
• Area (Polygon)
Polygon merupakan repr Contoh : Danau, Persil Tanah, dl
Gambar 2.5 Contoh Represe
ur Model Data Raster (D. Gumelar, 2003)
odel data vektor merupakan model data kan, model ini berbasiskan pada titik dinat (x, y) untuk membangun obyek bangun terbagi menjadi tiga bagian lagi garis (line), dan area (polygon) seperti
(D. Gumelar, 2003).
entasi grafis yang paling sederhana pada punyai dimensi tetapi dapat ditampilkan pada peta maupun dalam layar monitor.
sehatan, dll
uk linear yang menghubungkan dua atau ikan obyek dalam satu dimensi. Contoh :
epresentasi obyek dalam dua dimensi. h, dll.
2.8
Analisis Exponential Smoothing
Metode exponential smoothing menggunakan data masa lalu untuk memprediksi nilai sebuah variabel dengan memberi bobot atau faktor pengali yang berbeda-beda. Besarnya bobot berubah secara
eksponensial, semakin kecil untuk data yang semakin usang (Makridakis, 1999). Dalam analisa exponential smoothing ini ada tiga kategori atau metode yang berbeda yaitu single exponential smoothing, double exponential smoothing, dan triple exponential smoothing (Santoso, 2009). Berikut akan dijelaskan karakteristik masing-masing metode dan persamaan yang digunakan dalam penghitungan tiap metode.
2.8.1 Pemulusan Single Exponential Smoothing
Metode ini menggunakan sebuah parameterα, yang dibobotkan kepada data yang paling baru dan membobotkan nilai (1-α) kepada hasil peramalan periode sebelumnya. Harga α terletak antara 0 dan 1. Persamaan statistik pemulusan yang digunakan dalam peramalan terlihat pada persamaan 2.1 (Arsyad, 2001).
At = α[Yt + (1- α) Yt-1 + (1- α)2Yt-2 + ....] ...(2.1)
Dari persamaan 2.1 maka dapat dilakukan substitusi sederhana yang menghasilkan persamaan 2.2 :
At = αYt + (1- α) At-1 ...(2.2)
Dari persamaan statistik pemulusan 2.1 dan 2.2, jika nilai peramalan menjadi Y t+1 maka menghasilkan persamaan 2.3 :
Dari persamaan ini dapat pula ditulis menjadi persamaan 2.4
Y t+1 = Y t + α (et) ...(2.4)
Kemudian untuk nilai et dapat dihitung dengan persamaan 2.5
et= ( Yt -Y t ) ...(2.5)
Dimana :
Y t+1 : nilai ramalan untuk periode berikutnya
α : konstanta pemulusan (0<α<1)
Yt : data baru atau nilai Y yang sebenarnya pada periode t
Y t : nilai pemulusan atau rata-rata yang dimuluskan hingga
periode t-1
et : adalah kesalahan dalam peramalan t
2.8.2 Pemulusan Double Exponential Smoothing
menggunakan metode dari Brown dengan persamaan yang tertulis pada persamaan 2.6 sampai 2.10 (Arsyad, 2001) :
Persamaan statistik pemulusan tunggal :
At = αYt + (1- α) At-1 ...(2.6)
Persamaan statistik pemulusan ganda, atau lebih dikenal dengan nilai double exponential smoothing.
At’ = αAt + (1-α) At’-1 ...(2.7)
Selanjutnya berdasarkan model trend linier, cari selisih antara At
dan At’ dengan persamaan 2.8 dan 2.9 :
at = 2At-At’ ...(2.8)
(
- ')
1 t t
t A A
b
α α −
= ...(2.9)
Sedangkan persamaan untuk nilai peramalan Yt+pterlihat pada
persamaan 2.10 :
p b a
Yt+p = t + t ...(2.10)
Dimana :
α : konstanta pemulusan
t
A : pemulusan tahap pertama untuk periode t
' t
A : pemulusan tahap kedua untuk periode t
1
−
t
' 1
−
t A
: pemulusan tahap kedua untuk periode t - 1 at : nilai pemulusan baru selisih antara At dan At’ bt : estimasi trend / faktor penyesuaian tambahan Yt+p : ramalan untuk periode waktu t+ p
p : periode waktu yang diramalkan : 1,2,3,4,…
2.8.3 Pemulusan Triple Exponential Smoothing
Metode ini merupakan metode forecast yang dikemukakan oleh Brown, dengan menggunakan persamaan kwadrat. Metode ini lebih cocok dipakai untuk membuat forecast hal yang berfluktuasi atau mengalami gelombang pasang surut (Subagyo, 1986).
Prosedur pembuatan forecasting dengan metode ini sebagai berikut:
Carilah nilai S’t dengan rumus sebagai berikut
S`t = αXt+ (1− α)S`t-1 ...(2.11)
Untuk tahun pertama nilai S`t belum bisa dicari dengan rumus di
atas, maka boleh ditentukan dengan bebas. Biasanya ditentukan sama seperti nilai yang telah terjadi pada tahun pertama.
Carilah nilai S``t dengan rumus
S``t = α S`t+ (1− α)S`t-1...(2.12)
Pada tahun pertama biasanya nilai S``t ditentukan seperti nilai
yang terjadi pada tahun pertama. Carilah nilai S```t dengan rumus
Untuk tahun pertama biasanya nilai S```t dianggap sama dengan
data tahun pertama.
Carilah αt = 3 S`t -3 S``t + S```t... ...(2.14)
Carilah nilai bt =
( ) (6 − 5 )S`t − (10 − 8 )S``t + (4 − 3 )S```t ....(2.15)
Carilah nilai ct = ( ) (S`t − 2S``t + S```t ) ...(2.16)
Persamaan forecast-nya = + + ... (2.17) adalah jangka waktu ke depan, yaitu berapa tahun yang akan datang forecast dilakukan. αt , bt , ct adalah nilai yang telah dihitung
sesuai dengan rumus 2.14, 2.15 dan 2.16.
Pada penelitian ini menggunakan metode peramalan (forecast) dengan metode Triple Exponential Smoothing, dikarenakan metode tersebut cocok dipakai untuk peramalan yang berfluktuasi.
2.9
Ketepatan Metode Peramalan
Tingkat ketepatan peramalan suatu produk dipandang sebagai tolok ukur seberapa jauh model peramalan itu mampu memprediksi data yang telah diolahnya dengan baik. Dengan demikian perlu dilakukan evaluasi kesesuaian metode peramalan terhadap suatu kumpulan data yang diberikan.
Evaluasi dalam ketepatan metode ini dapat diukur melalui penghitungan berikut ini (Arsyad, 2001):
1. Error/kesalahan pada periode ke-t et = Yt -Yt x 100%
t
Y merupakan data aktual untuk periode t
∧
t
Y merupakan ramalan untuk periode t
2. Nilai tengah kesalahan mutlak (Mean Absolute Deviation) dari
3. Nilai tengah kesalahan kuadrat (Mean Squared Error)
∑
4. Nilai tengah kesalahan persentase (Mean Percentage Error)
n
5. Nilai tengah kesalahan persentase absolut (Mean Absolute