Non-Archimedean subjective probabilities in decision theory
and games
Peter J. Hammond
Department of Economics, Stanford University, Stanford, CA 94305-6072, USA
Abstract
To allow conditioning on counterfactual events, zero probabilities can be replaced by infinitesimal probabilities that range over a non-Archimedean ordered field. This paper considers a suitable minimal field that is a complete metric space. Axioms similar to those in Anscombe and Aumann [Anscombe, F.J., Aumann, R.J., 1963. A definition of subjective probability, Annals of Mathematical Statistics 34, 199–205.] and in Blume et al. [Blume, L., Brandenburger, A., Dekel, E., 1991. Lexicographic probabilities and choice under uncertainty, Econometrica 59, 61–79.] are used to characterize preferences which: (i) reveal unique non-Archimedean subjective probabilities within the field; and (ii) can be represented by the non-Archimedean subjective expected value of any real-valued von Neumann–Morgenstern utility function in a unique cardinal equivalence class, using the natural ordering of the field. 1999 Elsevier Science B.V. All rights reserved.
1. Introduction and outline
Recent game theory relies on players having conditional probabilistic beliefs after a counterfactual event, like a player deviating from a presumed equilibrium strategy. Suggested formal frameworks for dealing with such counterfactuals include complete conditional probability systems, lexicographic hierarchies of probabilities, and logarith-mic likelihood ratio functions. For a survey of these approaches and their relationship, see Hammond (1994).
Section 2 of this paper begins by pointing out a fundamental inadequacy of these previous suggestions. This arises because they do not permit a compound lottery to be reduced unambiguously.
Following some early steps taken in Hammond (1994, 1999c), this paper presents an alternative approach, using the smallest possible extension of the real number field that allows for infinitesimal probabilities. Such extensions require consideration of a
non-E-mail address: [email protected]. (P.J. Hammond)
Archimedean ordered algebraic field of possible probabilities, of the kind discussed in Section 3.
The key part of the paper begins with Section 4. First, for a general ordered field of possible probabilities, expected utility is derived from three axioms – ordering, independence, and an ‘‘algebraic continuity’’ axiom. Next, Section 5 introduces additional axioms, similar to those devised by Anscombe and Aumann (1963) for real-valued probabilities, and by Blume et al. (1991) (henceforth BBD) for lexicographic probabilities. These are used to prove existence of a unique cardinal equivalence class of real-valued von Neumann–Morgenstern utility functions and also, except in the case of universal indifference, unique (possibly infinitesimal) subjective probabilities.
Section 6 considers the special case when probabilities belong to R(e), the smallest ordered field including both the real line and at least one positive ‘‘basic’’ infinitesimal.
`
This is extended to the special field R (e) of all power series in e, as the smallest complete metric space that includes R(e) when the latter is given a suitable metric. In Section 7 this extension allows the algebraic continuity condition to be replaced by a more intuitive ‘‘extended continuity’’ condition. In this setting, moreover, applying the
`
natural ordering of R (e) to expected utilities induces a preference ordering which corresponds to a familiar lexicographic expected utility criterion, with a real-valued von Neumann–Morgenstern utility function and non-Archimedean subjective probabilities.
2. Non-reduction of compound lotteries
´
For dealing with counterfactuals, Renyi’s (1955) complete conditional probability systems (CCPSs) are intuitively appealing. They simply require P(E9uE ) to be specified
whenever event E9,E, even if E has probability zero. And the modified form
P(E0uE )5P(E0uE9)P(E9uE ) of Bayes’ rule is required to hold whenever E0,E9,E.
A crucial hypothesis of von Neumann and Morgenstern is that it should always be enough to analyse the normal form of a game, because the outcome should be invariant to alterations in the extensive form that leave the normal form unaffected. This invariance hypothesis is actually fundamental to orthodox game theory, and even more to its foundations in consequentialist single person decision theory.
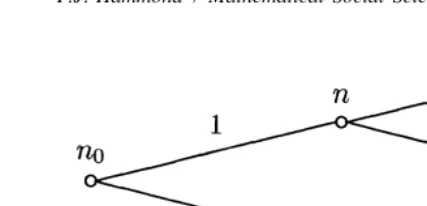
For this invariance hypothesis to hold, lotteries whose prizes are tickets for other lotteries must be reducible to equivalent simple lotteries merely by multiplying probabilities. Unfortunately, where CCPS are concerned, this reduction property may fail because there can be infinitely many different ways of compounding two lotteries which both involve zero probability events. A simple example to show this is illustrated in Fig. 1.
Fig. 1. Non-reduction of compound conditional probabilities
P(hajuha, b, cj)5P(hajuha, bj)P(ha, bjuha, b, cj)51
Also, because P(hajuha, b, cj)5P(hajuha, cj)P(ha, cjuha, b, cj)51 it must be true that P(hajuha, cj)51. Then all other conditional probabilities given the non-trivial eventsha, bj,ha, cjandha, b, cjmust be 0. But so far nothing determines the relative likelihoods of the two different ‘‘trembles’’ which result in states b and c respectively. Accordingly, the two other conditional probabilities P(hbjuhb, cj) and P(hcjuhb, cj) could be any real numbers in the interval [0, 1] which sum to 1. Hence, reduction of compound lotteries can only occur in a richer space allowing more information to be provided about the relative likelihood of the two trembles.
3. Non-Archimedean probabilities
3.1. Infinitesimals
Selten (1975) and many successors (including Myerson, 1978, 1986) have modelled a tremble as a vanishing sequence of positive probabilities – or, equivalently, as vanishing perturbations of the players’ (expected) payoff functions. Such vanishing sequences are obviously closely related to the ‘‘infinitesimals’’ used in the early development of ‘‘infinitesimal calculus’’ by Leibniz and many successors. Formally, a positive in-finitesimal is smaller than any positive rational number and so, because the rationals are dense in the reals, smaller than any positive real number. This obviously violates the ‘‘Archimedean’’ property of the real line, requiring that for every r.0 there should exist an integer n such that rn.1. So infinitesimals are only allowed in suitable non-Archimedean structures.
investigated several variant forms of non-Archimedean expected utility, especially those involving ‘‘matrix’’ probabilities associated with lexicographic utilities.
3.2. What range of probabilities?
Originally probabilities were rational numbers, usually with small denominators. Every monetary bet that has ever been made and settled on the precise agreed terms has involved a rational odds ratio. More sophisticated mathematical models of probability involve continuous distributions, which necessitate irrational but real probabilities. To date, real-valued probability measures have served us rather well. Yet the previous discussion suggests the need for infinitesimal probabilities in game theory. This forces us to face the question: How rich should the range of allowable probabilities be?
My provisional answer is: As small as possible, provided that some essential requirements are met. If the transfer principle of non-standard analysis is not an essential requirement, then there is no good reason to use every possible ‘‘hyperreal’’ between 0 and 1, as non-standard analysis seems to require. But the range should include some infinitesimal elements, it seems, as well as all real numbers in the interval [0, 1].
Probabilities need adding, because of finite additivity, and also multiplying when compounding lotteries. Furthermore, they need to be divided when calculating con-ditional probabilities by Bayesian updating. This suggests imposing the algebraic structure of a field. Finally, since the expectation of a real-valued von Neumann– Morgenstern utility function lies within the same field, and expected utilities should represent a complete preference ordering, there should be a linear or total order on the
1
field.
3.3. General non-Archimedean ordered fields
An ordered field kF, 1, ?, 0, 1, .l is a setF together with:
1. the two algebraic operations 1 (addition) and ? (multiplication); 2. the two corresponding identity elements 0 and 1;
3. the binary relation . which is a linear order on F satisfying 1.0.
Moreover,Fmust be closed under the two algebraic operations. The usual properties of real number arithmetic also have to be satisfied – i.e., addition and multiplication both have to be commutative and associative, the distributive law must hold, and every element x[F must have both an additive inverse 2x and a multiplicative inverse 1 /x,
except that 1 / 0 is undefined. The linear order . must satisfy y.z⇔y2z.0. Also, the set F1 of positive elements in F must be closed under both addition and multiplication.
Any ordered fieldF has distinct positive integer elements n51,2, . . . defined as the
1
sums n51111 ? ? ? 11 of n copies of the element 1[F. Obviously, it follows thatF
includes all rational numbers.
The ordered fieldFis Archimedean if, given any x[F , there exists such a positive
1
integer n for which nx.1. For any x[F, letuxudenote x if x$0 and 2x if x,0. Say
that any x[F\h0j is infinitesimal iff uxu,1 /n for every (large) positive integer n.
Evidently, a field is non-Archimedean iff it has infinitesimal elements, and is Archime-dean iff it is isomorphic to a subset of the real lineR. See Royden (1968), for example. In the rest of the paper, F will denote any ordered field that may or may not be Archimedean. Also, in the ensuing analysis, it will be convenient to use the notation (0, 1) to indicate the interval hx[Fu0,x,1j. This notation helps to distinguish this
F
possibly non-Archimedean interval from the usual real interval (0, 1), which will often be denoted by (0, 1) .R
4. Algebraic expected utility
4.1. Consequences and states of the world
Let Y be a fixed domain of possible consequences, and S a fixed finite set of possible
states of the world. No probability distribution over S is specified. An act, according to
Savage (1972), is a mapping a: S→Y specifying what consequence results in each
possible state. Inspired by the Arrow (1953, 1964) and Debreu (1959) device of ‘‘contingent’’ securities or commodities in general equilibrium theory, I refer instead to
contingent consequence functions, or CCFs for short. Also, each CCF will be considered
S
as a list y 5kys sl[S of contingent consequences in the Cartesian product space
S
Y :5
P
s[S Y , where each Y is a copy of the consequence domain Y.s sAnscombe and Aumann (1963) allowed subjective probabilities for the outcomes of ‘‘horse lotteries’’ or CCFs to be inferred from expected utility representations of preferences over compounds of horse and ‘‘roulette lotteries’’. Formally, Savage’s
S
(1972) framework is extended to allow preferences over D(Y ; R), the space of all
S S S
(finitely supported) simple roulette lotteries defined on Y . Eachl [D(Y ;R) specifies
S S S S
a real numberl ( y ) as the objective probability that the CCF is y [Y .
S S
Instead of D(Y ; R), this paper considers the space D(Y ; F) of F-valued simple
S S S S S S
lotteries on Y . Each l [D(Y ; F) satisfies l ( y )50 iff y is outside the finite
S S S S S S
support F,Y ofl . On F each probability l ( y )[F , and oS l ( y )51. That
1 y [F
S S S S S
is, l ( y ).0 for all y [F, even though l ( y ) could be infinitesimal.
4.2. Objective expected utility
utility maximization should be deduced before subjective probabilities are inferred. Accordingly, I assume:
• (O) Ordering. There exists a (reflexive, complete and transitive) preference ordering
S S
Axioms (O) and (I*) obviously extend standard conditions for real-valued probability
S S
distributions in D(Y ; R) to F-valued probability distributions in D(Y ; F). Even the
S
version of axiom (AC) forD(Y ;R) has appeared in the literature. However, the latter is usually derived from a more fundamental continuity assumption like the counterpart of condition (C) in Section 7.2 – see, for example, Hammond (1999a, b). For this reason, condition (AC) is discussed further in the special non-Archimedean framework of Sections 6 and 7.
Together these statements clearly imply the result. h
S S S S
In the following, s and | respectively denote the strict preference and indifference relations
corre-S
S
Say too that U satisfies the algebraic mixture preservation condition (AMP) provided that, whenever a[(0, 1) , then
probability 1 to the particular CCF y [Y .
S S S
Finally, say that the two functions U , V : D(Y ; F)→F are cardinally equivalent
S S S S
provided there exist constantsr[F andd[Fsuch that V (l )5d 1 rU (l ) for all
1
S S S S
l [D(Y ; F). Obviously, if U and V are cardinally equivalent, they must also be
]
The following Lemma is a simple adaptation of a result which is familiar for real-valued probabilities. Accordingly, the proof will not be provided here. For details see, for example, Fishburn (1970) or Hammond (1999a).
S
Lemma 2. Suppose that axioms (O ), (I*), and (AC ) are all satisfied onD(Y ;F). Then
S S
there exists a unique cardinal equivalence class of utility functions U : D(Y ; F)→F S
which represent ' and satisfy (AMP).
5. Algebraic subjective probability
5.1. The algebraic SEU hypothesis
The first aim of this section is to provide sufficient conditions like those of Anscombe
S S
and Aumann for the preference ordering' onD(Y ;F) to have a subjective expected
S S
utility (SEU) representation which, for eachl [D(Y ;F), takes the form
S S S S
U (l )5
O
l ( y )O
pv( y ) (1)s s
S S s[S y [Y
for a unique cardinal equivalence class of von Neumann–Morgenstern utility functions (NMUFs) v:Y→F, and for suitable unique subjective probabilities p [F satisfying
s 1
os[S ps51. The difference from Anscombe and Aumann is that the subjective probabilities p and utilities v( y) may belong to the general ordered field F, as may the
s
S S S S
objective probabilities l ( y ) determining the lottery l [D(Y ; F). In addition, the
subjective probabilities ps must be positive rather than merely non-negative. This
S
particular characterization of the preference ordering ' will be called the algebraic
SEU hypothesis.
F is non-Archimedean. To do so, I will introduce a new state-independent continuity axiom (SIC). Then only the probabilities, and not the utilities, are allowed to be non-Archimedean.
5.2. Reversal of order
In order to derive subjective probabilities, Anscombe and Aumann added three more axioms to their basic hypothesis that ‘‘roulette lotteries’’ would be chosen to maximize objective expected utility.
and any consequence y[Y, let
S S
ls( y):5
O
l ( y )S S
y [Y ( y)s
denote the marginal probability that y occurs in s. Then the probabilitiesl( y) ( y[Y ) s
specify the marginal distribution in state s[S.
The first of the three additional axioms is:
S S S
• (RO) Reversal of Order. Whenever l , m [D(Y ; F) have marginal distributions S S S
satisfying l 5 m for all s[S, then l | m .
s s
This condition owes its name to the fact that there is indifference between: (i) having
S S
the roulette lottery l determine the random CCF y before the horse lottery that resolves which state s[S and which ultimate consequence y occur; and (ii) resolving
s
the horse lottery first, before its outcome s[S determines which marginal roulette
lottery ls generates the ultimate consequence y.
5.3. The sure thing principle
The second of Anscombe and Aumann’s additional axioms concerns any event E,S, E
together with the product space Y :5
P
s[E Y of contingent CCFs taking the formsE E
y 5kyl [Y , and the existence of an associated contingent preference ordering s s[E
E E E
' . Here it is natural to assume that' is defined onD(Y ;F), the space ofF-valued
E
probability distributions, instead of only onD(Y ), the space of real-valued probability distributions. So the second extra axiom becomes:
• (STP) Sure Thing Principle. Given any event E,S, there exists a contingent
E E
preference ordering' on D(Y ;F) satisfying
E E E E S \E S E S \E
l ' m ⇔(l ,n )' (m ,n )
E E E S \E S \E E S \E
for all l , m [D(Y ; F) and n [D(Y ; F), where (l , n ) denotes the
E S \E
combination of the conditional lottery l if E occurs with n if S\E occurs, and
E S \E
However, following an idea due originally to Raiffa (1961) and then used by BBD, it is easy to show:
S Lemma 3. Suppose that the three axioms (O ), (I*), and (RO ) are all satisfied onD(Y ;
F). Then so is (STP).
Proof. See Hammond (1999b). h
Because of this result, (STP) will not be imposed as an axiom, but it will often be used in the ensuing proofs.
5.4. State independence
For each s[S, condition (STP) ensures the existence of a contingent preference
hsj
ordering ' on D(Y ;s F)5D(Y; F). The last axiom is:
• (SI) State Independence. Given any state s[S, the contingent preference ordering
hsj
' overD(Y;F) is independent of s.
S S
*
Let ' denote this state-independent preference ordering. When ' on D(Y ; F)
*
satisfies conditions (O), (I*) and (AC), so too must' onD(Y;F), because of (STP).
5.5. Subjective probabilities
The five axioms (O), (I*), (AC), (RO), and (SI) are assumed throughout the following, as is condition (STP).
Proof. By induction on the number of states in E. h
From now on, exclude the trivial case of universal indifference by assuming that there
] ]
D(Y ; F) whose marginal distribution in each state s[E is l 5 l, independent of s. s
* *
Lemma 5. The ordering ' on D(Y; F) is represented by a utility function U :D(Y;
S S and (AC), Lemma 2 of Section 4.2 implies that they can be represented by normalized
S S
*
] ] Because of the two normalizations in (2), the result follows immediately. h
S S
Proof. The proof by Fishburn (1970, Theorem 13.1, p. 176) of the corresponding result
S S
for the space D(Y ) of real-valued probabilities applies to D(Y ; F), with no change except that (AMP) replaces the usual mixture preservation property. See also Hammond (1999b). h
Lemma 7. There exists a unique cardinal equivalence class of NMUFs v:Y→F and,
unless there is universal indifference, unique subjective probabilities p (s[S ) such that s
S S
the ordering ' on D(Y ;F) is represented by the subjective expected utility function
S S
v could be replaced by any cardinally equivalent v: Y→F. But this is equivalent to
S S S
replacing U by a cardinally equivalent V : D(Y ; F)→F. Any such transformation leaves the ratio
of expected utility differences unaffected. This ensures that the subjective probabilities are unique. h
5.6. Real-valued utility
*
Lemmas 5 and 7 imply that the state-independent preference ordering' onD(Y;F) is represented by the expected value of each F-valued state-independent NMUF v:
also. Yet in game theory, the motivation for non-Archimedean probabilities is that players’ deviations from their presumed best responses can be given infinitesimal subjective probability. Where there is no uncertainty of this kind, but only risk in the form of specified objective probabilities, there is no good reason to depart from classical expected utility theory, which requires preferences over real-valued probability dis-tributions to be continuous, and expected utility to be real-valued – as in BBD, for
*
example. To ensure thatv is real-valued,' onD(Y;R) is assumed to satisfy an extra standard continuity axiom for real-valued probability distributions.
3
*
• (SIC) State Independent Continuity. For all l,m,n[D(Y; R) satisfying ls m
*
satisfied on D(Y ; F). Then, unless there is universal indifference, there exist unique
subjective probabilities p [D(S; F ) and a unique cardinal equivalence class of
s 1
Proof. By Lemma 7, there exist unique subjective probabilities p and a unique cardinals
equivalence class of NMUFs v:Y→F. Because there is not universal indifference, v
cannot be constant. So it can be normalized within the same cardinal equivalence class
] ] ] *
to make v(y)51 andv(y)50 for some pair y, y[Y satisfying 1 s 1 .
y y
S ] ] S ]
Next, let 'R denote the restriction of the ordering ' to the space D(Y; R) of
S
real-valued probability distributions. Note that 'R satisfies axioms (O), (I*), (SIC),
S
(RO) and (SI). By a standard result in utility theory,'R also satisfies (AC), and can be represented by the expected value of a real-valued NMUFv which can be normalized
R
S
]
to satisfy vR(y)51 andvR(y)50. The expected values of bothv andvR represent'R ]
on D(Y; R), so these two NMUFs are cardinally equivalent. Because of the common normalization, they must be identical. That is,v( y)5v ( y)[R for all y[Y, implying
R
that v: Y→R. h
3
This is sometimes called the Archimedean axiom – see, for instance, Karni and Schmeidler (1991, p. 1769). For obvious reasons I avoid this name here. Note that imposing axiom (AC) – or the counterpart of condition
S S
(C) as stated in Section 7.2 – on' restricted toD(Y ;R) would imply that all subjective probabilities are
S
*
`
6. The ordered fieldR (e) as a complete metric space
6.1. The ordered field R(e)
In Hammond (1994, 1999c), the search for a minimal suitable range of probabilities suggested the particular ordered field R(e), originally described by Robinson (1973). This is the smallest algebraic field that contains the real lineRas well as a basic positive infinitesimal elemente. One can regarde as a particular element of the ordered field of hyperreals used in non-standard analysis. Or perhaps more intuitively, as any vanishing
`
sequence ken nl 51 of positive real numbers.
The typical non-zero element of R(e) is a ratio of two ‘‘polynomial expressions’’ – i.e., a ‘‘rational expression’’ whose normalized form is
n
k i
ake 1
O
i5k11aie ]]]]]]f(e)5 m (6)
j
11
O
j51bjefor some unique integer k and non-zero leading coefficient a . Define the orderingk . on
R(e) so that f(e).0 iff ak.0. This makes . a lexicographic linear ordering onR(e), in effect. It also makesR(e) a non-Archimedean ordered field, with f(e) infinitesimal iff
k.0.
6.2. A metric
Section 7 will be concerned with finding weaker sufficient conditions for the algebraic continuity axiom (AC) of Section 4.2 to hold when probabilities are allowed to range overR(e). SoR(e) needs a topology such as that induced by Lightstone and Robinson’s (1975) metric.
Given the normalized form (6) of f(e), define k as the infinitesimal order v[ f(e)] of
f(e), with v[0]:5 ` for the zero element ofR(e). If f(e)±0, note that:
1. if k.0, then f(e) is an infinitesimal of order k;
2. if k,0, then f(e) is really an infinite number of order 2k, which can be regarded as
an infinitesimal of negative order;
3. if k50, then f(e) is infinitesimally different from a non-zero real number, in which case it is said to be of infinitesimal order 0.
Note too that, for all non-zero pairs f(e), g(e)[R(e), one has
v[ f(e)?g(e)]5v[ f(e)]1v[ g(e)] and v[ f(e)1g(e)]$ minhv[ f(e)],v[ g(e)]j
It follows that the infinitesimal order is an instance of what Robinson (1973) describes as a ‘‘non-Archimedean valuation’’.
Now define the function d: R(e)3R(e)→R so that
2v[ f (e)2g(e)]
2`
for every f(e), g(e)[R(e), with the obvious convention that 2 :50. Obviously,
d( f(e), g(e))5d( g(e), f(e)) and d( f(e), g(e))50 if and only if v[ f(e)2g(e)]5 `,
which is true iff f(e)5g(e). Finally, it is easy to verify that d is a metric because the triangle inequality is satisfied.
any zero terms of the sequence g (e) (n51, 2, . . . ), this requires that the infinitesimal
n
the numerator must become 0 for n sufficiently large. This is necessary and sufficient for convergence.
Note one important implication: An infinite sequence of real numbers converges iff it is eventually equal to a real constant. Thus, the (very fine) topology we have defined on
R(e) induces the discrete topology on the subspaceR, meaning that every subset ofRis open in the subspace topology. Just as ordinary continuity requires completing the space of rationals by going to the real lineRin which Cauchy sequences converge, here I will consider a similar completion
`
R (e) of R(e).
In R(e) many Cauchy sequences do not converge. Indeed, consider any sequence
n n k `
f (e)5ok50 ake (n51, 2, . . . ) with a non-recurring infinite sequence2 kak kl 51 of real
n k
coefficients – for example, ok50 e (n51, 2, . . . ). An analogy is the non-recurring]
Œ
decimal expansion of any irrational real number such as 2, which has no limit among
n
the set of rationals. The obvious limit of the sequence f (e) should be the power series ]
` k Œ
ok50 ake , just as the limit of the decimal expansion 1.41421356 . . . is 2. Yet a
` k
non-recurring power series ok50 ake does not correspond to a rational expression in
R(e), because multiplying by any polynomial expression always leaves an infinite power series, never a polynomial.
` k
series, but of the form ok5k0 ake where the leading power k0 could be negative.
` 4
Accordingly, define R (e) as the set of all such power series. Of course, any rational
` `
expression inR(e) can be expanded as a power series inR (e), soR (e) does extend
R(e).
` ` k
Each member ofR (e) can be conveniently written asok52` ake , where there must exist k such that a0 k50 for all k,k . Then the metric d on0 R(e) can obviously be Because the quotient space of limit equivalence classes of Cauchy sequences inR(e) is
` `
easily seen to be an ordered field which is isomorphic toR (e), it follows thatR (e) is effectively the smallest complete metric space containingR(e), just asRis the smallest complete metric space containing the ordered field of rationals.
7. Lexicographic expected utility
7.1. Continuity
`
In the special case when the ordered field Fis the complete metric space R (e), the unsatisfactory algebraic continuity (AC) axiom of Section 4.2 is implied by two weaker continuity axioms. Of these, the first is a non-Archimedean version of a familiar
S
continuity axiom for preferences over real-valued lotteries inD(Y ).
S S S S ` S S S
Before presenting the second continuity axiom, let me first re-state axiom (AC) for the
`
case when probabilities take values in R (e).
4 `
In factR(e) is a proper subset of the space+ described by Levi-Civita (1954) and by Laugwitz (1968),
` nk `
S S S S • (NAC) Non-Archimedean Continuity. Given any three lotteries l , m , n [D(Y ;
` S S S S S S ` k
R (e)) satisfying l s m andm s n , there existsa(e)5ok50 a ek [(0, 1) ` R (e)
S S S S
such thata(e)l 1[12a(e)]n | m .
Then it is evident that axiom (NAC) can only be satisfied if the following logically weaker axiom is as well:
Clearly, axiom (XC) is specific to the field R (e). When am(e) satisfies (7), any
m
positive probability perturbation of order e is strictly preferred, and any negative perturbation of the same order is strictly dispreferred. Then axiom (XC) requires there to
m11
be some perturbations of ordere that are strictly preferred, and others that are strictly dispreferred. Note the similarity here with the following weakening of axiom (C*) that
`
is familiar when the ordered field is R instead ofR (e):
S S S S ` S S S S S
It will now be shown that when probabilities take values in R (e), axioms (C*) and (XC) can together replace the questionable (NAC) among the sufficient conditions for the SEU hypothesis.
S `
Lemma 9. On the space D(Y ;R (e)) of probability distributions taking values in the
`
complete metric space R (e), the four axioms (O ), (I*), (C*) and (XC ) together imply (NAC ).
S S S S ` S S S S S S
Proof. Suppose that l , m , n [D(Y ; R (e)) satisfy l s m and m s n . The
following proof involves a recursive construction. This begins at stage m50 with a21(e):50 and the two disjoint subsets
S S S S
S S S S
B :0 5ha[(0, 1)Rual 1(12a)n a m j
of the real interval (0, 1) . Lemma 1 of Section 4.2 implies thatR a9 . a0 whenever a9[A anda0[B . So there is a unique a [(0, 1) satisfying a 5infA 5supB .
are non-empty. Applying Lemma 1 again, there must exist a unique a [Rsuch that m11
The following theorem gives sufficient conditions for the non-Archimedean version of the SEU hypothesis to hold, with a real-valued utility function:
Theorem 10. Suppose axioms (O ), (I*), (C*), (RO ), (SI ), (SIC ) and (XC ) are all S `
satisfied on D(Y ; R (e)). Unless there is universal indifference, there exist unique
`
strictly positive non-Archimedean subjective probabilities p(?; e)[D(S; R (e)) and a
1
unique cardinal equivalence class of real-valued NMUFs v:Y→R such that the
S S ` `
preference ordering ' onD(Y ;R (e)) is represented by the R (e)-valued subjective
expected utility expression
then using Lemma 9 to replace the particular axiom (NAC) with the two axioms (C*) and (XC). h
7.5. Lexicographic expected utility
`
For every s[S, the subjective probability p(s; e)[R (e) can be expressed as the
1
` k
power seriesok50 p (s)k e . Thus, the SEU expression (8) can be re-written as the power
S S ` S S k
series U (l ); ok50 u (k l )e where
S S
u (l ):5
O
p (s)O
l( y)v( y) (k50, 1, 2, . . . )k k s
s[S y[Y
S S S
But then l ' m if and only if the associated infinite hierarchies of coefficients
S S ` S S ` S S ` S S `
ku (k l )lk50 and ku (k m )lk50 satisfy ku (k l )lk50$Lku (k m )lk50 w.r.t. the usual
lex-` S
icographic total ordering .L on R . In this sense, the preference ordering' has a lexicographic expected utility representation.
Acknowledgements
My thanks to Don Brown for greatly improving my knowledge of non-standard analysis while he was a colleague at Stanford. Also to Giacomo Bonanno and an anonymous referee for helping me clear up some ambiguities, and giving concrete suggestions for how to produce a condensed version for inclusion in the published symposium. A more complete version, including more proofs and some discussion of the intuitive limitations of non-standard analysis, is available as Stanford Economics Department working paper 97-038, whose PDF form can be found on the internet at: http: / / www-econ.stanford.edu / econ / workp / swp97038.pdf
References
Anderson, R.M., 1991. Non-standard analysis with applications to economics. In: Hildenbrand, W., Son-nenschein, H. (Eds.), Handbook of Mathematical Economics, Vol. IV, North-Holland, Amsterdam, pp. 2145–2208.
Anscombe, F.J., Aumann, R.J., 1963. A definition of subjective probability. Annals of Mathematical Statistics 34, 199–205.
ˆ ` ´ ´
Arrow, K.J., 1953. Le role des valeurs boursieres pour la repartition la meilleure des risques. In: Econometrie, Centre National de la Recherche Scientifique, Paris, pp. 41–48. (Arrow (1953) is a translation of Arrow (1964))
Arrow, K.J., 1964. The role of securities in the optimal allocation of risk-bearing. Review of Economic Studies 31, 91–96.
Blume, L., Brandenburger, A., Dekel, E., 1991. Lexicographic probabilities and choice under uncertainty. Econometrica 59, 61–79.
Chernoff, H., 1954. Rational selection of decision functions. Econometrica 22, 422–443.
Fishburn, P.C., LaValle, I.H., 1993. On matrix probabilities in non-Archimedean decision theory. Journal of Risk and Uncertainty 7, 283–299.
Hammond, P.J., 1994. Elementary non-Archimedean representations of probability for decision theory and games. In: Humphreys, P. (Ed.), Probability and Probabilistic Causality, Patrick Suppes: Scientific Philosopher, Vol. I, Kluwer Academic, Dordrecht, pp. 25–59.
`
Hammond, P.J., 1999a. Objective expected utility: A consequentialist perspective. In: Barbera, S., Hammond, P.J., Seidl, C. (Eds.), Handbook of Utility Theory, Kluwer Academic, Dordrecht, ch. 5.
`
Hammond, P.J., 1999b. Subjective expected utility. In: Barbera, S., Hammond, P.J., Seidl, C. (Eds.), Handbook of Utility Theory, Kluwer Academic, Dordrecht, ch. 6.
Hammond, P.J., 1999c. Consequentialism, non-Archimedean probabilities, and lexicographic expected utility. In: Bicchieri, C., Jeffrey, R., Skyrms, B. (Eds.), The Logic of Strategy, Oxford University, Oxford. Karni, E., Schmeidler, D., 1991. Utility theory with uncertainty. In: Hildenbrand, W., Sonnenschein, H. (Eds.),
Handbook of Mathematical Economics, Vol. IV, North-Holland, Amsterdam, pp. 1763–1831.
LaValle, I.H., Fishburn, P.C., 1992. State-independent subjective expected lexicographic utility. Journal of Risk and Uncertainty 5, 217–240.
LaValle, I.H., Fishburn, P.C., 1996. On the varieties of matrix probabilities in non-Archimedean decision theory. Journal of Mathematical Economics 25, 33–54.
¨
Laugwitz, D., 1968. Eine nichtarchimedische Erweiterung angeordneter Korper. Mathematische Nachrichten 37, 225–236.
Levi-Civita, T., 1954. Sugli infiniti ed infinitesimali attuali: quali elementi analitici, Atti Istituto Veneto di scienze, lettere, ed arti, 7 (1892 / 3) 1765–1815; reprinted in: Opere Matematiche di Tullio Levi-Civita: Memorie e Note: Volume primo (1893–1900). Nicola Zanichelli, Bologna, 1954, pp. 1–39.
Lightstone, A.H., Robinson, A., 1975. Non-Archimedean Fields and Asymptotic Expansions, North-Holland, Amsterdam.
Myerson, R.B., 1978. Refinements of the Nash equilibrium concept. International Journal of Game Theory 7, 73–80.
Myerson, R.B., 1986. Multistage games with communication. Econometrica 54, 323–358.
Raiffa, H., 1961. Risk, ambiguity, and the Savage axioms: Comment. Quarterly Journal of Economics 75, 690–694.
Rajan, U., 1998. Trembles in the Bayesian foundations of solution concepts of games. Journal of Economics Theory. 82, 248–266.
´
Renyi, A., 1955. On a new axiomatic theory of probability. Acta Mathematica Academiae Scientiarum Hungaricae 6, 285–335.
Robinson, A., 1973. Function theory on some non-Archimedean fields. American Mathematical Monthly: Papers in the Foundations of Mathematics 80, S87–S109.
Royden, H.L., 1968. Real Analysis, 2nd ed, Macmillan, New York.
Savage, L.J. The Foundations of Statistics, John Wiley, New York, 1954; and Dover Publications, New York, 1972.