PERBANDINGAN ALGORITMA ALPHA BETA DAN GREEDY PADA PERMAINAN OTHELLO BERBASIS DESKTOP SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Komputer Program Studi Teknik Informatika

(1)

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Komputer

Program Studi Teknik Informatika

Oleh:

Damian Arif Pradana 135314047

PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

THESIS

Presented as Partial Fulfillment of the Requirements To Obtain the Sarjana Komputer Degree

Informatics Engineering Study Program

By:

Damian Arif Pradana 135314047

DEPARTMENT OF INFORMATICS ENGINEERING FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

(3)

(4)

(5)

v

HALAMAN PERSEMBAHAN

Hadapilah rasa pesimismu dengan selalu optimis.

Skripsi ini saya persembahkan kepada:

(6)

(7)

vii ABSTRAK

Permainan papan memiliki beberapa algoritma yang berjalan di dalamnya, antara lain Minimax, Minimax dengan Alpha-Beta, serta Greedy. Algoritma Alpha-Beta merupakan turunan dari algoritma Minimax dengan mengasumsikan pada langkah algoritma ini mengembil langkah terbaik di setiap posisi serta membuat lawan membuat kerugian maksimum, algoritma Greedy yang mengambil solusi dengan langkah yang mendekati optimum. Perbandingan algoritma ini dapat dilakukan dengan cara membuat kedua algoritma beradu misalnya algoritma A melawan algoritma B. Perbandingan ini bertujuan untuk menetahui algoritma yang paling baik digunakan dalam permainan papan terutama dalam permainan Othello. Maka, diharapkan dengan adanya penelitian ini, dapat diketahui algoritma mana yang baik dalam permainan Othello.

(8)

viii ABSTRACT

Board games have several algorithms running in them, including Minimax, Minimax with Alpha-Beta, and Greedy. Alpha-Beta Algorithm is a derivative of the Minimax algorithm by assuming that in the algorithm steps that take the best steps in making a decision that makes a loss, the Greedy algorithm takes the solution with optimal steps. This comparison algorithm can be done by making the second algorithm collide through algorithm A against algorithm B. This comparison aims to find the best algorithm in Othello's game. Therefore, it is expected that with this research, which algorithm can be good in Othello's game.

(9)

(10)

x

KATA PENGANTAR

Puji syukur atas Tuhan Yang Maha Esa yang telah memberikan rahmat dan berkahNya sehingga penulis dapat menyelesaikan laporan penelitian dengan judul “Algoritma Minimax Pada Permainan Othello Berbasis Desktop” ini dengan baik.

Tujuan dari penulisan skripsi ini guna memenuhi salah satu syarat untuk menempuh sarjana komputer pada Fakultas Sains dan Teknologi (FST) Program Studi Teknik Informatika. Dalam penulisan skripsi ini tentunya tidak lepas dari hambatan dan kesulitan, namun berkat bimbingan, bantuan, nasihat dan saran serta kerjasama dari berbagai pihak, segala hambatan tersebut akhirnya dapat diatasi.

Dalam kesempatan ini, penulis juga berterima kasih atas dukungannya yaitu kepada :

1. Tuhan Yang Maha Esa, karena diberikan rahmat dan berkahnya dalam pengerjaan skripsi ini.

2. Bapak Alb. Agung Hadhiatma, M.T., selaku dosen pembimbing skripsi pertama, dan Ibu Anastasia Rita sebagai dosen pembimbing selanjutnya yang mendampingi penulis selama pengerjaan skripsi ini.

3. Teman-teman dari Komunitas Sakura Blossom Sanata Dharma (Ara, Fina, Ani, Ume, Niar) yang memberikan dukungan dan hiburan selama pengerjaan skripsi ini.

(11)

(12)

xii DAFTAR ISI

HALAMAN JUDUL ... i

TITLE PAGE_{... ii}

HALAMAN PERSETUJUAN ... iii

HALAMAN PENGESAHAN SKRIPSI ... iv

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ... vi

ABSTRAK ... vii

ABSTRACT_{... viii}

PERSETUJUAN PUBLIKASI KARYA ILMIAH ... ix

KATA PENGANTAR ... x

1.5. Sistematika Penulisan ... 3

2. BAB II TINJAUAN PUSTAKA ... 5

2.1. Landasan Teori ... 5

2.1.1. Game ... 5

(13)

xiii

2.1.3. Java ... 7

2.1.4. Netbeans ... 8

2.1.5. Teori Graf ... 9

2.1.6. Depth-First Search (DFS) ... 10

2.2. Othello ... 11

2.2.1. Peraturan Othello ... 12

2.2.2. Tujuan Permainan dan Penilaian ... 14

2.2.3. Posisi dan Stabilitas ... 15

2.2.4. Evaluasi Posisi Othello ... 16

2.3. Algoritma yang Digunakan ... 18

2.3.1. Algoritma Minimax ... 18

2.3.1.1. Alpha-Beta Pruning ... 23

2.3.2. Algoritma Greedy ... 25

2.4. Kompleksitas Algoritma ... 27

3. BAB III PERANCANGAN DAN DESAIN ... 29

3.1. Kebutuhan Sistem ... 29

3.1.1. Perangkat Keras ... 29

3.1.2. Perangkat Lunak ... 29

3.1.3. Data ... 29

3.2.Perancangan Proses ... 31

3.2.1. Diagram dan Skenario Use Case ... 31

(14)

xiv

3.3. Desain Antarmuka ... 42

3.3.1. Menu ‘Single Play’ ... 42

3.3.2. Menu ‘AI vs. AI’ ... 43

4. BAB IV IMPLEMENTASI DAN ANALISIS HASIL ... 44

4.1. Implementasi Antarmuka Pemakai ... 44

4.1.1. Implementasi Antarmuka Menu ‘Single Play’ ... 45

4.1.2. Implementasi Antarmuka Menu ‘AI vs. AI’ ... 46

4.2. Implementasi Algoritma pada Sistem ... 47

4.2.1. Algoritma Alpha-Beta Pruning ... 47

4.2.2. Algoritma Greedy ... 48

4.3. Hasil Uji Algoritma ... 49

4.3.1. Algoritma Alpha-Beta dengan Greedy ... 49

4.3.2. Perbandingan Skor dan Grafik Waktu ... 51

5. BAB V KESIMPULAN DAN SARAN ... 87

5.1.Kesimpulan ... 87

5.2.Saran ... 88

(15)

1 BAB I PENDAHULUAN 1.1.Latar Belakang

Game telah menjadi suatu hal yang ada di dalam keseharian kita, bahkan

menjadi bagian dari gaya hidup manusia. Dulu, game hanya dijadikan sarana hiburan semata namun sekarang game telah menjadi luas fungsinya, misalnya game dijadikan sarana pembelajaran, lahan bisnis, dan dipertandingkan sebagai

salah satu dari cabang olahraga oleh para profesional, yang sekarang dinamakan e-sports. Perkembangan game juga dapat dilihat secara langsung oleh masyarakat, pada mulanya game hanya dapat dimainkan di komputer dan console tetapi sekarang sudah memasuki era mobile game.

Dalam hal ini, penulis tidak akan membahas mengenai mobile game, namun mengenai algoritma yang digunakan untuk mengiplementasikan game berbasis desktop dalam suatu Personal Computer (PC). Seperti yang kita ketahui bahwa aplikasi berbasis Desktop (Desktop Application) adalah suatu aplikasi yang dapat berjalan tanpa adanya koneksi internet. Selain itu kelebihan dari Desktop Application adalah pada bagian pengaturannya yang lebih mudah dimodifikasi, serta prosesnya lebih cepat dibanding dengan aplikasi yang membutuhkan koneksi internet, terutama untuk aplikasi game online.

(16)

2

Saat ini banyak algoritma yang digunakan untuk memecahkan berbagai masalah, salah satunya adalah memecahkan permasalahan dalam suatu permainan papan atau board games, maka dari itu penulis ingin membandingkan antara 2 algoritma yang nantinya diujikan dalam tugas akhir ini, serta penulis dari skripsi ini juga ingin membuat suatu game yang cukup terkenal dalam kalangan tertentu terutama untuk pemain yang mengetahui permainan jenis permainan papan yaitu Othello. Algoritmanya dalam permainan ini menggunakan algoritma Alpha-Beta dan Greedy. Penulis mengambil kedua algoritma ini karena kedua algoritma ini paling umum digunakan dalam permainan papan seperti Catur maupun Tic-Tac-Toe. Permainan Othello atau Reversi merupakan permainan yang menggunakan papan sebanyak 8 x 8 blok yang berbentuk kotak. Dalam permainan awal papan Othello diletakkan 2 kepingan warna hitam dan 2 kepingan warna putih di atas papan untuk menandakan mulai permainan sehingga Othello hanya dapat dimainkan oleh 2 pemain saja.

Alasan dibuatnya tugas akhir ini adalah penulis ingin berfokus pada algoritma yang biasa digunakan dalam permainan Othello, yaitu Alpha-Beta dan Greedy. Kedua algoritma ini memiliki keunikannya sendiri-sendiri dalam menentukan langkah dalam Othello, serta cara kedua algoritma ini dalam menentukan langkah yang diambil dalam suatu permainan yang akan dijelaskan pada bab berikutnya.

1.2.Rumusan Masalah

Dalam skripsi ini penulis merumuskan beberapa masalah yaitu sebagai berikut:

1. Bagaimana cara merancang game Othello berbasis desktop?

(17)

3 1.3.Tujuan

Dalam skripsi ini, penulis memiliki beberapa tujuan, yaitu sebagai berikut: 1. Mengimplementasikan algoritma Alpha-Beta dan Greedy dalam game

Othello.

2. Merancang aplikasi game Othello berbasis dekstop.

3. Mengetahui perbandingan algoritma Alpha-Beta dan Greedy dalam permainan othello.

1.4.Batasan Masalah

Dalam penelitian ini, ditentukan beberapa batasan masalah, yaitu sebagai berikut :

1. Game menggunakan platform desktop dengan pemrograman basis java. 2. Tidak ada level permainan.

3. Penghilangan (block) pada bagian pojok-pojok (corner) papan.

1.5.Sistematika Penulisan

Sistem penulisan skripsi ini adalah sebagai berikut: KATA PENGANTAR

DAFTAR ISI DAFTAR TABEL DAFTAR GAMBAR BAB I PENDAHULUAN

Bab ini berisi latar belakang dilakukannya suatu penelitian, rumusan masalah yang diselesaikan, tujuan serta sistematika penulisan penelitian.

BAB II TINJAUAN PUSTAKA

(18)

4 BAB III PERANCANGAN DAN DESAIN

Bab ini akan membahas dan menjelaskan tentang perancangan implementasi algoritma serta langkah program dalam pembuatan game ini. Selain itu juga akan dijelaskan tentang fitur – fitur yang ada di dalam aplikasi game ini.

BAB IV IMPLEMENTASI DAN ANALISIS HASIL

Bab ini menjelaskan mengenai implementasi algoritma yang digunakan penulis melalui permainan Othello.

BAB V KESIMPULAN DAN SARAN

(19)

5

BAB II

TINJAUAN PUSTAKA

2.1. Landasan Teori 2.1.1. Game

“Game” diartikan sebagai permainan. Permainan merupakan bagian dari bermain dan bermain juga bagian dari permainan yang keduanya saling berhubungan. Permainan dalam hal ini merujuk pada pengertian kelincahan intelektual (Intellectual Playability Game) yang dapat juga diartikan sebagai area keputusan dan aksi dari pemain tersebut. Dalam game, ada beberapa target yang ingin atau harus dicapai oleh pemain. Game juga mempunyai peraturan untuk membatasi perilaku pemain dan menentukan sebuah permainan itu sendiri.

Permainan adalah kegiatan yang kompleks yang didalamnya terdapat peraturan, play dan budaya. Sebuah permainan merupakan sebuah sistem dimana pemain terlibat dalam konflik buatan, disini pemain berinteraksi dengan sistem dan konflik dalam permainan merupakan rekayasa atau buatan, dalam permainan terdapat peraturan yang bertujuan untuk membatasi perilaku pemain dan menentukan permainan. Game bertujuan untuk menghibur, biasanya game banyak disukai oleh anak-anak hingga orang dewasa (Tim Pusat Bahasa DEPDIKNAS, 2008).

Permainan secara umum dapat juga diartikan sebagai aktivitas rekreasi dengan tujuan bersenang-senang, mengisi waktu luang, atau berolahraga ringan. Permainan biasanya dapat dilakukan sendiri atau bersama-sama, yang pada umumnya disebut multiplayer atau multi pemain.

2.1.2. Aplikasi Desktop

(20)

6

dengan sistem operasi atau platform tertentu, misalnya Windows Media Player, Winamp, Photoshop, dan lain-lain.

Aplikasi Desktop ini juga dapat mempermudah pengguna dalam memodifikasi pengaturan dalam aplikasi sehingga dapat sesuai dengan keinginan pengguna baik secara efektif dan efisien. Keuntungan yang dapat diperoleh dengan membangun Aplikasi Dekstop adalah sebagai berikut:

1. Tidak memerlukan koneksi internet.

2. Proses berjalannya aplikasi lebih cepat dibanding aplikasi yang menggunakan koneksi internet, karena mungkin saja koneksi internet yang berjalan lebih lambat dibanding dengan Aplikasi Desktop.

3. Tidak bergantung pada konektivitas. Aplikasi Web bergantung pada konektivitas, maka kemungkinan adanya gangguan koneksi akan lebih besar semisal ada gangguan koneksi seperti Denial of Service atau gangguan listrik.

Berikut ini adalah tahap-tahap dalam pelaksanaan pembuatan suatu aplikasi:

1. Perencanaan, dalam proses ini terjadi pemilihan desain suatu aplikasi hingga pembuatan dasar basis data (bila diperlukan). Tahap ini memerlukan pengumpulan beberapa data yang akan ditampilkan pada aplikasi yang akan direncanakan. Data yang sudah diperoleh lalu dianalisa berdasarkan kebutuhan (cepat tidaknya perubahan data, tingkat kerumitan penampilan, dan bagaimana data akan ditampilkan).

(21)

7

3. Penempatan, dari tahap ini suatu aplikasi akan diinstal ke komputer yang bersangkutan. Apabila ada desain dan pembuatan basis data maka akan diinstal juga ke dalam komputer server, dan selain itu dilakukan juga uji coba kelayakan aplikasi tersebut.

4. Perawatan, tahap ini dilakukan untuk menjamin apakah aplikasi masih layak dijalankan atau tidak, dan hal ini juga diperlukan untuk mengatasi kerusakan-kerusakan.

2.1.3. Java

(22)

8

Sintaks bahasa pemograman java merupakan pengembangan dari bahasa pemograman C/C++, sehingga dengan mereka yang sudah terbiasa dengan C/C++ tidak akan mengalami kesulitan mempelajari bahasa pemograman Java. Java adalah bahasa pemograman yang sederhana dan tangguh. Berikut ini adalah beberapa karakteristik dari Java sesuai dengan white paper dari Sun:

1. Berorientasi objek. Java mendorong pemograman yang bebas dengan kesalahan yang bersifat strongly typed dan memiliki run time checking. 2. Portable. Pemograman Java dapat berjalan pada sistem operasi apapun

yang memiliki Java Virtual Machine.

3. Multithreading. Java mendukung pemograman multitreading dan terintegrasi secara langsung dalam bahasa Java.

4. Dinamis. Program Java dapat melakukan sesuatu tindakan yang ditentukan pada saat eksekusi program dan pada saat kompilasi.

5. Sederhana. Java menggunakan bahasa yang sederhana dan mudah dipelajari.

6. Terdistribusi. Java didesain untuk berjalan pada lingkungan yang terdistribusi seperti halnya internet.

7. Aman. aplikasi yang dibuat dengan bahasa Java lebih dapat dijamin keamanannya terutama untul aplikasi internet.

8. Netral secara arsitektur. Java tidak terkait pada suatu mesin atau mesin operasi tertentu.

2.1.4. Netbeans

(23)

9

2.1.5. Teori Graf

Graf merupakan himpunan atau kumpulan titik yang dihubungkan dengan garis. Banyak persoalan yang menggunakan graf, misalnya dalam switching network, teori coding, kimia, maupun pemetaan. Penerapan graf adalah sebagai berikut: suatu graf G terdiri dari 2 himpunan yang berhingga, yaitu himpunan titik-titik yang tidak kosong dengan simbol V(G) dan himpunan garis dengan simbol E(G) yang ditulis dengan notasi G = (V,E).

Beberapa istilah yang berkaitan dengan graf adalah sebagai berikut: 1. Derajat (Degree)

Yaitu suatu simpul pada graf tak berarah yang memiliki jumlah sisi yang bersisian dengan simpul tersebut. Pada graf berarah, derajat simpul v dinyatakan dengan derajat masuk (in-degree), yaitu jumlah simpul yang masuk dalam simpul v atau disimbolkan dengan d v , dan derajat keluar (out-degree), yaitu jumlah simpul yang keluar dalam simpul v atau disimbolkan dengan d v , dimana d(v)=d v +d v .

2. Vertex atau Node Adalah simpul atau titik 3. Edge

Biasa disebut garis dan menghubungkan kedua titik. 4. Lintasan (Path)

Adalah barisan node dan edge secara berselang-seling dimana garisnya (edge) berbeda.

5. Siklus/Sirkuit (Cycle/Circuit)

Sebuah lintasan yang mempunyai awal dan akhir di titik yang sama. 6. Jarak (Distance)

Panjang garis antara kedua titik. 7. Graf Berbobot (Weighted Graph)

(24)

10

2.1.6. Depth-First Search (DFS)

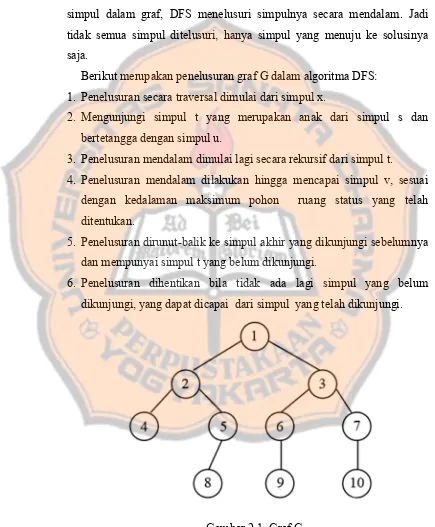
Merupakan salah satu dari algoritma traversal dalam graf. Algoritma traversal bekerja dengan cara menelusuri simpul-simpul yang ada secara sistematis. Berbeda dengan Breadth-First Search yang menelusuri seluruh simpul dalam graf, DFS menelusuri simpulnya secara mendalam. Jadi tidak semua simpul ditelusuri, hanya simpul yang menuju ke solusinya saja.

Berikut merupakan penelusuran graf G dalam algoritma DFS: 1. Penelusuran secara traversal dimulai dari simpul x.

2. Mengunjungi simpul t yang merupakan anak dari simpul s dan bertetangga dengan simpul u.

3. Penelusuran mendalam dimulai lagi secara rekursif dari simpul t.

4. Penelusuran mendalam dilakukan hingga mencapai simpul v, sesuai dengan kedalaman maksimum pohon ruang status yang telah ditentukan.

5. Penelusuran dirunut-balik ke simpul akhir yang dikunjungi sebelumnya dan mempunyai simpul t yang belum dikunjungi.

6. Penelusuran dihentikan bila tidak ada lagi simpul yang belum dikunjungi, yang dapat dicapai dari simpul yang telah dikunjungi.

(25)

11

Diambil sebuah ilustrasi seperti di atas, maka urutan simpul yang dikunjungi dengan algoritma DFS adalah : 1, 2, 4, 5, 8, 3, 6, 9, 7, 10.

2.2. Othello

Othello adalah permainan strategi game yang abstrak yang dimainkan oleh dua orang pemain pada sebuah papan berkukuran 8 kolom dan 8 baris dengan satu set disc berwarna berbeda pada kedua sisinya (yang biasanya berwarna gelap dan terang). masing-masing warna pada disk tersebut dikuasai oleh setiap pemain. Permainan ini pertama kali diciptakan di jepang oleh Goro Hasegawa bersama dengan James R Becker pada tahun 1971 yang terinspirasi dari game China GO dengan nama Othello. Hasegawa menginginkan suatu permainan yang kaya akan strategi namun tetap dapat dimainkan oleh pemain umum atau pemain awam. Becker menyebut permainan othello dengan tag “a minutes to learn, a lifetime to master”, mudah untuk dimainkan tetapi sangat sulit untuk menguasainya. Othello kemudian diperkenalkan kepada publik melalui Tsukada Original Co. pada tahun 1973 yang kemudian mengelola Japanese Othello Association.

(26)

12

2.2.1. Peraturan Othello

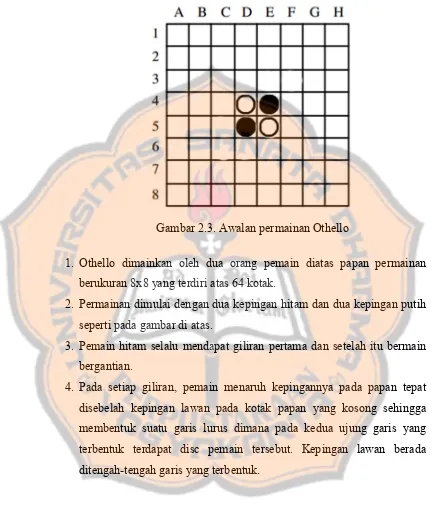
Gambar 2.3. Awalan permainan Othello

1. Othello dimainkan oleh dua orang pemain diatas papan permainan berukuran 8x8 yang terdiri atas 64 kotak.

2. Permainan dimulai dengan dua kepingan hitam dan dua kepingan putih seperti pada gambar di atas.

3. Pemain hitam selalu mendapat giliran pertama dan setelah itu bermain bergantian.

(27)

13

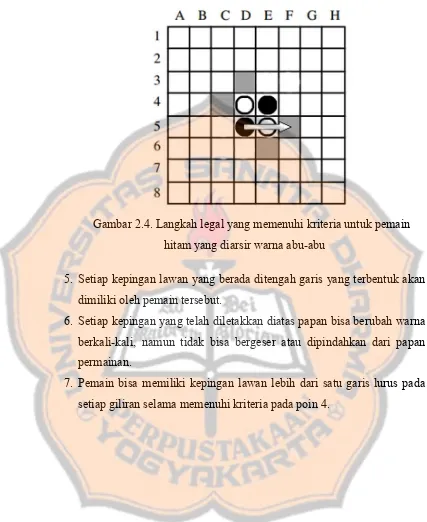
Gambar 2.4. Langkah legal yang memenuhi kriteria untuk pemain hitam yang diarsir warna abu-abu

5. Setiap kepingan lawan yang berada ditengah garis yang terbentuk akan dimiliki oleh pemain tersebut.

6. Setiap kepingan yang telah diletakkan diatas papan bisa berubah warna berkali-kali, namun tidak bisa bergeser atau dipindahkan dari papan permainan.

(28)

14

Gambar 2.5. Giliran putih bermain memiliki kepingan lawan pada 2 garis lurus.

8. Pemain tidak boleh melewati gilirannya (Pass), kecuali tidak ada lagi jalan yang legal.

9. Permainan berakhir jika tidak ada lagi jalan legal untuk kedua pemain atau seluruh papan telah terisi penuh oleh kepingan .

2.2.2. Tujuan Permainan dan Penilaian

Tujuan dari permainan ini adalah memperoleh sebanyak-banyaknya warna kepingan yang dimainkan oleh pemain tersebut. Pemain dengan jumlah kepingan terbanyak menjadi pemenang dari permainan reversi ini.

Penilaian atau skoring adalah menghitung seluruh jumlah warna yang didapatkan oleh setiap pemain. Seperti yang telah disebutkan diatas tentang tujuan permainan, maka pemain dengan jumlah skor terbanyak menjadi pemenang permainan.

Permainan akan berakhir apabila memenuhi salah satu syarat di bawah ini:

1. Kotak pada papan penuh dengan kepingan tanpa ada ruang kosong yang tersisa

(29)

15

Gambar 2.6. Pemain hitam memenangkan pertandingan dengan skor 33-31.

Dalam hal ini terdapat pengecualian yaitu apabila permainan menggunakan timer atau interval waktu tertentu, maka pemain yang kehabisan waktunya dinyatakan kalah tidak perduli bagaimana keadaan dan jumlah disc pada papan permainan.

2.2.3. Posisi dan Stabilitas

Begitu pentingnya posisi sudut membuat setiap pemain berusaha untuk mendapatkannya. Setiap kepingan yang diletakkan diatas papan permainan bisa jadi merupakan batu loncatan bagi lawan untuk memperoleh posisi sudut membuat setiap pemain harus berhati-hati dalam menentukan langkah nya.

(30)

16

diapit oleh kepingan yang berbeda warna. Ada 3 klasifikasi stabilitas kepingan: Stabil, semi-stabil, dan tidak stabil. Kepingan yang stabil adalah kepingan yang tidak dapat diapit saat permainan berlangsung, kepingan yang tidak stabil adalah kepingan yang dapat diapit oleh kepingan lain dalam langkah selanjutnya, sementara kepingan yang semi-stabil adalah kepingan yang berpotensi diapit oleh kepingan lain pada saat tertentu, namun kepingan tersebut berbeda dengan kepingan tidak stabil yang rentan diapit oleh kepingan lain.

2.2.4. Evaluasi Posisi Othello

Permainan Othello memiliki algoritma dan dalam suatu program, hal ini merupakan bagian yang penting. Pengaruh dari evaluasi ini memang kecil apabila algoritma yang digunakan memang sudah baik. Evaluasi ini dibagi menjadi 3 macam dan sebagian besar algoritma untuk Othello dapat ditempatkan pada salah satu kategori ini:

a. Disk-square tables

Ide dari evaluasi posisi ini adalah dari kotak yang berbeda memiliki nilai yang berbeda, dalam hal ini kotak/blok papan paling pojok memiliki nilai yang lebih tinggi daripada kotak di sebelahnya. ada 3 nilai juga untuk kotak/blok papan, yaitu kepingan hitam, kepingan putih, dan kosong. Pendekatan tertentu akan memiliki nilai yang berbeda untuk setiap posisi dalam tahap permainan yang berbeda, misalnya sudut lebih penting dalam awal permainan dan saat dimulainya pertengahan jalan permainan dibandingkan dengan akhir permainan.

(31)

17 b. Mobility-based evaluation

Pendekatan ini lebih baik dibanding pendekatan sebelumnya yang menggunakan tabel dari blok papan Othello. Kunci dari pendekatan ini adalah pemain berusaha untuk memaksimalkan mobilitas (jumlah kemungkinan langkah yang tersedia) dan meminimalkan disk frontier (kepingan yang berdekatan dengan blok kosong). Langkah atau pendekatan ini dapat berjalan dengan efisien apabila pemrogramannya juga efisien, serta dapat meningkatkan level kesulitan yang lebih tinggi. Kebanyakan program dengan fungsi evaluasi berbasis mobilitas juga memiliki fungsi mengenai konfigurasi tepi dan sudut serta berusaha untuk meminimalkan jumlah kepingan selama awal midgame, strategi ini juga digunakan oleh manusia.

c. Pattern-based evaluation

Seperti yang disebutkan di atas, evaluasi ini fokus pada pattern atau pola dalam papan Othello dengan cara menggabungkan konfigurasi tepi da sudut papan. Umumnya dengan memaksimalkan mobilitas dan meminimalisasi kepingan yang berdekatan dengan blok kosong. Evaluasi ini meminimalisir kepingan papan dengan cara yang sama seperti evaluasi sebelumnya. Implementasinya dilakukan dengan cara mengevaluasi setiap baris, kolom, diagonal dan konfigurasi sudut secara terpisah serta menambahkan nilai dalam evaluasi tersebut.

(32)

18

Dalam proses penentuan nilai relatif dari konfigurasi yang berbeda, seseorang harus memutuskan apa yang seharusnya diprediksi oleh fungsi evaluasi. Pilihan paling umum untuk memprediksi perbedaan kepingan akhir.

2.3. Algoritma yang Digunakan 2.3.1. Algoritma Minimax

Pencarian Minimax umumnya menggunakan depth-first search dalam suatu pohon permainan (tree). Hal ini didukung dengan mencari ke kedalaman pohon tertentu tergantung itu node min atau max. Algoritma ini digunakan untuk menemukan nilai akurat untuk sebuah posisi papan. Diasumsikan bahwa kedua pemain selalu mengambil langkah terbaik pada setiap posisi. Algoritma ini bekerja secara rekursif dengan mencari langkah yang membuat lawan mengalami kerugian maksimum. Ini berarti, pada langkah yang pertama komputer menganalisa seluruh pohon permainan dan untuk setiap langkahnya komputer akan memilih langkah yang membat lawan mendapatkan keuntungan minimum (dalam hal ini pemain disebut ‘max’ dalam pohon permainan, sedangkan komputer akan bekerja sebagai ‘min’). Berikut ini merupakan pseudocode algoritma Minimax:

1. Jika node merupakan leaf atau root maka mengembalikan nilai heuristik dari node tersebut.

2. Jika masuk ke node tersebut, deklarasikan alpha sebagai negatif infiniti, untuk setiap child node deklarasikan alpha sebagai max dengan node child dan kedalaman dikurangi satu dan mengembalikan nilai alpha.

(33)

19

Gambar 2.7. Pseudo-code Algoritma Minimax.

(34)

20

Gambar 2.8. Contoh pohon dengan nilai di tiap node.

Diasumsikan ada permainan yang melibatkan 2 pemain dan permainan dilakukan secara bergilir. Pemain selalu memilih langkah yang terbaik di tiap gilirannya. Pohon kemungkinan permainan akan terbentuk. Node root merupakan node awal permainan. Setiap node mempunyai anak/child untuk setiap posisi 1 langkah yang dilakukan oleh pemain. Pohon terbentuk dengan kedalaman tertentu (berdasarkan komputasi atau pemrograman). Node leaf akan menggunakan fungsi evaluasi untuk menentukan seberapa baik atau buruk posisi/langkah tersebut. Semakin tinggi angka yang didapat dalam langkah pemain tersebut, maka semakin kecil pula kemungkinan terburuk yang dialami pemain itu. Angka positif bisa digunakan untuk mengetahui posisi yang sering digunakan pemain, dan angka negatif untuk musuh agar mendapat keuntungannya.

(35)

21

Gambar 2.9. Contoh pengaplikasian algoritma Minimax pada pohon bagian awal.

Pada bagian node lingkaran di atas node leaf diberi nilai dengan asumsi kedua pemain memilih langkah terbaik, maka dalam node tersebut akan bernilai maksimum. Misalnya kita ambil pada bagian paling kiri akan ada pilihan node yang bernilai -8 dan node yang bernilai 12. Pemain memilih langkah yang terbaik sehingga dia mengambil node yang bernilai 12, dan nilai 12 ini mengisi node lingkaran tersebut.

(36)

22

Node di tingkat berikutnya merupakan node kotak sebagai langkah musuh. Pemain musuh juga mempunyai pilihan dengan asumsi menggunakan langkah terbaik, maka musuh akan menelusuri node dengan nilai minimum. Contohnya di node paling kiri akan diberikan pilihan node dengan nilai 12 dan 5. Pilihan terbaik adalah dengan node 5 (minimum), jadi diasumsikan musuh akan mengambil node tersebut. Otomatis node yang terisi adalah 5, dan secara lengkap digambarkan sebagai berikut.

Gambar 2.11. Contoh pengaplikasian algoritma Minimax pada pohon dalam mode minimum.

(37)

23

Gambar 2.12. Hasil akhir dari pohon algoritma Minimax.

2.3.1.1.Alpha-Beta Pruning

Alpha-Beta Prunning adalah sebuah algoritma yang sistemnya adalah dengan cara mengurangi jumlah simpul yang dieksplorasi dalam algoritma minimax. Dengan algoritma tersebut, waktu yang diperlukan dalam pencarian akan berkurang dengan membatasi waktu yang terbuang untuk mengevaluasi pohon permainan. Implementasi algoritma ini akan memberikan jalur terbaik dalam setiap kemungkinan permainan dalam pohon permainan (Prabawa, 2009).

(38)

24

Gambar 2.13. Pseudo-code Algoritma Alpha-Beta Pruning (Anggraeni, 2013).

Untuk menggambarkan proses dari pencarian Alpha-beta ditunjukkan pada gambar berikut:

Gambar 2.14. Pohon pencarian dengan Alpha-Beta Pruning (Anggraeni, 2013).

1. Hampiri node pertama pada leaf dengan nilai 5, naik ke parent pada level 2 masukkan nilai 5, hampiri 8, karena 8>5 maka ganti parent dengan 8, hampiri 3.

(39)

25

3. Hampiri node keempat pada leaf dengan nilai 9, naik ke parent pada level 2 masukkan nilai 9. Jika kita menghampiri leaf

berikutnya, kita mencari yang lebih tinggi dari 9, sementara pada level 1 kita mencari yang lebih kecil dari 8, maka leaf 3 dan 1 kita potong (tidak kita hampiri).

4. Begitu seterusnya hingga kita dapatkan hasil akhir dari tree di atas adalah seperti gambar 2.11.

Gambar 2.15. Pohon pencarian dengan Alpha-Beta Pruning (Anggraeni, 2013).

2.3.2. Algoritma Greedy

Algoritma greedy merupakan jenis algoritma yang menggunakan penyelesaian masalah dengan mencari nilai maksimum sementara pada setiap langkahnya. Nilai maksimum sementara ini dikenal dengan istilah local maximum. Pada kebanyakan kasus, algoritma ini tidak akan menghasilkan solusi paling optimal, namun algoritma ini memberikan solusi yang mendekati nilai optimum dalam waktu yang cukup cepat.

(40)

26

banyak pilihan yang perlu dieksplorasi. Oleh karena itu, pada setiap langkah harus dibuat keputusan yang terbaik dalam menentukan pilihan.

Sebagai contoh mudah dalam mempelajari algoritma ini adalah kasus memasukan barang ke dalam ransel. Misal ada sebuah ransel yang dapat memuat barang seberat 20 kilogram, dan ada 3 barang yang akan dimasukkan dalam ransel tersebut, barang A seberat 15 kilogram, barang B dan C seberat 10 kilogram. Normalnya orang akan memilih untuk memasukkan barang B dan C yang masing-masing seberat 10 kilogram karena totalnya sama dengan muatan ransel yaitu sebanyak 20 kilogram, namun dalam algoritma Greedy ini menggunakan cara pemecahan masalah dengan cara memasukkan barang terberat terlebih dahulu ke dalam ransel. Dalam hal ini, ia akan memilih berat 15 kg terlebih dahulu tanpa mempertimbangkan barang yang lain.

Persoalan optimasi algoritma greedy disusun oleh elemen-elemen berikut:

1. Himpunan kandidat, berisi elemen pembentuk solusi.

2. Himpunan solusi, berisi kandidat-kandidat yang terpilih sebagai solusi persoalan.

3. Fungsi seleksi, dinyatakan dengan predikat seleksi memilih kandidat yang paling memungkinkan mencapai solusi optimal pada setiap langkah.

4. Fungsi kelayakan, dinyatakan dengan predikat layak dengan memeriksa apakah kandidat yang dipilih dapat memberikan solusi yang layak dengan tidak melanggar constrains yang ada.

(41)

27

Gambar 2.16. Pseudo-code Algoritma Greedy.

Dalam hal ini S yang terdiri dari himpunan kandidat yang berisi elemen pembentuk solusi, saat himpunan kandidat itu tidak kosong maka himpunan tersebut akan diseleksi dan menghapus nilai kandidat dan mengembalikan nilai, jika solusi tersebut layak maka solusi tersebut tidak melanggar constraint yang ada dan mengembalikan nilai solusi.

2.4. Kompleksitas Algoritma

Kompleksitas yang ada dalam dua algoritma yang ada dalam skripsi ini dijelaskan sebagai berikut:

1. Algoritma Alpha-Beta

O( ) merupakan kompleksitas waktu terbaik untuk algoritma Alpha-Beta. Dengan rata-rata konstan faktor branching b, dan dengan kedalaman pencarian sebanyak d tingkat, nilai maksimum dari posisi node leaf yang sudah dievaluasi adalah O(bb...*b)= O( ) – sama seperti algoritma pencarian minimax, jika langkah pencarian merupakan pencarian optimal (yang artinya algoritma menggunakan langkah terbaik), posisi jumlah node yang dievaluasi adalah O(b*1*b*1*...*b) untuk kedalaman sementara dan O(b*1*b*1*...*1) untuk kedalaman yang paling dalam, atau

(42)

28

Penjelasan dari b*1*b*1*... adalah langkah pemain pertama yang ditelusuri agar mendapat yang terbaik, tapi untuk satu sama lain, hanya langkah pemain kedua yang terbaik diperlukan untuk mengakali penelusuran tersebut, namun dalam hal ini alpha-beta memastikan pergerakan pemain kedua yang perlu dipertimbangkan.

2. Algoritma Greedy

(43)

29

BAB III

PERANCANGAN DAN DESAIN

Dalam bab ini penulisan Tugas Akhir ini dibagi dalam beberapa sub bab. Pertama adalah kebutuhan sistem yang berisi tentang kebutuhan perangkat keras maupun perangkat lunak yang digunakan. Kedua adalah data yang dipakai dalam implementasi algoritma ke dalam game.

3.1.Kebutuhan Sistem

Dalam penelitian ini penulis menggunakan spesifikasi perangkat keras dan perangkat lunak sebagai berikut:

3.1.1. Perangkat Keras

Perangkat keras yang dibutuhkan dalam proses implementasi algoritma untuk game adalah sebagai berikut:

• Laptop : Processor minimum Intel Celeron, RAM minimum 1 GB, penyimpanan berukuran 512 MB, keyboard dan mouse.

3.1.2. Perangkat Lunak

Untuk perangkat lunak yang digunakan terutama untuk proses implementasi algoritma ke dalam game menggunakan sistem operasi Windows 7. Sedangkan untuk membangun aplikasi game yang berbasis desktop akan menggunakan aplikasi Netbeans, serta untuk bahasa pemrogramannya menggunakan Java.

3.1.3. Data

(44)

30

akan dibuat seperti papan Othello pada umumnya, namun dengan papan yang berukuran 8 x 8 blok.

Gambar 3.1. Koordinat papan Othello

(45)

31

Gambar 3.2. Keadaan permainan Othello saat ini (kiri) dan kemungkinan komputer/pemain lawan untuk meletakkan kepingan putih yang diarsir (kanan).

3.2.Perancangan Proses

3.2.1. Diagram dan Skenario Use Case

Dalam permainan Othello ini akan dirancang use case sebagai berikut:

Gambar 3.3. Diagram use case permainan Othello a. Nama Use Case : Memulai permainan

Aktor : Pengguna

(46)

32

Aksi Aktor Reaksi Sistem

1. Aktor memilih menu

Kondisi Awal : Aktor sudah berada di menu utama permainan Skenario :

1. Aktor memilih menu ‘Bantuan dan Info’.

2. Sistem menampilkan bantuan dan Info permainan Othello.

c. Nama Use Case : Keluar dari permainan Aktor : Pengguna

Kondisi Awal : Aktor sudah berada di menu utama permainan Skenario :

1. Aktor menekan tombol X (keluar).

(47)

33

3.2.2. Diagram Alur (Flowchart)

Gambar di bawah ini menunjukkan alur yang terjadi pada sistem. Sistem menunjukkan peran yang terjadi serta mengecek perbandingan algoritma dalam suatu permainan.

1. Diagram alur algoritma Greedy

Diagram alur untuk algoritma Greedy ditunjukkan dalam gambar berikut:

(48)

34

Diagram alur tersebut menggambarkan mulainya algoritma Greedy dengan inisialisasi awal papan Othello dengan nilai awal null serta nilai maksimum sama dengan nilai minimum, lalu dilanjutkan dengan membuat ukuran baris dan kolom pada papan Othello. Menuju percabangan apakah langkah pada Othello memang valid, bila iya maka langkah tersebut masuk sebagai poin, bila tidak maka akan mengembalikan nilai terbaik. Menuju percabangan apakah jika nilai lebih dari nilai maksimum, jika ya maka maxScore diinisialisasikan sebagai score tipe integer dan best dengan Point baru dan mengembalikan nilai terbaik, jika tidak maka membuat papan baru seperti sebelumnya dan mengembalikan nilai terbaik.

2. Diagram alur algoritma Alpha-Beta

Diagram alur untuk algoritma Alpha-Beta ditunjukkan dalam gambar berikut:

(49)

35

Gambar 3.5. Diagram alur method generateMoves algoritma Alpha-Beta.

(50)

36 b. Method minimax

Gambar 3.6. Diagram alur method minimax algoritma Alpha-Beta.

(51)

37

(52)

38 c. Method maxValue

(53)

39

(54)

40 d. Method minValue

(55)

41

(56)

42

3.3. Desain Antarmuka 3.3.1. Menu ‘Single Play’

Gambar 3.10. Menu ‘Single Play’ permainan Othello.

(57)

43

3.3.2. Menu ‘AI vs AI’

Gambar 3.11. Menu ‘AI vs AI’ permainan Othello.

(58)

44 BAB IV

IMPLEMENTASI DAN ANALISIS HASIL

Bab ini berisi tentang hasil penelitian mengenai sistem yang telah dibuat dari analisis serta perancangan yang dibahas pada bab-bab sebelumnya serta analisa mengenai hasil yang telah didapatkan. Aplikasi ini dibuat dengan perangkat lunak Netbeans IDE 8.0.2 pada laptop dengan RAM 4 GB dengan sistem operasi Windows 7. Berikut ini adalah pembahasan pada bagian antarmuka serta implementasi Othello dengan algoritma Alpha-Beta Pruning dan Greedy.

4.1. Implementasi Antarmuka Pemakai

Bagian ini menjelaskan mengenai implementasi dari perancangan

(59)

45

4.1.1. Implementasi Antarmuka Menu ‘Single Play’

Gambar 4.1. Implementasi antarmuka menu ‘Single Play’.

(60)

46

lawan, lalu ada tombol “Mulai Baru” yang mengulang permainan dari awal serta “Keluar” yang keluar dari permainan Othello.

4.1.2. Implementasi Antarmuka Menu ‘AI vs. AI’

Gambar 4.2. Implementasi antarmuka menu ‘AI vs. AI’.

(61)

47 4.2. Implementasi Algoritma pada Sistem

Dalam subbab ini akan dijelaskan mengenai implementasi 3 algoritma dalam permainan Othello, yaitu algoritma Alpha-Beta Pruning, algoritma Greedy, dan perbandingan antara kedua algoritma berdasarkan jumlah kepingan dalam Othello.

4.2.1. Algoritma Alpha-Beta Pruning

Dalam algoritma ini akan dijelaskan mengenai proses dalam pencarian node yang pada dasarnya menggunakan algoritma Minimax. Berikut ini merupakan proses jalannya algoritma Alpha-Beta Pruning: Pertama adalah membuat papan yang berukuran 8 x 8 yang mengambil dari method Board agar kepingan dapat melangkah.

Berikut adalah algoritma Alpha-Beta Pruning yang diimplementasikan dalam permainan Othello:

1. Menentukan koordinat papan dengan ListPoint.

2. Untuk setiap baris j sama dengan 0 dan j kurang dari size (yang

sebelumnya size diinisialisasi sebanyak 8), dan j bertambah, maka lakukan langkah selanjutnya.

3. Untuk setiap kolom i sama dengan 0 dan i kurang dari size (yang

sebelumnya size diinisialisasi sebanyak 8), dan j bertambah, maka lakukan langkah selanjutnya.

4. Perbarui papan pemainan dan tambahkan posisi kepingan yang

sudah ditandai.

Masuk ke method Minimax, jika kedalaman langkah kurang dari atau

sama dengan 0 atau game over maka tidak mengembalikan nilai apapun.

Jika tidak maka lakukan langkah selanjutnya.

1. Inisialisasi jumlah kepingan yang sedang berlangsung dengan nilai

(62)

48

2. Inisialisasi langkah current dan semua langkah yang telah

dilakukan.

3. Untuk setiap langkah yang dilakukan di tiap titik, inisialisasikan di

papan Othello dan buat langkah sementara (clone) dalam suatu

baris dan kolom papan, dan buat hasil langkah tersebut minimum. Masuk ke method minValue dan maxValue yang dal hal ini kedua method mengecek kedalaman langkah sampai akhir permainan yang kemudian diberlakukan algoritma Alpha-Beta Pruning yaitu pada nilai terbaik untuk simpul Max adalah negatif infiniti dan akan naik seiring berjalannya permainan sedangkan untuk simpul Min adalah positif infiniti dan akan menurun seiring berjalannya permainan.

4.2.2. Algoritma Greedy

Dalam algoritma ini akan dijelaskan mengenai proses dalam pencarian node yang menggunakan algoritma Greedy. Berikut ini merupakan proses jalannya algoritma:

1. Inisialisasi papan permainan yang digunakan (Othello

menggunakan papan berukuran 8x8).

2. Inisialisasi nilai maksimum merupakan nilai minimum.

3. Untuk setiap baris papan dengan nilai awal 0 dan kurang dari 8

serta kolom papan dengan nilai awal 0 dan kurang dari 8 maka lakukan langkah selanjutnya.

4. Jika kepingan Othello dalam suatu baris dan kolom papan

merupakan langkah yang valid maka hitung jumlah kepingan yang bewarna tertentu dalam papan tersebut dan lakukan langkah selanjutnya.

5. Ulangi langkah ketiga sampai papan tidak ada yang kosong atau

(63)

49 4.3. Hasil Uji Algoritma

4.3.1. Algoritma Alpha-Beta dengan Greedy

Kondisi permainan pertama adalah algoritma Alpha-Beta menggunakan kepingan hitam dan Greedy menggunakan kepingan putih.

Gambar 4.3. Perbandingan algoritma Alpha-Beta dengan Greedy.

(64)

50

maksimum dan minimum sehingga semua papan terisi dengan jumlah kepingan 17 banding 43.

Gambar 4.4. Perbandingan algoritma Alpha-Beta dengan Greedy.

(65)

51

didapat saat melangkah sehingga Alpha-Beta benar-benar mendominasi papan Othello.

4.3.2. Perbandingan Skor dan Grafik Waktu

Dalam bagian ini akan dijelaskan mengenai perbandingan algoritma dengan pengujian sebanyak 50 kali. Berikut ini merupakan hasil skor yang telah diujikan dalam permainan Othello:

1) Perbandingan algoritma Alpha-Beta Pruning sebagai kepingan hitam

dan Greedy sebagai kepingan putih

Tabel 4.1. Pengujian algoritma Alpha-Beta dengan Greedy.

Percobaan ke Alpha-Beta Pruning _{(Kepingan Hitam)} Greedy (Kepingan _Putih)

(66)

(67)

53

42 17 43

43 17 43

44 17 43

45 17 43

46 17 43

47 17 43

48 17 43

49 17 43

50 17 43

(68)

54

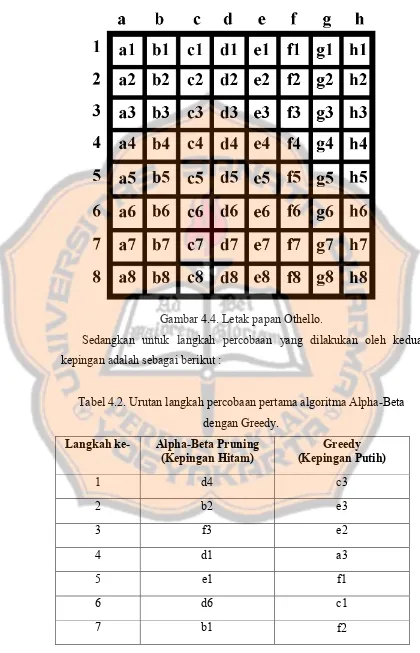
Gambar 4.4. Letak papan Othello.

Sedangkan untuk langkah percobaan yang dilakukan oleh kedua kepingan adalah sebagai berikut :

Tabel 4.2. Urutan langkah percobaan pertama algoritma Alpha-Beta dengan Greedy.

Langkah ke- Alpha-Beta Pruning

(Kepingan Hitam) (Kepingan Putih)Greedy

1 d4 c3

2 b2 e3

3 f3 e2

4 d1 a3

5 e1 f1

6 d6 c1

(69)

55

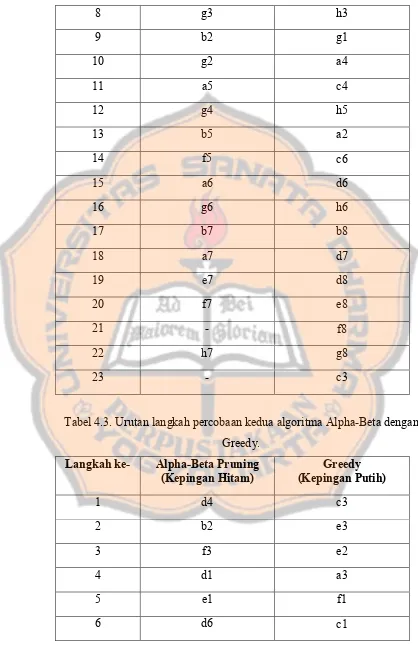
Tabel 4.3. Urutan langkah percobaan kedua algoritma Alpha-Beta dengan Greedy.

(70)

56

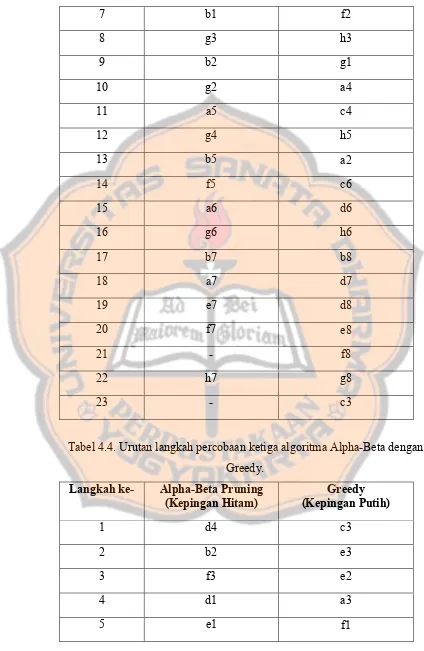
Tabel 4.4. Urutan langkah percobaan ketiga algoritma Alpha-Beta dengan Greedy.

1 d4 c3

2 b2 e3

3 f3 e2

4 d1 a3

(71)

57

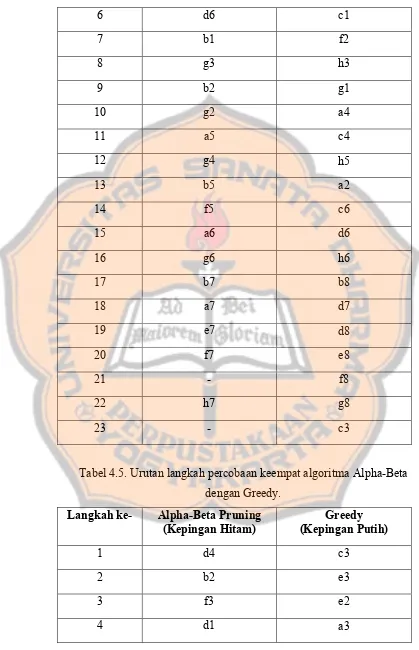
Tabel 4.5. Urutan langkah percobaan keempat algoritma Alpha-Beta dengan Greedy.

1 d4 c3

2 b2 e3

3 f3 e2

(72)

58

Tabel 4.6. Urutan langkah percobaan kelima algoritma Alpha-Beta dengan Greedy.

1 d4 c3

2 b2 e3

(73)

59

(74)

60

2) Perbandingan algoritma Greedy sebagai kepingan hitam dan

Alpha-Beta Pruning sebagai kepingan putih

Apabila kondisi kepingan kedua algoritma dibalik, maka akan diperoleh hasil berikut:

Tabel 4.7. Pengujian Algoritma Greedy dengan Alpha-Beta

Percobaan ke _{(Kepingan Hitam)}Greedy Alpha-Beta Pruning _{(Kepingan Putih)}

(75)

(76)

62

Dalam percobaan ini, algoritma Greedy sempat mengambil beberapa bagian sisi papan Othello, namun dengan penelusuran dari algoritma Alpha-Beta, serta pengambilan keputusan di tiap node, maka kepingan pada papan Othello dikuasai oleh kepingan putih (Alpha-Beta), sehingga permainan dimenangkan oleh Alpha-Beta secara mutlak. Berikut ini merupakan urutan langkah percobaan 1-5 yang dilakukan oleh kedua algoritma dengan kepingan hitam yang maju pertama.

Tabel 4.8. Urutan langkah percobaan pertama algoritma Greedy dengan Alpha-Beta.

Langkah ke- Greedy

(Kepingan Hitam) (Kepingan Putih)Alpha-Beta

(77)

63

Tabel 4.9. Urutan langkah percobaan kedua algoritma Greedy dengan Alpha-Beta.

(78)

64

15 b7 f5

16 b5 f1

17 - d6

18 - f7

Tabel 4.10. Urutan langkah percobaan ketiga algoritma Greedy dengan Alpha-Beta.

(79)

65

Tabel 4.11. Urutan langkah percobaan keempat algoritma Greedy dengan Alpha-Beta.

(80)

66

Tabel 4.12. Urutan langkah percobaan kelima algoritma Greedy dengan Alpha-Beta.

1 d3 c3

(81)

67

3) Perbandingan algoritma Alpha-Beta Pruning sebagai kepingan hitam

dan kepingan putih

Tabel 4.13. Pengujian Algoritma Alpha-Beta dengan Alpha-Beta

Percobaan ke Alpha-Beta Pruning _{(Kepingan Hitam)} Alpha-Beta Pruning _{(Kepingan Putih)}

(82)

(83)

69

48 28 32

49 28 32

50 28 32

Dalam tabel tersebut ditunjukkan perbandingan algoritma Alpha-Beta dengan memakai kedua kepingan hitam dan putih. Mulai dengan kepingan hitam dengan algoritma Alpha-Beta Pruning hingga akhir permainan dimenangkan oleh kepingan putih. Berikut ini merupakan grafik waktu yang dibutuhkan oleh Alpha-Beta saat eksekusi perbandingan algoritma.

Gambar 4.5. Grafik waktu jalannya algoritma Alpha-Beta dalam Othello.

(84)

70

papan karena daerah kosong yang tinggal sedikit, maka penelusurannya juga memakan waktu yang cukup singkat, berikut ini merupakan salah satu hasil eksekusi algoritma Alpha-Beta yang diimplementasikan dalam kedua kepingan dalam papan Othello.

Gambar 4.6. Perbandingan algoritma Alpha-Beta dalam Othello.

(85)

71

Tabel 4.14. Urutan langkah percobaan pertama algoritma Alpha-Beta dengan Alpha-Beta.

Langkah ke- Alpha-Beta

(86)

72

24 c8 d8

25 e8 f8

26 g8 -

Tabel 4.15. Urutan langkah percobaan kedua algoritma Alpha-Beta dengan Alpha-Beta.

(87)

73

Tabel 4.16. Urutan langkah percobaan ketiga algoritma Alpha-Beta dengan Alpha-Beta.

(88)

74

Tabel 4.17. Urutan langkah percobaan keempat algoritma Alpha-Beta dengan Alpha-Beta.

(89)

75

Tabel 4.18. Urutan langkah percobaan kelima algoritma Alpha-Beta dengan Alpha-Beta.

(90)

76

(91)

77

4) Perbandingan algoritma Greedy sebagai kepingan hitam dan kepingan

putih

Tabel 4.19. Pengujian Algoritma Greedy dengan Greedy

Percobaan ke Greedy (Kepingan _Hitam) Greedy (Kepingan _Putih)

(92)

(93)

79

48 35 25

49 35 25

50 35 25

Dalam tabel tersebut ditunjukkan perbandingan algoritma Greedy dengan memakai kedua kepingan hitam dan putih. Mulai dengan kepingan hitam dengan algoritma Greedy hingga akhir permainan dimenangkan oleh kepingan hitam. Berikut ini merupakan grafik waktu yang dibutuhkan oleh Greedy saat eksekusi perbandingan algoritma.

Gambar 4.7. Grafik waktu jalannya algoritma Greedy dalam Othello.

Grafik ini menunjukkan waktu yang dikerjakan kedua algoritma yang dalam hal ini sama-sama algoritma Greedy, berbeda dengan Alpha-Beta, algoritma ini membuat waktu yang lebih singkat dan lebih stabil karena algoritma ini mencari lebih banyak kemenangan dengan mengambil kemungkinan papan yang mendapatkan kepingan lebih banyak dari yang lain sehingga tidak diperlukan pencarian lebih lanjut dalam algoritma ini,

(94)

80

berikut ini merupakan salah satu hasil eksekusi algoritma Greedy yang diimplementasikan dalam kedua kepingan dalam papan Othello.

Gambar 4.8. Perbandingan algoritma Greedy dalam Othello.

(95)

81

Tabel 4.20. Urutan langkah percobaan pertama algoritma Greedy dengan Greedy.

(96)

82

24 e8 e1

25 h2 c8

Tabel 4.21. Urutan langkah percobaan kedua algoritma Greedy dengan Greedy.

(97)

83

Tabel 4.22. Urutan langkah percobaan ketiga algoritma Greedy dengan Greedy.

(98)

84

Tabel 4.23. Urutan langkah percobaan keempat algoritma Greedy dengan Greedy.

(99)

85

Tabel 4.24. Urutan langkah percobaan kelima algoritma Greedy dengan Greedy.

(100)

86

12 a6 c2

13 c1 a5

14 h7 b3

15 a4 f2

16 g3 g1

17 c6 f6

18 g4 g1

19 h3 b7

20 c7 a2

21 b8 a7

22 f8 g8

23 h5 e6

24 e8 e1

25 h2 c8

(101)

87 BAB V

KESIMPULAN DAN SARAN

5.1. Kesimpulan

Kesimpulan yang dapat diambil dari penelitian analisa perbandingan algoritma Alpha-Beta dan Greedy pada permainan Othello adalah:

1. Dalam hal waktu, Greedy lebih cepat dalam memproses eksekusi permainan Othello terutama bila dibandingkan dengan Alpha-Beta karena disamping kompleksitas waktu yang tidak begitu rumit serta dari grafik yang menunjukkan waktu prosesnya algoritma tersebut. 2. Algoritma Alpha-Beta dalam hal waktu tidak begitu baik di awal

karena proses pencarian cabang pohon permainan Othello pada kedalaman tertentu yang memerlukan waktu yang cukup lama, karena kemungkinan percabangan permainan Othello lebih banyak pada saat pertengahan permainan. Algoritma ini cukup efisien karena pencarian kemungkinan permainannya dibanding dengan algoritma Greedy yang sifatnya tamak. Langkah-langkah yang menjepit keping lawan terbanyak akan dievaluasi terlebih dahulu dan langkah yang kurang menguntungkan akan dibuang.

(102)

88 5.2.Saran

Peneliti ingin menyampaikan beberapa saran yang mungkin nantinya dapat berguna bagi kepentingan pihak-pihak yang peneliti sebutkan. Saran ini ditujukan bagi mahasiswa dan peneliti lain, yaitu:

1. Bagi mahasiswa

Diharapkan dari penelitian ini dapat membantu mahasiswa bahkan dapat menunjang pembelajaran maupun tugas akhir dengan topik yang relevan dengan tugas akhir ini.

2. Bagi peneliti lain

(103)

89

DAFTAR PUSTAKA

Anggraeni, D. 2012. Reversi Othello.

http://reversi-othello.blogspot.co.id/p/reversi.html, diakses 05 Januari 2017.

Anggraeni, D. R. 2013. Alpha-Beta Pruning. https://blog.ub.ac.id/dinaarizky/

2013/10/22/alpha-beta-pruning, diakses 20 Maret 2018.

Kosasi, S. 2014. Permainan Papan Strategi Menggunakan Algoritma Minimax.

Seminar Nasional Teknologi Informasi, Komunikasi dan Industri (SNTIKI) 6.

Pekanbaru, 24 September 2014.

Leouski, A. 1995. Learning of Position Evaluation in the Game of Othello.