PERBANDINGAN METODE RUNGE-KUTTA ORDE EMPAT DAN METODE ADAMS-BASHFORTH ORDE EMPAT DALAM PENYELESAIAN MASALAH NILAI AWAL ORDE SATU

PERBANDINGAN METODE RUNGE-KUTTA ORDE EMPAT DAN

METODE ADAMS-BASHFORTH ORDE EMPAT DALAM PENYELESAIAN

MASALAH NILAI AWAL ORDE SATU

Lilik Prasetiyo Pratama

Jurusan Matematika, FMIPA UNS

1.

LATAR BELAKANG

Tidak semua persamaan diferensial biasa dapat ditentukan penyelesaian eksaknya. Oleh

karena itu, diperlukan suatu metode untuk menjelaskan penyelesaian tersebut.

Salah satu

metode tersebut adalah metode numerik. Metode numerik yang digunakan untuk memperoleh

penyelesaian masalah nilai awal dapat berupa metode satu step maupun multistep. Dikatakan

metode satu step jika penyelesaian di titik

x

=

x

n

diperoleh berdasarkan penyelasaian di titik

sebelumnya,

x

=

x

n−1

. Jika dibutuhkan penyelesaian di beberapa titik sebelumnya, disebut

metode multistep.

Salah satu metode satu step adalah metode Runge-Kutta dam salah satu metode multistep

adalah Adams-Bashforth. Karena penyelesaian yang diperoleh dengan metode numerik adalah

penyelesaian pendekatan serta dalam proses mendapatkan penyelesaian pendekatan

membu-tuhkan waktu, maka terdapat eror dan lama waktu proses. Oleh karena itu, perlu diteliti

keakuratan dan efisiensi metode Runge-Kutta dan Adams-Bashforth, khususnya orde 4.

2.

PERUMUSAN MASALAH

Dari latar belakang dapat dirumuskan tiga masalah, yaitu

(1) bagaimana menurunkan ulang algoritma Runge-Kutta orde empat dan Adams-Bashforth

orde empat,

(2) bagaimana menerapkan algoritma Runge-Kutta orde empat dan Adams-Bashforth orde

empat pada suatu kasus, dan

(3) bagaimana keakuratan dan efisiensi metode Runge-Kutta orde empat dan Adams-Bashforth

orde empat.

3.

TUJUAN

Tujuan penulisan artikel ini adalah

(1) dapat menurunkan ulang algoritma Runge-Kutta orde empat dan Adams-Bashforth orde

empat,

(2) dapat menerapkan algoritma Runge-Kutta orde empat dan Adams-Bashforth orde empat

pada suatu kasus, dan

(3) dapat mengetahui keakuratan dan efisiensi metode Runge-Kutta orde empat dan

Adams-Bashforth orde empat.

4.

_PEMBAHASAN

Dalam penulisan ini, penurunan algoritma Runge-Kutta orde empat mengacu pada Gear

[3]. Sedangkan penurunan algoritma Adams-Bashforth orde empta mengacu pada Burden dan

Faires [2] dan Gear [3].

4.1.

Metode Runge-Kutta Orde Empat.

Bentuk umum metode Runge-Kutta orde empat

adalah:

y

n+1

=

y

n

+

h

(

c

1

k

1

+

c

2

k

2

+

c

3

k

3

+

c

4

k

4

)

for

n

= 0

,

1

,

2

, . . .

k

1

=

f

(

x

n

, y

n

)

k

2

=

f x

n

+

µh, y

n

+

hµk

1

k

3

=

f

(

x

n

+

λh, y

n

+

ρhk

2

+ (

λ

−

ρ

)

hk

1

)

k

4

=

f

(

x

n

+

νh, y

n

+

σhk

3

+

τ hk

2

+ (

ν

−

σ

−

τ

)

hk

1

)

.

Terdapat sepuluh konstanta

c

1

, c

2

, c

3

, c

4

, µ, λ, ρ, ν, σ

dan

τ

yang harus ditentukan sehingga eror

pemotongan lokalnya

O

(

h

4

) dan eror globalnya

O

(

h

5

). Dalam kasus ini diperoleh delapan

persamaan dengan sepuluh variabel:

c

1

+

c

2

+

c

3

+

c

4

= 1

,

µc

2

+

λc

3

+

νc

4

=

1

2

,

µ

2

c

2

+

λ

2

c

3

+

ν

2

c

4

=

1

3

,

µρc

3

+ (

λσ

+

µτ

)

c

4

=

1

6

,

µ

3

c

2

+

λ

3

c

3

+

ν

3

c

4

=

1

4

,

µ

2

_ρc

3

+ (

λ

2

σ

+

µ

2

τ

)

c

4

=

1

12

,

σµρc

4

=

1

24

,

µλρc

3

+ (

λσ

+

µτ

)

νc

4

=

1

8

.

Karena ada delapan persamaan dan sepuluh variabel, maka terdapat banyak sekali

penyele-saian. Jika setiap variabel dinyatakan dalam

µ

dan

λ

dan dipilih

µ

=

λ

=

1₂

, maka diperoleh

ρ

=

1

6

c

3

,

τ

= 1

−

3

c

3

,

ν

= 1

, c

1

=

1

6

,

c

2

=

2

3

−

c

3

,

c

4

=

1

6

.

Jika nilai

c

3

=

1₃

, diperoleh metode Runge-Kutta orde empat:

y

n+1

=

y

n

+

h

6

(

k

1

+ 2

k

2

+ 2

k

3

+

k

4

)

for

n

= 0

,

1

,

2

, . . .

k

1

=

f

(

x

n

, y

n

)

k

2

=

f

(

x

n

+

h

2

, y

n

+

h

2

k

1

)

k

3

=

f

(

x

n

+

h

2

, y

n

+

h

2

k

2

)

k

4

=

f

(

x

n

+

h, y

n

+

hk

3

)

4.2.

Metode Adams-Bashforth Orde Empat.

Metode Adams-Bashforth diturunkan

de-ngan mengintegralkan persamaan diferensial biasa,

y

0

=

f

(

x, y

) =

f

(

x, y

(

x

))

pada interval [

x

n−1

, x

n

], diperoleh

y

(

x

n

) =

y

(

x

n−1

) +

Z

xn

xn−1

f

(

x, y

(

x

))

dx.

(4.1)

Diperhatikan polinomial berderajat

k

−

1,

p

k−1

(

x

), yang menginterpolasi fungsi

f

(

x, y

(

x

))

pada persamaan (4.1) melalui titik-titik

x

n−1

,

x

n−2

,

. . .

, dan

x

n−k

. Dengan menggunakan

bentuk selisih mundur Newton diperoleh polinomial interpolasi

p

k−1

(

x

) =

k−1

X

i=0

∇

i

_f

n−1

i

!

h

i i−1

Y

j=0

(

x

−

x

n−1−j

)

.

(4.2)

Dari polinomial interpolasi (4.2), terdapat suatu bilangan

ξ

n−1

pada (

x

n−k

, x

n−1

) dengan

f

(

x, y

(

x

)) =

p

k−1

(

x

) +

f

(k)

(

ξ

n−1

, y

(

ξ

n−1

))

k

!

k−1

Y

j=0

(

x

−

x

n−1−j

)

.

(4.3)

Dimisalkan

x

=

x

n

+

sh

, dengan

dx

=

hds

, dan dengan menggunakan definisi fungsi binomial

1

i

!

h

i i−1

Y

j=0

(

x

−

x

n−1−j

) =

i−1

Y

j=0

s

+

j

i

!

= (−1)

i

₋

_s

i

,

polinomial interpolasi (4.2) menjadi

p

k−1

(

x

) =

k−1

X

i=0

(−1)

i

−

s

i

∇

i

f

n−1

.

(4.5)

Dengan memperhatikan persamaan (4.3) dan (4.5), persamaan (4.1) menjadi

y

(

x

n

) =

y

(

x

n−1

) +

"

Z

xn xn−1 k−1

X

i=0

(

−

1)

i

−

s

i

!

∇

i

f

n−1

dx

+

Z

xn xn−1

f

(k)

₍

_ξ

n−1

, y

(

ξ

n−1

))

k

!

k−1

Y

j=0

(

x

−

x

n−1−j

)

dx

#

=

y

(

x

n−1

) +

h

k−1

X

i=0

(

−

1)

i

∇

i

f

n−1

Z

1 0

−

s

i

!

ds

+

h

k+1

k

!

Z

1 0 k−1

Y

j=0

(

x

−

x

n−1−j

)

f

(k)

(

ξ

n−1

, y

(

ξ

n−1

))

ds.

Jika (

−

1)

i

R

1 0

−s i

ds

dievaluasi dengan

i

= 0

,

1

,

2

, . . . , k

−

1 dan

y

(

x

n

)

≈

y

n

serta

y

(

x

n−1

) =

y

n−1

,

diperoleh

y

n

=

y

n−1

+

h

1 +

1

2

∇

+

5

12

∇

2

+

3

8

∇

3

+

. . .

+ (

−

1)

i

Z

1 0

−

s

i

!

ds

∇

k−1

!

f

n−1

,

(4.6)

dengan eror lokal

T

n

=

h

k+1

k

!

Z

1 0 k−1

Y

j=0

(

x

−

x

n−1−j

)

f

(k)

(

ξ

n−1

, y

(

ξ

n−1

))

ds.

Ambil

i

= 3, maka persamaan (4.6) menjadi

y

n

=

y

n−1

+

h

(1 +

1

2

∇

+

5

12

∇

2

+

3

8

∇

3

)

f

n−1

.

(4.7)

Menurut Gear [3], selisih mundur dapat diekspresikan sebagai nilai fungsi di titik-titik sebelumnya,

yaitu

∇

q

f

n−1

=

q

X

j=0

(

−

1)

j

q

j

!

f

n−1−j

.

Akibatnya persamaan (4.7) menjadi

y

n

=

y

n−1

+

h

24

(55

f

n−1

−

57

f

n−2

+ 37

f

n−3

−

9

f

n−4

)

,

n

= 4

,

5

,

6

, . . .

yang merupakan metode Adams-Bashforth orde empat.

4.3.

Estimasi Eror.

Jika penyelesaian eksak masalah nilai awal tidak diketahui, maka eror perlu

di-estimasi dan digunakan ide ekstrapolasi Richardson untuk mengdi-estimasi eror (Apsley, [1]). Ide dari

ekstrapolasi RIchardson adalah menghitung eror global pada iterasi ke-

n

dengan mengambil ukuran

step

h

,

y

(

x

)

−

y

n

(

h

), dan 2

h

,

y

(

x

)

−

y

n

(2

h

). Selanjutnya kedua eror tersebut digunakan untuk

menges-timasi eror penyelesaian dengan ukuran step

h

.

Jika orde dari algorita yang diterapkan adalah

k

maka berlaku

y

(

x

)

−

y

n

(

h

)

≈

O

(

h

k

)

(4.8)

dan

y

(

x

)

−

y

n

(2

h

)

≈

2

k

O

(

h

k

)

.

(4.9)

Persamaan (4.8) dikalikan dengan 2

k

dan dikurangi dengan (4.9), diperoleh

y

(

x

)

−

y

n

(

h

)

≈

1

2

k

₋

₁

(

y

n

(

h

)

−

y

n

(2

h

))

.

(4.10)

Dari persamaan (4.10), maka estimasi eror penyelesaian dengan ukuran step

h

menggunakan algoritma

berorde

k

adalah

1

(

y

(

h

)

−

y

(2

h

)).

5.

PENERAPAN KASUS

Kasus 5.1.

Diberikan masalah nilai awal

y

0

=

2

x

y

+

x

2

e

x

,

1

≤

x

≤

2

,

y

(1) = 0

.

(5.1)

Masalah nilai awal (5.1) memiliki penyelesaian eksak

y

(

x

) = (

−

e

+

e

x

)

x

2

.

Masalah nilai awal (5.1) diselesaikan dengan metode Runge-Kutta dan Adams-Bashforth orde empat

dengan ukuran step

h

= 0

.

05, 0.025, 0.0125, dan 0.00625. Karena penyelesaian eksaknya diketahui,

maka eror dapat ditentukan dengan mudah. Eror mutlak penyelsaian yang terjadi ditunjukkan pada

Tabel 1 dan 2.

Tabel 1. Eror mutlak yang terjadi di lima titik, jika digunakan metode Runge-Kutta orde empat untuk

masalah nilai awal (5.1)

x

h

= 0

.

05

h

= 0

.

025

h

= 0

.

0125

h

= 0

.

00625

1.2

1

.

46608

×

10

−6

₉

_.

₇₂₀₀₅

_×

₁₀

−8

₆

_.

₂₅₆₇₅

_×

₁₀

−9

₃

_.

₉₆₈₄₄

_×

₁₀

−10

1.4

3

.

36821

×

10

−6

2

.

22485

×

10

−7

1

.

42949

×

10

−8

9

.

05837

×

10

−10

1.6

5

.

70824

×

10

−6

3

.

76061

×

10

−7

2

.

41308

×

10

−8

1

.

5281

×

10

−9

1.8

8

.

49846

×

10

−6

₅

_.

₅₈₇₇₂

_×

₁₀

−7

₃

_.

₅₈₁₉₇

_×

₁₀

−8

₂

_.

₂₆₇₁₄

_×

₁₀

−9

2.0

1

.

17557

×

10

−5

7

.

71724

×

10

−7

4

.

94326

×

10

−8

3

.

12744

×

10

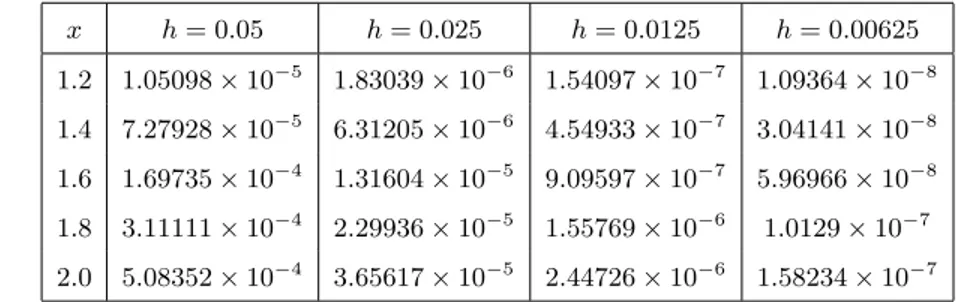
−9

Tabel 2. Eror mutlak yang terjadi di lima titik, jika digunakan metode Adams-Bashforth orde empat

untuk masalah nilai awal (5.1)

x

h

= 0

.

05

h

= 0

.

025

h

= 0

.

0125

h

= 0

.

00625

1.2

1

.

05098

×

10

−5

1

.

83039

×

10

−6

1

.

54097

×

10

−7

1

.

09364

×

10

−8

1.4

7

.

27928

×

10

−5

₆

_.

₃₁₂₀₅

_×

₁₀

−6

₄

_.

₅₄₉₃₃

_×

₁₀

−7

₃

_.

₀₄₁₄₁

_×

₁₀

−8

1.6

1

.

69735

×

10

−4

1

.

31604

×

10

−5

9

.

09597

×

10

−7

5

.

96966

×

10

−8

1.8

3

.

11111

×

10

−4

2

.

29936

×

10

−5

1

.

55769

×

10

−6

1

.

0129

×

10

−7

2.0

5

.

08352

×

10

−4

₃

_.

₆₅₆₁₇

_×

₁₀

−5

₂

_.

₄₄₇₂₆

_×

₁₀

−6

₁

_.

₅₈₂₃₄

_×

₁₀

−7

Orde dari kedua metode dapat ditunjukkan dengan menghitung rasio eror mutlak

eror

h

eror

h/2

dengan

h

= 0

.

05, 0.025, dan 0.0125 untuk masing-masing metode di titik yang sama. Hasil perhitungan dapat

dilihat pada Gambar 1, dengan garis hitam untuk

h

= 0

.

05, hitam tebal untuk

h

= 0

.

025, dan hitam

putus-putus untuk

h

= 0

.

0125.

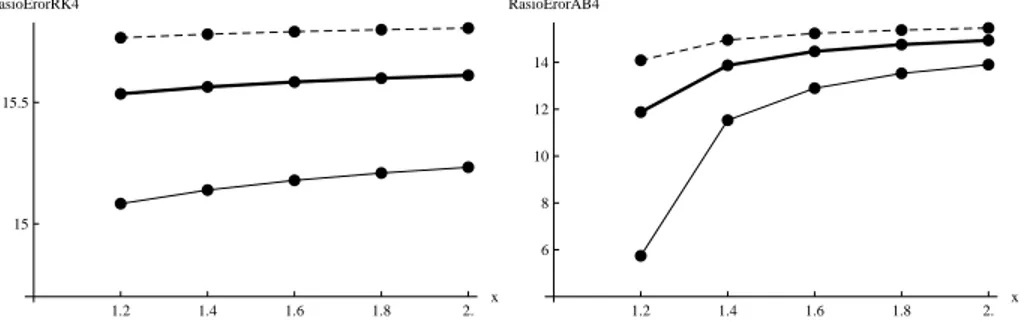
1.2 1.4 1.6 1.8 2. x 15 15.5 RasioErorRK4 1.2 1.4 1.6 1.8 2. x 6 8 10 12 14 RasioErorAB4

Gambar 1. Rasio eror mutlak

h

dan

h/

2 di lima titik, berturut-turut dengan metode Runge-Kutta

(kiri) dan Adams-Bashforth (kanan) orde empat.

Dari Gambar 1 terlihat bahwa untuk pengambilan

h

= 0

.

05, 0.025, dan 0.0125, rasio eror mutlak

eror

h

eror

h/2

≈

16. Hal ini menunjukkan bahwa orde dari algoritma yang diterapkan adalah empat.

Tabel 1 dan 2 menunjukkan bahwa pada ukuran step

h

yang sama, eror mutlak penyelesaian

de-ngan metode Runge-Kutta orde empat lebih kecil dibandingkan dede-ngan metode Adams-Bashforth orde

empat. Keakuratan kedua metode dapat dibandingkan dengan menghitung rasio eror mutlak

eror

AB4

eror

RK4

pada setiap pengambilan

h

di titik yang sama. Hasil perhitungan rasio ini dapat dilihat pada

Gam-bar 2, dengan garis hitam untuk

h

= 0

.

05, hitam tebal untuk

h

= 0

.

025, hitam putus-putus untuk

h

= 0

.

0125, dan hitam tebal putus-putus untuk

h

= 0

.

00625.

1.2 1.4 1.6 1.8 2. x 10

30 50 RasioRK4_AB4

Gambar 2. Rasio eror mutlak Runge-Kutta dan Adams-Bashforth orde empat untuk berbagai nilai

h

.

Gambar 2 menunjukkan bahwa untuk pengambilan

h

= 0

.

05, 0.025, 0.0125, dan 0.00625, semakin

kecil ukuran step

h

maka rasio eror mutlak

eror

AB4

eror

RK4

≈

50. Hal ini menunjukkan bahwa pada orde

empat, keakuratan Runge-Kutta adalah 50 kali metode Adams-Bashforth. Dapat disimpulkan, pada

orde empat, metode Runge-Kutta lebih akurat daripada metode Adams-Bashforth.

Efisiensi dapat dibandingkan dengan menghitung lama waktu program berjalan hingga diperoleh

penyelesaian pendekatan. Hasil perhitungan lama waktu dapat dilihat pada Tabel 3.

Tabel 3. Lama waktu proses dengan menggunakan metode Runge-Kutta dan metode Adams-Bashforth

orde empat dengan ukuran step

h

= 0

.

05, 0.025, 0.0125, dan 0.00625

h

0.05

0.025

0.0125

0.00625

Runge-Kutta orde 4

0.

0.

0.016

0.016

Adams-Bashforth orde 4

0.

0.

0.

0.015

Tabel 3 menunjukkan bahwa pada ukuran step

h

yang sama, dengan

h

= 0

.

05, 0.025, 0.0125, dan

0.00625, lama waktu proses program Adams-Bashforth orde empat lebih cepat daripada Runge-Kutta

orde empat. Dapat disimpulkan, pada orde empat, metode Adams-Bashforth lebih efisien daripada

metode Runge-Kutta.

Kasus 5.2.

Diberikan masalah nilai awal,

y

0

= 2

yx

2

+ 4

,

0

≤

x

≤

1

,

y

(0) = 1

(5.2)

dengan penyelesaian eksak tidak diketahui.

Masalah nilai awal (5.2) diselesaikan menggunakan metode Runge-Kutta dan Adams-Bashforth

orde empat dengan pengambilan

h

= 0

.

01, 0.005, 0.0025, dan 0.00125. Karena penyelsaian eksak tidak

diketahui, maka dihitung estimasi eror penyelesaian pendekatan masalh nilai awal (5.1) menggunakan

persamaan (4.10) dengan

k

= 4. Hasil dapat dilihat pada Tabel 4 dan 5.

Tabel 4. Estimasi eror mutlak yang terjadi di lima titik, jika digunakan metode Runge-Kutta orde

empat untuk masalah nilai awal (5.2)

x

h

= 0

.

01

h

= 0

.

005

h

= 0

.

0025

h

= 0

.

00125

0.2

1

.

00909

×

10

−11

5

.

92548

×

10

−13

3

.

5838

×

10

−14

2

.

25005

×

10

−15

0.4

7

.

31522

×

10

−11

₄

_.

₄₄₇₄₉

_×

₁₀

−12

₂

_.

₇₄₀₃₃

_×

₁₀

−13

₁

_.

₆₈₄₅₈

_×

₁₀

−14

0.6

2

.

34259

×

10

−10

1

.

43221

×

10

−11

8

.

84981

×

10

−13

5

.

45934

×

10

−14

0.8

6

.

45591

×

10

−10

3

.

93365

×

10

−11

2

.

42496

×

10

−12

1

.

4951

×

10

−13

1.0

3

.

26739

×

10

−9

₂

_.

₀₁₁₈

_×

₁₀

−10

₁

_.

₂₄₆₇₇

_×

₁₀

−11

₇

_.

₇₃₀₇

_×

₁₀

−13

Tabel 5. Estimasi eror mutlak yang terjadi di lima titik, jika digunakan metode Adams-Bashforth orde

empat untuk masalah nilai awal (5.2)

x

h

= 0

.

01

h

= 0

.

005

h

= 0

.

0025

h

= 0

.

00125

0.2

4

.

67395

×

10

−6

5

.

26968

×

10

−7

6

.

22673

×

10

−8

7

.

55733

×

10

−9

0.4

4

.

9679

×

10

−6

5

.

55097

×

10

−7

6

.

51684

×

10

−8

7

.

87897

×

10

−9

0.6

5

.

8923

×

10

−6

₆

_.

₄₁₂₁₂

_×

₁₀

−7

₇

_.

₃₈₇₅₉

_×

₁₀

−8

₈

_.

₈₃₁₅₁

_×

₁₀

−9

0.8

8

.

41693

×

10

−5

8

.

65814

×

10

−7

9

.

55323

×

10

−8

1

.

11123

×

10

−8

1.0

1

.

59121

×

10

−5

1

.

49251

×

10

−6

1

.

51566

×

10

−7

1

.

6622

×

10

−8

Orde dari kedua metode dapat ditunjukkan dengan menghitung rasio estimasi eror mutlak

esteror

h

esteror

h/2

dengan

h

= 0

.

01, 0.005, dan 0.0025 untuk masing-masing metode di titik yang sama. Hasil perhitungan

dapat dilihat pada Gambar 3, dengan garis hitam untuk

h

= 0

.

01, hitam tebal untuk

h

= 0

.

005, hitam

putus-putus untuk

h

= 0

.

0025.

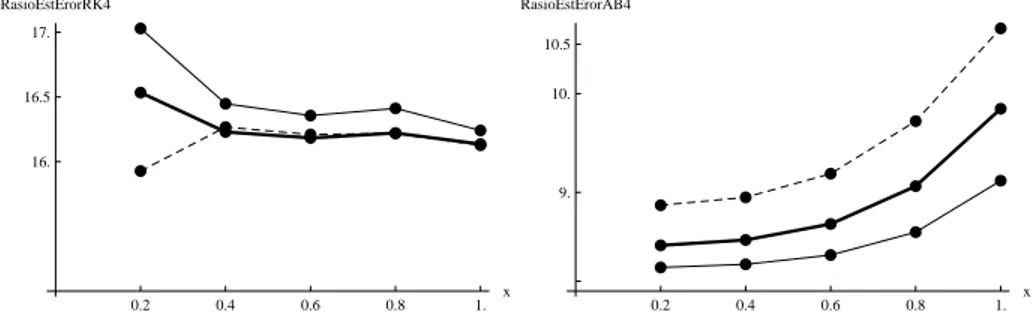
0.2 0.4 0.6 0.8 1. x 16. 16.5 17. RasioEstErorRK4 0.2 0.4 0.6 0.8 1. x 9. 10. 10.5 RasioEstErorAB4

Gambar 3. Rasio estimasi eror mutlak

h

dan

h/

2 di limat titik, berturut-turut dengan metode

Runge-Kutta (kiri) dan Adams-Bashforth (kanan) orde empat.

Dari Gambar 3 terlihat bahwa untuk pengambilan

h

= 0

.

01, 0.005, dan 0.0025 rasio estimasi eror

mutlak

esteror

h

esteror

h/2

≈

16. Hal ini menunjukkan bahwa orde dari algoritma yang diterapkan adalah

empat.

Tabel 4 dan 5 menunjukkan bahwa pada ukuran step

h

yang sama, estimasi eror mutlak penyelesaian

dengan metode Runge-Kutta orde empat lebih kecil dibandingkan dengan metode Adams-Bashforth

orde empat. Hal ini menunjukkan bahwa pada orde empat, pada orde empat, metode Runge-Kutta

lebih akurat daripada metode Adams-Bashforth.

Efisiensi dapat dibandingkan dengan menghitung lama waktu program berjalan hingga diperoleh

penyelesaian pendekatan. Hasil perhitungan lama waktu dapat dilihat pada Tabel 3.

Tabel 6. Lama waktu proses dengan menggunakan metode Runge-Kutta dan metode Adams-Bashforth

orde empat dengan ukuran step

h

= 0

.

01, 0.005, 0.0025, dan 0.00125

h

0.01

0.005

0.0025

0.00125

Runge-Kutta orde 4

0.

0.

0.015

0.031

Adams-Bashforth orde 4

0.

0.

0.

0.015

Tabel 6 menunjukkan bahwa pada ukuran step

h

yang sama, dengan

h

= 0

.

01, 0.005, 0.0025, dan

0.00125, lama waktu proses program Adams-Bashforth orde empat lebih cepat daripada Runge-Kutta

orde empat. Dapat disimpulkan, pada orde empat, metode Adams-Bashforth lebih efisien daripada

metode Runge-Kutta.

6.

KESIMPULAN

Dari pembahasan dan penerapan kasus, diperoleh kesimpulan

(1) Algoritma Runge-Kutta orde empat adalah

y

n+1

=

y

n

+

h

6

(

k

1

+ 2

k

2

+ 2

k

3

+

k

4

)

for

n

= 0

,

1

,

2

, . . .

k

1

=

f

(

x

n

, y

n

)

k

2

=

f

(

x

n

+

h

2

, y

n

+

h

2

k

1

)

k

3

=

f

(

x

n

+

h

2

, y

n

+

h

2

k

2

)

k

4

=

f

(

x

n

+

h, y

n

+

hk

3

)

dan algoritma Adams-Bashforth orde empat adalah

y

n

=

y

n−1

+

h

24

(55

f

n−1

−

57

f

n−2

+ 37

f

n−3

−

9

f

n−4

)

,

n

= 4

,

5

,

6

, . . . ,

(2) pada orde empat, metode Runge-Kutta lebih akurat dibandingkan metode Adams-Bashforth,

(3) pada orde empat, metode Adams-Bashforth lebih efisien daripada metode Runge-Kutta.

Pustaka

[1] Apsley, D.,Initial Value Problem, http://personalpages.umist.ac.uk/staff/david.d.apsley/lectures/numeric/initial-value.pdf

[2] Burden, R. L. and Faires, J. D.,Numerical Analysis, Brooks/Cole, California, 2001.

[3] Gear, J. A.,Numerical Solution of Ordinary Differential Equation, Royal Melbourne Institute of Technology Ltd, Melbourne, 1992.

Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, UNS, Jl. Ir. Sutami 36A,

Kentingan, Surakarta, 57126