ANALISIS KONDISI GINJAL PASIEN MENGGUNAKAN METODE JARINGAN SYARAF TIRUAN

ANALISIS KONDISI GINJAL PASIEN MENGGUNAKAN METODE JARINGAN SYARAF TIRUAN *)

R. Muhammad Subekti**) , Balza Achmad***), Gogot Suyitno****)

ANALISIS KONDISI GINJAL PASIEN MENGGUNAKAN METODE JARINGAN SYARAF TIRUAN. Penelitian kemampuan jaringan syaraf tiruan dalam menganalisis dan memprediksi kondisi ginjal pasien telah dilakukan dengan baik. Spektrum kondisi ginjal pasien merupakan hasil analisis dokter menggunakan alat renograf dual probe BI-756. Jaringan syaraf tiruan memiliki kemampuan untuk menganalisis pola yang spesifik maupun yang tidak spesifik. Hal ini sangat bermanfaat bagi pengembangan perangkat lunak untuk analisi ginjal. Tujuan penelitian adalah mengembangkan sistem jaringan syaraf tiruan yang dapat menganalisis kondisi ginjal pasien dengan tepat. Hasil tingkat optimal jaringan syaraf tiruan adalah system yang memiliki satu lapisan tersembunyi dengan jumlah neuron minimal 17 neuron. Dalam mencapai kondisi konvergen, semakin besar jumlah neuron jumlah iterasi cenderung semakin sedikit, tapi waktu proses semakin lama. Laju belajar optimal adalah 1,000, mometum optimalnya 0,000 dimana ralat sistem yang digunakan adalah 0,001. Sistem jaringan syaraf tiruan telah diujikan terhadap data pasien yang sesungguhnya dan kemampuan identifikasi 98 % diperoleh dari 618 data uji. Hasil ini menunjukkan bahwa system ini memiliki kemampuan baik dimana hanya dilatih dengan 6 data saja.

PATIENT’S KIDNEY CONDITION ANALYSING USING ARTIFICIAL NEURAL NETWORK METHOD. The research of artificial neural network to analyzing and predicting patient’s kidney condition has been done. The spectrum of patient’s kidney condition is result of doctor analysis using dual probe renograf (BI-756). The artificial neural network has capability for specific pattern analysis or unspecific pattern analysis. That is very important for the development of kidney analysis software. The objective of the research is to develop artificial neural network system that can analyze patient’s kidney condition exactly. The result of artificial neural network optimum level is systems that having a hidden layer with minimal neuron number are 17 neurons. The optimum learning rate is 1.000, the optimum momentum is 0.000 and system error that used is 0,001. The artificial neural network system has been tested to the real patient’s data and identification capability of 98% was obtained from 618 tested data. These results showed that the software has a good performance that trained by 6 data only.

*)

Diajukan untuk diterbitkan dalam Majalah Batan. **)

Staf P2TRR – BATAN, Serpong. ***)

Staf pengajar di Jurusan Teknik Nuklir, Fakultas Teknik, UGM, Yogyakarta. ****)

PENDAHULUAN

Kemampuan jaringan syaraf tiruan dalam suatu aplikasi kecerdasan buatan

sudah banyak diterapkan di berbagai bidang ilmu pengetahuan dan teknologi. Namun

dalam dunia kedokteran Indonesia, penerapan kecerdasan buatan sangat kurang sekali.

Oleh karena itu, studi kasus aplikasi jaringan syaraf tiruan di bidang kedokteran akan

memberikan jalan pembuka bagi penelitian jaringan syaraf tiruan untuk mengenali

pola-pola klinis. Penelitian jaringan syaraf tiruan mengambil suatu pola-pola klinis yang memiliki

kasus kompleks, yaitu spektrum ginjal pasien dimana spektrum ini dihasilkan oleh alat

kedokteran nuklir buatan BATAN bernama renograf dual probe (BI-756). Data

keluaran renograf dual probe (BI-756) adalah urutan angka hasil akuisis data

pencacahan yang membentuk spektrum sangat kompleks dan bersifat tidak spesifik,

sehingga analisis terhadap data tersebut cenderung memberikan penilaian subyektif

akibat penilaian visual spektrum renograf. Oleh karena itu, bantuan seorang dokter ahli

yang berpengalaman sangat dibutuhkan untuk memperoleh hasil analisa medis yang

benar. Sehingga keberadaan suatu aplikasi kecerdasan buatan dapat membantu seorang

dokter dalam memberikan keputusan klinis dimana perangkat ini memiliki pengetahuan

berbagai data kasus hasil analisis komprehensif dari para dokter ahli yang

berpengalaman..

Tujuan penelitian ini adalah menyediakan parameter-parameter optimal

perangkat lunak berbasis kecerdasan buatan yang telah dikembangkan supaya dapat

menganalisis kondisi ginjal pasien dengan tepat. Optimasi perangkat lunak berbasis

kecerdasan buatan dilakukan melalui penelitian mendalam terhadap struktur organisasi,

metode komputasi, dan kinerja parameter jaringan syaraf tiruan. Perangkat lunak

berbasis kecerdasan buatan yang dikembangkan menggunakan sistem jaringan syaraf

tiruan umpan maju dan perambatan ralat balik (backpropagation) dan metode optimasi

parameter adalah variasi parameter. Sistem ini mampu dilatih dengan menggunakan

data yang sudah diketahui hasilnya dan dapat mengklasifikasikan setiap pola yang telah

dilatihkan sesuai dengan hasil yang dikehendaki [1]. Jaringan syaraf buatan dilatih menggunakan beberapa konfigurasi data dan pengujian kemampuan identifikasinya

dilakukan pada setiap konfigurasi data pelatihan. Dengan demikian, dalam tahap akhir

pengembangan perangkat lunak ini, perlu sekali dilakukan penelitian dan pengujian

kecerdasan buatan untuk analisa ginjal pasien yang memiliki kemampuan identifikasi

maksimal.

Gambar 1. Ginjal normal [2] Gambar 2. Ginjal tidak normal [2]

DASAR TEORI

Masukan dan Keluaran Jaringan Syaraf Tiruan

Renogram seperti terlihat pada Gambar 1 adalah hasil rekaman renografi yang

menggambarkan keadaan fungsi ginjal pasien. Kurva renograf yang ditampilan oleh

perangkat komputer mampu memberikan informasi secara kuantitatif tentang kapasitas

ekskresi relatif untuk masing-masing ginjal [2]. Kondisi inilah yang dijadikan sebagai masukan jaringan syaraf tiruan. Deskripsi spektrum renograf terlihat pada Gambar 1

yang memperlihatkan kondisi ginjal normal dan Gambar 2 yang memperlihatkan bahwa

ginjal bagian kiri tidak normal karena ada gangguan sistem pengeluaran urine.

Keluaran perangkat lunak adalah hasil analisa terhadap gejala-gejala kondisi

ginjal normal maupun abnormal berdasarkan analisis grafik data fungsi ginjal pasien,

dimana kondisi ginjal yang tercatat pada data-data yang telah ada meliputi kondisi ginjal

normal, nephrectomy type, total obstruktive, partial obstruktive, parenchymal desease

dan renal artery stenosis. Analisa yang dihasilkan berupa hasil tunggal kondisi ginjal

pasien dan hasil gabungan lebih dari satu kondisi ginjal pasien seperti tersebut di atas.

Jadi, perangkat lunak ini mampu mengeluarkan hasil analisa ginjal normal saja atau

hasil analisa ginjal normal yang memiliki kecenderungan gejala partial obstruktive atau

Analisis Jaringan Syaraf Tiruan

Sistem jaringan syaraf tiruan merupakan suatu sistem yang memiliki

pengetahuan dalam menganalisa suatu masalah dan melakukan pekerjaan-pekerjaan

klasifikasi pola, pemodelan sistem dan memori asosiasi [1,3,4]. Klasifikasi pola digunakan untuk menganalisis pola-pola masukkan dengan cara mencari kemiripan pola-pola

masukan. Pemodelan sistem digunakan untuk pembuat simulasi sistem yang mampu

menghasilkan keluaran dari suatu pola masukan yang akan disimulasikan. Sedangkan

memori asosiasi digunakan untuk menganalisis pola masukan yang tidak lengkap,

misalnya pola masukan memiliki derau, terpotong-potong, rusak dan hanya bisa tampil

sebagian [1].

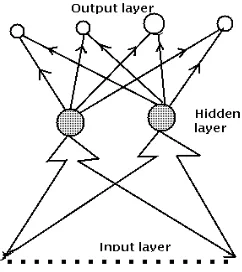
Gambar 3. Struktur jaringan syaraf tiruan umpan maju

Struktur jaringan syaraf tiruan umpan maju terlihat pada Gambar 5. Proses matematis

menggunakan persamaan sebagai berikut :

)

dengan : j = neuron pada lapisan tersembunyi ke-l

l = lapisan tersembunyi

Keluaran dari elemen proses di atas merupakan fungsi transfer yang umumnya

menggunakan fungsi sigmoid [1,5,6], persamaan umum sigmoid adalah sebagai berikut :

Proses yang terjadi untuk masing-masing lapisan tersembunyi adalah :

Untuk lapisan keluaran dimana l = L, maka :

)

Nilai ralat dari sistem ini merupakan hasil pengurangan keluaran sistem terhadap

keluaran yang kita inginkan [3,6]. Dengan demikian nilai ralat adalah sebagai berikut : ) dengan d_j(n) adalah elemen keluaran yang kita inginkan.

Ralat ini adalah ralat untuk masing-masing parameter keluaran, sehingga dari

persamaan (6) diperoleh ralat total :

( )

Proses belajar sistem jaringan syaraf tiruan ini menggunakan pelatihan

perambatan ralat balik (backpropagation) seperti terlihat pada Gambar 8. Perhitungan

perambatan ralat balik dimulai dari ralat keluaran sistem yang diumpankan ke belakang

merambat sampai ke lapisan aktif terdepan. Perambatan ralat ke belakang ini berfungsi

sebagai parameter pembanding dalam proses perbaikan nilai bobot yang telah diperoleh.

Persamaan gradien lokal pada masing-masing lapisan jaringan dapat ditulis sebagai

berikut :

dimana j menunjukkan posisi neuron pada lapisan tersembunyi l. Untuk lapisan

keluaran dimana l = L, persamaan yang digunakan :

(

1 ( )

)

dimana j adalah posisi neuron pada lapisan keluara L.

Dengan demikian, perbaikan bobot yang akan dilakukan oleh jaringan syaraf

tiruan tergantung pada hasil perhitungan gradien lokal yang melibatkan perambatan

Aliran proses generalisasi jaringan pada lapisan tersembunyi l adalah sebagai berikut : dimana : η = nilai laju belajar (learning-rate),

α = konstanta momentum (momentum constan).

Selanjutnya proses yang terjadi adalah proses iterasi dalam dengan syarat batas

adalah nilai ralat yang sudah ditentukan.

PEMBAHASAN NILAI OPTIMAL

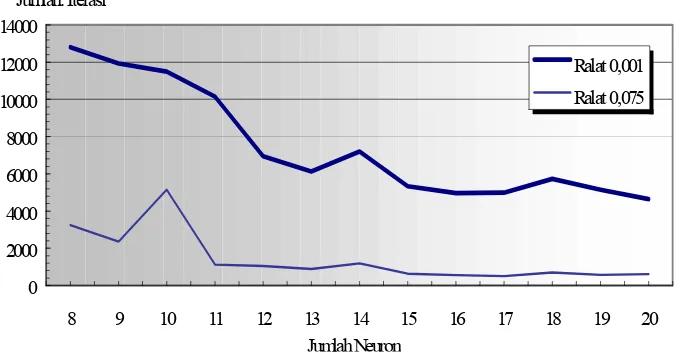
Pada Gambar 4, terlihat bahwa jumlah neuron optimal adalah lebih dari 10

neuron. Penentuan daerah optimal berdasarkan jumlah iterasi yang paling sedikit dan

jumlah neuron yang paling sedikit. Namun garis grafik yang curam di sebelah kiri perlu

diperhatikan dalam menentukan daerah optimal. Karena semakin dekat dengan daerah

curam, ruang ekspansi jaringan yang ditunjukkan oleh banyaknya neuron semakin

sedikit, meskipun kecepatan proses lebih baik dari pada menggunakan neuron yang

lebih banyak. Ruang ekspansi jaringan adalah parameter kemampuan jaringan dalam

menyerap materi belajar. Bila ruang ekspansi jaringan rendah, jaringan akan sulit sekali

mencapai konvergensi dalam proses pelatihan.

Gambar 4. Jumlah Iterasi terhadap Jumlah Neuron

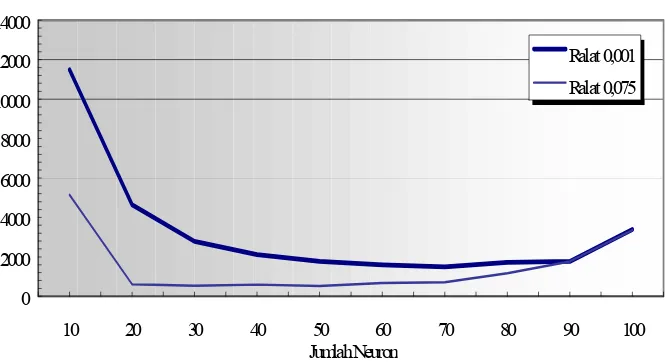
Gambar 5. Jumlah Iterasi terhadap Jumlah Neuron

Ruang ekspansi jaringan yang lebih diperlukan bila dilakukan pelatihan baru

dengan data yang lebih banyak. Semakin besar data tambahan untuk pelatihan baru,

semakin banyak ruang ekspansi jaringan yang harus disediakan. Tapi semakin besar

Ruang ekspansi jaringan, berarti semakin besar neuron yang harus disediakan dan ini

berakibat proses pelatihan akan berlangsung lebih lama meskipun jumlah iterasinya

relatif tidak banyak. Jumlah neuron yang cukup adalah optimal.

Pada Gambar 4, daerah optimal yang relatif aman adalah titik dengan jumlah

neuron lebih dari 17. Angka maksimal pada daerah optimal bersifat sangat relatif,

karena menyangkut kecepatan proses pelatihan dimana besar kecepatan tergantung pada

kecepatan sistem komputer secara keseluruhan. Sedangkan variasi parameter pelatihan

ditunjukkan dalam Tabel 1 dan Tabel 2

Tabel 1. Jumlah iterasi terhadap variasi momentum

Ralat

α

0,0750 0,0500 0,0250 0,0100 0,0075 0,0050 0,0025 0,0010

0,00 502 507 533 656 730 888 1388 2920

0,05 607 626 709 860 958 1173 1744 3629

0,10 602 642 750 973 1097 1311 2036 4140

0,20 645 654 672 867 985 1222 2015 4307

0 2000 4000 6000 8000 10000 12000 14000

10 20 30 40 50 60 70 80 90 100

Jumlah Neuron Jumlah. Iterasi

Ralat 0,001

Tabel 2. Jumlah iterasi terhadap variasi laju belajar

Ralat

η

0,0750 0,0500 0,0250 0,0100 0,0075 0,0050 0,0025 0,0010

1,00 502 507 533 656 730 888 1388 2920

0,95 620 625 663 804 877 1062 1598 3186

0,90 541 546 597 828 937 1177 1913 4033

0,80 549 554 594 851 997 1247 2030 4303

Tabel 3. Data-data pelatihan

Konfigurasi No Nama File Disket Bagian Vektor Keberhasilan (%)

Jumlah Kesalahan Identifikasi 1 Rn150.dat AR 01 RN Kiri 100000

2 Rn1.dat AR 09 RN Kanan 010000 3 Rn52.dat AR 10 RN Kanan 001000 4 Rn57.dat AR 10 RN Kanan 000100 I

5 Rn27.dat AR 10 RN Kanan 000010

94 35

1 Rn150.dat AR 01 RN Kiri 100000 2 Rn1.dat AR 09 RN Kanan 010000 3 Rn52.dat AR 10 RN Kanan 001000 4 Rn57.dat AR 10 RN Kanan 000100 5 Rn27.dat AR 10 RN Kanan 000010 II

6 Rn189.dat AR 03 RN Kanan 000100

98 10

1 Rn150.dat AR 01 RN Kiri 100000 2 Rn1.dat AR 09 RN Kanan 010000 3 Rn52.dat AR 10 RN Kanan 001000 4 Rn57.dat AR 10 RN Kanan 000100 5 Rn27.dat AR 10 RN Kanan 000010 6 Rn189.dat AR 03 RN Kanan 000100 III

7 Rn27.dat AR 10 RN Kiri 100000

98 12

Pada Tabel 3 terlihat bahwa kemampuan identifikasi 100% sulit diperoleh karena

spektrum grafik renogram untuk masing-masing kondisi memiliki kemiripan yang

tinggi dan bersifat tidak spesifik. Adapun nilai kemampuan identifikasi ini diperoleh

dari sistem yang telah mempelajari 6 data pelatihan saja. Penambahan 1 data pelatihan

mampu meningkatkan kemampuan identifikasinya menjadi 98%. Data pelatihan untuk

masing-masing konfigurasi ditunjukkan dalam Tabel 2. Penambahan 1 data pelatihan

menjadi 7 data pelatihan pada konfigurasi III akan menambah jumlah kesalahan

identifikasi meskipun tidak signifikan. Hal ini terjadi karena bobot yang sudah terbentuk

ginjal pasien tidak spesifik ditunjukkan dengan kemiripan spektrum ginjal yang sangat

tinggi, sehingga penambahan data pelatihan saat kemampuan identifikasinya mendekati

maksimal memiliki resiko penurunan kemampuan identifikasi. Perubahan bobot yang

bisa mengurangi kemampuan identifikasi ini bisa dihindari bila data yang ditambahkan

memiliki hasil keluaran yang spesifik terhadap suatu kondisi yang mewakili dan jumlah

kesalahan identifikasi terhadap data kondisi ginjal yang belum terwakili ini cukup

banyak.

KESIMPULAN

Konfigurasi sistem istem jaringan syaraf tiruan yang optimal dalam

mengidentifikasi grafik renogram adalah :

− Laju belajar = 1,00 − Momentum = 0,00 − Threshold = 0,10 − Lapisan tersembunyi = 1 − Jumlah neuron > 17

Persentase keberhasilan minimal sistem jaringan syaraf tiruan dalam

mengidentifikasi grafik renogram adalah 94%. Kemampuan identifikasi yang dimiliki

DAFTAR PUSTAKA

1. Haykin, S., Neural Networks, Macmillan College Publishing Company, New

York, 1994.

2. Prajitno, Petunjuk Perangkat Lunak dalam buku Petunjuk Renograf Model

BI-756, PPNY–BATAN, Yogyakarta, 1996.

3. Timothy, Advanced Algorithms for Neural Networks, John Wiley and Sons, Inc.

New York, 1995.

4. Harvey, R, Neural Network Principles, Prentice-Hall International, Inc, New

Jersey, 1994.

5. Kosko, B, Neural Networks and Fuzzy Systems, Prentice-Hall International, Inc.,

New Jersey, 1992

6. Timothy, Signal and Image Processing with Neural Networks, John Wiley and Sons,

Inc., New York, 1994.

7. Nelson, M. M., dan Illingworth, W. T, A Practical Guide to Neural Nets,

Addison-Wesley Publishing Company, Massachusetts, 1991.

8. Rubenking, N., Delphi Programming Problem Solver, IDG Books Worldwide, Inc.,