Aljabar Abstrak - Buku Aljabar Abstrak - Enos Lolang

Enos Lolang

Aljabar Abstrak

Aljabar Abstrak Copyright © September 2013

Penyusun dan Layout: Enos Lolang, S.Si., M.Pd.

Pembaca Naskah/ Edit or: Selvi R.T andiseru, S.Pd.,M.Sc., Syaiful Hamzah Nasution, S.Si.,S.Pd.,M.Pd.

Desain Sampul:

Lant ana Dioren Rumpa, S.Kom.

Hak cipt a dilindungi undang-undang All rights reserved

Dit erbit kan oleh UK I T oraja Press Jl. Nusant ara No.12 Makale, T elp.(0423)22887

Fax: (0423)22073 Email: ukit oraja@yahoo.com Websit e: ht t p:/ / www.ukit oraja.ac.id

KAT A PENGANTAR

Buku Aljabar Abst ak ini disusun untuk mengat asi kendala ket erbat asan bahan referensi bagi mahasiswa UK I T oraja, khususnya dalam mat a kuliah St rukt ur Aljabar. Buku-buku yang t ersedia di perpust akaan jumlahnya sangat t erbat as dan dit ulis dalam bahasa Inggris, sehingga mahasiswa t idak t erlalu berminat menggunakannya. Selain itu, penulis mengamat i bahwa sampai saat ini, buku rujukan ut ama dalam mat a kuliah St ruktur Aljabar belum pernah ada dan belum pernah diadakan.

Buku ini diberi judul Aljabar Abst rak, bukannya St ruktur Aljabar, karena sebagian besar rujukan yang digunakan dalam menyusun buku ini adalah buku yang berjudul Aljabar Abstrak, at au Aljabar Modern. Selain itu, jika diberi judul St rukt ur Aljabar, maka mahasiswa berpedoman sepenuhnya pada buku ini. Dengan kat a lain, meskipun buku ini dapat dijadikan sebagai rujukan ut ama, mahasiswa masih harus membaca berbagai sumber yang lain untuk memperkaya pemahaman mereka t erhadap t opik yang dipelajari.

Meskipun mungkin masih t erdapat banyak kekeliruan at au kesalahan dalam penulisan buku ini, penulis berharap bahwa dengan dit erbit kannya buku ini, dapat membantu mahasiswa dalam mengikut i proses perkuliahan, dan juga dapat menambah jumlah koleksi buku di perpust akaan. Penulis mengucapkan t erima kasih kepada semua pihak yang t elah memberikan dukungan sehingga penyusunan buku ini dapat direalisasikan, khususnya kepada Bapak Syaiful Hamzah Nasut ion,S.Pd.,S.Si.,M.Pd., dari Universit as Negeri Malang dan Ibu Selvi Rajuat i T andiseru,S.Pd.,M.Sc., dari Universit as K rist en Indonesia T oraja (UK I T oraja), yang t elah bert indak sebagai pembaca naskah dan edit or dalam penulisan buku ini.

DAFTAR I SI

K at a Pengant ar ... ii

Daft ar Isi... iii

Bab I: Pengant ar ... 1

A.T injauan Hist oris ... 1

B. Sejarah T eori Grup ... 4

Bab II: Himpunan ... 6

A.T eori Himpunan ... 6

A.1. Represent asi Himpunan ... 8

A.2. K esamaan Himpunan ... 8

A.3. Himpunan Berhingga dan T ak Hingga ... 9

A.4. Himpunan K osong dan Himpunan Disjoin ... 9

A.5. Singlet on ... 10

A.6. Subset ... 10

A.7. Proper Subset ... 11

A.8. Subset dan Superset ... 11

A.9. Proper dan Improper Subset ... 12

A.10. Power Set ... 12

A.11. Himpunan Comparable dan Non-Comparable ... 13

A.12. Himpunan Semest a ... 13

B. Operasi Himpunan ... 14

B.1. Gabungan dan Irisan ... 14

1. Gabungan Himpunan... 15

2. Irisan Himpunan ... 16

B.2.Partisi ... 16

B.3.Selisih Himpunan ... 18

B.4.K omplemen Himpunan ... 19

C. Sifat -Sifat Aljabar Himpunan ... 22

C.1. Sifat -Sifat Operasi Gabungan ... 22

C.3. Hukum-Hukum Dist ribut if ... 26

C.4. Sifat -Sifat Selisih Himpunan ... 27

C.5. Hukum De-Morgan ... 29

D. Definisi-Definisi ... 30

E. Pemet aan At au Fungsi ... 31

E.1. Domain, K odomain, dan Range ... 33

E.2. Pet a dan Invers Pet a ... 33

F. Operasi Biner ... 44

G. Soal-Soal... 50

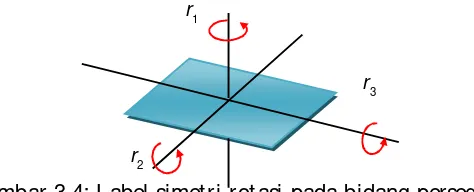
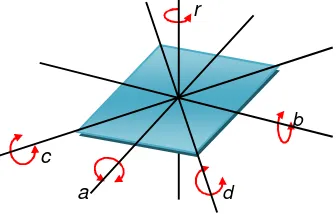
Bab III: Simet ri ... 63

A. Pengert ian Simet ri ... 63

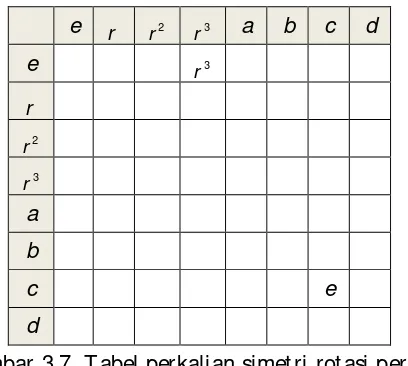
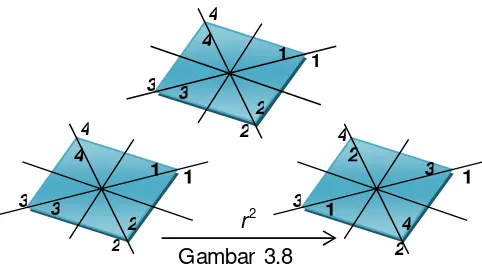
B. T abel Perkalian ... 69

C. Simet ri dan Mat riks ... 72

D. Permut asi ... 76

E. Soal-Soal ... 86

Bab IV: T eori Grup ... 90

A. Pendahuluan... 90

A.1. Operasi Biner ... 93

A.2. Definisi Grup ... 93

A.3. Grup Abelian ... 94

A.4. Subgrup ...102

A.5. K elas Ekuivalen ...119

A.6. Virtues of Abst ract ion ...121

A.7. Soal-Soal ...126

B. Dasar-Dasar T eori Grup ...127

B.1. Grup Dengan Orde K ecil ...130

B.2. Hukum Assosiat if Umum ...132

B.3. Subgrup dan Grup Cyclic ...135

B.4. Grup Siklik dan Subgrup Siklik ...137

B.5. Subgrup Dari Grup Siklik ...141

B.6. Grup Dihedral ...148

C. Homomorfisme dan Isomorfisme ... 155

D. Isomorfisma dan Aut omorfisma ... 160

E. Pet a Ident it as dan Pet a Invers ... 165

F. K ernel Homomorfisme ... 169

G. K oset dan T eorema Lagrange ... 176

H. Sifat -Sifat K oset ... 177

I. Relasi Ekivalensi dan Part isi Himpunan ... 178

J. Relasi Ekivalensi dan Pemet aan Surjekt if. ... 184

K K onjugasi ... 186

L. Soal-Soal ... 187

BAB I PENGANT AR

A. T injauan Historis

Bagaimana membukt ikan bahwa (-1)(-1)= 1? Pertanyaan ini menjadi beban bagi ahli mat emat ika Inggris pada awal abad ke-19 yang ingin melet akkan landasan aljabar pada dasar yang sama dengan geomet ri dengan memberikan pembukt ian-pembukt ian logika. Masalah t ersebut di at as juga merupakan salah sat u cont oh just ifikasi hukum-hukum arit met ika yang menyat akan hubungan antara arit met ika dengan aljabar abst rak, yang selanjutnya menghasilkan konsep-konsep ring, domain int egral, st ruktur, orde, dan aksima-aksioma.

bersifat spesifik, akan ekivalen jika simbol-simbol memiliki nilai dan bentuk yang berlaku secara umum.

Peacock menyat akan bahwa hukum-hukum arit met ika juga merupakan hukum dari aljabar simbolis suat u idea sama sekali t idak sama dengan pendekat an aksiomat ik t erhadap arit met ika. Jadi prinsip Peacock dapat digunakan untuk membukt ikan bahwa (-x)(-y)=xy. K arena

(

a−b c

)(

−d

)

= ac+bd−ad−bcjika a>b dan c>d, pernyat aan ini merupakan suat u hukum arit met ika dan oleh karena itu t idak perlu dibukt ikan. Pernyat aan ini menjadi hukum aljabar simbolis, jika t idak ada bat asan pada nilai at au bentuk a, b, c, dan d. Dengan memilih a = 0 dan c = 0, maka diperoleh (-b)(-c) = bd.

K ajian masalah yang sederhana dapat memunculkan berbagai pengembangan kasus, di ant aranya adalah sebagai berikut :

(a). Bagaimana membukt ikan bahwa (-1)(-1) = 1? Pert anyaan ini akan menuntun kita padaaksioma.K it a t idak dapat membukt ikan segalanya. (b). Aksioma apa yang dapat digunakan unt uk menjelaskan sifat -sifat

bilangan bulat? Pert anyaan ini memungkinkan kit a mengenal konsep-konsep ring, domain integral, ring berorde, dan prinsip urutan rapi (well ordering principle).

(c). Bagaimana memast ikan bila kit a sudah memiliki aksioma yang cukup? Di sini akan dipelajari t ent ang ide aksioma kelengkapan dari sekumpulan aksioma.

(d). Untuk apa mempelajari sifat -sifat bilangan bulat ? Sifat -sifat bilangan bulat akan menuntun kit a pada pengert ian isomorfisme.

(e). Dapat kah kit a menggunakan lebih sedikit aksioma unt uk memahami bilangan bulat ? Misalnya, kit a t idak memerlukan sifat a+b = b+a. Dalam kasus sepert i ini, kita akan menjumpai konsep independensi dari sekumpulan aksioma.

Bagaimana solusi bilangan bulat dari persamaan x2_{+ 2 = y}3_?

Persamaan ini adalah persamaan diophantine, yang merupakan salah satu bent uk persamaan Bachet yang t erkenal yait u x2_{+k = y}3_{. Persamaan ini t elah}

diperkenalkan pada abad ke-17 dan baru dapat diselesaikan secara t eorit is untuk sebarang nilai k pada abad ke-20. Permasalahan ini memadukan t eori bilangan dengan aljabar abst rak yang kemudian menghasilkan konsep domain fakt orisasi unik (unique factorization domain, UFD) dan domain eucledian yang merupakan cont oh pent ing dalam ring komut at if.

Untuk menent ukan penyelesaian dari persamaan diophant ine

2 2 2

x + y = z dengan (x, y) = 1, maka harus dicari semua solusi primit if t ripel Phyt hagorean. Meskipun solusi t ersebut t elah diket ahui sejak zaman Yunani kuno 2000 t ahun yang lalu, kit a t ert arik pada suat u bent uk solusi aljabar ist ilah yang baku sejak abad ke-19. Ide utama dari penyelesaian masalah ini adalah memfakt orkan ruas kiri dalam persamaan _x2_{+ y}2_{= z}2

sehingga didapat kan

(

_{x+ yi x}

)(

_−yi

)

_{= z}2_{dalam domain biulangan bulat Gaussian, yaitu}

=

{

a+bi a b: , ∈

}

.

Domain ini berhubungan dengan sifat fakt orisasi unik bilangan bulat sepert i yang t elah ditunjukkan oleh Gauss. K arena x+yi dan x yi adalah prima relat if di dalam (karena x dan y masing-masing adalah prima relat if dalam ) dan hasil perkaliannya berbent uk kuadrat , maka x+yi dan x yi adalah kuadrat dalam domain (hal ini berlaku unt uk sebarang domain fakt orisasi unik). Jadi x+yi = (a+bi)2

= (a2

b2

)+ 2abi. Dengan membandingkan bagian real dan imajiner, akan diperoleh x = a2

b2

, y = 2ab, dan karena x2

+y2

=z2

, makaz=a2

+b2

. Sebaliknya, dengan mudah dapat dit unjukkan bahwa untuk sebaranga,b , (a2

b2

, 2ab,a2

+b2

) adalah solusi dari x2

+y2

= z2

. Dengan demikian kit a dapat kan semua t ripel Pyt hagoras. Jadi dengan mudah dapat dipilih suatu solusi primitif di ant aranya.

K embali ke masalah x2

+ 2 = y3

, kit a melakukan langkah analogi dengan memfakt orkan ruas kiri sehingga diperoleh

(

)(

)

3

2 2 .

x+ i x−i = y

2

x− i merupakan fakt or pangkat t iga dalam domain , karena

(

)

3

2 2 .

x+ i = a+ bi Dengan aljabar sederhana dapat dit unjukkan bahwa nilai x = ± 5 dan y = 3. Fakt or-fakt or ini merupakan solusi dari 2 3

2 .

x + = y Perhit ungan t ersebut di at as menunjukkan bahwa nilai x dan nilai y yang diperoleh merupakan sat u-satunya solusi untuk persamaan t ersebut . Inilah cara Euler menyelesaikan soal t ersebut . Tent u kita dapat menunjukkan bahwa

adalah domain fakt orisasi unik.

Persamaan Fermat x3+ y3= z3dapat dianalisis dengan memandang bahwa_z3= _x3+ _y3=

(

_x+ _{y x}

)(

+ _yω

)

(

_x+ _yω2

)

_{adalah suat u persamaan dalam}

domain = {a+b :a,b } , adalah akar pangkat t iga primit if dari 1. Unt uk menyelesaikan ket iga persamaan diophant ine t ersebut di at as, diperlukan langkah-langkah yang lebih lanjut. Dalam hal ini diperlukan pemahaman mengenai domain faktorisasi unik dan domain eucledian sert a pembahasan beberapa sifat -sifat arit met ikanya. K et iga persamaan diophant ine dapat diselesaikan dengan cara yang t elah dit unjukkan di at as, karena domain-domain , , dan masing-masing merupakan domain fakt orisasi unik.

B. Sejarah T eori Grup

Pada t ahun 1854 pert ama kali Cayley memberikan definisi abst rak t ent ang grup. Pendefinisian t ersebut dilat arbelakangi oleh t ulisan Cauchy mengenai grup permut asi, dan secara khusus oleh Galois. Selain itu juga dilat arbelakangi oleh ahli mat emat ika berkebangsaan Inggris, ant ara lain Peacock, deMorgan, Hamilton, dan Boole. Cayley juga mendefinisikan grup berdasarkan t eori invarian Wussing.

awalnya hanya merupakan t eori bahwa t opik dalam aljabar bukanlah mengenai simbol-simbol dalam pernyat aan aljabar, melainkan hukum-hukum kombinasinya. Selanjut nya para ahli t ersebut juga memperkenalkan berbagai sist em yang memiliki sifat yang berbeda dengan yang sudah dikenal dalam sist em bilangan t radisional. Sist em ini ant ara lain kuart ernion dan bikuart ernion (Hamilt on), aljabar t ripel (deMorgan), Okt onion (Graves dan Cayley), A ljabar Boolean (Boole), dan mat riks (Cayley).

Cayley adalah salah seorang ahli mat emat ika sejat i yang memiliki pandangan generalit as dan berkeinginan menggabungkan beberapa sifat di at as dalam sat u rumpun. Bukt inya, dalam t eori grup Cayley menyusun permut asi, kuart ernion (dengan operasi t ambah), mat riks-mat riks invert ibel (dengan operasi kali), bentuk-bentuk kuadrat biner (dalam komposisi bent uk sepert i yang didefinisikan oleh Gauss pada t ahun 1801), grup yang muncul di dalam t eori fungsi elips, dan dua grup yang berorde delapan belas dan dua puluh t ujuh, yang didefinisikan menurut generat or dan relasi.

Definisi Cayley pada t ahun 1854 t ent ang grup hanya sedikit menarik perhat ian. Sat u-satunya sumber ut ama t eori grup pada masa it u adalah persamaan-persamaan aljabar sehingga hanya sedikit keinginan para ahli untuk membuat generalisasi. Selain it u, abst raksi dan aksioma-aksioma t idak t erlalu diminat i pada pert engahan abad XIX. Meskipun demikian, karya Cayley dalam bidang ini menjadi cont oh pert ama dari suat u sist em aljabar yang menjadi aksioma, bahkan Eves menganggapnya sebagai aksioma formal yang membedakan objek-objek dalam mat emat ika.

BAB I I HI M PUNAN

Sebelum memperdalam pemahaman mengenai Aljabar Abst rak, diperlukan penget ahuan yang memadai t entang T eori Himpunan, Pemet aan at au Fungsi, Operasi Biner, dan Sist em Bilangan. K ecuali Sist em Bilangan, masing-masing t opik t ersebut akan dijelaskan sat u demi satu pada bagian ini. Mahasiswa sudah cukup mendalami sist em bilangan melalui kuliah T eori Bilangan.

A. T eori Himpunan

Aljabar Abst rak (St ruktur Aljabar, Aljabar Modern) diawali dengan ident ifikasi masalah mat emat ika sepert i penyelesaian persamaan-persamaan polinomial dengan cara menent ukan akar at au menyusun bentuk geomet ris secara langsung. Dari penyelesaian masalah-masalah khusus, t erdapat t eknik-t eknik umum yang dapaeknik-t digunakan uneknik-t uk menyelesaikan masalah yang sama yang selanjut nya diuji apakah generalisasi t ersebut berlaku pada semua masalah yang sejenis, at au hanya berlaku pada persoalan t ert entu.

Salah sat u istilah yang t ak t erdefinisi sepert i yang dimaksud di at as adalah himpunan. K it a dapat membayangkan suat u himpunan sebagai koleksi at au kumpulan objek yang memungkinkan dit entukannya suatu objek sebagai anggot a himpunan at au bukan anggot a himpunan. Himpunan biasanya dinyat akan dengan huruf kapit al, at au dideskripsikan dengan mendaft arkan anggot a-anggot anya.

Beberapa buku tidak memberikan definisi himpunan dengan alasan bahwa definisi t ersebut pada hakikatnya masih memerlukan definisi lainnya. Penjelasan yang lain itu juga masih memerlukan penjelasan lebih lanjut, demikian set erusnya. T et api beberapa buku rujukan lainnya mendefinisikan himpunan sebagai kumpulan dari objek yang berhingga dan jelas berdasarkan persepsi atau pemikiran manusia. Himpunan dinyat akan dengan not asi huruf-huruf kapit al, misalnya A , B, C, , H, .

Definisi yang umumnya disepakat i adalah bagian-bagian yang membangun himpunan sert a sifat -sifat himpunan, misalnya anggot a himpunan, himpunan berhingga, himpunan t ak hingga, himpunan kosong, himpunan bagian, irisan, gabungan, dan beberapa sifat lainnya.

Objek-objek yang membentuk suatu himpunan dinamakan anggot a himpunan at au sering disebut elemen at au unsur himpunan. Anggot a himpunan biasanya dinyat akan dengan hruf-huruf kecil, sepert i a, b, c,d, e, f, dan set erusnya. Unt uk menyat akan bahwa suat u objek merupakan anggot a dari suat u himpunan t ert entu, digunakan simbol ∈. Sedangkan untuk menyat akan bahwa suatu objek bukan anggota dari himpunan t ert entu, digunakan simbol ∉. Jadi misalkan A adalah himpunan yang t erdiri at as bilangan-bilangan 1, 2, 3, 4, dan 5, maka not asi himpunan dan anggot a-anggot anya adalah:

A = { 1, 2, 3, 4, 5}

A.1. Representasi Himpunan

Untuk menyat akan suatu himpunan at au bukan himpunan, pada umumnya dikenal dua met ode yaitu met ode rast er at au t abulasi, dan met ode pembentuk himpunan. Dalam met ode rast er at au t abulasi, suat u himpunan dinyat akan dengan mendaft arkan semua anggot a himpunan t ersebut, masing-masing anggota dipisahkan dengan t anda koma, dan dilet akkan dalam kurung kurawal { } . Jadi untuk menyat akan himpunan A yang anggot a-anggot anya t erdiri at as bilangan-bilangan 1, 2, 3, 4, dan 5, maka himpunan A dit uliskan dengan not asi A = { 1, 2, 3, 4, 5} . Sedangkan dengan met ode pembentuk himpunan, suat u himpunan dinyat akan dengan mendefinisikan sifat pembentuk himpunannya. Himpunan S yang dinyat akan dengan not asi

( )

{

|

}

,

S= s P s menunjukkan bahwa himpunan S adalah suatu himpunan yang t erdiri at as anggot as yang bersifat P.

Cat at an:

Urut an anggot a dalam suat u himpunan t idak mempengaruhi sifat himpunan t ersebut . Himpunan { 2, 3, 4, 5} , { 4, 3, 5, 2} , { 2, 5, 4, 3} , { 4, 2, 5, 3} adalah himpunan-himpunan yang sama.

Pengulangan anggot a himpunan t idak mempengaruhi sifat himpunan. Himpunan {a, b, b, b, c, c, d, d, d, e, e} menyat akan himpunan yang sama dengan himpunan {a, b, c, d, e} , karena it u t idak dibenarkan menyat akan anggot a himpunan secara berulang.

A.2. Kesamaan Himpunan

Definisi 2.1. K esamaan Himpunan

Himpunan A dan B dikat akan himpunan yang sama dan dituliskan A = B, jika dan hanya jika set iap anggot a himpunan A adalah juga anggot a himpunan B. Untuk membukt ikan bahwa dua himpunan adalah himpunan yang sama maka harus dibukt ikan bahwa himpunan pert ama merupakan subset dari himpunan kedua, dan himpunan kedua merupakan subset dari himpunan pert ama. Jadi, harus ditunjukkan bahwa A ⊆B dan juga B ⊆A.

Strategi: Salah sat u met ode unt uk membukt ikan bahwa himpunan A B adalah menunjukkan suatu elemen yang merupakan anggot a A t et api t idak berada di B, at au anggot a himpunan B t et api tidak berada di A.

Contoh 2.1. Misalkan A = { 1, 1} , B = { -1, 1} , dan C = { 1} . T erlihat bahwa A B karena -1∈B t et api -1∉A. T erlihat juga bahwa A = B karena A⊆B dan A⊇B.

A.3. Himpunan Berhingga dan T ak Hingga

(i) Suatu himpunan dikat akan berhingga jika himpunan t ersebut memiliki anggot a yang berhingga banyaknya. Himpunan A yang t elah disebut kan di at as adalah himpunan berhingga, karena anggot a himpunannya berhingga banyaknya, yaitu sebanyak 5. Himpunan nama ibukota kabupat en di dalam suatu propinsi juga merupakan himpunan berhingga, karena nama kabupat en di dalam propinsi t ersebut berhingga banyaknya. (ii) Suatu himpunan dikat akan tak hingga jika himpunan t ersebut memiliki

anggot a yang tidak berhingga banyaknya.

A.4. Himpunan Kosong dan Himpunan Disjoin Definisi 2.2.Himpunan K osong dan Himpunan Disjoin.

adalah himpunan-himpunan yang disjoin karena { 1, -1}∩{ 0, 2} = . Hanya ada sat u himpunan kosong , dan adalah subset (himpunan bagian) dari set ioap himpunan. Dua himpunan t ak kosong dikat akan disjoin jika irisan kedua himpunan t ersebut t idak memiliki anggot a. Misalkan himpunan A = { 1, 3, 5, 7} dan B = { 2, 4, 6, 8} , maka himpunan A dan himpunan B adalah disjoin karena t idak memiliki anggot a himpunan irisan, at au t idak memiliki anggot a himpunan sekut u.

A.5. Singleton

Singlet on adalah himpunan yang hanya memiliki sat u anggot a himpunan. Singet on sering juga dinamakan himpunan sat uan, at au himpunan one-point. {Presiden Republik I ndonesia} merupakan cont oh himpunan singlet on. Demikian juga himpunan A = {p} , at au B = {q} . Perhat ikan bahwa dan { } t idak menyat akan himpunan yang sama, karena adalah himpunan kosong, sedangkan { } adalah singlet on.

A.6. Subset

Definisi 2.3. Subset. Misalkan A dan B adalah himpunan, maka A disebut subset dari B jika dan hanya jika set iap elemen A merupakan elemen-elemen B. Not asi A ⊆B at au B ⊇A menunjukkan bahwa A adalah subset dari B. Not asi A ⊆B dibaca A adalah subset dari B at au A t ermuat di dalam B . Demikian juga, B⊇A dibaca B memuat A . Simbol ∈ menyat akan anggot a, sedangkan simbol ⊆menyat akan subset .

T eorema 2.1.

Jika suat u himpunan memiliki n anggot a, maka banyaknya subset dari himpunan t ersebut ada 2n

.

Bukti

Banyaknya subset yang memiliki r anggot a sama dengan banyaknya kelompok yang memiliki r anggot a yang dapat dibent uk dari n elemen, yait u n

Jadi:

subset yang t idak memiliki anggot a ada sebanyak n

C0.

Subset yang memiliki 1 anggot a ada sebanyak n_C

1

Subset yang memiliki 2 anggot a ada sebanyak n

C2

Subset yang memiliki n anggot a ada sebanyakn_C n

T ot al subset adan

C0+ n

C1+

n

C2+ + n

Cn-2+ n

Cn-1+

n

Cn= 2

n

Contoh 2.2. K eanggot aan at au subset suatu himpunan dituliskan dengan simbol a∈{a, b, c, d} dan {a} ⊆{a, b, c, d} . Perhat ikan bahwaa⊆{a, b, c, d} dan {a} ∈{a, b, c, d} merupakan penggunaan simbol yang salah dalam not asi himpunan.

A.7. Proper Subset

Definisi 2.4. Proper Subset .

Jika A dan B adalah himpunan, maka A dinamakan proper subset dari B jika dan hanya jika A ⊆ B t et api A B. Proper subset sering juga dinyatakan dengan not asi A⊂B jika A adalah proper subset dari B.

Contoh 2.3. Proper subset dan kesamaan himpunan

{ 1, 2, 4} ⊂{ 1, 2, 3, 4, 5} (proper subset ) { a, c} = { c, a} (subset )

A.8. Subset dan Superset

Jika A dan B adalah dua himpunan t ak kosong sedemikian sehingga set iap anggot a himpunan A adalah juga anggot a himpunan B, maka:

A.9. Proper dan I mproper Subset

(i) Jika A dan B adalah dua himpunan t ak kosong dengan A⊆B dan A B, maka himpunan A dikat akan proper subset dari B dan dit uliskan A⊂B. (ii) Jika A dan B adalah dua himpunan t ak kosong sedemikian sehingga A⊆B

dan A= B, maka himpunan A dikat akan improper subset dari B dan dinyatakan dengan A⊂B. Not asi ⊄menyat akan bahwa A bukan proper subset dari B, dan not asi A B menyat akan A bukan superset dari B.

A.10. Power Set

Definisi 2.5. Powerset . Untuk himpunan A sebarang, powerset dari A yang dilambangkan dengan P(A) adalah himpunan dari semua subset A. P(A) = {x|x ⊆A} . Misalkan suat u himpunan A didefinisikan dengan A = { 1, 2} maka P(A ) = { , { 1} , { 2} , { 1, 2} } . Unt uk himpunan A yang memiliki n anggot a (n adalah bilangan bulat posit if), semua subset dari A dapat dituliskan. Misalkan A = {a, b, c} , maka subset dari himpunan A adalah , {a} , {b} , {c} , {a, b} , { a,c} , {b,c} , {a, b, c} .

Untuk memudahkan pemahaman, konsep himpunan biasanya dinyat akan dalam bent uk gambar at au diagram. Dengan membuat gambar at au diagram, diasumsikan bahwa semua himpunan dan irisan at au gabungannya merupakan subset dari suatu himpunan semest a, yang dilambangkan dengan U_{. Pada gambar di bawah ini, himpunan A dan B}

beririsan sat u sama lain dan keduanya merupakan subset dari himpunan semest aU _{yang digambarkan dalam bent uk persegi. Irisan himpunan A dan B}

A.11. Himpunan Comparable dan Non-comparable

(i) Jika himpunan A dan B adalah dua himpunan sedemikian sehingga t erdapat kemungkinan A ⊂ B at au B ⊂ A, maka himpunan A dan B masing-masing disebut comparable set (himpunan set ara). Misalkan A = { 1, 3, 5, 7} dan B = { 3, 5, 7} maka A dan B adalah himpunan comparable karena B⊂A.

(ii) Jika himpunan A dan B adalah dua himpunan sedemikian sehingga t idak ada kemungkinan A⊂B dan juga t idak ada kemungkinan B⊂A, maka himpunan A dan B masing-masing disebut himpunan yang Non-Comparable. Misalkan himpunan A = { 1, 3, 5, 7} dan B = { 2, 4, 6, 8} maka A dan B adalah himpunan-himpunan yangnon-comparable karena t idak t erdapat kemungkinan A⊂B maupun B ⊂A.

A.12. Himpunan Semesta

Himpunan semest a adalah suat u himpunan yang mengakibat kan semua himpunan lainnya menjadi subset . Contoh dapat diperlihat kan sebagai berikut :

A = {x|xadalah bilangan prima yang kurang dari 50} B = {x|xadalah kelapat an 6 ant ara 5 dan 55}

C = {x|xadalah fakt or dari 60}

Himpunan semest a dari ket iga himpunan t ersebut adalah himpunan bilangan asli dari 1 sampai dengan 60, at au U_{= { 1, 2, 3, , 60} . Jadi himpunan}

semest a t idak bersifat unik.

Contoh 2.5. Himpunan B yang t erdiri at as semua bilangan bulat t ak-negat if, dit uliskan sebagai B = { 0, 1, 2, 3, } . T iga t anda tit ik di belakang, disebut elipsis, menunjukkan bahwa elemen-elemen yang dit uliskan sebelum t anda elipsis, berlanjut sampai t ak hingga. Not asi { 0, 1, 2, 3, } dibaca himpunan yang anggot a-anggot anya adalah 0, 1, 2, 3, dan seterusnya. Anggot a dari suat u himpunan tidak perlu didaftar secara berulang. Himpunan yang anggot anya t erdiri at as elemen-elemen 1, 2, 3, t idak mengurangi maknanya dan t idak berbeda dengan himpunan yang anggot a-anggot anya t erdiri at as 1, 2, 2, 3, 3, 4, 5, 5, 5, .

Cara lain untuk menyat akan himpunan adalah dengan menggunakan notasi pembentuk himpunan (set-builder notation). Not asi pembent uk himpunan menggunakan t anda kurung kurawal untuk menyat akan sifat -sifat yang menyat akan kualifikasi keanggot aan himpunan t ersebut .

Contoh 2.6. Himpunan B pada Cont oh 2.5 dapat digambarkan dengan not asi pembentuk himpunan sebagai berikut : B = {x|x adalah bilangan bulat t ak-negat if} . Garis vert ikal digunakan unt uk menyatakan sedemikian sehingga dan dibaca B adalah himpunan dari semua x sedemikian sehingga x adalah bilangan bulat t ak-negat if

K eanggot aan suat u himpunan sering juga dit uliskan dengan not asi x ∈ yang menyat akan bahwa xadalah anggot a dari himpunan A dan x ∉

menyat akan x bukan anggot a dari himpunan A . Himpunan A dalam Cont oh 2.4 dapat dit uliskan 2∉A dan 7 ∉A.

B. Operasi Himpunan B.1. Gabungan dan I risan

Definisi 2.6.Himpunan Gabungan

Gabungan dua himpunan, misalnya himpunan A dan B, adalah himpunan yang anggot a-anggot anya t erdapat di A at au di B. I risan himpunan A dan B adalah himpunan yang anggot anya merupakan anggot a himpunan A dan juga anggot a himpunan B.

Contoh 2.7. Misalkan A = { 2, 4, 6} dan B = { 4, 5, 6, 7} , Maka A∪B = { 2, 4, 5, 6, 7} dan A∩B = { 4, 6} .

Contoh 2.8. Unt uk sebarang himpunan A dan B, maka A∪B = B∪A. A∪B = {x|x A at au x B}

= {x|x B at au x A} = B∪A

Berdasarkan fakt a bahwa A∪B = B∪A, maka dapat dikat akan bahwa operasi gabungan himpunan bersifat komut at if. Demikian juga, dengan menunjukkan bahwa A∩B = B∩A maka disimpulkan bahwa operasi irisan himpunan bersifat komut at if. Jika dua himpunan t idak memiliki anggot a himpunan irisan, maka irisannya disebut himpunan kosong. Misalkan A = { 1, -1} dan B = { 0, 2, 3} , maka A∩B t idak memiliki anggot a, dan dinyat akan sebagai himpunan kosong.

1. Gabungan Himpunan

(a) Gabungan dua himpunan.

Misalkan diket ahui himpunan A dan himpunan B, maka gabungan dari himpunan A dan B adalah himpunan dari semua anggot a himpunan A at au himpunan B, at au keduanya. Gabungan himpunan A dan himpunan B dinyat akan dengan not asi A∪B (dibaca A union B) dan didefinisikan A∪B = {x|x A at au x B} .

(b) Gabungan lebih dari dua himpunan

Misalkan diket ahui himpunan-himpunan A1, A2, ,An. Gabungan

himpunan dari semua himpunan t ersebut adalah himpunan semua anggot a himpunan dari semua himpunan tersebut . Gabungan himpunan A1, A2, ,An dit uliskan dengan not asi A1∪A2∪ ∪An,

at au n

i i= 1

A dan didefinisikan dengan pernyat aan sebagai berikut :

{

}

n i i = 1

A = x x| ∈A_i unt uk set idak-t idaknya sat ui

2. Irisan Himpunan

(a)Irisan dua himpunan

Misalkan diket ahui dua himpunan A dan himpunan B. Irisan dari himpunan A dengan B adalah himpunan dari semua anggot a himpunan A dan anggot a himpunan B. Irisan himpunan A dan B dituliskan dengan notasi A∩B (dibaca A int erseksi at au irisan B) dan didefinisikan A∩B = {x|x A dan x B} . Jika diket ahui himpunan A = { 1, 2, 3, 4} dan B = { 2, 3, 4, 5} , maka A∩B = { 2, 3, 4} .

(b) Irisan lebih dari dua himpunan

Misalkan diket ahui himpunan-himpunan A1, A2, A3 ,An, maka irisan

dari himpunan-himpunan ini adalah himpunan semua anggot a himpunan yang merupakan anggot a dari himpunan A1, A2, A3 ,An.

Irisan himpunan-himpunan A1, A2, A3 ,An, dituliskan dengan not asi

A1∩A2∩A3∩ ∩An at au

1

n i i

A

=

yang didefinisikan sebagai berikut :

1

n i i

A

=

= {x|x Ai unt uk set iap i}

B.2. Partisi

dinyatakan dengan X1 = {a, d} , X2 = {b, c, f} , X3 = {e} , karena dapat

dibent uk himpunan A sehingga A = X1∪X2∪X3,dimanaX1 , X2 , X3

dan X1∩X2 = , X1∩X3= , dan X∩X3= . K onsep part isi merupakan

t opik yang mendasar dalam mempelajari Aljabar Abst rak.

Operasi irisan, gabungan, dan komplemen dapat dikombinasikan dengan berbagai cara, sehingga dapat didapat kan beberapa kesamaan ant ara berbagai kombinasi t ersebut .

Contoh 2.10.Bukt ikan:

1. A∩(B∪C) = (A∩B)∪(A∩C) 2. A∪(B∩C) = (A∪B)∩(A∪C)

Sifat yang dit unjukkan pada kesamaan di at as adalah sifat dist ribut if. Hubungan yang pert ama dapat dibukt ikan sebagai berikut :

1. K esamaan himpunan dapat dibukt ikan dengan menunjukkan bahwa keduanya adalah himpunan yang memiliki anggot a yang t epat sama, yait u dua himpunan yang saling subset . Jadi akan ditunjukkan bahwa A∩(B∪C)⊆(A∩B)∪(A∩C) dan juga(A∩B)∪(A∩C) A∩ (B∪C). Ambil sebarangx A∩(B∪C)

Perhat ikan bahwa: x A∩(B∪C)

x A dan x (B∪C) x A dan x B at au x C

x A dan x B, at au x A dan x C x A∩B, at au x A∩C

x (A∩B)∪(A∩C)

Jadi, A∩(B∪C) (A∩B)∪(A∩C) (* )

Sebaliknya akan dibukt ikan juga bahwa (A∩B)∪(A∩C) A∩(B∪C). Dengan cara yang sama, misalkan bahwax (A∩B)∪(A∩C).

Perhat ikan bahwa: x (A∩B)∪(A∩C)

x A dan x B, at au x A dan x C x A, danx B at aux C

x A dan x (B∪C) x A∩(B∪C)

Jadi, (A∩B)∪(A∩C) A∩(B∪C) (* * )

Pembukt ian yang t elah dilakukan pada (* ) dan (* * ) menunjukkan bahwa A∩(B∪C) = (A∩B)∪(A∩C).

2. Sebagai lat ihan, mahasiswa dapat membukt ikan bagian (2) ini.

Bagian kedua dari pembuktian dapat diperoleh dari bagian pert ama, dengan cara membalik langkah-langkah pembukt ian, at au menelusuri pembukt ian mulai dari langkah t erakhir. Jika semua t anda digant i dengan t anda maka akan diperoleh implikasi yang benar. Fakt anya, pembukt ian kedua bagian dapat dilakukan dengan menggant i tanda menjadi , dimana

menyat akan makna jika dan hanya jika . Oleh karena it u, x A∩(B∪C)

x A dan x (B∪C) x A, dan x B at aux C

x A dan x B, at aux A dan x C x A∩B, at au x A∩C

x (A∩B)∪(A∩C)

Hubungan komplemen dengan gabungan at au irisan dijelaskan dengan Hukum De M organ,yait u(A∩B)C

= AC_∪

BC

dan(A∪B)C

= AC_∩

BC

.

B.3. Selisih Himpunan

Definisi 2.7.Selisih Himpunan.

B. Selisih himpunan A dan B dituliskan dengan not asi A B (A kurang B), dan didefinisikan A B = {x|x A, x B} . Jika himpunan A = { 1, 2, 3, 4, 5, 6} dan B = { 4, 5, 6} , maka A B = { 1, 2, 3} . Pada umumnya selisih dua himpunan yang berbeda t idak bersifat komutat if, art inya A B B A.

Contoh 2.11. Diket ahui himpunan A = { 1, 3, 5, 7, 9} dan B = { 3, 5, 7, 9, 11} . Berdasarkan Definisi 2.7. at au Definisi 2.1. , A B = { 1} dab B A = { 11} . Jadi, A B B A.

B.4. Komplemen Himpunan

Definisi 2.8. K omplemen Himpunan

Untuk sebarang subset A dan B dalam himpunan semesta U_,

komplemen B pada himpunan A didefinisikan A B = {x U_{|x A dan x B}.}

Not asi khusus A′ at au C

A menyat akan komplemen suat u himpunan dalam himpunan semest a. K omplemen himpunan A dit uliskan A′at au_AC_{= U A =}

{x U _{dan x A} .}

K omplemen dari himpunan A adalah himpunan semua anggot a himpunan semest a U_{, yang bukan merupakan anggot a himpunan A.}

K omplemen dari himpunan A dit uliskan dengan not asi C,

A yang didefinisikan

C

A = U _{A = {x|x} U_{, x A} . K omplemen himpunan dapat juga}

didefinisikan dengan cara lain, bahwa C

A adalah komplemen himpunan A di dalam U _{jika A∪A}C_{= U dan A∩A}C_{= .}

Contoh 2.12.Misalkan :

U_{= {x|xadalah bilangan bulat }}

A = {x|xadalah bilangan bulat genap} B = {x|xadalah bilangan bulat posit if} Maka:

A B = {x|xadalah bilangan bulat genap t ak-posit if} = { 0, -2, -4, -6, }

C

A = {x|xadalah bilangan bulat ganjil} = { , -5, -3, -1, 1, 3, 5, }

C

B = {x|xadalah bilangan bulat t ak-posit if} = { ,-3, -2, -1, 0}

Contoh 2.13. Gambar lingkaran berpot ongan di bawah ini menyat akan himpunan A dan B yang menandai daerah persegi U _{menjadi empat bagian,}

yait u daerah 1, 2, 3, dan 4. Masing-masing bagian menyat akan subset dari U_.

Banyak cont oh soal dan latihan di dalam buku ini meliput i sist em bilangan yang sudah umum dikenal, karena itu saya menggunakan simbol-simbol baku unt uk menyat akan sist em-sist em sepert i berikut ini:

: menyat akan himpunan semua bilangan bulat .

+ _{: menyat akan himpunan semua bilangan bulat posit if.}

: menyat akan himpunan semua bilangan rasional : menyat akan himpunan semua bilangan real

+

: menyat akan himpunan semua bilangan rela posit if. : menyat akan himpunan semua bilangan kompleks

Sepert i diket ahui, bilangan kompleks didefinisikan sebagai suatu bilangan yang berbentuk a+ bi dengan a dan b adalah bilangan real, dan i = −1.Demikian juga,bilangan real xdikat akan rasional jika dan hanya jikaxdapat dinyat akan dalam bent uk pembagian bilangan bulat yang penyebut nya t idak nol.

= mm ,n ,dan n 0 . n

 

 

 _{∈ ∈ ≠} 

 

 

 

 

Hubungan ant ara himpunan bilangan yang sat u dengan lainnya dapat dinyatakan dalam suatu diagram Venn berikut ini.

+ _{⊂ ⊂ ⊂ ⊂}

Operasi gabungan dan irisan dapat digunakan berulang-kali. Sebagai cont oh, dapat dibent uk irisan A dan B sehingga diperoleh A ∩ B, kemudian membent uk lagi irisan dari himpunan ini dengan suatu himpunan lain, misalnyaC. Dengan demikian irisan yang t erbent uk adalah (A∩B)∩C.

Himpunan (A∩B)∩C dan A∩(B∩C) adalah himpunan-himpunan yang sama karena:

(A∩B)∩C = {x|x A dan x B}∩C = {x|x A dan x B dan x C}

= A∩{x|x B danx C} = A∩(B∩C)

Analogi dengan sifat assosiat if (x+y)+z = x+ (y+z) pada operasi penjumlahan, operasi irisan pada himpunan juga bersifat assosiat if. Pada penjumlahan bilangan-bilangan, t anda kurung dapat dipindahkan at au dihilangkan sehingga diperoleh bent uk x+y+z =x+ (y+z) = (x+y)+z. Demikian juga operasi irisan pada himpunan,A∩B∩C = A∩(B∩C) = (A∩B)∩C.

Contoh 2.14. Misalkan diket ahui U _{= {a, b, c, d, ,x,y, z} dan A = {a, b, c} .}

Berdasarkan Definisi 2.8, C

A = {d, e, f, ,x,y, z} karena: (i) A∪ C

(ii) A∩Ac _{= {a, b,c} ∩{d, e, f, ,x,y,z} = .}

C. Sifat-sifat Aljabar Himpunan C.1. Sifat -sifat Operasi Gabungan

Sifat 1

JikaA danB adalah dua himpunan sebarang, maka: (i) A (A∪B)

(ii) B (A∪B)

Bukti:

(i) Misalkan xadalah sebarang anggot a himpunan A. Maka x A x A at aux B.

x (A∪B)

Jadi, set iap anggot a himpunan A merupakan juga anggot a dari himpunan A∪B. Oleh karena it uA (A∪B).

(ii) Mahasiswa dapat membukt ikan sendiri dengan cara yang sama dengan pembukt ian (i).

Sifat 2

JikaA adalah sebarang himpunan, maka: (i) A∪ = A

(ii) A∪A = A

(iii) A∪U ₌ U_{, dengan} U _{adalah himpunan semest a}

Bukt i:

(i) Untuk membukt ikan bahwa A∪ = A (ingat kesamaan himpunan) harus dit unjukkan bahwaA A∪ dan A∪ A. Berdasarkan Sifat 1, t elah dit unjukkan bahwaA A∪ (* )

sehingga dapat dipastikan bahwa x A. K arena x (A ∪ ) menunjukkan bahwa x A, maka (A∪ )=A A (* * ), karena unt uk set iap x (A∪ )= x A, makax A.

Dari persamaan (* ) dan (* *) A A ∪ dan (A ∪ ) A maka disimpulkan bahwaA = A∪

(ii) Mahasiswa dapat membuktikan sendiri.

(iii) Untuk membukt ikan bahwa A∪U ₌ U _{maka harus dibukt ikan dua}

hal yait u (A∪U₎ U _dan U _(A∪U_{). T elah diket ahui bahwa (A}∪ U₎ U _{karena semua himpunan merupakan subset dari himpunan}

semest a. (* ). Demikian juga, berdasarkan sifat 1, dapat dibukt ikan bahwa U _(A∪U_{). (* * ). Jadi dengan menggunakan (* ) dan (* * ),}

dapat dibukt ikan bahwa A∪U ₌ U_.

Sifat 3

Operasi gabungan himpunan bersifat komutatif. Jika A dan B adalah dua himpunan sebarang, makaA∪B = B ∪A.

Bukti:

x (A∪B) x A at au x B x B at au x A x (B∪A) Jadi A∪B = B∪A

Sifat 4

Operasi gabungan himpunan bersifat assosiatif. Misalkan diket ahui A, B, dan C adalah t iga himpunan sebarang, maka (A∪B)∪C = A∪(B∪C).

Bukti:

Misalkan P = (A∪B)∪C dan Q = A∪(B∪C). untuk membukt ikan bahwa P = Q, maka harus dit unjukkan bahwa P Q dan juga Q P.

(x A at au x B) at au x C. x A at au x B at au x C x A at au (x B at au x C) x A at au x (B∪C)

x Q.

Jadi P Q (* ), danQ P (bukt ikan!) (* *)

K arena P Q dan Q P maka disimpulkan bahwa P = Q.

C.2. Sifat-Sifat Operasi I risan

Sifat 1.

Misalkan A dan B adalah dua himpunan sebarang, maka: (i) (A∩B) A

(ii) (A∩B) B

Bukti

(i) Misalkan x adalah sebarang anggot a himpuan dari himpunan A B, maka berdasarkan definisi, x (A∩B) x A dan x B, berart i x A. Dengan demikian (A∩B) A.

(ii) Bukt ikan!

Sifat 2.

Jika A adalah sebarang himpunan, maka (i) A∩ =

(ii) A∩A = A

(iii) A∩U _{= A, dengan}U _{adalah himpunan semest a.}

Bukti

merupakan subset dari set iap himpunan, maka A∩ . (* * ). Jadi dari persamaan (* ) dan (* * ) t erbukt i bahwa A∩ = .

(ii) Mahasiswa dapat mencoba sendiri pembuktian ini.

(iii) Untuk membukt ikan bahwa A ∩ U _{= A, maka menurut definisi}

kesamaan himpunan, sepert i yang t elah dilakukan dalam pembuktian yang sebelumnya, akan ditunjukkan bahwa A∩U _{A dan A A∩}U_.

Berdasarkan Sifat 1, t elah ditunjukkan bahwa A ∩U _{A. (* ).}

Selanjut nya, misalkan x adalah sebarang anggot a himpunan dari himpunan A. K arena U _{adalah himpunan semest a, maka unt uk set iap}

x A x U_{. Dengan kat a lain x A}∩U_{. Jadi kesimpulannya A}

A∩U _{(* * ). Dari persamaan (* ) dan (* * ), t erbuktilah bahwa A∩}U ₌

A.

Sifat 3.

Irisan himpunan bersifat komutat if. Misalkan diket ahui himpunan A dan B adalah dua himpunan sebarang, maka A∩B = B∩A.

Bukti

x (A∩B)

x A dan x B x B dan x A x (B∩A)

Jadi t erbukt i bahwa A∩B = B∩A

Sifat 4.

Bukti:

Misalkan P = (A∩B)∩C, dan Q = A∩ (B∩C).

Untuk membuktikan bahwa P = Q, harus dit unjukkan bahwa P Q dan juga Q P.

x P x (A∩B) dan x C

(x A dan x B) dan x C x A dan x Bdan x C x A dan (x Bdan x C) x A dan x (B∩C) x A∩(B∩C)

x Q

K arena x P x Q, maka P Q. (* )Demikian pula sebaliknya (buktikan), Q P (* * ) maka P = Q yang menunjukkan bahwa operasi irisan himpunan merupakan operasi yang bersifat assosiat if.

C.3. Hukum-Hukum Distributif

Hukum 1: Operasi irisan himpunan bersifat distributif terhadap operasi gabungan himpunan. Misalkan diket ahui A, B, dan C adalah sebarang himpunan, maka A∩(B∩C) = (A∩B)∩(A∩C).

Bukti:

Untuk membukt ikan bahwa A ∩(B∪C) = (A∩B)∪(A∩C), maka harus ditunjukkan (kesamaan himpunan) bahwa:

(i) A∩(B∪C) (A∩B)∪(A∩C), dan (ii) (A∩B)∪(A∩C) A∩(B∪C)

Untuk membukt ikan hubungan (i), ambil sebarang xanggot a himpunan A∩(B ∪C). Dengan demikian,

x A∩(B∪C) x A dan x (B∪C)

x A dan (x B at au x C)

x (A∩B) at au x (A∩C) x (A∩B)∪ (A∩C)

K arena x A∩(B∪C) x (A∩B)∪(A∩C) maka dapat disimpulkan bahwa A∩(B∪C) (A∩B)∪ (A∩C).

Pembukt ian bagian (ii) untuk menunjukkan bahwa (A∩B)∪(A∩C) A∩(B∪C) agar dilat ih oleh mahasiswa, bahwa A∩(B∪C) = (A∩B)∪ (A∪ C). Dengan demikian Hukum I ini dapat dit erima.

Hukum 2: Operasi gabungan himpunan bersifat distributif terhadap operasi irisan himpunan.Misalkan diket ahui A, B, dan C adalah himpunan-himpunan sebarang, maka berlaku A∪(B∩C) = (A∪B)∩(A∪C).

Bukti:Sebagai latihan, mahasiswa dapat membuktikan hukum tersebut.

C.4. Sifat-sifat Selisih Himpunan

Sifat 1: A B B A. Dengan kat a lain, selisih dua himpunan t idak bersifat komut at if. Sebagai cont oh, misalkan A = { 1, 2, 3} dan B = { 3, 4, 5} . Selisih kedua himpunan t ersebut adalah A B = { 1, 2} dan B A = { 4, 5} . Dengan demikian t erbukt i bahwa A B B A (t idak bersifat komut at if).

Sifat 2: (A B) C A (B C), dengan kat a lain operasi pengurangan himpunan t idak bersifat assosiat if. Misalkan diketahui A = { 1, 2, 3} , B = { 3, 4, 5} , dan C = { 1, 5, 6} .

Maka:

(A B) C = { 1, 2} { 1, 5, 6} = { 2} (* ) dan

A (B C) = { 1, 2, 3} { 3, 4} = { 1, 2} (* * )

Sifat 3: (i). C ,

A∪A =U dengan U _{adalah himpunan semest a, dan}

(ii). C .

A∩A = ∅

Bukti:

(i) Untuk membuktikan A∪AC

= U _{maka harus ditunjukkan bahwa}

(A∪AC

) U_{, dan} U _(A∪AC

). K arena semua himpunan adalah subset dari himpunan semest a, maka (A ∪AC

) U _{(* ) adalah}

fakt a.

Selanjut nya untuk menunjukkan bahwa U _(A∪_AC_{), maka ambil}

sebarang x (A∪AC

). K arena x (A∪AC

) maka x A at au x AC

. x (A∪AC

) x A at au x AC

x A at au x (U _A)

x A at au (x U_{, x A)}

x A at au (x U _{dan x A)}

(x A at au x U_{) dan (x A at au x A)}

x A at au x U_{, mengimplikasikan x} U

x A at au x A, mengimplikasikan x U

x U

Oleh karena itu U _(A∪_AC_{) (* * )}

Dari (* ) dan (* * ), disimpulkan bahwa (A∪AC

) = U_.

(ii) Bukt ikan!

Sifat 4: (i) UC ₌

(ii) C

= U

Bukti:

(i). Akan dibuktikan bahwa C

U ⊆ ∅dan C

U

Perhat ikan bahwa untuk set iap x UC _{x U, dengan U adalah}

himpunan semest a. K arena semua anggot a himpunan merupakan anggot a himpunan semest a, maka x U _{mengimplikasikan bahwa x}

. Dengan demikian C

U (* ).

Selanjut nya, diket ahui bahwa C

U (* * ) (karena himpunan kosong merupakan subset dari semua himpunan). Jadi berdasarkan persamaan (* ) dan (* * ), disimpulkan bahwa C

U = .

(ii). Bukt ikan!

Sifat 5: (AC

)C

= A Bukti: (AC

)C

= {x|x Ac

} = {x|x A} = A.

C.5. Hukum de-Morgan (i). (A∪B)C

= AC∩

BC

(ii). (A∩B)C _{= A}C∪_BC

Bukti:

Misalkan U _{adalah himpunan semest a sedemikian sehingga untuk}

set iap xsebarang, maka xmerupakan anggot a dariU_.

(i) (A∪B)C

= {x|x (A∪B)} = {x|x A dan x B} = {x|x AC

dan x BC

} = AC _∩BC

D. Definisi-Definisi 1. Pasangan Terurut.

Suatu pasangan t erurut t erdiri at as dua elemen; misalkan a, b sedemikian sehinggaa dit empat kan pada posisi pert ama dan b dit empat kan pada posisi kedua. Pasangan t erurut ini dituliskan dengan notasi (a,b).

2. Perkalian Catesian Untuk Dua Himpunan

Misalkan A dan B adalah dua himpunan sebarang, maka himpunan semua pasangan t erurut (a, b) dengan a A dan b B, disebut hasilkali Cart esian dari A dan B. Hasilkali Cart esian dit uliskan dengan not asi A x B (dibaca A cross B). Definisi ini dit uliskan secara simbolis A x B = { (a,b)|a

A,b B} .

Contoh 2.15.

Misalkan A = { 1, 2, 3} dan B = {a, b} maka

A x B = { (1, a), (1, b), (2,a), (2, b), (3,a), (3,b)} dan

B x A = { (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)}

A x B B x A mengimplikasikan bahwa sifat komut at if t idak berlaku pada perkalian Cart esian.

3. Perkalian Cartesian Untuk T iga Himpunan

Misalkan diket ahui A, B, dan C adalah t iga himpunan sebarang, maka himpunan semua pasangan berurut an t riple (a, b,c) dianaa A, b B, dan c C, merupakan hasilkali Cart esian dari A , B, dan C, yait u A x B x C = { (a, b,c)|a A,b B, c C} .

4. Perkalian Cart esian untukn Himpunan

Misalkan diket ahui A1, A2, A3, , An adalah sebarang n himpunan, maka

himpunan dari semua pasangan berurut an n-tupel (a1, a2, a3, ,an), dimana

a1 A1, a2 A2, a3 A3, , an An, dinamakan hasilkali Cart esian dari

himpunan-himpunan A1, A2, A3, , An, yait u:

A1, A2, A3, , An= { (a1, a2, a3, ,an)|a1 A1, a2 A2, a3 A3, , an An}

E. Pemetaan atau Fungsi

K onsep fungsi merupakan hal yang mendasar dalam hampir semua bidang mat emat ika. Ist ilah fungsi sangat luas digunakan, t et api dalam aljabar, fungsi dan t ransformasi menjadi istilah t radisional. I stilah-ist ilah t ersebut digunakan unt uk menyat akan ket erkit an ant ara unsur-unsur yang dipelajari. Ide ut amanya adalah korespondensi dalam bent uk t ert ent u yang t imbul ant ara elemen-elemen dari dua himpunan. Art inya t erdapat aturan t ert entu yang menghubungkan elemen pada himpunan pert ama dengan elemen pada himpunan kedua. Hubungan t ersebut berlaku sedemikian sehingga unt uk set iap elemen pada himpunan pert ama, t erdapat sat u dan hanya sat u elemen pada himpunan kedua.

A

a

B

b (a, b) f

Definisi 2.9.Perkalian Cart esian

Untuk dua himpunan t ak kosong A dan B, perkalian Cart esian A x B adalah himpunan semua pasangan berurutan (a, b) dari elemen-elemen a A danb B, yait u A x B = { (a, b)|a A dan b B} .

Contoh 2.17. Misalkan diket ahui A = { 1, 2} dan B = { 3, 4, 5} ,maka A x B = { (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)} , sedangkan B x A = { (3, 1), (3, 2), (4, 1), (4, 2), (5, 1), (5, 2)} . Cont oh ini memperlihat kan bahwa untuk pasangan berurut an dari anggot a himpunan A dan B, maka A x B B x A.

Definisi 2.10. Pemet aan dan Pet a

Misalkan A dan B adalah himpunan-himpunan t ak kosong. Suatu subset f dari A x B dikat akan pemetaan dari A ke B jika dan hanya jika unt uk set iap a A t erdapat satu dan hanya sat u (unik) elemen b B sedemikian sehingga (a,b) f. Jikaf adalah pemet aan dari A ke B dan pasangan berurut an (a,b) f, maka dit uliskan b=f(a) dan b disebut peta dari a olehf.

Gambar di bawah ini menunjukkan pasangan ant ara a dengan f(a). Suatu pemet aan f dari A ke B sama dengan suat u fungsi dari A ke B, dan pet a a A oleh f adalah sama dengan nilai fungsi f di a. Dua pemet aan, misalnyaf memet akan A ke B dan g memet akan A ke B, dikat akan pemet aan yang sama jika dan hanya jikaf(x) = g(x) unt uk semua x A.

(sat u dan hanya satu) sedemikian sehingga (a, b) f. Pemet aan ini dapat dijelaskan dengan at uran pemet aan oleh f, yaitu f(a) = a2

, a A sebagai berikut :

E.1. Domain, Kodomain, dan Range

Definisi 2.11: Domain, K odomain, Range.

Misalkan f adalah suatu pemet aan dari A ke B, maka himpunan A disebut domain dari f, dan B disebut kodomain dari f. Range dari f adalah himpunan C = {y|y B dan y = f(x) untuk suatu x A} . Range dari f dilambangkan dengan f(A).

Contoh 2.19. Misalkan A = { -2, 1, 2} , B = { 1, 4, 9} , dan f adalah pemet aan yang didefinisikan sepert i pada cont oh sebelumnya, yait u f= { (a, b)|f(a)= a2

, a A}. Dalam kasus ini, domain f adalah A, kodomain fadalah B, dan rangef adalah { 1, 4} B.

E.2. Peta dan I nvers Peta

Definisi 2.12. Jika f: A Bdan S A, maka: f(S) = {y|y B dan y = f(x) untuk suatu x S} . Himpunan f(s) dinamakan pet a dari S oleh f Unt uk sebarang subset T dari B, invers pet a dari T dilambangkan dengan f -1

(T) = {x|x A dan f(x) T } .

Pet a f(A) sama dengan range dari f. Not asi-not asi f(S) dan f-1

(T) adalah himpunan, bukan nilai dari suatu pemet aan. Pernyat aan ini dapat dijelaskan dengan cont oh sebagai berikut : Misalkan f: A B. Jika S = { 1, 2} ,

A

B

-2

1

2

1

3

4

makaf(S) = { 1, 4} . Selanjut nya, dengan T = { 4, 9} , maka invers pet a dari T adalah f-1

(T ) = { -2, 2} .

Definisi 2.13.Pemet aan Ont o (Surjekt if)

Misalkan f: A B. maka f disebut onto at au surjekt if jika dan hanya jika B = f(A).

Cara st andar untuk menunjukkan bahwa pemet aan f: A B bersifat ont o adalah dengan mengambil sebarang b anggot a himpunan B kemudian menunjukkan bahwa t erdapat a A sehingga f(a)= b. Sebaliknya, untuk menunjukkan bahwa suat u pemet aan f: A B t idak bersifat ont o, hanya perlu ditunjukkan adanya suatu elemen b B, t et api t idak t erdapat a A sedemikian sehinggaf(x)= b sepert i ditunjukkan pada gambar berikut ini.

A

-2

9

B 1

S 2

f(S)

4

1 f

1 B

A

1

-2

f -1 (T)

2

4 T

9

f-1

A

B

b x

f(x)

A a₁

a₂

B f(a₁)=f(a2)

Misalkan diket ahui pemet aan f: A B, dengan A = { -1, 0, 1} , B = { 4, -4} , dan f = { (-1, 4), (0, 4), (1, 4)} . Pemet aan t ersebut tidak bersifat onto, karena t idak t erdapat a A yang memenuhi f(a) = -4 B.

Contohi 2.20. Misalkan f: , dengan adalah himpunan semua bilangan bulat . Jika f didefinisikan dengan f = { (a, 2-a)|a } , maka f(a) = 2 a, dimana a . Unt uk menunjukkan bahwa f bersifat ont o (surjekt if), diambil sebarang elemen b sehingga t erdapat 2 b sedemikian sehingga (2-b,b) f, karenaf(2 b)= 2 (2 b)= b.Jadi, f bersifat onto.

Definisi 2.14.Sat u-satu (Injekt if)

Misalkan pemet aan f: A B, maka f dikat akan one-to-one (sat u-satu) at au injekt if, jika dan hanya jika untuk set iap elemen yang berbeda di himpunan A, selalu memiliki pet a yang berbeda oleh pemet aan f.

Untuk menunjukkan bahwa f t idak bersifat sat u-sat u, hanya perlu dit emukan dua elemen himpunan A, yaitu a1 A dan a2 A sedemikian

sehingga jika a1 a2 maka f(a1) =f(a2). Pasangan elemen-elemen yang memiliki

sifat sedemikian itu diperlihat kan pada gambar di bawah ini.

Contoh 2.21. Misalkan diberikan pemet aan f: A B, dengan A = { -1, 0, 1} , B = { 4, -4}, dan f = { (-1, 4), (0, 4), (1, 4)} . Di sini dapat dilihat bahwaf t idak bersifat sat u-satu (one-to-one) karena f(-1)= f(0)= 4, t et api -1 0. Suatu pemet aan f: A B dikat akan sat u-satu jika dan hanya jika a1 a2 (yait u

elemen-elemen di A ) selalu mengakibat kan f(a1) f(a2) (yait u elemen di B).

Dengan kat a lain, unt uk set iap elemen yang berbeda di A , selalu menghasilkan pet a yang berbeda di B. Pernyat aan ini menimbulkan permasalahan t ersendiri, karena definisinya dinyat akan dalam bent uk ketaksamaan sedangkan umumnya manipulasi dalam mat emat ika dilakukan berdasarkan kesamaan. Mahasiswa lebih mudah memahami konsep kesamaan dibandingkan dengan konsep ket aksamaan. Oleh karena it u, pernyat aan sat u-sat u diubah ke dalam bent uk kont raposit ifnya, yait u f(a1) = f(a2) selalu menunjuk pada a1 = a2.

Untuk it u, pembukt ian bahwaf bersifat sat u-sat u (injekt if) dilakukan dengan mengasumsikan bahwaf(a1)=f(a2) kemudian memperlihat kan bahwaa1 = a2.

Contoh 2.22. Misalkan f: yang didefinisikan dengan f = { (a, 2-a)|a } . Untuk membukt ikan bahwa f bersifat sat u-satu (injekt if), maka diasumsikan bahwa unt uka1 dan a2 , sehinggaf(a1) = f(a2). Dengan demikian 2 a1 =

2 a2 dan hal ini mengimplikasikan bahwa a1 = a2. Jadi dalam hal ini f

bersifat sat u-satu (injekt if).

Definisi 2.15. Korespondensi Sat u-Satu, Bijeksi

Misalkan f: A B. Pemet aan f disebut bijektif jika dan hanya jika pemet aan t ersebut surjektif dan sekaligusinjektif. Pemet aan bijekt if dari A ke B disebut korespondensi satu-satu dari A ke B, at au bijeksi dari A ke B.

Contoh 2.23.

Contoh 2.24.

Pemet aan yang ont o t et api tidak sat u-satu dapat dit unjukkan pada suatu pemet aanh: yang didefinisikan sebagai berikut :

( )

2

2

jika genap

3

jika ganjil

2

x

x

h x

x

x

    

−

=

−

Untuk membukt ikan bahwa h ont o, ambil sebarang b dan suatu persamaan h(x) = b. Ada dua kemungkinan nilai untuk h(x), t ergant ung pada nilai x, genap at au ganjil. Nilai-nilai t ersebut 2 unt uk genap,

2 x

b x

− =

3

dan unt uk ganj il. 2

x

b x

− = Dengan menyelesaikan persamaan-persamaan ini

unt uk nilai-nilai x, diperoleh x= 2b+ 2 untuk xgenap, at au x= 2b+ 3 unt uk x ganjil. Perhat ikan bahwa 2b+ 2 = 2(b+ 1) menyat akan suat u bilangan bulat genap untuk sebarang elemen b . Demikian pula 2b+ 3 dapat dinyat akan dalam bent uk 2(b+ 1)+ 1, yang menunjukkan suau bilangan bulat ganjil unt uk sebarang b . Jadi t erdapat dua nilai, yaitu 2b + 2 dan 2b + 3 unt uk sebarang x sedemikian sehingga memenuhi h(2b+ 2) = b dan h(2b+ 3) = b. Hal ini menunjukkan bahwah bersifat ont o (surjekt if). K arena 2b + 2 2b + 3 dan h(2b+ 2 = h(2b+ 3) = b, maka t erbukt i juga bahwa h t idak bersifat sat u-sat u (injekt if).

Contoh 2.25.Misalkan suatu pemet aan f: didefinisikan dengan f(x)= 2x+ 1. Untuk membuktikan bahwa f ont o, ambillah sebarang elemen , misalkan b. Dengan demikian akan diperoleh

f(x)= b 2x+ 1 = b 2x= b 1,

f(m) = f(n) 2m+ 1 = 2n+ 1 2m = 2n

m = n

Cont oh ini menunjukkan bahwaf bersifat sat u-sat u (injekt if), meskipun t idak bersifat ont o (surjekt if).

Definisi 2.16.Pemet aan K omposit

Misalkan g: A B dan f: B C. Pemet aan komposit f g adalah pemet aan dari A ke C yang didefinisikan dengan (f g)(x) = f(g(x)) untuk semua x A. Proses

t erbent uknya pemet aan komposit dinamakan komposisi pemet aan, dan hasil dari f g disebut komposisi dari f dan g. Mahasiswa sudah t erbiasa dengan ist ilah aturan rantai melalui mat a kuliah kalkulus. K arena it u diasumsikan mahasiswa dapat melihat analogi komposisi pemat aan dengan at uran rant ai t ersebut . K omposisi pemet aan f g digambarkan pada diagram di at as. Perhat ikan bahwa domain dari f t erlebih dulu harus memuat range dari g sebelum komposisi f gdapat didefinisikan.

Contohi 2.26. Misalkan adalah himpunan semua bilangan bulat , A adalah himpunan bilangan bulat non-negatif, dan B adalah himpunan bilangan bulat non-posit if. Misalkan pemet aan-pemet aang danf didefinisikan sebagai berikut :

g: A, g(x)= x2

f: A B,f(x) = -x

Maka komposisi f g adalah pemet aan dari ke B dengan

(

f g x

)( )

= f(g(x))= -x2

. Perhat ikan bahwa f g t idak ont o, karena -3 B, t et api t idak t erdapat bilangan bulat sedemikian sehingga hubungan (f g)(x) = -x2

= -3

A

x

B

g(x)

C

f(g(x))

g f

t erpenuhi. Dalam kasus ini f g juga t idak sat u-sat u (injekt if) karena (f g)(-2) = -(-2)2

= -4 = (f g)(2) t et api -2 2.

Dalam komposisi pemet aan, not asi yang digunakan dalam set iap pernyat aan harus diperhat ikan dengan seksama. Beberapa ahli mat emat ika menggunakan not asi xf untuk manyat akan peta x oleh f. Jadi, not asi xf maupun f(x) menyatakan nilai f di x, at au dengan kat a lain pet a x oleh f. Apabila digunakan not asi xf, maka pemet aan dilakukan dari kiri ke kanan dan komposisi pemet aanf g didefinisikan dengan persamaan x(f g) = (xf)g. Not asi yang akan digunakan dalam buku ini adalahf(x) untuk menyat akan pemet aan xoleh f, dan (f g)(x) unt uk menyat akan kompisisi pemet aan f dengan g.

Jika pemet aan komposit dapat dibent uk, berarti suat u operasi yang t erdefinisi pada pemet aan t ersebut bersifat assosiatif. Jika h: A B, g: B C, danf: C D, maka

(

)

(

)

( ) (

) ( )

( )

( )

( )

(

)

(

)( )

(

)

(

)

(

)

( )

f g h x f g h x f g h x f g h x

f g h x

= = = =

untuk semua x A. Jadi komposisi

(

f g

)

h danf

(

g h

)

adalah pemet aan yang sama dari A ke D.

Definisi 2.17. 1. Pemet aan

Misalkan A dan B adalah dua himpunan t ak kosong, maka pemetaan (at au fungsi) dari suatu himpunan A ke suat u himpunan B adalah at uran yang memasangkan set iap elemen A dengan unik suatu elemen B. Pemet aan ini sering juga dinamakan transformator at au operator. Pemet aan at au fungsi dari A ke B sering dituliskan dengan not asi

f: A B at au _{A →}f _B

Misalkan f: A B, dan diket ahui x A, y B sedemikian sehingga f(x) = y, maka y dinamakan f-image (pet a f, at au pet a) dari x dan dituliskan dengan lambangf(x), sedangkan xadalah pra-pet a dari y.

3. Domain dan K odomain

Misalkan f: A B, dan misalkan x A, y B sedemikian sehingga f(x) = y, maka himpunan A disebut domain dari fungsi f dan himpunan B disebut co-domain f.

4. Range

Misalkan f: A B, maka himpunan pet a dari semua anggot a himpunan dari himpunan A disebut range dari f. Rangef dinyat akan denganf(A), dan didefinisikan f(A) = {f(x)|x A} .

Jenis-jenis Pemet aan 1. Pemet aan into

Misalkan f: A B sedemikian sehingga t erdapat set idak-t idaknya sat u anggot a himpunan B yang bukan merupakan pet a f (pet a) dari suat u elemen di A, makaf dikat akan pemet aan dari A ke B (mapping from A into B). Pemet aan dari A ke B dikat akan i nto _{jika dan hanya jika}

{f(x)} B, dimana x A dan {f(x)} = range dari f.

2. Pemet aan onto

Misalkan f: A B sedemikian sehingga set iap anggot a himpunan B merupakan pet a f (pet a) dari set idak-t idaknya sat u anggot a himpunan A, makaf disebut peta dari A ke B (mapping of A onto B). Pemet aan f: A B dikat akan onto jika dan hanya jika {f(x)} = B, dimana x A dan {f(x)} = range dari f. Pemet aan onto disebut juga pemet aan surjeksi at ausurjektif.

Misalkan f: A B sedemikian sehingga untuk set iap anggot a yang berbeda pada himpunan A memiliki pet a yang berbeda di himpunan B, maka fmerupakan pemet aan satu-sat u (one-to-one, one-one mapping). Pemet aanf: A B dikat akan sat u-sat u jika x1, x2 A, f(x1) = f(x2)

x1 = x2, at au jikax1 x2 makaf(x1) f(x2). Pemet aan satu-sat u disebut

juga pemet aan injeksi at au injektif. Pemet aan yang bersifat sat u-sat u dan sekaligus ont o, at au pemet aan yang surjekt if dan sekaligus injekt if, disebut pemet aan bijeksi at aubijektif.

4. Pemet aan banyak-ke-satu.

Misalkan f: A B sedemikian sehingga t erdapat dua at au lebih anggot a himpunan A memiliki pet a yang sama di himpunan B, maka f disebut pemet aan banyak-ke-sat u (many-one mapping). Pemet aan f: A

Bdikat akan banyak-ke-sat u jikax1,x2 A,f(x1) = f(x2) x1 x2.

5. Pemet aan I ndentitas.

Misalkan f: A A sedemikian sehingga masing-masing anggot a himpunan di A dipet akan pada dirinya sendiri, maka f disebut pemet aan identit as yang dilambangkan dengan I. Secara simbolis, pemet aan ident it as dituliskan dengan not asi f: A A jikaf(x) = x, x

A. Pemet aan ident it as bersifat one-to-one dan onto.

Contoh 2.27: Diket ahui A = { 1, 2, 3} dan B = { 4, 5} . K lasifikasikanlah pemet aan berikut ini:

(i) f = { (1, 4), (2, 5), (3, 5)} (ii) g = { (1, 4), (2, 5)}

(i) pemet aanfadalah pemet aan banyak-ke-sat u

(ii) pemet aan gt idak dapat didefinisikan karena t idak t erdapat pet a untuk 3.

Contoh 2.28.Diket ahui f: . K lasifikasikanlah pemet aan di bawah ini. (i) f(x) = 2x, dengan x .

(ii) f(x) =x2_{, dengan x .}

Jawab:

(i) pemet aanf(x) bersifat sat u-satu, dan ont o. (ii) Pemet aanf(x) bersifat banyak-ke-sat u, dan int o.

Contoh 2.29.Diket ahui f: . K lasifikasikanlah pemet aan di bawah ini. (i) f(x) =x2

(ii) f(x) = e x

(iii) f(x) = log (x) (iv) f(x) = t an x

Jawab:

(i) Pemet aanf(x) bersifat sat u-sat u, karena: f(x1) = f(x2) x12 = x22 x1 = x2.

Selanjut nya, karena set iap bilangan real a memiliki akar kuadrat, berart i

( ) ( )

2 .

f a = a = a Hal ini menunjukkan bahwa pet a f adalah semua bilangan real, dan karena itu pemet aan f t erhadap x bersifat onto. Dengan demikian pemet aan f(x) bersifat sat u-sat u danonto, at au bersifat bijektif.

(ii) Dapat ditunjukkan bahwa pemet aanf(x) bersifat sat u-sat u, karena

( )

( )

1 2

1 2

x x

f x = f x ⇒e = e yang mengimplikasikan bahwa x1 = x2.

Selanjut nya dengan memisalkan x adalah sebarang bilangan real posit if, makaf(x) = ex

adalah juga bilangan real posit if. Demikian pulaf(- x) = e- x

= 1 x

e adalah bilangan real posit if.

(iii) dan (iv) diselesaikan oleh mahasiswa sebagai lat ihan.

Misalkan f: A B dan g: A B, maka pemet aan oleh f dan g dikat akan pemet aan yang sama jikaf = g, x A.

b. Invers Pemet aan

Misalkan f: A B adalah pemet aan bijekt if (sat u-sat u dan ont o), maka pemet aan 1

f− : B A dimanaf(a) = b dengan b B adalah pet a dari a A oleh f, dinamakan invers pet a dari f.

T eorema 2.2.

Jikaf: A B adalah pemet aan yang bersifat satu-sat u dan onto, maka invers pemet aan 1

f− : B A juga adalah pemet aan yang bersifat sat u-satu dan onto.

Bukti:

Misalkan x1 dan x2 adalah sebarang anggot a himpunan A dengan x1 x2, yang

memiliki pet ay1 dan y2 sedemikian sehinggaf(x1) = y1 dan f(x2) = y2. (1).

Jika 1

f− adalah invers dari f, maka 1

( )

1 1

f− y = x dan 1

( )

2 2

f− y = x<