6
BAB II
DASAR TEORI
Dalam bab ini penulis akan menjelaskan teori – teori yang diperlukan untuk mewujudkan sistem penyamaan adaptif dengan algoritma galat kuadrat terkecil ternormalisasi pada suatu titik. Penyamaan tanggapan ruang akan diterapkan pada ruang CX01 dan C107. Dengan menggunakan standar pengukuran ruang[6], pendengar pada ruang dengar, jarak pendengar ke penyuara pada ruangan tersebut adalah 2 m berada pada medan jauh penyuara. Sudut yang dibentuk oleh pendengar dengan kedua penyuara 60 derajat. Teori-teori itu meliputi:
Pendekatan bentuk muka gelombang bunyi yang diterima oleh pendengar dari penyuara sangat tergantung pada jarak pendengar dari penyuara itu sendiri. Pada posisi ini, pendekatan bentuk muka gelombang bunyi yang diterima pendengar dari penyuara berbentuk bola (spherical). Penyamaan medan jauh penyuara yang dipengaruhi pendekatan bentuk muka gelombang bola tersebut akan dibahas pada subbab pertama.
Sistem penyama yang dirancang pada tugas akhir ini melakukan penyamaan berdasarkan tanggapan impuls sistem secara keseluruhan yang meliputi penguat audio, penyuara, dan ruangan tempat penyamaan dilakukan sampai pada titik di lokasi sekitar kepala pendengar. Penyamaan tersebut dilakukan dengan menggunakan algoritma galat kuadrat terkecil ternormalisasi. Algoritma galat kuadrat terkercil ternormalisasi menghitung ralat yang digunakan untuk menghitung tanggapan impuls penyama yang merupakan invers dari tanggapan sistem berdasarkan tanggapan impuls
7
sistem yang akan disamakan. Penggunaan algoritma tersebut yang akan diuraikan pada subbab kedua.
Dengan mencari kemiripan isyarat keluaran sistem (tanggapan impuls sistem) dengan masukan sistem (isyarat impuls) menggunakan korelasi silang, akan diperoleh fungsi pindah sistem. Penyama yang fungsi pindahnya merupakan invers dari fungsi pindah sistem yang akan disamakan memiliki kemungkinan tidak stabil jika sistem memiliki nol di luar lingkaran satuan (tidak berfase minimum)[4]. Tanggapan ruang terukur umumnya tidak berfase minimum[4]. Pembentukan sistem berfase minimum dilakukan menggunakan konsep alih ragam Hilbert[4] yang terdapat pada sistem perangkat lunak Raspberry Pi B. Dasar teori dari alih ragam Hilbert dijelaskan pada subbab ketiga.
Selain masalah kestabilan, sistem penyama dapat pula menghasilkan isyarat keluaran yang cacat karena tanggapan fase penyama yang tidak linear atau tundaan kelompok (Group Delay) penyama yang tidak konstan[4]. Hal ini dikarenakan tanggapan sistem yang terukur tidak berfase minimum Sehingga perlu dilakukan pendekatan tapis digital Finite Impulse Response (FIR) fase linear pada sistem penyama. Pendekatan ini dilakukan dengan mengubah bentuk tanggapan impuls penyama menjadi tapis digital FIR berfase linear melalui prose penjendelaan yang akan dibahas pada subbab keempat.
Isyarat yang digunakan untuk sebagai isyarat uji adalah isyarat maximum length sequence (MLS) dimana isyarat ini memiliki sifat seperti derau putih dengan tanggapan frekuensi yang rata pada jangkau frekuensi audio. Selain bersifat seperti derau putih, isyarat ini memiliki sifat yang tahan terhadap derau[7]. Untuk membangkitkan isyarat ini membutuhkan register geser dan sebuah gerbang logika XOR yang akan dijelaskan lebih lanjut pada subbab terakhir.
8 2.1 Penyamaan Medan Jauh Penyuara
Pendekatan bentuk muka gelombang yang diterima pendengar dari penyuara bergantung pada jarak pendengar dari penyuara itu sendiri. Pada medan jauh penyuara yang terletak pada lebih 2 meter dari penyuara, pola pancaran penyuara sama ke semua arah (omnidirectional)[8] sehingga pendekatan muka gelombang bunyi yang diterima oleh pendengar berbentuk bola (spherical). Sedangkan pada medan dekat penyuara, pola pancaran penyuara tidak omnidirectional[8] sehingga muka gelombang bunyi yang diterima oleh pendengar tidak beraturan.
Rentang nilai jarak pendengar ke penyuara yang bernilai 2 m atau lebih berada pada medan jauh penyuara, sehingga pendekatan bentuk muka gelombang bunyi yang diterima oleh pendengar pada posisi ini adalah bola (spherical). Standar pengukuran ruang[8] seperti yang ditunjukkan pada gambar berikut.
Gambar 2.1. Gambar pendekatan muka gelombang bunyi pada medan jauh penyuara.
Pendekatan bentuk muka gelombang tersebut menyebabkan jarak penyuara ke telinga kiri sama dengan jarak penyuara ke telinga kanan sehingga selisih persepsi binaural antara dua titik dengar manusia tersebut dapat diabaikan[8] (pada posisi pendengar terdapat dua titik dengar yang identik). Oleh karena itu, dalam melakukan
9
penyamaan medan jauh penyuara, cukup diketahui karakteristik medan jauh penyuara pada satu titik dengar saja. Karakteristik tersebut dapat diketahui dengan mengukur tanggapan impuls penyuara pada titik dengar.
2.2 Algoritma Galat Kuadrat Terkecil Ternormalisasi
Pada umumnya algoritma galat kuadrat terkecil ternormalisasi digunakan untuk memperoleh sebuah sistem sedemikian hingga isyarat keluarannya sesuai dengan sebuah isyarat acuan yang diinginkan. Algoritma ini berhasil apabila selisih (ralat) kuadrat antara isyarat keluaran sistem dan isyarat acuan yang diinginkan minimum atau mendekati nol.
Pada penerapannya dalam penyamaan tanggapan impuls sistem, penyamaan dengan menggunakan algoritma galat kuadrat terkecil ternormalisasi dilakukan dengan cara memperoleh invers tanggapan impuls sistem sedemikian hingga keluarannya rata pada frekuensi audio. Proses penyamaan berhasil dilakukan jika kuadrat dari isyarat ralat tanggapan impuls (jumlah antara isyarat tanggapan impuls sistem dengan inverse tanggapan impuls yang diinginkan) minimum atau mendekati nol. Diagram kotak sebuah sistem tapis adaptif secara umum ditunjukkan pada gambar berikut :
10
Gambar 2.2. Diagram kotak penyamaan dengan menggunakan algoritma galat kuadrat terkecil.
dimana:
x(n) adalah tanggapan impuls penyama; 𝑧−1(𝑛) adalah penunda;
h(n) adalah tanggapan impuls sistem; w(n) adalah tapis adaptif; dan
e(n) adalah ralat tanggapan impuls;
Pada aplikasinya, algoritma ini memerlukan 3 tahapan kerja untuk setiap proses iterasi sebagai berikut :
1. Keluaran 𝑦(𝑛) dihitung menggunakan persamaan
𝑦(𝑛) = ∑ 𝑤(𝑛)𝑥(𝑛 − 𝑖) 𝑁−1
𝑖=0
= 𝒘𝑇(𝑛)𝒙′(𝑛) … … … . … … … . … … (2.1)
2. Nilai perkiraan ralat dihitung dengan persamaan berikut
𝑒(𝑛) = 𝑑(𝑛) − 𝒘𝑇(𝑛)𝒙′(𝑛) … … … . … … … . (2.2) Sinyal 𝑑(𝑛) merupakan sinyal masukan 𝑥(𝑛) yang telah ditunda dan x’(n) merupakan isyarat masukan yang telah melalui sistem.
𝑧−1(𝑛) + ℎ(𝑛) ∑ 𝑤(𝑛) 𝑥(𝑛) 𝑒(𝑛) 𝑦(𝑛) 𝑑(𝑛) -
11
Koefisien filter diperbarui untuk proses iterasi selanjutnya menggunakan algorithma galat kuadrat terkecil ternormalisasi secara matematis menggunakan persamaan
𝒘(𝑛 + 1) = 𝒘(𝑛) + µ
𝒂 + 𝒙′𝑇(𝑛)𝒙′(𝑛)𝑒(𝑛)𝒙′(𝑛) … … … (2.3) Tapis adaptif normalized least mean square (NLMS) merupakan pengembangan dari tapis adaptif least mean square (LMS) [9]. Dengan tiap iterasi algoritma NLMS, koefisien dari tapis adaptif diperbarui sesuai dengan persamaan (2.3).
Di sini 𝑥(𝑛) merupakan masukan berupa vektor dengan nilai,
𝒙(𝑛) = [𝑥(𝑛) 𝑥(𝑛 − 1) 𝑥(𝑛 − 2) … 𝑥(𝑛 − 𝑁 + 1)]𝑇… … … . … … … . . (2.4) Vektor 𝑤(𝑛) adalah koefisien tapis yang diinginkan pada waktu n [5] sebagai berikut 𝒘(𝑛) = [𝑤0 (𝑛) 𝑤1(𝑛) 𝑤2(𝑛) … 𝑤𝑁−1(𝑛)]𝑇… … … . (2.5) Parameter µ adalah parameter ukuran langkah (step size) yang memiliki nilai tetap berupa bilangan positif yang kecil. Parameter step size ini mempengaruhi pembaharuan koefisien tapis adaptif. Jika nilai µ terlalu kecil, tapis adaptif akan mencapai nilai konvergen yang optimal dalam waktu yang lama. Sebaliknya, jika µ terlalu besar, tapis adaptif menjadi tidak stabil dan dapat menghasilkan keluaran divergen [9]. Nilai 𝑎 merupakan tetapan positif yang cukup kecil agar nilai w(n) konvergen.
2.3 Sistem Fase Minimum, Isyarat Analits, dan Alih Ragam Hilbert
Penggunaan tapis alih ragam Hilbert yang akan dilakukan pada pembentukan fase minimum sistem tersedia pada perintah – perintah dalam Raspberry Pi B yang
12
dikhususkan untuk pengolahan sinyal. Dasar teori dari penggunaan tapis alih ragam Hilbert tidak lepas dari analisis melalui isyarat analitis dan perannya pada pembentukan sistem fase minimum.
2.3.1 Isyarat Analitis
Suatu isyarat yang tidak memiliki komponen frekuensi negatif disebut isyarat analitis[10]. Dalam ranah waktu kontinyu setiap sinyal analitis direpresentasikan sebagai berikut 𝑧(𝑡) = 1 2𝜋∫ 𝑍(𝜔)𝑒 𝑗𝜔𝑡 ∞ 0 𝑑𝜔. . . … . (2.6)
Dimana Z(ω) merupakan representasi bilangan kompleks magnitudo dan fase frekuensi positif sinyal sinusoid kompleks exp(jωt) pada frekuensi ω
Setiap isyarat sinusoid nyata Acos(ωt+θ) dapat dikonversi ke dalam bentuk isyarat sinusoid kompleks Aexp[j(ωt+θ)] dengan membentuk komponen phase-quadrature Asin(ωt+θ) sebagai bagian imajiner
𝐴𝑒𝑗(𝜔𝑡+𝜃)= 𝐴𝑐𝑜𝑠(𝜔𝑡 + 𝜃) + 𝑗𝐴𝑠𝑖𝑛(𝜔𝑡 + 𝜃). . . … . (2.7) Untuk isyarat yang lebih rumit, misalnya dalam pengukuran dimana sinyal tersebut merupakan representasi dari jumlahan isyarat – isyarat sinusoid, sebuah tapis dapat dibentuk dimana tapis ini menggeser setiap isyarat sinusoid tersebut sebesar seperempat siklus (quarter cycle) yang disebut tapis alih ragam Hilbert.
Jika alih ragam sebuah tapis alih ragam Hilbert pada suatu isyarat x dalam ranah waktu t adalah ℋ𝑡{𝑥}, idealnya magnitudo dari sistem ini adalah 1 pada semua frekuensi dan menggeser fase isyarat x sebesar –π/2 pada setiap frekuensi positif dan +π/2 pada setiap frekuensi negatif. Ketika isyarat nyata x(t) dan alih ragam Hilbertnya y(t)= ℋ𝑡{𝑥} digunakan untuk membentuk suatu isyarat kompleks baru z(t)=x(t)+jℋ𝑡{𝑥} ; sehingga dapat kita dapat menyatakan isyarat z(t) merupakan
13
isyarat analitis dari x(t) dengan komponen frekuensi negatif yang telah ditapis. Untuk melihat bagaimana cara kerjanya, pergeseran fase pada isyarat sinusoidal kompleks dapat diperoleh dengan mengkalikan exp(± jπ/2) = ±j. Komponen frekuensi negatif dari pada frekuensi 𝜔0 adalah sebagai berikut
𝑥+(𝑡) ≜ 𝑒𝑗𝜔0𝑡. . . … . (2.8) 𝑥−(𝑡) ≜ 𝑒−𝑗𝜔0𝑡. . . … . (2.9) Kemudian pergeseran fasa sebesar -90 derajat pada komponen frekuensi positif dan +90 derajat pada komponen frekuensi negatif sehingga
𝑦+(𝑡) = 𝑒−𝜋 2⁄ 𝑒𝑗𝜔0𝑡 = −𝑗𝑒𝑗𝜔0𝑡. . . (2.10) 𝑦−(𝑡) = 𝑒𝜋 2⁄ 𝑒−𝑗𝜔0𝑡 = 𝑗𝑒−𝑗𝜔0𝑡. . . (2.11)
Dengan menjumlahkan keduanya didapat
𝑧+(𝑡) ≜ 𝑥+(𝑡) + 𝑗𝑦+(𝑡) = 𝑒𝑗𝜔0𝑡− 𝑗2𝑒𝑗𝜔0𝑡= 2𝑒𝑗𝜔0𝑡. . . (2.12) 𝑧−(𝑡) ≜ 𝑥−(𝑡) + 𝑗𝑦−(𝑡) = 𝑒−𝑗𝜔0𝑡+ 𝑗2𝑒−𝑗𝜔0𝑡= 0. . . (2.13) Dari persamaan diatas, dapat kita lihat bahwa komponen frekuensi negatif dihilangkan oleh tapis alih ragam Hilbert. Analisis teori alih ragam Hilbert secara lebih lanjut dapat dijelaskan dengan contoh kongkrit sebagai berikut. Diketahui suatu sinyal sinusoid nyata
𝑥(𝑡) = 2𝑐𝑜𝑠(𝜔0𝑡) = 𝑒𝑗𝜔0𝑡+ 𝑒−𝑗𝜔0𝑡. . . (2.14) Dengan mengaplikasihkan alih ragam Hilbert ideal, alih ragam Hilbert sinyal tersebut sebagai berikut
𝑦(𝑡) = 𝑒−𝑗𝜔0𝑡−𝜋 2⁄ + 𝑒−𝑗𝜔0𝑡+𝜋 2⁄ = −𝑗𝑒𝑗𝜔0𝑡+ 𝑗𝑒−𝑗𝜔0𝑡= 2𝑠𝑖𝑛(𝜔
0𝑡). . . … . (2.15) Dengan menggunakan identitas Euler, isyarat analitis didapat sebagai berikut
14
Sehingga pada penjumlahan x(t) + jy(t), komponen frekuensi negatif dari x(t) dan jy(t) saling menghilangkan dan hanya meninggalkan komponen frekuensi positif. Hal ini berlaku untuk semua isyarat x(t) yang bersifat real[10], tidak hanya sinusoid
Gambar 2.3. Pembentukan isyarat analitis 𝑧(𝑡)𝑒𝑗𝜔0𝑡 dari isyarat
Sinusoid nyata 𝑥(𝑡) = 𝑐𝑜𝑠(𝜔0𝑡) dan turunan phase-quadrature sinusoid
𝑦(𝑡) = 𝑠𝑖𝑛(𝜔0𝑡), pada domain frekuensi. a) spektrum 𝑥. b) spektrum 𝑦
15
Gambar 2.3 menunjukkan pembentukan isyarat analitis pada domain frekuensi. Gambar 2.3.a menunjukkan spektrum isyarat sinusoid 𝑐𝑜𝑠(𝜔0𝑡) yang terdiri dari impulse – impulse
frekuensi pada frekuensi 𝜔 = ±𝜔0 dan 0 pada semua frekuensi yang selain 𝜔0. 𝑐𝑜𝑠(𝜔0𝑡) dapat
direpresentasikan sebagai berikut
𝑐𝑜𝑠(𝜔0𝑡) =1 2 𝑒
𝑗𝜔0𝑡 + 1
2 𝑒
−𝑗𝜔0𝑡...(2.17)
Setiap impuls memiliki magnitudo ½ sama hal nya dengan 𝑠𝑖𝑛(𝜔0𝑡) dimana
𝑠𝑖𝑛(𝜔0𝑡) = −1 2 𝑗𝑒
𝑗𝜔0𝑡 + 1
2 𝑗 𝑒
−𝑗𝜔0𝑡...(2.18)
Spektrum impuls nya memiliki magnitudo -j ½ pada 𝜔 = 𝜔0 dan +j ½ pada 𝜔 = −𝜔0 perkalian j dengan y(t) menghasilkan
𝑠𝑖𝑛(𝜔0𝑡) =1 2 𝑒
𝑗𝜔0𝑡 − 1
2 𝑒
−𝑗𝜔0𝑡...(2.19)
Yang ditunjukkan pada gambar 2.3.c. kemudian jika ditambahkan dengan spektrum pada gambar 2.3.a maka akan menghasilkan persamaan (2.16) yaitu 𝑧(𝑡) = 𝑥(𝑡) + 𝑗𝑦(𝑡) . Penambahan ini akan menghasilkan unit impuls pada frekuensi 𝜔 = 𝜔0 dan menghasilkan 0 pada frekeuensi negatif 𝜔 = −𝜔0 sehingga menghasilkan isyarat analytical z(t). Dengan kata lain, komponen frekuensi negatif 𝑒−𝑗𝜔0𝑡 dihilangkan
dengan menjumlahkan 𝑐𝑜𝑠(𝜔0𝑡) dengan 𝑗𝑠𝑖𝑛(𝜔0𝑡) untuk menghasilkan isyarat analitis 𝑒𝑗𝜔0𝑡.
2.3.2 Sistem Fase Minimum
Sistem fase minimum adalah sistem yang fungsi pindahnya memiliki baik nol maupun kutub berada dalam lingkaran satuan[4]. Tanggapan ruang terukur umumnya tidak berfase minimum[4]. Dalam tugas akhir ini tanggapan ruang yang terukur harus berfase minimum karena tanggapan ruang sistem fase yang tidak minimum (memiliki nol di luar lingkaran satuan) jika diinversekan akan menyebabkan ketidakstabilan. Karena fungsi pindah penyama merupakan invers dari fungsi pindah sistem yang akan
16
disamakan maka untuk sistem penyamaan yang stabil, tanggapan sistem tersebut perlu dirubah kedalam sistem dengan fase minimum.
Sistem fase minimum Hm(ejω) memiliki sifat khusus, yakni komponen
magnitudo dan fasenya saling berhubungan melalui alih ragam Hilbert. Hubungan tersebut dapat dinyatakan seperti dalam persamaan berikut.
ℋ{ln |𝐻𝑚(𝑒𝑗𝜔)|} = ∅𝑚(𝑒𝑗𝜔) ……….………....(2.20) Dengan kata lain, jika Hm(ejω) merupakan sistem dengan fase minimum, maka
jika tapis alih ragam Hilbert diterapkan pada logaritma natural komponen magnitudonya akan didapat komponen fase minimum dari sistem tersebut. Dengan menggunakan hubungan tersebut, sistem fase minimum dapat dicari dengan proses sebagai berikut. Tanggapan frekuensi sistem sembarang H(ejω) terdiri dari komponen magnitudo dan komponen fase seperti yang ditunjukkan pada persamaan berikut. 𝐻(𝑒𝑗𝜔) = |𝐻(𝑒𝑗𝜔)|𝑒𝑗∅(𝑒𝑗𝜔)………...………....(2.21) Logaritma natural dari tanggapan frekuensi sistem tersebut akan menghasilkan persamaan di bawah ini.
𝐻̆(𝑒𝑗𝜔) = 𝑙𝑛|𝐻(𝑒𝑗𝜔)| + 𝑗∅(𝑒𝑗𝜔)………..………(2.22) Dengan menerapkan tapis alih ragam Hilbert pada logaritma natural tanggapan magnitudonya, akan dihasilkan komponen fase pengganti untuk memperoleh sistem fase minimum.
ℋ{ln 𝐻(𝑒𝑗𝜔)} = ∅𝑚(𝑒𝑗𝜔)……….………(2.23) Dengan mengganti komponen fase sistem dengan komponen fase minimum yang telah diperoleh dari tapis alih ragam Hilbert
𝐻𝑚(𝑒𝑗𝜔) = |𝐻(𝑒𝑗𝜔)|𝑒𝑗∅𝑚(𝑒
𝑗𝜔)
17
Alih ragam Fourier balik dari tanggapan frekuensi akan menghasilkan tanggapan impuls dengan fase minimum.
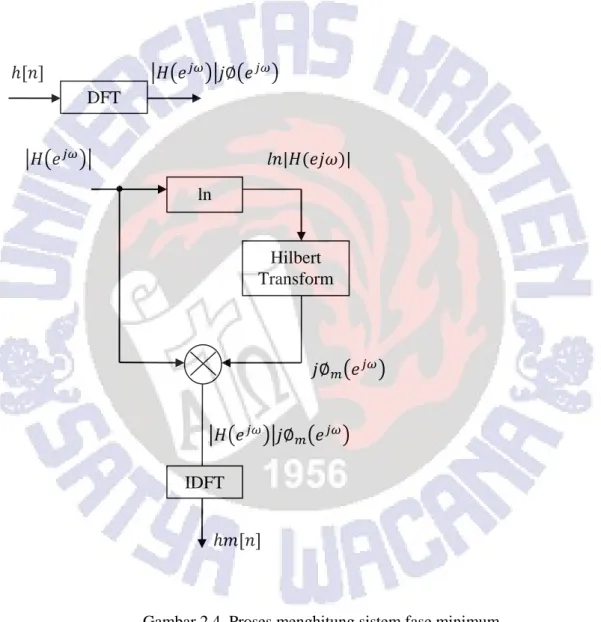
𝐻𝑚(𝑒𝑗𝜔) 𝐼𝐷𝐹𝑇 → ℎ𝑚[𝑛]……….(2.25) Pencarian sistem fase minimum mulai dari tanggapan impuls sistem ditunjukkan pada gambar diagram berikut
ℎ[𝑛] |𝐻(𝑒𝑗𝜔)|𝑗∅(𝑒𝑗𝜔) |𝐻(𝑒𝑗𝜔)| l𝑛|𝐻(𝑒𝑗𝜔)| 𝑗∅𝑚(𝑒𝑗𝜔) |𝐻(𝑒𝑗𝜔)|𝑗∅𝑚(𝑒𝑗𝜔) ℎ𝑚[𝑛]
Gambar 2.4. Proses menghitung sistem fase minimum dengan alih ragam Hilbert.
dimana:
h[n] adalah tanggapan impuls sistem fase tidak minimum; H(ejω) adalah tanggapan frekuensi sistem fase tidak minimum;
DFT
IDFT
Hilbert Transform ln
18
|H(ejω)| adalah komponen magnitudo sistem fase tidak minimum; ∅(𝑒𝑗𝜔) adalah fase tidak minimum sistem;
∅𝑚(𝑒𝑗𝜔) adalah fase pengganti untuk memperoleh sistem fase minimum; Hm(ejω) adalah tanggapan frekuensi sistem berfase minimum; dan
hm[n] adalah tanggapan impuls sistem fase minimum.
2.4 Metode Penjendelaan untuk Mendapatkan Tapis Digital Finite Impulse
Response Fase Linear
Tanggapan impuls penyama yang diperoleh melalui algoritma galat kuadrat terkecil mungkin memiliki tanggapan fase yang tidak linear (group delay tidak tetap) sehingga tidak dapat langsung digunakan dalam proses penyamaan. Untuk menanggulangi masalah tersebut, dilakukan pendekatan tapis FIR fase linear. Pendekatan ini dilakukan dengan mengubah bentuk tanggapan impuls penyama menjadi tapis digital FIR berfase linear melalui prose penjendelaan[3].
Secara umum, tapis FIR orde N dapat dinyatakan dalam persamaan selisih berikut.
𝑦[𝑛] = 𝑏0𝑥[𝑛] + 𝑏1𝑥[𝑛 − 1] + ⋯ + 𝑏𝑁−1𝑥[𝑛 − 𝑁 + 1] + 𝑏𝑁𝑥[𝑛 − 𝑁] ……….(2.26) dengan:
x[n] adalah masukan tapis; y[n] adalah keluaran tapis; dan b0, b1, … , bN adalah koefisien tapis.
Sesuai dengan namanya, tapis FIR memiliki panjang tanggapan impuls yang terbatas, yakni N+1 dengan N+1 koefisien tapis yang menentukan karakteristik tapis FIR tersebut. Tapis FIR memiliki beberapa kelebihan:
19 1. Stabil secara inheren
Semua kutub tapis FIR berada pada titik nol yang berarti semua kutubnya berada di dalam lingkaran satuan.
2. Tidak memerlukan sistem rangkai balik
Ralat pembulatan dalam operasi penjumlahan berulang yang menumpuk dalam tapis berumpan balik tidak akan terjadi.
3. Fase linear
Tapis berfase linear dapat dengan mudah dirancang dengan membuat koefisien tapis simetris.
Berdasarkan kelebihan tapis FIR ketiga, maka pada persamaan (2.26) tapis FIR fase linear dapat diperoleh dengan cara membuat koefisien tapis simetris, sehingga nilai b0 = bN, b1 = bN-1, b2 = bN-2, dst.
Pada tugas akhir ini, pembentukkan tapis digital FIR berkoefisien simetris dilakukan dengan metode penjendelaan (windowing). Pada metode ini, jumlah koefisien tapis digital dari tanggapan impuls penyama dibatasi dan diubah menjadi simetris dengan cara mengalikan tanggapan impuls penyama dengan koefisien-koefisien jendela yang digunakan. Jumlah koefisien-koefisien tapis digital yang terbentuk (orde tapis digital FIR yang diinginkan) sama dengan lebar jendela yang digunakan. Terdapat beberapa fungsi jendela yang dapat digunakan, yakni jendela kotak, Bartlett, Hann, Hamming, Blackman, dan Kaiser.
Persamaan lebar 2M+1 koefisien masing-masing jendela tersebut untuk -M ≤ n ≤ M dapat didefinisikan seperti persamaan-persamaan berikut [11].
Jendela kotak:
𝑤[𝑛] = {1, 𝑢𝑛𝑡𝑢𝑘 − 𝑀 ≤ 𝑛 ≤ 𝑀
20 Jendela Bartlett: 𝑤[𝑛] = 1 − |𝑛| 𝑀 + 1… … … . … … … . (2.28) Jendela Hann: 𝑤[𝑛] =1 2(1 + cos ( 2𝜋𝑛 2𝑀 + 1)) … … … . . … … … (2.29) Jendela Hamming: 𝑤[𝑛] = 0,54 + 0,46 cos ( 2𝜋𝑛 2𝑀 + 1) … … … (2.30) Jendela Blackman: 𝑤[𝑛] = 0,42 + 0,5 cos ( 2𝜋𝑛 2𝑀 + 1) + 0,08 cos ( 4𝜋𝑛 2𝑀 + 1) … … … (2.31) Jendela Kaiser : 𝑤[𝑛] = 𝐼0(𝛽√1 − 4𝑛 2 (𝑀 − 1)2) /𝐼0(𝛽) … … … (2.32) Dimana 𝐼0 merupakan fungsi Bessel orde-0 yang telah dimodifikasi. Untuk jendela Kaiser nilai M tidak sama dengan jendela yang lain yaiu ditentukan dengan persamaan berikut
−𝑀 − 1
2 ≤ 𝑛 ≤
𝑀 − 1
2 … … … (2.33)
2.4 Isyarat Maximum Length Sequence (MLS)
Maximum Length Sequence (MLS) merupakan sinyal periodik dengan panjang sebagai berikut
𝑃 = 2𝑁− 1……….……….………...(2.34)
dimana :
21 P merupakan perodisitas isyarat MLS
Isyarat MLS memiliki sifat – sifat yang unik salah satunya adalah autokorelasi dari isyarat tersebut merupakan unit impuls[12]. Secara statistik, sifat dari isyarat ini seperti isyarat derau putih dimana tanggapan frekuensinya rata di semua frekuensi disamping isyarat ini seluruh tanggapan impulsnya ditentukan oleh sebuah pembangkit register geser. Tanggapan impuls suatu sistem dapat diambil kembali dengan melakukan proses dekonvolusi salah satunya dengan korelasi silang atau dengan matriks transformasi Walsh-Hadamard[12].
Tanggapan impuls isyarat MLS dapat di hitung secara rekursif dengan persamaan berikut
𝑛(𝑘 + 3) = 𝑛(𝑘) ⊕ 𝑛(𝑘 + 2) … … … . … … … . . . (2.35) Dimana ⊕ merupakan operasi XOR, isyarat ini dapat dibangkitkan menggunakan register geser (biasanya nilai awal diberi nilai 1) dan sebuah gerbang XOR. Contoh pembangkit isyarat MLS dengan N = 3 sebagai berikut[12],
Gambar 2.5. Sistem umpan balik register geser biner sebagai pembangkit isyarat MLS dengan N = 3, dan P = 7
nilai biner dari MLS dikonversi menjadi isyarat dengan pemetaan 0 → 1 dan 1 → −1 jika isyarat MLS 𝑚[𝑛] dan tanggapan impuls suatu sistem adalah ℎ[𝑛] memiliki keluaran adalah 𝑦[𝑛] maka hubungan isyarat diatas
𝑦[𝑛] = 𝑚[𝑛] ∗ ℎ[𝑛] = ∑ 𝑚[𝑘]ℎ[𝑛 − 𝑘] +∞
𝑘=−∞
22
Dimana * merupakan operasi konvolusi linier. Dengan asumsi bahwa konvolusi linier secara matematis berlaku jika isyarat MLS tidak periodic, maka pendekatan ini hanya berlaku jika 𝑁 = ∞. Pendekatan matematis dengan konvolusi sirkular lebih tepat dalam hal ini. Jika ℎ′[𝑛] merupakan tanggapan impuls respon yang periodik, dengan diketahui unit impuls 𝛿[𝑛];
𝛿[𝑛] = {1, 𝑛 = 0
0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎… . … … … … . … … … . … … … . … … … . … (2.37) sedangkan unit impuls periodik 𝛿′[𝑛];
𝛿′[𝑛] = {1, 𝑛 𝑚𝑜𝑑𝑢𝑙𝑜 𝑃 = 0 0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎 … . … … … . … … … . … (2.38) sehingga ℎ′[𝑛] = ∑ 𝛿′[𝑘]ℎ[𝑛 − 𝑘] +∞ 𝑘=−∞ = ∑ ℎ[𝑛 + 𝑘𝑃] +∞ 𝑘=−∞ … … … . … … … … (2.39)
Tanggapan impuls periodik ℎ′[𝑛] merupakan tanggapan impuls sistem sebenarnya ℎ[𝑛] yang periodik dengan periode P jika isyarat MLS periodik 𝑚′[𝑛] dan isyarat keluaran periodik 𝑦′[𝑛], maka
𝑦′[𝑛] = 𝑚′[𝑛] ⊗ ℎ′[𝑛] = ∑ 𝑚′[𝑘]ℎ′[𝑛 − 𝑘] 𝑃−1
𝑘=0
… … … . … … … . … (2.40)
Dimana;
⊗ merupakan operasi konvolusi sirkular; [𝑛 − 𝑘] merupakan modulo P yang dihitung; 𝑦′[𝑛], 𝑚′[𝑛], dan ℎ′[𝑛] periodik dengan periode P
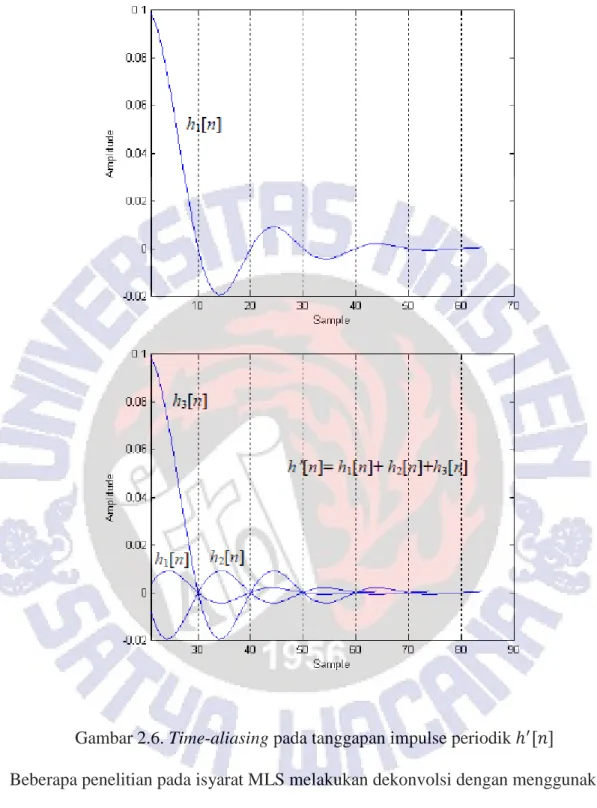
Nilai P sebaiknya dipilih cukup besar sehingga transien dari tanggapan impuls sebelumnya ℎ𝑘[𝑛] cukup kecil hingga tidak menyebabkan time-aliasing seperti yang ditunjukkan gambar dibawah ini[12]
23
Gambar 2.6. Time-aliasing pada tanggapan impulse periodik ℎ′[𝑛]
Beberapa penelitian pada isyarat MLS melakukan dekonvolsi dengan menggunakan metode korelasi silang [13]. Pada persamaan (2.3) hubungan isyarat MLS dengan tanggapan impuls dan isyarat keluaran
𝑦[𝑛] = 𝑚[𝑛] ∗ ℎ[𝑛] … … … . … … … . … … … . … … … (2.41) Persamaan dibawah ini akan memenuhi
24
dengan 𝑚[𝑛] ∗ ℎ[𝑛] = 𝛿′[𝑛] dan tidak terjadi time-aliasing.
Jika 𝑧[𝑛] = 𝑚[−𝑛] maka 𝑚[𝑛] ∗ 𝑧[𝑛] merupakan fungsi autokorelasi dari 𝑚[𝑛] dan memenuhi [𝑛] ∗ ℎ[𝑛] = 𝛿′[𝑛].
Dekonvolusi isyarat ℎ′[𝑛].ditunjukkan pada persamaan berikut
ℎ′[𝑛] = 1
𝑃 + 1(∑ 𝑦[𝑘]𝑚[𝑘 − 𝑛] 𝑃
𝑘=1
) … … … (2.43)
Ingat bahwa ℎ′[𝑛] merupakan tanggapan impuls ℎ[𝑛] yang periodik maka untuk P = 7
[ ℎ[0] ℎ[1] ℎ[2] ℎ[3] ℎ[4] ℎ[5] ℎ[6]] =1 8 [ 𝑚[0] 𝑚[1] 𝑚[2] 𝑚[3] 𝑚[4] 𝑚[5] 𝑚[6] 𝑚[1] 𝑚[2] 𝑚[3] 𝑚[4] 𝑚[5] 𝑚[6] 𝑚[0] 𝑚[2] 𝑚[3] 𝑚[4] 𝑚[5] 𝑚[6] 𝑚[0] 𝑚[1] 𝑚[3] 𝑚[4] 𝑚[5] 𝑚[6] 𝑚[0] 𝑚[1] 𝑚[2] 𝑚[4] 𝑚[5] 𝑚[6] 𝑚[0] 𝑚[1] 𝑚[2] 𝑚[3] 𝑚[5] 𝑚[6] 𝑚[0] 𝑚[1] 𝑚[2] 𝑚[3] 𝑚[4] 𝑚[6] 𝑚[0] 𝑚[1] 𝑚[2] 𝑚[3] 𝑚[4] 𝑚[5]] = [ 𝑦[0] 𝑦[1] 𝑦[2] 𝑦[3] 𝑦[4] 𝑦[5] 𝑦[6]] … … … (2.44)
Pada aplikasi DSP, matriks berisi nilai 𝑚[𝑛] disebut dengan matriks M-sequence. Deteksi
korelasi dengan menggunakan matriks M-sequence digunakan untuk mencari tanggapan impuls ruang.
25 2.5 Perangkat keras Wolfson Audio Card
Gambar 2.7 Perangkat Keras Wolfson Audio Card.
Meskipun perangkat keras raspberry pi model B memungkinkan untuk melakukan pengolahan audio, pengolahan audio dengan kualitas yang baik diperlukan perangkat keras lain yaitu Wolfson Audio Card yang dirancang khusus untuk digunakan dengan raspberry pi. Sistem pengolahan isyarat digital juga membutuhkan perangkat lain yaitu Coder-Decoder (CODEC) Perangkat keras Wolfson Audio Card ini menyediakannya dalam bentuk IC WM5102 dengan spesifikasi umum sebagai berikut [14] :
Audio hub CODEC dengan prosesor DSP terintegrasi.
Ketersediaan DSP yang dapat diprogram untuk keperluan pengolahan isyarat audio.
Pembangkit sinyal nada, PWM, dan derau.
Antarmuka isyarat digital dengan kecepatan cuplik standar dari 4KHz hingga 192KHz.
24-bit audio hub CODEC dengan 6/7 kanal terintegrasi dimana 6 ADC dengan 96 dB SNR dan 7 DAC dengan 113 db SNR.
26
Menyediakan beberapa fungsi pengolahan isyarat seperti wind noise, sidetone, dan tapis yang dapat diprogram.
Penguat daya stereo kelas D 2 x 2 Watt.
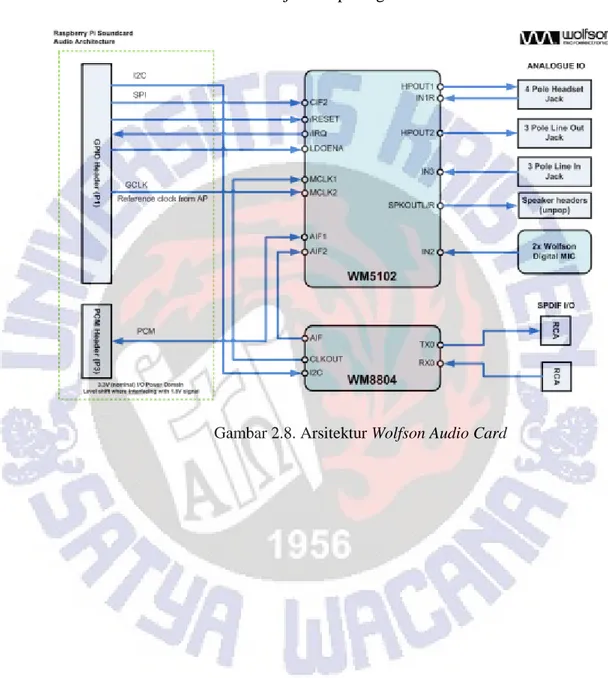
Arsitektur Wolfson Audio Card ditunjukkan pada gambar berikut