BAB III MINIMUM COVARIANCE DETERMINANT. Sebagaimana telah disinggung pada bab sebelumnya, salah satu metode

BAB III

MINIMUM COVARIANCE DETERMINANT

Sebagaimana telah disinggung pada bab sebelumnya, salah satu metode

robust untuk mendeteksi pencilan (outlier) dalam analisis komponen utama robust

yaitu metode Minimum Covariance Determinant (MCD). Sebelum dijelaskan lebih lanjut mengenai metode ini, akan dipaparkan terlebih dahulu mengenai pencilan, robust dan analisis komponen utama.

3.1 Pencilan (Outlier)

3.1.1 Definisi Pencilan

Ferguson (1961) mendefinisikan pencilan sebagai suatu pengamatan yang menyimpang dari sekumpulan pengamatan yang lain; Barnett (1981) mendefinisikan pencilan adalah pengamatan yang tidak mengikuti sebagian besar pola dan terletak jauh dari pusat pengamatan; selanjutnya Johnson (1992) mendefinisikan pencilan sebagai suatu pengamatan yang tak konsisten dengan kumpulan pengamatan lainnya.

Dari beberapa definisi yang sudah dipaparkan, dapat disimpulkan bahwa pencilan adalah suatu pengamatan yang menyimpang dari kumpulan pengamatan lainnya, sehingga tidak mengikuti sebagian besar pola. Akibatnya letaknya jauh dari pusat pengamatan.

3.1.2 Dampak Pencilan

Ketika sekumpulan data mengandung sejumlah pencilan, maka dalam hal ini akan mempengaruhi kenormalan distribusinya. Keberadaan pencilan pada suatu data dapat mengganggu proses analisis data, pencilan dapat menyebabkan hal-hal berikut:

a) Variansi pada data menjadi besar.

b) Taksiran interval memiliki rentang yang lebar. 3.1.3 Pendeteksian Pencilan

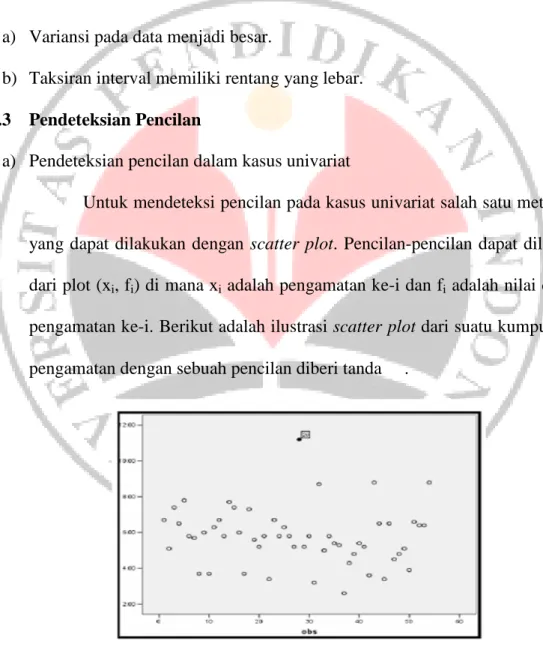
a) Pendeteksian pencilan dalam kasus univariat

Untuk mendeteksi pencilan pada kasus univariat salah satu metode yang dapat dilakukan dengan scatter plot. Pencilan-pencilan dapat dilihat dari plot (xi, fi) di mana xi adalah pengamatan ke-i dan fi adalah nilai dari

pengamatan ke-i. Berikut adalah ilustrasi scatter plot dari suatu kumpulan pengamatan dengan sebuah pencilan diberi tanda .

Gambar 3.1 Contoh Scatter Plot dari Suatu Kumpulan Pengamatan

Pada metode scatter plot, keputusan bahwa suatu pengamatan merupakan pencilan atau bukan sangatlah tergantung pada keputusan (judgement) peneliti, sehingga pengujian dengan scatter plot memiliki kelemahan. Pengujian yang paling banyak digunakan didasarkan pada penyimpangan maksimum dari rata-rata (maximum deviation from the

mean atau extreme studentized deviate (ESD) test),

i max µ σ − τ = i i x (3-1)

di mana τi merupakan suatu pengamatan dengan penyimpangan

maksimum dari rata-rata. Jika terdapat dua atau lebih pengamatan yang teridentifikasi sebagai pencilan, maka akan mengurangi keekstriman antar pengamatan. Hal ini mengakibatkan kesulitan untuk mendeteksi satu pencilan yang lebih ekstrim dari yang lainnya karena peningkatan pada rata-rata maupun variansinya sama. Pengaruh ini disebut masking (Rencher, 2002).

b) Pendeteksian pencilan dalam kasus multivariat

Pemeriksaan kenormalan multivariat lebih difokuskan pada uji

goodness-fit. Misalkan n pengamatan x1, x2, …, xn berada pada suatu

distribusi berdimensi p, suatu pengamatan yang terletak jauh dari ruang distribusinya diidentifikasi sebagai data pencilan.

Prosedur yang digunakan untuk memeriksa kenormalan multivaiat adalah berdasarkan pada jarak terstandarisasi dari pengamatan xi ke µ,

yang didefinisikan sebagai berikut

2 1

( µ) − ( µ), 1, 2,...,

= − t∑ _{− =}

i i i

di mana Di2= kuadrat jarak pengamatan ke-i dan xi = nilai pengamatan ke-i dengan, 1 2       = _{ }     M n x x X x , 1 2       = _{ }       M i i i pi x x x x , 1 2 µ µ µ µ       =_{ }       M p , dan 11 12 1 21 22 2 1 2 σ σ σ σ σ σ σ σ σ       ∑=_{ }       L L M M O M L p p n n np

jarak terstandarisasi ini sering disebut dengan jarak kuadrat Mahalanobis. Untuk mengidentifikasi pencilan pada kasus multivariat dilakukan dengan menghitung jarak dari setiap titik pengamatan ke suatu pusat pengamatan berdasarkan persamaan (3-2).

Dengan demikian, data pencilan merupakan suatu pengamatan yang memiliki jarak terbesar jika dibandingkan dengan pengamatan-pengamatan yang lain yang berada pada distribusi tertentu. Akibatnya sebuah pengamatan xi diidentifikasi sebagai pencilan pada kasus

multivariat, jika jarak Mahalanobis

1 2

(xi−µ)t∑− (xi−µ) > χp(1−α) (3-3) dengan probabilitas 1- α.

Pengidentifikasian pencilan pada kasus multivariat tidaklah mudah dilakukan karena sekumpulan pencilan mempunyai efek masking dan

swamping. Efek masking dan swamping pada jarak Mahalanobis sebagai

suatu kriteria pendeteksian pencilan. Efek masking menurunkan jarak Mahalanobisnya pada suatu pencilan yang mengakibatkan jarak antar titik terpencil saling berdekatan. Di lain pihak, efek swamping meningkatkan jarak Mahanalobisnya pada pengamatan yang tak terpencil (Penny dan Jolliffe, 2001).

Terdapat beberapa penyebab munculnya pencilan, salah satunya pencilan yang disebabkan oleh variabel bebas, dinamakan pencilan leverage. pencilan

leverage dideteksi dengan menggunakan jarak Mahalanobis (MDi) untuk setiap

pengamatan ke-i pada persamaan (3-2) sehingga dapat dituliskan,

0, ( ) 1, ≤  =  i jika MD C p leverage untuk lainnya (3-3)

di mana C(p) =

χ

2_p(1−

α

), C(p) dinyatakan sebagai nilai cut-off, yaitu pembatasan suatu ruang distribusi mayoritas data dari suatu pengamatan terpencil dengan p banyaknya variabel (derajat kebebasan) dan probabilitas 1-α. Pendeteksian pencilan leverage dengan menggunakan jarak Mahalanobis memiliki kesulitan karena efek masking maupun efek swamping.

3.1.4 Jenis-jenis Pencilan

Terdapat beberapa jenis pencilan dalam suatu data, berikut adalah uraiannya:

1. Good leverage merupakan pengamatan yang berada di ruang distribusi

tetapi sudah tidak berada di daerah mayoritas data.

2. Bad leverage merupakan pengamatan yang tidak berada baik dalam ruang distribusi pengamatan maupun daerah mayoritas data.

3. Pencilan ortogonal merupakan pengamatan yang mempunyai jarak yang sangat besar dari daerah mayoritas data sehingga pengamatan tersebut sudah tidak dapat dilihat dalam ruang distribusinya.

3.1.5 Tindakan pada Pencilan

Menurut Weissberg (1985), jika terdapat masalah yang berkaitan dengan pencilan maka diperlukan alat diagnosis yang dapat mengidentifikasi masalah pencilan, salah satunya dengan menyisihkan pencilan dari kelompok data kemudian menganalisis data tanpa pencilan. Terdapat dua pendekatan yang dapat dilakukan untuk mengatasi pencilan yaitu,

a. Pengidentifikasian: yaitu menghilangkan data pencilan kecuali pencilan memberikan informasi penting tentang model datanya. Pencilan dilihat dari posisi dan sebarannya terhadap pengamatan, selanjutnya dievaluasi apakah pencilan tersebut perlu dihilangkan atau tidak. Penghilangan pencilan yaitu dengan cara tidak mengikutsertakan pengamatan yang teridentifikasi sebagai pencilan dalam proses pengolahan data selanjutnya. Cara lain untuk mengatasi pencilan yaitu dengan cara transformasi data. Hamilton (dalam Osborne dan Overbay, 2004) mengemukakan bahwa dengan transformasi data nilai ekstrim (pencilan) tetap dapat disimpan pada data dan urutan relatif dari nilai akan tetap, juga kemiringan dan besarnya variansi dapat dikurangi.

b. Akomodasi: yaitu suatu metode yang menghasilkan suatu bentuk data yang tidak dipengaruhi banyak oleh pencilan.

3.2 Robust

Ketika sekumpulan data tidak menghasilkan informasi data yang diinginkan oleh peneliti, ini sering kali disebabkan oleh keberadaan pencilan. Untuk mengatasi keberadaan pencilan pada suatu data diperlukan suatu metode penaksir yang tak sensitif terhadap pencilan, metode tersebut disebut dengan metode robust. Karena pada dasarnya, robust selalu dikaitkan dengan pencilan.

3.2.1 Ke-robust-an (Robustness)

Kata “robust” biasanya dikonotasikan sebagai ketakkonsistenan dari suatu penaksir, artinya bahwa robustness adalah ketaksensitifan penyimpangan terhadap asumsinya. Metode robust lebih didekatkan pada parameter rata-rata dan variansi-kovariansi dari suatu penaksir tertentu (Huber, 1981), yaitu dengan menstandarisasikan penaksir untuk parameter rata-rata dan variansi-kovariansi sedemikian sehingga menghasilkan penaksir yang konsisten terhadap parameter-parameter tersebut. Dalam hal ini, dilakukan dengan bentuk pembatasan nilai pada penaksiran untuk parameter-parameternya. Dengan ke-robust-an, penaksirannya tidak akan menyimpang terlalu jauh.

3.2.2 Breakdown Point

Ketika data berasal dari data multivariat, sangatlah sulit menghilangkan pencilan secara keseluruhan dikarenakan efek swamping. Dalam hal ini, agar data tidak dipengaruhi banyak oleh pencilan, maka pencilan dalam data harus dibatasi. Hampel (1971, 1974) telah memperkenalkan konsep breakdown point, breakdown

point adalah jumlah pengamatan minimal yang dapat menggantikan sejumlah

pengamatan awal yang berakibat pada nilai taksiran yang dihasilkan sangat berbeda dari taksiran sebenarnya. Dengan kata lain, breakdown point sebagai suatu ukuran kerobutsan (robustness) dari suatu penaksir. Semakin besar nilai persen dari breakdown point pada suatu penaksir, maka penaksir tersebut semakin

robust.

3.2.3 Jarak Robust (Robust Distance)

Pada dasarnya, tujuan dari penaksiran robust adalah untuk mengkonstruk secara penuh efisiensi penyesuaian taksiran. Suatu pendekatan untuk mengidentifikasi pencilan multivariat yaitu dengan menggunakan metode robust pada penaksiran dari µ dan ∑. Sehingga metode ini meminimumkan pengaruh pencilan dalam penaksiran atau model fitting (Rencher, 2002).

Perkembangan dari jarak Mahalanobis adalah jarak robust, hal ini memiliki banyak keuntungan, karena jarak robust mendiagnosis pencilan leverage yang lebih reliabel (dapat dipercaya) daripada jarak Mahalanobis. Sehingga perluasan pendeteksian pencilan leverage pada persamaan (3-3) dengan menggunakan jarak robust (RDi) untuk setiap pengamatan ke-i menjadi,

0, ( ) 1, ≤  =  i jika RD C p leverage untuk lainnya (3-4)

Dengan nilai cut-off, C(p) =

χ

2_p(1−

α

) , di mana p banyaknya variabel (derajat kebebasan), probabilitas 1-α dan RD_i = (x_i −

µ

_R)t∑−_R1(x_i−

µ

_R) dengan µR dan

∑-1R masing-masing merupakan vektor rata-rata dan matriks invers

variansi-kovariansi dari penaksir robust.

3.3 Analisis Komponen Utama

Analisis komponen utama (AKU) merupakan suatu teknik analisis yang mentransformasi variabel-variabel asli yang masih berkolerasi menjadi satu kumpulan variabel baru yang tidak berkolerasi. Variabel-variabel baru tersebut disebut komponen utama (Johnson dan Wichern, 1982). Secara aljabar, komponen utama merupakan kombinasi linier (Y) dari p variabel acak X1, X2, X3, ... , Xp.

Secara geometris kombinasi linier ini merupakan sistem koordinat baru yang didapat dari rotasi sistem semula dengan X1, X2, X3, ... , Xp sebagai sumbu

koordinat yang tidak berkorelasi pada suatu ellipsoid. Sumbu baru tersebut merupakan arah dengan variabilitas maksimum dan memberikan variansi-kovariansi yang lebih sederhana.

Definisi AKU (3.3):

Analisis komponen utama bertujuan untuk menyederhanakan variabel-variabel yang diamati dengan cara mereduksi dimensinya. Hal ini dilakukan dengan menghilangkan korelasi diantara variabel melalui transformasi variabel asal (X) ke variabel baru (komponen utama Y) yang tak berkorelasi.

Komponen utama tergantung kepada matriks variansi-kovaransi Σ atau matriks korelasi ρ dari X1, X2, X3, ... , Xp, melalui matriks variansi-kovariansi

yaitu λ1 ≥ λ2 ≥ ... ≥ λp ≥ 0 dan vektor eigen-vektor eigen yaitu g1, g2, ... , gp.

Sasarannya adalah menemukan komponen utama k variabel di mana k < p, k diharapkan dapat memuat semua informasi yang terdapat pada p variabel asli sehingga data menjadi lebih sederhana. Menurut Dillon dan Goldstein (1984), tujuan analisis komponen utama untuk menentukan jumlah faktor (komponen utama) yang memaparkan banyaknya total variansi dalam data yang mungkin.

Jika Σ suatu matriks variansi-kovariansi yang merupakan suatu matriks semidefinit positif, maka semua nilai eigen dari Σ akan lebih besar atau sama dengan nol. Jadi jika λ = (λ1, λ2, …, λk, …, λp)t adalah vektor nilai eigen dari Σ, di

mana λ1 adalah nilai eigen terbesarnya, λ2 adalah nilai eigen terbesar kedua, dan

seterusnya, maka λ1 ≥ λ2 ≥ … ≥ λk ≥ ... ≥ λp ≥ 0. Ketika Σ mempunyai rank

lengkap, maka λ1 > λ2 > ... > λk > …. > λp > 0. Selanjutnya, asumsikan bahwa

di mana g.j adalah kolom-kolom vektor eigen ke-j pada Σ dan gtg = 1. Ini

terdefinisi dengan baik yang menghasilkan G suatu matriks ortogonal sedemikian hingga GtG = Ipxp dan 1 2 0 0 0 0 0 0 λ λ λ λ       ∑ _{= =}         L L M M O M L t p G G D (3-5)

Analisis komponen utama berbentuk linier sebagai berikut: (

µ

)

= t −

di mana X = (X1, X2,…., Xp)t , Y = (Y1, Y2,…., Yp)t dan G = (gij)pxp. Dengan

demikian dapat dituliskan menjadi,

Secara rinci dapat ditunjukkan sebagai berikut,

Persamaan di atas memperlihatkan bahwa Yi sebagai suatu kombinasi

linier dari X1, X2, X3, ... , Xp dengan penggunaan vektor eigen dari matriks

variansi-kovariansi X, untuk i = 1, 2, …, p. Atau dapat dibentuk menjadi,

. 1 (

µ

) = − = =

∑

p j j j X GY G Y (3-7)

Secara rinci dapat ditunjukkan sebagai berikut,

Teorema AKU (3.3.1):

Untuk analisis komponen utama yang didefinisikan oleh persamaan (3-6) atau persamaan (3-7), maka

1. Var (Yi) = λi, di mana Yi adalah komponen utama ke-i, dan λi adalah nilai

eigen terbesar untuk matriks variansi-kovariansi Σ, untuk semua i = 1, 2, …, p.

2. Cov (Yi, Yj) = 0, untuk i ≠ j, untuk semua i, j є (1, 2, …, p).

(Yang dan Trewn, 2004).

Bukti

Karena ( )= ( t( −

µ

))= t ( −

µ

)= t(

µ µ

− )=0

E Y E G x G E x G dari persamaan

(3-6), ini jelas bahwa matriks variansi-kovariansi dari Y adalah sebagai berikut

Dari persamaan (3-7), terbukti bahwa Var Y( )i =

λ

i,∀ =i 1, 2,...,p dan ( ,i j)=0, ≠

Cov Y Y i j ■

Teorema AKU (3.3.2):

Bukti

Bukti ini menjadi jelas karena λj dimuat oleh det (λI-∑) = 0, dan

■

Dari Teorema AKU (3.3.1) dan Teorema AKU (3.3.2), diperoleh sifat-sifat untuk analisis komponen utama yaitu:

a. Komponen utama Yt = (Y1, Y2, …, Yp) dari X yang variabel acak saling

bebas, dan variansi-variansinya yaitu λ1, λ2, ... , λp berturut-turut.

b. Jumlah dari total variansi-variansi pada X sama dengan total variansi dari komponen utama, yaitu

c. _{Dalam beberapa kasus, nilai eigen pada Σ, yaitu λ}1, λ2, ... , λp tidak sama

dalam besarnya (jarak). Beberapa nilai eigen lebih besar dari beberapa nilai eigen yang lainnya seperti λ1, λ2. Yaitu,

di mana k < p. Oleh karena itu,

Jadi, beberapa nilai eigen yang besar secara umum akan mendekati total variansi pada variabel acak multivariat X yang asli.

d. Selanjutnya, digunakan persamaan (3-7), 1 1 2 2 .1 1 .2 2 . ( ) ... µ µ µ µ −    ₋    − =_{ }≈ + + +   −     M k k p p X X X g Y g Y g Y X

sebagai suatu perkiraan pada

variabel acak multivariat X yang aslinya.

Pada kenyataannya, vektor rata-rata µ dan matriks variansi-kovariansi ∑ tidak diketahui. Untuk itu, diperlukan penaksir yang baik untuk menaksir vektor rata-rata µ dan matriks variansi-kovariansi ∑. Kedua parameter itu adalah

1 1 µ = =

∑

n i ki k x n dan 1 1 ( , ) ( )( ) 1 ₌ µ µ = = − − −

∑

n i j ij i j ki kj k s Cov X X x x n , i, j = 1, 2, …, p

Dengan demikian, analisis komponen utama berbentuk linier pada persamaan (3-6) menjadi,

( µ)

= t −

Y G X (3-8)

Dan menghasilkan komponen utama pada persamaan (3-7) menjadi,

(X −

µ

)=GY (3-9)

3.3.1 Prosedur

Penentuan komponen utama dimulai dari penyusunan kumpulan data dengan sebuah tabel yang terdiri dari p variabel dengan n pengamatan sampel untuk masing-masing variabel seperti pada tabel sebagai berikut:

Tabel 3.1

Bentuk Tabel untuk n Pengamatan Sampel terhadap p Variabel

X1 X2 Xp

1 x11 x12 x1p

2 x21 x22 x2p

n xn1 xn2 xnp

Rata-rata

Berikut adalah langkah-langkah penentuan komponen utama:

1) Nyatakan nilai-nilai yang terletak dalam tabel di atas menjadi sebuah matriks sebagai berikut:

11 12 1 21 22 1 1 2       =_{ }       L L M M O M L p p n n np x x x x x x X x x x (3-10)

Hitung matriks variansi dan kovariansi dari X dengan:

1 1 µ = =

∑

n i ki k x n (3-11) 2 1 1 ( ) ( ) 1 = µ = = − −

∑

n i ii i ki k s Var X x n 1 1 ( , ) ( )( ) 1 = µ µ = = − − −

∑

n i j ij i j ki kj k s Cov X X x x n , i, j = 1, 2, …, p (3-12)

Sehingga dapat dibentuk matriks variansi-kovariansinya sebagai berikut: pengamatan

11 12 1 21 22 1 1 2       ∑_{= =}         L L M M O M L p p p p pp s s s s s s S s s s (3-13)

Jika rij menyatakan korelasi antara Xi dan Xj maka

= ij ij ii jj s r s s (3-14)

Matriks korelasi untuk variabel X tersebut dapat dituliskan dengan,

11 12 1 21 22 1 1 2       =_{ }       L L M M O M L p p p p pp r r r r r r R r r r (3-15)

2) Tentukan nilai eigen dan vektor eigen

Agar variansi dari komponen utama ke-i maksimum serta antar komponen utama tidak adanya hubungan linier antar variabel bebas harus dipilih 1= g gti i dan 0= t i i g g sehingga diperoleh, 0 λ − = A I dan A−λI g_i=0

Untuk mencari nilai eigen λ dapat dilakukan dari matriks variansi-kovariansi S atau matriks korelasi R sehingga diperoleh,

0

λ

− =

S I dan S−λI gi =0 (3-16)

3) Tentukan komponen utama Yi

Dalam menentukan jumlah komponen utama yang ideal dapat dilakukan beberapa kriteria yaitu,

a. Kriteria proporsi total variansi sampel kumulatif yang dapat dijelaskan, yaitu sebanyak 80% (Rencher, 2002). Proporsi total variansi populasi untuk k komponen utama adalah

b. Nilai eigen lebih besar dari rata-rata nilai eigen . Untuk matriks korelasi, rata-rata ini adalah 1 atau ukuran relatif nilai eigen lebih besar dari 1 (Rencher, 2002).

c. Dengan mengamati scree plot dari nilai eigen dan jumlah komponen. Untuk menentukan jumlah komponen utama dengan memperhatikan patahan siku dari scree plot, dengan melihat dari kecuraman antar komponen sebelum ke komponen yang membentuk garis lurus antar komponen (menghasilkan beberapa nilai eigen kecil).

Dari langkah di atas akan menghasilkan suatu k komponen utama dari suatu sub ruang komponen utama berdimensi k yang sesuai dengan data.

3.3.2 Pendekatan Geometri

Secara geometri, komponen utama pertama merepresentasikan kecenderungan linier utama pertama yang memuat variansi maksimal, komponen utama kedua merepresentasikan kecenderungan linier utama kedua yang memuat variansi maksimal kedua dalam arah ortogonal, dan seterusnya (Huber, 1981; Rencher, 2002). Menurut Gnanadesikan (1997), komponen utama pertama sensitif pada pencilan-pencilan karena komponen utama pertama dipilih dari besarnya nilai eigen yang mewakili variansi maksimum data. Oleh karena itu, pereduksian dimensi data yang memuat sejumlah pencilan akan menghasilkan analisis komponen utama yang menyesatkan.

Gambar 3.2 memperlihatkan kecenderungan linier dari komponen utama pertama maupun kedua dari suatu ellipsoid yang saling ortogonal dengan

1 2

( , )

µ= µ µ dan panjang sumbu semimayor dan semiminor masing-masing adalah

$

1

c λ dan c λ$2 dalam suatu ellipsoid. Pengamatan yang berada di luar daerah

ellipsoid merupakan pengamatan terpencil atau pencilan. Garis yang dibentuk dengan sumbu utama dapat dianggap sebagai garis regresi. Akan tepat untuk titik-titiknya sehingga jarak perpendicular dari titik-titik-titiknya pada garis yang diminimalkan.

Gambar 3.2 Daerah Ellipsoid dari Komponen Utama Pertama dan

Komponen Utama Kedua pada 2-Dimensi

3.3.2.1 Pencilan Komponen Utama

Misalkan kombinasi linier Y_i =g_.t_i(X −

µ

)dengan vektor eigen

1 2

. ( , ,..., )

t

i i pi

i

g = g g g , berdasarkan persamaan (3-8) dinyatakan dengan

1 1 2 2

.( ) 1( ) 2 ( ) ... ( )

t

i i i i pi p p

Jika nilai pengamatan disubsitusikan pada persamaan di atas, maka menghasilkan nilai pengamatan dari komponen utama. Akibatnya persamaan (3-17) dapat dikatakan sebagai score komponen utama (nilai komponen utama). Perhatikan bahwa, jika setiap sisi ruas kiri dan ruas kanan dibagi dengan

λ

_i , maka diperoleh

(3-18) Karena Var(Yi) = λi maka Var Y( i λi)=1, jadi persamaan (3-18)

merupakan score komponen utama terstandarisasi. Dalam hal ini, score komponen utama terstandarisasi akan mengikuti distribusi normal standar. Bentuk komponen utama yang mempunyai score komponen utama yang tinggi, merupakan bentuk yang berpengaruh (pencilan). Penambahan atau penghilangan bentuk-bentuk ini biasanya akan secara drastis mempengaruhi hasil analisis komponen utama (Yang dan Trewn, 2004).

3.3.2.2 Meminimumkan Jarak Titik Perpendicular pada Komponen Utama

Seperti yang sudah dibahas, prosedur untuk memeriksa kenormalan multivariat dilakukan dengan jarak terstandarisasi. Misalkan untuk kasus dua komponen utama yang terpilih, sebuah sasaran kombinasi linier pada persamaan (3-17) yaitu komponen utama pertama dan komponen utama kedua, jika garis yang dibentuk oleh komponen utama pertama meminimumkan jarak

perpendicular dari titik-titik ke garis pada persamaan (3-17) yaitu Y₂=g_.2t(xi−µ),

maka jumlah total dari kuadrat jarak perpendicular adalah

2 2 2 .2 1 1 ( ) n n _t i i i i y g x µ = =   = _ − _  

∑

∑

di

mana g vektor _.2 eigen kedua dari ∑. Perhatikan bahwa karena .2( ) ( ) .2 t t i i g x −µ = x −µ g , sehingga

merupakan suatu jarak titik yang diminimumkan dari Var Y( )₂ =λ$2. Dengan

demikian, perluasannya menjadi 2 $ 1 ( 1) n i ij j y n λ = = −

∑

merupakan suatu jarak titik yang diminimumkan dari Var Y( )_i =λ$i. Jadi,

$

2

( 1) i ( 1) ( ) ( 1)

i i

Y = −n λ = −n Var Y = −n ∑,

akibatnya Yi2 mengikuti distribusi Wishart atau Yi2 W np( −1, )∑ . Distribusi Wishart

merupakan bentuk analog dari distribusi

χ

2. Berikut adalah ilustrasinya,

Gambar 3.3 Jarak Perpendicular dari Titik ke Garis Komponen Utama

Pertama

3.3.2.3 Plot Komponen Utama

Terdapat beberapa penelitian menghasilkan data yang tidak sama, dalam arti jumlah variabel dan jumlah pengamatannya, sehingga matriksnya menjadi tidak simetris. Oleh karena itu, digunakan Singular Value Decomposition untuk

memenuhi koordinat-koordinat pemplotan (Rencher, 2002). Menurut Yang dan Trewn (2004), pada persamaan (3-6) merupakan kombinasi linier pada dimensi-dimensi variansi di lokasi variabel yang berbeda, akan sangat sulit untuk memaparkan secara tepat maksud dari kombinasi linier tersebut. Sehingga akan digunakan persamaan (3-7), yang dapat dituliskan sebagai

$ 1 kxk t t nxp n nxk kxp X − µ =U D_λ V (3-19)

Persamaan (3-19) merupakan SVD dari matriks data terpusat sekitar rata-rata atau matriks lokasi data, 1n adalah vektor kolom yang semua elemennya

sama dengan 1, $

kxk

D_λ matriks diagonal (kxk), dan UtU = Ikxk = VtV di mana Ikxk

adalah matriks identitas berordo kxk.

Perkalian $

kxk

nxk

U D_λ pada persamaan (3-19) merupakan matriks score

komponen utama, karena V_kxpt adalah vektor eigen yang orthogonal dari matriks

simetris (Xnxp−1n

µ

t) (t Xnxp−1n

µ

t). $

kxk

nxk

U D_λ yang mewakili koordinat-koordinat dalam pemplotan komponen utama pada sub ruang komponen utama (Rencher, 2004: 532-535). Score komponen utama yang dibentuk merupakan

pentransformasian data asli ke dalam ruang komponen utama. Menurut Ke dan Kanade (2004), perhitungan SVD digunakan untuk:

1) Mendeteksi sisa pencilan-pencilan yang melanggar struktur korelasi dengan sub ruang rank rendah.

2) Menghitung sub ruang yang dapat dipercaya. 3) Sub ruang yang paling mendekati mayoritas data.

3.3.3 Pendeteksian Pencilan dalam Komponen Utama

Dalam perkembangan selanjutnya dihasilkan suatu alat diagnosis, alat diagnosis tersebut adalah plot diagnosis score. Plot diagnosis score mempunyai kelebihan dalam pendeteksian pencilan, selain dapat mendeteksi pencilan, juga dapat mengklasifikasi jenis-jenis pencilan. Plot diagnosis score dinyatakan dengan suatu sistem koordinat (Score Distance (SDi) versus Orthogonal Distance

(ODi)) untuk setiap pengamatan ke-i, di mana sumbu-x menyatakan SDi dan

sumbu-y menyatakan ODi, yang dibatasi dengan nilai cut-off yang menghasilkan

suatu daerah mayoritas data yang tidak dipengaruhi oleh pencilan.

3.3.3.1 Pengukuran Jarak Titik Pengamatan pada Komponen Utama

Dalam pendeteksian pencilan pada komponen utama dilakukan dengan

mengukur jarak untuk setiap pengamatan. Pengukuran ini dilakukan dengan Score

Distance dan Orthogonal Distance, untuk menghasilkan plot diagnosis score.

Berikut adalah prosedurnya,

Score Distance (SD)

Pada persamaan (3-17) merupakan bentuk yang berpengaruh (memuat titik terpencil atau pencilan) jika mempunyai score komponen utama yang tinggi. Sehingga dalam pengukuran jarak titik pada komponen utama dibentuk dari

Selanjutnya, meminimumkan jumlah kuadrat total jarak perpendicular dari titik-titik ke garis yang dibentuk oleh komponen utama, sehingga dari persamaan (3-18) terbentuklah Score Distance (SD) yaitu

$ $ 2 2 2 1 1 n k ij i i i _i j i y Y S D λ λ = =     = _{ } =  

∑

∑

atau $ 2 1 k ij i j i y SD λ = =

∑

(3-20)

dengan nilai cut-off, C(k) =

χ

_k2_;(1−α) dengan k banyaknya variabel yang terpilih (derajat kebebasan) dan probabilitas 1-α . Jadi, pengamatan ke-i dari komponen utama yang teridentifikasi sebagai pencilan jika SDi > C(k). Persamaan di atas

merupakan bentuk Score Distance pada tiap pengamatan, di mana yij merupakan

pengamatan ke-i pada kolom ke-j dari persamaan (3-20).

Gambar 3.4 Perbedaan Jenis-Jenis Pencilan Ketika Kumpulan Data pada

3-Dimensi di Proyeksi pada Sub Ruang Analisis Komponen Utama

2-Dimensi

Orthogonal Distance (OD)

Dari setiap pengamatan dapat diukur Orthogonal Distance (OD) pada sub ruang komponen utama. Menurut Härdle dan Hlávka (2007), kumpulan data

X pada n titik pengamatan dalam p dimensi, tampilan terbaik kumpulan data pada k dimensi di mana k < p, dapat ditemukan dengan mencari arah-arah vektor eigen g_{. j} di p-dimensi, j = 1, 2, …, q yaitu dengan memperkecil jaraknya.

Akan diproyeksikan pengamatan yi ke dalam arah g. j ke-j. Menurut Teorema proyeksi yaitu misalkan ruang-p direntang linier oleh vektor-vektor eigen g_{. j},g terdapat di ruang-p katakanlah W dan y_{. j} i ortogonal pada W.

Sehingga proyeksi ortogonal yi pada W adalah

(3-21) Dengan demikian diperoleh, bentuk jarak minimum Orthogonal Distance (OD) pada setiap pengamatan untuk sub ruang komponen utama yaitu

Atau,

( ) t

i i j i

OD = x −µ −g y (3-22)

Penentuan nilai cut-off untuk orthogonal distance tidak diketahui secara tepat. Menurut Box (1954), ukuran distribusi

χ

2 yaitu dengan

2 2 1 g

g

χ

sebagai perkiraan yang baik untuk distribusi tak diketahui. Untuk mengatasi ini, Wilson-Hilferty memperkirakan distribusi

χ

2 untuk orthogonal distance yaitu dengan dipangkatkan 2/3, yang merupakan perkiraan distribusi normal (Gaussian) dengan rata-rata 1/ 3 1 2 2 2 ( , ) (1 ) 9 g g g µ= − dan variansi-kovariansi 2 12 / 3 1/ 3 2 2 9 g g σ = , sehingga

nilai cut-offnya adalah _{( ) (( )}2 / 3_{, ( )}2 / 3 3₎ OD OD C k = N µ σ , dengan rata-rata 2 / 3 (

µ

OD) , variansi 2 / 3

(

σ

OD) dan probabilitas 1-α, yit adalah baris ke-i pada Ynxk.

Komponen utama ke-i teridentifikasi sebagai pencilan jika ODi > C(k).

Kombinasi kedua jarak SD dan OD

Dengan melakukan pengukuran jarak berdasarkan SD dan OD dengan masing-masing nilai cut-off yang telah ditentukan, menghasilkan tabel kombinasi kedua jarak SD dan OD sebagai berikut,

Tabel 3.2

Kombinasi Kedua Jarak SD dan OD

Jarak SD kecil SD besar

OD besar Pencilan ortogonal bad leverage-analisis komponen utama buruk OD kecil Pengamatan biasa good leverage-analisis

komponen utama baik

3.4 Metode Penaksir Robust

Banyak alternatif metode penaksir robust untuk menaksir vektor rata-rata dan matriks variansi-kovariansi yang tidak dipengaruhi banyak oleh pencilan. Dengan menggunakan metode penaksir robust untuk menaksir vektor rata-rata dan matriks variansi-kovariansi, baik efek masking maupun swamping dapat diatasi. Salah satu penaksir robust yang mempunyai kemampuan mengukur jarak

sekaligus mendeteksi jenis pencilan leverage adalah penaksir Minimum

Covariance Determinant.

3.4.1 Minimum Covariance Determinant

Minimum Covariance Determinant (MCD) adalah suatu metode pencarian

himpunan bagian dari X sejumlah h elemen di mana (n+ +p 1) / 2≤ ≤h n dengan menaksir rata-rata dan variansi-kovariansi yang menghasilkan determinan matriks variansi-kovariansi terkecil. Misalkan himpunan bagian tersebut adalah Xh,

terdapat n

h

   

  atau kombinasi himpunan bagian yang harus dicari untuk

mendapatkan penaksir MCD. Pada Tabel 3.3 menyajikan jumlah himpunan bagian yang harus ditemukan (kolom ketiga) berdasarkan jumlah pengamatan n (kolom pertama) dan jumlah variabel p tertentu (kolom kedua) yaitu,

Tabel 3.3

Jumlah Himpunan Minimal untuk Menghitung Penaksir MCD

Jumlah Pengamatan (n) Jumlah Variabel (p) Jumlah Kombinasi nCh

20 2 167960 7 38760 50 2 1.2155x1014 10 4.7129x1013 100 2 9.8913x1028 20 1.3746x1028

Berikut adalah definisi dari penaksir MCD yaitu,

Definisi MCD (3.4):

MisalkanX =( ,x x_{1 2},...,x_n)t merupakan kumpulan data sejumlah n pengamatan terdiri dari p-variabel di mana n≥ +p 1. Penaksir MCD merupakan pasangan

p

T∈ dan C adalah matriks definit positif simetris berdimensi pxp dari suatu sub

sampel berukuran h pengamatan di mana ( 1) 2 n p h n + + ≤ ≤ dengan 1 1 h i i T x h = =

∑

dan 1 1 ( )( ) h t i i i i i C x T x T h ₌ =

∑

− −

yang meminimumkan det C (Butler dkk, 1993).

Perhatikan Tabel 3.3, jika n kecil maka penaksir MCD cepat ditemukan. Tetapi jika n besar, ini membutuhkan waktu yang cukup lama dalam menemukan kombinasi sub sampel dari penaksir MCD. Keterbatasan ini kemudian dikembangkan oleh Rousseeuw dan Van Driessen (1999) dengan algoritma FAST-MCD yaitu Teorema C-Steps.

Teorema C-Steps (3.4.1):

Misalkan ( ,1 2,..., )

t n

X = x x x merupakan himpunan sejumlah n pengamatan terdiri dari p-variabel. Misal H1⊂

{

1, 2,...,n

}

dengan sejumlah elemen H1, jumlah (H1) =

h, tetapkan 1 1 h i i T x h = =

∑

dan 1 1 ( )( ) h t i i i i i C x T x T h =

=

∑

− − . Jika det(C₁)≠0 definisikan jarak relatif,

Selanjutnya ambil H2 sedemikian sehingga

{

d i ii( ); ∈H2

}

:=

{

( ) , ( )d1 i n; d1 2;n,..., ( )d1 h n;

}

, di mana ( )d1 i n; ≤( )d1 2;n ≤ ≤... ( )d1 n n; menyatakan urutan jarak, dan hitung T2 dan C2 berdasarkan kumpulan H2. Maka

2 1

det(C )≤det(C )dan akan sama jika dan hanya jika T1 = T2 dan C1 = C2

(Rousseeuw dan Van Driessen, 1999). (Bukti di lampiran B).

3.4.2 Penaksir Robust dalam Analisis Komponen Utama dengan Minimum

Covariance Determinant

Dari beberapa uraian di atas, maka analisis komponen utama yang robust

diperoleh dengan mengganti penaksir vektor rata-rata dan matriks variansi-kovariansi dengan penaksir robust MCD. Kemudian akan menghasilkan nilai

eigen maupun vektor eigen robust. Jadi, kombinasi linier Yi pada persamaan (3-6)

menjadi,

( )

t

MCD MCD

Y =G X −µ (3-23)

Berikut adalah tahap-tahap mendeteksi pencilan (outlier) dalam analisis

komponen utama robust dengan metode minimum covariance determinant:

Metode Analisis Komponen Utama

Tahap I

Sebelum melakukan pencarian komponen utama robust, akan dicari

jumlah k komponen yang terpilih dengan penaksir biasa. Diasumsikan data sampel dinyatakan dalam sebuah vektor acak X yaitu,

di mana elemen baris menyatakan n pengamatan dan banyaknya kolom menyatakan p variabel X1, X2, …, Xp.

Data diproses sedemikian sehingga data terletak dalam sub ruang yang dimensinya kurang dari p, dengan membangun matriks variansi-kovariansi S0

untuk menyeleksi jumlah komponen k dengan menggunakan salah satu dari beberapa kriteria yang sudah dibahas sebelumnya. Langkah ini menghasilkan sub ruang berdimensi k yang cocok dengan data, tahap ini dilakukan pada bagian 3.31. Langkah selanjutnya, titik-titik data diproyeksikan pada sub ruang ini.

Titik-titik data yang diproyeksi pada sub ruang yang sudah diperoleh, agar sub ruangnya menjadi sub ruang affine yang direntang oleh n pengamatan, cara mudah melakukan hal ini dengan SVD dari matriks data terpusat di rata-rata (the

mean centered-data matrix) menghasilkan

$ 0 _{0 0} 0 0 1 r xr t nxp n nxr r xp X −

µ

=U D_λ V (3-24)

di mana

µ

₀vektor rata-rata awal, 1n adalah vektor kolom yang semua elemennya

sama dengan 1 , r₀ =rank X( _nxp−1_nµ₀), $

0 0

r xr

D_λ matriks diagonal berordo r0 x r0,

dan UtU = Ir0 = VtV.

Untuk menghasilkan komponen utama robust dilakukan dengan menaksir vektor rata-rata dan matriks variansi-kovariansi secara robust oleh MCD. Akibatnya menghasilkan nilai eigen robust k positif

λ λ

$1,$2,...,

λ

$kdan vektor eigen

Pada tahap ini dicari titik pengamatan terkecil h, di mana h < n. Besarnya h = (n + p +1)/ 2, kemudian ditentukan probabilitas 1- α = h/n di mana α antara 0.5 sampai 1.

1. Untuk memberikan kemudahan dalam pencarian himpunan bagian h dari X untuk setiap xi dengan mencari titik terpencil terkecil h. Penentuan

titik-titik pencilan terkecil h, dilakukan melalui rumusan Stahel-Donoho yang diadaptasi dari persamaan (3-1), untuk setiap arah g∈A, di mana A memuat semua vektor tak nol kemudian diproyeksikan n titik pengamatan

xi padag. Ini petunjuk untuk keterpencilan dari suatu pengamatan, dengan

demikian pengamatan xi teridentifikasi sebagai keterpencilan jika,

$ $ $ $ 0 ( ) ( ) max ( ) t t i i i g A t t i i x g median x g out x median x g median x g ∈ − = − (3-25) di mana j = 1, 2, …, n

a. Asumsikan H0 merupakan himpunan bagian yang didapatkan dari

point 1, kemudian didapatkan rata-rata µ₁t dan matriks variansi-kovariansi S0. Dengan cara yang serupa, dicari vektor eigen dan nilai

eigen yang bersesuaian dari matriks variansi-kovariansi S0. Matriks

variansi-kovariansi sangat sensitif pada pencilan sehingga harus didekomposisi dari nilai eigen sebagai pendekatan untuk penaksiran sub ruangnya. Sehingga S0 didekomposisi spektral menjadi

$ 0 0 0 0 t S =G D G_λ (3-26)

Dengan $

$ $ $

0

1 2

( , ,..., r)

D_λ =diag

λ λ

λ

dan r ≤ r1. Matriks

variansi-kovariansi S0 digunakan untuk menentukan berapa banyak komponen

utama yang diperlukan k0 ≤ r. Penentuan komponen dapat dilakukan

dengan beberapa kriteria, salah satunya dengan nilai eigen lebih besar dari 1.

b. Sebagai langkah akhir, dilakukan proyeksi titik data pada sub ruang yang dibangkitkan oleh k0 komponen vektor eigen dari S0. Dari

persamaan (3-6) hasilnya dapat dibentuk menjadi

1 0 0 1 * 1 ( 1 t) r xk nxk nxr n Y = X −

µ

G (3-26)

di mana Gr xk1 0terdiri dari k0 kolom pertama dari G0 pada persamaan

(3-26).

Tahapan analisis komponen utama robust dengan penaksir minimum

covariance determinant selengkapnya sebagai berikut (Rousseuw dkk, 2003):

Metode Analisis Komponen Utama Robust dengan Penaksir Minimum

Covariance Determinant

Tahap II

Pada tahapan ini dilakukan perhitungan secara robust menaksir (estimasi) matriks scatter dari titik-titik pengamatan dalam

0 *

nxk

Y menggunakan penaksir MCD. Untuk menemukan titik-titik data yang mempunyai deteminan matriks variansi-kovariansi yang kecil. Akan digunakan Teorema C-Steps (Teorema 3.4.1)

karena mempunyai keuntungan dalam waktu yang digunakan untuk menghitung persamaan (3-26).

1. Dimulai dengan menerapkan Teorema C-steps dari y*i є

0 *

nxk

Y dengan

0

i∈H (indeks kumpulan H0 yang dimuat pada Tahap I) yang didefinisikan

sebagai berikut, misalkan m0 dan C0 merupakan rata-rata dan matriks

variansi-kovariansi pada h titik di H0. Jika det (C0) > 0, kemudian dihitung

C0-1 dan det(C0) beserta jarak Mahalanobis pada semua titik pengamatan

dengan m0 dan C0 yang dinotasikan sebagai,

1, 2, …, n (3-27)

2. Kemudian definisikan H1 sebagai himpunan bagian yang didapatkan dari

H0 dengan memilih h pengamatan yang mempunyai jarak Mahalanobis

0, 0( )

m C

d i terkecil. Pada himpunan bagian ini dihitung m1 dan C1

merupakan rata-rata dan matriks variansi-kovariansi pada h titik di H1.

Jika det (C1) > 0, kemudian dihitung C1-1 dan det(C1) beserta jarak

Mahalanobis

1, 1( )

m C

d i . Rousseeuw dan Van Driessen (1999) menjamin

bahwa det(C₁)≤det(C₀). Pembaharuan terus berlanjut sampai determinan pada matriks variansi-kovariansi konvergen.

Saat konvergen, dipenuhi suatu matriks data akan dinotasikan

1 *

nxk

Y , dengan variabel-variabel k₁≤k₀, dari himpunan bagian H1 dengan

pengamatan. Dengan demikian, didapatkan rata-rata dan variansi-kovariansi pengamatan tersebut yang merupakan penaksir robust MCD.

Tahap III

Pada tahapan ini akan dihitung jarak robust untuk

1 *

nxk

Y . Dalam setiap pengamatan dihitung vektor rata-rata dan matriks variansi-kovariansi pada persamaan (3-4). Kumpulan data akhir dinotasikan dengan Xnxk dengan k≤k₁.

Misal

µ

₂dan S1 menotasikan rata-rata dan matriks variansi-kovariansi pada

h-pengamatan yang ditemukan pada tahap II, dan

µ

2dan S2 rata-rata dan matriks variansi-kovariansi dicari dengan algoritma FAST-MCD, jika det (S1) < det (S2)

dilanjutkan perhitungannya yang didasari pada

µ

₂dan S1. Untuk itu, kumpulan

1 2

µ

=

µ

dan S3 = S1. Sebaliknya

µ

4 =

µ

3dan S3 = S2.

Untuk

µ

3 dan S4. S4 didekomposisi spektralkan yang ditulis dengan

$

2

2 2

4

t

S =G D G_λ , asumsikan kolom-kolom pada G =2 Gkxk memuat vektor eigen

pada S4 dan $ $

2 kxk

D_λ =D_λ adalah diagonal matriks dengan nilai eigen yang berkorespondensi. Score akhir diberikan dengan

* 2 5 ( nxk 1 t) nxk n Y = X −

µ

G (3-28)

Kemudian membentuk kembali kolom-kolom pada G2 pada p, hasil akhir komponen utama robust Gpxk. Vektor pusat robust akhir

µ

dimuat dengan

mentransformasikan

µ

5 kembali pada

p

St akhir dengan rank k diberikan dengan $ kxk t pxk pxk pxk S =G D_λ G dan perhitungan

score pada persamaan (3-28) dalam p, dapat dituliskan secara ekuivalen

dengan, Y_nxk =(X_nxk−1_n

µ

t)Gpxk

Mendeteksi pencilan dalam Analisis Komponen Utama Robust dengan

Metode Minimum Covariance Determinant

Tahap IV

Sebagai langkah terakhir dilakukan pengukuran Score Distance (SDi) dan

Orthogonal Distance (ODi) untuk menentukan jenis pencilan leverage untuk

setiap pengamatan ke-i pada score komponen utama, berdasarkan pada persamaan (3-20) dan (3-22).